NCERT Exemplar Class 11 Physics Solutions Chapter 2 Units and Measurement

Question:21

Name the device used for measuring the mass of atoms and molecules.

Answer:

The mass spectrograph is the device used for measuring the mass of atoms and molecules.

Name the device used for measuring the mass of atoms and molecules.

Question:22

Express unified atomic mass unit in kg.

Answer:

We know that the unified atomic mass unit or amu or $u= \frac{1}{12}$ is the mass of one $C^{12}$ atom
Mass of $6.023\times10^{23}$ carbon atoms $(_{6}C^{12})= 12\; gm$
Thus, the mass of one $_{6}C^{12}$ atom $= \frac{12}{6.023}\times 10^{-23}gm$
Now , 1 amu $= \frac{1}{12}\times \frac{12}{6.023}\times 10^{-23}\; gm$
$\Rightarrow 1 amu =1.66\times 10^{-24}\; gm$
Thus, 1 amu $= 1.66\times10^{-27}kg$

Question:23

A function $f(\theta )$ is defined as
$f(\theta )= 1-\theta +\frac{\theta ^{2}}{2!}-\frac{\theta ^{3}}{3!}+\frac{\theta ^{4}}{4!}+.........$
Why is it necessary for $\theta$ to be a dimensionless quantity?

Answer:

(i) $\theta$ is a dimensionless physical quantity since it is represented by an angle, viz., equal to arc/radius.
(ii) As $\theta$ is dimensionless, all its powers will also be dimensionless. Here, the first term is 1, viz., also dimensionless.
Hence, the L.H.S. $f(\theta)$ must be dimensionless so that all the terms in the R.H.S. are also dimensionless.

Question:24

Why length, mass and time are chosen as base quantities in mechanics?

Answer:

Length, mass & time is chosen as base quantities in mechanics because, unlike other physical quantities, they cannot be derived from any other physical quantities.

Question:26

Which of the following time-measuring devices is most precise?
(a) A wall clock.
(b) A stopwatch.
(c) A digital watch.
(d) An atomic clock.
Give a reason for your answer.

Answer:

The least count of the devices is as follows-
Wall clock = 1 sec

Stopwatch = $\frac{1}{10}$ sec

Digital watch = $\frac{1}{100}$ sec &

Atomic clock = $\frac{1}{10^{13}}$ sec.

Hence, the atomic clock is the most precise.

Question:27

The distance of a galaxy is of the order of 10²⁵ m. Calculate the order of magnitude of the time taken by light to reach us from the galaxy.

Answer:

It is given that the distance travelled by light from the galaxy to Earth = $10^{25}m.$
We know that speed of light = $3\times10^{8}m/s$
Thus, the required time, t = distance/speed
$\Rightarrow t = \frac{10^{25}}{3}\times10^{-8}\; sec$
$\Rightarrow t = \frac{1}{3}\times 10^{17}sec$
$\Rightarrow t = 3.3\bar{3}\times 10^{16}sec$

Question:28

The vernier scale of a travelling microscope has 50 divisions, which coincide with 49 main scale divisions. If each main scale division is 0.5 mm, calculate the minimum inaccuracy in the measurement of distance.

Answer:

Let ‘n’ be the no. of parts on the Vernier scale, n = 50
Now, the no. Of parts of M.S. coinciding with n parts of the vernier scale = (n-1)
Now, Least count of an instrument = L.C. of Mainscale/n = 0.5mm/50
Thus, the minimum accuracy will be 0.01 mm.

Question:29

During a total solar eclipse, the moon almost entirely covers the sphere of the sun. Write the relation between the distances and sizes of the sun and the moon.

Answer:

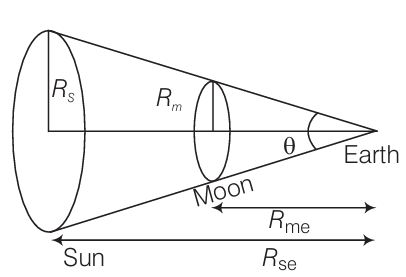
Consider the diagram given above
$R_{m e}=$ Distance of moon from earth
$R_{\text {se }}=$ Distance of sun from earth
Let the angle made by the sun and the moon be $\theta$, we can write

$
\theta=\frac{A_{\mathrm{sun}}}{R_{\mathrm{se}}^2}=\frac{A_{\mathrm{moon}}}{R_{\mathrm{me}}^2}
$
Here,
$A_{\text {sun }}=$ Area of the sun
$A_{\text {monn }}=$ Area of the moon

$
\begin{array}{ll}
\Rightarrow & \theta=\frac{\pi R_s^2}{R_{s e}^2}=\frac{\pi R_m^2}{R_{m e}^2} \\
\Rightarrow & \left(\frac{R_s}{R_{s e}}\right)^2=\left(\frac{R_m}{R_{m e}}\right)^2 \\
\Rightarrow & \frac{R_s}{R_{s e}}=\frac{R_m}{R_{m e}} \\
\Rightarrow & \frac{R_s}{R_m}=\frac{R_{s e}}{R_{m e}}
\end{array}
$

(Here, the radius of the sun and the moon represent their sizes, respectively)

Question:30

If the unit of force is 100 N, unit of length is 10 m and unit of time is 100 s, what is the unit of mass in this system of units?

Answer:

The dimensions of -
Force = $[M^{1}L^{1}T^{-2}]$=100 N ..........(i)
Length = $[L^{1}]$= 10 m ...........(ii)
Time = $[T^{1}]$= 100 sec ...........(iii)
Now let us substitute the values of eq. (ii) & (iii) in eq. (i)
We get,
$M\times10\times100^{-2}=100$

$\Rightarrow \frac{10M}{10000}=100$

Thus, $M=10^{5}kg, L=10^{1}m,F=10^{2}N \; and \; T=10^{2}seconds$

Question:31

Give an example of
(a) a physical quantity which has a unit but no dimensions.
(b) a physical quantity which has neither unit nor dimensions.
(c) a constant which has a unit.
(d) a constant which has no unit.

Answer:

(a) A plane angle is an example of a physical quantity which has a unit but no dimension since, plane angle = arc/radius in radian & solid angle.
(b) Relative density is a physical quantity which neither has units nor dimensions since µr (relative density) is a ratio of the same physical quantities.
(c) Gravitational constant (G) and Dielectric constant (k) are examples of constants that have a unit.
$G=6.67 \times 10^{-11}N-m^{2}-kg$
$k=9 \times 10^{9}N-m^{2}-C^{-2}(Vacuum)$
(d) Examples of the constant that has no units are the Reynolds no. & Avogadro’s no.

Question:32

Calculate the length of the arc of a circle of radius 31.0 cm which $\frac{\pi }{6}$ subtends an angle of at the centre.

Answer:

Given :radius = 31 cm
Angle = $\frac{\pi }{6}$
Length of arc =?
Now, we know that
Angle = length of arc/radius of arc
$\frac{\pi }{6}=\frac{x}{31}$
$x = 31 \times \frac{\pi }{6}$
$\Rightarrow x= 31 \times \frac{3.14 }{6}$
$\Rightarrow x = 16.22 \; cm$

Question:33

Calculate the solid angle subtended by the periphery of an area of $1cm^{2}$ at a point situated symmetrically at a distance of 5 cm from the area.

Answer:

We know that solid angle
$\begin{aligned} \Omega & =\frac{\text { Area }}{(\text { Distance })^2} \\ & =\frac{1 \mathrm{~cm}^2}{(5 \mathrm{~cm})^2}=\frac{1}{25}=4 \times 10^{-2} \text { steradian }\end{aligned}$

Question:34

The displacement of a progressive wave is represented by $y = A\; \sin (wt - k \; x ),$ where x is distance and t is time. Write the dimensional formula of (i) $\omega$ and (ii) k.

Answer:

According to the principle of homogeneity, the dimensional formula on L.H.S. & R.H.S. is equal.
Thus, the dimension of $A \; \sin (\omega t - kx)$ = Dimension of y
$\omega t-kx$ has no dimensions because it is an angle of sin.
$\frac{2\pi }{T}t=Kx$
$[M^{0}L^{0}T^{0}] = k[L]$
Thus, $\omega$ has no dimension & dimension of $k=[M^{0}L^{-1}T^{0}]$.

Question:35

Time for 20 oscillations of a pendulum is measured as $t_{1}= 39.6 \; s; t_{2} = 39.9 \; s; t_{3} = 39.5\; s$. What is the precision in the measurements? What is the accuracy of the measurement?

Answer:

Given data :
$t_{1}= 39.6 \; s$
$t_{2} = 39.9 \; s$
and $t_{3} = 39.5\; s$
L.C. of the instrument is 0.1 sec, hence, Precision (LC) = 0.1 sec.
Now,
For 20 oscillations, the mean value will be
$=\frac{39.6+39.9+39.5}{3}$
$=\frac{119}{2}$
$=39.7 \; s$
Now the absolute errors in measurement
$\left | \Delta t_{1} \right |=\left | \bar{t}- t_{1}\right |=\left | 39.7-39.6 \right |=\left | 0.1 \right |=0.1\; s$
$\left | \Delta t_{2} \right |=\left | \bar{t}- t_{2}\right |=\left | 39.7-39.9 \right |=\left | 0.2 \right |=0.2\; s$
$\left | \Delta t_{3} \right |=\left | \bar{t}- t_{3}\right |=\left | 39.7-39.5 \right |=\left | 0.2 \right |=0.2\; s$

Now, Mean absolute error $=\frac{0.1+0.2+0.2}{3}=\frac{0.5}{3}\cong 0.2\; s$
& Accuracy of measurement $=\pm 0.2\; s$

Question:37

The volume of a liquid flowing out per second of a pipe of length l and radius r is written by a student as
$V=\frac{\pi }{8}\frac{Pr^{4}}{\eta l}$
where P is the pressure difference between the two ends of the pipe and η is the coefficient of viscosity of the liquid having dimensional formula $ML^{-1}T^{-1}$. Check whether the equation is dimensionally correct.

Answer:

Let us write dimensions of -
Volume per second $(V)=\frac{V}{T}=[L^{3}T^{-1}]$
$P=\frac{F}{A}=[ML^{-1}T^{-2}]$
$\gamma =[L]$
$\eta =[ML^{-1}T^{-1}]$
$l =[L]$
Now, Dimensions of L.H.S.$=[M^{0}L^{3}T^{-1}]$
& dimensions of R.H.S. $=[M^{0}L^{3}T^{-1}]$
The equation is dimensionally correct since the dimensions of both sides are equal.

Question:38

A physical quantity X is related to four measurable quantities a, b, c and d as follows: $X = a^{2} b^{3} c^{\frac{5}{2}} d^{-2}$. The percentage error in the measurement of a, b, c and d are 1%, 2%, 3% and 4%, respectively. What is the percentage error in quantity X ? If the value of X calculated on the basis of the above relation is 2.763, to what value should you round off the result?

Answer:

As per the information given in the question, the percentage error in $a = (\frac{\Delta a}{a})(100) = 1\; %$
As per the information given in the question, the Percentage error in $b = (\frac{\Delta b}{b})(100) = 2\; %$
As per the information given in the question, the Percentage error in $c = (\frac{\Delta c}{c})(100) = 3\; %$
As per the information given in the question, the Percentage error in $d = (\frac{\Delta d}{d})(100) = 4\; %$

Percentage error in $X = (\frac{\Delta X}{X})(100)$

$\\\frac{\Delta X}{X}\times 100=\pm(2\times1+3\times2+2.5\times3+2\times4)\\\pm(2+6+7.5+8) =\pm 23.5\; ^{o}/_{o}$

Now, let us calculate the mean absolute error $=\pm \frac{23.5}{100}=\pm 0.235=0.24$ (after rounding up)
Therefore, we get ‘2.8’ after rounding X, i.e. $2.763.$

Question:39

In the expression $P=E\; I^{2}m^{-5}G^{-2}, E,m,I\; and\; G$ denote energy, mass, angular momentum and gravitational constant, respectively. Show that P is a dimensionless quantity.

Answer:

The dimensional formula of –
$E=[ML^{2}T^{-2}]$
$I=[ML^{2}T^{-1}]$
$G=[M^{-1}L^{3}T^{-2}]$
Now, let us find out the dimension of P
$P=EI^{2}m^{-5}G^{-2}$
$[P]=\frac{[E][I^{2}]}{[m^{5}][G^{2}]}=\frac{[ML^{2}T^{-2}][ML^{2}T^{-1}]^{2}}{[M]^{5}[M^{-1}L{3}T^{-2}]^{2}}$

$[P] =\frac{M^3L^{6}T^{-4}}{M^3L^{6}T^{-4}}$

$[P] = [M^{0}L^{0}T^{0}]$
Hence, it is clear that P is a dimensionless quantity.

Question:40

If velocity of light c, Planck’s constant h and gravitational constant G are taken as fundamental quantities then express mass, length and time in terms of the dimensions of these quantities.

Answer:

Let us first write down the dimensions of-
$h=\frac{E}{v}= \frac{[ML^{2}T^{-2}]}{[T^{-1}]}=[ML^{2}T^{-1}]$
$C=[LT^{-1}]$
$G = [M^{-1}L^{3}T^{-2}]$
(i) Let us consider that Mass m is directly proportional to $[h]^{a}[C]^{b}[G]^{c}$
$[M^{1}L^{0}T^{0}] = k [ML^{2}T^{-1}]^{a}[LT^{-1}]^{b}[M^{-1}L^{3}T^{-1}]^{c}$

$[M^{1}L^{0}T^{0}] = k [M^{a-c}L^{2a+b+3c}T^{-a-b-2c}]$

Comparing the powers on R.H.S. & L.H.S.
$a-c=1$
Thus, $a=c+1$
$2a+b+3c=0\; \; \; \; \; \; \; .....(i)$
$-a-b-2c=0 \; \; \; \; \; \; \; ..... (ii)$
Substituting the value of a in eq (i) & (ii)
$2(c+1) + b + 3c = 0$
$2c + 2 + b + 3c =0$
$b+5c = -2 \; \; \; \; \; \; \; \; ..... (iii)$
$-(c+1)-b-2c = 0$
$-b-3c=1 \; \; \; \; \; \; \; ...... (iv)$
By adding (iii) & (iv), we get,
$c=\frac{1}{2}$
$now, a = c+1$
Thus, $a = \frac{-1}{2}+1 = \frac{1}{2}$
Substituting these values in the equation. (iii)
$b + 5(-1/2) = -2$
$b = -2 + \frac{2}{5}$
$b = \frac{1}{2}$
Thus, $m = kh^{\frac{1}{2}}C^{\frac{1}{2}}G^{\frac{-1}{2}}$
$M=k\sqrt{\frac{hc}{G}}$
Now, let $L\; \alpha \; C^{a}h^{b}G^{c}$
Thus, $[L^{1}] = k[LT^{-1}]^{a}[ML^{2}T^{-1}]^b[M^{-1}L^{3}T^{2}]^{c}$
$=k[M^{b-c}L^{a+2b+3c}T^{-a-b-2c}]$
Equating the powers on both sides
$b-c=0$
Thus,$b=c$
$a+2b+3c = 1 \; \; \; \; \; \; \; ...... (i)$
$-a-b-2c = 0 \; \; \; \; \; \; .... (ii)$
Now, since $b=c$
$a+2b+3b=1$ becomes
$a+5b=1 \; \; \; \; \; \; .....(iii)$
& eq. (ii)
$a+b+2c = 0$ becomes
$a + 3b = 0\; \; \; \; \; \; \; \; ...... (iv)$
Subtracting eq (iv) from eq (iii), we get,
$b=\frac{1}{2}$
Thus, $c=\frac{1}{2}$
And eq (iv) will be
$a +3(\frac{1}{2}) = 0$
$a=\frac{-3}{2}$
Therefore, $I = k\; C^{\frac{3}{2}}h^{\frac{1}{2}}G^{\frac{1}{2}}$
$L=k\sqrt{\frac{hG}{c^{3}}}$
Let us consider $T\; \alpha \; G^{a}h^{b}C^{c}$
Thus, $[M^{0}L^{0}T^{-1}] = k[M^{-1}L^{3} T^{-2}]^{a}[ML^{2}T^{-1}][LT^{-1}]^{c}$
$= k[M^{-a+b} L^{3a+2b+c}T^{-2a-b-c}]$
$-a+b=0 \; \; \; \; \; \; \; ... (i)$
$3a + 2b + c = 0 \; \; \; \; \; \; ....... (ii)$
$-2a-b-c = 1 \; \; \; \; \; \; \; \; .... (iii)$
On adding eq (ii) & (iii), we get,
$a+b=1 \; \; \; \; \; \: \: \: \: \: ..... (iv)$
From eq (i) &(iv)
$b=\frac{1}{2}$
$a=\frac{1}{2}$
Thus, $c=\frac{-5}{2}$
$T = k\; G^{\frac{1}{2}}h^{\frac{1}{2}}C^{\frac{-5}{2}}$
Thus, $T = k\sqrt{\frac{hG}{c^{5}}}$

Question:41

An artificial satellite is revolving around a planet of mass M and radius R, in a circular orbit of radius r. From Kepler’s third law about the period of a satellite around a common central body, square of the period of revolution T is proportional to the cube of the radius of the orbit r. Show using dimensional analysis that $T=\frac{k}{R}\sqrt{\frac{r^3}{g}}$ where k is a dimensionless constant and g is acceleration due to gravity.

Answer:

According to Kepler’s 3rd law of planetary motion,
$T^{2}\; \alpha \; \; r^{3}$
$T\; \alpha \; \; r^{\frac{3}{2}}$
Now, R & g also affects T
Thus,
$T \; \; \; \alpha\; \; \; g^{a}R^{b}r^{\frac{3}{2}}$
$T = K[LT^{-2}]^{a}[L^{b}][L]^{\frac{3}{2}}$
$[T^{1}] = K[L^{a+b+\frac{3}{2}}T^{-2a}]$
Now, comparing M, L & T according to the principle of homogeneity
$a+b+\frac{3}{2} = 0 \; \; \; \; \; \; ..... (i)$
$-2a = 1 \; \; \; \; \; \; ..... (ii)$
$a=\frac{-1}{2}$
Thus, $\frac{-1}{2} + b + \frac{3}{2} = 0$

$b+1=0$
$b=-1$
$-2a=1$
$T=Kg^{\frac{-1}{2}}R^{-1}r^{\frac{3}{2}}$
i.e., $T=\frac{K}{R}\sqrt{\frac{r^{3}}{g}}$

An artificial satellite is revolving around a planet of mass M and radius R in a circular orbit of radius r. From Kepler's third law about the period of a satellite around a common central body, the square of the period of revolution T is proportional to the cube of the radius of the orbit r. Show using dimensional analysis that where k is a dimensionless constant and g is the acceleration due to gravity.

Question:42

In an experiment to estimate the size of a molecule of oleic acid, 1mL of oleic acid is dissolved in 19mL of alcohol. Then 1mL of this solution is diluted to 20mL by adding alcohol. Now, 1 drop of this diluted solution is placed on water in a shallow trough. The solution spreads over the surface of water, forming one molecule-thick layer. Now, lycopodium powder is sprinkled evenly over the film we can calculate the thickness of the film, which will give us the size of the oleic acid molecule.
Read the passage carefully and answer the following questions:
a) Why do we dissolve oleic acid in alcohol?
b) What is the role of lycopodium powder?
c) What would be the volume of oleic acid in each mL of solution prepared?
d) How will you calculate the volume of n drops of this solution of oleic acid?
e) What will be the volume of oleic acid in one drop of this solution?

Answer:

(a) Oleic acid does not dissolve in water; hence, it is dissolved in alcohol.
(b) Lycopodium powder spreads over the entire surface of the water when it is sprinkled evenly. When a drop of prepared solution is dropped on water, oleic acid does not dissolve in water. Instead, it spreads on the water surface, pushing the lycopodium powder away to clear a circular area where the drop falls. We can therefore measure the area over which oleic acid spreads.
(c) In each mL of solution prepared, volume of oleic acid $=\frac{1}{20} \mathrm{~mL} \times \frac{1}{20}=\frac{1}{400} \mathrm{~mL}$
(d) Volume of $n$ drops of this solution of oleic acid can be calculated by means of a burette and measuring cylinder, and measuring the number of drops.
(e) If $n$ drops of the solution make 1 mL, the volume of oleic acid in one drop will be $\frac{1}{(400) n} \mathrm{~mL}$.

Question:43

a) How many astronomical units (AU) make 1 parsec?
b) Consider the sun like a star at a distance of 2 parsec. When it is seen through a telescope with 100 magnification, what should be the angular size of the star? Sun appears to be (1/2) degree from the earth. Due to atmospheric fluctuations, eye cannot resolve objects smaller than 1 arc minute.
c) Mars has approximately half of the earth’s diameter. When it is closer to the earth it is at about ½ AU from the earth. Calculate at what size it will disappear when seen through the same telescope.

Answer:

(a)1 A.U. long arc subtends the angle of 1s or 1 arc sec at a distance of 1 parsec.
Thus, angle 1 sec = $\frac{1 A.U.}{1}$ parsec

Thus, 1 parsec = $\frac{1 A.U.}{1}$ arc sec

Thus, 1 parsec= $\frac{630(3600)}{11}=206182.8=2\times10^{5}A.U.$

(b)Angle of the sun’s diameter $\left ( \frac{1}{2} \right )^{o}$ is subtended by 1 A.U. since the distance from the sun increases the angle subtended in the same ratio.
Now,
$2\times10^{5} A.U.$ will form an angle of $\theta =\left ( \frac{1}{4\times10^{5}} \right )^{o}$, since the diameter is the same angle subtended on earth by 1 parsec will be the same.
If the sunlike star is at 2 parsecs, the angle becomes half $= (1.25 \times 10^{-6})^{o}$
Thus, angle $= 75 \times 10^{-6}$ min
When it is seen with a telescope that has a magnification of 100, the angle formed will be $7.5 \times 10^{-3}$ min, viz., less than a minute.
Hence, it can’t be observed by a telescope.

(c)

Given that $\quad \frac{D_{\text {mars }}}{D_{\text {earth }}}=\frac{1}{2}....…(i)$
where $D$ represents the diameter.
From answer 25(e)
We know that,

$
\begin{aligned}
& \frac{D_{\text {earth }}}{D_{\text {sun }}}=\frac{1}{100} \\
& \frac{D_{\text {mars }}}{D_{\text {sun }}}=\frac{1}{2} \times \frac{1}{100} -------[from Eq. (i)]
\end{aligned}
$

$
\begin{aligned}
& \text { At } 1 \mathrm{AU} \text { sun's diameter }=\left(\frac{1}{2}\right)^{\circ} \\
& \therefore \quad \text { mar's diameter }=\frac{1}{2} \times \frac{1}{200}=\frac{1}{400} \\
& \text { At } \frac{1}{2} \mathrm{AU} \text {, mar's diameter }=\frac{1}{400} \times 2^{\circ}=\left(\frac{1}{200}\right)^{\circ} \\
& \text { With } 100 \text { magnification, Mar's diameter }=\frac{1}{200} \times 100^{\circ}=\left(\frac{1}{2}\right)^{\circ}=30^{\prime}
\end{aligned}
$

This is larger than the resolution limit due to atmospheric fluctuations. Hence, it looks magnified.

Question:44

Einstein’s mass-energy relation emerging out of his famous theory of relativity relates mass (m) to energy (E) as E = mc², where c is speed of light in vacuum. At the nuclear level, the magnitudes of energy are very small. The energy at nuclear level is usually measured in MeV where $1 MeV = 1.6 \times 10^{-13}J$, the masses are measured in unified equivalent of 1u is 931.5 MeV.
a) Show that the energy equivalent of 1 u is 931.5 MeV.
b) A student writes the relation as $1 u = 931.5 MeV$. The teacher points out that the relation is dimensionally incorrect. Write the correct relation.

Answer:

(a) Given :
$m=1$
$u=1.67\times10^{-27}kg$
$c=3\times10^{8}m/s$
By the formula $E=mc^{2}$
$E=1.67\times10^{-27}\times3\times10^{8}\times3\times10^{8}$

$\Rightarrow E=1.67\times10^{-27+16}\times9J$

$\Rightarrow E=\frac{(1.67)(9)(10^{-11})}{(1.6)(10^{-13})}MeV$

$\Rightarrow E=939.4\; MeV \cong 931.5\; MeV$

(b) 1 u mass converted into total energy will be released by 931.5 MeV.
However, 1 amu = 931.5 MeV is dimensionally incorrect.
$E=mc^{2}\rightarrow 1uc^{2}\cong 931.5\; MeV$, will be dimensionally correct.