NCERT Exemplar Class 11 Physics Solutions Chapter 4 Motion in a Plane
Have you ever thought about how a football goes flying round in the air, or why a bicycle rider leans to make a turn, or why a ball will travel in a curved line when a person throws it into the air? These daily experiences are all dictated by the principles of the two-dimensional motion, which are the main content of NCERT Class 11 Physics Chapter 4 - Motion in a Plane. This chapter makes students realize the way in which motion takes place when an object moves simultaneously in more than one direction.
This Story also Contains
- NCERT Exemplar Class 11 Physics Solutions Chapter 4: MCQI
- NCERT Exemplar Class 11 Physics Solutions Chapter 4: MCQII
- NCERT Exemplar Class 11 Physics Solutions Chapter 4: Very Short Answer
- NCERT Exemplar Class 11 Physics Solutions Chapter 4: Short Answer
- NCERT Exemplar Class 11 Physics Solutions Chapter 4: Long Answer
- NCERT Exemplar Class 11 Physics Solutions Chapter 4: Important Concepts and Formulas
- Advantages of NCERT Exemplar Class 11 Physics Solutions Chapter 4 Motion in a Plane
- Approach to Solve Exemplar Questions of Chapter 4 Motion in a Plane
- NCERT Exemplar Class 11 Physics Solutions Chapter-Wise
- NCERT Exemplar Solutions Class 11 Subject-wise
- NCERT Solutions for Class 11 Physics Chapter-wise
NCERT Exemplar Class 11 Physics Chapter 4 Motion in a Plane, addresses crucial topics such as scalars and vectors, addition of vectors, relative velocity, projectile motion and uniform circular motion. The concepts are very fundamental in the explanation of motions in real life, and they are often examined in board and competitive exams. The NCERT Exemplar Solutions for Class 11 Physics Chapter 4 Motion in a Plane are developed in a simple step-wise way, in which complex numericals and derivations of vectors are easily understood and applied. The NCERT Exemplar Solutions Class 11 Physics Chapter 4 has been developed by subject matter experts and is completely consistent with the most recent CBSE syllabus and NCERT guidelines. The NCERT Exemplar solutions are all aimed at creating a solid conceptual clarity, preventing typical errors that can be committed by students and teaching them to think logically in solving the problem. These are the questions that can be practised regularly to improve analytical skills and confidence.
NCERT Exemplar Class 11 Physics Solutions Chapter 4: MCQI
NCERT Exemplar Class 11 Physics Chapter 4 Motion in a Plane: MCQ I provides accurate and well-explained answers to objective questions designed as per the NCERT Exemplar pattern. These NCERT solutions assist students in their conceptual knowledge testing, enhance accuracy, and effectively practise questions that have a multi-choice format that are examination oriented.
Question:4.1
The angle between $A=\hat{i}+\hat{j}$ and $B=\hat{i}-\hat{j}$ is
(a) $45^{o}$
(b) $90^{o}$
(c) $-45^{o}$
(d)$180^{o}$
Answer:
The answer is option (b), $90^{o}$Explanation :
We know from the formula that $A.B=\left \| A \right \|\left \| B \right \|\cos \theta$
Given that $\vec{A}=\hat{\iota }+\hat{J}$ and $\vec{B}=\hat{\iota }-\hat{J}$
$\cos \theta =\frac{(\hat{\iota }+\hat{J})(\hat{\iota }-\hat{J})}{\sqrt{1^{2}+1^{2}}(\sqrt{1^{2}+(-1^{2})})}$
$=0=\cos 90$
Hence the angle is $90^{o}$
Question:4.2
Which one of the following statements is true?
(a) A scalar quantity is the one that is conserved in a process.
(b) A scalar quantity is the one that can never take negative values.
(c) A scalar quantity is the one that does not vary from one point to another in space.
(d) A scalar quantity has the same value for observers with different orientations of the axes.
Answer:
The answer is option (d). A scalar quantity has the same value for observers with different orientations of the axes.Explanation:
Unlike vector quantities, a scalar quantity has no dependence on direction, and hence its value remains the same for all orientations of the axes.
Question:4.3
Figure 4.1 shows the orientation of two vectors u and v in the XY plane.
If $u=a\hat{i}+b\hat{j}$ and
$v=p\hat{i}+q\hat{j}$
Which of the following is correct?
(a) a and p are positive while b and q are negative.
(b) a, p and b are positive while q is negative.
(c) a, q and b are positive while p is negative.
(d) a, b, p and q are all positive.
Answer:
The answer is option (b) a, p and b are positive while q is negative.Explanation:
Now, $\vec{u}=a\hat{\iota }+b\hat{J}$ and $\vec{v}=p\hat{\iota }+q\hat{J}$
For vector u, both the components a and b are in the positive direction of the x-axis. Hence, they are positive.
For vector v, p is in the positive direction, but q is in the opposite direction. Hence, p is positive, and q is negative.
Question:4.4
The component of a vector r along X-axis will have maximum value if
(a) r is along positive Y-axis
(b) r is along positive X-axis
(c) r makes an angle of 45° with the X-axis
(d) r is along negative Y-axis
Answer:
The answer is option (b) r is along the positive X-axisExplanation: if a vector B forms an angle $\theta$ along the x-axis. Then its components along the x-axis can be written as B Cos θ.
The maximum value of $\cos \theta =1$, which is when $\theta =0$.
Hence, for the vector r, the maximum value will be when it is along the positive x-axis.
Question:4.5
The horizontal range of a projectile fired at an angle of $15^{o}$ is 50 m. If it is fired with the same speed at an angle of $45^{o}$, its range will be
a) 60 m
b) 71 m
c) 100 m
d) 141 m
Answer:
The answer is option (c) 100 mExplanation:
According to the formula:
$R=\frac{u^{2}\sin {2\theta }}{g}$
Given in the question:
$\theta =15,R=50\; m$
Putting in the formula, we get:
$u^{2}=100\; g$
For $\theta =45,$
The value of the range is:
$R=\frac{100\; g\times \sin{90}}{g}=100\; m$
Question:4.6
Consider the quantities pressure, power, energy, impulse gravitational potential, electric charge, temperature, area. Out of these, the only vector quantities are
a) impulse, pressure, and area
b) impulse and area
c) area and gravitational potential
d) impulse and pressure
Answer:
The answer is the option (b), impulse and areaExplanation:
Impulse is a vector quantity and not a scalar quantity, as the impulse is the rate of change of momentum, and it involves direction.
The area is a vector quantity
Question:4.7
In a two dimensional motion, instantaneous speed v0 is a positive constant. Then which of the following are necessarily true?
a) the average velocity is not zero at any time
b) average acceleration must always vanish
c) displacements in equal time intervals are equal
d) equal path lengths are traversed in equal intervals
Answer:
The answer is the option (d), equal path lengths are traversed in equal intervals.Explanation: when instantaneous speed is positive and constant, since speed is a scalar quantity, equal paths will be covered in an equal amount of time.
Question:4.8
In a two dimensional motion, instantaneous speed $v_{0}$ is a positive constant. Then which of the following are necessarily true?
a) the acceleration of the particle is zero
b) the acceleration of the particle is bounded
c) the acceleration of the particle is necessarily in the plane of motion
d) the particle must be undergoing a uniform circular motion
Answer:
The answer is the option (c), the acceleration of the particle is necessarily in the plane of motionExplanation: In a two-dimensional motion, the instantaneous speed is positive and constant. Since velocity is constant, acceleration, which is the rate of change in velocity, is also constant. Hence, the acceleration will be in the plane of motion.
Question:4.9
Three vectors A,B and C add up to zero. Find which is false.
(a) (A * B) * C is not zero unless B,C are parallel
(b) (A * B).C is not zero unless B,C are parallel
(c) If A,B,C define a plane, (A * B) *C is in that plane
(d) $(A^{*}B).C=\left | A \right |\left | B \right |\left | C \right |\rightarrow C^{2}=A^{2}+B^{2}$
Answer:
The answer is the option (a) and (c)Explanation:
Given $\vec{A}+\vec{B}+\vec{C}=0$
Option a : $\vec{B}\times (\vec{A}+\vec{B}+\vec{C})=\vec{B}\times 0=0$
$0=\vec{B}\times \vec{A}+\vec{B}\times \vec{B}+\vec{B}\times \vec{C}$
$0=\vec{B}\times \vec{A}+0+\vec{B}\times \vec{C}$
$\vec{A}\times \vec{B}=\vec{B}\times \vec{C}$(this cannot be zero)
Only if B and C are antiparallel or parallel $\vec{B}\times \vec{C}$ will be zero
Hence, for the whole quantity to be zero, $\vec{B}\parallel \vec{C}$ should be true.
Option C : $\vec{A}\times \vec{B}=\vec{X}$
X is perpendicular to the planes which have vector A and vector B
Vector Y is perpendicular to the planes which have vector A and vector B
Vector Y is perpendicular to the plane containing X and C, which is, in turn, the plane containing vectors A, B and C
Question:4.10
It is found that $\left | A+B \right |=\left | A \right |.$ This necessarily implies,
(a)$B=0$
(b) A,B are antiparallel
(c) A,B are perpendicular
(d) $A.B\leq 0$
Answer:
The answer is the option (a) $B=0$Explanation :
Squaring both sides and opening the brackets, we get,
$\left | \vec{A} \right |^{2}+\left |\overrightarrow{B} \right |^{2}+2\left | \vec{A} \right |\left | \overrightarrow{B} \right |\cos \theta =\left | \vec{A} \right |^{2}$
$\left | \overrightarrow{B} \right |^{2}+2\left | \vec{A} \right |\left | \overrightarrow{B} \right |\cos \theta =0$
$cos\theta=\frac{-B}{2A}$
$if B=0$
$cos\theta=0$
NCERT Exemplar Class 11 Physics Solutions Chapter 4: MCQII
Physics Class 11 NCERT Exemplar Chapter 4 Motion in a Plane: MCQ II is centered on the solution of higher-order objective questions, such as assertion-reason questions, concept-based questions in MCQs. These Motion in a Plane NCERT Exemplar Class 11 Physics Solutions assist the students to reason logically, to clear the major mistakes, and to be confident with their ability to answer the advanced objective questions.
Question:4.11
Two particles are projected in air with speed $v_{0}$, at angles $\theta _{1}$ and $\theta _{2}$ to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then tick the right choices
a) angle of project: $q_{1} > q_{2}$
b) time of flight: $T_{1} > T_{2}$
c) horizontal range: $R_{1} > R_{2}$
d) total energy: $U_{1} > U_{2}$
Answer:
The answer is the option (a) and (b)Explanation:
According to the formula, the maximum height of a projectile is
$H = \frac{u^{2} \sin^{2} {\theta }}{2g}$
Option a :$H1>H2$
$\sin ^{2}\theta 1>\sin ^{2}\theta 2$
$(\sin \theta 1+\sin \theta 2)(\sin \theta 1-\sin \theta 2)>0$
So, $(\sin \theta 1+\sin \theta 2)>0 \; or(\sin \theta 1-\sin \theta 2)>0$
So, $\theta 1>\theta 2$ and $\theta$ lies etween 0 and 90 degree i.e. acute
Option b :
$\frac{T1}{T2}=\frac{\sin \theta 1}{\sin \theta 2}$
$T1\sin \theta 2=T2\sin \theta 1$
Since $\sin \theta 1>\sin \theta 2$
$T1>T2$
Question:4.12
A particle slides down a frictionless parabolic $(y=x^{2})$ track $(A - B - C)$ starting from rest at point A (Fig. 4.2). Point B is at the vertex of parabola and point C is at a height less than that of point A. After C, the particle moves freely in air as a projectile. If the particle reaches highest point at P, then
(a) KE at P = KE at B
(b) height at P = height at A
(c) total energy at P = total energy at A
(d) time of travel from A to B = time of travel from B to P.
Answer:
The answer is the option (c)Explanation: total energy at a point in the path remains the same, as there is no friction between air and plane on paths A, B and C
As we know through the energy conservation law, the total energy at point P will be the same as the total energy at point A.
Hence, option c is correct.
Question:4.13
Following are four different relations about displacement, velocity, and acceleration for the motion of a particle in general. Choose the incorrect one(s) :
(a) $V_{av}=\frac{1}{2}\left [ V(t_{1})+V(t_{2}) \right ]$
(b) $V_{av}=\frac{r(t_{2})-r(t_{1})}{t_{2}-t_{1}}$
(c) $r=\frac{1}{2}\left ( V(t_{2})-V(t_{1}) \right )\left ( t_{2}-t_{1} \right )$
(d) $a_{av}=\frac{V(t_{2})-V(t_{1})}{t_{2}-t_{1}}$
Answer:
The answer is the option (a) and (c)Explanation:
Option a:
The given relation is correct when the acceleration is uniform
Option c:
$\vec{r}=\frac{1}{2}\left ( \vec{v}(t_{2})-\vec{v}(t_{1}) \right )\div \left ( t_{2}-t_{1} \right )$
This is the relationship given in the question, but it is not possible as the LHS and RHS dimensions $\left [ M^{0}L^{1}T^{0} \right ]$ and $\left [ M^{0}L^{1}T^{2} \right ]$do not match and hence the relationship cannot be considered valid.
Question:4.14
For a particle performing uniform circular motion, choose the correct statement(s) from the following:
(a) Magnitude of particle velocity (speed) remains constant.
(b) Particle velocity remains directed perpendicular to radius vector.
(c) Direction of acceleration keeps changing as particle moves.
(d) Angular momentum is constant in magnitude but direction keeps changing.
Answer:
The answer is the option (a), (b), and (c)Explanation:
Option a: speed is constant at all times in the case of uniform circular motion
Option b: In the case of velocity, in a circular motion, it is measured tangentially to the direction of motion of the particle, which is in turn perpendicular to the radius.
Option c: The direction of the acceleration is always in the direction of the force. This can concur with the newton’s second law of motion. So as the particle moves in a circular motion, the direction of force keeps on changing, and hence that of acceleration also changes.
Question:4.15
For two vectors A and B, $|A + B| = |A - B|$ is always true when
(a) $\left | A \right |=\left | B \right |\neq 0$
(b) $\left | A \right |\perp \left | B \right |$
(c) $\left | A \right |= \left | B \right |\neq 0$ and A and B are parallel or anti parallel
(d) when either $\left | A \right |$ or $\left | B \right |$ is zero.
Answer:
The answer is the option (b) and (d)Explanation:
Given : $\left | \vec{A}+\vec{B} \right |=\left | \vec{A}-\vec{B} \right |$
Now we square both sides and open the brackets to get:
$\left | \vec{A} \right |^{2}+\left | \vec{B} \right |^{2}+2\left | \vec{A} \right |\left | \vec{B} \right |\cos \theta =\left | \vec{A} \right |^{2}+\left | \vec{B} \right |^{2}-2\left | \vec{A} \right |\left | \vec{B} \right |\cos \theta$
$4\left | \vec{A} \right |\left | \vec{B} \right |\cos \theta=0$
So, we have, $\theta =90$ degree and $\left | \vec{A} \right |=\left | \vec{B} \right |=0$
Hence, option b and option d are correct.
NCERT Exemplar Class 11 Physics Solutions Chapter 4: Very Short Answer
Motion in a Plane NCERT Exemplar Class 11 Physics Solutions: Very short answer provides brief and precise answers to questions that would examine the simple concepts and definitions. These responses suit rapid revision and allow students to remember important concepts in a minimal amount of time and reinforce the basics.
Question:4.16
Answer:
To calculate acceleration in a circular motion, we have a formula.$A=\frac{v^{2}}{R}$
Given, $R=1000 \; m, v = 10\; m/s$
Hence, $A=10\times \frac{10}{1000}=\frac{1}{10}=0.1\; m/s^{2}$
Question:4.17
Answer:
A particle travelling in a projectile motion will definitely have a path which is parabolic in nature. The velocity of such a particle is always measured tangentially to the path of motion. Point B is where the particle reaches maximum height during the projectile motion.
Here we have the vertical and horizontal components of B, which are $V_{y}=0$ and $V_{x}=u\cos \theta$
Question:4.18
Answer:
The ball is thrown from point O. The angle with the horizontal is 45 degrees. As the height increases from O to A, the speed decreases. At B, the speed becomes equal to its initial speed. The height decreases further from B to C and becomes maximum at point C.
$V_{x}=u\; \cos 45=\frac{u}{\sqrt{2}}\; m/s$
a) greatest speed of the ball is at c as $V_{y}$ and $V_{x}=u\; \cos\; 45=\frac{u}{\sqrt{2}}\; m/s$
b) slowest speed will be at point A. here $V_{y}=0$, and the horizontal speed is $V_{x}=\frac{u}{\sqrt{2}}$
c) The greatest acceleration will be the one caused by the gravitational force downward, which will be equal to g.
Question:4.19
A football is kicked into the air vertically upwards. What is its
a) acceleration
b) velocity at the highest point
Answer:
a) When the football is kicked into the air, the only force working on it is the gravitational force. Hence, the acceleration will be caused by this force, which will be in the downward direction towards the centre of the Earth.b) When the ball is thrown upward, no horizontal forces act on it, and hence the horizontal component velocity becomes nil. The vertical component of velocity at the highest point is $V_{y}=0$. Hence, the net velocity when the ball reaches the highest point is also zero.
Question:4.20
Answer:
Given: A, B, and C are non-collinear and no co-planar vectors.For finding out the direction, we used the right-hand grip rule.
For $(\vec{B}\times\vec{C})$, the direction will be in a plane perpendicular to the plane containing $\vec{B}$ and $\vec{C}$.
However, for the direction of $\vec{A}\times(\vec{B}\times\vec{C}):$ it will be perpendicular to both $\vec{A}$ and the plane which has $(\vec{B}\times\vec{C}).$
NCERT Exemplar Class 11 Physics Solutions Chapter 4: Short Answer
Class 11 Physics chapter 4 Motion in a Plane: Short Answer gives explicit and logically presented answers to the questions requiring a brief explanation and argument for the answer. These responses assist the students in enhancing conceptual clarity, organising their answers well and even in examinations.
Question:4.21
Answer:
Let v be the vertical velocity, and u be the horizontal velocity of the car.
In the case of the ball, as it has both horizontal and vertical components of velocity, it will have a parabolic path when a person standing on a footpath sees the trajectory.
When a boy sitting in the same car sees the ball, the path will be vertical up and down. However, he will be able to catch up with the ball provided the car moves at a constant velocity.
Question:4.22
Answer:
Given : $u=36\; km/h=10\; m/s$
$u_{x}=u\; \cos 60=5\; m/s$
Now, in the direction of the ball, the speed of the car is $18\times \frac{5}{18}=5\; m/s$
Since the horizontal speeds are the same, in the situation of a ball thrown by the boy as soon as the car passes him, they also cover equal horizontal distances.
Now, when vertical components are considered, $u_{y}=u\; \cos 30=5\sqrt{3}\; m/s$ and the motion of the ball is vertically up-down as seen by the boy.
Question:4.23
Answer:
When we are dealing with projectile motion, we neglect the air resistance. But if air resistance is included, the horizontal component of velocity will not be constant and obviously trajectory will change.
Due to air resistance, particle energy, as well as the horizontal component of velocity, keep on decreasing, making the fall steeper than the rise, as shown in the figure.
When we are neglecting air resistance path was a symmetric parabola (OAC). When air resistance is considered path is an asymmetric parabola (OAB).
Question:4.23
Answer:
The horizontal and vertical components of the velocity decrease due to air resistance. So, as a result, the max height also becomes less than in the ideal case.
Now, $R=u^{2}\sin 2\; \theta/g$ and max height $H=u^{2}\sin^{2} \; \theta/2g$
So, $h_1<h_2\;and\; R_1<R_2$
But, in the second case, when $h1<h2$, due to the smaller time taken to rise, the overall time of flight for both cases stands equal
Question:4.24
Answer:
$u=720\; km/h=200\; m/s$
We assume that the bomb is dropped by the pilot t seconds vertically above Q, before the target T
vertical component velocity of the bomb will be zero, and the horizontal component value will be equal to that of the plane. So, the bomb covers the distance TQ as a free fall.
Now, $u=0,H=1.5,g=10$
So, $H=ut+\frac{1}{2}gt^{2}=0+\frac{1}{2}10\times t\times t=1500$
So, we get, $t=10\sqrt{3}\; s$
ut is the distance covered by the plane or the bomb equal to PQ
hence, $PQ=ut=200\sqrt{3}\; m$
now, $\tan \theta =\frac{TQ}{PQ}=\sqrt{\frac{3}{4}}=23^{o}42'$
Question:4.25
a) Earth can be thought of as a sphere of radius 6400 km. Any object is performing circular motion around the axis of earth due to earth’s rotation. What is the acceleration of object on the surface of the earth towards its centre? What is it at latitude $\theta$? How does these accelerations compare with $g=9.8\; m/s^{2}?$
b) Earth also moves in circular orbit around sun once every year with an orbital radius of $1.5\times 10^{11}\; m.$ What is the acceleration of earth towards the centre of the sun? How does this acceleration compare with $g=9.8\; m/s^{2}?$
$\left ( Hint: acceleration\frac{V^{2}}{R}=\frac{4\pi ^{2}R}{T^{2}} \right )$
Answer:
The angular acceleration will have its direction towards the centre, and the value will be $a=w^{2}R$Now, $w=\frac{2\pi }{T}$
$R=6.4\times 10^{6}m\;$ and $T=24\times 3600=86400s$
Acceleration of the person on the surface of the Earth,
$a=w^{2}R=\left ( \frac{2\pi }{T} \right )^{2}\times R$
$=\frac{4\times22\times22\times6.4\times10^{6}}{7\times 7\times 24\times 24\times 3600\times 3600}=\frac{1210}{81\times49\times9}=0.034\; m/s^{2}$
Now, at the equator latitude = 0
Hence $\frac{a}{g}=\frac{0.034}{9.8}=\frac{1}{288}=0.0034$ which is much smaller than the previous case.
b) acceleration of Earth revolving around the sun
$R=1.5\times10^{11}m$ and $w=\frac{2\pi }{T}$
$T=365\times24\times3600=3.15\times10^{7}seconds$
Now, $a=w^{2}R=(\frac{2\pi }{T})^{2}\times R$
$=\frac{4\times 3.14\times3.14\times1.5\times10^{11}}{3.15\times3.15\times10^{7}\times10^{7}}=6\times10^{-3}m/s^{2}$
Also, $\frac{a}{g}=\frac{0.0006}{9.8}$
Question:4.26
| Column I | Column II |
| a) a+b=c |  |
| 5b) a-c=b |  |
| c) b - a = c |  |
| d) a+b+c=0 |  |
Answer:
a) $\vec{a}+\vec{b}=\vec{c}$ matches with (iv)b) $\vec{c}+\vec{b}=\vec{a}$ matches with (iii)
c) $\vec{a}+\vec{c}=\vec{b}$ matches with (i)
d) $\vec{a}+\vec{c}+\vec{b}=0$ matches with (ii)
Question:4.27
If $\left | A \right |=2$ and $\left | B \right |=4$, then match the relations in column I with the angle $\theta$ between A and B in column II.
Column I Column II
(a) $A.B=0$ (i) $\theta =0$
(b) $A.B=+8$ (ii) $\theta =90^{o}$
(c) $A.B=4$ (iii) $\theta =180^{o}$
(d) $A.B=-8$ (iv) $\theta =60^{o}$
Answer:
a) Matches with (ii)$\left | \vec{A} \right |\left | \vec{B} \right |\; \cos \theta =0$
$\cos \theta =0$
$\theta =90$
b) Matches with (i)
$\left | \vec{A} \right |\left | \vec{B} \right |\; \cos \theta =8$
$2\times4 \cos \theta =8$
$\cos \theta =1$
$\theta =0$
c) Matches with (iv)
$\left | \vec{A} \right |\left | \vec{B} \right |\; \cos \theta =4$
$2\times4 \cos \theta =84$
$\cos \theta =\frac{1}{2}$
$\theta = 60$
d) Matches with (iii)
$\left | \vec{A} \right |\left | \vec{B} \right |\; \cos \theta =-8$
$2\times4 \cos \theta =-8$
$\cos \theta =-1$
$\theta =180$
Question:4.28
If $\left | A \right |=2$ and $\left | B \right |=4$ then match the relations in column I with the angle $\theta$ between A and B in column II.
Column I Column II
(a)$\left | A\times B \right |=0$ (i) $\theta =30^{o}$
(b) $\left | A\times B \right |=8$ (ii) $\theta =45^{o}$
(c) $\left | A\times B \right |=4$ (iii) $\theta =90^{o}$
(d) $\left | A\times B \right |=4\sqrt{2}$ (iv) $\theta =0^{o}$
Answer:
Given : $\left | \vec{A} \right |=2$ and $\left | \vec{B} \right |=4$a) Matches with (iv)
$\left | \vec{A}\times \vec{B} \right |=0$
$\left | \vec{A} \right |\left | \vec{B} \right |\sin \theta =0$
$2\times4\; \sin \theta =0$
$\sin \theta =\sin 0$
$\theta =0$
b) matches with (iii)
$\left | \vec{A}\times \vec{B} \right |=8$
$\left | \vec{A} \right |\left | \vec{B} \right |\sin \theta =8$
$2\times4\; \sin \theta =8$
$\sin \theta =1$
$\theta =90$
c) matches with (i)
$\left | \vec{A}\times \vec{B} \right |=4$
$\left | \vec{A} \right |\left | \vec{B} \right |\sin \theta =4$
$2\times4\; \sin \theta =4$
$\sin \theta =\frac{1}{2}$
$\theta =30$
d) matches with (ii)
$\left | \vec{A}\times \vec{B} \right |=4\sqrt{2}$
$\left | \vec{A} \right |\left | \vec{B} \right |\sin \theta =4\sqrt{2}$
$2\times4\; \sin \theta =4\sqrt{2}$
$\sin \theta =\frac{1}{\sqrt{2}}$
$\theta =45$
NCERT Exemplar Class 11 Physics Solutions Chapter 4: Long Answer
NCERT Exemplar Class 11 Physics Solutions Chapter 4 Motion in a Plane (Long Answer) provides detailed, step-by-step explanations to help students understand complex vector concepts and two-dimensional motion. These solutions focus on clear reasoning, proper use of formulas, and well-structured derivations as required in long-answer questions. Practising them strengthens conceptual clarity, improves presentation skills, and prepares students effectively for board and competitive examinations.
Question:4.29
Answer:
Packet speed = 125 m/s, height of hill = 500m
In order to cross the hill, the vertical component of the packet should be reduced to make the height of 500m attainable. The distance between the canon and the hill should also be half of that of the packet’s range.
$V^{2}-u^{2}=2gh$
$U_{y}=\sqrt{2gh}=\sqrt{10000}=100\; m/s$
Now, $U=u{_{x}}^{2}+u{_{y}}^{2}$
$u{_{x}}^{2}=125\times125-(100\times100)$
$u_{x}=75\; m/s$
Now we consider the packet's vertical motion,
$v_{y}=u_{y}+gt$
t= total time of flight = 10 sec
so, $v_{y}=75\times10=750$
So the distance between the canon and the hill is 750m
distance for which the canon needs to move$=800-750=50m$
time taken for the canon to move $50m=\frac{50}{2}=25 sec$
So the total time taken by the packet $=25+10+10=45\; seconds$
Question:4.3
A gun can fire shells with maximum speed $v_{0}$ and the maximum horizontal range that can be achieved is $R=v{_{0}}^{2}/g$
If a target farther away by $\Delta x$ beyond R has to be hit with the same gun as shown in the figure. Show that it could be achieved by rating the gun to a height at least
$h=\Delta x[1+\frac{\Delta x}{R}]$
Answer:
The solution to this problem can be given in two ways:
i) the target is present at the horizontal distance of $(R+\Delta x)$ and is h meters below the projection point. $Y=-h$
ii) the motion of a projectile starting from point P till reaching point T. The vertical height covered is -h, and the horizontal range is $\Delta x$
max range of a projectile is given by $R=\frac{v^{2}}{g}$
here, $\theta =45$
We assume that the gun is raised to a height h to hit the target T
total range $=(R+\Delta x)$
the horizontal component of velocity is, $v\; \cos \theta$
horizontal velocity at $P=V_{x}=-V\; \cos \theta$
vertical velocity at $P=V_{y}=V\sin \theta$
now, $h=ut+\frac{1}{2}at^{2}$
So, $h=-V\; \sin \theta t+\frac{1}{2}gt^{2}\; \; \; \; \; \; ---------------(1)$
$V\; \cos \theta .t=(R+\Delta x)$
$t=\frac{(R+\Delta x)}{V\; \cos \theta }$
Substituting the value of t in (1), we get,
$h=-V\; \sin \theta \left ( \frac{(R+\Delta x)}{V\; \cos \theta } \right )+\frac{1}{2}g\left ( \frac{(R+\Delta x)}{V\; \cos \theta } \right )^{2}$
$h=-(R+\Delta x)+\frac{1}{R}(R^{2}+\Delta x^{2}+2R\; \Delta x)=-R-\Delta x+R+\frac{\Delta x^{2}}{R}+2\Delta x$
$h=\Delta x[1+\frac{\Delta x}{R}]$
hence proved.
Question:4.31
Answer:
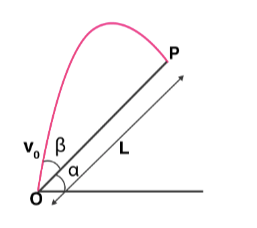
Now, $a_{y}=-g\; \cos \alpha$ and $a_{x}= g\; \sin \alpha$
$Y=0$ at O and P,
So
$U_{y}=v\; \sin \beta$ where t = T
We calculate the Time of Flight Part (b) before Part (a)
b) motion of particle along the Y axis
$s=ut+\frac{1}{2}gt^{2}$
$s=0,u=v\; \sin \beta , g=a=-g\; \cos \alpha ,t=T$
$0=v\; \sin \beta .T+\frac{1}{2}(-g\; \cos \alpha )T^{2}$
$T[v\; \sin \beta -T.\frac{g}{2}\cos \alpha ]=0$
$\frac{Tg}{2}.\cos \alpha =v\sin \beta$
So, $T=2v\; \sin \beta /g.\cos \alpha$
a) Now we continue part a
$T=2v\; \sin \beta /g.\cos \alpha$
$s=ut+\frac{1}{2}gt^{2}$
$L=v\; \cos \beta (T)+\frac{1}{2}(-g\; \sin \alpha )T^{2}$
$L=2\; v^{2}\; \sin \beta[\cos \beta \cos \alpha -\sin \beta \sin \alpha ]/g \cos ^{2}\alpha$
$L=2\; v^{2}\; \sin \beta \times \cos [\alpha +\beta ]/g \cos ^{2}\alpha$
c) on the axis X, L will be maximum when $\sin \beta \cos [\alpha +\beta ]$ will be maximum
let $z=\sin \beta \cos [\alpha +\beta ]$
$=\sin \beta [\cos \beta \cos \alpha -\sin \beta \sin \alpha ]$
$=\frac{1}{2}[\cos \alpha\; 2\sin\; \beta +\sin \alpha \cos \; 2\; \beta-\sin \alpha ]$
$=\frac{1}{2}[\sin(2\beta +\alpha )-\sin\; \alpha ]$
In order to make Z maximum, we put $[\sin(2\beta +\alpha )-\sin\; \alpha ]=1$
Opening the brackets, we get $(2\beta +\alpha )=90$
$2\beta =90-\alpha$
$\beta =45-\frac{\alpha }{2}$radian
Question:4.32
Answer:
The particle rebounds from P. when it strikes a plane inclined at v0 speed. Hence, the speed of the particle after it rebounds from P will be v0. We assume the new axis X’OX and YOY’ axis at P as origin ‘O’. The components of g and v0 in the new OX and OY axes are:
Focusing on the motion of the particle from O to A,
$s=ut+\frac{1}{2}gt^{2}$
Here, t=T which is the time of flight
$0=T[v\; \cos\; \theta -\frac{1}{2}g\; \sin\; \theta \; T]$
So, either $T=0\; or \left [ v\; \cos\; \theta -\frac{1}{2}g\; \sin\; \theta \; T \right ]=0$
$S_{x}=u_{x}t+\frac{1}{2}a_{x}t^{2}$
$L=[\frac{2v}{g}]v\; \sin \theta +\frac{1}{2}g\; \sin\; \theta [\frac{2v}{g}]^{2}$
$L=\frac{4v^{2}}{g}.\sin \theta$
Question:4.33
Answer:
Let the north direction be i and the south direction be jThe velocity of rain is $v=a\hat{i}+b\hat{J}$
Case 1 (v=5i)
The velocity of rain with respect to the girl is:
$v_{r}-v_{g}=(a\hat{i}+b\hat{j})-5\hat{i}=(a-5)\hat{i}+b\hat{j}$
Since the horizontal component is zero, $a-5=0 \; or\; a=5$
Case 2 (v=10i)
$v_{r}-v_{g}=(a\hat{i}+b\hat{j})-10\hat{i}=(a-10)\hat{i}+b\hat{j}$
The angle of rain appears to be 45 degrees.
$\tan 45=\frac{b}{a}=\frac{b}{-5}$
$b=-5$
So,
$\left | v_{r} \right |=\sqrt{5^{2}+(-5)^{2}}=\sqrt{50}=5\sqrt{2}\; m/s$
Question:4.34
A river is flowing due east with a speed 3m/s. A swimmer can swim in still water at a speed of 4 m/s (Fig. 4.8).
(a) If swimmer starts swimming due north, what will be his resultant velocity (magnitude and direction)?
(b) If he wants to start from point A on south bank and reach opposite point B on north bank,
(a) which direction should he swim?
(b) what will be his resultant speed?
(c) From two different cases as mentioned in (a) and (b) above, in which case will he reach opposite bank in shorter time?
Answer:
a) If a swimmer starts swimming due north, what will be his resultant velocity
$V_{s}=4\; m/s$ due north
$V_{r}=4\; m/s$ due east
Now, since both directions are perpendicular,
$\left | V_{r} \right |^{2}=4^{2}+3^{2}=5\; m/s$
$\tan \; \theta =\frac{V_{r}}{V_{s}}=0.75=36^{o}54'$ in the North direction
b) The swimmer wants to start from point A on the south bank and reach the opposite point B on the north bank
The swimmer makes an angle $\theta$ with the north.
From the figure, we have the relation,
$V^{2}=v{_{s}}^{2}-v{_{r}}^{2}=16-9=7$
Henece$v=\sqrt{7}\; m/s$
Now we calculate the value of θ through the following formula,
$\tan \theta =\frac{v_{r}}{v}=\frac{3\sqrt{7}}{7}=1.13$
So, $\theta =48^{o}29'30''$ in th edirection from North to West
c) we need to find from the above two scenarios that for the swimmer to reach the opposite bank in the shortest time
We know that the velocity component perpendicular to the river is 4m/s
Let us assume the width of the river to be ‘w’
Time taken - North
$\frac{w}{4}=t1$
time taken in part b) when $v=\sqrt{7}\; m/s$
$\frac{w}{\sqrt{7}}=t2$
taking ratio,
$\frac{t1}{t2}=\frac{(\frac{w}{4})}{(\frac{w}{\sqrt{7}})}$
$4\; t1=\sqrt{7}\; t2$
Now as, $4>\sqrt{7}$
$t1<t2$
So, the swimmer will take a shorter time in case a)
Question:4.35
A cricket fielder can throw the cricket ball with a speed vo. If he throws the ball while running with speed u at an angle $\theta$ to the horizontal, find
a) the effective angle to the horizontal at which the ball is projected in the air as seen by a spectator
b) what will be time of flight?
c) what is the distance from the point of projection at which the ball will land?
d) find $\theta$ at which he should throw the ball that would maximise the horizontal range as found c)
e) how does $\theta$ for maximum range change if $u>v_{o}=v_{o}$ and $u<v_{o}$
f) how does $\theta$ in e) compare with that for u = 0?
Answer:
a) u is the horizontal velocity with which the cricketer runs. The ball is thrown by him while running, and hence the speed of the ball also contains a component of the cricketer’s speed.
$U_{x}=u+v\; \cos \; \theta$
Vertical component,
$U_{y}=v\; \sin \; \theta$
$\tan \theta =\frac{v\; \sin \theta }{u+v\cos \theta }$
$\theta =\tan ^{-1}[\frac{v\; \sin\; \theta }{u+v\; \cos \; \theta }]$
b) Time of flight
$S_{y}=U_{y}t+\frac{1}{2}a_{y}t^{2}$
Since the ball returns back to the same position, Sy = 0
$U_{y}=v\; \sin \theta$
So,$0=v\; \sin \theta (T)-\frac{1}{2}g\; T^{2}$
$T[v\; \sin \theta -\frac{1}{2}g\; T]=0$
Since T cannot be zero, we have
$T=2v\; \sin \frac{\theta }{g}$
c) Maximum range
For the max range, the condition is
$\frac{dR}{d\theta} =0$
$d\frac{\left \{ \frac{v}{g}[2u]\sin \; \theta +\frac{v}{g}\; \sin 2\theta \right \}}{d\; \theta }=0$
$\theta =\cos ^{-1}\left [ \frac{-u\pm \sqrt{u^{2}+8\; v_{0}^{2}}}{4v_{0}} \right ]$
$\cos \; \theta =\left [ \frac{-u\pm \sqrt{u^{2}+8\; v_{0}^{2}}}{4v_{0}} \right ]$
e) In the case when $u=v,\cos \theta =$
$\frac{-v_{0}\pm \sqrt{v_{0}^{2}+8v_{0}^{2}}}{4v_{0}}$
$=\frac{-v_{0}+3v_{0}}{4v_{0}}$
$\cos\; \theta =-1+\frac{(-3)}{4}$
$\cos\; \theta =\frac{1}{2}$ (as $\theta$ is taken as an acute angle here)
hence, $\theta =60^{o}$
for the case of u << v
$\cos \theta =-u+\frac{(-2\sqrt{2}v)}{4v}$
Since $\theta$ is an acute angle here,
As u << v here, we can neglect the last term
$\cos \theta =\frac{1}{\sqrt{2}}$
$\theta =\frac{\pi }{4}$
For u >> v,
$\cos\; \theta =\frac{-u+(-u)}{4v}$
$\cos\; \theta =0=\cos 90$
$\theta =\frac{\pi }{2}$
f) when $u=0$
$\cos\; \theta =\frac{-u\pm \sqrt{u^{2}+8v_{0}^{2}}}{4v_{0}}$
$\cos\; \theta =\frac{2\sqrt{2}v}{4v}=\frac{1}{\sqrt{2}}$
$\cos\; \theta =45$
$\cos\; \theta =\frac{\pi }{4}$
Question:4.36
Motion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in Cartesian co-ordinates $A=A_{x}\hat{i}+A_{y}\hat{j}$ where $\hat{i}$ and $\hat{j}$ are unit vector long x and y directions, respectively and $A_{x}$ and $A_{y}$ are corresponding components of A (fig.4.9). Motion can also be studied by expressing vectors in circular polar co-ordinates as $A=A_{r}\hat{r}+A_{\theta }\hat{\theta }$ where $\hat{r}=\frac{r}{r}=\cos \theta \hat{i}+\sin \theta \hat{j}$ and $\hat{\theta }=-\sin \theta \hat{i}+\cos \theta \hat{j}$ are unit vectors along direction in which 'r' and $'\theta '$ are increasing.
(a) Express $\hat{i}$ and $\hat{j}$ in terms of $\hat{r}$ and $\hat{\theta }$
(b) Show that both $\hat{r}$ and $\hat{\theta }$ are unit vectors and are perpendicular to each other.
(c) Show that $\frac{d}{dt}(\hat{r})=\omega \hat{\theta }$ where $\omega =\frac{d\theta }{dt}$ and $\frac{d}{dt}(\theta )=-\omega \hat{r}$
(d) For a particle moving along a spiral given by $r=a\theta \hat{r},$ where $a=1$ (unit), find the dimensions of 'a'.
(e) Find velocity and acceleration in polar vector representation for the particle moving along the spiral described in (d) above.
Answer:
a) $\hat{r}=\cos\; \theta \hat{i}+\sin\; \theta \hat{J}\; \; \; \; \; \; -------(1)$$\hat{\theta }=-\sin\; \theta \hat{i}+\cos \theta \hat{J}\; \; \; \; ----------(2)$
When we multiply 1 by $\sin \theta$ and 2 by $\cos \theta$, we get :
$\hat{r}\sin \theta +\hat{\theta }\cos \theta =(\sin^{2}\theta +\cos^{2}\theta )\hat{J}$
$\hat{r}\sin \theta +\hat{\theta }\cos \theta =\hat{J}\; \; \; \; \; \; \; \; ---------(3)$
When we multiply 1 by $\cos \theta$ and 2 by $\sin \theta$ we get :
$\hat{r}\cos \theta =\cos^{2}\theta \hat{i}+\sin \theta \cos \theta \hat{J}\; \; \; \; \; -----(4)$
$\hat{\theta }\sin \theta =-\sin^{2}\theta \hat{i}+\sin \theta \cos \theta \hat{J}\; \; \; \; \; -----(5)$
Subtracting equation 5 from 4 and comparing the coefficients we get,
$\hat{r}\cos\theta -\hat{\theta }\sin \theta =\hat{i}$
$\hat{r}\sin\theta -\hat{\theta }\cos \theta =\hat{J}$
b) from equations 1 and 2, through the dot product method, we get,
$\hat{r}.\hat{\theta }=\left ( \cos\; \theta \hat{i}+\sin \theta \hat{J} \right ).\left ( -\sin\; \theta \hat{i}+\cos\; \theta \hat{J} \right )$
$\left | \hat{r} \right |\left | \hat{\theta } \right |\cos\; \theta =0$
Since LHS elements cannot be zero,
$\cos \theta =0$
and $\theta =90$
c) $\hat{r}=\cos\; \theta \hat{i}+\sin \theta \hat{J}$
$\frac{d\; \hat{r}}{dt}=\frac{d(\cos\; \theta \hat{i}+\sin \theta \hat{J})}{dt}$
$=\left ( -\sin \theta \hat{i} +\cos \theta \hat{J}\right )\frac{d\; \theta }{dt}$
Since, $\omega =\frac{d\theta }{dt}$
$\frac{d\hat{r}}{dt}=\omega \hat{\theta }$
d) $\hat{r}=\left | \hat{a} \right |\left | \hat{\theta } \right |\hat{r}$
Now looking at the dimensions of the quantities on the LHS and the RHS,
$[a]=\frac{[\hat{r}]}{[\hat{\theta }][\hat{r}]}$
$=\frac{[M^{0}L^{1}T^{0}]}{[M^{0}L^{0}T^{0}][M^{0}L^{0}T^{0}]}$
$=[M^{0}L^{1}T^{0}]$
e) $a=1$
$\hat{r}=\hat{\theta }[\cos\; \theta \hat{i}+\sin\; \theta \hat{J}]$
$V=\frac{d\hat{r}}{dt}=\frac{d\theta }{dt}\hat{r}+\theta (-\sin \theta \hat{i}+\cos \theta \hat{J})\frac{d\; \theta }{dt}$
$V=\omega \hat{r}+\theta .\hat{\theta }\omega$
$\vec{a}=\frac{dv}{dt}$
$=\frac{d(\omega \hat{r}+\theta .\hat{\theta }\omega )}{dt}$
$=d^{2}\frac{\theta }{dt^{2}}\hat{r}+d\frac{\theta }{dt}d\; \hat{r}\frac{\hat{r}}{dt}+d^{2}\frac{\theta }{dt^{2}}(\theta .\hat{\theta })+d\frac{\theta }{dt}(\theta .\hat{\theta })$
$=d^{2}\frac{\theta }{dt^{2}}\; \hat{r}+\omega \left ( \frac{-\sin\; \theta \hat{i}\; d}{dt}+\frac{\cos\; \theta \hat{J}\; d\; \theta }{dt} \right )+\frac{d^{2}\theta }{dt^{2}}(\theta .\hat{\theta })+\frac{\omega \; d\; \theta }{dt}(\theta .\hat{\theta })$
$=\frac{d^{2}\theta }{dt^{2}\hat{r}}+\omega ^{2}\hat{\theta }+\frac{d^{2}\theta }{dt^{2}}(\theta .\hat{\theta })+\omega ^{2}\hat{\theta }+\omega ^{2}(-\hat{r})$
$\vec{a}=\left ( \frac{d^{2}\theta }{dt^{2}-\omega ^{2}} \right )\hat{r}+\left ( \frac{2\omega ^{2+}d^{2}\theta }{dt^{2}\theta } \right )\hat{\theta }$
Question:4.37
Answer:
Since PQ is the diagonal, we can use Pythagoras theorem to find out,
$PQ=\sqrt{50\times 50+50\times 50}=50\sqrt{2}\; meters$
$AC=\sqrt{100\times 100+100\times 100}=100\sqrt{2}\; meters$
Now, let us calculate the time taken by the man to travel the path A-P-Q-C,
$T1=\frac{AC-PQ}{1}+\frac{PQ}{v}=\frac{100\sqrt{2}-50\sqrt{2}}{1}+\frac{50\sqrt{2}}{v}$
$T1=50\sqrt{2}[1+\frac{1}{v}]$
Now, let us calculate the time taken by the man to travel the path A-R-C,
$T2=2\; AR$
$AR=\left ( \frac{100\sqrt{2}}{2} \right )^{2}+\left ( \frac{50\sqrt{2}}{2} \right )^{2}$
$AR=25\sqrt{10}$
$T2=50\sqrt{10}$
The case when,
$T1>T2$
We get,
$50\sqrt{2}\left [ 1+\frac{1}{v} \right ]<50\sqrt{10}$
$\frac{1}{v}<\sqrt{5}-1$
$v<0.82\; m/s$
NCERT Exemplar Class 11 Physics Solutions Chapter 4: Important Concepts and Formulas
The chapter Motion in a Plane lays the foundation for understanding two-dimensional motion using vectors. It helps students analyse motion involving both magnitude and direction, which is essential for topics like projectile motion and circular motion. Mastery of concepts and formulas from this chapter is crucial for solving numericals accurately in board and competitive examinations. NCERT Exemplar questions strengthen both conceptual clarity and mathematical application.
1. Scalars and Vectors
Scalar quantities are characterised by magnitude alone, but vector quantities are characterised by both magnitude and direction. The study of two-dimensional motion, like velocity and acceleration in a plane, needs to be represented in vectors.
2. Position and Displacement Vectors
Position vector is the position of a particle in relation to the origin, whereas displacement vector indicates the change in position of a particle. These vectors assist in tracing motion in a two-dimensional coordinate system.
$\vec{r}=x \hat{i}+y \hat{j}$
3. Vector Addition
The process of adding two or more vectors to obtain a resultant vector is called vector addition. It may be accomplished with either the triangle law, the parallelogram law or the polygon law, depending on the number of vectors.
$R=\sqrt{A^2+B^2+2 A B \cos \theta}$
4. Resolution of Vectors
A vector is said to be resolved when it is broken into two orthogonal parts, usually along the x-axis and y-axis. This makes the plane analysis of motion simpler.
$A_x=A \cos \theta, \quad A_y=A \sin \theta$
5. Velocity and Acceleration in a Plane
The rate of change of the position vector is velocity, and the rate of change ofthe velocity vector is acceleration. In a plane motion, the two are represented in terms of their x and y components.
$\vec{v}=\frac{d \vec{r}}{d t}, \quad \vec{a}=\frac{d \vec{v}}{d t}$
6. Relative Velocity
Relative velocity is the velocity of one object as observed from another moving object. It is obtained by vector subtraction of their velocities.
$\vec{v}_{A B}=\vec{v}_A-\vec{v}_B$
7. Projectile Motion
Projectile motion is the motion of an object projected into the air under gravity, moving in a parabolic path. Horizontal motion occurs with constant velocity, while vertical motion has uniform acceleration due to gravity.
- Time of flight: $T=\frac{2 u \sin \theta}{g}$
- Maximum height: $H=\frac{u^2 \sin ^2 \theta}{2 g}$
- Range: $R=\frac{u^2 \sin 2 \theta}{g}$
8. Uniform Circular Motion
In circular motion, an object travels at a constant speed around a circular path, but the velocity of the object is constantly varying because of a direction change. The centripetal acceleration needed is always directed towards the centre of a circle.
$a_c=\frac{v^2}{r}=\omega^2 r$
Advantages of NCERT Exemplar Class 11 Physics Solutions Chapter 4 Motion in a Plane
The chapter Motion in a Plane presents students with two-dimensional motion through vectors, which is quite difficult to learn initially for many students. The NCERT Exemplar Class 11 Physics solutions Chapter 4 are aimed at streamlining such concepts by making the explanations and answers well-organised and easy to understand. They assist the students to be familiar with, practise, and apply physics concepts during exams with confidence.
- The solutions describe complicated concepts such as vectors and projectile motion in a very simple way. The steps are easy to follow, even for students who have only a basic knowledge of physics.
-
All numerical and theoretical questions are answered in steps. This assists the students to learn how to approach a problem and not memorise the end result.
-
The solutions are concerned with why a formula is applied and how it is applied. This will establish a solid conceptual foundation and minimise usual errors during exams.
-
Exemplar questions of the NCERT are said to be a bit higher level. These solutions are also a good method of preparing students for board exams and entrance examinations such as JEE.
-
Plane motion deals with directions and angles, and these can be best represented diagrammatically. The solutions have straightforward diagrams and vectors that simplify the learning process.
-
Regular practice with Exemplar solutions reduces fear of numerical problems. Students are assured that they can solve projectile motion and relative velocity problems.
-
A structured response will make revision time efficient and fast before exams. Important steps and formulas are easy to recall when needed.
Approach to Solve Exemplar Questions of Chapter 4 Motion in a Plane
Chapter 4 Motion in a Plane mainly deals with vectors, directions, and two-dimensional motion, which can feel tricky at first. NCERT Exemplar questions not only test the application of the formula, but also assess conceptual knowledge. By adhering to a definite and procedural method, it can become much easier and more precise to solve these questions.
- The first thing is to read the question slowly and attempt to visualise the motion. Determine the nature of the problem (i.e. vectors, relative velocity, projectile motion, or circular motion) before leaping to formulae.
- A simple diagram showing directions, angles, and axes helps a lot. Drawing even a basic sketch reduces confusion, especially in vector addition and projectile motion problems.
- Decide the x-axis and y-axis in a convenient direction, usually along the motion. This makes resolving vectors into components much simpler.
- Split velocity, displacement, or acceleration into horizontal and vertical components. Most two-dimensional problems become easy once they are reduced to one-dimensional components.
- Select formulas according to the type of motion involved. Avoid mixing up projectile motion formulas with relative velocity or circular motion formulas.
- Write each step clearly instead of jumping to the final answer. This helps avoid calculation errors and also fetches step-wise marks in exams.
- Always check units and direction of the final result. A quick review ensures the answer makes physical sense.
NCERT Exemplar Class 11 Physics Solutions Chapter-Wise
NCERT Exemplar Class 11 Physics Solutions Chapter-Wise Links provide students with a structured and organised way to study physics concepts chapter by chapter. These links make it easy to access well-explained solutions for numericals, conceptual questions, and derivations as per the latest NCERT and CBSE guidelines. They help students revise efficiently, strengthen conceptual understanding, and prepare confidently for board and competitive examinations.
NCERT Exemplar Solutions Class 11 Subject-wise
NCERT Exemplar Solutions Class 11 Subject-Wise Links offer a convenient and organised way for students to access solutions for Physics, Chemistry, and Mathematics in one place. The links enable the students to study each topic in a systematic manner with correct step-by-step directions that strictly adhere to the latest NCERT syllabus. They are suitable for rapid revision, clarity of the concepts and proper preparation in exams in all science subjects in Class 11.
NCERT Solutions for Class 11 Physics Chapter-wise
NCERT Solutions for Class 11 Physics Chapter-Wise Links help students study physics in a well-organised and systematic manner. By accessing solutions chapter by chapter, learners can easily understand concepts, numericals, and derivations as prescribed by the latest NCERT syllabus. These solutions support effective revision, strengthen fundamentals, and assist students in preparing confidently for school exams and competitive examinations.
Also, Read NCERT Solution subject-wise -
- NCERT Solutions for Class 11 Maths
- NCERT Solutions for Class 11 Chemistry
- NCERT Solutions for Class 11 Biology
Check NCERT Notes subject-wise -
- NCERT Notes Class 11 Maths
- NCERT Notes for Class 11 Physics
- NCERT Notes for Class 11 Chemistry
- NCERT Notes for Class 11 Biology
Also, check NCERT Books and NCERT Syllabus here
Frequently Asked Questions (FAQs)
Q: What is the difference between scalar and vector quantities in Motion in a Plane?
A:
In Motion in a Plane, the key difference between scalar and vector quantities is:
Scalar Quantities: These have only magnitude and no direction. Examples include speed, distance, time, and mass.
Vector Quantities: These have both magnitude and direction. Examples include velocity, displacement, acceleration, and force.
Q: What are the key concepts of relative velocity in two dimensions?
A:
Relative velocity in two dimensions is the velocity of one object relative to another, calculated by subtracting their velocity vectors. It involves breaking down velocity into horizontal and vertical components.
Q: Why is uniform circular motion considered accelerated motion?
A:
Uniform circular motion is accelerated because the direction of velocity constantly changes, resulting in centripetal acceleration towards the center, even though speed remains constant.
Q: What are some tricky numerical problems in NCERT Exemplar Physics Chapter 4?
A:
Tricky problems in Chapter 4 include:
Projectile motion: Finding range, height, or flight time.
Relative velocity: Solving with objects moving in different directions.
Circular motion: Calculating forces, tension, or angular velocity.
Acceleration in a plane: Resolving forces in 2D/3D motion.
Q: What are the real-life applications of concepts from Motion in a Plane?
A:
Real-life applications include:
Projectile motion: Sports (e.g., throwing a ball, shooting a basketball).
Relative velocity: Navigation (e.g., airplanes, trains).
Circular motion: Satellites orbiting Earth, car turns on a circular track.
Acceleration: Motion of vehicles, falling objects under gravity.
Articles
Upcoming School Exams
Popular Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters