NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections
Have you ever noticed the shape of satellite dishes, car headlights, or even the paths of planets? These shapes come from conic sections, a key topic in geometry. This chapter, conic sections, is a continuation of the last chapter of straight lines, and here we will discuss mainly four other curves: Circle, Hyperbola, Parabola, and Ellipse. “Conic” means “Cone” and “Sections” means “Intersection”. These curves are called “Conic sections” because they can be formed by the intersection of a plane with a double-napped right circular cone. Now, strengthening the basic concepts is necessary, and the Class 11 NCERT Solutions will help to command the concepts.
This Story also Contains
- NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections: Download Free PDF
- NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections: Exercise Questions
- Conic Sections Class 11 NCERT Solutions: Exercise-wise
- Class 11 Maths NCERT Chapter 10: Extra Question
- Conic Sections Class 11 Chapter 10: Topics
- Conic Sections Class 11 Solutions: Important Formulae
- Approach to Solve Questions of Conic Sections Class 11
- What Extra Should Students Study Beyond the NCERT for JEE?
- Why are Class 11 Maths Chapter 10 Conic Sections question answers important?
- NCERT Solutions for Class 11 Maths: Chapter Wise
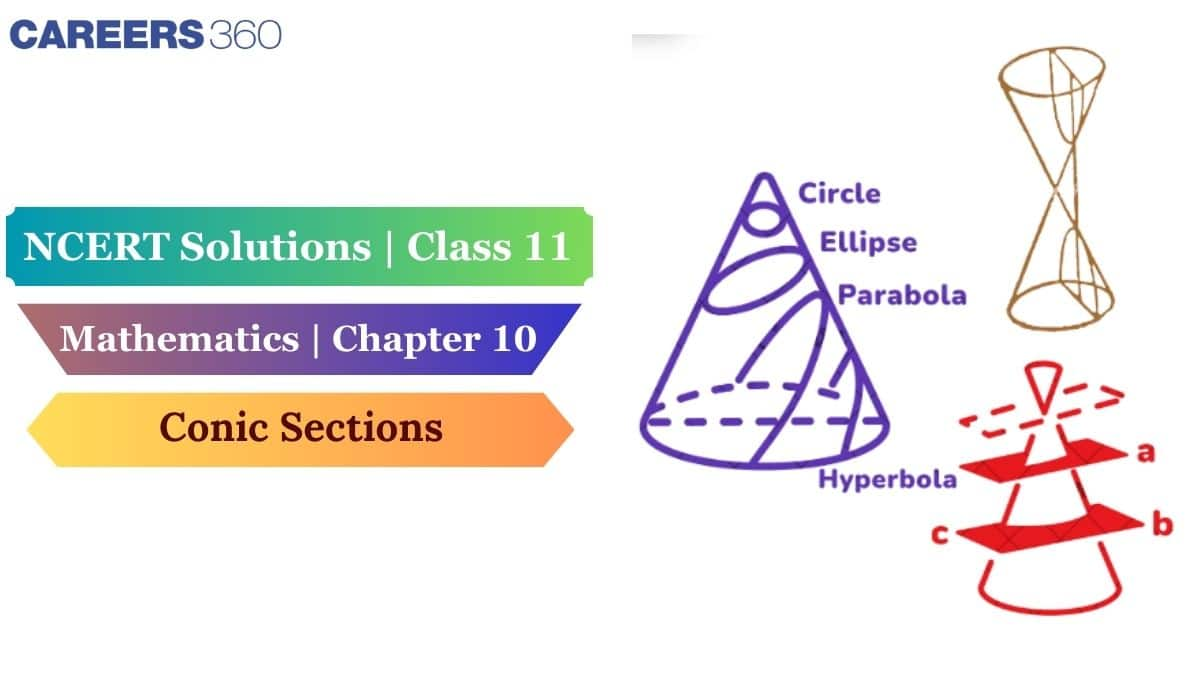
This article will explain all the Conic Sections class 11 questions and answers of NCERT based on the latest NCERT 2025-26 syllabus in detail. Many teachers recommend NCERT Solutions because they closely match the exam pattern. Conic sections NCERT solutions are not only useful for CBSE board exams but also for competitive exams like JEE Mains, JEE Advanced, VITEEE, and BITSAT. Learnings from this chapter can be used in real-life applications like wheels, satellite dishes, headlights, GPS, planetary orbits, MRI machines, and many more. For a quick revision, students can use the PDFS of Class 11 Maths NCERT solutions. Students can also use the Conic Section Class 11 Maths Chapter Notes and the NCERT Exemplar Solutions for Class 11 Maths Chapter Conic Sections to master this chapter and gain deeper knowledge. Check this NCERT article for complete syllabus coverage along with NCERT Books, Solutions, Syllabus, and Exemplar Problems with Solutions.
NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections: Download Free PDF
Careers360 brings you NCERT Class 11 Maths Chapter 10 Conic Sections solutions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF is available — click the link below to access it.
NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections: Exercise Questions
Below, you will find the NCERT Class 11 Maths Chapter 10 Conic Sections question answers explained step by step.
| Conic Sections Class 11 Question Answers Exercise: 10.1 Page Number: 158-159 Total Questions: 11 |
Question 1: Find the equation of the circle with centre (0,2) and radius 2.
Answer:
As we know, the equation of the circle with centre (h, k) and radius r is given by:
$(x-h)^2+(y-k)^2=r^2$
Here, $(h,k)=(0,2)$ and $r=2$
So the equation of the circle is:
$(x-0)^2+(y-2)^2=2^2$
$⇒x^2+y^2-4y+4=4$
$⇒x^2+y^2-4y=0$
Question 2: Find the equation of the circle with centre (–2,3) and radius 4.
Answer:
As we know,
The equation of the circle with centre (h, k) and radius r is given by:
$(x-h)^2+(y-k)^2=r^2$
Here $(h,k)=(-2,3)$ and $r=4$
So the equation of the circle is:
$(x-(-2))^2+(y-3)^2=4^2$
$⇒x^2+4x+4+y^2-6y+9=16$
$⇒x^2+y^2+4x-6y-3=0$
Question 3: Find the equation of the circle with centre $\left(\frac{1}{2},\frac{1}{4} \right )$ and radius $\frac{1}{12}$.
Answer:
As we know, the equation of the circle with centre ( h, k) and radius r is given by:
$(x-h)^2+(y-k)^2=r^2$
Here, $(h,k)=\left ( \frac{1}{2},\frac{1}{4} \right )$ and $r=\frac{1}{12}$
So the equation of the circle is:
$\left ( x-\frac{1}{2}\right )^2+\left ( y-\frac{1}{4}\right )^2=\left ( \frac{1}{12}\right )^2$
$⇒x^2-x+\frac{1}{4}+y^2-\frac{1}{2}y+\frac{1}{16}=\frac{1}{144}$
$⇒x^2+y^2-x-\frac{1}{2}y-\frac{11}{36}=0$
$⇒36x^2+36y^2-36x-18y-11=0$
Question 4: Find the equation of the circle with centre (1,1) and radius $\sqrt2$.
Answer:
As we know,
The equation of the circle with centre (h, k) and radius r is given by:
$(x-h)^2+(y-k)^2=r^2$
Here $(h,k)=(1,1)$ and $r=\sqrt{2}$
So the equation of the circle is:
$(x-1)^2+(y-1)^2=(\sqrt{2})^2$
$⇒x^2-2x+1+y^2-2y+1=2$
$⇒x^2+y^2-2x-2y=0$
Question 5: Find the equation of the circle with centre $(-a,-b)$ and radius $\sqrt{a^2 - b^2}$.
Answer:
As we know,
The equation of the circle with centre ( h, k) and radius r is given by:
$(x-h)^2+(y-k)^2=r^2$
Here $(h,k)=(-a,-b)$ and $r=\sqrt{a^2-b^2}$
So the equation of the circle is:
$(x-(-a))^2+(y-(-b))^2=(\sqrt{a^2-b^2})^2$
$⇒x^2+2ax+a^2+y^2+2by+b^2=a^2-b^2$
$⇒x^2+y^2+2ax+2by+2b^2=0$
Question 6: Find the centre and radius of the circles: $(x+5)^2 + (y-3)^2 = 36$
Answer:
As we know,
The equation of the circle with centre (h, k) and radius r is given by:
$(x-h)^2+(y-k)^2=r^2$
Here, $(x+5)^2 + (y-3)^2 = 36$
It can also be written in the form: $(x-(-5))^2 + (y-3)^2 = 6^2$
After comparing, we can see that,
$r=6$
Hence, the radius of the circle is 6.
Question 7: Find the centre and radius of the circles: $x^2 + y^2 -4x - 8y - 45 = 0$
Answer:
As we know,
The equation of the circle with centre (h, k) and radius r is given by:
$(x-h)^2+(y-k)^2=r^2$
Here $x^2 + y^2 -4x - 8y - 45 = 0$
It can also be written in the form: $(x-2)^2 + (y-4)^2 =(\sqrt{65})^2$
After comparing, we can see that,
$r=\sqrt{65}$
Hence, the radius of the circle is $\sqrt{65}$.
Question 8: Find the centre and radius of the circles: $x^2 + y^2 -8x +10y -12 = 0$
Answer:
As we know,
The equation of the circle with centre (h, k) and radius r is given by:
$(x-h)^2+(y-k)^2=r^2$
Here, $x^2 + y^2 -8x +10y -12 = 0$
It can also be written in the form: $(x-4)^2 + (y-(-5))^2 = (\sqrt{53})^2$
After comparing, we can see that
$r=\sqrt{53}$
Hence, the radius of the circle is $\sqrt{53}$.
Question 9: Find the centre and radius of the circles: $2x^2 + 2y^2 - x = 0$
Answer:
As we know,
The equation of the circle with centre (h, k) and radius r is given by:
$(x-h)^2+(y-k)^2=r^2$
Here, $2x^2 + 2y^2 - x = 0$
It can also be written in the form: $\left ( x-\frac{1}{4}\right )^2 + \left ( y-0 \right )^2 = \left ( \frac{1}{4} \right )^2$
After comparing, we can see that,
$r=\frac{1}{4}$
Hence, centre of the circle is the $\left ( \frac{1}{4},0\right )$ and radius of the circle is $\frac{1}{4}$.
Answer:
As we know,
The equation of the circle with centre (h, k) and radius r is given by:
$(x-h)^2+(y-k)^2=r^2$
Condition 1: The circle passes through points (4,1) and (6,5).
$(4-h)^2+(1-k)^2=r^2$
$(6-h)^2+(5-k)^2=r^2$
Here,
$(4-h)^2+(1-k)^2=(6-h)^2+(5-k)^2$
$⇒(4-h)^2-(6-h)^2+(1-k)^2-(5-k)^2=0$
$⇒(-2)(10-2h)+(-4)(6-2k)=0$
$⇒-20+4h-24+8k=0$
$⇒4h+8k=44$
Condition 2: Centre is on the line $4x + y = 16$.
So, $4h+k=16$
From conditions 1 and 2, we get,
$h=3$ and $k=4$
Substituting the values of h and k in condition 1, we get,
$(4-3)^2+(1-4)^2=r^2$
$⇒1+9=r^2$
$⇒r=\sqrt{10}$
$\therefore$ Final Equation of the circle is:
$(x-3)^2+(y-4)^2=(\sqrt{10})^2$
$⇒x^2-6x+9+y^2-8y+16=10$
$⇒x^2+y^2-6x-8y+15=0$
Answer:
As we know,
The equation of the circle with centre ( h, k) and radius r is given by ;
$(x-h)^2+(y-k)^2=r^2$
Condition 1: The circle passes through points (2,3) and (–1,1).
$(2-h)^2+(3-k)^2=r^2$
$(-1-h)^2+(1-k)^2=r^2$
Here,
$(2-h)^2+(3-k)^2=(-1-h)^2+(1-k)^2$
$⇒(2-h)^2-(-1-h)^2+(3-k)^2-(1-k)^2=0$
$⇒(3)(1-2h)+(2)(4-2k)=0$
$⇒3-6h+8-4k=0$
$⇒6h+4k=11$
Condition 2: The centre is on the line $x - 3y - 11 = 0$
So, $h-3k=11$
From condition 1 and condition 2, we get,
$h=\frac{7}{2}$ and $k=\frac{-5}{2}$
Substituting the values of h and k in condition 1, we get,
$\left ( 2-\frac{7}{2}\right )^2+\left (3+\frac{5}{2}\right )^2=r^2$
$⇒\frac{9}{4}+\frac{121}{4}=r^2$
$⇒r^2=\frac{130}{4}$
$\therefore$ Final Equation of the circle is:
$\left(x-\frac{7}{2}\right )^2+\left(y+\frac{5}{2}\right)^2=\frac{130}{4}$
$⇒x^2-7x+\frac{49}{4}+y^2+5y+\frac{25}{4}=\frac{130}{4}$
$⇒x^2+y^2-7x+5y-\frac{56}{4}=0$
$⇒x^2+y^2-7x+5y-14=0$
Question 12: Find the equation of the circle with radius 5, whose centre lies on the x-axis and passes through the point (2,3).
Answer:
As we know,
The equation of the circle with centre (h, k) and radius r is given by:
$(x-h)^2+(y-k)^2=r^2$
So let the circle be,
$(x-h)^2+(y-k)^2=r^2$
Since its radius is 5 and its centre lies on the x-axis,
$(x-h)^2+(y-0)^2=5^2$
And since it passes through the point (2,3).
$(2-h)^2+(3-0)^2=5^2$
$⇒(2-h)^2=25-9$
$⇒(2-h)^2=16$
$⇒(2-h)=4$ or, $(2-h)=-4$
$⇒h=-2$ or, $h=6$
When $h=-2$, the equation of the circle is:
$(x-(-2))^2+(y-0)^2=5^2$
$⇒x^2+4x+4+y^2=25$
$⇒x^2+y^2+4x-21=0$
When $h=6$, the equation of the circle is:
$(x-6)^2+(y-0)^2=5^2$
$⇒x^2-12x+36+y^2=25$
$⇒x^2+y^2-12x+11=0$
Question 13: Find the equation of the circle passing through (0,0) and making intercepts a and b on the coordinate axes.
Answer:
Let the equation of circle be $(x-h)^2+(y-k)^2=r^2$
Now, since this circle passes through (0, 0),
$(0-h)^2+(0-k)^2=r^2$
$⇒h^2+k^2=r^2$
Now, this circle makes an intercept of a and b on the coordinate axes. it means the circle passes through the points (a, 0) and (0, b).
So,
$(a-h)^2+(0-k)^2=r^2$
$⇒a^2-2ah+h^2+k^2=r^2$
$⇒a^2-2ah=0$
$⇒a(a-2h)=0$
$⇒a=0$ or $a-2h=0$
Since $a\neq0$, So, $a-2h=0$
$⇒h=\frac{a}{2}$
Similarly,
$(0-h)^2+(b-k)^2=r^2$
$⇒h^2+b^2-2bk+k^2=r^2$
$⇒b^2-2bk=0$
$⇒b(b-2k)=0$
Since b is not equal to zero.
$k=\frac{b}{2}$
So the final equation of the Circle is:
$\left ( x-\frac{a}{2} \right )^2+\left ( y-\frac{b}{2} \right )^2=\left ( \frac{a}{2} \right )^2+\left ( \frac{b}{2} \right )^2$
$⇒x^2-ax+\frac{a^2}{4}+y^2-bx+\frac{b^2}{4}=\frac{a^2}{4}+\frac{b^2}{4}$
$⇒x^2+y^2-ax-bx=0$
Question 14: Find the equation of a circle with a centre (2,2) and passes through the point (4,5).
Answer:
Let the equation of the circle be:
$(x-h)^2+(y-k)^2=r^2$
Now, since the centre of the circle is (2,2), our equation becomes:
$(x-2)^2+(y-2)^2=r^2$
Now, since this passes through the point (4,5),
$(4-2)^2+(5-2)^2=r^2$
$⇒4+9=r^2$
$⇒r^2=13$
Hence, The Final equation of the circle becomes:
$(x-2)^2+(y-2)^2=13$
$⇒x^2-4x+4+y^2-4y+4=13$
$⇒x^2+y^2-4x-4y-5=0$
Question 15: Does the point (–2.5, 3.5) lie inside, outside or on the circle $x^2 + y^2 = 25$?
Answer:
Given, a circle $x^2 + y^2 = 25$
As we can see, the centre of the circle is (0, 0).
Now the distance(d) between (0,0) and (–2.5, 3.5) is:
$d=\sqrt{(-2.5-0)^2+(3.5-0)^2}$
$⇒d=\sqrt{6.25+12.25}$
$⇒d=\sqrt{18.5}\approx 4.3<5$
Since the distance between the given point and the centre of the circle is less than the radius of the circle, the point lies inside the circle.
| Conic Sections Class 11 Question Answers Exercise: 10.2 Page Number: 186-187 Total Questions: 12 |
Answer:
Given a parabola with equation $y^2 =12x$
This is a parabola of the form $y^2=4ax$, which opens towards the right.
So, by comparing the given parabola equation with the standard equation, we get,
$4a=12$
$⇒a=3$
Hence,
Coordinates of the focus :
$(a,0)=(3,0)$
Axis of the parabola:
It can be seen that the axis of this parabola is the X-axis.
The equation of the directrix:
$x=-a$
$\Rightarrow x=-3$
$\Rightarrow x+3=0$
The length of the latus rectum:
$4a=4(3)=12$
Answer:
Given a parabola with equation $x^2 =6y$
This is a parabola of the form $x^2=4ay$, which opens upward.
So, by comparing the given parabola equation with the standard equation, we get,
$4a=6$
$⇒a=\frac{3}{2}$
Hence,
Coordinates of the focus :
$(0,a)=\left (0,\frac{3}{2}\right)$
Axis of the parabola:
It can be seen that the axis of this parabola is the Y-axis.
The equation of the directrix:
$y=-a$
$\Rightarrow y=-\frac{3}{2}$
$\Rightarrow y+\frac{3}{2}=0$
The length of the latus rectum:
$4a=4(\frac{3}{2})=6$
Answer:
Given a parabola with equation $y^2 =-8x$
This is a parabola of the form $y^2=-4ax$, which opens towards the left.
So, by comparing the given parabola equation with the standard equation, we get,
$-4a=-8$
$⇒a=2$
Hence,
Coordinates of the focus :
$(-a,0)=(-2,0)$
Axis of the parabola:
It can be seen that the axis of this parabola is the X-axis.
The equation of the directrix:
$x=a$
$\Rightarrow x=2$
$\Rightarrow x-2=0$
The length of the latus rectum:
$4a=4(2)=8$
Answer:
Given a parabola with equation $x^2 =-16y$
This is a parabola of the form $x^2=-4ay$, which opens downward.
So, by comparing the given parabola equation with the standard equation, we get,
$-4a=-16$
$⇒a=4$
Hence,
Coordinates of the focus :
$(0,-a)=(0,-4)$
Axis of the parabola:
It can be seen that the axis of this parabola is the Y-axis.
The equation of the directrix
$y=a$
$\Rightarrow y=4$
$\Rightarrow y-4=0$
The length of the latus rectum:
$4a=4\times4=16$
Answer:
Given a parabola with equation $y^2 =10x$
This is a parabola of the form $y^2=4ax$, which opens towards the right.
So, by comparing the given parabola equation with the standard equation, we get,
$4a=10$
$⇒a=\frac{10}{4}=\frac{5}{2}$
Hence,
Coordinates of the focus :
$(a,0)=\left(\frac{5}{2},0\right)$
Axis of the parabola:
It can be seen that the axis of this parabola is the X-axis.
The equation of the directrix:
$x=-a$
$\Rightarrow x=-\frac{5}{2}$
$\Rightarrow x+\frac{5}{2}=0$
$\Rightarrow 2x+5=0$
The length of the latus rectum:
$4a=4\times(\frac{5}{2})=10$
Answer:
Given a parabola with an equation $x^2 =-9y$
This is a parabola of the form $x^2=-4ay$, which opens downward.
So, by comparing the given parabola equation with the standard equation, we get,
$-4a=-9$
$⇒a=\frac{9}{4}$
Hence,
Coordinates of the focus :
$(0,-a)=\left (0,-\frac{9}{4}\right)$
Axis of the parabola:
It can be seen that the axis of this parabola is the Y-axis.
The equation of the directrix:
$y=a$
$\Rightarrow y=\frac{9}{4}$
$\Rightarrow y-\frac{9}{4}=0$
The length of the latus rectum:
$4a=4\left(\frac{9}{4}\right)=9$
Question 7: Find the equation of the parabola that satisfies the given conditions: Focus (6,0); directrix $x = - 6$
Answer:
Given, in a parabola,
Focus : (6,0) And Directrix : $x = - 6$
Here,
Focus is of the form (a, 0), which means it lies on the X-axis.
Directrix is of the form $x=-a$, which means it lies left to the Y-Axis.
These are the conditions when the standard equation of a parabola is. $y^2=4ax$
Hence, the Equation of the Parabola is $y^2=4ax$
Here, it can be seen that: $a=6$
Hence, the Equation of the Parabola is:
$\Rightarrow y^2=4ax$
$\Rightarrow y^2=4(6)x$
$\Rightarrow y^2=24x$ .
Question 8: Find the equation of the parabola that satisfies the given conditions: Focus (0,–3); directrix $y = 3$
Answer:
Given, in a parabola,
Focus : Focus (0,–3); directrix $y = 3$
Here,
Focus is of the form (0, -a), which means it lies on the Y-axis.
Directrix is of the form $y=a$, which means it lies above the X-axis.
These are the conditions when the standard equation of a parabola is $x^2=-4ay$. Hence, the Equation of the Parabola is
$x^2=-4ay$
Here, it can be seen that:
$a=3$
Hence, the Equation of the Parabola is:
$\Rightarrow x^2=-4ay$
$\Rightarrow x^2=-4(3)y$
$\Rightarrow x^2=-12y$
Question 9: Find the equation of the parabola that satisfies the given conditions: Vertex (0,0); focus (3,0)
Answer:
Given,
Vertex (0,0) and focus (3,0)
As the vertex of the parabola is (0,0) and the focus lies on the positive X-axis, the parabola will open towards the right. The standard equation of such a parabola is
$y^2=4ax$
Here, it can be seen that $a=3$
So, the equation of a parabola is
$\Rightarrow y^2=4ax$
$\Rightarrow y^2=4(3)x$
$\Rightarrow y^2=12x$
Question 10: Find the equation of the parabola that satisfies the given conditions: Vertex (0,0); focus (-2,0)
Answer:
Given: Vertex (0,0) and focus (-2,0)
As the vertex of the parabola is (0,0) and the focus lies on the negative X-axis, the parabola will open towards the left, and the standard equation of such a parabola is $y^2=-4ax$
Here, it can be seen that $a=2$
So, the equation of a parabola is:
$\Rightarrow y^2=-4ax$
$\Rightarrow y^2=-4(2)x$
$\Rightarrow y^2=-8x$
Question 11: Find the equation of the parabola that satisfies the given conditions: Vertex (0,0) passing through (2,3) and axis is along the x-axis.
Answer:
Given
The Vertex of the parabola is (0,0).
The parabola is passing through (2,3), and the axis is along the x-axis; it will open towards the right. and the standard equation of such a parabola is
$y^2=4ax$
Now, since it passes through (2,3)
$3^2=4a(2)$
$⇒9=8a$
$⇒a=\frac{9}{8}$
So the Equation of the Parabola is:
$\Rightarrow y^2=4\left(\frac{9}{8}\right)x$
$\Rightarrow y^2=\left(\frac{9}{2}\right)x$
$\Rightarrow 2y^2=9x$
Answer:
Given a parabola with Vertex (0,0), passing through (5,2) and symmetric with respect to the y-axis.
Since the parabola is symmetric with respect to the Y-axis, its axis will be the Y-axis. And since it passes through the point (5,2), it must go through the first quadrant.
So the standard equation of such a parabola is
$x^2=4ay$
Now, since this parabola is passing through (5,2)
$5^2=4a(2)$
$⇒25=8a$
$⇒a=\frac{25}{8}$
Hence, the equation of the parabola is:
$\Rightarrow x^2=4\left ( \frac{25}{8} \right )y$
$\Rightarrow x^2=\left ( \frac{25}{2} \right )y$
$\Rightarrow 2x^2=25y$
| Conic Sections Class 11 Question Answers Exercise: 10.3 Page Number: 195 Total Questions: 20 |
Answer:
The equation of the ellipse $\frac{x^2}{36} + \frac{y^2}{16} = 1$
As we can see from the equation, the major axis is along the X-axis, and the minor axis is along the Y-axis.
On comparing the given equation with the standard equation of an ellipse, which is
$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$
We get,
$a=6$ and $b=4$
So,
$c=\sqrt{a^2-b^2}=\sqrt{6^2-4^2}=\sqrt{20}=2\sqrt5$
Hence,
Coordinates of the foci:
$(c,0)$ and $(-c,0)=(2\sqrt{5},0)$ and $(-2\sqrt{5},0)$
The vertices:
$(a,0)$ and $(-a,0)=(6,0)$ and $(-6,0)$
The length of the major axis:
$2a=2(6)=12$
The length of the minor axis:
$2b=2(4)=8$
The eccentricity :
$e=\frac{c}{a}=\frac{2\sqrt{5}}{6}=\frac{\sqrt{5}}{3}$
The length of the latus rectum:
$\frac{2b^2}{a}=\frac{2(4)^2}{6}=\frac{32}{6}=\frac{16}{3}$
Answer:
The equation of the ellipse $\frac{x^2}{4} + \frac{y^2}{25} =1$
As we can see from the equation, the major axis is along the Y-axis, and the minor axis is along the X-axis.
On comparing the given equation with the standard equation of such an ellipse, which is
$\frac{x^2}{b^2} + \frac{y^2}{a^2} = 1$
We get,
$a=5$ and $b=2$
So,
$c=\sqrt{a^2-b^2}=\sqrt{5^2-2^2}=\sqrt{21}$
Hence,
Coordinates of the foci:
$(0,c)$ and $(0,-c)=(0,\sqrt{21})$ and $(0,-\sqrt{21})$
The vertices:
$(0,a)$ and $(0,-a)=(0,5)$ and $(0,-5)$
The length of the major axis:
$2a=2(5)=10$
The length of the minor axis:
$2b=2(2)=4$
The eccentricity :
$e=\frac{c}{a}=\frac{\sqrt{21}}{6}$
The length of the latus rectum:
$\frac{2b^2}{a}=\frac{2(2)^2}{5}=\frac{8}{5}$
Answer:
The equation of the ellipse $\frac{x^2}{16} + \frac{y^2}{9} = 1$
As we can see from the equation, the major axis is along the X-axis, and the minor axis is along the Y-axis.
On comparing the given equation with the standard equation of an ellipse, which is
$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$
We get,
$a=4$ and $b=3$
So,
$c=\sqrt{a^2-b^2}=\sqrt{4^2-3^2}=\sqrt7$
Hence, the Coordinates of the foci:
$(c,0)$ and $(-c,0)=(\sqrt{7},0)$ and $(-\sqrt{7},0)$
The vertices:
$(a,0)$ and $(-a,0)=(4,0)$ and $(-4,0)$
The length of the major axis:
$2a=2(4)=8$
The length of the minor axis:
$2b=2(3)=6$
The eccentricity :
$e=\frac{c}{a}=\frac{\sqrt{7}}{4}$
The length of the latus rectum:
$\frac{2b^2}{a}=\frac{2(3)^2}{4}=\frac{18}{4}=\frac{9}{2}$
Answer:
The equation of the ellipse $\frac{x^2}{25} + \frac{y^2}{100} = 1$
As we can see from the equation, the major axis is along the Y-axis, and the minor axis is along the X-axis.
On comparing the given equation with the standard equation of such an ellipse, which is
$\frac{x^2}{b^2} + \frac{y^2}{a^2} = 1$
We get,
$a=10$ and $b=5$
So,
$c=\sqrt{a^2-b^2}=\sqrt{10^2-5^2}=\sqrt{75}=5\sqrt3$
Hence, the Coordinates of the foci:
$(0,c)$ and $(0,-c)=(0,5\sqrt{3})$ and $(0,-5\sqrt{3})$
The vertices:
$(0,a)$ and $(0,-a)=(0,10)$ and $(0,-10)$
The length of the major axis:
$2a=2(10)=20$
The length of the minor axis:
$2b=2(5)=10$
The eccentricity :
$e=\frac{c}{a}=\frac{5\sqrt{3}}{10}=\frac{\sqrt{3}}{2}$
The length of the latus rectum:
$\frac{2b^2}{a}=\frac{2(5)^2}{10}=\frac{50}{10}=5$
Answer:
The equation of ellipse $\frac{x^2}{49} + \frac{y^2}{36} = 1\Rightarrow \frac{x^2}{7^2} + \frac{y^2}{6^2} = 1$
As we can see from the equation, the major axis is along the X-axis, and the minor axis is along the Y-axis.
On comparing the given equation with the standard equation of an ellipse, which is
$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$
We get,
$a=7$ and $b=6$ .
So,
$c=\sqrt{a^2-b^2}=\sqrt{7^2-6^2}=\sqrt{13}$
Hence, the Coordinates of the foci:
$(c,0)\:and\:(-c,0)=(\sqrt{13},0)\:and\:(-\sqrt{13},0)$
The vertices:
$(a,0)\:and\:(-a,0)=(7,0)\:and\:(-7,0)$
The length of the major axis:
$2a=2(7)=14$
The length of the minor axis:
$2b=2(6)=12$
The eccentricity :
$e=\frac{c}{a}=\frac{\sqrt{13}}{7}$
The length of the latus rectum:
$\frac{2b^2}{a}=\frac{2(6)^2}{7}=\frac{72}{7}$
Answer:
The equation of the ellipse $\frac{x^2}{100} + \frac{y^2}{400} =1\Rightarrow \frac{x^2}{10^2} + \frac{y^2}{20^2} =1$
As we can see from the equation, the major axis is along the Y-axis, and the minor axis is along the X-axis.
On comparing the given equation with the standard equation of such an ellipse, which is
$\frac{x^2}{b^2} + \frac{y^2}{a^2} = 1$
We get,
$a=20$ and $b=10$ .
So,
$c=\sqrt{a^2-b^2}=\sqrt{20^2-10^2}$
$⇒c=\sqrt{300}=10\sqrt{3}$
Hence,
Coordinates of the foci:
$(0,c)\:and\:(0,-c)=(0,10\sqrt{3})\:and\:(0,-10\sqrt{3})$
The vertices:
$(0,a)\:and\:(0,-a)=(0,20)\:and\:(0,-20)$
The length of the major axis:
$2a=2(20)=40$
The length of the minor axis:
$2b=2(10)=20$
The eccentricity :
$e=\frac{c}{a}=\frac{10\sqrt{3}}{20}=\frac{\sqrt{3}}{2}$
The length of the latus rectum:
$\frac{2b^2}{a}=\frac{2(10)^2}{20}=\frac{200}{20}=10$
Answer:
The equation of the ellipse $36x^2 + 4y^2 =144$
$\Rightarrow \frac{36}{144}x^2 + \frac{4}{144}y^2 =1$
$\Rightarrow \frac{1}{4}x^2 + \frac{1}{36}y^2 =1$
$\frac{x^2}{2^2} + \frac{y^2}{6^2} = 1$
As we can see from the equation, the major axis is along the Y-axis, and the minor axis is along the X-axis.
On comparing the given equation with the standard equation of such an ellipse, which is
$\frac{x^2}{b^2} + \frac{y^2}{a^2} = 1$
We get,
$a=6$ and $b=2$ .
So,
$c=\sqrt{a^2-b^2}=\sqrt{6^2-2^2}$
$⇒c=\sqrt{32}=4\sqrt{2}$
Hence, the Coordinates of the foci:
$(0,c)\:and\:(0,-c)=(0,4\sqrt{2})\:and\:(0,-4\sqrt{2})$
The vertices:
$(0,a)\:and\:(0,-a)=(0,6)\:and\:(0,-6)$
The length of the major axis:
$2a=2(6)=12$
The length of the minor axis:
$2b=2(2)=4$
The eccentricity :
$e=\frac{c}{a}=\frac{4\sqrt{2}}{6}=\frac{2\sqrt{2}}{3}$
The length of the latus rectum:
$\frac{2b^2}{a}=\frac{2(2)^2}{6}=\frac{8}{6}=\frac{4}{3}$
Answer:
The equation of the ellipse $16x^2 + y^2 = 16$
$\frac{16x^2}{16} + \frac{y^2}{16} = 1$
$\frac{x^2}{1^2} + \frac{y^2}{4^2} = 1$
As we can see from the equation, the major axis is along the Y-axis, and the minor axis is along the X-axis.
On comparing the given equation with the standard equation of such an ellipse, which is
$\frac{x^2}{b^2} + \frac{y^2}{a^2} = 1$
We get,
$a=4$ and $b=1$ .
So,
$c=\sqrt{a^2-b^2}=\sqrt{4^2-1^2}$
$⇒c=\sqrt{15}$
Hence, the Coordinates of the foci:
$(0,c)\:and\:(0,-c)=(0,\sqrt{15})\:and\:(0,-\sqrt{15})$
The vertices:
$(0,a)\:and\:(0,-a)=(0,4)\:and\:(0,-4)$
The length of the major axis:
$2a=2(4)=8$
The length of the minor axis:
$2b=2(1)=2$
The eccentricity :
$e=\frac{c}{a}=\frac{\sqrt{15}}{4}$
The length of the latus rectum:
$\frac{2b^2}{a}=\frac{2(1)^2}{4}=\frac{2}{4}=\frac{1}{2}$
Answer:
The equation of the ellipse $4x^2 + 9y^2 =36$
$⇒\frac{4x^2}{36} + \frac{9y^2}{36} = 1$
$⇒\frac{x^2}{9} + \frac{y^2}{4} = 1$
$⇒\frac{x^2}{3^2} + \frac{y^2}{2^2} = 1$
As we can see from the equation, the major axis is along the X-axis, and the minor axis is along the Y-axis.
On comparing the given equation with the standard equation of an ellipse, which is
$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$
We get,
$a=3$ and $b=2$ .
So,
$c=\sqrt{a^2-b^2}=\sqrt{3^2-2^2}$
$⇒c=\sqrt{5}$
Hence, the Coordinates of the foci:
$(c,0)\:and\:(-c,0)=(\sqrt{5},0)\:and\:(-\sqrt{5},0)$
The vertices:
$(a,0)\:and\:(-a,0)=(3,0)\:and\:(-3,0)$
The length of the major axis:
$2a=2(3)=6$
The length of the minor axis:
$2b=2(2)=4$
The eccentricity :
$e=\frac{c}{a}=\frac{\sqrt{5}}{3}$
The length of the latus rectum:
$\frac{2b^2}{a}=\frac{2(2)^2}{3}=\frac{8}{3}$
Question 10: Find the equation for the ellipse that satisfies the given conditions: Vertices (± 5, 0), foci (± 4, 0)
Answer:
Given, in an ellipse,
Vertices (± 5, 0), foci (± 4, 0)
Here Vertices and focus of the ellipse are on the X-axis, so the major axis of this ellipse will be the X-axis.
Therefore, the equation of the ellipse will be of the form:
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
Where $a$ and $b$ are the length of the semimajor axis and semiminor axis, respectively.
So, on comparing standard parameters( vertices and foci) with the given one, we get
$a=5$ and $c=4$
Now, as we know the relation,
$a^2=b^2+c^2$
$⇒b^2=a^2-c^2$
$⇒b=\sqrt{a^2-c^2}$
$⇒b=\sqrt{5^2-4^2}$
$⇒b=\sqrt{9}$
$⇒b=3$
Hence, The Equation of the ellipse will be :
$\frac{x^2}{5^2}+\frac{y^2}{3^2}=1$
$⇒\frac{x^2}{25}+\frac{y^2}{9}=1$ .
Question 11: Find the equation for the ellipse that satisfies the given conditions: Vertices (0, ± 13), foci (0, ± 5)
Answer:
Given, in an ellipse, Vertices (0, ± 13), foci (0, ± 5)
Here Vertices and focus of the ellipse are on the Y-axis, so the major axis of this ellipse will be the Y-axis.
Therefore, the equation of the ellipse will be of the form:
$\frac{x^2}{b^2}+\frac{y^2}{a^2}=1$
Where $a$ and $b$ are the length of the semimajor axis and semiminor axis, respectively.
So, on comparing standard parameters( vertices and foci) with the given one, we get
$a=13$ and $c=5$
Now, as we know the relation,
$a^2=b^2+c^2$
$⇒b^2=a^2-c^2$
$⇒b=\sqrt{a^2-c^2}$
$⇒b=\sqrt{13^2-5^2}$
$⇒b=\sqrt{169-25}$
$⇒b=\sqrt{144}$
$⇒b=12$
Hence, The Equation of the ellipse will be :
$\frac{x^2}{12^2}+\frac{y^2}{13^3}=1$
$⇒\frac{x^2}{144}+\frac{y^2}{169}=1$ .
Question 12: Find the equation for the ellipse that satisfies the given conditions: Vertices (± 6, 0), foci (± 4, 0)
Answer:
Given, in an ellipse, Vertices (± 6, 0), foci (± 4, 0)
Here Vertices and focus of the ellipse are on the X-axis, so the major axis of this ellipse will be the X-axis.
Therefore, the equation of the ellipse will be of the form:
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
Where $a$ and $b$ are the length of the semimajor axis and semiminor axis, respectively.
So, on comparing standard parameters( vertices and foci) with the given one, we get
$a=6$ and $c=4$
Now, as we know the relation,
$a^2=b^2+c^2$
$⇒b^2=a^2-c^2$
$⇒b=\sqrt{a^2-c^2}$
$⇒b=\sqrt{6^2-4^2}$
$⇒b=\sqrt{36-16}$
$⇒b=\sqrt{20}$
Hence, The Equation of the ellipse will be :
$\frac{x^2}{6^2}+\frac{y^2}{(\sqrt{20})^2}=1$
$⇒\frac{x^2}{36}+\frac{y^2}{20}=1$ .
Answer:
Given, in an ellipse,
Ends of the major axis (± 3, 0), ends of minor axis (0, ± 2)
Here, the major axis of this ellipse will be the X-axis.
Therefore, the equation of the ellipse will be of the form:
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
Where $a$ and $b$ are the lengths of the semimajor axis and semiminor axis, respectively.
So, on comparing standard parameters( ends of the major and minor axis ) with the given ones, we get $a=3$ and $b=2$
Hence, The Equation of the ellipse will be :
$\frac{x^2}{3^2}+\frac{y^2}{2^2}=1$
$⇒\frac{x^2}{9}+\frac{y^2}{4}=1$ .
Answer:
Given, in an ellipse,
Ends of the major axis (0, ± $\sqrt{5}$ ), ends of minor axis (± 1, 0)
Here, the major axis of this ellipse will be the Y-axis.
Therefore, the equation of the ellipse will be of the form:
$\frac{x^2}{b^2}+\frac{y^2}{a^2}=1$
Where $a$ and $b$ are the lengths of the semimajor axis and semiminor axis, respectively.
So on comparing standard parameters( ends of the major and minor axis ) with the given one, we get $a=\sqrt{5}$ and $b=1$
Hence, The Equation of the ellipse will be :
$\frac{x^2}{1^2}+\frac{y^2}{(\sqrt{5})^2}=1$
$⇒\frac{x^2}{1}+\frac{y^2}{5}=1$ .
Question 15: Find the equation for the ellipse that satisfies the given conditions: Length of major axis 26, foci (± 5, 0)
Answer:
Given, in an ellipse,
Length of major axis 26, foci (± 5, 0)
Here, the focus of the ellipse is on the X-axis, so the major axis of this ellipse will be the X-axis.
Therefore, the equation of the ellipse will be of the form:
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
Where $a$ and $b$ are the lengths of the semimajor axis and semiminor axis, respectively.
So on comparing standard parameters( Length of semimajor axis and foci) with the given one, we get $2a=26\Rightarrow a=13$ and $c=5$
Now, as we know the relation,
$a^2=b^2+c^2$
$⇒b^2=a^2-c^2$
$⇒b=\sqrt{a^2-c^2}$
$⇒b=\sqrt{13^2-5^2}$
$⇒b=\sqrt{144}$
$⇒b=12$
Hence, The Equation of the ellipse will be :
$\frac{x^2}{13^2}+\frac{y^2}{12^2}=1$
$⇒\frac{x^2}{169}+\frac{y^2}{144}=1$ .
Question 16: Find the equation for the ellipse that satisfies the given conditions: Length of minor axis 16, foci (0, ± 6).
Answer:
Given, in an ellipse,
Length of minor axis 16, foci (0, ± 6).
Here, the focus of the ellipse is on the Y-axis, so the major axis of this ellipse will be the Y-axis.
Therefore, the equation of the ellipse will be of the form:
$\frac{x^2}{b^2}+\frac{y^2}{a^2}=1$
Where $a$ and $b$ are the lengths of the semimajor axis and semiminor axis, respectively.
So, on comparing standard parameters( length of semi-minor axis and foci) with the given ones, we get
$2b=16$
$\Rightarrow b=8$
and $c=6$
Now, as we know the relation,
$a^2=b^2+c^2$
$⇒a=\sqrt{b^2+c^2}$
$⇒a=\sqrt{8^2+6^2}$
$⇒a=\sqrt{64+36}$
$⇒a=\sqrt{100}$
$⇒a=10$
Hence, The Equation of the ellipse will be :
$\frac{x^2}{8^2}+\frac{y^2}{10^3}=1$
$⇒\frac{x^2}{64}+\frac{y^2}{100}=1$ .
Question 17: Find the equation for the ellipse that satisfies the given conditions: Foci (± 3, 0), a = 4
Answer:
Given, in an ellipse, V Foci (± 3, 0), a = 4
Here, foci of the ellipse is in the X-axis, so the major axis of this ellipse will be the X-axis.
Therefore, the equation of the ellipse will be of the form:
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
Where $a$ and $b$ are the length of the semimajor axis and semiminor axis, respectively.
So, on comparing standard parameters( vertices and foci) with the given one, we get
$a=4$ and $c=3$
Now, as we know the relation,
$a^2=b^2+c^2$
$⇒b^2=a^2-c^2$
$⇒b=\sqrt{a^2-c^2}$
$⇒b=\sqrt{4^2-3^2}$
$⇒b=\sqrt{7}$
Hence, The Equation of the ellipse will be :
$\frac{x^2}{4^2}+\frac{y^2}{(\sqrt{7})^2}=1$
$⇒\frac{x^2}{16}+\frac{y^2}{7}=1$ .
Question 18: Find the equation for the ellipse that satisfies the given conditions: b = 3, c = 4, centre at the origin; foci on the x-axis.
Answer:
Given: In an ellipse, b = 3, c = 4, centre at the origin; foci on the x-axis.
Here, foci of the ellipse is in the X-axis, so the major axis of this ellipse will be the X-axis.
Therefore, the equation of the ellipse will be of the form:
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
Where $a$ and $b$ are the length of the semimajor axis and semiminor axis, respectively.
Also Given,
$b=3$ and $c=4$
Now, as we know the relation,
$a^2=b^2+c^2$
$⇒a^2=3^2+4^2$
$⇒a^2=25$
$⇒a=5$
Hence, The Equation of the ellipse will be :
$\frac{x^2}{5^2}+\frac{y^2}{3^2}=1$
$⇒\frac{x^2}{25}+\frac{y^2}{9}=1$ .
Answer:
Given, in an ellipse
Centre at (0,0), major axis on the y-axis and passes through the points (3, 2) and (1,6).
Since the major axis of this ellipse is on the Y-axis, the equation of the ellipse will be of the form:
$\frac{x^2}{b^2}+\frac{y^2}{a^2}=1$
Where $a$ and $b$ are the length of the semimajor axis and semiminor axis, respectively.
Now, since the ellipse passes through points (3, 2)
$\frac{3^2}{b^2}+\frac{2^2}{a^2}=1$
$⇒{9a^2+4b^2}={a^2b^2}$
Since the ellipse also passes through points (1, 6).
$\frac{1^2}{b^2}+\frac{6^2}{a^2}=1$
$⇒a^2+36b^2=a^2b^2$
On solving these two equations, we get,
$a^2=40$ and $b^2=10$
Thus, the equation of the ellipse will be
$\frac{x^2}{10}+\frac{y^2}{40}=1$
Answer:
Given, in an ellipse
Major axis is on the x-axis and passes through the points (4,3) and (6,2).
Since the major axis of this ellipse is on the X-axis, the equation of the ellipse will be of the form:
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
Where $a$ and $b$ are the length of the semimajor axis and semiminor axis, respectively.
Now, since the ellipse passes through the point (4,3)
$\frac{4^2}{a^2}+\frac{3^2}{b^2}=1$
$⇒{16b^2+9a^2}={a^2b^2}$
Since the ellipse also passes through the point (6, 2).
$\frac{6^2}{a^2}+\frac{2^2}{b^2}=1$
$⇒4a^2+36b^2=a^2b^2$
On solving these two equations, we get,
$a^2=52$ and $b^2=13$
Thus, the equation of the ellipse will be
$\frac{x^2}{52}+\frac{y^2}{13}=1$
| Conic Sections Class 11 Question Answers Exercise: 10.4 Page Number: 202 Total Questions: 15 |
Answer:
Given a Hyperbola equation, $\frac{x^2}{16} - \frac{y^2}{9} = 1$
It can also be written as $\frac{x^2}{4^2} - \frac{y^2}{3^2} = 1$
Comparing this equation with the standard equation of the hyperbola, we get,
$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$
We get,
$a=4$ and $b=3$
Now, as we know the relation in a hyperbola,
$c^2=a^2+b^2$
$⇒c=\sqrt{a^2+b^2}$
$⇒c=\sqrt{4^2+3^2}$
$⇒c=5$
Here, as we can see from the equation, the axis of the hyperbola is the X-axis.
So, the Coordinates of the foci are:
$(c,0)$ and $(-c,0)=(5,0)$ and $(-5,0)$
The Coordinates of the vertices:
$(a,0)$ and $(-a,0)=(4,0)$ and $(-4,0)$
The Eccentricity:
$e=\frac{c}{a}=\frac{5}{4}$
The Length of the latus rectum :
$\frac{2b^2}{a}=\frac{2(3)^2}{4}=\frac{18}{4}=\frac{9}{2}$
Question 2: Find the coordinates of the foci and the vertices, the eccentricity and the length of the latus rectum of the hyperbolas: $\frac{y^2}{9} - \frac{x^2}{27} = 1$
Answer:
Given a Hyperbola equation, $\frac{y^2}{9} - \frac{x^2}{27} = 1$
It can also be written as $\frac{y^2}{3^2} - \frac{x^2}{(\sqrt{27})^2} = 1$
Comparing this equation with the standard equation of the hyperbola:
$\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1$
We get,
$a=3$ and $b=\sqrt{27}$
Now, as we know the relation in a hyperbola,
$c^2=a^2+b^2$
$⇒c=\sqrt{a^2+b^2}$
$⇒c=\sqrt{3^2+(\sqrt{27})^2}$
$⇒c=\sqrt{36}$
$⇒c=6$
Here, as we can see from the equation, the axis of the hyperbola is the Y-axis.
So, the Coordinates of the foci are:
$(0,c)$ and $(0,-c)=(0,6)$ and $(0,-6)$
The Coordinates of the vertices:
$(0,a)$ and $(0,-a)=(0,3)$ and $(0,-3)$
The Eccentricity:
$e=\frac{c}{a}=\frac{6}{3}=2$
The Length of the latus rectum :
$\frac{2b^2}{a}=\frac{2(27)}{3}=\frac{54}{3}=18$
Answer:
Given a Hyperbola equation, $9 y^2 - 4 x^2 =36$
It can also be written as
$\frac{9y^2}{36} - \frac{4x^2}{36} = 1$
$⇒\frac{y^2}{2^2} - \frac{x^2}{3^2} = 1$
Comparing this equation with the standard equation of the hyperbola:
$\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1$
We get,
$a=2$ and $b=3$
Now, as we know the relation in a hyperbola,
$c^2=a^2+b^2$
$⇒c=\sqrt{a^2+b^2}$
$⇒c=\sqrt{2^2+3^2}$
$⇒c=\sqrt{13}$
Hence, the Coordinates of the foci:
$(0,c)$ and $(0,-c)=(0,\sqrt{13})$ and $(0,-\sqrt{13})$
The Coordinates of vertices:
$(0,a)$ and $(0,-a)=(0,2)$ and $(0,-2)$
The Eccentricity:
$e=\frac{c}{a}=\frac{\sqrt{13}}{2}$
The Length of the latus rectum :
$\frac{2b^2}{a}=\frac{2(9)}{2}=\frac{18}{2}=9$
Answer:
Given a Hyperbola equation, $16x^2 - 9y^2 = 576$
It can also be written as:
$\frac{16x^2}{576} - \frac{9y^2}{576} = 1$
$⇒\frac{x^2}{36} - \frac{y^2}{64} = 1$
$⇒\frac{x^2}{6^2} - \frac{y^2}{8^2} = 1$
Comparing this equation with the standard equation of the hyperbola:
$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$
We get,
$a=6$ and $b=8$
Now, as we know the relation in a hyperbola,
$c^2=a^2+b^2$
$⇒c=\sqrt{a^2+b^2}$
$⇒c=\sqrt{6^2+8^2}$
$⇒c=10$
Therefore, the Coordinates of the foci are:
$(c,0)$ and $(-c,0)=(10,0)$ and $(-10,0)$
The Coordinates of vertices:
$(a,0)$ and $(-a,0)=(6,0)$ and $(-6,0)$
The Eccentricity:
$e=\frac{c}{a}=\frac{10}{6}=\frac{5}{3}$
The Length of the latus rectum :
$\frac{2b^2}{a}=\frac{2(8)^2}{6}=\frac{128}{6}=\frac{64}{3}$
Answer:
Given a Hyperbola equation, $5y^2 - 9x^2 = 36$
It can also be written as:
$\frac{5y^2}{36} - \frac{9x^2}{36} = 1$
$⇒\frac{y^2}{\frac{36}{5}} - \frac{x^2}{4} = 1$
$⇒\frac{y^2}{(\frac{6}{\sqrt{5}})^2} - \frac{x^2}{2^2} = 1$
Comparing this equation with the standard equation of the hyperbola:
$\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1$
We get,
$a=\frac{6}{\sqrt{5}}$ and $b=2$
Now, as we know the relation in a hyperbola,
$c^2=a^2+b^2$
$⇒c=\sqrt{a^2+b^2}$
$⇒c=\sqrt{(\frac{6}{\sqrt{5}})^2+2^2}$
$⇒c=\sqrt{\frac{56}{5}}$
$⇒c=2\sqrt{\frac{14}{5}}$
Here, as we can see from the equation, the axis of the hyperbola is the Y-axis.
So, the Coordinates of the foci are:
$(0,c)$ and $(0,-c)=\left(0,2\sqrt{\frac{14}{5}}\right)$ and $\left(0,-2\sqrt{\frac{14}{5}}\right)$
The Coordinates of vertices:
$(0,a) $ and $(0,-a)=\left(0,\frac{6}{\sqrt{5}}\right)$ and $\left(0,-\frac{6}{\sqrt{5}}\right)$
The Eccentricity:
$e=\frac{c}{a}=\frac{2\sqrt{\frac{14}{5}}}{\frac{6}{\sqrt{5}}}=\frac{\sqrt{14}}{3}$
The Length of the latus rectum :
$\frac{2b^2}{a}=\frac{2(4)}{\frac{6}{\sqrt{5}}}=\frac{4\sqrt{5}}{3}$
Answer:
Given a Hyperbola equation, $49y^2 - 16x^2 = 784$
It can also be written as:
$\frac{49y^2}{784} - \frac{16x^2}{784} = 1$
$⇒\frac{y^2}{16} - \frac{x^2}{49} = 1$
$⇒\frac{y^2}{4^2} - \frac{x^2}{7^2} = 1$
Comparing this equation with the standard equation of the hyperbola:
$\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1$
We get,
$a=4$ and $b=7$
Now, as we know the relation in a hyperbola,
$c^2=a^2+b^2$
$⇒c=\sqrt{a^2+b^2}$
$⇒c=\sqrt{4^2+7^2}$
$⇒c=\sqrt{65}$
Therefore,
Coordinates of the foci:
$(0,c)$ and $(0,-c)=(0,\sqrt{65})$ and $(0,-\sqrt{65})$
The Coordinates of vertices:
$(0,a)$ and $(0,-a)=(0,4)$ and $(0,-4)$
The Eccentricity:
$e=\frac{c}{a}=\frac{\sqrt{65}}{4}$
The Length of the latus rectum :
$\frac{2b^2}{a}=\frac{2(49)}{4}=\frac{98}{4}=\frac{49}{2}$
Question 7: Find the equations of the hyperbola satisfying the given conditions: Vertices (± 2, 0), foci (± 3, 0)
Answer:
Given, in a hyperbola: Vertices (± 2, 0), foci (± 3, 0)
Here, Vertices and foci are on the X-axis, so the standard equation of the Hyperbola will be ;
$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$
By comparing the standard parameter (Vertices and foci) with the given one, we get
$a=2$ and $c=3$
Now, as we know, the relation in a hyperbola
$c^2=a^2+b^2$
$⇒b^2=c^2-a^2$
$⇒b^2=3^2-2^2$
$⇒b^2=9-4=5$
Hence,The Equation of the hyperbola is $\frac{x^2}{4}-\frac{y^2}{5}=1$.
Question 8: Find the equations of the hyperbola satisfying the given conditions: Vertices (0, ± 5), foci (0, ± 8)
Answer:
Given, in a hyperbola: Vertices (0, ± 5), foci (0, ± 8)
Here, Vertices and foci are on the Y-axis, so the standard equation of the Hyperbola will be:
$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$
By comparing the standard parameter (Vertices and foci) with the given one, we get
$a=5$ and $c=8$
Now, as we know, the relation in a hyperbola
$c^2=a^2+b^2$
$⇒b^2=c^2-a^2$
$⇒b^2=8^2-5^2$
$⇒b^2=64-25=39$
Hence, The Equation of the hyperbola is: $\frac{y^2}{25}-\frac{x^2}{39}=1$.
Question 9: Find the equations of the hyperbola satisfying the given conditions: Vertices (0, ± 3), foci (0, ± 5)
Answer:
Given, in a hyperbola Vertices (0, ± 3), foci (0, ± 5)
Here, Vertices and foci are on the Y-axis, so the standard equation of the Hyperbola will be:
$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$
By comparing the standard parameter (Vertices and foci) with the given one, we get
$a=3$ and $c=5$
Now, as we know, the relation in a hyperbola
$c^2=a^2+b^2$
$⇒b^2=c^2-a^2$
$⇒b^2=5^2-3^2$
$⇒b^2=25-9=16$
Hence, The Equation of the hyperbola is $\frac{y^2}{9}-\frac{x^2}{16}=1$.
Answer:
Given, in a hyperbola: Foci (± 5, 0), the transverse axis is of length 8.
Here, the foci are on the X-axis, so the standard equation of the Hyperbola will be:
$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$
By comparing the standard parameter (transverse axis length and foci) with the given one, we get
$2a=8\Rightarrow a=4$ and $c=5$
Now, as we know, the relation in a hyperbola
$c^2=a^2+b^2$
$⇒b^2=c^2-a^2$
$⇒b^2=5^2-4^2$
$⇒b^2=25-16=9$
Hence, The Equation of the hyperbola is $\frac{x^2}{16}-\frac{y^2}{9}=1$ .
Answer:
Given, in a hyperbola: Foci (0, ±13), the conjugate axis is of length 24.
Here, the foci are on the Y-axis, so the standard equation of the Hyperbola will be:
$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$
By comparing the standard parameter (length of conjugate axis and foci) with the given one, we get
$2b=24\Rightarrow b=12$ and $c=13$
Now, as we know, the relation in a hyperbola
$c^2=a^2+b^2$
$⇒a^2=c^2-b^2$
$⇒a^2=13^2-12^2$
$⇒a^2=169-144=25$
Hence, The Equation of the hyperbola is $\frac{y^2}{25}-\frac{x^2}{144}=1$.
Question 12: Find the equations of the hyperbola satisfying the given conditions: Foci $(\pm 3\sqrt5, 0)$, the latus rectum is of length 8 .
Answer:
Given, in a hyperbola: Foci $(\pm 3\sqrt5, 0)$, the latus rectum is of length 8.
Here, foci are on the X-axis, so the standard equation of the Hyperbola will be ;
$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$
By comparing the standard parameter (length of latus rectum and foci) with the given one, we get
$c=3\sqrt{5}$ and
$\frac{2b^2}{a}=8$
$\Rightarrow 2b^2=8a$
$\Rightarrow b^2=4a$
Now, as we know, the relation in a hyperbola
$c^2=a^2+b^2$
$⇒c^2=a^2+4a$
$⇒a^2+4a=(3\sqrt{5})^2$
$⇒a^2+4a=45$
$⇒a^2+9a-5a-45=0$
$⇒(a+9)(a-5)=0$
$⇒a=-9$ or, $a=5$
Since $a$ can never be negative,
$a=5$
$⇒a^2=25$
So, $b^2=4a=4(5)=20$
Hence, The Equation of the hyperbola is $\frac{x^2}{25}-\frac{y^2}{20}=1$ .
Question 13: Find the equations of the hyperbola satisfying the given conditions: Foci (± 4, 0), the latus rectum is of length 12
Answer:
Given, in a hyperbola: Foci (± 4, 0), the latus rectum is of length 12
Here, foci are on the X-axis, so the standard equation of the Hyperbola will be:
$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$
By comparing the standard parameter (length of latus rectum and foci) with the given one, we get
$c=4$ and
$\frac{2b^2}{a}=12$
$\Rightarrow 2b^2=12a$
$\Rightarrow b^2=6a$
Now, as we know, the relation in a hyperbola
$c^2=a^2+b^2$
$⇒c^2=a^2+6a$
$⇒a^2+6a=4^2$
$⇒a^2+6a=16$
$⇒a^2+8a-2a-16=0$
$⇒(a+8)(a-2)=0$
$⇒a=-8$ or, $a=2$
Since $a$ can never be negative,
$a=2$
$⇒a^2=4$
So, $b^2=6a=6(2)=12$
Hence, The Equation of the hyperbola is $\frac{x^2}{4}-\frac{y^2}{12}=1$ .
Question 14: Find the equations of the hyperbola satisfying the given conditions: vertices (± 7,0), $e = \frac{4}{3}$
Answer:
Given, in a hyperbola: vertices (± 7,0), and $e = \frac{4}{3}$
Here, Vertices is on the X-axis, so the standard equation of the Hyperbola will be:
$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$
By comparing the standard parameter (Vertices and eccentricity) with the given one, we get,
$a=7$ and
$e=\frac{c}{a}$
$⇒\frac{4}{3}=\frac{c}{7}$
$⇒c=\frac{28}{3}$
Now, as we know, the relation in a hyperbola
$c^2=a^2+b^2$
$⇒b^2=c^2-a^2$
$⇒b^2=\left(\frac{28}{3}\right)^2-7^2$
$⇒b^2=\left(\frac{784}{9}\right)-49$
$⇒b^2=\left(\frac{784-441}{9}\right)=\frac{343}{9}$
Hence, The Equation of the hyperbola is $\frac{x^2}{49}-\frac{9y^2}{343}=1$ .
Question 15: Find the equations of the hyperbola satisfying the given conditions: Foci $(0,\pm\sqrt{10})$, passing through (2,3)
Answer:
Given, in a hyperbola: Foci $(0,\pm\sqrt{10})$, passing through (2,3)
Since the foci of the hyperbola is on the Y-axis, the equation of the hyperbola will be of the form:
$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$
By comparing the standard parameter (foci) with the given one, we get
$c=\sqrt{10}$
Now, as we know, in a hyperbola
$a^2+b^2=c^2$
$⇒a^2+b^2=10—----(1)$
Now, as the hyperbola passes through the point (2,3),
$\frac{3^2}{a^2}-\frac{2^2}{b^2}=1$
$⇒9b^2-4a^2=a^2b^2—------(2)$
Solving Equations (1) and (2), we get,
$9(10-a^2)-4a^2=a^2(10-a^2)$
$⇒a^4-23a^2+90=0$
$⇒(a^2)^2-18a^2-5a^2+90=0$
$⇒(a^2-18)(a^2-5)=0$
$⇒a^2=18$ or, $a=5$
Now, as we know in a hyperbola $c$ is always greater than $a$,
we choose the value $a^2=5$
So, $b^2=10-a^2=10-5=5$
Hence The Equation of the hyperbola is $\frac{y^2}{5}-\frac{x^2}{5}=1$.
| Conic Sections Class 11 Question Answers Exercise: Miscellaneous Exercise Page Number: 204 Total Questions: 8 |
Question 1: If a parabolic reflector is 20 cm in diameter and 5 cm deep, find the focus.
Answer:
Let the parabolic reflector open towards the right.
So, the equation of the parabolic reflector will be $y^2=4ax$
Now, since this curve will pass through the point (5,10), if we assume origin at the optical centre,
So,
$10^2=4a(5)$
$⇒a=\frac{100}{20}=5$
Hence, the focus of the parabola is $(a,0)=(5,0)$.
Alternative Method:
As we know, on any concave curve, the focus, $f=\frac{R}{2}$
$\therefore$ Focus, $f=\frac{R}{2}=\frac{10}{2}=5$
Hence, the focus is 5 cm right to the optical centre.
Answer:
Since the Axis of the parabola is vertical, let the equation of the parabola be $x^2=4ay$
it can be seen that this curve will pass through the point ($\frac52$, 10) if we assume the origin at the bottom end of the parabolic arch.
So,
$\left(\frac{5}{2}\right)^2=4a(10)$
$⇒a=\frac{25}{160}=\frac{5}{32}$
Hence, the equation of the parabola is:
$x^2=4\times\frac{5}{32}\times y$
$⇒x^2=\frac{20}{32} y$
$⇒x^2=\frac{5}{8} y$
Now, when y = 2 the value of x will be:
$x=\sqrt{(\frac{5}{8}\times2)}=\sqrt{\frac{5}{4}}=\frac{\sqrt{5}}{2}$
Hence, the width of the arch at this height is:
$2x=2\times\frac{\sqrt{5}}{2}=\sqrt{5}$
Answer:
Given,
The width of the parabolic cable = 100m
The length of the shorter supportive wire attached = 6m
The length of the longer supportive wire attached = 30m
Since the rope opens upwards, the equation will be of the form $x^2=4ay$
Now, if we consider the origin at the centre of the rope, the equation of the curve will pass through points: (50, 30-6) = (50,24)
$50^2=4a\times 24$
$⇒a=\frac{625}{24}$
Hence, the equation of the parabola is
$x^2=4\times \frac{625}{24}\times y$
$⇒x^2= \frac{625}{6}\times y$
Now, at a point 18 m right from the centre of the rope, the x coordinate of that point will be 18.
So, by the equation, the y-coordinate will be:
$y=\frac{x^2}{4a}=\frac{18^2}{4\times \frac{625}{24}}\approx 3.11$ m
Hence, the length of the supporting wire attached to the roadway from the middle is
(3.11 + 6)m = 9.11 m
Answer:
The equation of the semi-ellipse will be of the form $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\:,y>0$
Now, according to the question,
the length of major axis = 2a = 8
$\Rightarrow a=4$
The length of the semi-major axis = 2
$\Rightarrow b=2$
Hence, the equation will be,
$\frac{x^2}{4^2}+\frac{y^2}{2^2}=1\:,y>0$
$⇒\frac{x^2}{16}+\frac{y^2}{4}=1\:,y>0$
Now, at point 1.5 cm from the end, the x coordinate is $4-1.5 = 2.5$
So, the height at this point is
$\frac{(2.5)^2}{16}+\frac{y^2}{4}=1$
$\Rightarrow y=\sqrt{4(1-\frac{2.5^2}{16})}$
$⇒y\approx 1.56$ m
Hence, the height of the required point is 1.56 m.
Answer:
Let $\theta$ be the angle that the rod makes with the ground.
Now, at a point 3 cm from the end,
$\cos\theta=\frac{x}{9}$
At the point of touching the ground
$\sin\theta=\frac{y}{3}$
Now, as we know the trigonometric identity,
$\cos^2\theta+\sin^2\theta=1$
$⇒\left (\frac{x}{9} \right )^2+\left ( \frac{y}{3} \right )^2=1$
$⇒\frac{x^2}{81}+\frac{y^2}{9}=1$
Hence, the equation is $\frac{x^2}{81}+\frac{y^2}{9}=1$
Answer:
Given the parabola, $x^2=12y$
Comparing this equation with $x^2=4ay$, we get, $a=3$
Now, as we know, the coordinates of the ends of the latus rectum are:
$(2a,a)$ and $(-2a,a)$
So, the coordinates of the latus rectum are,
$(2a,a)$ and $(-2a,a)=(6,3)$ and $(-6,3)$
Now the area of the triangle with coordinates (0,0),(6,3) and (-6,3)
Width of the triangle $= 2 \times 6=12$
Height of the triangle = 3
So, the area of the triangle
= $\frac{1}{2}\times$ Base $\times$ height
= $\frac{1}{2}\times12\times3$
= $18$
Hence, the required area is 18 square units.
Answer:
As we know, if a point moves in a plane in such a way that its distance from two points remains constant, then the path is an ellipse.
Now, according to the question,
The distance between the point from where the sum of the distance from a point is constant = 10
$\Rightarrow 2a=10$
$\Rightarrow a=5$
Now, the distance between the foci = 8
$\Rightarrow 2c=8$
$\Rightarrow c=4$
Now, as we know the relation,
$c^2=a^2-b^2$
$⇒b^2=a^2-c^2$
$⇒b=\sqrt{a^2-c^2}=\sqrt{5^2-4^2}=\sqrt{25-16}=\sqrt{9}=3$
Hence, the equation of the ellipse is:
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
$\Rightarrow \frac{x^2}{5^2}+\frac{y^2}{3^2}=1$
$\Rightarrow \frac{x^2}{25}+\frac{y^2}{9}=1$
Hence, the path of the man will be:
$\Rightarrow \frac{x^2}{25}+\frac{y^2}{9}=1$
Answer:
Given an equilateral triangle inscribed in a parabola with the equation $y^2 = 4 ax$
The one coordinate of the triangle is A(0,0).
Now, let the other two coordinates of the triangle are
$B(x,\sqrt{4ax})$ and $C(x,-\sqrt{4ax})$
Now, since the triangle is equilateral,
$BC=AB=CA$
$⇒2\sqrt{4ax}=\sqrt{(x-0)^2+(\sqrt{4ax}-0)^2}$
$⇒x^2=12ax$
$⇒x=12a$
The coordinates of the points of the equilateral triangle are,
$(0,0),(12,\sqrt{4a\times 12a}),(12,-\sqrt{4a\times 12a})$
$=(0,0),(12,4\sqrt{3}a)$ and $(12,-4\sqrt{3}a)$
So, the side of the triangle is:
$2\sqrt{4ax}=2\times4\sqrt{3}a=8\sqrt{3}a$
Conic Sections Class 11 NCERT Solutions: Exercise-wise
Exercise-wise NCERT Solutions of Conic Sections Class 11 Maths Chapter 10 are provided in the links below.
Class 11 Maths NCERT Chapter 10: Extra Question
Question:
The distance between the foci of a hyperbola is 16, and its eccentricity is $\sqrt{2}$. Its equation is:
Solution:
Let the equation of the hyperbola be $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$
Given that Foci=( $\pm a e, 0)$
Distance between foci=2ae=16
$
\begin{aligned}
& 2 × a × \sqrt{2}=16 \\
& a=4 \sqrt{2} \\
& b^2=a^2\left(e^2-1\right)=(4 \sqrt{2})^2\left((\sqrt{2})^2-1\right) \\
& =32(2-1)=32
\end{aligned}
$
Thus, equation is $\frac{x^2}{32}-\frac{y^2}{32}=1$
Hence, the correct answer is "x2 – y2 = 32".
Conic Sections Class 11 Chapter 10: Topics
The topics discussed in the NCERT Solutions for class 11, chapter 10, Conic sections are:
Conic Sections Class 11 Solutions: Important Formulae
| Circle | |
|
Description |
Equation/Formulae |
|
Equation of a circle |
(x - h)2 + (y - k)2 = r2 |
|
General equation of a circle |
x2 + y2 + 2gx + 2fy + c = 0 |
|
Centre of the circle |
Centre: (-g, -f) |
|
Radius of the circle |
Radius (r) = $\sqrt{g^2+f^2-c}$ |
|
Parametric equation of a circle |
x = r cos(θ), y = r sin(θ) |
|
Parametric equation of a circle (centre at h, k) |
x = h + r cos(θ), y = k + r sin(θ) |
| Parabola | |
|
Description |
Equations/Forms |
|
Equation forms of a parabola |
y2 = 4ax, y2 = -4ax, x2 = 4ay, x2 = -4ay |
|
Axis of the parabola |
y = 0 (for first two forms), x = 0 (for last two forms) |
|
Directrix of the parabola |
x = -a (1st form), x = a (2nd form), y = -a (3rd form), y = a (4th form) |
|
Vertex of the parabola |
(0, 0) (for all forms) |
|
Focus of the Parabola |
(a, 0) (1st form), (-a, 0) (2nd form), (0, a) (3rd form), (0, -a) (4th form) |
|
Length of the latus rectum |
4a (for all forms) |
|
Ellipse | |
|
Description |
Equation/Forms |
|
Equation forms of an ellipse | $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b$ And $\frac{x^2}{b^2}+\frac{y^2}{a^2}=1(a>b)$ |
|
Major Axis |
y = 0 (1st form), x = 0 (2nd form) |
|
Length of Major Axis |
2a (for both forms) |
|
Minor Axis |
x = 0 (1st form), y = 0 (2nd form) |
|
Length of Minor Axis |
2b (for both forms) |
|
Directrix of the ellipse | x = $\pm \frac ae$ (1st form), y = $\pm \frac ae$ (2nd form) |
|
Vertex of the ellipse |
(±a, 0) (1st form), (0, ±a) (2nd form) |
|
Focus of the ellipse |
(±ae, 0) (1st form), (0, ±ae) (2nd form) |
|
Length of the latus rectum | $\frac{2b^2}a$ (for both forms) |
|
Eccentricity (e) |
$\sqrt{\frac{a^2+b^2}{a^2}}$(for both forms) |
| Hyperbola | |
|
Description |
Equations/Forms |
|
Equation forms of the hyperbola | $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ And $\frac{x^2}{b^2}+\frac{y^2}{a^2}=-1$ |
|
Coordinates of centre |
(0, 0) (for both forms) |
|
Coordinates of vertices |
(±a, 0) (for both forms) |
|
Coordinates of foci |
(±ae, 0) (for both forms) |
|
Length of Conjugate axis |
2b (for both forms) |
|
Length of Transverse axis |
2a (for both forms) |
|
Equation of Conjugate axis |
x = 0 (for both forms) |
|
Equation of Transverse axis |
y = 0 (for both forms) |
|
Equation of Directrix |
x = $\pm\frac ae$ (for both forms) |
|
Eccentricity (e) |
$\sqrt{\frac{(a^2+b^2)}{a^2}}$(for both forms) |
|
Length of the latus rectum |
$\frac{2b^2}a$ (for both forms) |
Approach to Solve Questions of Conic Sections Class 11
Using these approaches, students can tackle the Conic Sections Class 11 Chapter 10 Question Answers with greater confidence.
Standard equations: It is very important to understand the standard equations of all the conic shapes, such as circle, parabola, hyperbola, and ellipse, so that students can understand from the general equations which type of conic it is.
Key elements: Learn the definitions of all the key elements, like focus, vertex, axis, and latus rectum, to find them from standard forms. These types of questions are very common in the exams.
Prioritise Latus rectum: These are the formulas to find the latus rectum from standard equations of different conics. Memorise this very well.
- Parabola: Length $=4 a$
- Ellipse: $\frac{2 b^2}{a}$
- Hyperbola: $\frac{2 b^2}{a}$
Symmetry: The usage of symmetry is very important to guess the coordinates of missing points, as conics are Symmetric about their axes. It also saves time and errors during the plotting of graphical questions.
Conversion: Convert normal equations into standard forms of conics to identify centre, axes, etc.
Eccentricity: It is also an option to identify the conic. For example, if the eccentricity is less than 1, it is an ellipse; greater than 1, it is a hyperbola. If the eccentricity is 1, it is a parabola.
What Extra Should Students Study Beyond the NCERT for JEE?
Here are a few key topics outside the NCERT syllabus that students should study for JEE. Learning these will give you an extra edge during the exam.
|
Concept Name |
JEE |
NCERT |
|
✅ |
✅ | |
|
✅ |
✅ | |
|
Equation of parabola when equation of axis and tangent at vertex and latus rectum are given |
✅ |
✅ |
|
✅ |
✅ | |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
Normal in point and Parametric, and Slope form of a parabola |
✅ | ❌ |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
✅ |
✅ | |
|
✅ |
✅ | |
|
✅ | ❌ | |
|
✅ |
✅ | |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
✅ |
✅ | |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
✅ | ❌ | |
|
✅ | ❌ |
Why are Class 11 Maths Chapter 10 Conic Sections question answers important?
This Conic Sections chapter helps us understand shapes like circles, parabolas, ellipses, and hyperbolas that are formed by cutting a cone. It builds our geometry and algebra skills together. These Class 11 Maths chapter 10 Conic Sections question answers help us practise how to find and use their equations easily.
- These solutions teach you how to recognise and draw different conic shapes on a graph.
- Students learn how to find equations and important terms like focus, directrix, and eccentricity.
- Solving Class 11 Maths chapter 10 Conic Sections question answers helps us in Class 12 and higher studies, especially in coordinate geometry and physics.
- It improves our problem-solving and visual understanding, which is useful in real-life applications like engineering and astronomy.
NCERT Solutions for Class 11 Maths: Chapter Wise
Access all NCERT Class 11 Maths solutions from one place using the links below.
Also, read,
NCERT Solutions For Class 11: Subject-wise
Students can use the following links to check the solutions of the other subjects to achieve good marks in the exam.
- NCERT Solutions for Class 11 Biology
- NCERT Solutions for Class 11 Chemistry
- NCERT Solutions for Class 11 Physics
NCERT Books and NCERT Syllabus
After studying the NCERT books for fundamental knowledge, students can solve problems from other books. Also, they can check the latest NCERT syllabus to stay updated using the following links.
Frequently Asked Questions (FAQs)
You can find the free NCERT solutions on the NCERT's official websites.
Careers360's official website offers detailed, free solutions prepared by experienced experts; these solutions explain every detail and provide extra information.
Conic sections chapter in class 11 Covers the following topics:
- Introduction
- Sections of Cone
- Circle
- Parabola
- Ellipse
- Hyperbola
There are also many important sub-topics like latus rectum, standard equations of the conic sections, foci, major/minor axis, directrix, and eccentricity.
Before solving the conic sections problems, familiarise yourself with all the basics, general equations, key properties, and important formulae of this chapter. Then follow the following steps.
- First, identify the type of standard equations given. Whether it is a circle, parabola, ellipse or hyperbola.
- Use the necessary formulas to find properties like directrix, coordinates of foci, latus rectum, and eccentricity.
- Analyze all the solved examples first before moving to the exercises.
- Start with easier problems first and gradually increase the difficulty level of questions.
- Draw the conic section to visualise its focus, directrix and axis, if necessary.
Here are some real-life uses of different conic sections.
| Circle | It can be used in clocks, wheels, planetary motions, CDs & DVDs, etc. |
| Parabola | It can be used in Satellite dishes, radio telescopes, Car headlights & flashlights, Projectile motions, Suspension bridges, etc. |
| Ellipse | It can be used in planetary orbits, MRI, Whispering galleries, Car & train tracks, etc. |
| Hyperbola | It can be used in navigation, GPS systems, Nuclear radiation detection, optical lenses, cooling towers, boomerangs, telescopes, etc. |
| Features | Ellipse | Parabola | Hyperbola |
| Definition | A set of points where the sum of the distances from two fixed foci is constant. | A set of points equidistant from a fixed point called the focus and a fixed line called the directrix. | A set of points where the absolute difference of distances from two fixed foci is constant. |
| Shape | Oval shaped | U-shaped | Two separate open curves(Look like two infinite bows) |
| Standard Equation | $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ | $y^2=4 a x$ | $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ |
| Foci | $( \pm c, 0) \text {, where } c^2=a^2-b^2$ | $(a, 0)$ | $( \pm c, 0) \text {, where } c^2=a^2+b^2$ |
| Eccentricity (e) | $0<e<1$ | $e=1$ | $e>1$ |
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
