NCERT Solutions for Class 11 Maths Chapter 3 Trigonometric Functions

Question 1: Find the radian measures corresponding to the following degree measures:

(i) $25 ^\circ$
(ii) $-47 ^\circ$ $30'$
(iii) $240^\circ$
(iv) $520^\circ$

Answer:

It is solved using the relation between degree and radian
(i) $25^\circ$
We know that $180^\circ$ = $\pi$ radian
So, $1^\circ = \frac{\pi }{180}$ radian
$25^\circ = \frac{\pi }{180}\times 25$ radian $=\frac{5\pi }{36}$ radian

(ii) $-47^\circ30'$
We know that
$-47^\circ30' = -47\frac{1}{2}^\circ = -\frac{95}{2}^\circ$
Now, we know that $180^\circ = \pi \Rightarrow 1^\circ = \frac{\pi}{180}$ radian
So, $-\frac{95}{2}^\circ = \frac{\pi}{180}\times \left (-\frac{95}{2} \right )$ radian $= \frac{-19\pi}{72}$ radian

(iii) $240^\circ$
We know that
$180^\circ = \pi \Rightarrow 1^\circ = \frac{\pi}{180}$ radian
So, $240^\circ = \frac{\pi}{180}\times 240 = \frac{4\pi}{3}$ radian

(iv) $520^\circ$
We know that
$180^\circ = \pi \Rightarrow 1^\circ = \frac{\pi}{180}$ radian
So, $520^\circ = \frac{\pi}{180}\times 520$ radian $= \frac{26\pi}{9}$ radian

Question 2: Find the degree measures corresponding to the following radian measures. (Use $\small \pi =\frac{22}{7}$)

$\small (i) \frac{11}{16}$
$\small (ii) -4$
$\small (iii) \frac{5\pi }{3}$
$\small (iv) \frac{7\pi }{6}$

Answer:

(i) $\frac{11}{16}$
We know that
$\pi$ radian $= 180^\circ \Rightarrow 1\ radian = \frac{180}{\pi}^\circ$
So, $\frac{11}{16}\ radian = \frac{180}{\pi}\times \frac{11}{16}^\circ$ (we need to take $\pi = \frac{22}{7}$ )
$\frac{11}{16}\ radian = \frac{180\times 7}{22}\times \frac{11}{16}^\circ = \frac{315}{8}^\circ$
(we use $1^\circ = 60'$ and 1' = 60'')
Here 1' represents 1 minute and 60" represents 60 seconds
Now,
$\frac{315}{8}^\circ=39\frac{3}{8}^\circ =39^\circ +\frac{3\times 60}{8}' = 39^\circ +22' + \frac{1}{2}' = 39^\circ +22' +30''= \frac{315}{8}^\circ = 39^\circ22'30''$

(ii) $-4$
We know that
$\pi$ radian $= 180^\circ \Rightarrow 1\ radian = \frac{180}{\pi}^\circ$ (we need to take $\pi = \frac{22}{7}$ )
So, $-4\ radian = \frac{-4\times 180}{\pi}= \frac{-4\times 180\times 7}{22} = -\frac{2520}{11}^\circ$
(we use $1^\circ = 60'$ and 1' = 60'')
$\Rightarrow \frac{-2520}{11}^\circ= -229\frac{1}{11}^\circ =-229^\circ + \frac{1\times 60}{11}' = -229^\circ + 5' + \frac{5}{11}' = -229^\circ +5' +27''= -229^\circ5'27''$

(iii) $\frac{5\pi}{3}$
We know that
$\pi$ radian $= 180^\circ \Rightarrow 1\ radian = \frac{180}{\pi} ^\circ$ (we need to take $\pi = \frac{22}{7}$ )
So, $\frac{5\pi}{3}\ radian = \frac{180}{\pi}\times \frac{5\pi}{3}^\circ = 300^\circ$

(iv) $\frac{7\pi}{6}$
We know that
$\pi$ radian $= 180^\circ \Rightarrow 1\ radian = \frac{180}{\pi} ^\circ$ (we need to take $\pi = \frac{22}{7}$ )
So, $\frac{7\pi}{6}\ radian = \frac{180}{\pi}\times \frac{7\pi}{6} = 210^\circ$

Question 3: A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?

Answer:
Number of revolutions made by the wheel in 1 minute = 360
$\therefore$ Number of revolutions made by the wheel in 1 second = $\frac{360}{60} = 6$
($\because$ 1 minute = 60 seconds)
In one revolution, the wheel will cover $2\pi$ radian
So, in 6 revolutions it will cover = $6\times 2\pi = 12\pi$ radian
$\therefore$ In 1 the second wheel will turn $12\pi$ radian.

Question 4: Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm (use $\small \pi =\frac{22}{7}$ )

Answer:
We know that
$l = r\theta$ ( where $l$ is the length of the arc, $r$ is the radius of the circle and $\theta$ is the angle subtended)
here $r$ = 100 cm
and $l$ = 22 cm
Now,
$\theta = \frac{l}{r} = \frac{22}{100}$ radian
We know that
$\pi\ radian = 180^\circ$
So, 1 radian = $\frac{180}{\pi}^\circ$
$\therefore \frac{22}{100}\ radian = \frac{180}{\pi}\times\frac{22}{100}^\circ= \frac{180\times7}{22}\times\frac{22}{100} = \frac{63}{5}^\circ$
So, $\frac{63}{5}^\circ = 12\frac{3}{5}^\circ = 12^\circ + \frac{3\times60}{5}' = 12^\circ + 36' = 12 ^\circ36'$
Thus, the angle subtended at the centre of a circle $\theta = 12^\circ36'$.

Question 5: In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.

Answer:
Given: radius ($r$) of circle = $\frac{Diameter}{2} = \frac{40}{2} = 20$ cm
length of chord = 20 cm
We know that
$\theta = \frac{l}{r}$ ($r$ = 20 cm , $l$ = ? , $\theta$ = ?)
Now,

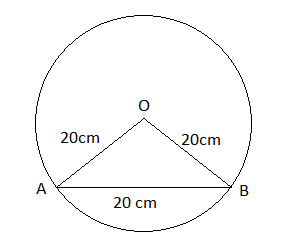
AB is the chord of length 20 cm and OA and OB are radii of circle i.e. 20 cm each
The angle subtended by OA and OB at centre = $\theta$
$\because$ OA = OB = AB
$\therefore$ $\Delta$ OAB is equilateral triangle
So, each angle is $60^\circ$
$\therefore$ $\theta = 60^\circ$ $= \frac{\pi}{3}$ radian
Now, we have $\theta$ and $r$
So, $l = r\theta = 20\times\frac{\pi}{3}=\frac{20\pi}{3}$
$\therefore$ the length of the minor arc of the chord ($l$) = $\frac{20\pi}{3}$ cm.

Question 6: If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii.

Answer:
Given: $\theta_1 = 60^\circ, \theta_2 = 75^\circ\\$ and $l_1 = l_2$
We need to find the ratio of their radii $\frac{r_1}{r_2}$
We know that arc length $l = r \theta$
So, $l_1 = r_1 \theta_1$ and $l_2 = r_2\theta_2$
Now, $l_1 = l_2$
So, $\frac{ r_1 }{ r_2}= \frac{\theta_2}{\theta_1} = \frac {75}{60} = \frac{5}{4}$, which is the ratio of their radii.

Question 7: Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
(i) 10 cm
(ii) 15 cm
(iii) 21 cm

Answer:
(i) We know that
$l = r \theta$
Now,
$r$ = 75 cm
$l$ = 10 cm
So,
$\theta = \frac{l}{r} = \frac{10}{75} = \frac{2}{15}$ radian

(ii) We know that
$l = r \theta$
Now,
$r$ = 75 cm
$l$ = 15 cm
So,
$\theta = \frac{l}{r} = \frac{15}{75} = \frac{1}{5}$ radian

(iii) We know that
$l = r \theta$
Now,
$r$ = 75 cm
$l$ = 21 cm
So,
$\theta = \frac{l}{r} = \frac{21}{75} = \frac{7}{25}$ radian

Question 1: Find the values of other five trigonometric functions as $\small \cos x = -\frac{1}{2}$ , $x$ lies in third quadrant.

Answer:
$\cos x = -\frac {1}{2}$
$\because \sec x = \frac{1}{\cos x} = \frac{1}{-\frac {1}{2}} = -2$
$x$ lies in III quadrants. Therefore sec x is negative
$\sin ^{2}x +\cos^{2}x = 1 ⇒ \sin^{2}x = 1 - \cos^{2}x$
$⇒ \sin^{2}x = 1 -\left ( -\frac{1}{2} \right )^{2}⇒ \sin^{2}x = 1 - \frac{1}{4} = \frac{3}{4}⇒ \sin x = \sqrt{\frac{3}{4}} = \pm \frac{\sqrt{3}}{2}$
$x$ lies in III quadrants. Therefore sin x is negative
$\therefore \sin x= - \frac{\sqrt{3}}{2}$
$\because cosec \ x = \frac {1}{\sin x}= \frac{1}{- \frac{\sqrt{3}}{2}} =- \frac{2}{\sqrt{3}}$
$x$ lies in III quadrants. Therefore cosec x is negative
$\tan x = \frac{\sin x}{\cos x} = \frac {-\frac{\sqrt{3}}{2}}{-\frac{1}{2}} = \sqrt{3}$
$x$ lies in III quadrants. Therefore tan x is positive
$\cot x = \frac{1}{\tan x} = \frac{1}{\sqrt{3}}$
$x$ lies in III quadrants. Therefore cot x is positive.

Question 2: Find the values of other five trigonometric functions as $\small \sin x = \frac{3}{5}$, $x$ lies in second quadrant.

Answer:
$\sin x = \frac {3}{5}$
$cosec \ x = \frac{1}{\sin x}=\frac {1}{\frac {3}{5}} = \frac {5}{3}$
$x$ lies in the second quadrant. Therefore cosec x is positive
$\sin^{2}x + \cos ^{2}x = 1⇒ \cos ^{2}x = 1 - \sin ^{2}x$
$⇒ \cos ^{2}x = 1 - \left ( \frac{3}{5} \right )^{2}⇒ \cos ^{2}x = 1 - \frac {9}{25} = \frac {16}{25}⇒ \cos x = \sqrt{\frac {16}{25}} = \pm \frac {4}{5}$
$x$ lies in the second quadrant. Therefore cos x is negative
$\therefore \cos x = - \frac {4}{5}$
$\sec x = \frac {1}{\cos x} = \frac{1}{- \frac {4}{5}} = -\frac {5}{4}$
$x$ lies in the second quadrant. Therefore sec x is negative
$\tan x = \frac {\sin x}{\cos x} = \frac {\frac{3}{5}}{-\frac{4}{5}} = -\frac {3}{4}$
$x$ lies in the second quadrant. Therefore tan x is negative
$\cot x = \frac {1}{\tan x} = \frac {1}{-\frac {3}{4}} = -\frac{4}{3}$
$x$ lies in the second quadrant. Therefore cot x is negative.

Question 3: Find the values of other five trigonometric functions as $\small \cot x = \frac{3}{4}$, $x$ lies in third quadrant.

Answer:
$\cot x= \frac {3}{4}$
$\tan x = \frac{1}{\cot x}= \frac{1}{\frac {3}{4}} = \frac {4}{3}$
$1 + \tan ^ {2}x = \sec ^{2}x⇒ 1+\frac{4^2}{3^2} = \sec ^{2}x⇒ 1 + \frac {16}{9} = \sec ^{2}x⇒ \frac {25}{9} = \sec ^{2}x$
$⇒ \sec x = \sqrt {\frac {25}{9}} = \pm \frac {5}{3}$
$x$ lies in x lies in third quadrant. therefore sec x is negative
$\sec x = -\frac{5}{3}$
$\cos x = \frac {1}{\sec x} = \frac {1}{-\frac{5}{3}} = -\frac{3}{5}$
$\sin ^{2 }x+ \cos ^{2}x = 1⇒ \sin ^{2 }x = 1 - \cos ^{2}x$
$⇒ \sin ^{2 }x = 1 -\left ( -\frac{3}{5} \right )^{2}⇒ \sin ^{2 }x = 1 - \frac {9}{25}⇒ \sin ^{2 }x = \frac{16}{25}⇒ \sin x = \sqrt {\frac{16}{25}} = \pm \frac{4}{5}$
$x$ lies in third quadrant. Therefore sin x is negative
$\sin x = -\frac {4}{5}$
$cosec \ x = \frac {1}{\csc} = \frac {1}{-\frac{4}{5}} = - \frac{5}{4}$.

Question 4: Find the values of other five trigonometric functions as $\small \sec x = \frac{13}{5}$, $x$ lies in fourth quadrant.

Answer:
$\sec x = \frac {13}{5}$
$\cos x = \frac {1}{\sec x} = \frac{1}{\frac {13}{5}} = \frac {5}{13}$
$\sin^{2}x + \cos^{2}x = 1⇒ \sin^{2}x = 1 - \cos^{2}x$
$⇒ \sin^{2}x = 1 - (\frac {5}{13})^2⇒ \sin^{2}x = 1 - \frac {25}{169} = \frac {144}{169}⇒ \sin x = \sqrt { \frac {144}{169}} = \pm \frac {12}{13}$
$x$ lies in fourth quadrant. Therefore $\sin x$ is negative.
$\sin x =- \frac {12}{13}$
$\csc x = \frac {1}{\sin x} = \frac {1}{-\frac {12}{13}} = -\frac {13}{12}$
$\tan x = \frac {\sin x}{\cos x} = \frac {-\frac{12}{13}}{\frac{5}{13}} = -\frac {12}{5}$
$\cot x = \frac {1}{\tan x} = \frac {1}{-\frac{12}{5}} = -\frac{5}{12}$.

Question 5: Find the values of the other five trigonometric functions as $\small \tan x = -\frac{5}{12}$, $x$ lies in second quadrant.

Answer:
$\tan x = -\frac {5}{12}$
$\cot x = \frac {1}{\tan x} = \frac {1}{-\frac{5}{12}} = -\frac {12}{5}$
$1 + \tan^{2}x = \sec^{2}x⇒ 1 + \left ( -\frac{5}{12} \right )^{2} = \sec^{2}x⇒ 1 + \frac {25}{144} = \sec^{2}x⇒ \frac {169}{144} = \sec^{2}x$
$⇒ \sec x = \sqrt {\frac {169}{144}} = \pm \frac {13}{12}$
$x$ lies in second quadrant. Therefore the value of $\sec x$ is negative
$\sec x = - \frac {13}{12}$
$\cos x = \frac{1}{\sec x}= \frac{1}{-\frac{13}{12}} = -\frac {12}{13}$
$\sin^{2}x + \cos^{2}x = 1⇒ \sin^{2}x = 1 - \cos^{2}x$
$⇒ \sin^{2}x = 1 - \left ( -\frac{12}{13} \right )^{2}⇒ \sin^{2}x = 1 - \frac{144}{169}⇒\sin^{2}x = \frac {25}{169}⇒ \sin x = \sqrt {\frac{25}{169}} = \pm \frac{5}{13}$
$x$ lies in the second quadrant.
Therefore the value of $\sin x$ is positive.
$\sin x = \frac {5}{13}$
$\csc = \frac {1}{\sin x} = \frac {1}{\frac {5}{13}} = \frac {13}{5}$.

Question 6: Find the values of the trigonometric functions $\small \sin 765^\circ$

Answer:
We know that values of $\sin x$ repeat after an interval of $2\pi$ or $360^\circ$
$\sin765^\circ = \sin (2\times360^\circ + 45^\circ ) = \sin45^\circ = \frac {1}{\sqrt{2}}$.

Question 7: Find the values of the trigonometric functions $\small cosec \ (-1410^\circ)$

Answer:
We know that value of $\operatorname{cosec} x$ repeats after an interval of $2\pi$ or $360^\circ$.
$\operatorname{cosec} (-1410^\circ) = \operatorname{cosec} (360^\circ\times4+(-1410^\circ))= \operatorname{cosec}\ 30^\circ = 2$

Question 8: Find the values of the trigonometric functions $\small \tan \frac{19\pi }{3}$

Answer:
We know that $\tan x$ repeats after an interval of $\pi$ or 180$^\circ$.
$\tan (\frac{19\pi}{3}) = \tan (6\pi+\frac{\pi}{3})= \tan \frac{\pi}{3} =\tan 60^\circ = \sqrt{3}$

Question 9: Find the values of the trigonometric functions $\sin\left ( -\frac{11\pi}{3} \right )$

Answer:
We know that $\sin x$ repeats after an interval of $2\pi$ or $360^\circ$
$\sin \left ( -\frac{11\pi}{3} \right ) = \sin \left (4\pi +(-\frac{11\pi}{3}) \right ) = \sin \frac{\pi}{3} = \frac {\sqrt{3}}{2}$

Question 10: Find the values of the trigonometric functions $\small \cot \left ( -\frac{15\pi }{4} \right )$

Answer:
We know that $\cot x$ repeats after an interval of $\pi$ or 180$^\circ$.
$\cot \left ( -\frac{15\pi}{4} \right ) = \cot \left (4\pi +(-\frac {15\pi}{4}) \right ) = \cot \left ( \frac{\pi}{4} \right ) = 1$

We know that
$\cos2x=1-2\sin^{2}x$
We use this in our problem
$\cos 4x = \cos 2(2x)$
= $1-2\sin^{2}2x$
= $1-2(2\sin x \cos x)^{2}$ $(\because \sin2x = 2\sin x \cos x)$
= $1-8\sin^{2}x\cos^{2}x=$ R.H.S.

Question 25: Prove the following $\small \cos6x = 32\cos^{6}x -48\cos^{4}x + 18\cos^{2}x-1$

Answer:
We know that
$\cos 3x = 4 \cos^{3}x - 3\cos x$
We use this in our problem
we can write $\cos 6x$ as $\cos 3(2x)$
$\cos 3(2x) = 4 \cos^{3}2x - 3\cos 2x$
= $4(2\cos^{2}x - 1)^{3} - 3(2\cos^{2}x - 1) (\because \cos 2x = 2\cos^{2}x - 1)$
= $4[(2\cos^{2}x)^{3} -(1)^{3}-3(2\cos^{2}x)^{2}(1) + 3(2\cos^{2}x)(1)^{2}]-6\cos^{2}x + 3[(a-b)^{3} = a^{3} - b^{3} - 3a^{2}b+ 3ab^{2}]$
= $32\cos^{6}x - 4 - 48 \cos^{4}x + 24 \cos^{2}x - 6\cos^{2}x + 3$
= $32\cos^{6}x - 48 \cos^{4}x + 18\cos^{2}x - 1 =$ R.H.S.

Question 1: Prove that $\small 2\cos\frac{\pi }{13}\cos\frac{9\pi }{13}+\cos\frac{3\pi }{13}+\cos\frac{5\pi }{13}=0$

Answer:
We know that
cos A+ cos B = $2\cos(\frac{A+B}{2})\cos(\frac{A-B}{2})$
we use this in our problem
$\small 2\cos\frac{\pi }{13}\cos\frac{9\pi }{13}+2\cos\frac{(\frac{3\pi }{13}+\frac{5\pi}{13})}{2}\cos\frac{(\frac{3\pi}{13}-\frac{5\pi }{13})}{2}$
= $\small 2\cos\frac{\pi }{13}\cos\frac{9\pi }{13}+2\cos\frac{4\pi }{13}\cos\frac{-\pi}{13}$ ( we know that cos(-x) = cos x )
= $\small 2\cos\frac{\pi }{13}\cos\frac{9\pi }{13}+2\cos\frac{4\pi }{13}\cos\frac{\pi}{13}$
= $\small 2\cos\frac{\pi }{13}(\cos\frac{9\pi }{13}+\cos\frac{4\pi }{13})$
again use the above identity
= $\small 2\cos\frac{\pi }{13}(2\cos(\frac{\frac{9\pi }{13}+\frac{4\pi }{13}}{2})\cos(\frac{\frac{9\pi }{13}-\frac{4\pi }{13}}{2})$
= $\small 2\cos\frac{\pi }{13}2\cos\frac{\pi }{2}\cos\frac{5\pi }{26}$
we know that $\small \cos\frac{\pi }{2}$ = 0
So, $\small 2\cos\frac{\pi }{13}2\cos\frac{\pi }{2}\cos\frac{5\pi }{26}$ = 0 = R.H.S.

Question 2: Prove that $\small (\sin 3x + \sin x)\sin x + (\cos 3x - \cos x )\cos x = 0$

Answer:
We know that
$\sin3x=3\sin x - 4\sin^{3}x$ and $\cos3x=4\cos^{3}x - 3\cos x$
We use this in our problem
$\small (\sin 3x + \sin x)\sin x + (\cos 3x - \cos x )\cos x$
= $(3\sin x - 4\sin^{3}x+ \sin x) \sin x$ + $(4\cos^{3}x - 3\cos x- \cos x)\cos x$
= (4sinx - 4 $\small \sin^{3}x$ )sin x + (4 $\small \cos^{3}x$ - 4cos x)cos x
Now take the 4sinx common from 1st term and -4cosx from 2nd term
= 4 $\small \sin^{2}x$ (1 - $\small \sin^{2}x$ ) - 4 $\small \cos^{2}x$ (1 - $\small \cos^{2}x$ )
= 4 $\small \sin^{2}x$ $\small \cos^{2}x$ - 4 $\small \cos^{2}x$ $\small \sin^{2}x$ ($\small \because \cos^{2}x = 1 - \sin^2x$ and $\sin^{2}x = 1 -\cos^{2}x$)
= 0 = R.H.S.

Question 3: Prove that $\small (\cos x + \cos y)^{2} + (\sin x - \sin y)^{2} = 4 \cos^{2}\left ( \frac{x+y}{2} \right )$

Answer:
We know that $(a+b)^{2} = a^{2} + 2ab + b^{2}$ and $(a-b)^{2} = a^{2} - 2ab + b^{2}$
We use these two in our problem
$(\sin x-\sin y)^{2} = \sin^{2}x - 2\sin x\sin y + \sin^{2}y$ and $(\cos x+\cos y)^{2} = \cos^{2}x + 2\cos x\cos y + \cos^{2}y$
$\small (\cos x + \cos y)^{2} + (\sin x - \sin y)^{2}$ = $\cos^{2}x + 2\cos x\cos y + \cos^{2}y$ + $\sin^{2}x - 2\sin x\sin y + \sin^{2}y$
= 1 + 2 cos x cos y + 1 - 2 sin x sin y $\left ( \because \sin^{2}x + \cos^{2}x = 1\ and \ \sin^{2}y + \cos^{2}y = 1 \right )$
= 2 + 2(cos x cos y - sin x sin y)
= 2 + 2cos(x + y)
= 2(1 + cos(x + y) )
Now we can write
$\cos(x + y) =2\cos^{2}\frac{(x + y)}{2} - 1$ $\left ( \because \cos2x = 2\cos^{2}x - 1 \ \Rightarrow \cos x = 2\cos^{2}\frac{x}{2} - 1\right )$
= $2(1 + 2\cos^{2}\frac{(x + y)}{2} - 1)$
= $4\cos^{2}\frac{(x + y)}{2}$
= R.H.S.

Question 4: Prove that $\small (\cos x-\cos y)^{2} + (\sin x - \sin y)^{2} = 4\sin^{2}\left ( \frac{x-y}{2} \right )$

Answer:
We know that $(a+b)^{2} = a^{2} + 2ab + b^{2}$ and $(a-b)^{2} = a^{2} - 2ab + b^{2}$
We use these two in our problem
$(\sin x-\sin y)^{2} = \sin^{2}x - 2\sin x\sin y + \sin^{2}y$ and $(\cos x-\cos y)^{2} = \cos^{2}x - 2\cos x\cos y + \cos^{2}y$
$\small (\cos x - \cos y)^{2} + (\sin x - \sin y)^{2}$ = $\cos^{2}x - 2\cos x\cos y + \cos^{2}y$ + $\sin^{2}x - 2\sin x\sin y + \sin^{2}y$
= 1 - 2cos x cos y + 1 - 2sin x sin y $\left ( \because \sin^{2}x + \cos^{2}x = 1\ and \ \sin^{2}y + \cos^{2}y = 1 \right )$
= 2 - 2(cos x cos y + sin x sin y)
= 2 - 2cos(x - y) $\small (\because \cos(x-y) =\cos x \cos y + \sin x \sin y)$
= 2(1 - cos(x - y) )
Now we can write
$\cos(x - y) = 1 -2\sin^{2}\frac{(x - y)}{2}$ $\left ( \because \cos2x = 1 - 2\sin^{2}x \ \Rightarrow \cos x = 1 - 2\sin^{2}\frac{x}{2} \right )$
So, $2(1 - \cos(x - y) ) = 2(1 - ( 1 -2\sin^{2}\frac{(x - y)}{2}))$
= $4\sin^{2}\frac{(x - y)}{2}$ = R.H.S.

Question 5: Prove that $\small \sin x + \sin 3x + \sin 5x + \sin 7x = 4\cos x\cos2x \sin4x$

Answer:
we know that $\sin A + \sin B =2\sin\frac{A+B}{2}\cos\frac{A-B}{2}$
We use this identity in our problem
If we notice we need sin4x in our final result so it is better if we need a combination of sin7x and sin x , sin3x and sin5x to get sin4x.
$(\sin7x + \sin x) + (\sin5x + \sin3x) = 2\sin\frac{7x+x}{2}\cos\frac{7x-x}{2}$ $+2\sin\frac{5x+3x}{2}\cos\frac{5x-3x}{2}$
$=$ $2\sin4x\cos3x + 2\sin4x\cos x$
take 2sin4x common
= 2sin4x(cos3x + cosx)
We know that
$\cos A + \cos B =2\cos\frac{A+B}{2}\cos\frac{A-B}{2}$
We use this
$\cos3x + \cos x =2\cos\frac{3x+x}{2}\cos\frac{3x-x}{2}$
= $2\cos2x\cos x$
Now 2sin4x(cos3x + cosx) = 2sin4x( $2\cos2x\cos x$)
= $4\cos x \cos2x\sin4x$ = R.H.S.

Question 6: Prove that $\small \frac{(\sin 7x + \sin 5x) + (\sin9x + \sin 3x)}{(\cos7x + \cos5x) + (\cos9x + \cos3x)} = \tan6x$

Answer:
We know that
$\sin A + \sin B = 2\sin\frac{A+B}{2}\cos\frac{A-B}{2}$
$\cos A + \cos B =2\cos\frac{A+B}{2}\cos\frac{A-B}{2}$
We use these two identities in our problem
sin7x + sin5x = $2\sin\frac{7x+5x}{2}\cos\frac{7x-5x}{2}$ = $2\sin6x\cos x$
sin 9x + sin 3x = $2\sin\frac{9x+3x}{2}\cos\frac{9x-3x}{2}$ = $2\sin6x\cos 3x$
cos 7x + cos5x = $2\cos\frac{7x+5x}{2}\cos\frac{7x-5x}{2}$ = $2\cos6x\cos x$
cos 9x + cos3x = $2\cos\frac{9x+3x}{2}\cos\frac{9x-3x}{2}$ = $2\cos6x\cos 3x$
$\small \frac{(\sin 7x + \sin 5x) + (\sin9x + \sin 3x)}{(\cos7x + \cos5x) + (\cos9x + \cos3x)}$ = $\small \frac{(2\sin 6x\cos x) + (2\sin6x \cos3x)}{(2\cos6x cos x) + (2\cos6x \cos3x)}$
= $\small \frac{2\sin6x(\cos x + \cos3x)}{2\cos6x (\cos x + \cos3x)} = \tan6x$ = R.H.S. $\small \left ( \because \frac{\sin x}{\cos x} = \tan x\right )$

Question:7: Prove that $\small \sin3x + \sin2x - \sin x = 4\sin x \cos\frac{x}{2}\cos\frac{3x}{2}$

Answer:
We know that
$\cos A + \cos B = 2\cos\frac{A+B}{2}\cos\frac{A-B}{2}$
$\sin A - \sin B = 2\cos\frac{A+B}{2}\sin\frac{A-B}{2}$
We use these identities
$\sin3x - \sin x = 2\cos\frac{3x+x}{2}\sin\frac{3x-x}{2}$
$= 2\cos2x\sin x$
sin2x + $2\cos2x\sin x$ = 2sinx cosx + $2\cos2x\sin x$
take 2 sinx common
$2\sin x ( \cos x + \cos2x) = 2\sin x(2\cos\frac{2x+x}{2}\cos\frac{2x-x}{2})$
$= 2\sin x(2\cos\frac{3x}{2}\cos\frac{x}{2})$
$= 4\sin x\cos\frac{3x}{2}\cos\frac{x}{2} =$ R.H.S.

Question 8: Find $\small \sin\frac{x}{2} , \cos\frac{x}{2} , and \tan\frac{x}{2}$ in $\small \tan x = - \frac{4}{3}$ , x in quadrant II.

Answer:
tan x = $-\frac{4}{3}$
We know that ,
$\sec^{2}x = 1 + \tan^{2}x$
$= 1 +\left ( -\frac{4}{3} \right )^{2}$
$= 1 + \frac{16}{9}$ = $\frac{25}{9}$
$\sec x = \sqrt{\frac{25}{9}}$ = $\pm\frac{5}{3}$
x lies in II quadrant thats why sec x is -ve
So, $\sec x =-\frac{5}{3}$
Now, $\cos x = \frac{1}{\sec x}$ = $-\frac{3}{5}$
We know that,
$\cos x = 2\cos^{2}\frac{x}{2}- 1$ ( $\because \cos2x = 2\cos^{2}x - 1 \Rightarrow \cos x = 2\cos^{2}\frac{x}{2} - 1$ )
⇒ $-\frac{3}{5}+ 1 = 2$ $\cos^{2}\frac{x}{2}$
⇒ $\frac{-3+5}{5}$ = $2\cos^{2}\frac{x}{2}$
⇒ $\frac{2}{5}$ = $2\cos^{2}\frac{x}{2}$
⇒ $\cos^{2}\frac{x}{2}$ = $\frac{1}{5}$
⇒ $\cos\frac{x}{2}$ = $\sqrt{\frac{1}{5}}$ = $\pm\frac{1}{\sqrt5}$
x lies in II quadrant so value of $\cos\frac{x}{2}$ is +ve
$\cos\frac{x}{2}$ = $\frac{1}{\sqrt5} = \frac{\sqrt5}{5}$
we know that
$\cos x =1 - 2\sin^{2}\frac{x}{2}$
⇒ $2\sin^{2}\frac{x}{2}$ = 1 - $(-\frac{3}{5})$ = $\frac{8}{5}$
⇒ $\sin^{2}\frac{x}{2} = \frac{4}{5}\\ \\=\sin\frac{x}{2} = \sqrt{ \frac{4}{5}} = \pm \frac{2}{\sqrt{5}}$
x lies in II quadrant So value of sin x is +ve
$\sin\frac{x}{2} = \frac{2}{\sqrt{}5} = \frac{2\sqrt5}{5}$
$\tan \frac{x}{2} = \frac{\sin\frac{x}{2}}{\cos\frac{x}{2}} = \frac{\frac{2\sqrt5}{5}}{\left ( \frac{\sqrt5}{5} \right )} = 2$

Question 9: Find $\small \sin\frac{x}{2} , \cos\frac{x}{2} , and \tan\frac{x}{2}$ in $\small \cos x = -\frac{1}{3}$ , x in quadrant III

Answer:
$\pi < x < \frac{3\pi}{2}⇒ \frac{\pi}{2} < \frac{x}{2} < \frac{3\pi}{4}$
We know that
cos x = $2\cos^{2}\frac{x}{2} - 1$
$2\cos^{2}\frac{x}{2} =$ cos x + 1 = $\left ( -\frac{1}{3} \right )$ + 1 = $\left ( \frac{-1+3}{3} \right )$ = $\frac{2}{3}$
⇒ $\cos\frac{x}{2} = \sqrt{ \frac{1}{3}} = \pm \frac{1}{\sqrt3}$
⇒ $\cos\frac{x}{2} = - \frac{1}{\sqrt3} = - \frac{\sqrt3}{3}$ (As x lies in 3rd quadrant)
we know that
cos x = $1 - 2\sin^{2}\frac{x}{2}$
⇒ $2\sin^{2}\frac{x}{2} = 1 - \cos x$ = 1 - $\left ( -\frac{1}{3} \right )$ = $\frac{3+1}{3}$ = $\frac{4}{3}$
⇒ $2\sin^{2}\frac{x}{2} = \frac{4}{3}⇒ \sin^{2}\frac{x}{2} = \frac{2}{3}⇒ \sin\frac{x}{2} = \pm \sqrt{ \frac{2}{3}} = \frac{\sqrt6}{3}$
Because $\sin\frac{x}{2}$ is +ve in given quadrant
$\tan\frac{x}{2} = \frac{\sin\frac{x}{2}}{\cos\frac{x}{2}} = \frac{\frac{\sqrt6}{3}}{\frac{-\sqrt3}{3}} = - \sqrt2$

Question 10: Find $\small \sin\frac{x}{2} , \cos\frac{x}{2} , and \tan\frac{x}{2}$ in $\small \sin x = \frac{1}{4}$ ,x in quadrant II

Answer:
$\frac{\pi}{2} < x < \pi⇒ \frac{\pi}{4} < \frac{x}{2} < \frac{\pi}{2}$ all functions are positive in this range
We know that
$\cos^{2}x = 1 - \sin^{2}x$ = 1 - $\left ( \frac{1}{4} \right )^{2}$ = $1 - \frac{1}{16}$ = $\frac{15}{16}$
cos x = $\sqrt\frac{15}{16} = \pm \frac{\sqrt15}{4} = - \frac{\sqrt15}{4}$ (cos x is -ve in II quadrant)
We know that
cosx = $2\cos^{2}\frac{x}{2} - 1$
$2\cos^{2}\frac{x}{2} = \cos x + 1 = -\frac{\sqrt15}{4} + 1 = \frac{-\sqrt15+4}{4}$
$\cos^{2}\frac{x}{2} = \frac{-\sqrt15+4}{8}$
$\cos\frac{x}{2} = \pm \sqrt\frac{-\sqrt15+4}{8} = \frac{\sqrt{-\sqrt15+4}}{2\sqrt2} = \frac{\sqrt{8-2\sqrt15}}{4}$ (because all functions are posititve in given range)
Similarly,
cos x = $1-2\sin^{2}\frac{x}{2}$
$2\sin^{2}\frac{x}{2} = 1 - \cos x⇒ 2\sin^{2}\frac{x}{2} = 1 -\left (\frac{-\sqrt15}{4} \right ) = \frac{4+\sqrt15}{4}$
$\sin\frac{x}{2} = \pm \sqrt\frac{\sqrt15+4}{8} = \frac{\sqrt{\sqrt15+4}}{2\sqrt2} = \frac{\sqrt{8+2\sqrt15}}{4}$ (because all functions are posititve in given range)
$\tan\frac{x}{2} = \frac{\sin\frac{x}{2}}{\cos\frac{x}{2}} = \frac{\frac{\sqrt{8+2\sqrt15}}{4}}{\frac{\sqrt{8-2\sqrt15}}{4}} = \frac{{8+2\sqrt15}}{\sqrt{64 - 15\times4}} = \frac{{8+2\sqrt15}}{\sqrt{4}} = 4 + \sqrt15$