NCERT Solutions for Class 11 Maths Chapter 9 Straight Lines

A straight line is defined as a line traced by a point travelling in a constant direction with zero curvature. In other words, the shortest distance between two points is called a straight line. It lacks width, depth, or curvature, and it extends infinitely in both directions. It is a 1-D entity that can be placed within spaces of greater dimensions. Key topics in Chapter 9 of Class 11 Mathematics include definitions of the straight line, line slope, collinearity of two points, the angle between points, horizontal and vertical lines, the general equation of a line, and conditions for parallel or perpendicular lines, as well as the distance from a point to a line. The main objective of these Class 11 NCERT solutions is to prepare students efficiently and boost their confidence for the board exam and other competitive exams.

This article on NCERT solutions for class 11 Maths Chapter 9 Straight Lines offers clear and step-by-step solutions for the exercise problems given in the NCERT book. This chapter holds significant importance for the final examination of CBSE class 11, as well as for various competitive tests such as JEE Mains, JEE Advanced, BITSAT, and others. It is advisable to work through all the NCERT problems, including examples and the miscellaneous exercises, to master this chapter. For syllabus, notes, and PDF, refer to this link: NCERT.

Class 11 Maths Chapter 9 question answer PDF Free Download

Download PDF

Straight lines class 11 NCERT solutions (Exercise)

Class 11 Maths Chapter 9 question answer - Exercise: 9.1 (Page no. 158, Total questions- 11)

Question:1 Draw a quadrilateral in the Cartesian plane, whose vertices are $(-4,5),(0,7),(5,-5)$ and $(-4,-2)$. Also, find its area.

Answer:

Area of $A B C D=$ Area of $A B C+$ Area of $A C D$ Now, we know that the area of a triangle with vertices $\left(x_1, y_1\right),\left(x_2, y_2\right)$ and $\left(x_3, y_3\right)$ is given by $A=\frac{1}{2}\left|x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right|$. Therefore, Area of triangle $\mathrm{ABC}=\frac{1}{2}|-4(7+5)+0(-5-5)+5(5-7)|=\frac{1}{2}|-48-10|=\frac{58}{2}=29$

Similarly, the Area of triangle ACD

$ = \frac{1}{2} \left|-4(-5+2)+5(-2-5)+-4(5+5) \right| = \frac{1}{2} \left|12-35-40\right| = \frac{63}{2} \text {Now,}$

Area of $A B C D=$ Area of $A B C+$ Area of $A C D$

$= \frac{121}{2} \text {units}$

Question:2 The base of an equilateral triangle with side $2a$ lies along the $y$ -axis such that the mid-point of the base is at the origin. Find the vertices of the triangle.

Answer:

It is given that it is an equilateral triangle and the length of all sides is 2a
The base of the triangle lies on the y-axis, such that the origin is the midpoint.
Therefore,
Coordinates of point A and B are $(0,a)$ and $(0,-a)$ respectively
Now,
Apply Pythagoras theorem in triangle AOC.
$AC^2=OA^2+OC^2$
$(2a)^2=a^2+OC^2$
$OC^2= 4a^2-a^2=3a^2$
$OC=\pm \sqrt3 a$
Therefore, the coordinates of the vertices of the triangle are
$(0,a),(0,-a) and(\sqrt3a,0) \ \ or \ \ (0,a),(0,-a) and(-\sqrt3a,0)$

Question:3(i) Find the distance between $P(x_1,y_1)$ and $Q(x_2,y_2)$ when :

PQ is parallel to the $y$ -axis.

Answer: When PQ is parallel to the y-axis
then, x coordinates are equal i.e. $x_2 = x_1$
Now, we know that the distance between two points is given by
$D = |\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}|$
Now, in this case, $x_2 = x_1$
Therefore,
$D = |\sqrt{(x_2-x_2)^2+(y_2-y_1)^2}| = |\sqrt{(y_2-y_1)^2}|= |(y_2-y_1)|$
Therefore, the distance between $P(x_1,y_1)$ and $Q(x_2,y_2)$ when PQ is parallel to y-axis is $|(y_2-y_1)|$

Question:3(ii) Find the distance between $P(x_1,y_1)$ and $Q(x_2,y_2)$ when :

PQ is parallel to the $x$ -axis.

Answer:

When PQ is parallel to the x-axis
then, x coordinates are equal i.e. $y_2 = y_1$
Now, we know that the distance between two points is given by
$D = |\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}|$
Now, in this case, $y_2 = y_1$
Therefore,
$D = |\sqrt{(x_2-x_1)^2+(y_2-y_2)^2}| = |\sqrt{(x_2-x_1)^2}|= |x_2-x_1|$
Therefore, the distance between $P(x_1,y_1)$ and $Q(x_2,y_2)$ when PQ is parallel to the x-axis is $|x_2-x_1|$

Question:4 Find a point on the x-axis, which is equidistant from the points $(7,6)$ and $(3,4)$.

Answer:

The point is on the x-axis, therefore, the y-coordinate is 0
Let's assume the point is (x, 0)
Now, it is given that the given point (x, 0) is equidistant from points (7, 6) and (3, 4)
We know that
The distance between two points is given by
$D = |\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}|$
Now,
$D_1 = |\sqrt{(x-7)^2+(0-6)^2}|= |\sqrt{x^2+49-14x+36}|= |\sqrt{x^2-14x+85}|$
and
$D_2 = |\sqrt{(x-3)^2+(0-4)^2}|= |\sqrt{x^2+9-6x+16}|= |\sqrt{x^2-6x+25}|$
Now, according to the given condition
$D_1=D_2$
$|\sqrt{x^2-14x+85}|= |\sqrt{x^2-6x+25}|$
Squaring both sides
$x^2-14x+85= x^2-6x+25\\ 8x = 60\\ x=\frac{60}{8}= \frac{15}{2}$
Therefore, the point is $( \frac{15}{2},0)$

Question:5 Find the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points $P(0,-4)$ and $B(8,0)$.

Answer:

Mid-point of the line joining the points $P(0,-4)$ and $B(8,0)$ . is
$l = \left ( \frac{8}{2},\frac{-4}{2} \right ) = (4,-2)$
It is given that the line also passes through the origin, which means it passes through the point (0, 0)
Now, we have two points on the line, so we can find the slope of a line by using the formula.
$m = \frac{y_2-y_1}{x_2-x_1}$
$m = \frac{-2-0}{4-0} = \frac{-2}{4}= \frac{-1}{2}$
Therefore, the slope of the line is $\frac{-1}{2}$

Question:6 Without using the Pythagoras theorem, show that the points $(4,4),(3,5)$ and $(-1,-1),$ are the vertices of a right angled triangle.

Answer:

It is given that point A(4,4) , B(3,5) and C(-1,-1) are the vertices of a right-angled triangle
Now,
We know that the distance between two points is given by
$D = |\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}|$
Length of AB $= |\sqrt{(4-3)^2+(4-5)^2}|= |\sqrt{1+1}|= \sqrt2$
Length of BC $= |\sqrt{(3+1)^2+(5+1)^2}|= |\sqrt{16+36}|= \sqrt{52}$
Length of AC $= |\sqrt{(4+1)^2+(4+1)^2}|= |\sqrt{25+25}|= \sqrt{50}$
Now, we know that Pythagoras' theorem is
$H^2= B^2+L^2$
Is clear that
$(\sqrt{52})^2=(\sqrt{50})^2+(\sqrt 2)^2\\ 52 = 52\\ i.e\\ BC^2= AB^2+AC^2$
Hence proved

Question:7 Find the slope of the line, which makes an angle of $30^{\circ}$ with the positive direction of $y$ -axis measured anticlockwise.

Answer:

It is given that the line makes an angle of $30^{\circ}$ with the positive direction of $y$ -axis measured anticlockwise
Now, we know that
$m = \tan \theta$
line makes an angle of $30^{\circ}$ with the positive direction of $y$ -axis
Therefore, the angle made by the line with the positive x-axis is = $90^{^\circ}+30^{^\circ}= 120^\circ$
Now,
$m = \tan 120^\circ = -\tan 60^\circ = -\sqrt3$
Therefore, the slope of the line is $-\sqrt3$

Question:8 Without using the distance formula, show that points $(-2,-1),(4,0),(3,3)$ and $(-3,2)$ are the vertices of a parallelogram.

Answer:

Given points are $A(-2, -1),B(4,0),C(3,3)$ and $D(-3,2)$
We know the pair of opposite sides are parallel to each other in a parallelogram.
Which means their slopes are also equal
$Slope = m = \frac{y_2-y_1}{x_2-x_1}$
The slope of AB =

$\frac{0+1}{4+2} = \frac{1}{6}$

The slope of BC =

$\frac{3-0}{3-4} = \frac{3}{-1} = -3$

The slope of CD =

$\frac{2-3}{-3-3} = \frac{-1}{-6} = \frac{1}{6}$

The slope of AD

= $\frac{2+1}{-3+2} = \frac{3}{-1} = -3$
We can see that
The slope of AB = Slope of CD (which means they are parallel)
and
The slope of BC = Slope of AD (which means they are parallel)
Hence, a pair of opposite sides are parallel to each other.
Therefore, we can say that points $(-2,-1),(4,0),(3,3)$ and $(-3,2)$ are the vertices of a parallelogram

Question:9 Find the angle between the x-axis and the line joining the points $(3,-1)$ and $(4,-2)$.

Answer:

We know that
$m = \tan \theta$
So, we need to find the slope of the line joining the points (3,-1) and (4,-2)
Now,
$m = \frac{y_2-y_1}{x_2-x_1}= \frac{-2+1}{4-3} = -1$
$\tan \theta = -1$
$\tan \theta = \tan \frac{3\pi}{4} = \tan 135^\circ$
$\theta = \frac{3\pi}{4} = 135^\circ$
Therefore, the angle made by the line with the positive x-axis when measured in anti-clockwise direction is $135^\circ$

Question:10 The slope of a line is twice the slope of another line. If the tangent of the angle between them is $\frac{1}{3},$ find the slopes of the lines.

Answer:

Let $m_1 \ and \ m_2$ are the slopes of lines and $\theta$ is the angle between them
Then, we know that
$\tan \theta = \left | \frac{m_2-m_1}{1+m_1m_2} \right |$
It is given that $m_2 = 2m_1$ and

$\tan \theta = \frac{1}{3}$
Now,
$\frac{1}{3}= \left | \frac{2m_1-m_1}{1+m_1.2m_1} \right |$
$\frac{1}{3}= \left | \frac{m_1}{1+2m^2_1} \right |$
Now,
$3|m_1|= 1+2|m^2_1|\\ 2|m^2_1|-3|m_1|+ 1 = 0\\ 2|m^2_1|-2|m_1|-|m_1|+1=0\\ (2|m_1|-1)(|m_1|-1)= 0\\ |m_1|= \frac{1}{2} \ \ \ \ \ or \ \ \ \ \ \ |m_1| = 1$
Now,
$m_1 = \frac{1}{2} \ or \ \frac{-1}{2} \ or \ 1 \ or \ -1$
According to which value of $m_2 = 1 \ or \ -1 \ or \ 2 \ or \ -2$
Therefore, $m_1,m_2 = \frac{1}{2},1 \ or \ \frac{-1}{2},-1 \ or \ 1,2 \ or \ -1,-2$

Question:11 A line passes through $(x_1,y_1)$ and $(h,k)$ . If the slope of the line is $m$, show that $k-y_1=m(h-x_1)$.

Answer:

Given that A line passes through $(x_1,y_1)$ and $(h,k)$ and slope of the line is m
Now,
$m = \frac{y_2-y_1}{x_2-x_1}$
$\Rightarrow m = \frac{k-y_1}{h-x_1}$
$\Rightarrow (k-y_1)= m(h-x_1)$
Hence proved

Straight lines class 11 solutions - Exercise: 9.2 (Page no. 163, Total questions- 19)

Question:1 Find the equation of the line that satisfies the given conditions:

Write the equations for the $x$ -and $y$ -axes.

Answer:

The equation of the x-axis is y = 0
and
The equation of the y-axis is x = 0

Question:2 Find the equation of the line which satisfies the given conditions:

Passing through the point $(-4,3)$ with slope $\frac{1}{2}$ .

Answer:

We know that , equation of line passing through point $(x_1,y_1)$ and with slope m is given by
$(y-y_1)=m(x-x_1)$
Now, equation of line passing through point (-4,3) and with slope $\frac{1}{2}$ is
$(y-3)=\frac{1}{2}(x-(-4))\\ 2y-6=x+4\\ x-2y+10 = 0$
Therefore, the equation of the line is $x-2y+10 = 0$

Question:3 Find the equation of the line which satisfies the given conditions:

Passing through $(0,0)$ with slope $m$ .

Answer:

We know that the equation of the line passing through the point $(x_1,y_1)$ and with slope m is given by
$(y-y_1)=m(x-x_1)$
Now, the equation of the line passing through the point (0,0) and with slope m is
$(y-0)=m(x-0)\\ y = mx$
Therefore, the equation of the line is $y = mx$

Question:4 Find the equation of the line which satisfies the given conditions:

Passing through $(2,2\sqrt{3})$ and inclined with the x-axis at an angle of $75^{\circ}$.

Answer:

We know that the equation of the line passing through the point $(x_1,y_1)$ and with slope m is given by
$(y-y_1)=m(x-x_1)$
We know that
$m = \tan \theta$
Where $\theta$ is the angle made by the line with the positive x-axis, measured in the anti-clockwise direction
$m = \tan75^\circ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because \theta=75^\circ \ given)$
$m = \frac{\sqrt3+1}{\sqrt3-1}$
Now, the equation of the line passing through the point $(2,2\sqrt3)$ and with slope $m = \frac{\sqrt3+1}{\sqrt3-1}$ is
$(y-2\sqrt3)=\frac{\sqrt3+1}{\sqrt3-1}(x-2)\\ \\ (\sqrt3-1)(y-2\sqrt3)=(\sqrt3+1)(x-2)\\ (\sqrt3-1)y-6+2\sqrt3= (\sqrt3+1)x-2\sqrt3-2\\ (\sqrt3+1)x-(\sqrt3-1)y = 4(\sqrt3-1)$
Therefore, the equation of the line is $(\sqrt3+1)x-(\sqrt3-1)y = 4(\sqrt3-1)$

Question:5 Find the equation of the line which satisfies the given conditions:

Intersecting the $x$ -axis at a distance of $3$ units to the left of origin with slope $-2$.

Answer:

We know that the equation of the line passing through the point $(x_1,y_1)$ and with slope m is given by
$(y-y_1)=m(x-x_1)$
Line Intersecting the $x$ -axis at a distance of $3$ units to the left of the origin, which means the point is (-3,0)
Now, the equation of the line passing through the point (-3,0) and with slope -2 is
$(y-0)= -2(x-(-3))\\ y = -2x-6\\ 2x+y+6=0$
Therefore, the equation of the line is $2x+y+6=0$

Question:6 Find the equation of the line which satisfies the given conditions:

Intersecting the $y$ -axis at a distance of $2$ units above the origin and making an angle of $30^{\circ}$ with the positive direction of the x-axis.

Answer:

We know that , equation of line passing through point $(x_1,y_1)$ and with slope m is given by
$(y-y_1)=m(x-x_1)$
Line Intersecting the y-axis at a distance of 2 units above the origin, which means the point is (0,2)
We know that

$m = \tan \theta \Rightarrow m = \tan 30^\circ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because \theta = 30 ^\circ \ given)\\ m = \frac{1}{\sqrt3}$
Now, the equation of the line passing through the point (0,2) and with slope $\frac{1}{\sqrt3}$ is
$(y-2)= \frac{1}{\sqrt3}(x-0)\\ \sqrt3(y-2)= x\\ x-\sqrt3y+2\sqrt3=0$
Therefore, the equation of the line is $x-\sqrt3y+2\sqrt3=0$

Question:7 Find the equation of the line which satisfies the given conditions:

Passing through the points $(-1,1)$ and $(2,-4)$ .

Answer:

We know that , equation of line passing through point $(x_1,y_1)$ and with slope m is given by
$(y-y_1)=m(x-x_1)$
Now, it is given that the line passes through the point (-1, 1) and (2, -4)
$m = \frac{y_2-y_1}{x_2-x_1}\\ \\ m = \frac{-4-1}{2+1}= \frac{-5}{3}$
Now, equation of line passing through point (-1,1) and with slope $\frac{-5}{3}$ is
$(y-1)= \frac{-5}{3}(x-(-1))\\ \\3(y-1)=-5(x+1)\\ 3y-3=-5x-5\\ 5x+3y+2=0$

Question:8 The vertices of $\Delta \hspace{1mm}PQR$ are $P(2,1),Q(-2,3)$ and $R(4,5)$ . Find the equation of the median through the vertex $R$.

Answer:

The vertices of $\Delta \hspace{1mm}PQR$ are $P(2,1),Q(-2,3)$ and $R(4,5)$
Let m be the median through vertex R
Coordinates of M (x, y ) = $\left ( \frac{2-2}{2},\frac{1+3}{2} \right )= (0,2)$
Now, the slope of line RM
$m = \frac{y_2-y_1}{x_2-x_1} = \frac{5-2}{4-0}= \frac{3}{4}$
Now, equation of line passing through point $(x_1,y_1)$ and with slope m is
$(y-y_1)= m(x-x_1)$
The equation of the line passing through the point (0, 2) and with slope $\frac{3}{4}$ is
$(y-2)= \frac{3}{4}(x-0)\\ \\ 4(y-2)=3x\\ 4y-8=3x\\ 3x-4y+8=0$
Therefore, the equation of the median is $3x-4y+8=0$

Question:9 Find the equation of the line passing through $(-3,5)$ and perpendicular to the line through the points $(2,5)$ and $(-3,6)$ .

Answer:

It is given that the line passing through $(-3,5)$ and perpendicular to the line through the points $(2,5)$ and $(-3,6)$
Let the slope of the line passing through the point (-3,5) be m and
The slope of the line passing through points (2,5) and (-3,6)
$m' = \frac{6-5}{-3-2}= \frac{1}{-5}$
Now this line is perpendicular to the line passing through the point (-3,5)
Therefore,
$m= -\frac{1}{m'} = -\frac{1}{\frac{1}{-5}}= 5$

Now, equation of line passing through point $(x_1,y_1)$ and with slope m is
$(y-y_1)= m(x-x_1)$
The equation of the line passing through the point (-3, 5) and with slope 5 is
$(y-5)= 5(x-(-3))\\ \\ (y-5)=5(x+3)\\ y-5=5x+15\\ 5x-y+20=0$
Therefore, the equation of the line is $5x-y+20=0$

Question:10 A line perpendicular to the line segment joining the points $(1,0)$ and $(2,3)$ divides it in the ratio $1:n$. Find the equation of the line.

Answer:

Co-ordinates of point which divide line segment joining the points $(1,0)$ and $(2,3)$ in the ratio $1:n$ is
$\left ( \frac{n(1)+1(2)}{1+n},\frac{n.(0)+1.(3)}{1+n} \right )= \left ( \frac{n+2}{1+n},\frac{3}{1+n} \right )$
Let the slope of the perpendicular line be m
And Slope of line segment joining the points $(1,0)$ and $(2,3)$ is
$m'= \frac{3-0}{2-1}= 3$
Now, the slope of the perpendicular line is
$m = -\frac{1}{m'}= -\frac{1}{3}$
Now, equation of line passing through point $(x_1,y_1)$ and with slope m is
$(y-y_1)= m(x-x_1)$
equation of line passing through point $\left ( \frac{n+2}{1+n},\frac{3}{1+n} \right )$ and with slope $-\frac{1}{3}$ is
$(y- \frac{3}{1+n})= -\frac{1}{3}(x- (\frac{n+2}{1+n}))\\ 3y(1+n)-9=-x(1+n)+n+2\\ x(1+n)+3y(1+n)=n+11$
Therefore, equation of line is $x(1+n)+3y(1+n)=n+11$

Question:11 Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point $(2,3)$.

Answer:

Let (a, b) be the intercept on the x and the y-axis respectively.
Then, the equation of the line is given by
$\frac{x}{a}+\frac{y}{b}= 1$
Intercepts are equal, which means a = b
$\frac{x}{a}+\frac{y}{a}= 1\\ \\ x+y = a$
Now, it is given that the line passes through the point (2,3)
Therefore,
$a = 2+ 3 = 5$
Therefore, the equation of the line is $x+ y = 5$

Question:12 Find the equation of the line passing through the point $(2,2)$ and cutting off intercepts on the axes whose sum is $9$.

Answer:

Let (a, b) be the intercept on the x and y axes respectively.
Then, the equation of the line is given by
$\frac{x}{a}+\frac{y}{b}= 1$
It is given that
a + b = 9
b = 9 - a
Now,
$\frac{x}{a}+\frac{y}{9-a } = 1\\ \\ x(9-a)+ay= a(9-a)\\ 9x-ax+ay=9a-a^2$
It is given that the line passes through the point (2, 2)
So,
$9(2)-2a+2a=9a-a^2\\ a^2-9a+18=0\\ a^2-6a-3a+18=0\\ (a-6)(a-3)= 0\\ a=6 \ \ \ \ \ \ or \ \ \ \ \ \ a = 3$

case (i) a = 6 b = 3
$\frac{x}{6}+\frac{y}{3}= 1\\ \\ x+2y = 6$

case (ii) a = 3 , b = 6
$\frac{x}{3}+\frac{y}{6}= 1\\ \\ 2x+y = 6$
Therefore, equation of line is 2x + y = 6 , x + 2y = 6

Question:13 Find equation of the line through the point $(0,2)$ making an angle $\frac{2\pi }{3}$ with the positive $x$ -axis. Also, find the equation of the line parallel to it and cross the $y$ -axis at a distance of $2$ units below the origin.

Answer:

We know that
$m = \tan \theta \\ m = \tan \frac{2\pi}{3} = -\sqrt3$
Now, the equation of the line passing through the point (0, 2) and with slope $-\sqrt3$ is
$(y-2)= -\sqrt3(x-0)\\ \sqrt3x+y-2=0$
Therefore, equation of line is $\sqrt3x+y-2=0$ -(i)

Now, it is given that the line crossing the $y$ -axis at a distance of $2$ units below the origin, which means the coordinates are (0,-2)
This line is parallel to the above line, which means the slope of both lines is equal.
Now, the equation of the line passing through the point (0, -2) and with slope $-\sqrt3$ is
$(y-(-2))= -\sqrt3(x-0)\\ \sqrt3x+y+2=0$
Therefore, the equation of the line is $\sqrt3x+y+2=0$

Question:14 The perpendicular from the origin to a line meets it at the point $(-2,9)$, find the equation of the line.

Answer:

Let the slope of the line be m
The slope of a perpendicular line that passes through the origin (0, 0) and (-2, 9) is
$m' = \frac{9-0}{-2-0}= \frac{9}{-2}$
Now, the slope of the line is
$m = -\frac{1}{m'}= \frac{2}{9}$
Now, the equation of the line passes through the point (-2, 9) and has slope $\frac{2}{9}$ is
$(y-9)=\frac{2}{9}(x-(-2))\\ \\ 9(y-9)=2(x+2)\\ 2x-9y+85 = 0$
Therefore, the equation of the line is $2x-9y+85 = 0$

Question:15 The length $L$ (in centimetres) of a copper rod is a linear function of its Celsius temperature $C$. In an experiment, if $L=124.942$ when $C=20$ and $L=125.134$ when $C=110$ , express $L$ in terms of $C$

Answer:

It is given that
If $C=20$ then $L=124.942$
and If $C=110$ then $L=125.134$
Now, if we assume C along the x-axis and L along the y-axis
Then, we will get the coordinates of two points (20, 124.942) and (110, 125.134)
Now, the relation between C and L is given by the equation.
$(L-124.942)= \frac{125.134-124.942}{110-20}(C-20)$
$(L-124.942)= \frac{0.192}{90}(C-20)$
$L= \frac{0.192}{90}(C-20)+124.942$
Which is the required relation

Question:16 The owner of a milk store finds that he can sell 980 litres of milk each week at $Rs\hspace{1mm}14/litre$ and $1220$ litres of milk each week at $Rs\hspace{1mm}16/litre$. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at $Rs\hspace{1mm}17/litre$

Answer:

It is given that the owner of a milk store sells
980 litres milk each week at $Rs\hspace{1mm}14/litre$
and $1220$ litres of milk each week at $Rs\hspace{1mm}16/litre$
Now, if we assume the rate of milk as the x-axis and the Litres of milk as the y-axis
Then, we will get the coordinates of two points, i.e. (14, 980) and (16, 1220)
Now, the relation between litres of milk and Rs/litre is given by the equation.
$(L-980)= \frac{1220-980}{16-14}(R-14)$
$(L-980)= \frac{240}{2}(R-14)$
$L-980= 120R-1680$
$L= 120R-700$
Now, at $Rs\hspace{1mm}17/litre$ he could sell
$L= 120\times 17-700= 2040-700= 1340$
He could sell 1340 litres of milk each week at $Rs\hspace{1mm}17/litre$

Question:17$P(a,b)$ is the mid-point of a line segment between axes. Show that equation of the line is $\frac{x}{a}+\frac{y}{b}=2$ .

Answer:

Now, the coordinates of point A are (0, y) and of point B are (x, 0)
The,
$\frac{x+0}{2}= a \ and \ \frac{0+y}{2}= b$
$x= 2a \ and \ y = 2b$
Therefore, the coordinates of point A are (0, 2b) and of point B are (2a, 0)
Now, the slope of the line passing through the points (0,2b) and (2a,0) is
$m = \frac{0-2b}{2a-0} = \frac{-2b}{2a}= \frac{-b}{a}$
Now, equation of line passing through point (2a,0) and with slope $\frac{-b}{a}$ is
$(y-0)= \frac{-b}{a}(x-2a)$
$\frac{y}{b}= - \frac{x}{a}+2$
$\frac{x}{a}+\frac{y}{b}= 2$
Hence proved

Question:18 Point $R(h,k)$ divides a line segment between the axes in the ratio $1:2$. Find the equation of the line.

Answer:

Let the coordinates of Point A be (x,0) and of Point B be (0,y)
It is given that point R(h, k) divides the line segment between the axes in the ratio $1:2$
Therefore,
R(h , k) $=\left ( \frac{1\times 0+2\times x}{1+2},\frac{1\times y+2\times 0}{1+2} \right )=\left ( \frac{2x}{3},\frac{y}{3} \right )$
$h = \frac{2x}{3} \ \ and \ \ k = \frac{y}{3}$
$x = \frac{3h}{2} \ \ and \ \ y = 3k$
Therefore, coordinates of point A is $\left ( \frac{3h}{2},0 \right )$ and of point B is $(0,3k)$
Now, slope of line passing through points $\left ( \frac{3h}{2},0 \right )$ and $(0,3k)$ is
$m = \frac{3k-0}{0-\frac{3h}{2}}= \frac{2k}{-h}$
Now, equation of line passing through point $(0,3k)$ and with slope $-\frac{2k}{h}$ is
$(y-3k)=-\frac{2k}{h}(x-0)$
$h(y-3k)=-2k(x)$
$yh-3kh=-2kx$
$2kx+yh=3kh$
Therefore, the equation of the line is $2kx+yh=3kh$

Question:19 By using the concept of the equation of a line, prove that the three points $(3,0),(-2,-2)$ and $(8,2)$ are collinear.

Answer:

Points are collinear if they lie on the same line
Now, given points are $A(3,0),B(-2,-2)$ and $C(8,2)$
The equation of the line passing through points A and B is
$(y-0)=\frac{0+2}{3+2}(x-3)$
$y=\frac{2}{5}(x-3)\Rightarrow 5y= 2(x-3)$
$2x-5y=6$
Therefore, the equation of the line passing through A and B is $2x-5y=6$

Now, the Equation of the line passing through points B and C is
$(y-2)=\frac{2+2}{8+2}(x-8)$
$(y-2)=\frac{4}{10}(x-8)$
$(y-2)=\frac{2}{5}(x-8) \Rightarrow 5(y-2)=2(x-8)$
$5y-10=2x-16$
$2x-5y=6$
Therefore, the Equation of the line passing through points B and C is $2x-5y=6$
When can we see that the Equation of the line passing through points A and B and through B and C is the same
By this we can say that points $A(3,0),B(-2,-2)$ and $C(8,2)$ are collinear points

Straight lines class 11 NCERT solutions - Exercise: 9.3 (Page no. 167, Total questions- 17)

Question:1(i) Reduce the following equations into slope-intercept form and find their slopes and the $y$ - intercepts.

$x+7y=0$

Answer:

Given the equation is
$x+7y=0$
We can rewrite it as
$y= -\frac{1}{7}x$ -(i)
Now, we know that the Slope-intercept form of the line is
$y = mx+C$ -(ii)
Where m is the slope and C is some constant
On comparing equation (i) with equation (ii)
We will get
$m =- \frac{1}{7}$ and $C = 0$
Therefore, slope and y-intercept are $-\frac{1}{7} \ and \ 0$ respectively

Question:1(ii) Reduce the following equations into slope-intercept form and find their slopes and the y-intercepts.

$6x+3y-5=0$

Answer:

Given the equation is
$6x+3y-5=0$
We can rewrite it as
$y= -\frac{6}{3}x+\frac{5}{3}\Rightarrow y = -2x+\frac{5}{3}$ -(i)
Now, we know that the Slope-intercept form of the line is
$y = mx+C$ -(ii)
Where m is the slope and C is some constant
On comparing equation (i) with equation (ii)
We will get
$m =- 2$ and $C = \frac{5}{3}$
Therefore, slope and y-intercept are $-2 \ and \ \frac{5}{3}$ respectively

Question:1(iii) Reduce the following equations into slope-intercept form and find their slopes and the y-intercepts.

$y=0.$

Answer:

Given the equation is
$y=0$ -(i)
Now, we know that the Slope-intercept form of the line is
$y = mx+C$ -(ii)
Where m is the slope and C is some constant
On comparing equation (i) with equation (ii)
We will get
$m =0$ and $C = 0$
Therefore, slope and y-intercept are $ 0$and $ 0$ respectively

Question:2(i) Reduce the following equations into intercept form and find their intercepts on the axes.

$3x+2y-12=0$

Answer:

Given the equation is
$3x+2y-12=0$
We can rewrite it as
$\frac{3x}{12}+\frac{2y}{12} = 1$
$\frac{x}{4}+\frac{y}{6} = 1$ -(i)
Now, we know that the intercept form of the line is
$\frac{x}{a}+\frac{y}{b} = 1$ -(ii)
Where a and b are intercepted on the x and y axes respectively
On comparing equation (i) and (ii)
We will get
a = 4 and b = 6
Therefore, intercepts on the x and y axes are 4 and 6 respectively

Question:2(ii) Reduce the following equations into intercept form and find their intercepts on the axes.

$4x-3y=6$

Answer:

Given the equation is
$4x-3y=6$
We can rewrite it as
$\frac{4x}{6}-\frac{3y}{6} = 1$
$\frac{x}{\frac{3}{2}}-\frac{y}{2} = 1$ -(i)
Now, we know that the intercept form of the line is
$\frac{x}{a}+\frac{y}{b} = 1$ -(ii)
Where a and b are intercepted on the x and y axes respectively
On comparing equation (i) and (ii)
We will get
$a = \frac{3}{2}$ and $b = -2$
Therefore, intercepts on x and y axis are $\frac{3}{2}$ and -2 respectively

Question:2(iii) Reduce the following equations into intercept form and find their intercepts on the axes.

$3y+2=0$

Answer:

Given the equation is
$3y+2=0$
We can rewrite it as
$y = \frac{-2}{3}$
Therefore, intercepts on y-axis are $\frac{-2}{3}$
And there is no intercept on the x-axis.

Question:3 Find the distance of the point $(-1,1)$ from the line $12(x+6)=5(y-2)$ .

Answer:

Given the equation of the line is
$12(x+6)=5(y-2)$
We can rewrite it as
$12x+72=5y-10$
$12x-5y+82=0$
Now, we know that
$d= \frac{|Ax_1+By_1+C|}{\sqrt{A^2+B^2}}$ where A and B are the coefficients of x and y and C is some constant and $(x_1,y_1)$ is point from which we need to find the distance
In this problem A = 12 , B = -5 , c = 82 and $(x_1,y_1)$ = (-1 , 1)
Therefore,
$d = \frac{|12.(-1)+(-5).1+82|}{\sqrt{12^2+(-5)^2}} = \frac{|-12-5+82|}{\sqrt{144+25}}=\frac{|65|}{\sqrt{169}}=\frac{65}{13}= 5$
Therefore, the distance of the point $(-1,1)$ from the line $12(x+6)=5(y-2)$ is 5 units

Question:4 Find the points on the x-axis, whose distances from the line $\frac{x}{3}+\frac{y}{4}=1$ are $4$ units.

Answer:

Given the equation of the line is
$\frac{x}{3}+\frac{y}{4}=1$
We can rewrite it as
$4x+3y-12=0$
Now, we know that
$d = \frac{|Ax_1+By_1+C|}{\sqrt{A^2+B^2}}$
In this problem A = 4 , B = 3 C = -12 and d = 4
point is on x-axis therefore $(x_1,y_1)$ = (x ,0)
Now,
$4= \frac{|4.x+3.0-12|}{\sqrt{4^2+3^2}}= \frac{|4x-12|}{\sqrt{16+9}}= \frac{|4x-12|}{\sqrt{25}}= \frac{|4x-12|}{5}$
$20=|4x-12|\\ 4|x-3|=20\\ |x-3|=5$
Now if x > 3
Then,
$|x-3|=x-3\\ x-3=5\\ x = 8$
Therefore, the point is (8,0)
and if x < 3
Then,
$|x-3|=-(x-3)\\ -x+3=5\\ x = -2$
Therefore, the point is (-2,0)
Therefore, the points on the x-axis, whose distances from the line $\frac{x}{3}+\frac{y}{4}=1$ are $4$ units are (8, 0) and (-2, 0)

Question:5(i) Find the distance between parallel lines $15x+8y-34=0$ and $15x+8y+31=0$.

Answer:

Given the equations of the lines are
$15x+8y-34=0$ and $15x+8y+31=0$
It is given that these lines are parallel.
Therefore,
$d = \frac{ |C_2-C_1|}{\sqrt{A^2+B^2}}$
$A = 15 , B = 8 , C_1= -34 \ and \ C_2 = 31$
Now,
$d = \frac{|31-(-34)|}{\sqrt{15^2+8^2}}= \frac{|31+34|}{\sqrt{225+64}}= \frac{|65|}{\sqrt{289}} = \frac{65}{17}$
Therefore, the distance between two lines is $\frac{65}{17} \ units$

Question:5(ii) Find the distance between parallel lines $l(x+y)+p=0$ and $l(x+y)-r = 0$

Answer:

Given the equations of the lines are
$l(x+y)+p=0$ and $l(x+y)-r = 0$
It is given that these lines are parallel.
Therefore,
$d = \frac{ |C_2-C_1|}{\sqrt{A^2+B^2}}$
$A = l , B = l , C_1= -r \ and \ C_2 = p$
Now,
$d = \frac{|p-(-r)|}{\sqrt{l^2+l^2}}= \frac{|p+r|}{\sqrt{2l^2}}= \frac{|p+r|}{\sqrt{2}|l|}$
Therefore, the distance between two lines is $\frac{1}{\sqrt2}\left | \frac{p+r}{l} \right |$

Question:6 Find the equation of the line parallel to the line $3x-4y+2=0$ and pass through the point $(-2,3)$.

Answer:

It is given that the line is parallel to the line $3x-4y+2=0$ which implies that the slopes of both lines are equal.
We can rewrite it as
$y = \frac{3x}{4}+\frac{1}{2}$
The slope of line $3x-4y+2=0$ = $\frac{3}{4}$
Now, the equation of the line passing through the point $(-2,3)$ and with slope $\frac{3}{4}$ is
$(y-3)=\frac{3}{4}(x-(-2))$
$4(y-3)=3(x+2)$
$4y-12=3x+6$
$3x-4y+18= 0$
Therefore, the equation of the line is $3x-4y+18= 0$

Question:7 Find equation of the line perpendicular to the line $x-7y+5=0$ and having $x$ intercept $3$.

Answer:

It is given that the line is perpendicular to the line $x-7y+5=0$
we can rewrite it as
$y = \frac{x}{7}+\frac{5}{7}$
Slope of line $x-7y+5=0$ ( m' ) = $\frac{1}{7}$
Now,
The slope of the line is $m = \frac{-1}{m'} = -7 \ \ \ \ \ \ \ \ \ \ \ (\because lines \ are \ perpendicular)$
Now, the equation of the line with $x$ intercept $3$ i.e. (3, 0) and with slope -7 is
$(y-0)=-7(x-3)$
$y = -7x+21$
$7x+y-21=0$

Question:8 Find angles between the lines $\sqrt{3}x+y=1$ and $x+\sqrt{3}y=1$ .

Answer:

Given the equations of the lines are
$\sqrt{3}x+y=1$ and $x+\sqrt{3}y=1$

Slope of line $\sqrt{3}x+y=1$ is, $m_1 = -\sqrt3$

And
Slope of line $x+\sqrt{3}y=1$ is , $m_2 = -\frac{1}{\sqrt3}$

Now, if $\theta$ is the angle between the lines
Then,

$\tan \theta = \left | \frac{m_2-m_1}{1+m_1m_2} \right |$

$\tan \theta = \left | \frac{-\frac{1}{\sqrt3}-(-\sqrt3)}{1+(-\sqrt3).\left ( -\frac{1}{\sqrt3} \right )} \right | = \left | \frac{\frac{-1+3}{\sqrt3}}{1+1} \right |=| \frac{1}{\sqrt3}|$

$\tan \theta = \frac{1}{\sqrt3} \ \ \ \ \ \ \ or \ \ \ \ \ \ \ \ \tan \theta = -\frac{1}{\sqrt3}$

$\theta = \frac{\pi}{6}=30^\circ \ \ \ \ \ \ \ or \ \ \ \ \ \ \theta =\frac{5\pi}{6}=150^\circ$

Therefore, the angle between the lines is $30^\circ \ and \ 150^\circ$

Question:9 The line through the points $(h,3)$ and $(4,1)$ intersects the line $7x-9y-19=0$ at right angle. Find the value of $h$.

Answer:

Line passing through the points ( h,3) and (4,1)

Therefore, the Slope of the line is

$m =\frac{y_2-y_1}{x_2-x_1}$

$m =\frac{3-1}{h-4}$

This line intersects the line $7x-9y-19=0$ at a right angle
Therefore, the Slope of both the lines is negative times the inverse of each other
Slope of line $7x-9y-19=0$ , $m'=\frac{7}{9}$
Now,
$m=-\frac{1}{m'}$
$\frac{2}{h-4}= -\frac{9}{7}$
$14=-9(h-4)$
$14=-9h+36$
$-9h= -22$
$h=\frac{22}{9}$
Therefore, the value of h is $\frac{22}{9}$

Question:10 Prove that the line through the point $(x_1,y_1)$ and parallel to the line $Ax+By+C=0$ is $A(x-x_1)+B(y-y_1)=0.$

Answer:

It is given that the line is parallel to the line $Ax+By+C=0$
Therefore, their slopes are equal.
The slope of line $Ax+By+C=0$ , $m'= \frac{-A}{B}$
Let the slope of the other line be m
Then,
$m =m'= \frac{-A}{B}$
Now, the equation of the line passing through the point $(x_1,y_1)$ and with slope $-\frac{A}{B}$ is
$(y-y_1)= -\frac{A}{B}(x-x_1)$
$B(y-y_1)= -A(x-x_1)$
$A(x-x_1)+B(y-y_1)= 0$
Hence proved

Question:11 Two lines passing through the point $(2,3)$ intersect each other at an angle of $60^{\circ}$. If the slope of one line is $2$, find the equation of the other line.

Answer:

Let the slopes of two lines be $ m_1$and $ m_2$ respectively.
It is given the lines intersect each other at an angle of $60^{\circ}$ and the slope of the line is 2
Now,
$m_1 = m\ and \ m_2= 2 \ and \ \theta = 60^\circ$
$\tan \theta = \left | \frac{m_2-m_1}{1+m_1m_2} \right |$
$\tan 60^\circ = \left | \frac{2-m}{1+2m} \right |$
$\sqrt3 = \left | \frac{2-m}{1+2m} \right |$
$\sqrt3 = \frac{2-m}{1+2m} \ \ \ \ \ \ or \ \ \ \ \ \ \ \ \ \sqrt 3 = -\left ( \frac{2-m}{1+2m} \right )$
$m = \frac{2-\sqrt3}{2\sqrt3+1} \ \ \ \ \ \ or \ \ \ \ \ \ \ \ \ \ m = \frac{-(2+\sqrt3)}{2\sqrt3-1}$
Now, the equation of the line passing through the point (2,3) and with slope $\frac{2-\sqrt3}{2\sqrt3+1}$ is
$(y-3)= \frac{2-\sqrt3}{2\sqrt3+1}(x-2)$
$(2\sqrt3+1)(y-3)=(2-\sqrt3)(x-2)$
$x(\sqrt3-2)+y(2\sqrt3+1)=-1+8\sqrt3$ -(i)

Similarly,
Now, the equation of the line passing through the point (2, 3) and with slope $\frac{-(2+\sqrt3)}{2\sqrt3-1}$ is
$(y-3)=\frac{-(2+\sqrt3)}{2\sqrt3-1}(x-2)$
$(2\sqrt3-1)(y-3)= -(2+\sqrt3)(x-2)$
$x(2+\sqrt3)+y(2\sqrt3-1)=1+8\sqrt3$ -(ii)

Therefore, equation of line is $x(\sqrt3-2)+y(2\sqrt3+1)=-1+8\sqrt3$ or $x(2+\sqrt3)+y(2\sqrt3-1)=1+8\sqrt3$

Question:12 Find the equation of the right bisector of the line segment joining the points $(3,4)$ and $(-1,2)$.

Answer:

Right bisector means a perpendicular line that divides the line segment into two equal parts.
Now, the lines are perpendicular, which means their slopes are negative times the inverse of each other.
Slope of line passing through points $(3,4)$ and $(-1,2)$ is
$m'= \frac{4-2}{3+1}= \frac{2}{4}=\frac{1}{2}$
Therefore, the Slope of the bisector line is
$m = - \frac{1}{m'}= -2$
Now, let (h, k) be the point of intersection of two lines.
It is given that point (h,k) divides the line segment joining point $(3,4)$ and $(-1,2)$ into two equal parts, which means it is the midpoint.
Therefore,
$h = \frac{3-1}{2} = 1\ \ \ and \ \ \ k = \frac{4+2}{2} = 3$
$(h,k) = (1,3)$
Now, the equation of the line passing through the point (1,3) and with slope -2 is
$(y-3)=-2(x-1)\\ y-3=-2x+2\\ 2x+y=5$
Therefore, the equation of the line is $2x+y=5$

Question 13 Find the coordinates of the foot perpendicular from the point $(-1,3)$ to the line $3x-4y-16=0$.

Answer:

Let's suppose the foot of the perpendicular is $(x_1,y_1)$
We can say that line passing through the point $(x_1,y_1) \ and \ (-1,3)$ is perpendicular to the line $3x-4y-16=0$
Now,
The slope of the line $3x-4y-16=0$ is , $m' = \frac{3}{4}$
And
The slope of the line passing through the point $(x_1,y_1) \ and \ (-1,3)$ is, $m = \frac{y-3}{x+1}$
Lines are perpendicular
Therefore,
$m = -\frac{1}{m'}\\ \frac{y_1-3}{_1+1} = -\frac{4}{3}\\ 3(y_1-3)=-4(x_1+1)\\ 4x_1+3y_1=5 \ \ \ \ \ \ \ \ \ -(i)$
Now, the point $(x_1,y_1)$ also lies on the line $3x-4y-16=0$
Therefore,
$3x_1-4y_1=16 \ \ \ \ \ \ \ \ \ \ \ -(ii)$
On solving equations (i) and (ii)
We will get
$x_1 = \frac{68}{25} \ and \ y_1 =-\frac{49}{25}$
Therefore, $(x_1,y_1) = \left ( \frac{68}{25},-\frac{49}{25} \right )$

Question:14 The perpendicular from the origin to the line $y=mx+c$ meets it at the point $(-1,2)$. Find the values of $m$ and $c$.

Answer:

We can say that line passing through point $(0,0) \ and \ (-1,2)$ is perpendicular to line $y=mx+c$
Now,
The slope of the line passing through the point $(0,0) \ and \ (-1,2)$ is , $m = \frac{2-0}{-1-0}= -2$
Lines are perpendicular
Therefore,
$m = -\frac{1}{m'} = \frac{1}{2}$ - (i)
Now, the point $(-1,2)$ also lies on the line $y=mx+c$
Therefore,
$2=\frac{1}{2}.(-1)+C\\ C = \frac{5}{2} \ \ \ \ \ \ \ \ \ \ \ -(ii)$
Therefore, the value of m and C is $\frac{1}{2} \ and \ \frac{5}{2}$ respectively

Question:15 If $p$ and $q$ are the lengths of perpendiculars from the origin to the lines $x\cos \theta -y\sin \theta =k\cos 2\theta$ and $x\sec \theta +y\hspace{1mm}cosec\hspace{1mm}\theta =k$, respectively, prove that $p^2+4q^2=k^2$.

Answer:

Given equations of lines are $x\cos \theta -y\sin \theta =k\cos 2\theta$ and $x\sec \theta +y\hspace{1mm}cosec\hspace{1mm}\theta =k$
We can rewrite the equation $x\sec \theta +y\hspace{1mm}cosec\hspace{1mm}\theta =k$ as
$x\sin \theta +y\cos \theta = k\sin\theta\cos\theta$
Now, we know that
$d = \left | \frac{Ax_1+By_1+C}{\sqrt{A^2+B^2}} \right |$
In equation $x\cos \theta -y\sin \theta =k\cos 2\theta$
$A= \cos \theta , B = -\sin \theta , C = - k\cos2\theta \ and \ (x_1,y_1)= (0,0)$

$p= \left | \frac{\cos\theta .0-\sin\theta.0-k\cos2\theta }{\sqrt{\cos^2\theta+(-\sin\theta)^2}} \right | = |-k\cos2\theta|$
Similarly,
in the equation $x\sin \theta +y\cos \theta = k\sin\theta\cos\theta$

$A= \sin \theta , B = \cos \theta , C = -k\sin\theta\cos\theta \ and \ (x_1,y_1)= (0,0)$

$q= \left | \frac{\sin\theta .0+\cos\theta.0-k\sin\theta\cos\theta }{\sqrt{\sin^2\theta+\cos^2\theta}} \right | = |-k\sin\theta\cos\theta|= \left | -\frac{k\sin2\theta}{2} \right |$
Now,

$p^2+4q^2=(|-k\cos2\theta|)^2+4.(|-\frac{k\sin2\theta}{2})^2= k^2\cos^22\theta+4.\frac{k^2\sin^22\theta}{4}$
$=k^2(\cos^22\theta+\sin^22\theta)$
$=k^2$
Hence proved

Question:16 In the triangle $ABC$ with vertices $A(2,3)$ , $B(4,-1)$ and $C(1,2)$ , find the equation and length of altitude from the vertex $A$ .

Answer:

Let suppose foot of perpendicular is $(x_1,y_1)$
We can say that line passing through point $(x_1,y_1) \ and \ A(2,3)$ is perpendicular to line passing through point $B(4,-1) \ and \ C(1,2)$
Now,
Slope of line passing through point $B(4,-1) \ and \ C(1,2)$ is , $m' = \frac{2+1}{1-4}= \frac{3}{-3}=-1$
And
Slope of line passing through point $(x_1,y_1) \ and \ (2,3)$ is , $m$
Lines are perpendicular
Therefore,
$m = -\frac{1}{m'}= 1$
Now, the equation of the line passing through the point (2,3) and with a slope with 1
$(y-3)=1(x-2)$
$x-y+1=0$ -(i)
Now, equation line passing through point $B(4,-1) \ and \ C(1,2)$ is
$(y-2)=-1(x-1)$
$x+y-3=0$
Now, the perpendicular distance of (2,3) from the $x+y-3=0$ is
$d= \left | \frac{1\times2+1\times3-3}{\sqrt{1^2+1^2}} \right |= \left | \frac{2+3-3}{\sqrt{1+1}} \right |= \frac{2}{\sqrt{2}}=\sqrt2$ -(ii)

Therefore, the equation and length of the line are $x-y+1=0$ and $\sqrt2$ respectively.

Question:17 If $p$ is the length of the perpendicular from the origin to the line whose intercepts on the axes are $a$ and $b$, then show that $\frac{1}{p^2}=\frac{1}{a^2}+\frac{1}{b^2}$.

Answer:

We know that the intercept form of the line is
$\frac{x}{a}+\frac{y}{b} = 1$
We know that
$d = \left | \frac{Ax_1+bx_2+C}{\sqrt{A^2+B^2}} \right |$
In this problem
$A = \frac{1}{a},B = \frac{1}{b}, C =-1 \ and \ (x_1,y_1)= (0,0)$
$p= \left | \frac{\frac{1}{a}\times 0+\frac{1}{b}\times 0-1}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}}} \right | = \left | \frac{-1}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}}} \right |$
On squaring both sides
We will get
$\frac{1}{p^2}= \frac{1}{a^2}+\frac{1}{b^2}$
Hence proved

Straight lines NCERT solutions - Miscellaneous Exercise (Page no. 172, Total questions- 23)

Question:1(a) Find the values of $k$ for which the line $(k-3)x-(4-k^2)y+k^2-7k+6=0$ is

Parallel to the x-axis.

Answer:

Given the equation of a line is
$(k-3)x-(4-k^2)y+k^2-7k+6=0$
And the equation of the x-axis is $y=0$
It is given that these two lines are parallel to each other.
Therefore, their slopes are equal.
Slope of $y=0$ is , $m' = 0$
and
Slope of line $(k-3)x-(4-k^2)y+k^2-7k+6=0$ is , $m = \frac{k-3}{4-k^2}$
Now,
$m=m'$
$\frac{k-3}{4-k^2}=0$
$k-3=0$
$k=3$
Therefore, the value of k is 3

Question:1(b) Find the values of $k$ for which the line $(k-3)x-(4-k^2)y+k^2-7k+6=0$ is

Parallel to the y-axis.

Answer:

Given the equation of the line is
$(k-3)x-(4-k^2)y+k^2-7k+6=0$
And the equation of the y-axis is $x = 0$
It is given that these two lines are parallel to each other
Therefore, their slopes are equal.
Slope of $y=0$ is , $m' = \infty = \frac{1}{0}$
and
Slope of line $(k-3)x-(4-k^2)y+k^2-7k+6=0$ is , $m = \frac{k-3}{4-k^2}$
Now,
$m=m'$
$\frac{k-3}{4-k^2}=\frac{1}{0}$
$4-k^2=0$
$k=\pm2$
Therefore, the value of k is $\pm2$

Question:1(c) Find the values of k for which the line $(k-3)x-(4-k^2)y+k^2-7k+6=0$ is passing through the origin.

Answer:

Given the equation of a line is
$(k-3)x-(4-k^2)y+k^2-7k+6=0$
It is given that it passes through the origin (0,0)
Therefore,
$(k-3).0-(4-k^2).0+k^2-7k+6=0$
$k^2-7k+6=0$
$k^2-6k-k+6=0$
$(k-6)(k-1)=0$
$k = 6 \ or \ 1$
Therefore, the value of k is $6 \ or \ 1$

Question:2 Find the equations of the lines, which cut-off intercepts on the axes whose sum and product are $\small 1$ and $\small -6$, respectively.

Answer:

Let the intercepts on the x and y-axis be a and b respectively.
It is given that
$a+b = 1 \ \ and \ \ a.b = -6$
$a= 1-b$
$\Rightarrow b.(1-b)=-6$
$\Rightarrow b-b^2=-6$
$\Rightarrow b^2-b-6=0$
$\Rightarrow b^2-3b+2b-6=0$
$\Rightarrow (b+2)(b-3)=0$
$\Rightarrow b = -2 \ and \ 3$
Now, when $b=-2\Rightarrow a=3$
and when $b=3\Rightarrow a=-2$
We know that the intercept form of the line is
$\frac{x}{a}+\frac{y}{b}=1$

Case (i) when a = 3 and b = -2
$\frac{x}{3}+\frac{y}{-2}=1$
$\Rightarrow 2x-3y=6$

Case (ii) when a = -2 and b = 3
$\frac{x}{-2}+\frac{y}{3}=1$
$\Rightarrow -3x+2y=6$
Therefore, equations of lines are $2x-3y=6 \ and \ -3x+2y=6$

Question:3 What are the points on the $\small y$ -axis whose distance from the line $\small \frac{x}{3}+\frac{y}{4}=1$ is $\small 4$ units.

Answer:

Given the equation of the line is
$\small \frac{x}{3}+\frac{y}{4}=1$
We can rewrite it as
$4x+3y=12$
Let's take the point on the y-axis as $(0,y)$
It is given that the distance of the point $(0,y)$ from line $4x+3y=12$ is 4 units
Now,
$d= \left | \frac{Ax_1+By_1+C}{\sqrt{A^2+B^2}} \right |$
In this problem $A = 4 , B=3 , C =-12 ,d=4\ \ and \ \ (x_1,y_1) = (0,y)$
$4 = \left | \frac{4\times 0+3\times y-12}{\sqrt{4^2+3^2}} \right |=\left | \frac{3y-12}{\sqrt{16+9}} \right |=\left | \frac{3y-12}{5} \right |$

Case (i)

$4 = \frac{3y-12}{5}$
$20=3y-12$
$y = \frac{32}{3}$
Therefore, the point is $\left ( 0,\frac{32}{3} \right )$ -(i)

Case (ii)

$4=-\left ( \frac{3y-12}{5} \right )$
$20=-3y+12$
$y = -\frac{8}{3}$
Therefore, the point is $\left ( 0,-\frac{8}{3} \right )$ -(ii)
Therefore, points on the $\small y$ -axis whose distance from the line $\small \frac{x}{3}+\frac{y}{4}=1$ is $\small 4$ units are $\left ( 0,\frac{32}{3} \right )$ and $\left ( 0,-\frac{8}{3} \right )$

Question:4 Find the perpendicular distance from the origin to the line joining the points $(\cos \theta,\sin \theta )$ and $(\cos \phi,\sin \phi ).$.

Answer:

Equation of line passing through the points $(\cos \theta ,\sin \theta )$ and $(\cos \phi ,\sin \phi )$ is
$(y-\sin \theta )= \frac{\sin \phi -\sin \theta}{\cos \phi -\cos \theta}(x-\cos\theta)$
$\Rightarrow (\cos \phi -\cos \theta)(y-\sin \theta )= (\sin \phi -\sin \theta)(x-\cos\theta)$
$\Rightarrow y(\cos \phi -\cos \theta)-\sin \theta(\cos \phi -\cos \theta)=x (\sin \phi -\sin \theta)-\cos\theta(\sin \phi -\sin \theta)$
$\Rightarrow x (\sin \phi -\sin \theta)-y(\cos \phi -\cos \theta)=\cos\theta(\sin \phi -\sin \theta)-\sin \theta(\cos \phi -\cos \theta)$ $\Rightarrow x (\sin \phi -\sin \theta)-y(\cos \phi -\cos \theta)=\sin(\theta-\phi)$
$(\because \cos a\sin b -\sin a\cos b = \sin(a-b) )$
Now, distance from origin(0,0) is
$d = \left | \frac{(\sin\phi -\sin\theta).0-(\cos\phi-\cos\theta).0-\sin(\theta-\phi)}{\sqrt{(\sin\phi-\sin\theta)^2+(\cos\phi-\cos\theta)^2}} \right |$
$d = \left | \frac{-\sin(\theta-\phi)}{\sqrt{(\sin^2\phi+\cos^2\phi)+(\sin^2\theta+\cos^2\theta)-2(\cos\theta\cos\phi+\sin\theta\sin\phi)}} \right |$
$d = \left | \frac{-\sin(\theta-\phi)}{1+1-2\cos(\theta-\phi)} \right |$ $(\because \cos a\cos b +\sin a\sin b = \cos(a-b) \ \ and \ \ \sin^2a+\cos^2a=1)$
$d = \left |\frac{ - \sin(\theta-\phi)}{2(1-\cos(\theta-\phi))} \right |$
$d = \left | \frac{-2\sin\frac{\theta-\phi}{2}\cos \frac{\theta-\phi}{2}}{\sqrt{2.(2\\sin^2\frac{\theta-\phi}{2})}}\right |$
$d = \left | \frac{-2\sin\frac{\theta-\phi}{2}\cos \frac{\theta-\phi}{2}}{2\sin\frac{\theta-\phi}{2}}\right |$
$d = \left | \cos\frac{\theta-\phi}{2} \right |$

Question:5 Find the equation of the line parallel to the y-axis and draw through the point of intersection of the lines $\small x-7y+5=0$ and $\small 3x+y=0$.

Answer:

Point of intersection of the lines $\small x-7y+5=0$ and $\small 3x+y=0$
$\left ( -\frac{5}{22},\frac{15}{22} \right )$
It is given that this line is parallel to the - axis, i.e. $x=0$, which means their slopes are equal.
Slope of $x=0$ is , $m' = \infty = \frac{1}{0}$
Let the Slope of line passing through point $\left ( -\frac{5}{22},\frac{15}{22} \right )$ is m
Then,
$m=m'= \frac{1}{0}$
Now, equation of line passing through point $\left ( -\frac{5}{22},\frac{15}{22} \right )$ and with slope $\frac{1}{0}$ is
$(y-\frac{15}{22})= \frac{1}{0}(x+\frac{5}{22})$
$x = -\frac{5}{22}$
Therefore, equation of line is $x = -\frac{5}{22}$

Question:6 Find the equation of a line drawn perpendicular to the line $\small \frac{x}{4}+\frac{y}{6}=1$ through the point, where it meets the $\small y$ -axis.

Answer:

Given the equation of a line is
$\small \frac{x}{4}+\frac{y}{6}=1$
We can rewrite it as
$3x+2y=12$
Slope of line $3x+2y=12$ , $m' = -\frac{3}{2}$
Let the Slope of the perpendicular line be m
$m = -\frac{1}{m'}= \frac{2}{3}$
Now, the ponit of intersection of $3x+2y=12$ and $x =0$ is $(0,6)$
Equation of line passing through point $(0,6)$ and with slope $\frac{2}{3}$ is
$(y-6)= \frac{2}{3}(x-0)$
$3(y-6)= 2x$
$2x-3y+18=0$
Therefore, the equation of a line is $2x-3y+18=0$

Question:7 Find the area of the triangle formed by the lines $\small y-x=0,x+y=0$ and $\small x-k=0$.

Answer:

Given the equations of the lines are
$y-x=0 \ \ \ \ \ \ \ \ \ \ \ -(i)$
$x+y=0 \ \ \ \ \ \ \ \ \ \ \ -(ii)$
$x-k=0 \ \ \ \ \ \ \ \ \ \ \ -(iii)$
The point of intersection of (i) and (ii) is (0,0)
The point of intersection of (ii) and (iii) is (k,-k)
The point of intersection of (i) and (iii) is (k,k)
Therefore, the vertices of the triangle formed by the three lines are $(0,0), (k,-k) \ and \ (k,k)$
Now, we know that the area of a triangle whose vertices are $(x_1,y_1),(x_2,y_2) \ and \ (x_3,y_3)$ is
$A = \frac{1}{2}|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|$
$A= \frac{1}{2}|0(-k-k)+k(k-0)+k(0+k)|$
$A= \frac{1}{2}|k^2+k^2|$
$A= \frac{1}{2}|2k^2|$
$A= k^2$
Therefore, the area of a triangle is $k^2 \ square \ units$

Question:8 Find the value of $\small p$ so that the three lines $\small 3x+y-2=0,px+2y-3=0$ and $\small 2x-y-3=0$ may intersect at one point.

Answer:

Point of intersection of lines $\small 3x+y-2=0$ and $\small 2x-y-3=0$ is $(1,-1)$
Now, $(1,-1)$ must satisfy equation $px+2y-3=0$
Therefore,
$p(1)+2(-1)-3=0$
$p-2-3=0$
$p=5$
Therefore, the value of p is $5$

Question:9 If three lines whose equations are $y=m_1x+c_1,y=m_2x+c_2$ and $y=m_3x+c_3$ are concurrent, then show that $m_1(c_2-c_3)+m_2(c_3-c_1)+m_3(c_1-c_2)=0$ .

Answer:

Concurrent lines mean they all intersect at the same point.
Now, given the equations of the lines are
$y=m_1x+c_1 \ \ \ \ \ \ \ \ \ \ \ -(i)$
$y=m_2x+c_2 \ \ \ \ \ \ \ \ \ \ \ -(ii)$
$y=m_3x+c_3 \ \ \ \ \ \ \ \ \ \ \ -(iii)$
Point of intersection of equation (i) and (ii) $\left ( \frac{c_2-c_1}{m_1-m_2},\frac{m_1c_2-m_2c_1}{m_1-m_2} \right )$

Now, lines are concurrent which means point $\left ( \frac{c_2-c_1}{m_1-m_2},\frac{m_1c_2-m_2c_1}{m_1-m_2} \right )$ also satisfy equation (iii)
Therefore,
$\frac{m_1c_2-m_2c_1}{m_1-m_2}=m_3.\left ( \frac{c_2-c_1}{m_1-m_2} \right )+c_3$
$m_1c_2-m_2c_1= m_3(c_2-c_1)+c_3(m_1-m_2)$
$m_1(c_2-c_3)+m_2(c_3-c_1)+m_3(c_1-c_2)=0$
Hence proved

Question:10 Find the equation of the lines through the point $\small (3,2)$ which makes an angle of $\small 45^{\circ}$ with the line $\small x-2y=3$.

Answer:

Given the equation of the line is
$\small x-2y=3$
The slope of line $\small x-2y=3$ , $m_2= \frac{1}{2}$
Let the slope of the other line be, $m_1=m$
Now, it is given that both the lines make an angle $\small 45^{\circ}$ with each other.
Therefore,
$\tan \theta = \left | \frac{m_2-m_1}{1+m_1m_2} \right |$
$\tan 45^\circ = \left | \frac{\frac{1}{2}-m}{1+\frac{m}{2}} \right |$
$1= \left | \frac{1-2m}{2+m} \right |$
Now,

Case (i)
$1=\frac{1-2m}{2+m}$
$2+m=1-2m$
$m = -\frac{1}{3}$
Equation of line passing through the point $\small (3,2)$ and with slope $-\frac{1}{3}$
$(y-2)=-\frac{1}{3}(x-3)$
$3(y-2)=-1(x-3)$
$x+3y=9 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$

Case (ii)
$1=-\left ( \frac{1-2m}{2+m} \right )$
$2+m=-(1-2m)$
$m= 3$
Equation of line passing through the point $\small (3,2)$ and with slope 3 is
$(y-2)=3(x-3)$
$3x-y=7 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(ii)$

Therefore, the equations of lines are $3x-y=7$ and $x+3y=9$

Question:11 Find the equation of the line passing through the point of intersection of the lines $4x+7y-3=0$ and $2x-3y+1=0$ that has equal intercepts on the axes.

Answer:

Point of intersection of the lines $4x+7y-3=0$ and $2x-3y+1=0$ is $\left ( \frac{1}{13},\frac{5}{13} \right )$
We know that the intercept form of the line is
$\frac{x}{a}+\frac{y}{b}= 1$
It is given that a line makes equal intercepts on the x and y axes.
Therefore,
a = b
Now, the equation reduces to
$x+y = a$ -(i)
It passes through point $\left ( \frac{1}{13},\frac{5}{13} \right )$
Therefore,
$a = \frac{1}{13}+\frac{5}{13}= \frac{6}{13}$
Put the value of an in equation (i)
We will get
$13x+13y=6$
Therefore, the equation of a line is $13x+13y=6$

Question:12 Show that the equation of the line passing through the origin and making an angle $\small \theta$ with the line $\small y=mx+c$ is $\small \frac{y}{x}=\frac{m\pm \tan \theta }{1\mp m\tan \theta }$.

Answer:

Slope of line $\small y=mx+c$ is m
Let the slope of the other line be m'.
It is given that both the line makes an angle $\small \theta$ with each other.
Therefore,
$\tan \theta = \left | \frac{m_2-m_1}{1+m_1m_2} \right |$
$\tan \theta = \left | \frac{m-m'}{1+mm'} \right |$
$\mp(1+mm')\tan \theta =(m-m')$
$\mp\tan \theta +m'(\mp m\tan\theta+1)= m$
$m'= \frac{m\pm \tan \theta}{1\mp m\tan \theta}$
Now, the equation of the line passing through the origin (0,0) and with slope $\frac{m\pm \tan \theta}{1\mp m\tan \theta}$ is
$(y-0)=\frac{m\pm \tan \theta}{1\mp m\tan \theta}(x-0)$
$\frac{y}{x}=\frac{m\pm \tan \theta}{1\mp m\tan \theta}$
Hence proved

Question:13 In what ratio, the line joining $\small (-1,1)$ and $\small (5,7)$ is divided by the line $x+y=4$ ?

Answer:

Equation of line joining $\small (-1,1)$ and $\small (5,7)$ is
$(y-1)= \frac{7-1}{5+1}(x+1)$
$\Rightarrow (y-1)= \frac{6}{6}(x+1)$
$\Rightarrow (y-1)= 1(x+1)$
$\Rightarrow x-y+2=0$
Now, point of intersection of lines $x+y=4$ and $x-y+2=0$ is $(1,3)$
Now, let's suppose point $(1,3)$ divides the line segment joining $\small (-1,1)$ and $\small (5,7)$ in $1:k$
Then,
$(1,3)= \left ( \frac{k(-1)+1(5)}{k+1},\frac{k(1)+1(7)}{k+1} \right )$
$1=\frac{-k+5}{k+1} \ \ and \ \ 3 = \frac{k+7}{k+1}$
$\Rightarrow k =2$
Therefore, the line joining $\small (-1,1)$ and $\small (5,7)$ is divided by the line $x+y=4$ in ratio $1:2$

Question:14 Find the distance of the line $\small 4x+7y+5=0$ from the point $\small (1,2)$ along the line $\small 2x-y=0$.

Answer:

point $\small (1,2)$ lies on line $2x-y =0$
Now, point of intersection of lines $2x-y =0$ and $\small 4x+7y+5=0$ is $\left ( -\frac{5}{18},-\frac{5}{9} \right )$
Now, we know that the distance between two points is given by
$d = |\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}|$
$d = |\sqrt{(1+\frac{5}{18})^2+(2+\frac{5}{9})^2}|$
$d = |\sqrt{(\frac{23}{18})^2+(\frac{23}{9})^2}|$
$d = \left | \sqrt{\frac{529}{324}+\frac{529}{81}} \right |$
$d = \left | \sqrt{\frac{529+2116}{324}} \right | = \left | \sqrt\frac{2645}{324} \right | =\frac{23\sqrt5}{18}$
Therefore, the distance of the line $\small 4x+7y+5=0$ from the point $\small (1,2)$ along the line $\small 2x-y=0$ is $\frac{23\sqrt5}{18} \ units$

Question:15 Find the direction in which a straight line must be drawn through the point $\small (-1,2)$ so that its point of intersection with the line $\small x+y=4$ may be at a distance of $3$ units from this point.

Answer:

Let $(x_1,y_1)$ be the point of intersection
It lies on the line $\small x+y=4$
Therefore,
$x_1+y_1=4 \\ x_1=4-y_1\ \ \ \ \ \ \ \ \ \ \ -(i)$
Distance of point $(x_1,y_1)$ from $\small (-1,2)$ is 3
Therefore,
$3= |\sqrt{(x_1+1)^2+(y_1-2)^2}|$
Square both sides and put the value from equation (i)
$9= (5-y_1)^2+(y_1-2)^2\\ 9=y_1^2+25-10y_1+y_1^2+4-4y_1\\ 2y_1^2-14y_1+20=0\\ y_1^2-7y_1+10=0\\ y_1^2-5y_1-2y_1+10=0\\ (y_1-2)(y_1-5)=0\\ y_1=2 \ or \ y_1 = 5$
When $y_1 = 2 \Rightarrow x_1 = 2$ point is $(2,2)$
and
When $y_1 = 5 \Rightarrow x_1 = -1$ point is $(-1,5)$
Now, slope of line joining point $(2,2)$ and $\small (-1,2)$ is
$m = \frac{2-2}{-1-2}=0$
Therefore, the line is parallel to the x-axis -(i)

or
slope of line joining point $(-1,5)$ and $\small (-1,2)$
$m = \frac{5-2}{-1+2}=\infty$
Therefore, the line is parallel to the y-axis -(ii)

Therefore, the line is parallel to the -axis or parallel to the y-axis

Question:16 The hypotenuse of a right-angled triangle has its ends at the points $\small (1,3)$ and $\small (-4,1)$ Find an equation of the legs (perpendicular sides) of the triangle.

Answer:

The slope of lines OA and OB are negative times the inverse of each other.
Slope of line OA is , $m=\frac{3-y}{1-x}\Rightarrow (3-y)=m(1-x)$
Slope of line OB is , $-\frac{1}{m}= \frac{1-y}{-4-x}\Rightarrow (x+4)=m(1-y)$
Now,

Now, for a given value of m, we get these equations.
If $m = \infty$
$1-x=0 \ \ \ \ and \ \ \ \ \ 1-y =0$
$x=1 \ \ \ \ and \ \ \ \ \ y =1$

Question:17 Find the image of the point $\small (3,8)$ to the line $x+3y=7$ assuming the line to be a plane mirror.

Answer:

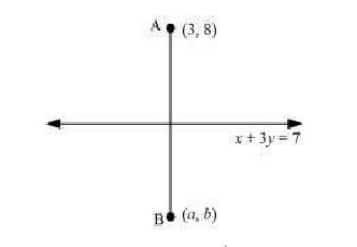
Let point $(a,b)$ is the image of point $\small (3,8)$ w.r.t. to line $x+3y=7$
line $x+3y=7$ is perpendicular bisector of line joining points $\small (3,8)$ and $(a,b)$
Slope of line $x+3y=7$ , $m' = -\frac{1}{3}$
Slope of line joining points $\small (3,8)$ and $(a,b)$ is , $m = \frac{8-b}{3-a}$
Now,
$m = -\frac{1}{m'} \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because lines \ are \ perpendicular)$
$\frac{8-b}{3-a}= 3$
$8-b=9-3a$
$3a-b=1 \ \ \ \ \ \ \ \ \ \ \ -(i)$
Point of intersection is the midpoint of line joining points $\small (3,8)$ and $(a,b)$
Therefore,
Point of intersection is $\left ( \frac{3+a}{2},\frac{b+8}{2} \right )$
Point $\left ( \frac{3+a}{2},\frac{b+8}{2} \right )$ also satisfy the line $x+3y=7$
Therefore,
$\frac{3+a}{2}+3.\frac{b+8}{2}=7$
$a+3b=-13 \ \ \ \ \ \ \ \ \ \ \ \ \ -(ii)$
On solving equations (i) and (ii) we will get
$(a,b) = (-1,-4)$
Therefore, the image of the point $\small (3,8)$ with respect to the line $x+3y=7$ is $(-1,-4)$

Question:18 If the lines $\small y=3x+1$ and $\small 2y=x+3$ are equally inclined to the line $\small y=mx+4$, find the value of $m$.

Answer:

Given the equations of the lines are
$\small y=3x+1 \ \ \ \ \ \ \ \ \ \ -(i)$
$\small 2y=x+3 \ \ \ \ \ \ \ \ \ \ -(ii)$
$\small y=mx+4 \ \ \ \ \ \ \ \ \ \ -(iii)$
Now, it is given that lines (i) and (ii) are equally inclined to line (iii)
Slope of line $\small y=3x+1$ is , $\small m_1=3$
Slope of line $\small 2y=x+3$ is , $\small m_2= \frac{1}{2}$
Slope of line $\small y=mx+4$ is , $\small m_3=m$
Now, we know that
$\tan \theta = \left | \frac{m_1-m_2}{1+m_1m_2} \right |$
Now,
$\tan \theta_1 = \left | \frac{3-m}{1+3m} \right |$ and $\tan \theta_2 = \left | \frac{\frac{1}{2}-m}{1+\frac{m}{2}} \right |$

It is given that $\tan \theta_1=\tan \theta_2$
Therefore,
$\left | \frac{3-m}{1+3m} \right |= \left | \frac{1-2m}{2+m} \right |$
$\frac{3-m}{1+3m}= \pm\left ( \frac{1-2m}{2+m} \right )$
Now, if $\frac{3-m}{1+3m}= \left ( \frac{1-2m}{2+m} \right )$
Then,
$(2+m)(3-m)=(1-2m)(1+3m)$
$6+m-m^2=1+m-6m^2$
$5m^2=-5$
$m= \sqrt{-1}$
Which is not possible
Now, if $\frac{3-m}{1+3m}= -\left ( \frac{1-2m}{2+m} \right )$
Then,
$(2+m)(3-m)=-(1-2m)(1+3m)$
$6+m-m^2=-1-m+6m^2$
$7m^2-2m-7=0$
$m = \frac{-(-2)\pm \sqrt{(-2)^2-4\times 7\times (-7)}}{2\times 7}= \frac{2\pm \sqrt{200}}{14}= \frac{1\pm5\sqrt2}{7}$

Therefore, the value of m is $\frac{1\pm5\sqrt2}{7}$

Question:19 If the sum of the perpendicular distances of a variable point $\small P(x,y)$ from the lines $\small x+y-5=0$ and $\small 3x-2y+7=0$ is always $\small 10$. Show that $\small P$ must move on a line.

Answer:

Given the equation of the line are
$x+y-5=0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$
$3x-2y+7=0 \ \ \ \ \ \ \ \ \ \ \ -(ii)$
Now, perpendicular distances of a variable point $\small P(x,y)$ from the lines are

$d_1=\left | \frac{1.x+1.y-5}{\sqrt{1^2+1^2}} \right |$ $d_2=\left | \frac{3.x-2.y+7}{\sqrt{3^2+2^2}} \right |$
$d_1=\left | \frac{x+y-5}{\sqrt2} \right |$ $d_2=\left | \frac{3x-2y+7}{\sqrt{13}} \right |$
Now, it is given that.
$d_1+d_2= 10$
Therefore,
$\frac{x+y-5}{\sqrt2}+\frac{3x-2y+7}{\sqrt{13}}=10$
$(assuming \ x+y-5 > 0 \ and \ 3x-2y+7 >0)$
$(x+y-5)\sqrt{13}+(3x-2y+7)\sqrt2=10\sqrt{26}$

$x(\sqrt{13}+3\sqrt{2})+y(\sqrt{13}-2\sqrt{2})=10\sqrt{26}+5\sqrt{13}-7\sqrt2$

Which is the equation of the line
Hence proved

Question:20 Find the equation of the line that is equidistant from parallel lines $9x+6y-7=0$ and $3x+2y+6=0$.

Answer:

Let's take the point $p(a,b)$ which is equidistance from parallel lines $9x+6y-7=0$ and $3x+2y+6=0$
Therefore,
$d_1= \left | \frac{9.a+6.b-7}{\sqrt{9^2+6^2}} \right |$ $d_2= \left | \frac{3.a+2.b+6}{\sqrt{3^2+2^2}} \right |$
$d_1= \left | \frac{9a+6b-7}{\sqrt{117}} \right |$ $d_2= \left | \frac{3a+2b+6}{\sqrt{13}} \right |$
It is that $d_1=d_2$
Therefore,
$\left | \frac{9a+6b-7}{3\sqrt{13}} \right |= \left | \frac{3a+2b+6}{\sqrt{13}} \right |$
$(9a+6b-7)=\pm 3(3a+2b+6)$
Now, case (i)
$(9a+6b-7)= 3(3a+2b+6)$
$25=0$
Therefore, this case is not possible.

Case (ii)
$(9a+6b-7)= -3(3a+2b+6)$
$18a+12b+11=0$

Therefore, the required equation of the line is $18a+12b+11=0$

Question:21 A ray of light passing through the point $(1,2)$ reflects on the $x$ -axis at point $A$ and the reflected ray passes through the point $(5,3)$. Find the coordinates of $A$.

Answer:

From the figure above we can say that
The slope of line AC $(m)= \tan \theta$
Therefore,
$\tan \theta = \frac{3-0}{5-a} = \frac{3}{5-a} \ \ \ \ \ \ \ \ \ \ (i)$
Similarly,
The slope of line AB $(m') = \tan(180^\circ-\theta)$
Therefore,
$\tan(180^\circ-\theta) = \frac{2-0}{1-a}$
$-\tan\theta= \frac{2}{1-a}$
$\tan\theta= \frac{2}{a-1} \ \ \ \ \ \ \ \ \ \ \ \ \ -(ii)$
Now, from equation (i) and (ii) we will get
$\frac{3}{5-a} = \frac{2}{a-1}$
$\Rightarrow 3(a-1)= 2(5-a)$
$\Rightarrow 3a-3= 10-2a$
$\Rightarrow 5a=13$
$\Rightarrow a=\frac{13}{5}$
Therefore, the coordinates of $A$ . is $\left ( \frac{13}{5},0 \right )$

Question:22 Prove that the product of the lengths of the perpendiculars drawn from the points $\small (\sqrt{a^2-b^2},0)$ and $\small (-\sqrt{a^2-b^2},0)$ to the line $\small \frac{x}{a}\cos \theta +\frac{y}{b}\sin \theta =1$ is $\small b^2$.

Answer:

Given the equation id line is
$\small \frac{x}{a}\cos \theta +\frac{y}{b}\sin \theta =1$
We can rewrite it as
$xb\cos \theta +ya\sin \theta =ab$
Now, the distance of the line $xb\cos \theta +ya\sin \theta =ab$ from the point $\small (\sqrt{a^2-b^2},0)$ is given by
$d_1=\left | \frac{b\cos\theta.\sqrt{a^2-b^2}+a\sin \theta.0-ab}{\sqrt{(b\cos\theta)^2+(a\sin\theta)^2}} \right | = \left | \frac{b\cos\theta.\sqrt{a^2-b^2}-ab}{\sqrt{(b\cos\theta)^2+(a\sin\theta)^2}} \right |$
Similarly,
The distance of the line $xb\cos \theta +ya\sin \theta =ab$ from the point $\small (-\sqrt{a^2-b^2},0)$ is given by
$d_2=\left | \frac{b\cos\theta.(-\sqrt{a^2-b^2})+a\sin \theta.0-ab}{\sqrt{(b\cos\theta)^2+(a\sin\theta)^2}} \right | = \left | \frac{-(b\cos\theta.\sqrt{a^2-b^2}+ab)}{\sqrt{(b\cos\theta)^2+(a\sin\theta)^2}} \right |$
$d_1.d_2 = \left | \frac{b\cos\theta.\sqrt{a^2-b^2}-ab}{\sqrt{(b\cos\theta)^2+(a\sin\theta)^2}} \right |.\times\left | \frac{-(b\cos\theta.\sqrt{a^2-b^2}+ab)}{\sqrt{(b\cos\theta)^2+(a\sin\theta)^2}} \right |$
$=\left | \frac{-((b\cos\theta.\sqrt{a^2-b^2})^2-(ab)^2)}{(b\cos\theta)^2+(a\sin\theta)^2} \right |$
$=\left | \frac{-b^2\cos^2\theta.(a^2-b^2)+a^2b^2)}{(b\cos\theta)^2+(a\sin\theta)^2} \right |$
$=\left | \frac{-a^2b^2\cos^2\theta+b^4\cos^2\theta+a^2b^2)}{b^2\cos^2\theta+a^2\sin^2\theta} \right |$
$=\left | \frac{-b^2(a^2\cos^2\theta-b^2\cos^2\theta-a^2)}{b^2\cos^2\theta+a^2\sin^2\theta} \right |$
$=\left | \frac{-b^2(a^2\cos^2\theta-b^2\cos^2\theta-a^2(\sin^2\theta+\cos^2\theta))}{b^2\cos^2\theta+a^2\sin^2\theta} \right | \ \ \ \ (\because \sin^2a+\cos^2a=1)$
$=\left | \frac{-b^2(a^2\cos^2\theta-b^2\cos^2\theta-a^2\sin^2\theta-a^2\cos^2\theta)}{b^2\cos^2\theta+a^2\sin^2\theta} \right |$
$=\left | \frac{+b^2(b^2\cos^2\theta+a^2\sin^2\theta)}{b^2\cos^2\theta+a^2\sin^2\theta} \right |$
$=b^2$
Hence proved

Question:23 A person standing at the junction (crossing) of two straight paths represented by the equations $\small 2x-3y+4=0$ and $\small 3x+4y-5=0$ wants to reach the path whose equation is $\small 6x-7y+8=0$ in the least time. Find the equation of the path that he should follow.

Answer:

point of intersection of lines $\small 2x-3y+4=0$ and $\small 3x+4y-5=0$ (junction) is $\left ( -\frac{1}{17},\frac{22}{17} \right )$
Now, a person reaches the path $\small 6x-7y+8=0$ in the least time when it follows the path perpendicular to it.
Now,
Slope of line $\small 6x-7y+8=0$ is , $m'=\frac{6}{7}$
Let the slope of a line perpendicular to it be, m
Then,
$m= -\frac{1}{m}= -\frac{7}{6}$
Now, equation of line passing through point $\left ( -\frac{1}{17},\frac{22}{17} \right )$ and with slope $-\frac{7}{6}$ is
$\left ( y-\frac{22}{17} \right )= -\frac{7}{6}\left ( x-(-\frac{1}{17}) \right )$
$\Rightarrow 6(17y-22)=-7(17x+1)$
$\Rightarrow 102y-132=-119x-7$
$\Rightarrow 119x+102y=125$

Therefore, the required equation of the line is $119x+102y=125$

If you are interested in the class 11 maths chapter 10 question-answer exercises, then these are listed below.

• Straight Lines Class 11 exercises 10.1
• Straight Lines Class 11 exercises 10.2
• Straight Lines Class 11 exercises 10.3
• Straight Lines Class 11 miscellaneous exercises

Class 11 Maths NCERT Chapter 9: Extra Question

Question: The ratio in which the line 3x + 4y + 2 = 0 divides the distance between the lines 3x + 4y + 5 = 0 and 3x + 4y – 5 = 0 is:

Solution:
Given lines are 3x+4y+5=0…....(i)
3x+4y-5=0…....(ii)
and 3x+4y+2=0….......(iii)
Since the coefficients of x and y are the same, (i), (ii), and (iii) are parallel to each other.
Distance between two parallel lines is $d=\frac{\left | c_{1}-c_{2} \right |}{\sqrt{A^{2}+B^{2}}}=\frac{\left | 5-2 \right |}{\sqrt{3^{2}+(4)^{2}}}=\frac{\left | 3 \right |}{\sqrt{9+16}}=\left | \frac{3}{5} \right |$
Similarly in case of ii and iii distance between two parallel lines is $d=\frac{\left | c_{1}-c_{2} \right |}{\sqrt{A^{2}+B^{2}}}=\frac{\left | -5-2 \right |}{\sqrt{3^{2}+(4)^{2}}}=\frac{\left | -7 \right |}{\sqrt{9+16}}=\left |- \frac{7}{5} \right |$
Ratio between the distance = $\frac{3}{5}:\frac{7}{5}=3:7$
Hence, the correct answer is $3:7$.

Straight Lines Class 11 Chapter 9: Topics

Given below are the topics discussed in the NCERT Solutions for class 11, chapter 9, Straight lines:

• Introduction
• Slope of a Line
• Various Forms of the Equation of a Line
• Distance of a Point From a Line

Straight lines NCERT solutions- Important Formulae

Distance Formula:

The distance between two points A $(x_1, y_1)$ and B $(x_2,y_2)$ is given by:

• $AB = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Distance of a Point from the Origin:

The distance of a point $A(x, y)$ from the origin $O(0, 0)$ is given by:

• $OA = \sqrt{x^2+y^2}$

Section Formula for Internal Division:

The coordinates of the point that divides the line segment joining $(x_1, y_1)$ and $(x_2,y_2)$ in the ratio $m:n$ internally is:

• $\frac{mx_2 + nx_1}{ m + n}, \frac{my_2 + ny_1}{m + n}$

Section Formula for External Division:

The coordinates of the point that divides the line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ in the ratio m:n externally is:

• $\frac{mx_2 - nx_1}{ m - n}, \frac{my_2 - ny_1}{m - n}$

Midpoint Formula:

The midpoint of the line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ is:

• $\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}$

Coordinates of Centroid of a Triangle:

For a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$, the coordinates of the centroid are:

• $\frac{x_1 + x_2 + x_3}{3}, \frac{y_1+y_2+y_3}{3}$

Area of a Triangle:

The area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$is given by:

• $\frac{1}{2} \left|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2) \right|$

Collinearity of Points:

If the points $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$are collinear, then:

• $x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)=0$

Slope or Gradient of a Line:

The slope (m) of a line passing through points P$(x_1, y_1)$and Q$(x_2, y_2)$is given by:

• $m = \frac{y_2-y_1}{x_2-x_1}$

The angle between Two Lines:

The angle ($\theta$) between two lines with slopes $m_1$ and $m_2$ is given by:

• $\tan \theta = \left|\frac{m_2-m_1 }{1 +m_1\cdot m_2}\right|$

Point of Intersection of Two Lines:

Let the equations of lines be $a_1 x + b_1 y + c_1 = 0$ and $a_2 x + b_2 y + c_2 = 0$. The point of intersection is:

• $\frac{b_1 c_2 – b_2c_1}{a_1b_2 – a_2 b_1}, \frac{a_2 c_1 -a_1 c_2}{a_1 b_2 – a_2 b_1}$

Distance of a Point from a Line:

The perpendicular distance (d) of a point P$(x_1, y_1)$from the line $Ax + By + C = 0$ is given by:

• $d = \left|\frac{Ax_1 +By_1+C}{\sqrt{A^2 + B^2}}\right|$

Distance Between Two Parallel Lines:

The distance (d) between two parallel lines $y = mx + c_1$ and $y = mx + c_2$ is given by:

• $d = \frac{|c_1 - c_2|}{\sqrt{1 + m^2}}$

Different Forms of Equation of a Line:

Various forms of the equation of a line include:

• Normal form: $x \cos\alpha + y \sin\alpha = p$
• Intercept form: $ \frac{x}{a} + \frac{y}{b} = 1$
• Slope-intercept form: $y = mx + c$
• One-point slope form: $y – y_1 = m(x – x_1)$
• Two-point form: $y – y_1 = \frac{y_2 – y_1}{x_2 – x_1} \cdot (x - x_1)$

Approach to Solve Questions of Straight lines Class 11

Here are some steps on how to approach the questions of the Straight lines:

• Understand the Expansion Format
  Use the binomial expansion: $(a+b)^n=\sum_\limits{r=0}^n\binom{n}{r} a^{n-r} b^r$

• Understand Binomial Coefficients
  Apply the formula:
  $\binom{n}{r}=\frac{n!}{r!(n-r)!}$
  Practice Pascal's Triangle with small numbers.

• Apply the General Term Formula
  The (r + 1)^th term in the expansion of $(a + b)^n$ is:
  $T_{r+1}=\binom{n}{r} a^{n-r} b^r$

• Formula for the Middle Term(s)
  For even n, the middle term is at r = $\frac{n}{2}$
  For odd n, two middle terms at r = $\frac{n-1}{2}$ and r = $\frac{n+1}{2}$

• When the Coefficient is Requested
  Just find the combination C(n, r), without involving the variables.

• Apply Symmetry of Coefficients
  C(n, r) = C(n, n - r). It will help with the lengthy calculations.

What Extra Should Students Study Beyond NCERT for JEE?

Here is a comparison list of the concepts in Straight lines that are covered in JEE and NCERT, to help students understand what extra they need to study beyond the NCERT for JEE:

NCERT solutions for class 11 mathematics - Chapter Wise

Given below is the chapter-wise list of the NCERT Class 11 Maths solutions with their respective links:

Also Read,

• NCERT Exemplar Class 11 Maths Solutions Chapter 9 Straight Lines
• NCERT Notes Class 11 Maths Solutions Chapter 9 Straight Lines

NCERT solutions for class 11- Subject-wise

Given below are some useful links for NCERT books and the NCERT syllabus for class 10:

• NCERT solutions for class 11 biology
• NCERT solutions for class 11 maths
• NCERT solutions for class 11 chemistry
• NCERT solutions for Class 11 physics

NCERT Books and NCERT Syllabus

Here are the subject-wise links for the NCERT solutions of class 10:

• NCERT Books Class 11 Maths
• NCERT Syllabus Class 11 Maths
• NCERT Books Class 11
• NCERT Syllabus Class 11