Straight Lines Class 11th Notes - Free NCERT Class 11 Maths Chapter 10 notes - Download PDF

Class 11 Straight Lines Notes PDF – Download Free Study Material

Students who wish to access these NCERT Class 11 Maths Chapter 9 Notes can click on the link below to download the entire notes in PDF.

Download PDF

Straight Lines Class 11 Notes

Careers360 experts have curated these NCERT Class 11 Maths Chapter 9 Notes to help students revise quickly and confidently.

Important formulas

1. The distance between two points $\mathrm{P}\left(\mathrm{x}_1, \mathrm{y}_1\right)$ and $\mathrm{Q}\left(\mathrm{x}_2, \mathrm{y}_2\right)$ is $d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}$

2. The coordinate of the point which cuts a line segment joining by $P\left(x_1, y_1\right)$ and $Q\left(x_2, y_2\right)$ internally in ratio $m:n$ is $\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}\right)$

3. If the ratio of $\mathrm{m}: \mathrm{n}=1: 1$ then the coordinate of the point is $\left(\frac{x_2+x_1}{2}, \frac{y_2+y_1}{2}\right)$

4. Area of the triangle whose vertices are $P\left(x_1, y_1\right), Q\left(x_2, y_2\right)$, and $R\left(x_3, y_3\right)$ is given by:
$A=\frac{1}{2}\left|x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right|$

Slope of A Line

The steepness of a line is known as the slope of the line.

A line that is nonparallel to the x-axis cuts the x-axis at two angles. The angles are supplementary to each other. A line that makes an angle with the positive direction x-axis and the angle is measured anti-clockwise, then θ is the inclination of the line.

Definition: If a line makes an angle θ with the positive direction x-axis, then tanθ is the slope of the line.

The slope of a line is also denoted by the letter m.

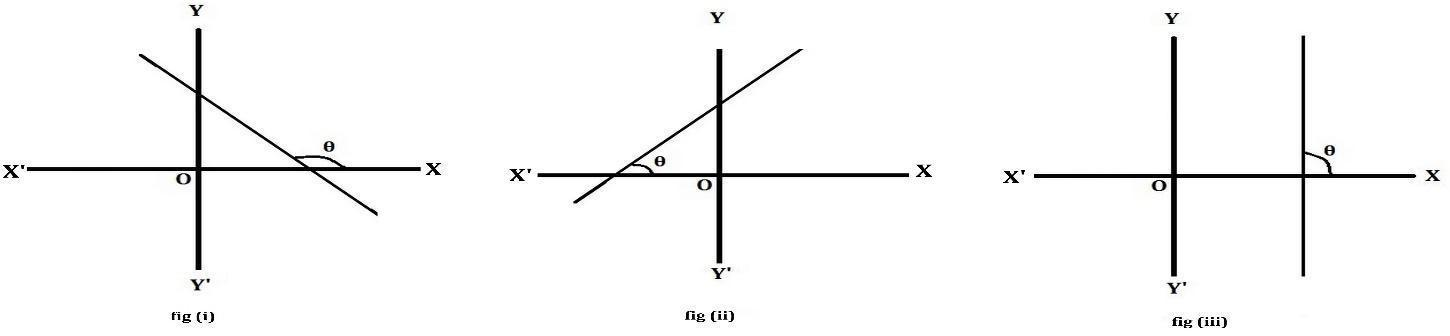
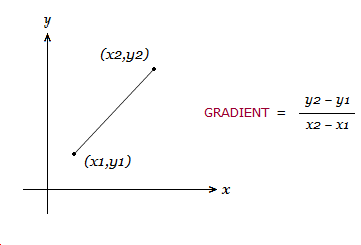
Slope of a line when the coordinates of any two points on the line are given

When two points are given as (x₁, y₁) and (x₂, y₂) the slope is $m=\frac{y_2-y_1}{x_2-x_1}$

Conditions for Parallelism and Perpendicularity of Lines in Terms of Their Slopes

Parallel Lines

Let two lines l₁ and l₂ be parallel to each other. The slopes of lines l₁ and l₂ are m₁ and m_2. The inclinations of the lines l₁ and l₂ are α and β, respectively. The diagram is shown below

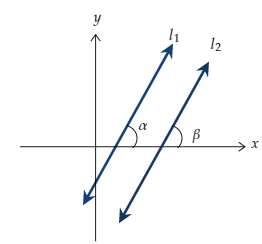
Since the lines are parallel to each other so the angle of inclination is also equal.

Hence, $α=β$

Taking $\tan$ both sides

$\tan α = \tan β$ and m₁ = m₂

The slope of line l₁ = The slope of line l₂

If the lines are parallel, then the slopes of the lines are also equal.

Perpendicular Lines

Let two lines l₁ and l₂ be perpendicular to each other. The slopes of lines l₁ and l₂ are m₁ and m₂. The inclinations of the lines l₁ and l₂ are α and β, respectively. The diagram is shown below

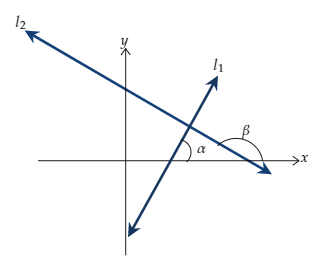
So, $β= α+90°$

Taking $\tan$ both sides

$\begin{aligned} & \tan \beta=\tan \left(\alpha+90^{\circ}\right) \\ &⇒ \tan \beta=-\cot \alpha \\ &⇒ \tan \beta=-\frac{1}{\tan \alpha} \\ &⇒ \tan \alpha \cdot \tan \beta=-1 \\ &⇒ m_1 m_2=-1\end{aligned}$

Two lines l₁ and l₂ are said to be perpendicular if m₁m₂ = -1

The Angle Between Two Lines

The inclination of two lines be θ₁ and θ₂ and θ₁, θ₂ ≠ 90°

The slopes of the lines are m₁ = tanθ₁ and m₂ = tanθ₂

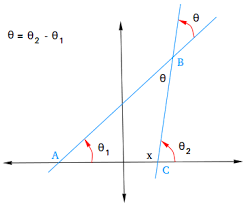
Assume that θ is the angle between the lines.
So,
$\begin{aligned} \tan \theta & =\tan \left(\theta_1-\theta_2\right) \\ & =\frac{\tan \theta_1-\tan \theta_2}{1+\tan \theta_1 \tan \theta_2} \\ & =\frac{m_1-m_2}{1+m_1 m_2}\end{aligned}$

Example 3.4
Find the acute angle between the lines $2x-y+3=0$ and $x+y+2=0$
Solution
Let $m_1$ and $m_2$ be the slopes of $2 x-y+3=0$ and $x+y+2=0$
Now $m_1=2, m_2=-1$
Let $\theta$ be the angle between the given lines
$ \tan \theta =\left|\frac{m_1-m_2}{1+m_1 m_2}\right| $
$ \Rightarrow \tan \theta=\left|\frac{2+1}{1+2(-1)}\right|=3 $
$⇒\theta =\tan ^{-1}{(3)}$

Collinearity Of Three Points

Let three points be A(1,4), B(4,6), and C(10,10) lie on the same line.

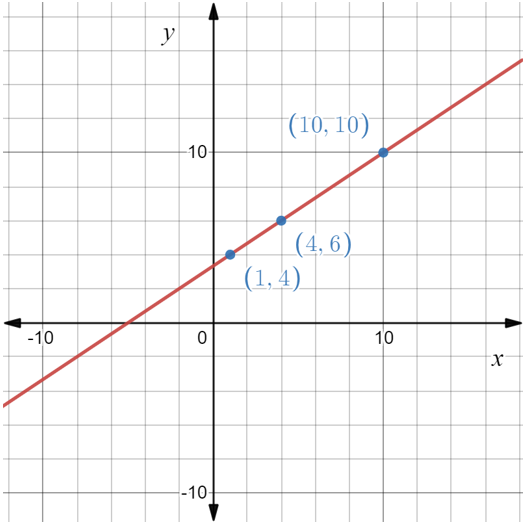
The slope of the line that passes through the points $A(1,4)$ and $B(4,6)$ is $\frac{6-4}{4-1}=\frac{2}{3}$

The slope of the line that passes through points $B(4,6)$ and $C(10,10)$ is $\frac{10-6}{10-4}=\frac{2}{3}$

So, m_AB = m_BC = $\frac{2}{3}$

If the points lie on the same line, then the slope of the line joining any two points is always the same.

Various Forms of the Equation of a Line

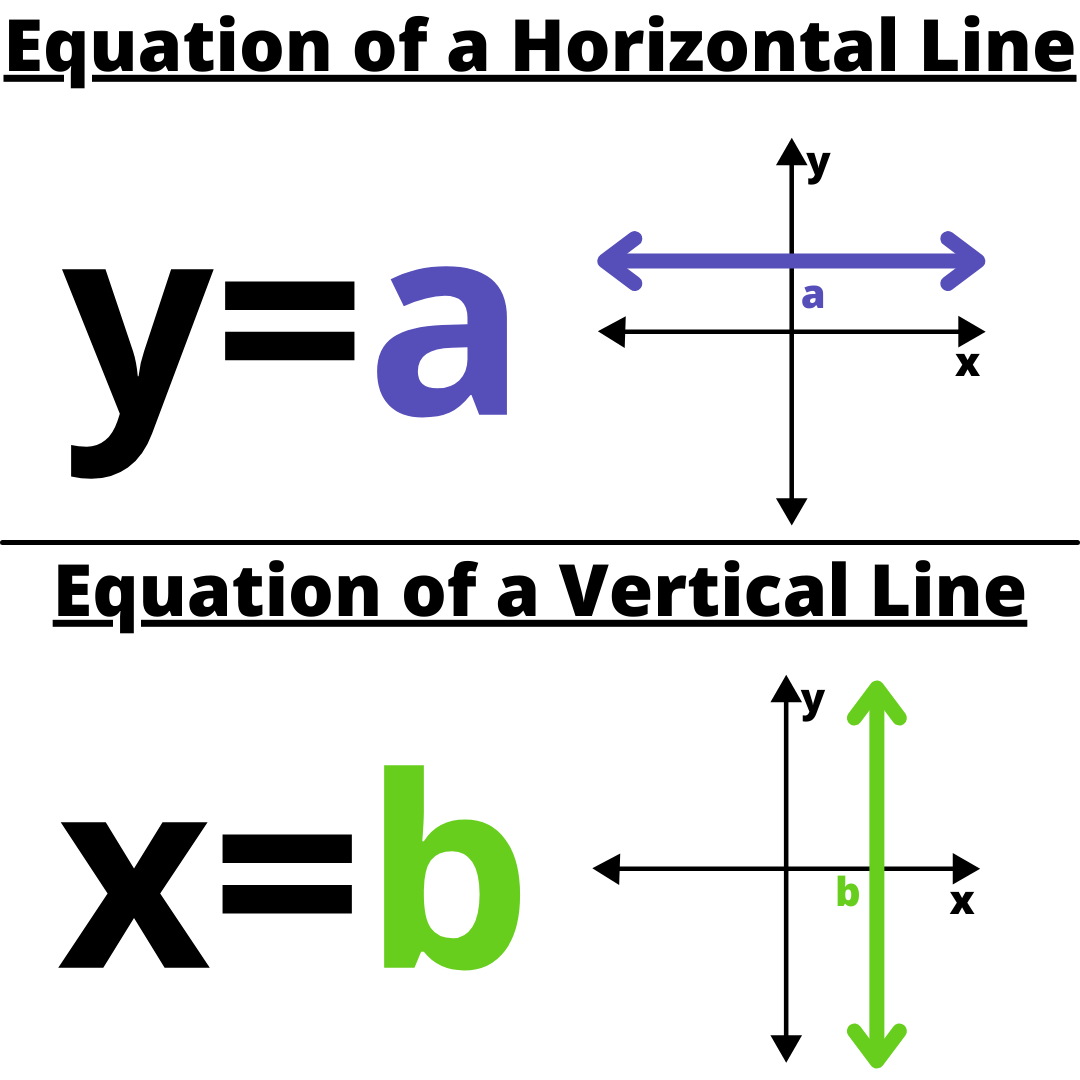
Horizontal and vertical lines

If a line is parallel to the x-axis, and the distance of the line from the x-axis is b units. Then the equation of the line is

Either $y=b$ or $y =-b$.

If a line is parallel to the y-axis, and the distance of the line from the y-axis is a unit. Then the equation of the line is

Either $x=a$ or $x=-a$

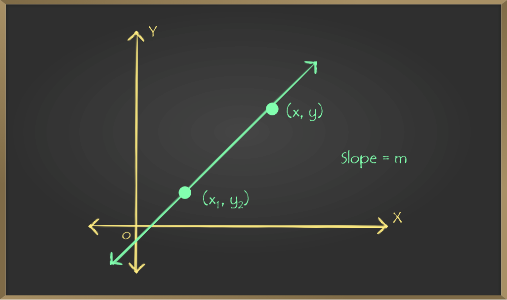
Point-Slope Form

Let a fixed point be (x₁,y₁) and an arbitrary point be (x,y).

Let m be the slope of the line.

Then $\frac{y-y_1}{x-x_1}=m$

$y-y_1=m\left(x-x_1\right)$

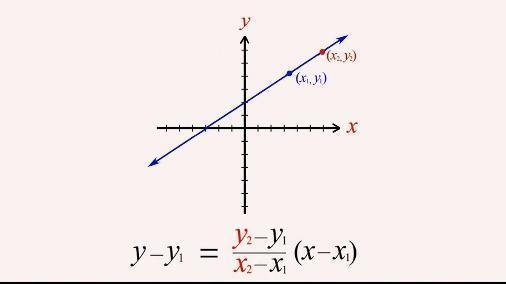
Two-point form

Let two points be (x₁,y₁) and (x₂,y₂) then

$y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right)$

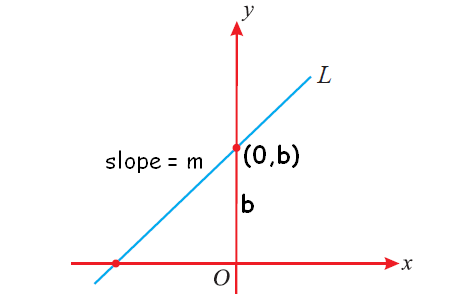
Slope-Intercept Form

Let the point on the y-axis be (0,b), and m is the slope of the line

Then the formula is $y=mx+b$

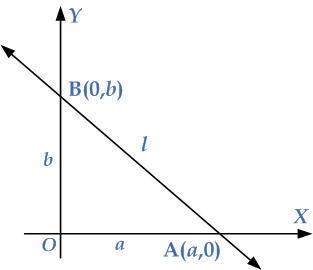
Intercept - Form

Let the points on the coordinate axes be (a, 0) and (0, b)

Then the equation

$\frac{x}{a}+\frac{y}{b}=1$

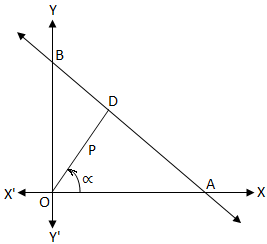
Normal Form

$x \cos \alpha+y \sin \alpha=p$

General Equation Of A Line

The general equation goes by $Ax+By+C=0$

Different forms of $Ax+By+C=0$

Slope-intercept form

$\begin{aligned} & B y=-A x-C \\ & y=-\frac{A}{B} x-\frac{C}{B} \\ & m=-\frac{A}{B} \text { and } c=-\frac{C}{B}\end{aligned}$

Intercept form

$\begin{aligned} & A x+B y+C=0 \\ &⇒ A x+B y=-C \\ &⇒ \frac{x}{-\frac{C}{A}}+\frac{y}{C}=1 \\ &⇒ \frac{x}{a}+\frac{y}{b}=1 \\ &⇒ a=-\frac{C}{A} \text { and } b=-\frac{C}{B}\end{aligned}$

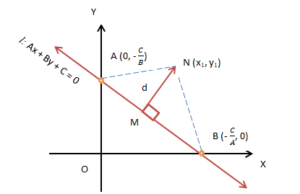
Distance of a Point from a Line

Let P(x₁, y₁) be a point that does not lie on the line $Ax+By+C=0$.

Then the distance of the point P(x₁, y₁) from the line is

$d=\left|\frac{A x_1+B y_1+C}{\sqrt{A^2+B^2}}\right|$

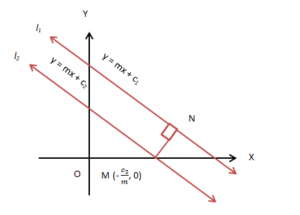
Distance Between Two Parallel Lines

Suppose the equations of two parallel lines be $Ax+By+C_1 = 0$ and $Ax+By+C_2 = 0$

Then the distance between two parallel lines is $d=\left|\frac{C_1-C_2}{\sqrt{A^2+B^2}}\right|$

Straight Lines Class 11 Notes: Previous Year Question and Answer

Given below are selected previous year question answers for NCERT Class 11 Maths Chapter 9 Straight Lines, collected from various examinations.

Question 1:
The graph of the equation $x=a(a \neq 0)$ is a_____.

Solution:
Given: $x=a(a \neq 0)$
A diagram that shows the change of one variable to one or more other variables, such as a collection of one or more points, lines, line segments, curves, or regions.
The value of $x$ = The value of $a$ = 1, 2, 3, and so on to infinity.
The value of $y$ = constant (assume $y=4$)
As a result, the graph these points create will be a straight line parallel to the y-axis.
Hence, the correct answer is "a line parallel to the y-axis".

Question 2:
What is the slope of the line parallel to the line passing through the points (5, –1) and (4, –4)?

Solution:
Given: The points are (5, –1) and (4, –4).
$\text{Slope}=\frac{y_2–y_1}{x_2–x_1}$
Substitute the given values in the above formula, and we get,
$\frac{–4–(–1)}{4–5}=\frac{–3}{–1}$
So, the slope of the given line is 3. The slope of the line parallel to this line is also the same.
Hence, the correct answer is $3$.

Question 3:
At what point does the line $2x–3y = 6$ cut the Y-axis?

Solution:
Given:
The equation is $2x–3y = 6$
The Y-axis can be expressed as $x = 0$.
So, both lines should be satisfied at the intersection.
Substitute $x=0$ in the equation, $2x–3y = 6$, we get,
$(2×0)–3y = 6$
⇒ $y = –2$
The point is (0, –2), which satisfies both lines.
Hence, the correct answer is (0, –2).

Importance of NCERT Class 11 Maths Chapter 9 Notes

NCERT Class 11 Maths Chapter 9 Notes play a vital role in helping students grasp the core concepts of the chapter easily and effectively, so that they can remember these concepts for a long time. Some important points of these notes are:

• Effective Revision: These notes provide a detailed overview of all the important theorems and formulas, so that students can revise the chapter quickly and effectively.
• Clear Concepts: With these well-prepared notes, students can understand the basic concepts effectively. Also, these notes will help the students remember the key concepts by breaking down complex topics into simpler and easier-to-understand points.
• Time Saving: Students can look to save time by going through these notes instead of reading the whole lengthy chapter.
• Exam Ready Preparation: These notes also highlight the relevant content for various exams, so that students can get the last-minute guidance for exams.

NCERT Class 11 Maths Notes Chapter-Wise Links

For students' preparation, Careers360 has gathered all Class 11 Maths NCERT Notes here for quick and convenient access.

Subject-Wise NCERT Exemplar Solutions

After finishing the textbook exercises, students can use the following links to check the NCERT exemplar solutions for a better understanding of the concepts.

• NCERT Exemplar Class 11 Solutions
• NCERT Exemplar Class 11 Maths
• NCERT Exemplar Class 11 Physics
• NCERT Exemplar Class 11 Chemistry
• NCERT Exemplar Class 11 Biology

Subject-Wise NCERT Solutions

Students can also check these well-structured, subject-wise solutions for class 11.

• NCERT Solutions for Class 11 Mathematics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 11 Biology

NCERT Books and NCERT Syllabus

Before the start of a new academic year, students should refer to the latest syllabus to determine the chapters they’ll be studying. Below are the updated syllabus links, along with some recommended reference books.

• NCERT Books Class 11 Maths
• NCERT Syllabus Class 11 Maths
• NCERT Books Class 11
• NCERT Syllabus Class 11