Oscillations Class 11th Notes - Free NCERT Class 11 Physics Chapter 14 Notes - Download PDF

NCERT Notes for Class 11 Physics Chapter 13: Download PDF

These NCERT Class 11 Physics Chapter 13 Notes would help the students have a proper and clear method to revise the concept of oscillations and other concepts. The PDF contains the most important formulas, solved problems, illustrations, and questions to be studied in order to prepare for exams and learn quickly. These notes can enable the students to reinforce their knowledge, revise effectively, and improve problem-solving capabilities to pass the CBSE board exam, the JEE, and the NEET.

Download PDF

NCERT Notes for Class 11 Physics Chapter 13

The NCERT Class 11 Physics Chapter 13 Notes provide a clear and easy-to-follow summary of oscillations, breaking down complex ideas into simple explanations. With diagrams, solved examples, and essential formulas, these notes help students grasp concepts quickly and revise effectively. Perfect for board exam preparation and competitive exams like JEE and NEET, they make studying more efficient and organised.

Periodic Motion

• A motion that repeats itself after a fixed interval of time is called periodic motion. e.g., orbital motion of the Earth around the Sun, motion of the second’s arm of a clock, motion undergone by a simple pendulum, etc.

Oscillatory Motion

• A periodic motion which undergoes a to and fro else back and forth motion about a fixed point, is known as oscillatory motion, e.g., motion shown by a simple pendulum, motion of a spring, etc.
• Note that all oscillatory motions are periodic motions, but not all periodic motions are oscillatory motions. Thus, vice versa is not true.

• Harmonic Oscillation: The oscillation that is expressed in terms of a single harmonic function, which is a sine or cosine function, is a harmonic oscillation.

• Simple Harmonic Motion: A Simple harmonic motion is such that it will move in accordance with to and fro along a straight line. Under restoring force magnitude is directly proportional to that of the displacement.

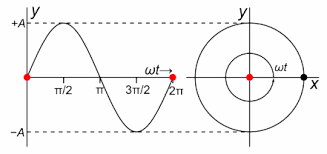
An SHM can be expressed in the following manner:

y = a sin ωt

or

y = a cos ωt

a = amplitude of oscillation.

• Non-harmonic Oscillation

A non-harmonic oscillation is the combination of at least two harmonic oscillations.

Non-harmonic Oscillation is expressed as:

y = a sin ωt + b sin 2ωt

Terms Related to SHM

The following are the important terms related to Simple harmonic Motion-

1. Time Period: The Time taken by a body to complete one whole oscillation is known as the time period. It is symbolised by T.

2. Frequency: The number of oscillations completed by the body in one second is the frequency. It is symbolised by v.

SI unit = ‘Hertz’ or ‘second-1

Frequency = 1 / Time period

3. Angular Frequency: The product of frequency and the factor 2π is called angular frequency. It is symbolised by ω.

Angular frequency (ω) = 2πv

SI unit = ‘Hertz’ or ‘second-1.

4. Displacement: A physical quantity which changes uniformly with respect to time in a periodic motion is displacement. It is symbolised by y.

5. Amplitude: The maximum displacement in any direction with respect to the mean position is called amplitude. It is symbolised by a.

6. Phase: A physical quantity which shows the position and direction of motion of an oscillating particle is known as a phase. It is symbolised by φ.

SHM as Circular Motion

• SHM is defined as the projection of the uniform circular motion on a circle of any diameter as a reference.

• Some Important Formulae of SHM

1. Displacement in SHM at any instant is shown as:

y = a sin ωt

or

y = a cos ωt , where a = amplitude and ω = angular frequency.

2. Velocity of a particle undergoing SHM at any instant is expressed as :

v = ω √(a2 – y2)

When at mean position, y = 0 and v = maximum

vmax = aω

When at an extreme position, y = a and v=0.

3. The acceleration of a particle undergoing SHM at any instant is shown by

A or a = – ω2 y

The acceleration is towards the mean position, and so the negative sign signifies the opposite of an increase in displacement

At the mean position, y = 0 and acceleration = 0.

At the extreme position, y = a and acceleration = maximum

Amax = – aω2

4. Time period in SHM is shown by T = 2π √Displacement / Acceleration

Graphical Representation

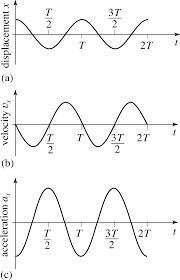
• The acceleration is maximum when the velocity is minimum and vice versa.
• In case a particle is undergoing SHM, the phase difference between

(i) Instantaneous displacement and Instantaneous velocity = (π / 2)

(ii) Instantaneous velocity and Instantaneous acceleration = (π / 2)

(iii) Instantaneous acceleration and Instantaneous displacement = π

The graph of velocity versus displacement for a particle executing SHM is elliptical.

Force in SHM

• Acceleration of body in SHM is α = -ω2 x
• Applying the equation of motion F = ma,

F = – mω2 x = -kx

Where, ω = √k / m and k = mω2 and ‘k’ constant and sometimes it is called the elastic constant.

• The force is proportional and opposite to the displacement ( in SHM).

Energy in SHM

• The Kinetic energy of a particle is K = 1 / 2 mω2 (A2 – x2)
• From the above expression, we can see that the kinetic energy is maximum at the centre (x = 0) and 0 at the extremes of the oscillation (that is, x ± A).
• The Potential energy of the particle, U =mω2 x2/2
• The above expression says, the potential energy has a minimum value at the centre (x = 0) and increases as the particle approaches either extreme of the oscillation (that is x ± A).
• Total energy is obtained by adding potential and kinetic energies. Thus,

E = K + U = [m2 ω2(A2 – x2) + mω2x2]/2= mω2A2/2

where A = amplitude

m = mass of particle executing SHM.

ω = angular frequency and

v = frequency

• Changes that occur in kinetic and potential energies during oscillations.

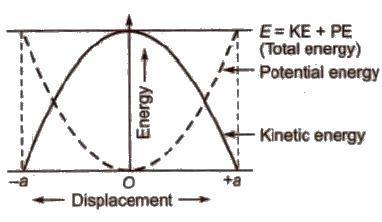
• The frequency of the total energy of particles executing SHM equals zero, as the total energy in SHM remains constant at every position.
• When a particle of mass m undergoes SHM with a constant angular frequency (I), then the time period of oscillation (T)

Simple Pendulum

• A simple pendulum has a heavy point mass which is suspended through a rigid support with the help of an inextensible elastic string.
• The time period of a simple pendulum is expressed as :

T = 2π √(l / g)

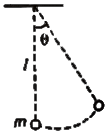
where l = effective length of pendulum and g = acceleration due to gravity.

• Vibrations of a Loaded Spring

The restoring force acts on the spring under the condition that the spring is stretched or compressed through a small distance y.

Restoring force (F) = – ky; Here k = force constant of spring.

In equilibrium, mass m is suspended from a spring system.

mg = kl

This expression is also used for Hooke's law.

The time period of a loaded spring is expressed in terms as follows:

T = 2π √m / k

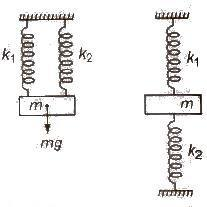
Let the two springs of force constants k1 and k2.

These two constants are connected in parallel to mass m.

1. The effective force constant will therefore be,

k = k1 + k2

(ii) Time period

T = 2π √m / (k1 + k2)

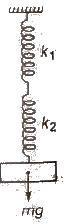
These two constants are connected in series to mass m.

(i) The effective force constant will therefore be,

1 / k = 1 / k1 + 1 / k2

(ii) Time period is expressed as follows: T = 2π √m(k1 + k2) / k1k2

Class 11 Physics Chapter 13 Oscillations: Previous Year Question and Answer

The Class 11 Physics Chapter 13 Oscillations Previous Year Questions and Answers provide students with a comprehensive look at commonly asked problems in past exams. These solved questions help understand exam patterns, practice effectively, and strengthen problem-solving skills. Ideal for board exam preparation and competitive exams like JEE and NEET, they allow quick revision of key concepts and formulas.

Q1: The displacement of a particle is represented by the equation $y=\sin ^3 \omega t$. The motion is:

(a) non-periodic

(b) periodic but not simple harmonic

(c) simple harmonic with period $\frac{2 \pi}{\omega}$

(d) simple harmonic with period $\frac{\pi}{\omega}$

Answer:

Periodic Motion:
- A motion is periodic if it repeats itself after a fixed interval of time. The function $\sin ^3(\omega t)$ is derived from $\sin (\omega t)$, which is periodic with a period $T=\frac{2 \pi}{\omega}$. Since $\sin ^3(\omega t)$ repeats itself every $T$, the motion is periodic.

Simple Harmonic Motion (SHM):
- A motion is simple harmonic if it can be expressed as $y(t)=A \sin (\omega t+\phi)$, where:
- $A$ is the amplitude.
- $\omega$ is the angular frequency.
- $\phi$ is the phase constant.
- The function $\sin ^3(\omega t)$ is not a pure sine wave. Instead, it involves higher harmonics and can be expanded using trigonometric identities.

So the motion is periodic but not simple harmonic. Hence, the answer is the option (b).

Q2: A particle is acted simultaneously by mutually perpendicular simple harmonic motion $x=a \cos \omega t ,$ and $ y=a \sin \omega t$. The trajectory of motion of the particle will be:

(a) an ellipse

(b) a parabola

(c) a circle

(d) a straight line

Answer:

Resultant displacement $=x+y =a \cos \omega t+a \sin \omega t$

Thus,

$\begin{aligned}
y^{\prime}&=a(\cos \omega t+a \sin \omega t)\\
&= a \sqrt{2}\left[\frac{\cos \omega t}{\sqrt{2}}+\frac{\sin \omega t}{\sqrt{2}}\right] \\
& =a \sqrt{2}\left[\cos \omega t \cos 45^{\circ}+\sin \omega t \sin 45^{\circ}\right]
\end{aligned}$

(particle is acted simultaneously by mutually perpendicular directions)
$y^{\prime}=a \sqrt{2} \cos s\left(\omega t-45^{\circ}\right)$.

Thus, the displacement can neither be a straight line nor a parabola

Now, let us square and add $x$ \& $y$,

$x^2+y^2=a^2 \cos ^2 \omega t+a^2 \sin ^2 \omega t$

Thus, $x^2+y^2=a^2$

This represents a circle.

Q3: A particle executing S.H.M. has a maximum speed of $30 \frac{\mathrm{~cm}}{\mathrm{~s}}$ and a maximum acceleration of $60 \frac{\mathrm{~cm}}{\mathrm{~s}^2}$. The period of oscillation is

Answer:

Thus, $y=a \sin \omega t$

$\begin{aligned}
v&=\frac{d y}{d t} \\
&=a \omega \cos \omega t \quad\ldots(i)\\
a&=\frac{d v}{d t} \\
&=-a \omega^2 \sin \omega t \quad\ldots(ii)\\
V_{\text {max }}&=30 \frac{\mathrm{~cm}}{\mathrm{~s}}
\end{aligned}$

From (i),

$V_{\max }=a \omega$

Thus, $a \omega=30 \quad\ldots(iii)$

From (ii),
Now, $a_{\max }=a \omega^2=60 \quad\ldots(iv)$

Thus, $60=\omega \times 30$

Therefore, $\omega=2 \frac{\mathrm{rad}}{\mathrm{s}}$

Now, $\frac{2 \pi}{T}=2$
Thus, $T=\pi$.

Importance of Class 11 Physics Chapter 13 Oscillations

Class 11 Physics Chapter 13 Oscillations is the basic chapter that provides an insight into periodic and repetitive motions in both nature and technology. Learning from this chapter enables students to have a strong background in wave motion, sound, and AC circuits. It is essential for board exams and competitive exams such as JEE and NEET, and improves conceptual understanding and problem-solving.

• Foundation for Wave Mechanics: It is the study of oscillatory motion and the beginning of waves, sound propagation, and vibration phenomena that are important to advanced physics studies.
• Real-Life Applications: The concepts of simple harmonic motion (SHM) can be used directly in pendulums, clocks, musical instruments, and in the vibrations of molecules.
• Competition Exam Preparation: Oscillations are common in JEE, NEET, and other entrance exams, usually in numerical or conceptual questions about mass-spring systems, pendulums, and energy relationships.
• Enhances Analytical Thinking: SHM Problems on displacement, velocity, acceleration, phase, and energy help students develop more mathematical reasoning and analytical abilities.
• Energy Understanding: The chapter focuses on understanding how kinetic energy and potential energy interact in oscillatory systems, assisting the students to imagine energy conservation in dynamic systems.
• Graphical Interpretation Skills: Students are taught the interpretation of displacement-time, velocity-time, and acceleration-time graphs, and this is an important skill needed in the analysis of experiments and in problem solving.
• Connection to Higher Topics: The understanding of oscillations will be used to build the knowledge of AC circuits, resonance and the use of modern physics in electronics and in mechanical systems.
  

NCERT Class 11 Notes Chapter-Wise

The chapter-by-chapter notes of NCERT Class 11 Physics are well edited and designed so that students can revisit each subject in the most effective manner. Such notes comprise formulas, significant concepts, solved problems, and practice questions, and learning is fast and efficient. They are aimed at making complicated subjects easy to understand and will help in the preparation for CBSE board exams and some of the competitive exams, such as JEE and NEET. These structured chapter-by-chapter notes will enable the students to reinforce their basics and enhance their ability to solve problems.

Subject Wise NCERT Exemplar Solutions

• NCERT Exemplar Class 11 Solutions
• NCERT Exemplar Class 11 Maths
• NCERT Exemplar Class 11 Physics
• NCERT Exemplar Class 11 Chemistry
• NCERT Exemplar Class 11 Biology

Subject Wise NCERT Solutions

• NCERT Solutions for Class 11 Mathematics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Physics

• NCERT Solutions for Class 11 Biology