NCERT Class 11 Physics Chapter 12 Notes Thermodynamics - Download PDF
Suppose there is a cup of tea on the table that is hot--you see it cools down slowly till it reaches the temperature of the room. This simple observation is a beautiful explanation of the principles of thermodynamics, the science of physics, which is concerned with the interrelation of heat, work, temperature, and energy. Class 11 Physics Chapter 11 - Thermodynamics is a very important chapter that addresses these ideas in detail and is important in understanding how energy transformation takes place in many physical processes.
This Story also Contains
- NCERT Notes for Class 11 Physics Chapter 11: Download PDF
- NCERT Notes for Class 11 Physics Chapter 11
- Class 11 Physics Chapter 11 Thermodynamics: Previous Year Question and Answer
- How to Master Class 11 Physics Chapter 11 Thermodynamics?
- Importance of NCERT Notes for Class 11 Physics Chapter 11
- How to Use NCERT Class 11 Physics Chapter 12: Thermodynamics Notes Effectively?
- NCERT Class 11 Notes Chapter-Wise
- Subject-Wise NCERT Exemplar Solutions
- Subject-Wise NCERT Solutions
- NCERT Books and Syllabus

To simplify complex topics, the NCERT Notes for Class 11 Physics Chapter 11 Thermodynamics are well drafted by experts in the subject to ensure that students can learn and understand the handy materials. These NCERT notes are clear explanations of important concepts such as thermal equilibrium, the zero law, internal energy, the first and second law, and such processes as the isothermal and adiabatic changes. These NCERT notes are prepared in line with the new CBSE syllabus and are invaluable to students who are about to take CBSE board exams, JEE, NEET, and other competitive exams. These NCERT Notes for Class 11 Physics Chapter 11 Thermodynamics are easy to revise due to simplified derivations, significant formulas, definitions, clearly labelled diagrams, and solved examples. Not only do they enhance conceptual knowledge, but they also enable students to solve real-life as well as exam-level problems with the confidence of applying thermodynamic concepts.
Also, students can refer to
NCERT Notes for Class 11 Physics Chapter 11: Download PDF
The Class 11 Physics Chapter 11 Thermodynamics Notes can be downloaded easily by the students in order to get well-structured and exam-oriented study material. The Thermodynamics Class 11 Physics notes are in a structured form with brief explanations, major formulas, and derivations, which one can revise within a short period. Created by professionals according to the newest CBSE standards, they assist students in enhancing their conceptual understanding and train well to sit CBSE, JEE, and NEET exams.
NCERT Notes for Class 11 Physics Chapter 11
The Thermodynamics Class 11 Physics Chapter 11 CBSE notes assist students in knowing the connections between heat and work, as well as how these entities relate to energy within a physical system. These Thermodynamics Class 11 Physics notes include all the significant concepts, such as thermal equilibrium, laws of thermodynamics, and heat transfer, in a simple and sequential manner. They are ready-made and based on the latest CBSE syllabus; hence, they are ideal in terms of revision within a short time and performing highly in board and competitive exams.
Mechanics vs. Thermodynamics
- In thermodynamics, we focus exclusively on the state of the object, evaluating macroscopic variables such as pressure, volume, and temperature. whereas mechanics is concerned with the motion of an object, taking into account parameters such as velocity and acceleration.
Thermal Equilibrium
- When two systems have identical temperatures, we say they are in thermal equilibrium. In mechanics, a system is considered in equilibrium when its net force is zero. Equilibrium in thermodynamics refers to the stability of all macroscopic variables over time, including pressure, temperature, and volume.
- Different Types of Equilibrium: Various types of equilibrium characterise different aspects of physical systems:
- Thermal equilibrium: Thermal equilibrium occurs when two systems' temperatures remain constant over time.
- Chemical equilibrium: Chemical equilibrium occurs when two systems' compositions remain constant over time.
- Mechanical equilibrium: Mechanical equilibrium occurs when two systems' pressures do not vary over time.
System and Surroundings
- System: Any distinct part of the universe surrounded by a boundary that allows for the exchange of heat or energy.
- Surroundings: Everything outside of the defined system that makes up the broader environment.
- Different System Types:
- Open System: Characterised by the unrestricted exchange of energy and matter with its environment. An everyday example is a cup of coffee boiling in an open pan, allowing heat and water vapour to escape freely.
- Closed System: A closed system allows for the exchange of energy but restricts the flow of matter. A gas-filled balloon is an example of a closed system because it allows for energy transfer (thermal expansion or contraction) while maintaining a constant volume of gas.
- Isolated System: There is no exchange of matter or energy with the surroundings. A thermos flask is a classic example of how insulation prevents heat loss or gain, allowing the contents to remain at a constant temperature for an extended period of time.
- Different Types of Walls:
- Adiabatic wall: The adiabatic wall acts as an insulating barrier, preventing heat transfer between systems. This type of wall keeps the temperatures of the interacting systems constant over time.
- Diathermic wall: The diathermic wall acts as a conducting barrier, allowing heat to be transferred between two systems. A diathermic wall, as opposed to an adiabatic wall, allows heat to flow through it, allowing temperature adjustments between connected systems.
Thermodynamics' Zeroth Law
- According to the Zeroth Law of Thermodynamics, if two systems are in thermal equilibrium with a third system on their own, they are also in thermal equilibrium with each other. This fundamental principle provides a foundation for defining and measuring temperature by emphasising thermal equilibrium as a transitive relation.

Thermodynamic state variables
- Thermodynamic state variables are macroscopic quantities that define an equilibrium state in a system. These variables contain important information about the system's properties.
- Examples of Thermodynamic State Variables:
- Extensive Variables: These variables are proportional to the system's size and are influenced by its mass or particle count. Examples include volume, mass, and internal energy. For example, when dealing with a larger mass system, the volume and internal energy are larger as well, demonstrating the system's size dependence.
- Intensive variables: Intensive variables are unaffected by the system's size. These parameters remain constant regardless of the system's mass or number of particles. Intensive variables include pressure and temperature. These variables maintain their values regardless of system size.
- Equation of State:
The equation of state establishes a link between key variables such as pressure, mass, volume, and density, describing the state of matter when certain physical conditions are met. In the case of an ideal gas, this equation provides information about its behaviour under various conditions, making it a useful tool for understanding and predicting its state.
Consider an ideal gas, whose state equation is
$P V=\mu R T$
Here, P, V, and T are state variables, with μ = no. of moles.
Heat, Work and Internal Energy
- Heat: Heat is the energy exchanged between a system and its surroundings when the temperature differs. This transfer occurs due to the thermal gradient, resulting in changes in the system's internal energy.
- Work: Work occurs when a body or system moves in response to a force. Work, mathematically expressed as,
$\mathrm{dW}=\mathrm{PdV}$
Where P is the pressure of the gas in the cylinder.
- Internal energy: The internal energy (U) of a system of molecules is the sum of their kinetic and potential energies. Internal energy, denoted by U = Ek + Ep, where Ek and Ep are the molecular kinetic and potential energies, is a macroscopic variable that is solely determined by the state of the system. It is not determined by the path taken, but rather by the energy resulting from molecular motion and configuration within the system.
- Unlike internal energy, heat and work are not state variables. They are forms of energy transfer to a system that cause an internal energy change.
Thermodynamics First Law
- The First Law of Thermodynamics is synonymous with the principle of energy conservation, which states that energy cannot be created or destroyed but can be transformed into other forms.
- According to the First Law of Thermodynamics, the change in internal energy of a closed system equals the heat added to the system minus the work done by the system on its surroundings.
- Examples: Consider a ball dropping from a building's roof. Initially, the ball possesses potential energy at the top, which diminishes as it falls, transforming into kinetic energy. By the time it reaches the ground, the ball only has kinetic energy.
- Mathematically,
$\Delta Q=\Delta U+\Delta W$
- For Cyclic Process
$\sum \Delta Q=\sum \Delta W$
Where: ΔQ is the heat provided to the system by the environment.
ΔW denotes the amount of work done by the system in relation to the environment.
And ΔU is the change in the system's internal energy.
Relation between CP and CV
- Mayer's Formula describes the relationship between the specific heat at constant pressure (CP) and the specific heat at constant volume (CV) for an ideal gas. According to Mayer's relation, an ideal gas:
CP - CV = R
Specific Heat Capacity
- Specific heat capacity is the amount of heat required to raise the temperature of a substance per unit mass.
$S=\frac{\Delta Q}{m \Delta T}$
Where,
m is the body's mass, ΔQ is the quantity of heat that a substance absorbs or rejects, and ΔT stands for temperature change.
Molar Specific Heat Capacity
- The heat capacity per mole is the amount of heat (in moles) absorbed or rejected (instead of mass m in kg) by a substance to change its temperature by one unit.
$C=S / \mu=\Delta Q / \mu \Delta T$
Where: μ= the mass of a material in moles, C is the substance's molar specific heat capacity, ΔQ is the quantity of heat that a substance absorbs or rejects, and ΔT stands for temperature change.
- At constant pressure, molar specific heat capacity (CP): The equivalent molar specific heat capacity at constant pressure is called molar specific heat capacity at constant pressure if the gas is retained at constant pressure during the heat transfer (CP).
- At constant volume, the molar specific heat capacity (CV): The equivalent molar specific heat capacity at constant volume is called molar specific heat capacity at constant volume if the volume of the gas is maintained during the heat transfer (CV).
Isothermal Processes
- An Isothermal Process is defined as a condition in which the temperature of a system undergoing a thermodynamic process remains constant throughout. In other words, during an isothermal process, the system's other thermodynamic variables change (such as pressure, volume, or internal energy), but the temperature remains constant.
- The equation for an ideal gas undergoing an isothermal process describes the relationship between pressure (P), volume (V), and temperature (T):
PV=constant
This means that the product of pressure and volume for an ideal gas remains constant as long as the process takes place at the same temperature. A hyperbolic curve is commonly used to represent the behaviour of an isothermal process on a pressure-volume (PV) diagram.
- Graphically,
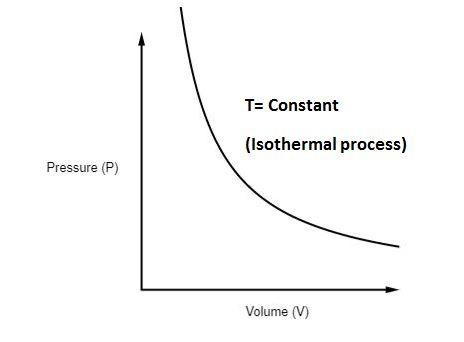
Points in the Graph of the Isothermal Process:
- Isotherms are curves on the pressure-volume (P-V) graph that form during an isothermal process. These isotherms have a hyperbolic shape.
- The slope of an isothermal curve on the P-V graph:
$\tan \theta=\frac{d P}{d V}=\frac{-P}{V}$
- The area between the isothermal curve and the volume axis on the P-V graph represents the work done during the isothermal process.
- The magnitude of work done in the isothermal process:
$\begin{aligned} & W=n R T \log _e\left(\frac{V_f}{V_i}\right)=2.303 n R T \log _{10}\left(\frac{V_f}{V_i}\right) \\ & W=n R T \log _e\left(\frac{P_i}{P_f}\right)=2.303 n R T \log _{10}\left(\frac{P_i}{P_f}\right)\end{aligned}$
Adiabatic Processes
- An Adiabatic process is a thermodynamic process in which no heat is exchanged between the system and its surroundings. In other words, the system is thermally isolated, which prevents heat from entering or leaving the system.
- Equations of Adiabatic process:
$\begin{gathered}P V^\gamma=\text { constant; where } \gamma=\frac{C_P}{C_V} \\ T V^{\gamma-1}=\text { constant } \Rightarrow T_1 V_1^{\gamma-1}=T_2 V_2^{\gamma-1} \text { or } T \propto V^{1-\gamma} \\ \frac{T^\gamma}{P^{\gamma-1}}=\text { constant } \\ \Rightarrow T_1^\gamma P_1^{1-\gamma}=T_2^\gamma P_2^{1-\gamma} \text { or } T \propto P^{\frac{\gamma-1}{\gamma}} \text { or } P \propto T^{\frac{\gamma}{\gamma-1}}\end{gathered}$
Isochoric Processes
- Isochoric Process refers to a thermodynamic process in which the system's volume remains constant while other variables, such as pressure and temperature, vary. Because the volume is constant in an isochoric process, no work is done to or by the gas.
ΔW =0
Isobaric Processes
- The term "Isobaric Process" is derived from the combination of "iso," meaning the same, and "baric," which refers to pressure. In an isobaric process, pressure remains constant throughout the operation, whereas volume and temperature may fluctuate.
$\begin{aligned} & W=\mu R\left(V_2-V_1\right) \\ & \Delta Q=\Delta U+\mu R\left(T_2-T_1\right)\end{aligned}$
Cyclic Processes
- The process by which the system returns to its original condition.
ΔU = 0
This means that the entire amount of heat absorbed is equal to the amount of work done by the system.
Heat Engines
- A Heat Engine is a device that allows heat to be supplied and absorbed by placing a body in alternating contact with hot and cold bodies.
- A heat engine, to put it simply, is a mechanism that turns thermal energy into mechanical energy.
Thermodynamics' Second Law
- The Second Law of Thermodynamics states that any spontaneous process will inevitably result in an increase in the total entropy (S) of the universe. Simply put, this law states that the entropy of an isolated system does not decrease over time.
- Under certain conditions, such as thermodynamic equilibrium or a reversible process, the total entropy of a system and its surroundings remains constant. The Law of Increased Entropy is an alternative term for the second law, emphasising the tendency of systems to progress towards greater disorder over time.
Reversible and Irreversible Process
- Reversible Process: A thermodynamic process is considered reversible if it can be reversed, restoring the system and its surroundings to their original states while causing no net change in the universe. Reversible processes allow the system to transition from an initial state to a final state and then seamlessly reverse back to the initial state. Examples include isothermal expansion and compression, as well as electrolysis.
- Irreversible Process: Irreversible processes are those that cannot be reversed in any practical way. Irreversible processes typically happen quickly. Examples include plastic deformation, combustion, diffusion, and water flow downhill. Irreversible processes cause an increase in entropy and lack reversibility.
Carnot Engine

- The Carnot Engine was named after the scientist Carnot.
- It's a reversible heat engine that can operate at two different temperatures.
- It achieves a level of efficiency that no other engine can match.
- Processes in a Carnot engine's cycle

Any heat engine's basic function is to transfer heat Q1 from a hot reservoir at temperature T1 to a cool reservoir at temperature T2.
It is isothermal expansion because the system absorbs heat. At temperature T1, the engine absorbs heat Q1.
Inside the engine, an adiabatic process occurs, causing the temperature of the engine to rise from T1 to T2, but with no heat flow.
Isothermal contraction occurs as the system releases heat. At temperature T2, the engine produces heat Q2.
An adiabatic process occurs once more, changing the system's temperature from T2 to T1.
Isothermal expansion, followed by the adiabatic process, and then isothermal contraction, followed by the adiabatic process, make up one cycle of the Carnot engine.
This will continue to happen.
- The efficiency of the Carnot engine is given by:-
$\eta=\frac{W}{Q_1-Q_2}=1-\frac{T_2}{T_1}$
Class 11 Physics Chapter 11 Thermodynamics: Previous Year Question and Answer
The Class 11 Physics Chapter 11 - Thermodynamics Previous Year Questions and Answers can guide the students to know the kind of questions that are asked in board and competitive exams. The questions are to enhance the conceptual knowledge and accuracy of problem-solving in terms of heat, energy, and laws of thermodynamics. By regularly practising them, the students can learn to recognise critical subject matter, can become faster, and gain confidence in tests such as CBSE, JEE and NEET.
Q1: An ideal gas undergoes an isothermal process from some initial state I to final state f. Choose the correct alternatives
a) dU = 0
b) dQ = 0
c) dQ = dU
d) dQ = dW
Answer:
Since the process is isothermal $\Delta T=0$ or T is constant For an ideal gas, dU=Change in internal energy=nCvdT $\mathrm{dT}=0$; Thus $\mathrm{dU}=0$
$
\begin{gathered}
d Q=d U+d W \\
d Q=d W
\end{gathered}
$
Hence, the answers are options (a) and (d) only.
Q2: An ideal gas undergoes a cyclic process ABCDA as shown in the given P-V diagram (Figure). The amount of work done by the gas is:
Answer:
Let us take the $P-V$ diagram. In this figure, the work done in the process of $A B C D$ is equal to the area of the rectangle in ABCDA.
$\Rightarrow$ work done in the process of $A B C D=$ area of the rectangle in $A B C D A$.
$\Rightarrow$ work done in the process of $A B C D=A B \times B C$
$\Rightarrow$ work done in the process of $\mathrm{ABCD}=\left(3 V_o-V_o\right) \times\left(2 P_o-P_o\right)$
$\Rightarrow$ work done in the process of $\mathrm{ABCD}=2 V_o \times P_o$
$\Rightarrow$ work done in the process of $\mathrm{ABCD}=2 V_o P_o$
Here we can see that the process is in an anti-clockwise direction, therefore, work done in the process of $\mathrm{ABCD}=-2 V_o P_o$
Q3: An ideal gas undergoes four different processes from the same initial state (Figure). Four processes are adiabatic, isothermal, isobaric and isochoric. Out of 1, 2, 3 and 4, which one is adiabatic
.
Answer:
For curve 4, pressure is constant, so this is an isobaric process.
For curve 1, volume is constant, so it is an isochoric process. Between curves 3 and 2, curve 2 is steeper, so it is adiabatic, and curve 3 is isothermal
Q4: A monoatomic gas having $\gamma=\frac{5}{3}$ is stored in a thermally insulated container, and the gas is suddenly compressed to $\left(\frac{1}{8}\right)^{\text {th }}$ of its initial volume. The ratio of final pressure and initial pressure is:
($\gamma$ is the ratio of specific heats of the gas at constant pressure and at constant volume)
Answer:
$\begin{aligned} & P_i V_i^\gamma=P_f V_f^\gamma \\ & \frac{P_f}{P_i}=\left(\frac{V_i}{V_f}\right)^\gamma=(8)^{5 / 3} \\ & \frac{P_f}{P_i}=32\end{aligned}$
Q5:
An ideal gas has undergone the cyclic process as shown in the figure. Work done by the gas in the entire cycle is _____ $\times 10^{-1} \mathrm{~J}$.
(Take $\pi=3.14$ )
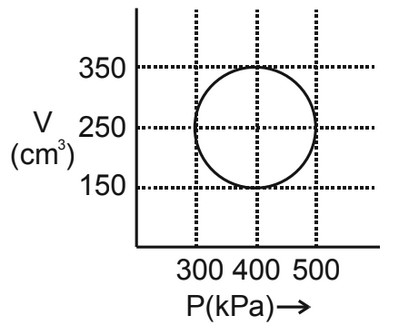
Answer:
Area of circle, $W=\frac{\pi}{4} d_1 d_2$
$
\begin{aligned}
& \mathrm{W}=\frac{\pi}{4}(500-300) \times 10^3(350-150) \times 10^{-6} \\
& \mathrm{~W}=31.4 \text { Joule } \\
& \mathrm{W}=314 \times 10^{-1} \text { Joule }
\end{aligned}
$
Hence, the answer is 314.
How to Master Class 11 Physics Chapter 11 Thermodynamics?
Thermodynamics is concerned with the behaviour of heat, work and internal energy, and the determination of the patterns of flow of energy between systems and the environment. The chapter proposes important laws such as the First and Second Laws of Thermodynamics, heat engines, refrigerators, and efficiency. Since the concepts are very basic and most common in physics and engineering, the learning of this chapter enhances logical thinking. Having conceptual clarity as well as numerical practice, Thermodynamics is considered among the scoring chapters in Class 11.
- Begin with some fundamental concepts such as system, surroundings, systems of various types and state variables such as pressure, volume, temperature and internal energy.
- The Zeroth Law is important and should be understood well since it is the foundation of temperature measurement and thermal equilibrium.
- Develop a good understanding of the First Law of Thermodynamics and revise the sign conventions of heat and work in order to avoid the most frequent mistakes.
- Solve numerical problems of heat exchange, work done in PV curves and change of internal energy to reinforce the applications of the First Law.
- Learn the various thermodynamic processes isochoric, isobaric, isothermal and adiabatic and their PV curves and equations.
- Learn the adiabatic equations and practice problems involving adiabatic processes involving work done and change in temperature.
- Study the Second Law of Thermodynamics conceptually, focusing on entropy, spontaneous processes, and direction of heat flow.
- Learn the principles of heat engines and the Carnot theorem using a simple example.
- Solve all NCERT and Exemplar numericals, as many competitive and school exam questions directly come from them.
- Keep a formula sheet with a summary of the relations of PV, work done in various processes, formulae of efficiency and thermodynamics laws to revise easily.
- Draw and revise PV diagrams frequently because many questions require identifying the process from the graph.
- The conceptual questions should be practised on a regular basis to develop some intuition on the topic of heat, work and energy flow, as this is vital in mastering the chapter.
Importance of NCERT Notes for Class 11 Physics Chapter 11
The Thermodynamics Class 11 Notes are essential to understand one of the most basic aspects of physics, the connection between heat, work, and energy. These notes make complex laws and derivations less challenging, thereby assisting students in establishing a solid conceptual foundation. Not only are they required to score well in CBSE board examinations, but they are also the basis
- Breaks down Complex Concepts: The notes also simplify complex concepts such as the laws of thermodynamics, internal energy, enthalpy and heat engines into simple explanations, thus making the learning process easier and less daunting.
- Helps in Quick Revision: These notes are easy to revise, and the main formulas, definitions and derivations are underlined so that students may revise these notes effectively prior to CBSE board exams or competitive exams such as JEE/NEET.
- Enhances Conceptual Clarity: The notes also facilitate learning of the underlying principle of transfer of energy and work by giving step-by-step explanations, examples, and worked-out problems so that the students are not memorising formulas but comprehending the principles of energy transfer and work.
- Useful for Problem-Solving: Examples with detailed derivations and numerical illustrations allow the students to develop problem-solving skills that are essential in solving both theoretical and application-based questions in an examination.
- Bridges Classroom and Preparation of Examinations: Such notes are a supplement to classroom instructions as they reduce bulky chapters to specific points and enable students to concentrate on relevant issues in board and competitive exams.
- Improves Memorising using Visual Aids: The notes contain labelled diagrams, graphs and illustrations, which enable the students to visualise processes such as isothermal, adiabatic and cyclic processes, as a way of understanding and retaining.
- Foundation for Advanced Studies: Thermodynamics is fundamental to higher-level physics, engineering, and chemistry. These notes build a strong base for advanced concepts encountered in Class 12, IIT-JEE, NEET, and other entrance exams.
How to Use NCERT Class 11 Physics Chapter 12: Thermodynamics Notes Effectively?
The Class 11 Physics chapter 11 Thermodynamics Notes on this chapter present the basic concepts of thermodynamics in a simple and understandable manner, and thus students find it easy to comprehend concepts such as heat, work and energy transfer. These Class 11 Physics chapter 11 Thermodynamics Notes can be used to make the learning process simpler, faster, and achieve better results in exams when applied properly.
- Begin by checking out the Thermodynamics NCERT Notes to gain a rough idea of the chapter, and then proceed to the specific theory.
- Learn several important terms (thermodynamic systems, laws of thermodynamics, internal energy, heat, and work) using simple real-life examples.
- Write a list of important formulas and memorise them separately so that they are easily remembered in exams.
- Do the numeric problems after reading the Thermodynamics Class 11 Notes to increase your skills in applying the formulae properly.
- Pay attention to the diagrams and solved problems in the notes because they allow understanding the thermodynamic processes and remembering the concepts more easily
- Keep on revising the Class 11 Thermodynamics Notes, particularly prior to tests and exams, to retain the concepts in your mind.
- In case you have problems with some of the concepts or feel confused, consult the textbook rather than brushing off the doubt.
NCERT Class 11 Notes Chapter-Wise
These Class 11 Physics chapter-wise notes of NCERT offer students a simplified and structured study guide on all aspects of the syllabus. These notes are designed by experts in the subject, comprising important formulas, important definitions, solved examples, and practice questions, to ensure that the student can revise at an efficient pace. They are also perfect for preparing for exams in a short time, whether they are CBSE board exams or competitive exams, such as the JEE and NEET. These notes can be read online or downloaded by the students as PDF files so that they can study them at any time and place.
Subject-Wise NCERT Exemplar Solutions
NCERT Exemplar Solutions for Class 11 provide additional practice through higher-order and application-based questions. The subject-wise links help students strengthen conceptual clarity and improve problem-solving skills for exams and competitive tests.
Subject-Wise NCERT Solutions
NCERT Solutions for Class 11 offer detailed, step-by-step answers to all textbook questions across subjects. These subject-wise links make learning organised and help students prepare effectively for school exams.
NCERT Books and Syllabus
NCERT Books and the NCERT Syllabus for Class 11 form the backbone of the academic curriculum. Easy access to these links helps students understand the prescribed course structure and study systematically as per the latest guidelines.
Frequently Asked Questions (FAQs)
It is, in fact, very important chapter as far as JEE and NEET are concerned because it acts as a foundation to several conceptual and numerical questions on heat, energy, and the efficiency of a system.
Thermodynamics is a part of physics that concerns the correlation between heat, work and energy. it discusses the transfer of energy in a system and surrounding.
The NCERT notes provide well-written explanations, essential formulas, derivations and diagram-based revision for last-minute revision
Devices such as ACs, engines, other power plants, and even biological metabolism in organisms are based on thermodynamics.
The Second Law of Thermodynamics Asserts that a hot object will naturally give heat to a cold object until both are at the same temperature.
No, the NCERT notes for Class 11 Physics Chapter 11 do not include all of the important derivations. This NCERT note provides a summary of the chapter's main themes and equations and can be used to review Thermodynamics.
From the notes for Class 11 Physics chapter 11, students should expect 4 to 6 mark questions, and they can use this note for quick revision to help them improve their grades.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters


