NCERT Solutions for Class 11 Physics Chapter 10 Thermal Properties of Matter
Have you never observed that a chair made of metal is colder than one made of wood, though both are at the same temperature? Or why blacksmiths heat rims of iron and put them in wooden wheels? This is explained in Chapter 10 - Thermal Properties of Matter of Class 11 Physics. This chapter presents the concept of heat, temperature, thermal expansion, calorimetry, specific heat capacity and various methods used in transferring heat, such as conduction, convection, and radiation.
This Story also Contains
- Thermal Properties of Matter NCERT Solutions: Download Solution PDF
- Thermal Properties of Matter NCERT Solutions - Exercise Questions
- Class 11 Physics Chapter 10 - Thermal Properties of Matter: Higher Order Thinking Skills (HOTS) Questions
- Class 11 Physics Chapter 10 - Thermal Properties of Matter: Topics
- Class 11 Physics Chapter 10 - Thermal Properties of Matter: Important Formulae
- How Can NCERT Solutions for Class 11 Physics Chapter 10 Help in Exam Preparation?
- Approach to Solve Questions of Class 11 Physics Chapter 10 - Thermal Properties of Matter
- Importance of NCERT Solutions for Class 11 Physics Chapter 10: Thermal Properties of Matter
- What Students Learn from NCERT Solutions for Class 11 Physics Chapter 10: Thermal Properties of Matter?
- What Extra Should Students Study Beyond NCERT for JEE/NEET?
- NCERT Solutions for Class 11 Physics Chapter-Wise
- NCERT solutions for class 11 subject-wise
.jpg)
NCERT Solutions for Class 11 Physics Chapter 10 - Thermal Properties of Matter are made by experienced teachers, and it is presented in a step-by-step explanation of all the questions in the exercise. These NCERT solutions make complicated concepts much easier, enhance problem-solving abilities and enable students to relate theory with practical life examples such as boiling water, land winds, sea winds or thermal conductivity of metals. They are very useful in CBSE board examinations and competitive exams of JEE, NEET, and Olympiads are also good preparation material. These NCERT Solutions for Class 11 Physics Chapter 10 - Thermal Properties of Matter should be practised regularly so that a firm foundation is laid and the performance in exams is enhanced
Also Read
- NCERT Exemplar Class 11 Physics Solutions Chapter Thermal Properties Of Matter
- NCERT Class 11 Physics Chapter 10 Notes Thermal Properties of Matter - Download PDF
Thermal Properties of Matter NCERT Solutions: Download Solution PDF
The Class 11 Physics Chapter 10 - Thermal Properties of Matter question answers can be downloaded as a free PDF file, which allows students to prepare for exams easily. The class 11 physics chapter 10 Thermal Properties of Matter question answers are in steps and are made in accordance with the recent CBSE syllabi, and facilitate fast revision. Here, the download link of the Thermal Properties of Matter NCERT Solutions PDF is provided, which you can study and practice very easily without any complications.
Thermal Properties of Matter NCERT Solutions - Exercise Questions
The Thermal Properties of Matter class 11 question answers address every question in the exercises with step-by-step explanations. Students develop an insight into topics such as heat transfer, heat expansion, and specific heat, and can solve numerical problems, and prepare better to take board exams, JEE, and NEET.
Answer:
The relation between the Kelvin and Celsius scales is T oK = T oC + 273.15
Triple Point of Neon in Kelvin T oK = 24.57 K
Triple Point of Neon in Celcius T oC = T oK -273.15 = 24.57 -273.15 =-248.58 C
Triple Point of carbon dioxide in Kelvin T oK = 216.55 K
Triple Point of carbon dioxide in Celcius T oC = T oK -273.15 = 216.55 - 273.15 = -56.60 C
The relation between Celcius and Fahrenheit scale is $T_{F}=\frac{9}{5}T_{C} + 32$
Triple Point of Neon in Fahrenheit is
$T_{F}=\frac{9}{5}\times (-248.58) + 32$
TF = -415.44 oC
The triple point of carbon dioxide in Fahrenheit is
$T_{F}=\frac{9}{5}\times (-56.60) + 32$
TF = -69.88 oC
Answer:
200 A = 273 K
$T_{K}=\frac{273}{200}T_{A}$
350 B = 273 K
$T_{K}=\frac{273}{350}T_{B}$
Equating T K from the above two equations, we have
$\frac{273}{200}T_{A}=\frac{273}{350}T_{B}$
$T_{A}=\frac{4}{7}T_{B}$
Q. 10.3 The electrical resistance in ohms of a certain thermometer varies with temperature according to the approximate law:$R=R_{0}\left [ 1+\alpha (T-T_{0}) \right ]$ The resistance is $101.6\Omega$ at the triple-point of water $273.16\; K,$ and $165.5\; \Omega$ at the normal melting point of lead $(600.5\; K).$ What is the temperature when the resistance is $123.4\; \Omega$?
Answer:
$R=R_{0}\left [ 1+\alpha (T-T_{0}) \right ]$
R 0 = $101.6\Omega$
T 0 = $273.16 K$
R = $165.5\; \Omega$
T = $600.5 K$
Putting the above values in the given equation, we have
$\\\alpha =\frac{165.5-101.6}{600.5-27316}\\ $
$\alpha =1.92\times 10^{-2}\ K^{-1}$
For R = $123.4\; \Omega$
$\\T=T_{0}+\frac{1}{\alpha }\left ( \frac{R}{R_{0}}-1 \right )\\ $
$T=273.16+\frac{1}{1.92\times 10^{-2}}\left ( \frac{123.4}{101.6}-1 \right )\\ $
$T=384.75K$
Answer:
Unlike the melting point of ice and the boiling point of water, the triple point of water has a fixed value of 273.16 K. The melting point of ice and the boiling point of water vary with pressure.
Answer:
The other fixed point on the Kelvin scale is 0 K. 0K is the absolute zero
Answer:
This is because 0 °C on the Celsius scale corresponds to the melting point at standard pressure is equal to 273.15 K, whereas 273.16 K is the triple point of water. The triple point of water is 0.01oC , not 0 °C
Answer:
Let at a certain temperature, the readings on the Fahrenheit and Kelvin Scales be T F and T K, respectively
$T_{F}-32=\frac{9}{5}(T_{K}-273)$ $(i)$
Let at another temperature, the reading on the Fahrenheit and Kelvin Scales be T' F and T' K respectively
$T'_{F}-32=\frac{9}{5}(T'_{K}-273)$ $(ii)$
Subtracting equation (ii) from (i)
$T_{F}-T'_{F}=\frac{9}{5}(T_{K}-T'_{K})$
For T K - T' K = 1 K,
T F - T' F = 9/5
Therefore, corresponding to 273.16 K, the absolute scale whose unit interval size is equal to that of the Fahrenheit scale
$\\T_{F}=\frac{9}{5}\times 273.16\\ $
$T_{F}=491.688$
Q. 10.5 (a) Two ideal gas thermometers A and B use oxygen and hydrogen respectively. The following observations are made :
Answer:
$\\PV=nRT\\$
$\frac{P}{T}=\frac{nR}{V}$
As the moles of oxygen and hydrogen inside the thermometers and the volume occupied by the gases remain constant, P/T would remain constant.
The triple point of water(T1 ) = 273.16 K
Pressure in thermometer A at a temperature equal to the triple point of water (P1) = $1.250\times 10^{5}Pa$
Pressure in thermometer A at a temperature equal to the Normal melting point of sulphur (P2) = $1.797\times 10^{5}Pa$
The normal melting point of sulphur, as read by thermometer A, T2, would be given as
$T_{2}=\frac{P_{2}T_{1}}{P_{1}}$
$\\T_{2}=\frac{1.797\times 10^{5}\times 273.16}{1.250\times 10^{5}}\\ $
$T_{2}=392.69\ K$
Pressure in thermometer B at a temperature equal to the triple point of water (P1') = $0.200\times 10^{5}Pa$
Pressure in thermometer B at a temperature equal to the Normal melting point of sulphur (P2') = $0.287\times 10^{5}Pa$
The normal melting point of sulphur, as read by thermometer B, T2', would be given as
$\\T'_{2}=\frac{P'_{2}T_{1}}{P'_{1}}\\ $
$T'_{2}=\frac{0.287\times 10^{5}\times 273.16}{0.200\times 10^{5}}\\$
$ T'_{2}=391.98\ K$
Q. 10.5 (b) Two ideal gas thermometers, A and B, use oxygen and hydrogen, respectively. The following observations are made :
Answer:
The slight difference in the answers of thermometers A and B occurs because the gases used in the thermometers are not ideal gases. To reduce this discrepancy, the experiments should be carried out at low pressures where the behaviour of real gases tends closer to that of ideal gases.
Answer:
At 27 oC, the 63 cm ($l1$) mark on the steel tape would be measuring exactly 63 cm as the tape is calibrated at 27 oC
Coefficient of linear expansion of steel $=1.20\times 10^{-5}K^{-1}$
Actual length when the scale is giving a reading of 63 cm at 45°C is $l2$
$\\l_{2}=l_{1}(1+\alpha \Delta T)\\ =63\times (1+1.20\times 10^{-5}\times (45-27))\\ =63.013608cm$
The actual length of the steel rod on a day when the temperature is 45 °C is 63.013608 cm.
Length of the same steel rod on a day when the temperature is 63cm.
Answer:
Diameter of the steel shaft at 27 oC (T1) d1 = 8.70 cm
The diameter of the central hole in the wheel, d2 = 8.69 cm
Coefficient of linear expansion of the steel $\alpha _{steel}=1.20\times 10^{-5}K^{-1}$ .
The wheel will slip on the shaft when the diameter of the steel shaft becomes equal to the diameter of the central hole in the wheel.
Let this happen at temperature T
$\\d_{2}=d_{1}(1+\alpha (T-T_{1}))\\ 8.69=8.7(1+1.2\times 10^{5}(T-27))\\ $
$T=-68.79\ ^{o}C$
Answer:
Coefficient of linear expansion of copper $\alpha$ $=1.70\times 10^{-5}K^{-1}.$
Coefficient of superficial expansion of copper is $\beta$
$\beta =2\alpha \\ $
$\beta =2\times 1.7\times 10^{-5}\\ $
$\beta =3.4\times 10^{-5}K^{-1}$
Diameter of the hole at 27 oC (d1) = 4.24 cm
Area of the hole at 227 oC is
$A_{2}=A_{1}(1+\beta \Delta T)\\ $
$A_{2}=\pi \left ( \frac{4.24}{2} \right )^{2}(1+3.4\times 10^{-5}(227-27))$
$A_{2}=14.215\ cm^{2}$
Let the diameter at 227 °C be d2
$\\\pi \left ( \frac{d_{2}}{4} \right )^{2}=14.215\\$
$ d_{2}=4.254cm$
Change in diameter is d2 -d1 = 4.24 -4.254 = 0.014 cm.
Answer:
Youngs Modulus of Brass, $Y=0.91\times 10^{11}$
Co-efficient of linear expansion of Brass, $\alpha =2.0\times 10^{-5}K^{-1}$
The diameter of the given brass wire, d = 2.0 mm
Length of the given brass wire, $l$ = 1.8 m
Initial Temperature T1 = 27 oC
Final Temperature T2 = -39 oC
$\\Y=\frac{Stress}{Strain}\\ $
$Y=\frac{\frac{F}{A}}{\frac{\Delta l}{l}}\\ $
$F=\frac{\Delta lAY}{l}\\ $
$F=\frac{(l\alpha \Delta T)AY}{l}\\ $
$F=\alpha \Delta TAY\\ $
$F=\alpha \Delta TY\pi \frac{d^{2}}{4}\\ $
$F=\frac{2.0\times 10^{-5}\times (-39-27)\times 0.91\times 10^{11}\times \pi \times (2\times 10^{-3})^{2}}{4}$
$F=-378N$
The tension developed in the wire is 378 N. The negative sign signifies that this tension is inward.
Answer:
Length of the rods $l$ = 50 cm
Co-efficient of linear expansion of brass, $\\\alpha _{b}=2\times 10^{-5}K^{-1}$
Co-efficient of linear expansion of steel, $\\\alpha _{s}=1.2\times 10^{-5}K^{-1}$
Initial Temperature T1 = 40.0 oC
Final Temperature T2 = 250 oC
Change in the length of the brass rod is
$\\\Delta l_{t}=l_{t}\alpha_{b} \Delta T\\ $
$\Delta l_{t}=50\times 2.0\times 10^{-5}\times (250-40)\\ $
$\Delta l_{t}=0.21cm$
A change in the length of the steel rod is
$\\\Delta l_{s}=l_{s}\alpha_{s} \Delta T\\ $
$\Delta l_{s}=50\times 1.2\times 10^{-5}\times (250-40)\\ $
$\Delta l_{s}=0.126cm$
Change in the length of the combined rod is
$\\\Delta l=\Delta l_{s}+\Delta l_{b}\\ $
$\Delta l=0.126+0.21\\ $
$\Delta l=0.336cm$
Answer:
Coefficient of volume expansion of glycerine is $\gamma =49\times 10^{-5}K^{-1}$
Let the initial volume and mass of a certain amount of glycerine be V and m, respectively.
Initial density is
$\rho =\frac{m}{V}$
Change in volume for a 30 o C rise in temperature will be
$\\\Delta V=V(\gamma \Delta T)\\ $
$\Delta V=V(49\times 10^{-5}\times 30)\\ $
$\Delta V=0.0147V$
Final Density is
$\\\rho' =\frac{m}{V+\Delta V}\\ $
$\rho'=\frac{m}{1.0147V}\\ $
$\rho'=\frac{0.986m}{V}$
The fractional change in density is
$\\\frac{\rho'-\rho}{\rho}\\ =\frac{\frac{0.986m}{v}-\frac{m}{v}}{\frac{m}{v}}\\ =-0.014$
The negative sign signifies that with an increase in temperature, density will decrease.
Answer:
Power of the drilling machine, P = 10 kW
Time. t = 2.5 min
Total energy dissipated, E, is
$\\E=Pt\\$
$ E=10\times 10^{3}\times 2.5\times 60\\ $
$E=1.5\times 10^{6}J$
The thermal energy absorbed by the aluminium block is
$\\\Delta Q=\frac{E}{2}\\$
$ \Delta Q=\frac{1.5\times 10^{6}}{2}\\ $
$\Delta Q=7.5\times 10^{5}J$
Mass of the aluminium block, m = 8.0 kg
Specific heat of aluminium, c = 0.91 J g -1 K -1
Let the rise in temperature be $\Delta T$
$\\mc\Delta T=\Delta Q\\ $
$\Delta T=\frac{\Delta Q}{mc}\\ $
$\Delta T=\frac{7.5\times 10^{5}}{0.91\times 8\times 10^{3}}\\ $
$\Delta T=103.02\ ^{o}C$
Answer:
Mass of copper block m = 2.5 kg
Initial Temperature of the copper block, T 1 = 500 o C
Final Temperature of Copper block, T 2 = 0 o C
Specific heat of copper, c = 0.39 J g -1 K -1
Thermal Energy released by the copper block is $\Delta Q$
$\\\Delta Q=mc\Delta T\\ $
$\Delta Q=2.5\times 10^{3}\times 0.39\times 500\\ $
$\Delta Q=487500\ J$
Latent heat of fusion of water, L = 335 j g -1
The amount of ice that can melt is
$\\w=\frac{\Delta Q}{L}\\ $
$w=\frac{487500}{335}\\$
$ w=1455.22g$
1.455 kg of ice can melt using the heat released by the copper block.
Answer:
Let the specific heat of the metal be c.
Mass of metal block m = 200 g
Initial Temperature of the metal block = 150 oC
Final Temperature of the metal block = 40 oC
The heat released by the block is
$\\\Delta Q=mc\Delta T\\ $
$\Delta Q=200\times c\times (150-40)\\ $
$\Delta Q=22000c$
Initial Temperature of the calorimeter and water = 27 °C
Final Temperature of the calorimeter and water = 40 °C
Amount of water = 150 cm
Mass of water = 150 g
Water equivalent of calorimeter = 25 g
Specific heat of water = 4.186 J g -1 K -1
Heat absorbed by the Calorimeter and water is $\\\Delta Q'$
$\\\Delta Q'=(150+25)\times 4.186\times (40-27)\\ $
$\Delta Q'=9523.15J$
The heat absorbed by the Calorimeter and water is equal to the heat released by the block
$\\\Delta Q=\Delta Q'\\ 22000c=9523.15\\ c=0.433\ J\ g^{-1}\ K^{-1}$
The above value would be less than the actual value since some heat must have been lost to the surroundings as well, which we haven't accounted for.
Q. 10.15 Given below are observations on molar specific heats at room temperature of some common gases.
Answer:
Monoatomic gases have only a translational degree of freedom, but diatomic gases have rotational degrees of freedom as well. The temperature increases with an increase in the spontaneity of motion in all degrees. Therefore, to increase the temperature of diatomic gases, more energy is required than that required to increase the temperature of monoatomic gases by the same value, owing to higher degrees of freedom in diatomic gases.
If we only consider rotational modes of freedom, the molar specific heat of the diatomic gases would be given as
$\\c=\frac{fR}{2}$
$ c=\frac{5}{2}\times 1.92$
$ c=4.95\ cal\ mol^{-1}\ K^{-1}$
The number of degrees of freedom = 5 (3 translational and 2 rotational)
The values given in the table are more or less in accordance with the above calculated ones. The larger deviation from the calculated value in the case of chlorine is because of the presence of vibrational motion as well.
Answer:
Initial Temperature of the boy = 101°F
Final Temperature of the boy = 98°F
Change in Temperature is
$\\\Delta T=3\ ^{o}F\\ $
$\Delta T=3\times \frac{5}{9}\\ $
$\Delta T=1.67\ ^{o}C$
Mass of the child is m = 30 kg
Specific heat of human body = 1000 cal kg -1 °C -1
Heat released is $\\\Delta Q$
$\\\Delta Q=mc\Delta T\\$
$\Delta Q=30\times 1000\times 1.67\\ $
$\Delta Q=50000\ cal$
Latent heat of evaporation of water = 580 cal g -1
The amount of heat lost by the child's body has been absorbed by water.
Let the mass of water which has evaporated be m'
$\\\Delta Q=m'L\\ $
$ m'=\frac{Q}{L}\\ $
$m'=\frac{50000}{580}\\$
$ m'=86.2\ g$
Time in which the water has evaporated, t = 20 min.
The rate of evaporation is m'/t
$\\\frac{m'}{t}=\frac{86.2}{20}\\ $
$\frac{m'}{t}=4.31\ g\ min^{-1}$
Answer:
Side of the box s = 30 cm
Area available for conduction A
A = 6s 2
A=6(30) 2
A=5400 cm 2 = 0.54 m 2
Temperature difference = 45 °C
Coefficient of thermal conductivity of thermacole is k = 0.01 J s -1 m -1 K -1
Width of the box is d = 5 cm
Heat absorbed by the box in 6 hours is $\Delta Q$
$\\\Delta Q=\frac{kA\Delta T}{l}\\ $
$\Delta Q=\frac{0.01\times 0.54\times 45\times 6\times 60\times 60}{0.05}\\ $
$\Delta Q=104976\ J$
The heat of fusion of water is $L=335\times 10^{3}\ J\ kg^{-1}$
The amount of ice which has melted is m'
$\\m'=\frac{\Delta Q}{L}\\ $
$m'=\frac{104976}{335\times 10^{3}}\\ $
$m'=0.313\ kg$
Amount of ice left after 6 hours = 4 - 0.313 = 3.687 kg
Answer:
The rate at which water boils, R = 6.0 kg min -1
The heat of vaporisation of water, $L=2256\times 10^{3}\ J\ kg^{-1}$
The rate at which heat enters the boiler
$\\\frac{dQ}{dT}=RL\\ $
$\frac{dQ}{dT}=\frac{6\times 2256\times 10^{3}}{60}\\ $
$\frac{dQ}{dT}=2.256\times 10^{5}Js^{-1}$
The base area of the boiler, A = 0.15 m 2
Thickness, $l$ = 1.0 cm
Thermal conductivity of brass $=109\; J\; s^{-1}m^{-1}K^{-1};$
The temperature inside the boiler = Boiling point of water = 100 °C
Let the temperature of the flame in contact with the boiler be T
The amount of heat flowing into the boiler is
$\begin{aligned}
& \frac{d Q}{d t}=\frac{K A \Delta T}{l} \\
& 2.256 \times 10^5=\frac{109 \times 0.15 \times(T-100)}{1 \times 10^{-2}} \\
& T-100=137.98 \\
& T=237.98^{\circ} \mathrm{C}
\end{aligned}$
The temperature of the flame in contact with the boiler is 237.98 oC
Q. 10.19 (a) Explain why a body with large reflectivity is a poor emitter
Answer:
A body with a large reflectivity is a poor absorber. As we know, a body which is a poor absorber will also be a poor emitter. Therefore, a body with large reflectivity is a poor emitter.
Q10.19 (b) Explain why a brass tumbler feels much colder than a wooden tray on a chilly day
Answer:
Brass is a good conductor of heat. Therefore, once someone touches brass, heat from their body flows into it, and it feels cold. In the case of a wooden tray, no such conduction of heat from the body takes place, as wood is a very poor conductor of heat.
Q. 10.19 (c) Explain why an optical pyrometer (for measuring high temperatures) calibrated for an ideal black body radiation gives too low a value for the temperature of a red hot iron piece in the open but gives a correct value for the temperature when the same piece is in the furnace
Answer:
An optical pyrometer relates the brightness of a glowing body to its temperature. In the open, because of other sources of light, the sensor in the optical pyrometer does not detect the true brightness of a red-hot piece of iron and thus does not predict its temperature correctly, whereas in the furnac,e the piece of iron is the only source of light and the sensor detects its brightness correctly thus giving the correct value of the temperature.
Q. 10.19 (d) Explain why the Earth without its atmosphere would be inhospitably cold
Answer:
The sun's rays contain infrared radiation. These are reflected back by the lower part of the atmosphere after being reflected by the surface of the Earth and are trapped inside the atmosphere, thus maintaining the Earth's temperature at a hospitable level. Without these rays being trapped, the temperature of the Earth would go down severely, and thus the Earth without its atmosphere would be inhospitably cold.
Q. 10.19 (e) Explain why heating systems based on circulation of steam are more efficient in warming a building than those based on circulation of hot water
Answer:
Heating systems based on the circulation of steam are more efficient in warming a building than those based on the circulation of hot water because the same amount of steam at 100 °C contains more energy available for heat dissipation than the same amount of water at 100 °C in the form of latent heat of vaporisation.
Answer:
Let a body initially be at temperature T 1
Let its final Temperature be T 2
Let the surrounding temperature be T 0
Let the temperature change over time t.
According to Newton's Law of Cooling
$\\-\frac{dT}{dt}=K(T-T_{0})\\ $
$\frac{dT}{T-T_{0}}=-Kdt\\$
$ \int_{T_{1}}^{T_{2}}\frac{dT}{T-T_{0}}=-K\int_{0}^{t}dt\\$
$ \left [ ln(T-T_{0}) \right ]_{T_{1}}^{T_{2}}=-K[t]_{0}^{t}\\ $
$ln\left ( \frac{T_{2}-T_{0}}{T_{1}-T_{0}} \right )=-Kt$
where K is a constant.
We have been given that the body cools from 80 oC to 50 oC in 5 minutes when the surrounding temperature is 20 oC.
T 2 = 50 o C
T 1 = 80 o C
T 0 = 20 o C
t = 5 min = 300 s.
$\\ln\left ( \frac{50-20}{80-20} \right )=-K\times 300\\ K=\frac{ln(2)}{300}\\$
For T 1 = 60 o C and T 2 = 30 o C we have
$\\ln\left ( \frac{30-20}{60-20} \right )=-\frac{ln2}{300}t\\ $
$t=\frac{ln(4)\times 300}{ln(2)} \\$
$t=\frac{2ln(2)\times 300}{ln(2)}\\ $
$t=600\ s\\ $
$t= 10\ min$
The body will take 10 minutes to cool from 60 o C to 30 o C at the surrounding temperature of 20 o C.
Class 11 Physics Chapter 10 - Thermal Properties of Matter: Higher Order Thinking Skills (HOTS) Questions
The Class 11 Physics NCERT Chapter 10 HOTS (Higher Order Thinking Skills) Questions are designed to challenge students' understanding of thermal properties of matter beyond textbook exercises. These questions encourage critical thinking, application-based learning, and problem-solving skills, preparing students for competitive exams like JEE and NEET.
Q1: When 100 g of liquid A at 100 °C is added to 50 g of liquid B at a temperature of 75 °C, the temperature of the mixture becomes 90 °C. The temperature of the mixture (in oC), if 100 g of liquid A at 100 °C is added to 50 g of liquid B at 50 °C, will be :
Answer:
Specific Heat -
$
\begin{aligned}
& S=\frac{Q}{m \cdot \Delta \theta} \\
& \text { - wherein } \\
& \mathrm{S}=\text { specific heat } \\
& \Delta \theta=\text { Change in temperature } \\
& \mathrm{m}=\text { Amount of mass } \\
& \text { For (I) } \\
& 100 \times S_A \times(100-90)=50 \times S_B \times(90-75) \\
& S_A=\frac{1.5}{2} S_B=\frac{3}{4} S_B \cdots(1) \\
& \text { now for }(\mathrm{II}) \\
& 100 \times S_A \times(100-T)=50 \times S_B \times(T-50) \\
& \Rightarrow 2 S_A(100-T)=S_B(T-50) \cdots(2)
\end{aligned}
$
From (1) & (2)
$
\begin{aligned}
& 2 \times \frac{3}{4} \times(100-T)=(T-50) \\
& 3(100-T)=2(T-50) \\
& 300-3 T=2 T-100 \\
& 400=5 T \\
& T=80^{\circ} \mathrm{C}
\end{aligned}
$
Q2: If the length of the cylinder on heating increases by 2%, then the area of the base of the cylinder will increase by
Answer:
Assuming the initial length of the cylinder is $\ell_1$, the linear expansion coefficient is $\alpha$, and the temperature rise is $\Delta \mathrm{t}^{\circ} \mathrm{C}$,
$
\begin{aligned}
& \Delta \ell=\ell \alpha \Delta \mathrm{t} \Rightarrow \frac{\Delta \ell}{\ell} \times 100=\alpha \Delta \mathrm{t} \times 100 \\
& \therefore 2=\alpha \Delta \mathrm{t} \times 100
\end{aligned}
$
Now, for the area
$
\begin{aligned}
& \Delta A=A \beta \Delta t \Rightarrow \frac{\Delta A}{A}=\beta \Delta t \\
& \Rightarrow \frac{\Delta A}{A} \times 100=\beta \Delta t \times 100 \\
& \% \text { change in area }=\beta \Delta t \times 100 \\
& =\beta \Delta t \times 100
\end{aligned}
$
We know that $2 \times \alpha \times \Delta \mathrm{t}=\beta \times \Delta \mathrm{t}$
$
\begin{aligned}
& =2 \alpha \Delta \mathrm{t} \times 100 \\
& =2(\alpha \Delta \mathrm{t} \times 100) \\
& =2 \times 2 \\
& =4 \%
\end{aligned}
$
Q3: A cylindrical metal rod of length L0 is shaped into a ring with a small gap, as shown in the Figure. On heating the system,
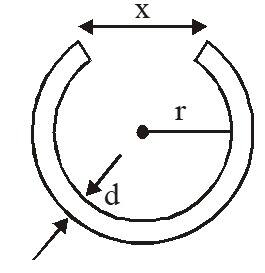
A. x will decrease, r will increase
B. Both x and r will decrease
C. Both x and r will increase
D. r will increase, x will remain the same
Answer:
Linear Expansion - When a solid is heated and its length increases, then the Expansion is called linear Expansion.
On heating the system, x and r both will increase since the expansion of isotropic solids is similar to true photographic enlargement.
Q4: The coefficient of thermal expansion of a rod varies with temperature as $\alpha=\alpha_0+\alpha_0 \frac{T}{T_0}$ where T is the temperature of the body and all others are positive constants. If the temperature of the rod of length $\ell_0$ is changed from $T_0 / 2$ to $T_0$ uniformly with time, then what is the ratio of the rate of fractional change of length initially and finally?
Answer:
We know the coefficient of thermal expansion is given as
$
\begin{gathered}
\quad \frac{\mathrm{d} L}{L \mathrm{~d} T}=\alpha \\
\Rightarrow \frac{\mathrm{d} L}{L \mathrm{dt}}=\alpha \frac{\mathrm{d} T}{\mathrm{~d} t} \\
\frac{\left(\frac{d L}{L d t}\right)_1}{\left(\frac{d L}{L d t}\right)_2}=\frac{\alpha_1 \frac{d T}{d t}}{\alpha_2 \frac{d T}{d t}} \\
\Rightarrow \frac{\left(\frac{d L}{L d}\right)_1}{\left(\frac{d L}{L d t}\right)_2}=\frac{\alpha_1}{\alpha_2} \\
\Rightarrow
\frac{\alpha_0+\alpha_0 \frac{T_0 / 2}{T_0}}{\alpha_0+\alpha_0 \frac{T_0}{T_0}}=\frac{3 / 2}{2}=\frac{3}{4}
\end{gathered}
$
Q5: A red-hot iron (mass 25 g) has a temperature of 100ºC. It is immersed in a mixture of ice and water at thermal equilibrium. The volume of the mixture is found to be reduced by $0.15 \mathrm{~cm}^3$with the temperature of the mixture remaining constant. Find the specific heat (in cal gm ${ }^0 \mathrm{C}$) of the metal.
Given specific gravity of ice = 0.92, specific gravity of water at $0^{\circ} \mathrm{C}=1.0$, latent heat of fusion of ice $=80 \mathrm{calg}^{-1}$.
Answer:
As the ice melts, its density changes, which causes change in volume. Let m g of ice melt.
$\begin{aligned} & \frac{m}{\rho_{i c e}}-\frac{m}{\rho_{\mathrm{H}_2 \mathrm{O}}}=0.15 \\ & m=\frac{0.15 \times 0.92}{0.08} \\ & \therefore \quad H_{\text {lost }}=H_{\text {gaired }} \\ & \Rightarrow \quad 25 \times S \times 100=\frac{0.15 \times 0.92}{0.08} \times 80 \\ & S=0.06 \mathrm{cal} \mathrm{gm}^{\circ} \mathrm{C}\end{aligned}$
Class 11 Physics Chapter 10 - Thermal Properties of Matter: Topics
Chapter 10: Thermal Properties of Matter: Key topics include heat, temperature, thermal expansion and heat conduction. The chapter describes temperature-dependent behaviour of matter and the physics behind the phenomena we experience in our daily lives, such as the boiling of water, expansion of metals and sea breezes. These are the basic points of thermodynamics to understand and the applications in real life.
10.1 Introduction
10.2 Temperature And Heat
10.3 Measurement Of Temperature
10.4 Ideal-Gas Equation And Absolute Temperature
10.5 Thermal Expansion
10.6 Specific Heat Capacity
10.7 Calorimetry
10.8 Change Of State
10.8.1 Latent Heat
10.9 Heat Transfer
10.9.1 Conduction
10.9.2 Convection
10.9.3 Radiation
10.9.4 Blackbody Radiation
10.10 Newton’s Law of Cooling
Class 11 Physics Chapter 10 - Thermal Properties of Matter: Important Formulae
Thermal Properties of Matter class 11 question answers include all essential equations related to heat, temperature, thermal expansion, and heat transfer. These formulas help students solve numerical problems effectively and are crucial for board exams, JEE, NEET, and other competitive tests. Mastery of these formulas simplifies the understanding and application of thermal concepts.
1. Heat and Temperature Relation
$
Q=m c \Delta T
$
Where:
$
\begin{aligned}
& Q=\text { heat added or removed } \\
& m=\text { mass } \\
& c=\text { specific heat capacity } \\
& \Delta T=\text { change in temperature }
\end{aligned}
$
2. Specific Heat Capacity
$c=\frac{Q}{m \Delta T}$
3. Heat Capacity
$\begin{aligned} & C=m c \\ & C=\frac{Q}{\Delta T}\end{aligned}$
4. Latent Heat
$
Q=m L
$
Where:
$L=$ latent heat of fusion or vaporisation
(Use for phase changes with no temperature change)
5. Linear, Areal and Volume Expansion
$
\Delta L=L \alpha \Delta T
$
$
\Delta A=A \beta \Delta T
$
Where $\beta=2 \alpha$
$
\Delta V=V \gamma \Delta T
$
Where $\gamma=3 \alpha$
8. Calorimetry Principle
Heat lost=Heat gained
(Applies to thermal equilibrium problems)
9. Thermal Conduction
$
Q=\frac{k A\left(T_1-T_2\right) t}{d}
$
Where:
$k=$ thermal conductivity
$A=$ area
$d=$ thickness
$t=$ time
$T_1-T_2=$ temperature difference
10. Newton’s Law of Cooling
$\frac{d T}{d t} \propto\left(T-T_{\text {env }}\right)$
How Can NCERT Solutions for Class 11 Physics Chapter 10 Help in Exam Preparation?
Class 11 physics chapter 10 Thermal Properties of Matter question answers can assist the students to study and pass the exams because it contains stepwise explanations of all the concepts and numerical problems at a time, in a clear and understandable manner. They make concepts such as thermal expansion, heat transfer, and Newton's law of cooling easier to learn so that students can learn how heat influences various materials. The Thermal Properties of Matter class 11 question answers also cover well-explained derivation, solved examples and conceptual questions that help in a solid base to the board exam, as well as competitive examinations such as JEE and NEET. With such Thermal Properties of Matter NCERT Solutions, students will be able to improve problem-solving skills, work on the accuracy of the numerical questions, and memorise all essential formulas and definitions in a short time before the exams. Thermal Properties of Matter class 11 question answers also assist students in connecting theoretical concepts with real-life examples, and this improves conceptual clarity and retention.
Approach to Solve Questions of Class 11 Physics Chapter 10 - Thermal Properties of Matter
To solve the problems presented in Class 11 Physics Chapter 10 - Thermal Properties of Matter, one should pay attention to the application of concepts instead of memorisation of formulae. The questions in this chapter tend to challenge your capacity to relate heat, temperature and expansion of heat to real-life scenarios. A logical step-by-step method will enable students not only to simplify issues, but also to prevent the confusion of various processes in heat transfer and to develop precision in board exams and in competitive examinations.
- To start with, read the chapter carefully to get a clear idea of the impacts of heat on solids, liquids, and gases, and how an increase or decrease in temperature causes expansion or contraction of materials.
- Learn important terms like thermal expansion, specific heat, and latent heat by real-life examples like how the railway tracks expand, or the ice melts.
- When working on numerical problems, understand what you are given and what you are to find, and can use such formulas as Q=mcΔT or Q= mL correctly.
- Observations of graphical representations like heating curves are also important since they can be used to visualise phase changes.
- Revise important laws such as Newton's Law of Cooling and the interrelationship between Celsius, Fahrenheit, and Kelvin temperature scales.
- Practice derivations and numerical problems step-by-step to strengthen conceptual understanding and accuracy.
- Wherever possible, use diagrams to make your answers clearer, such as in describing conduction, convection, and radiation.
- Lastly, go through solved NCERT problems and NCERT questions of the last few years to have an idea of the nature of problems asked in general and to gain speed and certainty during the exam.
Importance of NCERT Solutions for Class 11 Physics Chapter 10: Thermal Properties of Matter
Class 11 Physics chapter 10 Thermal Properties of Matter solutions are of particular importance since the chapter introduces students to the behaviour of materials in response to the change of heat and temperature. It is the connection between such daily activities as heating, cooling, and expansion to science and measurements.
- Helps students have a clear understanding of the distinction between heat and temperature, which is usually confusing.
- Discusses the thermal expansion of solids, liquids, and gases, which proves handy in the real-world example of railway tracks and bridges.
- Introduces heat exchange between bodies and specific heat capacity and calorimetry, which assist students in analysing heat exchange.
- Establishes the groundwork of more advanced topics such as thermodynamics and the kinetic theory of gases.
- Enhances the knowledge of the phase change phenomena, which include: melting, boiling and latent heat.
- Improves the numerical precision by offering structured solutions to the calculation-based problems.
- Useful for CBSE board exams, where conceptual clarity and formula-based numericals are equally important.
- Relates physics knowledge to everyday life, e.g., cooking, climate change, temperature regulation, etc.
What Students Learn from NCERT Solutions for Class 11 Physics Chapter 10: Thermal Properties of Matter?
The chapter Thermal Properties of Matter introduces the students to the behaviour of substances when they take in or give out heat. Through Class 11 Physics chapter 10 Thermal Properties of Matter question answers, students are able to know how thermal energy reacts with matter, which results in the variation of temperature, size, and state of matter under varying conditions.
- Students learn the way that temperature is measured and the reason why there are different temperature scales.
- Students get the idea of thermal expansion and the reason why materials either expand or contract as they are either heated or cooled.
- Students learn specific heat capacity and the variation in the absorption of heat by various substances.
- Students learn the principles of calorimetry and heat exchange between bodies.
- They learn the processes of change of state, i.e. melting, boiling, and condensation.
- They learn about the latent heat and its action in the phases of transition.
- They learn how heat transfer occurs through conduction, convection, and radiation.
- Develop skills to solve numerical problems involving heat, temperature, and expansion accurately.
- Get an understanding of real-life applications such as thermal insulation, thermal control and material design.
What Extra Should Students Study Beyond NCERT for JEE/NEET?
This comparison table shows the divergence between textbook focus, depth and the kind of questions that are asked in a competitive examination like JEE and NEET on the topic of thermal properties of matter. NCERT gives a good conceptual knowledge along with a basic practice set, whereas JEE/NEET questions require application of techniques, application-based reasoning and advanced numerical practice. This table assists the students in areas they need to focus on in preparation for the exams.
NCERT Solutions for Class 11 Physics Chapter-Wise
NCERT solutions for class 11 subject-wise
Also, Check NCERT Books and NCERT Syllabus here
- NCERT Books Class 11 Physics
- NCERT Syllabus Class 11 Physics
- NCERT Books Class 11
- NCERT Syllabus Class 11
Subject-wise NCERT Exemplar solutions
Frequently Asked Questions (FAQs)
Thermal properties of matter describe the behaviour of substances when heat is added or removed, such as temperature changes, expansion, heat transfer and phase changes.
Metals are good conductors of heat and hence they tend to conduct heat away at a very fast rate from our body and thus they feel colder, whereas wood is a poor conductor and does not conduct heat at a high rate.
Heat is a type of energy that is exchanged between bodies with respect to a difference in temperature whereas temperature is a measure of how hot or cold a body is.
Specific heat capacity is used to establish the amount of heat energy needed to increase the temperature of one unit mass of a substance by 1 °C (or 1 K), commonly encountered in calculations-based questions.
Yes, a lot of conceptual and numerical questions, depending on the heat transfer, thermal expansion, and calorimetry, are regularly asked in JEE, NEET, and other entrance tests.
No, all in-text questions and additional questions have thorough answers included in the PDF. This guarantees that you can practice and check your understanding as you go through the chapter.
Indeed, the chapter on thermal properties of matter is crucial for competitive tests like the NEET. It is a component of the broader "Thermal Physics" unit, which is always given a lot of weight.
The solutions have easy to understand formula and examples of the linear, area and volume expansion, and it is easier to apply the concepts of the same in numerical problems.
Calorimetry assists in the analysis of the exchange of heat among bodies. This concept is explained in the NCERT Solutions with the concept of heat balance.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
