NCERT Solutions for Class 11 Physics Chapter 2 Motion In a Straight Line
When you imagine a car travelling along a straight road, you are actually looking at one of the most basic and most critical concepts in Physics, the straight line motion. This is the most basic chapter that is presented to us in class 11 Physics Chapter 2, and with the assistance of the NCERT Solutions of Motion in a Straight Line, learning will become an ordered and simple process. These solutions address all the main concepts, such as displacement, distance, speed, velocity, acceleration, equations of motion, and the motion graph, and they dictate everything in steps, thus making it easier to understand.
This Story also Contains
- Motion in a straight line class 11 Question Answers: Download PDF
- Motion in a Straight Line NCERT Solutions: Exercise Questions
- Class 11 Physics Chapter 2 - Motion in a Straight Line Question Answers: Topics
- Class 11 Physics Chapter 2 - Motion in a Straight Line Summary
- How Can NCERT Solutions for Class 11 Physics Chapter 2 Help in Exam Preparation?
- What Extra Should Students Study Beyond NCERT for JEE?
- NCERT Solutions for Class 11 Physics Chapter-Wise
The NCERT Solutions for Class 11 Physics Chapter 2 - Motion in a straight line are based on the recent CBSE syllabus and provide elaborate answers to questions in the textbook, problems in exercises, and additional numerical work. Higher Order Thinking Skills (HOTS) questions, additional solved problems, and conceptual descriptions are also there in these NCERT solutions, which enhance our problem-solving ability. These are extremely convenient in board exams and class tests, homework, and assignments, and form the foundation of competitive exams such as JEE, NEET, and Physics Olympiads. Also, understanding this chapter will be a foundation for more complicated chapters, such as plane motion and laws of motion by Newton, so this chapter is a pillar in further Physics studies. These NCERT Solutions for Class 11 Physics Chapter 2 - Motion in a straight line will help us to clear our concepts, score more marks, as well as develop good analytical skills that can be used in our future.
Motion in a straight line class 11 Question Answers: Download PDF
Class 11 Physics Chapter 2 - Motion in a straight line question answers provide clear and step-by-step answers to all textbook questions, helping students understand concepts like displacement, speed, velocity, and motion graphs. These class 11 physics chapter 2 Motion in a straight line question answers are available in a free downloadable PDF format, making it easy for students to revise anytime and prepare effectively for exams like CBSE, JEE, and NEET.
Download Solutions PDF
Motion in a Straight Line NCERT Solutions: Exercise Questions
Exercise Solutions of Class 11 Physics Chapter 2 - Motion in a straight line provide a step-by-step explanation to each of the back exercise questions, and can help one understand straight-line motion more easily. The class 11 physics chapter 2 Motion in a straight line question answers sharpen the problem-solving technique and are also very practical in exam practice, along with competitive exams such as the JEE and NEET.
A railway carriage is moving without jerks between two stations.
View Solution
Answer: Since the length of a railway carriage is quite small compared to the distance between two stations, it could be considered as a point object.
A monkey is sitting on top of a man cycling smoothly on a circular track.
View Solution
Answer: The monkey can be considered a point object as its size is quite small compared to the circumference of the circular track.
A spinning cricket ball that turns sharply on hitting the ground.
View Solution
Answer: The ball cannot be considered as a point object because the distance covered around the instant when it hits the ground is comparable to its size.
A tumbling beaker that has slipped off the edge of a table
View Solution
Answer: Since the size of the beaker is comparable to the distance it travels after slipping off the edge of the table, it cannot be considered to be a point object.
(a) (A/B) lives closer to the school than (B/A)
View Solution
Answer: It is clear from the graph that A lives closer to the school than B.
(b) (A/B) starts from the school earlier than (B/A)
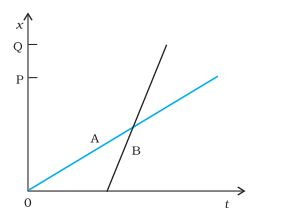
View Solution
Answer: From the graph, we can see that the position of A starts changing at time t = 0, whereas in case of B, it starts changing at some finite time. Therefore, A starts from the school earlier than B.
(c) (A/B) walks faster than (B/A)
View Solution
Answer: The velocity of a particle is equal to the slope of its position-time (x-t) graph. Since the graph of B is steeper, B walks faster than A.
(d) A and B reach home at the (same/different) time
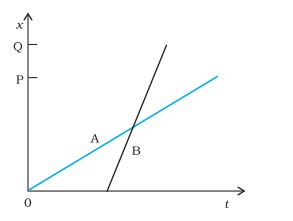
View Solution
Answer: The time (x-coordinate) is different for both A and B when their position (y-coordinate) is equal to that of their home. Therefore, A and B reach home at different times.
(e) (A/B) overtakes (B/A) on the road (once/twice)
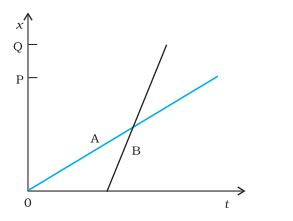
View Solution
Answer: B starts after A at a higher speed, and B overtakes A on the road once.
View Solution
Answer:
Distance between the office and the home = 2.5 Km
The speed of the woman = 5 km h-1
Time taken by the woman to reach the office is:
2.5 / 5 = 0.5 h = 30 min
At 9:30 am, the woman is at the office till 5 pm.
The speed of the auto = 25 km h-1
The time taken by the woman to reach back home is:
2.5 / 25 = 0.1 h = 6 min
At 5:06 pm, the woman reaches home.
The position-time graph will be:
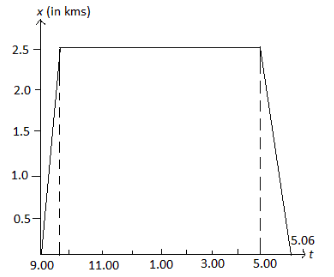
View Solution
Answer:
| Time | 0 | 5 | 8 | 13 | 16 | 21 | 24 | 29 | 32 | 37 |
| Distance Covered | 0 | 5 | 2 | 7 | 4 | 9 | 6 | 11 | 8 | 13 |
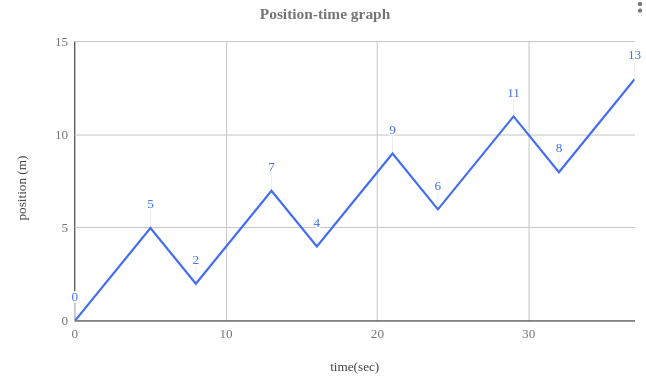
At time t = 37 s, the man falls into a pit at 13 meters from the start.
View Solution
Answer:
Initial velocity (u) = 126 km h–1 = 35 m s–1
Final velocity (v) = 0
Distance travelled before coming to rest (s) = 200 m
Using the third equation of motion:
$v^2 - u^2 = 2as$
$a = \frac{v^2 - u^2}{2s} = \frac{-35^2}{200} = -3.0625\ \text{m/s}^2$
Using the first equation of motion:
$v = u + at$
$t = \frac{v - u}{a} = \frac{0 - 35}{-3.0625} = 11.428\ \text{s}$
Conclusion: The retardation of the car is $3.0625\ \text{m/s}^2$ and it takes $11.428$ seconds for the car to stop.
Q 2.6(a) A player throws a ball upwards with an initial speed of 29.4 ms -1.
(a) What is the direction of acceleration during the upward motion of the ball?
View Solution
Answer: The acceleration of the ball will always be in the downward direction, irrespective of its position and direction of motion, since the gravitational force always acts in the downward direction.
Q 2.6 (b) A player throws a ball upwards with an initial speed of 29.4 ms -1 .
(b) What are the velocity and acceleration of the ball at the highest point of its motion?
View Solution
Answer: The velocity is 0 m s–1 and the acceleration is 9.8 m s–2
Q 2.6 (c) A player throws a ball upwards with an initial speed of 29.4 ms -1.
(c) Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of the x-axis, and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
View Solution
Answer: The sign of velocity is positive during the motion in the downward direction and negative during motion in the upward direction. The signs of position and acceleration are positive during motion in both directions.
Q 2.6 (d) A player throws a ball upwards with an initial speed of 29.4 ms -1 .
(d) To what height does the ball rise, and after how long does the ball return to the player’s hands? (Take g = 9.8 m s -2 and neglect air resistance).
View Solution
Consider the motion from the instant the ball starts travelling in the upward direction to the instant it reaches the highest point. Let the upwards direction be positive.
At the highest point, its velocity $v$ is 0 m s–1.
Initially, the velocity $u$ is 29.4 m s–1.
Acceleration is $-g = -9.8$ m s–2
Using the third equation of motion:
$v^{2} - u^{2} = 2as$
$s = \frac{v^{2} - u^{2}}{2a}$
$s = \frac{0^{2} - 29.4^{2}}{2 \times (-9.8)} = 44.1\ \text{m}$
Now consider the motion from the instant the ball starts travelling in the upward direction to the instant it reaches back to the player's hand.
The displacement during this period is $s = 0$ m.
Initial velocity $u = 29.4$ m s–1, Acceleration $a = -9.8$ m s–2
Using the second equation of motion:
$s = ut + \frac{1}{2}at^2$
$0 = 29.4t - 4.9t^2$
$t = 0\ \text{s or}\ t = 6\ \text{s}$
Conclusion: The ball, therefore, reaches back to the player's hand in 6 seconds.
Note: The solution $t = 0$ signifies the starting instant of the motion.
Q 2.7 (a) Read each statement below carefully and state with reasons and examples, if it is true or false.
(a ) A particle in one-dimensional motion with zero speed at an instant may have non-zero acceleration at that instant
View Solution
Answer: True, since non-zero velocity is not at all a necessary condition for non-zero acceleration. A ball thrown upwards at its highest point in motion has zero velocity but non-zero acceleration due to gravity.
Q 2.7 (b) Read each statement below carefully and state with reasons and examples, if it is true or false.
(b) A particle in one-dimensional motion with zero speed may have non-zero velocity
View Solution
Answer: True, since non-zero velocity is not at all a necessary condition for non-zero acceleration. A ball thrown upwards at its highest point in motion has zero velocity but non-zero acceleration due to gravity.
Q 2.7 (b) Read each statement below carefully and state with reasons and examples, if it is true or false.
(b) A particle in one-dimensional motion with zero speed may have non-zero velocity
View Solution
Answer: False, as speed is the magnitude of velocity. Therefore, a non-zero velocity would imply a non-zero speed.
Q 2.7 (c) Read each statement below carefully and state with reasons and examples, if it is true or false.
(c) A particle in one-dimensional motion with constant speed must have zero acceleration
View Solution
Answer: True. A particle moving in a straight line with constant speed will have constant velocity since its direction of motion is constant, and as acceleration is defined as the rate of change of velocity, its acceleration will be zero.
Q 2.7 (d) Read each statement below carefully and state with reasons and examples, if it is true or false.
(d) A particle in one-dimensional motion with a positive value of acceleration must be speeding up
View Solution
Answer: False. The answer to this question depends on the choice of a positive direction. If a ball is thrown upwards and the downward direction is chosen to be positive, then its acceleration will be positive, but its speed will still be decreasing.
View Solution
At time t = 0, velocity is 0
Initial velocity, u = 0
Acceleration = 10 m s–2
Height, s = 90 m
$ \begin{aligned} & s = ut + \frac{1}{2} a t^2 \\ & 90 = 0 \times t + \frac{1}{2} \times 10 t^2 \\ & t = 3\sqrt{2} \\ & t = 4.242\ \text{s} \\ & v = u + a t = 10 \times 3\sqrt{2} = 30\sqrt{2}\ \text{m/s} \end{aligned} $
The above is the speed with which the ball will collide with the ground. After colliding, the upward velocity becomes:
$ \begin{aligned} u & = 30\sqrt{2} \times \frac{9}{10} \\ u & = 27\sqrt{2}\ \text{m/s} \end{aligned} $
Acceleration $a = -10$ m s–2
While falling again, velocity = $-27\sqrt{2}$ m s–1
Let the time between successive collisions be $t$:
$ \begin{aligned} v &= u + a t \\ t &= \frac{v - u}{a} = \frac{-27\sqrt{2} - 27\sqrt{2}}{-10} = 5.4\sqrt{2} = 7.635\ \text{s} \end{aligned} $
After the first collision, its speed will become 0 in time $2.7\sqrt{2}$ s
Total time = 4.242 + 7.635 = 11.87 s
After this, it bounces again with velocity:
$ \begin{aligned} v = 27\sqrt{2} \times \frac{9}{10} = 24.3\sqrt{2}\ \text{m/s} \end{aligned} $
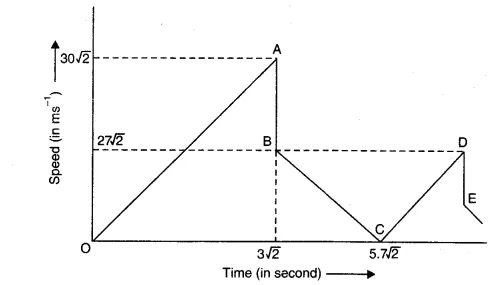
$v_E = 24.3\sqrt{2}$ m s–1
Q 2.9 (a) Explain clearly, with examples, the distinction between :
(a) the magnitude of displacement (sometimes called distance) over an interval of time, and the total length of the path covered by a particle over the same interval
View Solution
Answer: The magnitude of displacement is defined as the shortest distance between the initial and final position of a particle, whereas the total length of the path covered by a particle is the actual distance it has travelled. For example, a ball thrown upwards which goes to a height h and comes down to its starting position has its magnitude of displacement as zero, but the total length of the path covered by the ball is 2h. In the case of one-dimensional motion, the two will be equal if the particle moves only in one direction.
Q 2.9 (b) Explain clearly, with examples, the distinction between :
(b) magnitude of average velocity over an interval of time, and the average speed over the same interval. [Average speed of a particle over an interval of time is defined as the total path length divided by the time interval.] Show in both (a) and (b) that the second quantity is either greater than or equal to the first. When is the equality sign true? [For simplicity, consider one-dimensional motion only]
View Solution
Answer: The magnitude of average velocity over an interval of time is defined as total displacement divided by the time taken, whereas the average speed over the same interval is defined as the actual distance travelled by the particle divided by the total time taken. For example, a ball thrown upwards which goes to a height h in time t and comes down to its starting position in the same time has the magnitude of average velocity zero, whereas the average speed of the ball is h/t. In the case of one-dimensional motion, the two will be equal if the particle moves only in one direction.
View Solution
Answer:
(a)(i) Time taken by the man to reach the market is $t_1$:
$t_1 = \frac{2.5}{5} = 0.5\ h = 30\ \text{min}$
Displacement in 30 minutes is $d_1 = 2.5$ km
Magnitude of average velocity = $d_1 / t_1 = 5$ km h–1
(b)(i) Distance travelled in 30 minutes is $s_1 = 2.5$ km
Average speed = $s_1 / t_1 = 5$ km h–1
In the first 30 minutes, the man travels from his home to the market.
During the next 10 minutes, he travels with a speed of 7.5 km h–1 towards his home, covering a distance $s_3$:
$s_3 = 7.5 \times \frac{10}{60} = 1.25\ \text{km}$
$t_3 = 40$ min
Magnitude of average velocity = $(2.5 - 1.25)/t_3 = 1.875$ km h–1
Average speed = $(2.5 + 1.25)/t_3 = 5.625$ km h–1
Q 2.11 The instantaneous speed is always equal to the magnitude of the instantaneous velocity. Why?
View Solution
Answer: Instantaneous speed is defined as the first derivative of distance travelled with respect to time, and the magnitude of instantaneous velocity is the first derivative of the magnitude of displacement with respect to time. The time interval considered is so small that it is safe to assume that the particle won't change its direction of motion during it, and therefore the magnitude of displacement during this interval will be the same as the distance travelled. Hence, instantaneous speed is always equal to the magnitude of instantaneous velocity.
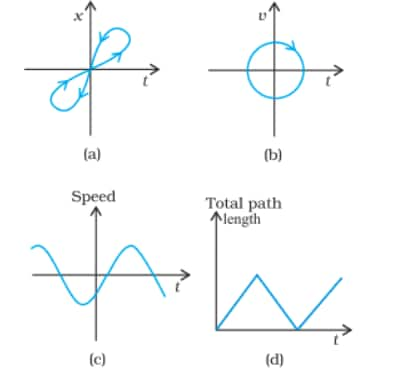
View Solution
Answer:
(a) The given x-t graph cannot represent the one-dimensional motion of a particle, as the particle cannot be at two positions at the same instant.
(b) The given v-t graph cannot represent the one-dimensional motion of a particle, as the particle cannot be travelling at two velocities at the same instant.
(c) The given speed-time graph cannot represent the one-dimensional motion of a particle, as the particle cannot have negative speed.
(d) The given path length-time graph cannot represent the one-dimensional motion of a particle, as the total path length cannot decrease.
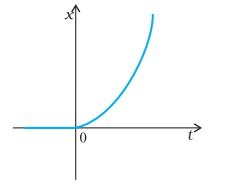
View Solution
Answer: It cannot be said from the above-given graph whether the particle is moving along a straight line or along a parabolic path, as the x-t graph does not tell us about the trajectory taken by the particle. From the given graph, we can only say that the position of the particle along the x-axis does not change till time t = 0, and after that it starts increasing in a non-linear manner.
View Solution
Answer:
Muzzle speed of the bullet is $V_B = 150$ m/s = 540 km/h
Speed of the police van is $V_V = 30$ km/h
Resultant speed of the bullet = $V = 540 + 30 = 570$ km/h
Speed of the thief's car = $V_T = 192$ km/h
Speed with which the bullet hits the thief's car = $V - V_T = 570 - 192 = 378$ km/h = 105 m/s
Q 2.15 Suggest a suitable physical situation for each of the following graphs.
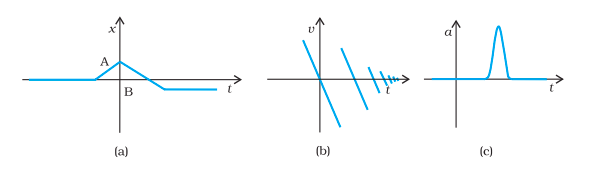
View Solution
Answer:
(a) The particle is initially at rest. Then it starts moving with a constant velocity for some time, and then its velocity changes instantaneously, and it starts moving in the opposite direction, crosses the point where it was at rest initially and then comes to a halt.
A similar physical situation arises when a bowler throws a ball towards the batsman. The ball travels towards the batsman with some constant speed, and after the batsman hits it, the ball goes past the bowler and gets caught by a fielder, and its velocity comes down to zero within an instant.
(b) The velocity of a particle starts coming down to zero from some velocity with some constant acceleration, goes to zero and changes its direction. Then suddenly the direction of velocity changes and the magnitude decreases.
This is the case when a ball is thrown in the air. It starts moving with some velocity and gets retarded by gravity. Its velocity becomes zero at the highest point, then changes direction, and as it hits the ground, it loses some of its speed and rebounds. This keeps happening till it comes to rest.
(c) The acceleration of a body is zero. It increases to some value for a very small period of time and again comes to zero.
This is the case when a football travelling horizontally hits a wall or is kicked by a player.
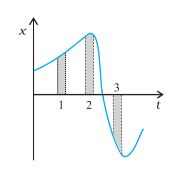
View Solution
Answer: The average speed is greatest in interval 3 and least in interval 2, as the average of the magnitude of the slope is maximum in interval 3 and minimum in interval 2.
Average velocity is positive in interval 1 and interval 2 as the slope is positive over these intervals, and average velocity is negative in interval 3 as the slope is negative over this interval.
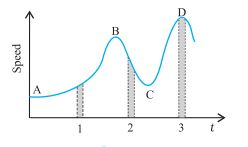
View Solution
Answer:
The average acceleration is greatest in magnitude in interval 2 as in this interval the magnitude of change in speed is the greatest.
The average speed is greatest in interval 3.
| v | a | |
| Interval 1 | Positive | Positive |
| Interval 2 | Positive | Negative |
| Interval 3 | Positive | Zero |
In interval 1, speed increases; in interval 2, it decreases; and in interval 3, it remains constant.
At points A, B, C, and D, acceleration is zero as at these points the curve is parallel to the time axis.
Class 11 Physics Chapter 2 - Motion in a Straight Line Question Answers: Topics
NCERT Solutions Class 11 Physics Chapter 2: Motion in a Straight Line - This chapter concentrates on fundamental topics in motion, such as displacement, distance, average speed, instantaneous velocity, equations of motion and motion graphs. These are some of the aspects that form an effective background to learn about advanced topics in mechanics and competitive exam-oriented learning.
2.1 Introduction
2.2 Instantaneous velocity and speed
2.3 Acceleration
2.4 Kinematic equations for uniformly accelerated motion
Class 11 Physics Chapter 2 - Motion in a Straight Line Summary
The chapter “Motion in a Straight Line” (also called Rectilinear Motion) introduces the fundamental concepts of kinematics, which deals with the description of motion without considering its causes. It focuses on how objects move along a straight path and how their motion can be measured and represented mathematically. Students learn key terms such as position, displacement, distance, speed, velocity, and acceleration, and how to distinguish between uniform and non-uniform motion.
Basic Introduction
- Motion is the change in position of an object with time
- The study of the motion of objects along a straight line is known as rectilinear motion.
- In Kinematics, we study ways to describe motion without going into the causes of motion.
- Point objects are objects that are much smaller than the distance they move in a reasonable duration of time
Position, Pathlength and Displacement
-
The coordinate system with time constitutes a frame of reference.
- If one or more coordinates of an object change with time, we say that the object is in motion
- The description of an event depends on the frame of reference chosen for the description.
- The magnitude of displacement may or may not be equal to the path length (distance) traversed by an object, or in other words, the distance travelled is always greater than or equal to the magnitude of displacement.
Distance $\geq \mid$ Displacement $\mid$
- If an object moving along a straight line covers equal distances in equal intervals of time, it is said to be in uniform motion along a straight line.
Instantaneous Velocity And Speed
-
Instantaneous speed tells us how fast a particle moves at an instant, and instantaneous velocity tells us in what direction and with what speed a particle moves at an instant of time.
- Instantaneous velocity $=\overrightarrow{\mathrm{v}}_{\text {inst }}=\lim _{\Delta t \rightarrow 0} \frac{\Delta \overrightarrow{\mathrm{X}}}{\Delta \mathrm{t}}=\frac{\mathrm{d} \vec{x}}{\mathrm{dt}}$
- Instantaneous speed $=\mathrm{v}_{\text {inst }}=\lim _{\Delta t \rightarrow 0} \frac{\Delta \mathrm{x}}{\Delta \mathrm{t}}=\frac{\mathrm{d} x}{\mathrm{dt}}$
- For uniform motion, the instantaneous velocity is the same as the average velocity at all instants.
Average And Instantaneous Acceleration
-
The acceleration gives us an idea about how the velocity is changing with respect to changes in time.
-
A body is said to be accelerated if there is:
1. Change in speed (magnitude)
2. Change in direction of velocity
3. Changes in both.
-
The average acceleration over a time interval is defined as the change of velocity divided by the time interval
$
\begin{aligned}
& \text { Averge acceleration }=\frac{\text { Change in velocity }}{\text { Total time interval }} \\
& \vec{d}_{\text {avg }}=\frac{\vec{v}_2-\vec{v}_1}{t_2-t_1}=\frac{\Delta \vec{v}}{\Delta t}
\end{aligned}
$
- Instantaneous acceleration is defined as the limit of the average acceleration as the time interval tends to zero.
$
\begin{aligned}
& \text { Instantaneous acceleration }=\frac{\text { Infinitesimal change in velocity }}{\text { Infintesimal time interval }} \\
& \vec{a}_{\text {inst }}=\lim _{\Delta t \rightarrow 0} \frac{\Delta \vec{v}}{\Delta t}=\frac{\mathrm{d} \vec{v}}{\mathrm{~d} t}
\end{aligned}
$
How Can NCERT Solutions for Class 11 Physics Chapter 2 Help in Exam Preparation?
The NCERT Solutions to Class 11 Physics Chapter 2 - Motion in a Straight Line are aimed at helping students to pass the exams by simplifying basic laws of kinematics, such as displacement, velocity, speed, and acceleration. These Motion in a straight line class 11 question answers give step-wise methods to solve problems, and it becomes easier to understand motion along a straight path and how to use formulas to get the right solution. Students will be encouraged to practice all in-text and exercise questions to improve their problem-solving skills and learn to formulate accurate answers to board exams. The Motion in a straight line class 11 question answers consist of diagrams and numerical examples as well, which help in gaining visual understanding and enhance confidence in exams. Frequent use of such solutions guarantees complete revision, faster memorisation of formulas, and increased readiness to pass the board exams to CBSE and competitive exams such as JEE and NEET.
What Extra Should Students Study Beyond NCERT for JEE?
In JEE preparation, NCERT gives a good foundation of Motion in a Straight Line, which can not be sufficient to solve some complicated questions. Students should study more than the basics and learn higher-level problem-solving, graphical analysis, relative motion and calculus-based applications to improve their concepts and increase accuracy in exams.
NCERT Solutions for Class 11 Physics Chapter-Wise
The NCERT Solutions of Class 11 Physics (Chapter-wise) answer all questions in the textbooks in detail and step by step, and thus, students can learn complex concepts without any trouble. Such solutions are developed by subject experts based on the current CBSE syllabus (2025-26) in order to develop a solid conceptual base. They will be highly useful in not only preparing students for the CBSE board but also in competitive exams such as JEE and NEET due to the clear explanations, numerical problem-solving methods and diagram-based solutions. The NCERT Physics Class 11 Solutions PDFs on chapters are available to students in chapter-wise PDFs and enable them to study them at their convenience and reinforce their knowledge, which is topic by topic.
Frequently Asked Questions (FAQs)
Q: How can students learn kinematics concepts with the NCERT Motion in a Straight Line Solutions?
A:
NCERT Solutions break down difficult kinematic equations and graph interpretations into easily understood portions and offer step-by-step explanations for every textbook problem. Students frequently struggle with applying mathematical concepts to real-world motion situations. After going over solutions, students can work through related problems on their own. These thorough solutions close the gap between theoretical concepts and the practical problem-solving abilities necessary for mastering physics.
Q: In what ways do the NCERT solutions for class 11 Physics motion in a straight line handle numerical problems?
A:
NCERT Solutions offer systematic solutions for numerical problems that demonstrate appropriate formula selections, unit conversions, and calculations with understandable logic. Students who are proficient in numbers gain confidence and are better prepared for competitive exams which rely on quick problem-solving abilities.
Q: Is there a Motion in a Straight Line Class 11 Solutions PDF available for download?
A:
Yes, the solutions PDF for Motion in a Straight Line in Class 11 is available and includes both theory-based and numerical questions with easy-to-follow answers.
Q: What topics are covered in Motion in a Straight Line Class 11 numericals with Solutions PDF?
A:
The PDF includes solved numerical problems based on displacement, speed, velocity, acceleration, and motion graphs, all designed to strengthen your understanding and improve problem-solving skills.
Q: What can I expect in Motion in a Straight Line Class 11 questions and answers?
A:
You will find textbook exercises, conceptual questions, and additional problems to test your understanding and prepare well for exams.
Q: Is it possible for a moving object to have zero acceleration?
A:
Yes, when an object is moving with constant velocity (no change in speed or direction), its acceleration is zero.
Q: What does a horizontal line in a velocity-time graph represent?
A:
A horizontal line in a velocity-time graph means the object is moving with uniform velocity (zero acceleration).
Articles
Upcoming School Exams
Popular Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Courses After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters