NCERT Class 11 Physics Chapter 5 Notes Laws of Motion - Download PDF

NCERT Class 11 Physics Chapter 4 Notes: Download PDF

Master the fundamentals of Newton’s laws, friction, and the motion of objects with these well-structured notes. The downloadable PDF simplifies key concepts, formulas, and examples, making it easier for Class 11 students to revise quickly and prepare for exams like CBSE, JEE, and NEET.

Download PDF

NCERT Class 11 Physics Chapter 4 Notes

NCERT Class 11 Physics Chapter 4 Notes Laws of Motion give a clear explanation of the laws of Newton, inertia, momentum, as well as friction, with real-life examples. Such notes enable students to enhance problem-solving and develop a solid base with regard to board exams and other competitive exams such as JEE and NEET.

Aristotle’s Fallacy

Aristotle, a Greek philosopher, posed a view that for a body to be in motion and keep moving, something external is required. He said that motion had to be caused by a force. To explain why an arrow kept flying after the bow string was no longer pushing on it, he said that the air rushed around behind the arrow and pushed it forward.

Aristotle gave his law of motion, which may be phrased as "An external force is required to keep a body in motion." But this is wrong, because an arrow shot in a vacuum chamber does not instantly drop to the floor as soon as it leaves the bow. Most of Aristotle's ideas on motion are now known to be wrong and need not concern us, as the flaw in Aristotle's argument can be understood by taking an example of a ball rolling on a floor that comes to rest after a while due to the external force of friction on the ball by the floor, which opposes its motion. Now, to keep that ball moving on the floor, we need to give some external force to it to move. But when the ball is moving in uniform motion, there is no net external force acting in its direction of motion. This is due to the fact that the force given by us to move a ball cancels the force of friction by the floor. In simple language, we may say that to keep a ball in uniform motion, we would not be required to apply any external force in the absence of friction. This is the reason why we need external sources to overcome opposing forces like friction (solids) and viscous drag (for fluids), which are always present in the natural world.

The Law of Inertia

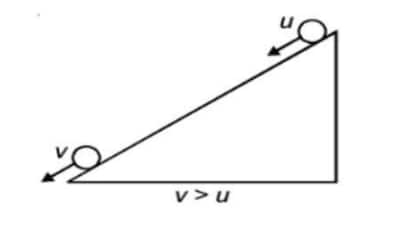
As we have seen, before Galileo, it was thought that a force was required to keep a body moving with uniform velocity. Galileo observed that the speed of a ball increases as it rolls down an inclined plane.

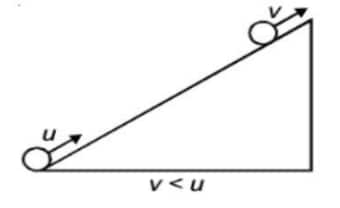
The speed of that ball decreases as it is rolled up that inclined plane.

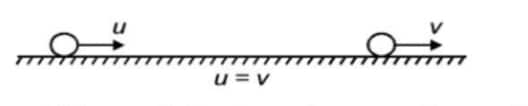
So, what should happen if it is rolled on a horizontal plane? As this case is just in between the situations discussed, the result must also be in between, i.e., the speed of the ball should remain constant.

Explanation :
When you move down, speed increases.
When you move up, speed decreases.
Moving horizontally (i.e., neither up nor down), speed should remain constant (neither increase nor decrease.

Newton’s First Law of Motion (Law of Inertia)

Statement:

If no external force acts on a body, it stays at rest or keeps moving in a straight line with the same speed.

This is called the Law of Inertia.

It explains:

• No force → no change in motion.
• If something changes (starts/stops/turns), a force must be acting.

Types of Inertia:

1. Inertia of Rest: An Object stays still unless something moves it.
2. Inertia of Motion: A Moving object keeps going unless stopped.
3. Inertia of Direction: The Object keeps moving in the same direction unless forced to turn.

Balanced and Unbalanced Forces

Balanced Forces:

• Two equal forces pulling/pushing in opposite directions
• Motion doesn’t change
  Example: In a tug of war, both teams pull equally → The rope doesn’t move.

Unbalanced Forces:

• Forces are not equal
• They cause objects to move, stop, or change shape
  Example: In tug of war, if one team pulls harder → the rope moves towards them.

Linear Momentum

• Linear momentum is a vector quantity (has both magnitude and direction).

• It’s the product of an object’s mass (m) and velocity (v).
  $\overrightarrow{p}=m\overrightarrow{v}$

• SI Unit: kg·m/s

• CGS Unit: g·cm/s

• Dimension: [MLT^-1]

Note: If two objects have the same momentum but different masses, the lighter object will have a higher velocity.

Newton’s Second Law of Motion

The rate of change of momentum of a body is directly proportional to the applied external force, and this change happens in the direction of the force.

In Simple Words:

Force is what causes momentum to change.
More force → faster change in motion.

Mathematically:

Let a body of mass m move with velocity v.
Its momentum: p = m × v

If a force (F) is applied, then:

$\overrightarrow{F}=\frac{dp}{dt}=\frac{d}{dt}(m\overrightarrow{v})=m\frac{d\overrightarrow{v}}{dt}=m\overrightarrow{a}($ from $a=\frac{d\overrightarrow{v}}{dt})$

This formula tells us:
Force = mass × acceleration. It’s one of the most important equations in Physics!

Impulse

Impulse is the effect of a force applied to an object for a short time, causing a sudden change in its motion. It helps explain how quickly an object speeds up, slows down, or changes direction when hit or pushed. For example, when you kick a football or hit a cricket ball with a bat, you give it an impulse that changes its speed and direction instantly. Even airbags in cars use the concept of impulse—they increase the time of impact during a crash to reduce the force on passengers. In simple words, impulse shows how a quick force can create a big change in how something moves.

$\overrightarrow{I}={\int }_{t_1}^{t_2}\overrightarrow{F}dt$

• Impulse is a vector quantity, so it has both magnitude and direction.
• Dimension of impulse: [MLT^-1]

• SI unit- Newton-second or Kg-m-s^-1 and CGS unit- Dyne-second or gm-cm-s^-1

Newton’s Third Law of Motion

Newton's Third Law of Motion says that for every action, there is an equal and opposite reaction. This means that if one object applies a force on another, the second object pushes back with the same amount of force but in the opposite direction. If we say ${\overrightarrow{F}}_{AB}$ is the force that object B applies on object A (action), and ${\overrightarrow{F}}_{BA}$ is the force that object A applies on object B (reaction), then these forces are equal in size but opposite in direction, written as:

${\overrightarrow{F}}_{AB}=-{\overrightarrow{F}}_{BA}$

This law helps explain things like how a swimmer pushes water backwards and moves forward, or how a rocket launches by pushing gas downward and lifting upward.

Conservation of Momentum

According to the Law of Conservation of Linear Momentum, when no external forces act on an isolated system, its total linear momentum remains constant. In other words, the total momentum of a closed system of interacting objects remains constant over time, assuming no external forces influence it.

According to this law, $\overrightarrow{F}=\frac{d\overrightarrow{p}}{dt}$

In the absence of external forces, if F equals 0, then p is constant.

i.e, $P_{\text{system}}=P_1+P_2+P_3+P_4+\dots \dots \dots ..=$ constant

Applications of the Law of Conservation of Linear Momentum

(i) Recoil velocity of a Gun: When a bullet is fired from a gun, the gun recoils or gives a kick in the backwards direction.

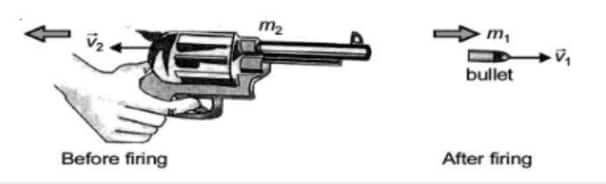
Let ${\overrightarrow{v}}_1\to$ velocity of bullet after firing
${\overrightarrow{v}}_2\to$ velocity of gun after firing
$m_1\to$ mass of the bullet
$m_2\to$ mass of the gun
According to the law of conservation of linear momentum,
Linear momentum before firing = Linear momentum after firing

$0=m_1{\overrightarrow{v}}_1+m_2{\overrightarrow{v}}_2$

or

$\begin{array}{r}{m}_2{\overrightarrow{v}}_2=-m_1{\overrightarrow{v}}_1\\ {\overrightarrow{v}}_2=-\frac{m_1}{m_2}{\overrightarrow{v}}_1\end{array}$

where ${\overrightarrow{v}}_2\to$ recoil velocity of a gun, the negative sign shows that the gun moves backwards.
(ii)Rocket propulsion: Before firing the rocket, the total momentum of the system is zero because the rocket is in the state of rest. When it is fired, chemical fuels inside the rocket are burnt and the hot gases are passed through the nozzle at a greater speed. According to the law of conservation of momentum, the total momentum after firing must be equal to zero. As the hot gases gain momentum to the rear on leaving the rocket, the rocket acquires equal momentum in the upward (i.e.) opposite direction.

Equilibrium of a Particle

In mechanics, a body is in equilibrium when it is at rest or moving with constant velocity in an inertial frame of reference. A hanging lamp, a suspension bridge, an aeroplane flying straight and level at a constant speed are all examples of equilibrium situations.

The essential physical principle is Newton's first law: When a particle is at rest or is moving with constant velocity in an inertial frame of reference, the net force acting on it, i.e., the vector sum of all the forces acting on it, must be zero.

$\mathrm{\Sigma }\overrightarrow{F}=0\text{(Particle in equilibrium vector form)}$

We most often use this equation in component form :

$\mathrm{\Sigma }{\overrightarrow{F}}_x=0;\mathrm{\Sigma }{\overrightarrow{F}}_y=0$

and $\mathrm{\Sigma }{\overrightarrow{F}}_z=0$
Equilibrium under concurrent forces (i.e., those forces which act on the same particle at the same time) may be seen as

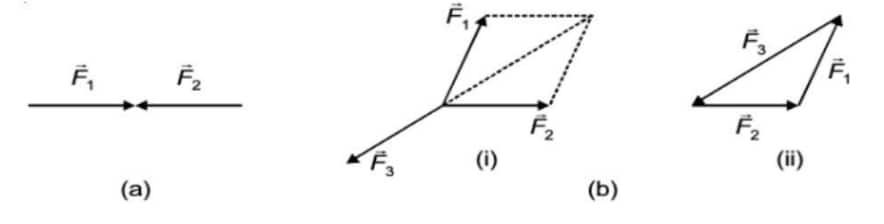
In Fig. (a),

${\overrightarrow{F}}_1+{\overrightarrow{F}}_2=0$

In Fig. (b)-(i) and (b)-(ii),

${\overrightarrow{F}}_1+{\overrightarrow{F}}_2+{\overrightarrow{F}}_3=0$

Common Forces in Mechanics

In mechanics, we come across many types of forces: Some of the common forces are given below:
1. Weight : The weight of a body is the gravitational force with which the earth pulls the body.
2. Spring Force : When a spring is extended, it pulls the body attached to its ends towards its centre and if compressed, it pushes the body away from its centre.
If the extension or compression is not too large, the force exerted by the spring is proportional to the change in its length from its natural length.
i.e., $F\propto x$, where $x$ is the elongation or compression
or $\overrightarrow{F}=-k\overrightarrow{x}$
where $k$ is a positive constant called the spring constant or force constant. Negative sign indicates that the force is opposite to the displacement from the unstretched or uncompressed state.

3. Tension Force: The pulling force transmitted through a string, rope, or wire

4. Normal Reaction: Normal reaction is a contact force between two surfaces in contact, which is always perpendicular to the surfaces in contact. The following diagrams show the normal reaction between two surfaces

Block pushes ground downward with force $R$ and ground pushes the block back with force $R$.

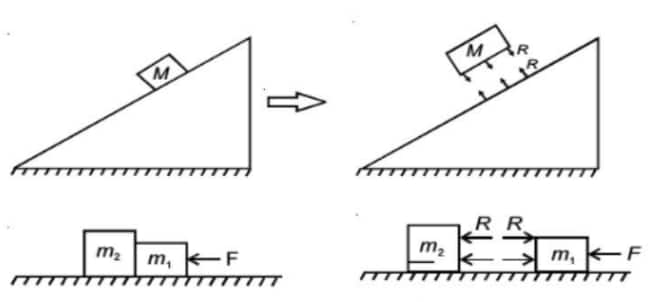
Here $m_1$ pushes $m_2$ towards left by force $R$ and $m_2$ pushes $m_1$ towards right by force $R$

5. Friction

Friction is a force that occurs at the point of contact between two surfaces and works to oppose relative or approaching motion between them.

Friction can be categorised into three main types:

• Static Friction: Acts on stationary objects, preventing them from initiating motion. The force of static friction increases with the applied force until motion is initiated.
  $f_{\mathrm{s}}\le {\mu }_{\mathrm{s}}N$
• The maximum static frictional force ${\left({\mathrm{f}}_{\mathrm{s}}\right)}_{max}={\mu }_{\mathrm{s}}N$
• Kinetic friction: Kinetic friction is the force that arises between two surfaces when they are moving relative to one another.

  The kinetic frictional force ($f_{\mathrm{k}}$) is proportional to the normal force ($N$) and can be expressed as $f_{\mathrm{k}}={\mu }_{\mathrm{k}}N$

• Rolling friction: Rolling friction is the force that opposes the motion of an object as it rolls across a surface. It occurs when there is relative motion between the surface and the part of the object that makes contact with it. it is similar to kinetic friction.

Factors Affecting Friction :

1. Nature of the medium of contact between two bodies :
   Roughness: It increases friction between the two surfaces.
   Smoothness: It reduces the friction.

2. Normal reaction: The force of friction also depends on the normal reaction also. As the normal reaction increases, the interlocking between two surfaces in contact increases as they press harder against each other and hence, friction increases.
3. Area of contact: Force of friction is independent of area of contact.

Angle of Friction: The angle $(\lambda )$ between the resultant maximum possible contact force $(F)$ and the normal force $(N)$ is called the angle of friction.

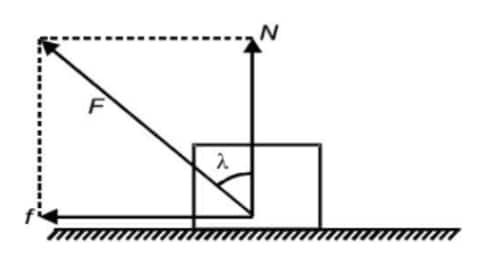
From the figure, clearly $\tan \lambda =\frac{f}{N}=\frac{{\mu }_{s}N}{N}$
i.e., $\tan \lambda ={\mu }_{\mathrm{s}}$
or $\lambda ={\tan }^{-1}\left({\mu }_s\right)$

Angle of repose $(\alpha )$: It is the maximum angle of inclination $(\alpha )$ of a rough inclined plane with the horizontal such that the block kept on it remains at rest.

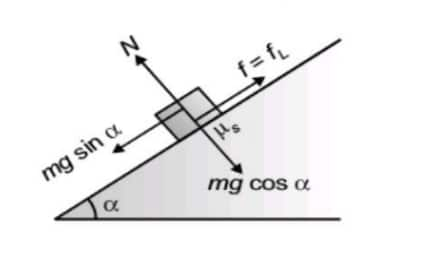
At the angle of repose,

$\begin{array}{r}\text{Driving force = Limiting friction}\\ mg\sin \alpha ={\mu }_{s}N\\ mg\sin \alpha ={\mu }_{s}mg\cos \alpha \\ \tan \alpha ={\mu }_s\end{array}$
Again, we have

$\begin{array}{r}\tan \theta ={\mu }_s(\theta =\text{angle of friction})\\ \therefore & \text{Angle of friction}=\text{Angle of repose}\end{array}$

Circular Motion

• Angular Displacement(θ): The angular displacement of an object moving around a circular path is defined as the angle traced out by the radius vector at the center of the circular path over time. This is a vector quantity.θ= s/r, where s is the arc length and r is the radius.
• Angular Velocity (ω): The angular velocity of an object in circular motion is defined as the rate at which its angular displacement changes over time.
  ω= Δθ/Δt, where Δθ is the change in angular displacement, and Δt is the change in time.
• Angular Acceleration (α): The angular acceleration of an object in circular motion is defined as the rate at which its angular velocity changes over time. α= Δt/Δω, where Δω is the change in angular velocity, and Δt is the change in time
• Uniform Circular Motion: Uniform circular motion occurs when a point object moves along a circular path at a constant speed.

  In this type of motion, the speed remains constant while the direction changes continuously, resulting in circular motion. a_c=v²/r, where r is the radius

Solving Problems in Mechanics

(i) Draw a diagram showing schematically the various parts of the assembly of bodies, the links, supports, etc.
(ii) Choose a convenient part of the assembly as one system.
(iii) Draw a separate diagram which shows this system and all the forces on the system by the remaining part of the assembly. Include also the forces on the system by other agencies. Do not include the forces on the environment by the system. A diagram of this type is known as a free-body diagram. (Note this does not imply that the system under consideration is without a net force).
(iv) In a free-body diagram, include information about forces (their magnitudes and directions) that are either given or you are sure of (e.g., the direction of tension in a string along its length). The rest should be treated as unknowns to be determined using the laws of motion.
(v) If necessary, follow the same procedure for another choice of the system. In doing so, employ Newton's third law. That is, if in the free-body diagram of $A$, the force on $A$ due to $B$ is shown as $\mathbf{F}$, then in the free-body diagram of $B$, the force on $B$ due to $A$ should be shown as $-\mathbf{F}$.

Laws of Motion: Previous Year Questions and Answers

Q1:

Two billiard balls $A$ and $B$, each of mass 50 g and moving in opposite directions with speed of 5 m s-1 each, collide and rebound with the same speed. If the collision lasts for $10^{-3} s$, which of the following statements are true?
(a) The impulse imparted to each ball is $0.25 \mathrm{~kg} \mathrm{~m} \mathrm{~s}^{-1}$ and the force on each ball is 250 N .
(b) The impulse imparted to each ball is $0.25 \mathrm{~kg} \mathrm{~m} \mathrm{~s}^{-1}$ and the force exerted on each ball is $25 \times 10^{-5} \mathrm{~N}$.
(c) The impulse imparted to each ball is 0.5 Ns .
(d) The impulse and the force on each ball are equal in magnitude and opposite in direction.

Answer:

The correct answers:

(c) The impulse imparted to each ball is 0.5 Ns .
(d) The impulse and force on each ball are equal in magnitude and opposite in direction.

Let m be the mass of each ball, $\mathrm{m}=0.05 \mathrm{~kg}$
Let $v$ be the speed of each ball, $v=5 \mathrm{~m} / \mathrm{s}$
We know that the initial momentum of each ball will be

$
\begin{aligned}
& \overrightarrow{p_i}=m \vec{v} \\
& \overrightarrow{p_i}=(0.05)(5)=0.25 \mathrm{kgms}^{-1} \\
& =0.25 \mathrm{~N}-\mathrm{s}
\end{aligned}
$
After the collision, on rebounding, the direction of the velocity of each ball is reversed; hence, the final momentum of each ball will be

$
\begin{aligned}
& \vec{p}=m(-\vec{v}) \\
& =-0.25 \mathrm{~N}-\mathrm{s} .
\end{aligned}
$
Hence, statement (d) is verified.
Thus, it is clear that the impulse imparted to each ball is equal to the change in momentum of each ball

$
\begin{aligned}
& =p_f-p_i \\
& =-0.25-(0.25) \\
& =-0.50 \mathrm{~kg} \mathrm{~ms}^{-1} \\
& =-0.50 \mathrm{~N}-\mathrm{s}
\end{aligned}
$
Here, statement (c) is also verified.

Q2:

In the Figure, the coefficient of friction between the floor and the body B is 0.1. The coefficient of friction between the bodies $B$ and $A$ is 0.2. A force $F$ is applied as shown on $B$. The mass of $A$ is $\frac{m}{2}$ and of $B$ is $m$. Which of the following statements are true?

(a) The bodies will move together if F = 0.25 mg.
(b) The body A will slip with respect to B if F = 0.5 mg.
(c) The bodies will move together if F = 0.5 mg.
(d) The bodies will be at rest if F = 0.1 mg.
(e) The maximum value of F for which the two bodies will move together is 0.45 mg.

Answer:

Explanation: By opt (e) the max. The force by which bodies move together is 0.45 mg, Newton.

$
\mathrm{mA}=\frac{m}{2}=\mathrm{mB}=\mathrm{m}
$
Consider the acceleration of the bodies A and B to be ' a '.
Both the bodies $\mathrm{A} \& \mathrm{~B}$ will keep moving by force F until the force of friction between their surface is larger or equal to 0 than the force acting on A.

$
a=\frac{F-f_1}{m_A-m_B}=\frac{F-f_1}{\frac{m}{2}+m}=\frac{2\left(F-f_1\right)}{3 m}
$

Thus, the force on

$
A=m_A a=\frac{m}{2} \frac{\left(F-f_1\right)}{3 m}
$
Hence, the force on A is

$
F_{A B}=\frac{\left(F-f_1\right)}{3}
$
The body $A$ will move along with body $B$ only if $\mathrm{F}_{A B}$ is equal or smaller than $\mathrm{f}_2$.
Hence, $F_{A B}=f_2$

$
\mu N=\frac{\left(F-f_1\right)}{3}
$

$0.2 \times m_A g=\frac{\left(F-f_1\right)}{3}$

N is the reaction force by B on A

$
f_1=\mu N B=\mu\left(m_A+m_B\right) g
$

$\qquad$ (here, $\mathrm{N}_{\mathrm{B}}$ is the normal reaction on B along with A by the surface)

$
\begin{aligned}
& 0.1 \times\left(m_A+m_B\right) g \\
& f_1=0.1 \times \frac{3}{2} m g=0.15 \mathrm{mg}
\end{aligned}
$
Now,

$
\begin{aligned}
& F-f_1=3 \times 0.2 \mathrm{mAg} \\
& F-0.15 \mathrm{mg}=0.6 \times \frac{\mathrm{m}}{2} \mathrm{~g} \\
& F_{\max }=0.3 \mathrm{mg}+0.15 \mathrm{mg}=0.45 \mathrm{mg}
\end{aligned}
$
Thus, the max force on B is 0.45 mg, therefore, $\mathrm{A} \& \mathrm{~B}$ can move together.
Hence, opt (e).
Both the bodies $\mathrm{A} \& \mathrm{~B}$ will keep moving by force F until the force of friction between their surface is larger or equal to 0 than the force acting on A, i.e., 0.45 mg Newton, hereby opt (c) is rejected.

Now, for opt (d), the minimum force which can move $A \& B$ together is,

$
\begin{aligned}
& F_{\text {in }} \geq f_1+f_2 \\
& \geq 0.15 \mathrm{mg}+0.2 \times \frac{\mathrm{m}}{2} \mathrm{~g} \quad \ldots . .[\text { from (i) \& (ii) }] \\
& F_{\text {in }} \geq 0.25 \mathrm{mg} \text { Newton }
\end{aligned}
$
Since $0.1 \mathrm{mg}<0.25 \mathrm{mg}$, opt (d) is verified, which states that the body will be at rest if $\vec{F}=0.1 \mathrm{mg}$.

Q3:

A body of mass 5 kg is acted upon by a force $F=(-3 \widehat{i}+4 \widehat{j}) N$. If its initial velocity at $\mathrm{t}=0$ is $v=(6 \widehat{i}-12 \widehat{j}) \mathrm{ms}^{-1}$, the time at which it will just have velocity along the $y$-axis is

(a) never

(b) 10s

(c) 2s

(d) 15s

Answer:

Explanation:
Initial velocity $(u)=(6 \widehat{i}+12 \widehat{j}) \mathrm{ms}^{-1}$
Force, $F=(-3 \widehat{i}+4 \widehat{j}) N, \operatorname{Mass}(\mathrm{~m})=5 \mathrm{~kg}$

$
\vec{a}=\frac{\vec{F}}{m}=\left(\frac{-3}{5} \widehat{i}+\frac{4}{5} \widehat{j}\right) m s^{-2}
$
Since there is only the Y component in the final velocity and the X component is zero,

$
\begin{aligned}
& v_x=u_x+a_x t \\
& 0=6+\frac{-3}{5} t \rightarrow \frac{3}{5} t=6 \\
& \mathrm{t}=10 \mathrm{~s}
\end{aligned}
$
Hence, the answer is the option (b).

Importance of Laws of Motion Class 12 Notes

Basic of Mechanics

• The NCERT Class 11 Physics Chapter 4 Notes give a solid conceptual foundation of mechanics, which is among the most significant subjects of physics in CBSE Board examinations, JEE and NEET.

Explanation of Newton's Laws

• The laws of motion, known as the first, second, and third Newton laws, are well organised and explained with solved examples to enable easier understanding of how these laws are applied to vehicles, rockets and projectiles in real-life situations.

Time Saving Revising Aid

• These NCERT Class 12 Physics Notes assist students in revising their briefs before an exam by learning summarised formulas, definitions, and derivations.

Enhances Competitive Exam Preparation

• Most of the high-weightage questions in JEE Main, JEE Advanced, and NEET physics directly depend on the concept of force, friction, equilibrium, and circular motion; therefore, these notes prove to be of great importance.

Conceptual Knowledge with Applications

• The notes emphasise real-life applications of concepts like motion of lifts, banking of roads and tension in strings, which reinforce the linkage between theory and the physics of the real world.

Error-Free Learning Material

• The notes are ready because the subject specialists prepared them, and in this way, the confusion is cleared, and they are presented in a simple-to-understand format of derivations, diagrams and problem-solving techniques.

Exam-Oriented Preparation

• Short tricks, key formulas, and references to questions of the previous year in Laws of Motion notes are known to enable students to achieve better marks in the board exams as well as in the competitive exams.

NCERT Class 11 Notes Chapter-Wise

Preparing for Class 11 exams becomes easier with well-structured notes covering every chapter of Physics, Chemistry, Maths, and Biology. These Physics NCERT Class 11 Notes provide simplified explanations, key formulas, and important concepts to help in both CBSE board exams and competitive exams like JEE & NEET. Click on the chapter-wise links below to access complete notes for quick and effective revision.

Subject-Wise NCERT Exemplar Solutions

• NCERT Exemplar Class 11 Solutions
• NCERT Exemplar Class 11 Maths
• NCERT Exemplar Class 11 Physics
• NCERT Exemplar Class 11 Chemistry
• NCERT Exemplar Class 11 Biology

Subject-Wise NCERT Solutions

• NCERT Solutions for Class 11 Mathematics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 11 Biology

NCERT Books and Syllabus