NCERT Solutions for Class 11 Physics Chapter 4 Laws Of Motion

Q4.1 (a) Give the magnitude and direction of the net force acting ona drop of rain falling down at a constant speed

Answer:

Since the drop is falling with constant speed, so the net acceleration of the drop is zero. This means net force on the drop is zero.

Q4.1 (b) Give the magnitude and direction of the net force acting on a cork of mass 10 g floating on water,

Answer:

Since the cork is floating on the water, that implies the gravitational force of cork is balanced by the buoyant force. Thus net force acting on cork is zero.

Q4.1 (c) Give the magnitude and direction of the net force acting on a kite skillfully held stationary in the sky,

Answer:

Since the kite is stationary in the sky, thus according to Newton's law, the net force on the kite is zero.

Q4.1 (d) Give the magnitude and direction of the net force acting on a car moving with a constant velocity of 30 km/h on a rough road,

Answer:

Since the car is moving with constant velocity thus the net acceleration of the car is zero. Thus net force acting on the car is zero.

Q4.1 (e) Give the magnitude and direction of the net force acting ona high-speed electron in space far from all material objects, and free of electric and magnetic fields.

Answer:

Since the electron is free from the electric and magnetic field so net force acting on the electron is zero.

Q4.2 (a) A pebble of mass 0.05 kg is thrown vertically upwards. Give the direction and magnitude of the net force on the pebble, during its upward motion

Answer:

During upward motion, the force acting on the pebble is only the gravitational force which is acting in a downward direction .

The gravitational force :

=mg=0.05(10)N=0.5N

Q4.2 (b) A pebble of mass 0.05 kg is thrown vertically upwards. Give the direction and magnitude of the net force on the pebble, during its downward motion

Answer:

Since the pebble is moving in the downward direction the net force acting is also in the downward direction .

The net force is the gravitational force.

Gravitational force:-

=mg=0.(05)10=0.5N

Q4.2 (c) A pebble of mass 0.05 kg is thrown vertically upwards. Give the direction and magnitude of the net force on the pebble, at the highest point where it is momentarily at rest. Do your answers change if the pebble was thrown at an angle of 45° with the horizontal direction? Ignore air resistance.

Answer:

At the highest point velocity becomes zero for a moment. At this point also, the net force acting is the gravitational force which acts in the downward direction .

Gravitational force:-

$=mg=(0.05)10=0.5N$

When a pebble is thrown at 45⁰ with the horizontal direction then also net force will be the same gravitational force.

Q4.3 (a) Give the magnitude and direction of the net force acting on a stone of mass 0.1 kg,just after it is dropped from the window of a stationary train, Neglect air resistance throughout.

Answer:

Since the train is stationary so the net force acting on the stone is the gravitational force which acts in the downward direction .

Gravitational force :

$F=ma=mg$

or $F=(0.1)10$

or $F=1N$

Q4.3 (b) Give the magnitude and direction of the net force acting on a stone of mass 0.1 kgjust after it is dropped from the window of a train running at a constant velocity of 36 km/h, Neglect air resistance throughout.

Answer:

Since the train is travelling with the constant speed so the acceleration of the train is zero. Thus there is no force on stone due to train.

The net force acting on the stone will be the gravitational force which acts in a downward direction.

Gravitational force:-

$F=mg$

or $F=(0.1)10N$

or $F=1N$

Q4.3 (c) Give the magnitude and direction of the net force acting on a stone of mass 0.1 kg, (c) just after it is dropped from the window of a train accelerating with $1m{s}^{-2}$ , Neglect air resistance throughout.

Answer:

Just after the stone is dropped, the stone is free from the acceleration of the train. Thus the force acting on the stone will be just the gravitational force which acts in the downward direction.

The gravitational force is given by:-

$F=mg$

or $F=(0.1)10$

or $F=1N$

Q4.3 (d) Give the magnitude and direction of the net force acting on a stone of mass 0.1 kg,lying on the floor of a train which is accelerating with 1 m s^-2 , the stone being at rest relative to the train. Neglect air resistance throughout.

Answer:

As the stone is in contact with the train thus the acceleration of stone is the same as that of train i.e. 1 m/s ² .

Thus force acting on the stone is given by :

$F=ma$

or $F=0.1\times 1=0.1N$

This force is acting in the horizontal direction.

Q4.4 One end of a string of length l is connected to a particle of mass m and the other to a small peg on a smooth horizontal table. If the particle moves in a circle with speed v the net force on the particle (directed towards the centre) is :

(i) $T$

(ii) $T-\frac{m{v}^2}{l}$

(iii) $T+\frac{m{v}^2}{l}$

(iv) 0

$T$ is the tension in the string. [Choose the correct alternative].

Answer:

When the particle is moving in a circular path, the centripetal force will be :

$F_c=\frac{m{v}^2}{r}$

This centripetal force will be balanced by the tension in the string.

So, the net force acting is :

$F=T=\frac{m{v}^2}{r}$

Q4.5 A constant retarding force of 50 N is applied to a body of mass 20 kg moving initially with a speed of $15m{s}^{-1}$ . How long does the body take to stop?

Answer:

We are given the retarding force. So we can find the deacceleration this force is causing.

By Newton's second law of motion, we get :

$F=ma$

or $-50=(20)a$

or $a=\frac{50}{20}=-2.5m/s^2$

Now we will use the first equation of motion,

$v=u+at$

The final velocity, in this case, will be zero (Since the vehicle stops).

$0=15+(-2.5)t$

Thus $t=\frac{15}{2.5}=6s$

Thus the time taken to stop the vehicle is 6 sec.

Q4.6 A constant force acting on a body of mass 3.0 kg changes its speed from $2.0m{s}^{-1}$ to $3.5m{s}^{-1}$ in 25 s. The direction of the motion of the body remains unchanged. What is the magnitude and direction of the force?

Answer:

Since the velocity of the body is increased by applying the force. This is possible only when the force is applied in the direction of the motion.

For finding the magnitude of the force, we need to calculate acceleration.

By using first equation of the motion,

$v=u+at$

or $3.5=2+a(25)$

or $a=\frac{3.5-2}{25}=0.06m/s^2$

Thus force can be written as :

$F=ma$

$F=3\times 0.06$

$F=0.18N$

Q4.7 A body of mass 5 kg is acted upon by two perpendicular forces 8 N and 6 N. Give the magnitude and direction of the acceleration of the body.

Answer:

The magnitude of the resulting force can be found by :

$R=\sqrt{F_1^2+F_2^2}$

or $R=\sqrt{8^2+6^2}$

or $R=10N$

Now force direction,

$\tan \theta =\frac{6}{8}$

or $\theta ={37}^{\circ }$

The acceleration of the body is given by :

$a=\frac{F}{m}$

or $a=\frac{10}{5}=2m/s^2$

Hence acceleration of the body is $2m/s^2$ and its direction is the same as of the resultant force.

Q4.8 The driver of a three-wheeler moving with a speed of 36 km/h sees a child standing in the middle of the road and brings his vehicle to rest in 4.0 s just in time to save the child. What is the average retarding force on the vehicle? The mass of the three-wheeler is 400 kg and the mass of the driver is 65 kg.

Answer:

Total mass of the system = 400 + 65 = 425 kg

Using first law of motion, we get

$v=u+at$

Since the car comes to rest, thus final velocity will be zero.

$0=10+a(4)$

or

$a=\frac{-10}{4}=-2.5m/s^2$

So the force required :

$F=ma$

or $F=465\times (-2.5)$

or $F=-1162.5N$

So the magnitude of the force is 1162.5 N and it is retarding force.

Q4.9 A rocket with a lift-off mass 20,000 kg is blasted upwards with an initial acceleration of $5.0m{s}^{-2}$ . Calculate the initial thrust (force) of the blast.

Answer:

Let the initial thrust be F Newton.

Using Newton's second law of motion, we get

$F-mg=ma$

or $F=ma+mg$

$F=m(a+g)N$

Substituting values in this equation, we get :

$F=20000(5+10)$

or $F=3\times {10}^{5}N$

Q4.10 A body of mass 0.40 kg moving initially with a constant speed of $10m{s}^{-1}$ to the north is subject to a constant force of 8.0 N directed towards the south for 30 s. Take the instant the force is applied to be $t=0$ , the position of the body at that time to be $x=0$ , and predict its position at $t=-5s,25s,100s$ .

Answer:

The acceleration of force is given by :

$a=\frac{F}{m}$

$a=\frac{-8}{0.4}=-20m/s^2$

At t = - 5 s :

There is no force acting so acceleration is zero and u = 10 m/s

$s=ut+\frac{1}{2}a{t}^2$

or $s=10(-5)+\frac{1}{2}.0.t^2$

or $s=-50m$

At t = 25 s :

Acceleration is - 20 m/s ² and u = 10 m/s

$s=ut+\frac{1}{2}a{t}^2$

or $s=10(25)+\frac{1}{2}(-20){25}^2$

or $s=-6000m$

At t = 100 s

We have acceleration for first 30 sec, and then it will move with constant speed.

So for 0 < t < 30 :

$s=ut+\frac{1}{2}a{t}^2$

or $s=10(30)+\frac{1}{2}(-20){30}^2$

or $s=-8700m$

Now for t > 30 s :

We need to calculate velocity at t = 30 sec which will be used as the initial velocity for 30 < t < 100.

$v=u+at$

or $v=10+(-20)30=-590m/s$

Now $s=vt+\frac{1}{2}a{t}^2$

or $s=(-590)70+\frac{1}{2}.0.t^2$

or $s=-41300m$

Hence total displacement is : - 8700 + (- 41300 ) = - 50000 m.

Q4.11 (a) A truck starts from rest and accelerates uniformly at $2.0m{s}^{-2}$ . At $t=10s$ , a stone is dropped by a person standing on the top of the truck (6 m high from the ground). What is the velocity of the stone at $t=11s$ ? (Neglect air resistance.)is

Answer:

The initial velocity of the truck is given as zero.

We need to find the final velocity (at t = 10 s), so we will use the equation of motion :

$v=u+at$

or $v=0+(2)10=20m/s$

This is the velocity imparted to stone by the truck that's why it is a horizontal component of velocity.

The stone is dropped at t = 10 sec. so it has travelled 1 sec in the air (11 - 10 = 1 s). We need to find the final vertical velocity.

$v=u+at$

$v=0+10(1)=10m/s$

Thus resultant of both the component is the required velocity.

$R=\sqrt{v_h^2+v_v^2}$

or $R=\sqrt{{20}^2+{10}^2}$

or $R=22.36m/s$

Direction :

$\tan \theta =\frac{v_v}{v_h}=\frac{10}{20}$

or $\theta ={26.57}^{\circ }$

Q4.11 (b) A truck starts from rest and accelerates uniformly at $2.0m{s}^{-2}$ . At $t=10s$ , a stone is dropped by a person standing on the top of the truck (6 m high from the ground). What is the acceleration of the stone at $t=11s$ ? (Neglect air resistance.)

Answer:

When the stone is dropped, the stone comes only in effect of gravity.

So the acceleration of stone is 10 m/s ² and it acts in the downward direction.

Q4.12 (a) A bob of mass 0.1 kg hung from the ceiling of a room by a string 2 m long is set into oscillation. The speed of the bob at its mean position is $1m{s}^{-1}$ . What is the trajectory of the bob if the string is cut when the bob is at one of its extreme positions?

Answer:

At the extreme positions, the velocity of the bob will become zero for a moment. So if we cut the string at this time, then Bob will fall vertically downward due to gravity.

Q4.12 (b) A bob of mass 0.1 kg hung from the ceiling of a room by a string 2 m long is set into oscillation. The speed of the bob at its mean position is $1m{s}^{-1}$ . What is the trajectory of the bob if the string is cut when the bob is at its mean position?

Answer:

At the mean position, the bob will have velocity tangential to the circular path (it will be completely horizontal). If the bob is cut at this place then it will follow a parabolic path having only horizontal velocity.

Q4.13 (b) A man of mass 70 kg stands on a weighing scale in a lift which is moving downwards with a uniform acceleration of $5m{s}^{-2}$. What would be the readings on the scale?

Answer:

Using Newton&##39;s law of motion, we have :

$R+mg=ma$

or $R-70(10)=70(-5)$ (Since we took downward direction as negative and upward as positive).

or $R=700-350=350N$

Thus the reading on the weighing scale will be :

$=\frac{R}{g}=\frac{350}{10}=35Kg$

Q4.13 (c) A man of mass 70 kg stands on a weighing scale in a lift which is moving upwards with a uniform acceleration of $5m{s}^{-2}$ . What would be the readings on the scale?

Answer:

The acceleration of lift is given to be 5 m/s ² . Let us assume the upward direction to be positive.

Using Newton's law of motion, we can write :

$R-mg=ma$

or $R-70(10)=70(5)$

or $R=350+700=1050N$

Thus the reading of the weighing scale will be :

$=\frac{R}{g}=\frac{1050}{10}=105Kg$

Q44.13 (d) A man of mass 70 kg stands on a weighing scale in a lift which is moving What would be the reading if the lift mechanism failed and it hurtled down freely under gravity?

Answer:

If the lift falls freely then the acceleration of lift will be acceleration due to gravity.

Using Newton's law of motion we can write :

$R-mg=ma$

or $R-mg=m(-g)$

or $R=m(-g)+mg=0N$

Thus the reading of weighing scale will also be zero since there is no normal force.

This state is called the state of weightlessness.

Q4.14 (a) Figure shows the position-time graph of a particle of mass 4 kg. What is the force on the particle for $t<0,t>4s,0<t<4s$ ?

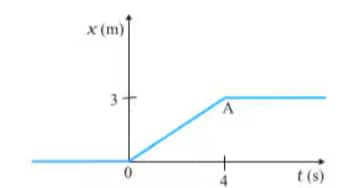
Answer:

(i) For t < 0 :

In this range the position of particle coincides with time, that implies no motion takes place. Hence net force on the particle is zero.

(ii) For t > 4 :

In this range displacement of the particle is not changed so the net force is zero.

(iii) For 0 < t < 4 :

In this range the slope of the position-time graph is constant that means the particle is moving with constant speed. And hence net force, in this case, is zero.

Q4.14 (b) Figure shows the position-time graph of a particle of mass 4 kg. What is the impulse at t = 0 and t = 4 s ? (Consider one-dimensional motion only).

Answer:

Impulse is defined by :

$J=mv-mu$ (Change in momentum).

At t = 0 s :

$u=0andv=\frac{3}{4}m/s$

or $J=4(\frac{3}{4})-0$

or $J=3Kgm/s$

At t = 4 s :

$u=\frac{3}{4}m/s$ and $v=0$

Thus $J=0-4\left(\frac{3}{4}\right)$

or $J=-3Kgm/s$

Q4.15 (i) Two bodies of masses 10 kg and 20 kg respectively kept on a smooth, horizontal surface are tied to the ends of a light string. A horizontal force F = 600 N is applied to A along the direction of the string. What is the tension in the string?

Answer:

We will consider A and B in a system. So total mass in the system is = 10 + 20 = 30 Kg.

Thus acceleration of the system is given by :

$a=\frac{F}{m}$

or $a=\frac{600}{30}=20m/s^2$

When force is applied at block A :

Using Newton's law of motion :

$F-T=m_{1}a$

or $600-T=10\times 20$

Thus $T=400N$

Q4.15 (ii) Two bodies of masses 10 kg and 20 kg respectively kept on a smooth, horizontal surface are tied to the ends of a light string. A horizontal force F = 600 N is applied to B along the direction of the string. What is the tension in the string?

Answer:

We will consider A and B in a system. So total mass in the system is = 10 + 20 = 30 Kg.

Thus acceleration of the system is given by :

$a=\frac{F}{m}$

or $a=\frac{600}{30}=20m/s^2$

When force is applied at block B :

Using Newton's law of motion, we can write

$F-T=m_{2}a$

or $600-T=20(20)$

Thus $T=200N$

Q4.16 Two masses 8 kg and 12 kg are connected at the two ends of a light inextensible string that goes over a frictionless pulley. Find the acceleration of the masses, and the tension in the string when the masses are released.

Answer:

Since both the masses are connected with string so they will have the same acceleration, let say 'a'.

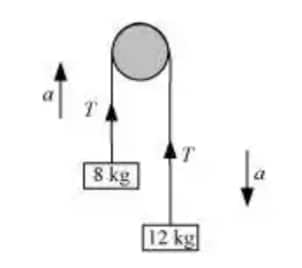
We will apply Newton's law for each block individually.

For smaller block (8 Kg) :

$T-m_{s}g=m_{s}a$ ...................................................(i)

For larger block (12 Kg) :

The equation of motion is given by :

$m_{l}g-T=m_{l}a$ ......................................................(ii)

Adding both the equations we get :

The acceleration is given by :

$a=\left(\frac{m_l-m_s}{m_l+m_s}\right)g$

or $a=\left(\frac{12-8}{12+8}\right)10$

or $a=2m/s^2$

Now put the value of acceleration in any of the equations to get the value of T.

$T=(m_l-\frac{m_l^2-m_s{m}_l}{m_s+m_l})g$

or $T=\left(\frac{2m_s{m}_l}{m_s+m_l}\right)g$

or $T=\left(\frac{2\times 12\times 8}{12+8}\right)10$

$T=96N$

Thus the tension in the string is 96 N.

Q4.17 Anucleus is at rest in the laboratory frame of reference. Show that if it disintegrates into two smaller nuclei the products must move in opposite directions.

Answer:

Let the mass of parent nuclei be m.

And the mass of daughter nuclei be m ₁ and m ₂ .

Initial momentum is zero since the nuclei is at rest.

But after dissociation, the momentum becomes :

$M=m_1{v}_1+m_2{v}_2$

Using conservation of momentum,

$0=m_1{v}_1+m_2{v}_2$

or $v_1=\frac{-m_2{v}_2}{m_1}$

Thus both velocities have opposite direction.

Q4.18 Two billiard balls each of mass 0.05 kg moving in opposite directions with speed $6m{s}^{-1}$ collide and rebound with the same speed. What is the impulse imparted to each ball due to the other?

Answer:

Impulse imparted can be calculated by knowing the change in momentum.

The initial momentum of each ball is :

$p_i=mu=(0.05)6=0.3Kgm/s$

The final momentum is given by :

$p_f=mv=(0.05)(-6)=-0.3Kgm/s$

So the impulse is :

$J=p_f-p_i$

or $J=-0.3-0.3$

or $J=-0.6Kgm/s$

Q4.19 A shell of mass 0.020 kg is fired by a gun of mass 100 kg. If the muzzle speed of the shell is $80m{s}^{-1}$ , what is the recoil speed of the gun?

Answer:

In this question, we will use the conservation of momentum.

Final momentum = Initial momentum

For initial momentum :

Both gun and shell are at rest initially so momentum is zero.

For final momentum :

The direction of the velocity of the shell is opposite to that of the gun.

So, $p_f=m_s{v}_s-m_g{V}_g$

The recoil speed of the gun :

$V_g=\frac{m_s{v}_s}{m_g}$

or $V_g=\frac{0.020\times 80}{100\times 1000}=0.016m/s$

Q4.20 A batsman deflects a ball by an angle of 45° without changing its initial speed which is equal to 54 km/h. What is the impulse imparted to the ball? (The mass of the ball is 0.15 kg.)

Answer:

The situation is shown below :

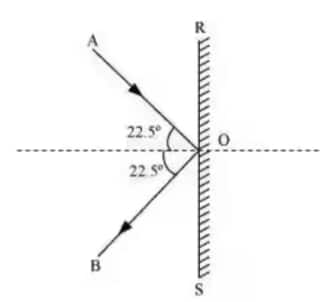
The horizontal components of velocity are to be considered for imparting impulse as vertical components are in the same direction thus impulse in the vertical direction is zero.

The impulse is given by a change in momentum.

Initial momentum = $-mv\cos \theta$

Final momentum = $mv\cos \theta$

Thus impulse is, J $=mv\cos \theta -(-mv\cos \theta )=2mv\cos \theta$

or $J=2\times 0.15\times 15\cos {22.5}^{\circ }$

or $J=4.16Kgm/s$

Q4.21 A stone of mass 0.25 kg tied to the end of a string is whirled round in a circle of radius 1.5 m with a speed of 40 rev./min in a horizontal plane. What is the tension in the string? What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?

Answer:

We are given, frequency :

$n=\frac{40}{60}=\frac{2}{3}$

So, the angular velocity becomes :

$\omega =2\mathrm{\Pi }n$

By Newton's law of motion, we can write :

$T=F_{centripetal}$

or $T=\frac{m{v}^2}{r}=m{w}^{2}r$

or $T=(0.25){(2\times \mathrm{\Pi }\times \frac{2}{3})}^2(1.5)$

or $T=6.57N$

Now, we are given maximum tension and we need to find the maximum velocity for that :

$T_{max}=\frac{m{v}_{max}^2}{r}$

Thus, $v_{max}=\sqrt{\frac{T_{max}.r}{m}}$

or $v_{max}=\sqrt{\frac{200\times 1.5}{0.25}}$

or $v_{max}=34.64m/s$

Q4.22 (a) If, in Exercise 4.21, the speed of the stone is increased beyond the maximum permissible value, and the string breaks suddenly, which of the following correctly describes the trajectory of the stone after the string breaks :

(a) the stone moves radially outwards,

Answer:

The stone should move in the direction of velocity at that instant. Since velocity is tangential at that moment the stone will not move radially outward.

Q4.22 (b) If, in Exercise 4.21, the speed of the stone is increased beyond the maximum permissible value, and the string breaks suddenly, which of the following correctly describes the trajectory of the stone after the string breaks :

(b) the stone flies off tangentially from the instant the string breaks,

Answer:

(b) This statement is correct as the direction of velocity at the instant of the breaking of the string is tangential thus stone will move tangentially.

Q4.22 (c) If, in Exercise 4.21, the speed of the stone is increased beyond the maximum permissible value, and the string breaks suddenly, which of the following correctly describes the trajectory of the stone after the string breaks :

(c) the stone flies off at an angle with the tangent whose magnitude depends on the speed of the particle.

Answer:

The direction of velocity at the instant of breakage of the string is tangential so the stone will fly tangentially. Hence given statement is false.

Q4.23 (a) Explain whya horse cannot pull a cart and run in empty space

Answer:

The horse moves forward by pushing ground backwards. The ground will then give the normal force to the horse (action-reaction pair), which is responsible for the movement of the horse. In an empty space, no such force is present so the horse cannot get the push to run forward. Thus, a horse cannot pull a cart and run in empty space.

Q4.23 (b) Explain whypassengers are thrown forward from their seats when a speeding bus stops suddenly

Answer:

This is because of inertia. When the bus is moving our body has the same speed. But when the bus comes to rest, the inertia of our body opposes to stop and continues its motion. That's why passengers are thrown forward from their seats when a speeding bus stops suddenly.

Q4.23 (c) Explain whyit is easier to pull a lawnmower than to push it

Answer:

Because when you pull the lawnmower at some angle, one component of force is in the upward direction and one in horizontal (to move). The vertical force reduces the effective weight of the motor which makes it easier. But in case of a push, the vertical force is directed downward which makes its effective weight even greater than before. That's why it is said 'pull is easier than push'.

Q4.23 (d) Explain whya cricketer moves his hands backwards while holding a catch.

Answer:

According to Newton's law, we can write :

$F=ma$

or $F=m\frac{dv}{dt}$

Thus $F\propto \frac{dv}{dt}$

It can be seen from the equation that if we increase the impact time then the experienced force will be lesser.

So a cricketer increases the impact time by taking his hands backward while holding a catch, resulting in less force on their hand.

Class 11 Physics NCERT Chapter 4: Higher Order Thinking Skills (HOTS) Questions

Q1. Consider a block and trolley system as shown in the figure. If the coefficient of kinetic friction between the trolley and the surface is 0.4, the acceleration of the system ${\mathrm{ms}}^{-2}$ is: ( Consider that the string is massless and unstretchable and the pulley is also massless and frictionless)

Answer:

$\begin{array}{rl}50-T& =5a\to (1)\\ T-f& =10a\to (2)\end{array}$

$\begin{array}{rl}& 10=15a\\ & a=\frac{2}{3}\mathrm{m}/{\mathrm{s}}^2\end{array}$

Hence, The answer is 2/3.

Q.2 The system shown in the figure is in equilibrium and at rest. The spring and string are massless. Now the string between B and C is cut. Find the acceleration of A, B and C just after the string is cut. $(g=10\mathrm{m}/{\mathrm{s}}^2)$

Answer:

At equilibrium, the free body diagrams are-

For block A,

$\begin{array}{rl}{T}_A& =mg+kx\\ & =3mg\end{array}$

For block B,

$\begin{array}{rl}kx& =T_B+mg\\ & =2mg\end{array}$

For block C,

$T_B=mg$

When string is cut $T_B$ will be equal to zero. Net force acting on block A is zero

Block A $a_a=0$
Block B $a_B=\frac{(2mg-mg)}{m}=g$
Block C $a_c=g$

Q.3 The reading of the spring balance (mass-stress) in the figure given below is $(m_2>m_1)$

Answer:

FBD of the block of mass m₁

$T-mg=m_{1}a$......(1)

FBD of block mass m₂

$m_{2}g-T=m_{2}a$.......(2)

For massless spring balance reading $=\mathrm{kx}=\mathrm{T}$
From the equation (1) and (2), we get-

$\begin{array}{rl}& m_{2}g-m_{1}g=(m_1+m_2)a\\ & \Rightarrow a=\left(\frac{m_2-m_1}{m_1+m_2}\right)g\end{array}$
$T=m_{1}g+m_{1}a=m_{1}g+\frac{m_1{m}_{2}g}{m_1+m_2}-\frac{m_1^2+g}{(m_1+m_2)}$
$T=\frac{2m_1{m}_{2}g}{m_1+m_2}$
Spring balance reading

$=\frac{2m_1{m}_{2}g}{m_1+m_2}$

Q.4 The arrangement is shown in the given figure. If the coefficient of friction between the 2kg block and the table is 0.2 . What would be the maximum value of m (in kg) such that two blocks do not move?(10=m/s²⁾ ?

Answer:

Given-
mass of block on table $=2\mathrm{kg}$,
coefficient of friction, $\mu =0.2$
As we keep on increasing the value of $m$ from zero the tension as well as friction force increases to kepp the blocks at rest. For the maximum value of $m$ the friction force is maximum and the blocks are just about to move. Therefore at that instant the friction force is limiting.

Let the tension in the string be $T$.
F.B.D of a block of mass $m$ -

For equilibrium-

$\mathrm{T}=\mathrm{mg}\dots (1)$

F.B.D of a block of mass 2 kg -

$N=20$
Limiting friction-

${\mathrm{f}}_{\mathrm{l}}=\mu \mathrm{N}=4$
For equilibrium-

$\mathrm{T}={\mathrm{f}}_{\mathrm{l}}=4\dots (2)$
From equation (1) and (2) -

$\begin{array}{rl}& \mathrm{mg}=4\\ & \Rightarrow \mathrm{m}=0.4\end{array}$

Q.5 A bob is hanging over a pulley inside a car through a string. The second end of the string is in the hand of a person standing in the car. The car is moving with constant acceleration 'a' directed horizontally as shown in the figure. The other end of the string is pulled with constant acceleration ' a ' vertically downward.The tension in the string is equal to :

Answer:

As we learned

Newton's 2nd Law -

$F=ma$

Apply the concept of pseudo force as shown in the below figure

Applying Newton's law perpendicular to string $mg\sin \theta =ma\cos \theta$

$\Rightarrow \tan \theta =\frac{a}{g}$
Applying Newton's law along string,

$\begin{array}{rl}& T-mg\cos \theta -ma\sin \theta =ma\\ & \Rightarrow T=m\sqrt{g^2+a^2}+ma\end{array}$