NCERT Class 11 Physics Chapter 7 notes System of Particles and Rotational Motion - Download PDF

NCERT Notes for Class 11 Physics Chapter 6: Download PDF

System of Particles and Rotational Motion Class 11 Notes come in a well-organised and easy-to-download PDF format to enable students to study efficiently. These brief notes have clear explanations, formulae, and examples that have been solved, and thus, a last-minute preparation is fast and efficient. The downloadable PDF makes access easy anytime, such that the students are able to reinforce their mastery and enhance their performance in examinations such as CBSE, JEE, and NEET.

Download PDF

System of Particles and Rotational Motion Class 11 Notes

The NCERT Notes for Class 11 Physics Chapter 6 present an explanation of key physics concepts in a simplified form with having structured format. To simplify and shorten the revision time, these notes contain the summaries of the major derivations, formulas, and examples. Prepared in line with the current CBSE Class 11 Physics syllabus, they assist the students in enhancing clarity and being more precise in the context of preparing to take board as well as JEE/NEET exams.

Rotational Motion

• Rotational motion describes the movement of an object as it spins or revolves around an axis. Consider a spinning top, a rotating wheel, or the Earth turning on its axis; these are all examples of rotational motion.
• In this type of motion, each point in the object follows a circular path around a fixed line known as the axis. The motion is a rotation rather than a linear translation.

Centre of Mass

• The centre of mass is an imaginary point in a system where all of the system's mass is concentrated. When two bodies are joined, their centre of mass is along the line that connects them.

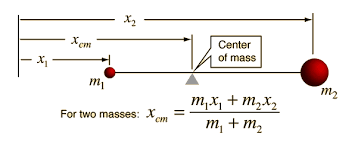
(Here, m1 & m2 are two bodies in which m1 is at a distance x1, & m2 at a distance x2 from the origin O).

• The coordinates of a system's centre of mass (X, Y, Z) are generally given by $\sum \frac{m_i \vec{r}_i}{m}$
• Considering a thin rod of length $l$, the origin is at the geometric centre of the rod. and the X-axis is along the length of the rod, and for every element dm of the rod at x, there is an element of the same mass dm located at x.

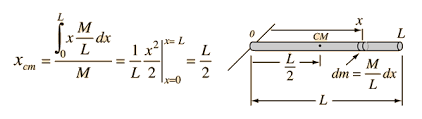
• The total contribution of each such integral and the integral x dm is zero. Therefore, the COM coincides with its geometric centre.

• The centre of mass coincides with the geometric centre, and with the same geometry applies to homogenous rings, discs, spheres, or even thick rods of circular or rectangular cross-sections;

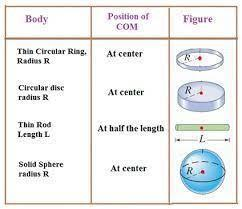
Motion of COM

• The centre of mass of a system of particles moves in a manner such that the entire mass of the system is considered to be concentrated at the centre, and all external forces are treated as if they act solely on that point.

$M \vec{R}=\sum m_i \overrightarrow{r_i}=m_1 \overrightarrow{r_1}+m_2 \overrightarrow{r_2}+\ldots \ldots m_n \overrightarrow{r_n}$$$

Differentiating w.r.t. time, we get,

$\begin{aligned} M \frac{\overrightarrow{d R}}{d t} & =m_1 \frac{\overrightarrow{d r_1}}{d t}+m_2 \frac{\overrightarrow{d r_2}}{d t}+\ldots \ldots m_n \frac{\overrightarrow{d r_n}}{d t} \\ M \vec{v} & =m_1 \overrightarrow{v_1}+m_2 \overrightarrow{v_2} \ldots \ldots+m_n \overrightarrow{v_n}\end{aligned}$$\begin{array}{r}\end{array}$

Again, differentiating w.r.t. time, we get,

$\begin{aligned} & M \vec{a}=m_1 \overrightarrow{a_1}+m_2 \overrightarrow{a_2} \ldots \ldots+m_n \overrightarrow{a_n} \\ & M \vec{a}=\overrightarrow{F_{\text {ext }}}\end{aligned}$

• Instead of considering extended bodies as single particles, we can consider them as systems of particles.

• The translational component of their motion could be attained by taking the mass of the whole system and all the external forces on the system to be acting at the centre of mass.

Linear Momentum of a System of Particles

• The linear momentum of a system of particles is the product of the system's total mass and the velocity of its centre of mass. This relationship is expressed as follows:
• Linear Momentum=Total Mass×Velocity of Center of Mass

$\begin{aligned}
&\begin{aligned}
& \vec{p}=\vec{p}_1+\vec{p}_2+\ldots+\vec{p}_n \\
& \vec{p}=\mathrm{m} 1 \vec{v}_1+\mathrm{m} 2 \vec{v}_2+\ldots+\mathrm{mn} \vec{v}_n \\
& \vec{p}=M \vec{v}
\end{aligned}\\
&\text { Where } \vec{p}=\text { Momentum particles and } \vec{v}=\text { Velocity of COM }
\end{aligned}$

• Newton's Second Law of Motion, in reference to the system of particles, is represented by the following expression:

$\frac{\overrightarrow{d p}}{d t}=\vec{F}_{e x t}$$\frac{\stackrel{}{}}{}$

• In case when the total external force acting on a system of particles is zero $\left(\vec{F}_{\text {ext }}=0\right)$, then, in that case, the total linear momentum of the system is constant and can be represented as:

$(\frac{\overrightarrow{d p}}{d t}=0 ; \vec{p}=$ constant $)$

• The Centre of mass having velocity also remains constant (Since $\vec{p}=m \vec{v}=$ Constant).

• If the total external force on a body is zero, then the internal forces cause complex trajectories of individual particles in spite of the COM moving with a constant velocity.

Angular Velocity & Linear Velocity

• Each particle of a rotating body is considered to move in a circle. We define the angular displacement of a given particle about its centre in unit time as angular velocity.

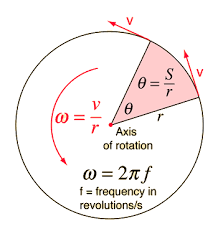
• Average angular velocity =∆θ/∆t
• Instantaneous angular velocity, ω=dθ/dt
• In a pure rotation motion, all the parts of the moving body have the same angular velocity.
• It is a vector quantity
• $\vec{v}=\vec{\omega} \times \vec{r}$; where $\vec{v}$ is the linear velocity of a particle and r is the radius of the circle​​​​​​.$\stackrel{}{}$
  $\stackrel{}{}$
• Angular acceleration is outlined as the rate of change of angular speed with respect to time. $\vec{\alpha}=\frac{\overrightarrow{d \omega}}{d t}$$\frac{\stackrel{}{}}{}$

Torque & Angular Momentum

• The rotational analogue of force is a moment of force, which is also known as Torque.

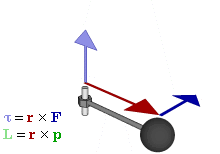
• Torque is a vector quantity.

Equilibrium of a Rigid Body

• The translational state of the motion of the rigid body is due to the changes in force, i.e. its total linear momentum changes.

• The rotational state of motion of the rigid body is due to the changes in torque, i.e. the total angular momentum of the body changes.

• Unless stated otherwise, only external forces and torques should be dealt.

• A rigid body is said to be in mechanical equilibrium when both its linear momentum and angular momentum are constant with time. This means

Total force zero = Translational Equilibrium

Total torque zero = Rotational Equilibrium

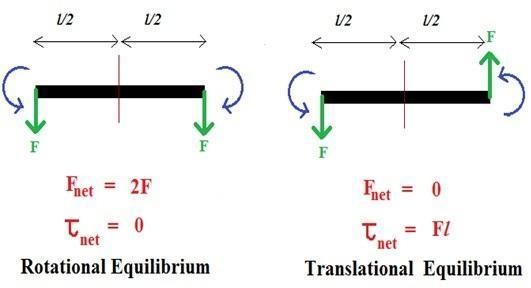
• A couple or torque can be defined as a pair of equal and opposite forces with different lines of action is termed a couple or torque.
• Without translation, the couple can produce the rotation. For example, when you open the lid of a jar, you put a couple on it.

Centre of Gravity

• The centre of gravity of a body is the point on the body where the total gravitational torque on the body is zero.
• In uniform gravity or gravity-free space, the centre of gravity of the body coincides with the centre of mass.
• The condition for the centre of gravity and centre of mass will not coincide is that if the value of g varies from part to part of the body.

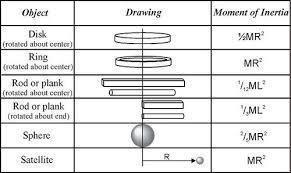
Moment of Inertia

• Moment of inertia (I) is the analogue of mass in rotational motion.
• A change in rotational motion is resisted by the moment of inertia about a given axis of rotation. It can be regarded as a measure of rotational inertia of the body.
• It is a measure of how the different parts of the body are distributed at different distances from the axis.
• The moment of inertia of a rigid body depends on the mass of the body, its form and size, and therefore the distribution of mass concerning the axis of rotation.

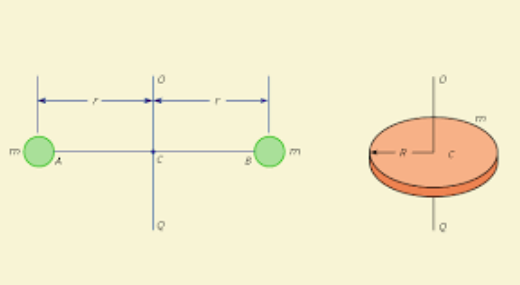
• The radius of gyration of a body with respect to an axis is defined as the distance from the axis of a mass whose mass is up to the mass of the total body and whose moment of inertia is up to the moment of inertia of the body concerning the axis.

I = Mk2, where k is the radius of gyration.

The Theorem of Perpendicular Axis

• Perpendicular Axis Theorem: The moment of inertia of a two-dimensional body (lamina) regarding an axis perpendicular to its plane is the sum of its moments of inertia regarding two perpendicular axes synchronous with the perpendicular axis and lying within the plane of the body.

• It is applicable only to planar bodies.

The Theorem of Parallel Axis

• Parallel Axis Theorem: The moment of inertia of a body about an axis parallel to an axis passing through the centre of mass is equal to the sum of the moment of inertia of the body about an axis passing through the centre of mass and the product of mass & square of the distance between the two axes. This theorem is applicable to a body of any form.

Kinematics of Rotational Motion for a Fixed Axis

We can derive equations of motion similar to translational motion.

Translational motion

v=v_o+at

x=x_o+v_ot+0.5at²

v²=v_o²+2as

Rotational Motion

ω=ω_o+αt

θ=θ_o+ω_ot+0.5αt²

ω²=ω_o²+2αθ

Dynamics of Rotational Motion for a Fixed Axis

• The components of torques are considered along the direction of the fixed axis, and this is so because the component of the torque is perpendicular to the axis of rotation, and this will tend to turn the axis from its position.
• The forces that lie in planes perpendicular to the axis are only considered. Forces parallel to the axis give torques perpendicular to the axis.
• Also, the components of the position vectors which are perpendicular to the axis are only considered. Components of position vectors on the axis can lead to torques perpendicular to the axis.

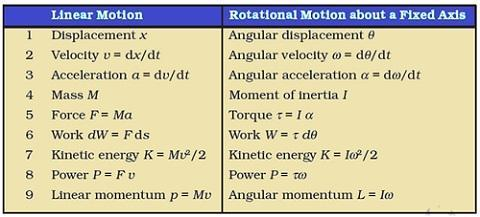
Class 11 Physics Chapter 6 System of Particles and Rotational Motion: Previous Year Question and Answer

System of Particles and Rotational Motion Previous Year Questions and Answers encourage students to have knowledge of the kind of questions that could be asked in board and competitive exams. These answered questions provide an understanding of some critical concepts, derivations, and numerical trends of previous papers. Their practice enhances the preparation for exams and confidence in achieving high marks in Class 11 Physics, JEE, and NEET.

Q1: The net external torque on a system of particles about an axis is zero. Which of the following are compatible with it?

a) The forces may be acting radially from a point on the axis

b) The forces may be acting on the axis of rotation

c) The forces may be acting parallel to the axis of rotation

d) The torque caused by some forces may be equal and opposite to that caused by other forces

Answer:

Torque is given by $\vec{\tau}=\vec{r} \times \vec{F}$
Or
$\tau=r F \sin \theta \hat{n}$ where $\theta$ is the angle between both the vectors and $\hat{n}$ is the unit vector perpendicular to the plane of $\vec{r}$ and $\vec{F}$
1. When the force is acting radially in the direction of $\vec{r}, \theta=0$
$\ tau=r F sin 0=0 $

2. $\text{When the forces are acting on the axis of rotation, then}$ $\theta=0$ $ \text{and thus}$ $\tau=0$
3. The component of forces in the plane of $\vec{r}$ and $\vec{F}$ when they are parallel to the axis of rotation is $F \cos 90^{\circ}$, which is equal to 0 . Hence $\tau=0$
4. When torques are equal in magnitude but opposite in direction, the net resultant is 0.

Hence, the answers are options (a) and (b).

Q2: A Merry-go-round, made of a ring-like platform of radius $R$ and mass $M$, is revolving with angular speed $\omega$$$. A person of mass $M$ is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round afterwards is

Answer:

As no external torque acts on the system, angular momentum should be conserved.
Hence. $I \omega=$ constant ,
where $I$ is the moment of inertia of the system and $\omega$ is the angular
velocity of the system.
From Eq. (i), $I_1 \omega_1=I_2 \omega_2$
(where $\omega_1$ and $\omega_2$ are angular velocities before and after jumping)

$
\Rightarrow I \omega=\frac{I}{2} \times \omega_2
$

(As mass is reduced to half, hence moment of inertia is also reduced to half)

$
\Rightarrow \omega_2=2 \omega
$

Q3: Which of the following points A, B and C is the likely position of the centre of mass of the system shown in Fig. 7.1?

Answer:

The volume of the hollow sphere is occupied equally by the air and sand. Since the pressure exerted by the air region is less than that of sand, the mass of sand is greater than the air. The centre of mass shifts towards a heavier portion, which in this case is sand. B is exactly at the line dividing air and sand, so it is incorrect. D is at the farthest end and divides the sand area very unequally, so it also cancels out. C is almost at the centre with regard to the mass.

Importance of Class 11 Physics Chapter 6 System of Particles and Rotational Motion Notes

Class 11 Physics Chapter 6 System of Particles and Rotational Motion Notes play an essential role in the foundation of good work on mechanics. They make complex concepts such as torque, angular momentum, and rotational dynamics easier to comprehend by presenting brief explanations and solved problems. The notes allow students to understand theoretical and numerical knowledge effectively, and they are very useful in preparing for the CBSE examination, the JEE, and the NEET.

Clear Understanding of Fundamentals

• Systems of particles, centre of mass, and rotational motion are described in a simplified form by the NCERT Notes for Class 11 Physics Chapter 6, which allow students to construct a strong conceptual clarity.

Time-Saving for Revision

• Properly organised System of Particles and Rotational Motion Class 11 Notes save time when it comes to last-minute revision, as all the formulas, derivations, and important definitions are consolidated in a single location.

Increases Board Exam Prep

• These are the notes that are prepared in accordance with the recent NCERT syllabus, and they assist students in receiving higher marks in CBSE Class 11 Physics exams.

Competitive Exam Readiness

• These NCERT Notes for Class 11 Physics Chapter 6 notes are highly relevant for JEE Main, JEE Advanced, NEET, and other competitive exams, as topics like torque, angular momentum, and equilibrium frequently appear in the question papers.

Easy Formula Retention

• All significant formulae of rotational motion, moment of inertia, and centre of mass can be found, and students find it easy to revise and memorise.

Application-Based Learning

• NCERT Notes for Class 11 Physics Chapter 6 relate theory to applied applications such as the motion of planets, spinning objects, and rolling motion in real life, making learning more interactive.

Error-Free Learning Resource

• Since the notes are based on NCERT Class 11 Physics, students can trust them as authentic and reliable study material.

NCERT Class 11 Notes Chapter-Wise

NCERT Class 11 Notes Chapter-Wise contain brief, clearly organised and simple summaries of every chapter. These are notes on major concepts, formulas, derivations and diagrams as per the newest CBSE syllabus that enable students to revise quickly. They are of great utility in board exams and also in competitive exams as JEE and NEET.

Subject-Wise NCERT Exemplar Solutions

• NCERT Exemplar Class 11 Solutions
• NCERT Exemplar Class 11 Maths
• NCERT Exemplar Class 11 Physics
• NCERT Exemplar Class 11 Chemistry
• NCERT Exemplar Class 11 Biology

Subject-Wise NCERT Solutions

• NCERT Solutions for Class 11 Mathematics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 11 Biology

NCERT Books and Syllabus