NCERT Solutions for Class 11 Physics Chapter 6 System Of Particles And Rotational Motion
When a rubber ball is compressed, it alters its shape; when a metal rod is bent under pressure, it becomes deformed. In Physics, however, to make things simpler, we frequently consider such objects to be rigid bodies that neither change shape in response to forces exerted on them. With this assumption, we could simplify the study of their motion. Chapter 6, Class 11 Physics System of Particles and Rotational Motion presents students with some of the most significant concepts of mechanics, such as: torque, angular momentum, moment of inertia, and rotational dynamics. These principles are the foundation of the knowledge of motion and rotation of bodies in the real world.
This Story also Contains
- System of Particles and Rotational Motion Class 11 Question Answers: Download PDF
- System of Particles and Rotational Motion NCERT Solutions: Exercise Questions
- System of Particles and Rotational Motion NCERT Solutions: Higher Order Thinking Skills (HOTS) Questions
- Class 11 Physics Chapter 6 - System of Particles and Rotational Motion: Topics
- System of Particles and Rotational Motion NCERT Solutions: Key Formulas
- Approach to Solve Questions of Class 11 Physics Chapter 6 - System of Particles and Rotational Motion
- Importance of NCERT Solutions for Class 11 Physics Chapter 6: System of Particles and Rotational Motion
- What Students Learn from NCERT Solutions for Class 11 Physics Chapter 6: System of Particles and Rotational Motion?
- What Extra Should Students Study Beyond NCERT for JEE/NEET
- NCERT Solutions for Class 11 Physics Chapter-Wise
NCERT Solutions for Class 11 Physics Chapter 6 - System of Particles and Rotational Motion are well organised and prepared by subject experts so that they can give a step-by-step explanation of all concepts, derivations, formulas and numerical problems. These resources, which contain NCERT solutions to in-text and exercise questions in detail, simplify even complex concepts further and allow understanding and application. The chapter is very important not only to CBSE board exams but also to competitive exams such as JEE and NEET, where questions on rotational motion are often asked. Regular practice with NCERT Solutions for Class 11 Physics Chapter 6 - System of Particles and Rotational Motion assists the students to improve upon their basics, perform well in school examinations, and gain a strong foundation to continue their education in physics.
System of Particles and Rotational Motion Class 11 Question Answers: Download PDF
The Class 11 Physics Chapter 6 - System of Particles and Rotational Motion question answers provide solutions to all the questions in the book, and teach students what the centre of mass is, how torque and angular momentum work, and what determines the rotational dynamics. The PDF version can be downloaded and works well in helping to revise as well as prepare for both board exams and competitive exams like JEE and NEET.
System of Particles and Rotational Motion NCERT Solutions: Exercise Questions
System of Particles and Rotational Motion class 11 question answers enable the students to understand the important concepts such as centre of mass, torque, angular momentum and rotational dynamics. These are step-wise class 11 physics chapter 6 System of Particles and Rotational motion question answers that will help understand concepts, sharpen problem-solving and also equip students for school tests and competitive exams such as JEE and NEET.
Answer:
For uniform mass density, the location of the centre of mass is the same as that of the geometric centre.
No, it is not necessary that the centre of mass lies inside the body. For example, in the case of a ring, the centre of mass is outside the body.
Answer:
Let us assume that the centre of mass of the molecule is x cm away from the chlorine atom.
So, we can write
$\frac{m\left ( 1.27\ -\ x \right )\ +\ 35.5mx}{m\ +\ 35.5 }\ =\ 0$
or $x\ =\ \frac{-1.27}{\left ( 35.5-1 \right )}\ =\ -\ 0.037 Å$
Here negative sign indicates that the centre of mass lies leftward of the chlorine atom.
Answer:
Since the child and trolley are considered in a system, the speed of the centre of mass changes only when an external force acts on the system. When the child starts to move on the trolley, the force produced is the internal force of the system, so this will produce no change in the velocity of the CM.
Answer:
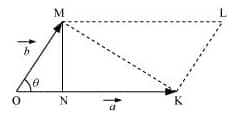
Let a and b be two vectors having an angle $\theta$ between them.
Consider $\Delta$ MON,
$\sin \theta \ =\ \frac{MN}{MO}$
or $\sin \theta \ =\ \frac{MN}{|\vec{b}|}$
or $MN\ =\ b\sin \theta$
$\left | \vec{a}\times \vec{b} \right |\ =\ \left | \vec{a} \right |\left | \vec{b} \right |\sin \theta$= 2 (Area of $\Delta$ MOK)
Therefore the area of $\Delta$ MOK = One half of $\left | \vec{a}\times \vec{b} \right |$ .
Answer:
A parallelepiped is shown in the figure given below:-
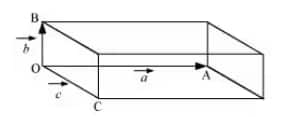
Volume is given by: abc
We can write :
$|\vec{b}\times \vec{c}|\ =\ |\vec{b}||\vec{c}|\sin \theta\ \widehat{n}$ (The direction of $\widehat{n}$ is in the direction of vector $\vec{a}$)
$\Rightarrow |\vec{b}\times \vec{c}|=\ |b||c|\sin 90^{\circ}\ \widehat{n}$
$\Rightarrow |\vec{b}\times \vec{c}|=\ |b||c|\ \widehat{n}$
Now,
$\vec{a}.(\vec{b}\times \vec{c})\ =\ \vec{a}.(bc)\ \widehat{n}$
$=\ abc \cos \theta$
$=\ abc \cos 0^{\circ}$
$=\ abc$
This is equal to the volume of a parallelepiped.
Q6.6 Find the components along the $x,y,z$ axes of the angular momentum $1$ of a particle, whose position vector is $\vec{r}$ with components $x,y,z$ and momentum is $\vec{p}$ with components $p_{x}$, $p_{y}$ and $p_{z}$. Show that if the particle moves only in the $x-y$ plane, the angular momentum has only a z-component.
Answer:
Linear momentum of a particle is given by :
$\overrightarrow{p}\ =\ p_x \widehat{i}\ +\ p_y \widehat{j}\ +\ p_z \widehat{k}$
And the angular momentum is :
$\overrightarrow{l}\ = \overrightarrow{r}\times \overrightarrow{p}$
$\Rightarrow \overrightarrow{l}\ = \left ( x \widehat{i}\ +\ y \widehat{j}\ +\ z \widehat{k} \right ) \times \left ( p_x \widehat{i}\ +\ p_y \widehat{j}\ +\ p_z \widehat{k} \right )$
$\Rightarrow \overrightarrow{l}\ =\begin{vmatrix} i &j &k \\ x &y &z \\ P_x &P_y &P_z \end{vmatrix}$
$\Rightarrow \overrightarrow{l}\ =\ \widehat{i}\left ( yp_z - zp_y \right )\ -\ \widehat{j}\left ( xp_z - zp_x \right )\ +\ \widehat{k}\left ( xp_y - yp_x \right )$
When a particle is confined to the x-y plane, then z = 0 and pz = 0.
When we put the value of z and p z in the equation of linear momentum, then we observe that only the z component is non-zero.
Answer:
Assume two points (say A, B) separated by distance d.
So the angular momentum of a point about point A is given by: $=\ mv \times d\ =\ mvd$
And about point B : $=\ mv \times d\ =\ mvd$
Now, assume a point between A and B as C, which is at a distance y from point B.
Now the angular momentum becomes : $=\ mv \times \left ( d-y \right )\ +\ mv \times y=\ mv d$
Thus, it can be seen that angular momentum is independent of the point about which it is measured.
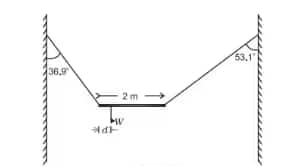
Answer:
The FBD of the given bar is shown below :
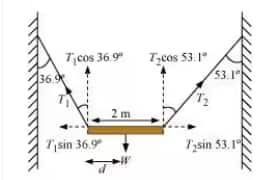
Since the bar is in equilibrium, we can write :
$T_1 \sin 36.9 ^{\circ}\ =\ T_2 \sin 53.1 ^{\circ}$
or $\frac{T_1}{T_2}\ =\ \frac{0.800}{0.600}\ =\ \frac{4}{3}$
or $T_1\ =\ \frac{4}{3}T_2$ .....................................................(i)
For the rotational equilibrium :
$T_1 \cos 36.9 ^{\circ}\times d\ =\ T_2 \cos 53.1 ^{\circ}\times \left ( 2-d \right )$ (Use equation (i) to solve this equation)
or $d\ =\ \frac{1.2}{1.67}\ =\ 0.72\ m$
Thus, the centre of gravity is at 0.72 m from the left.
Answer:
The FBD of the car is shown below :
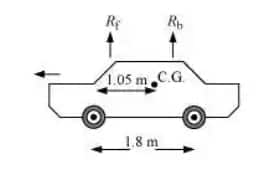
We will use the conditions of equilibrium here :
$R_f\ +\ R_b\ =\ mg$
$\Rightarrow \ 1800\times 9.8\ =\ 17640\ N$ ....................................(i)
For rotational equilibrium :
$R_f\left ( 1.05 \right )\ =\ R_b(1.8-1.05)$
or $1.05R_f\ =\ 0.75R_b$
$R_b\ =\ 1.4R_f$ ..............................(ii)
From (i) and (ii) we get :
$R_f\ =\ \frac{17640}{2.4}\ =\ 7350\ N$
and $R_b\ =\ 17640-7350\ =\ 10290\ N$
Thus force exerted by the front wheel is = 3675 N
and force exerted by the back wheel = 5145 N.
Answer:
The moment of inertia of a hollow cylinder is given by $=\ mr^2$
And the moment of inertia of a solid cylinder is given by: $=\ \frac{2}{5}mr^2$
We know that : $\tau \ =\ I\alpha$
Let the torque for the hollow cylinder be $\tau_1$ and for the solid cylinder let it be $\tau_2$.
According to the question : $\tau_1\ =\ \tau_2$
So we can write the ratio of the angular acceleration of both objects.
$\frac{\alpha _2}{\alpha _1}\ =\ \frac{I_1}{I_2}\ =\ \frac{mr^2}{\frac{2}{5}mr^2}\ =\ \frac{2}{5}$
Now for angular velocity,
$\omega \ =\ \omega _o\ +\ \alpha t$
Clearly, the angular velocity of the solid sphere is more than the angular velocity of the hollow sphere. (As the angular acceleration of a solid sphere is greater).
Answer:
Firstly, we will calculate the moment of inertia of the solid cylinder:
$I_c =\ \frac{1}{2}mr^2$
$\Rightarrow I_c=\ \frac{1}{2}(20)(0.25)^2\ =\ 0.625\ Kg\ m^2$
So the kinetic energy is given by :
$E_k = \frac{1}{2}I\omega ^2= \frac{1}{2}\times (6.25)\times (100) ^2=3125J$
And the angular momentum is given by: $= I\omega= 0.625\times 100= 62.5 Js$
Answer:
We are given the initial angular speed and the relation between the moment of inertia of both cases.
Here, we can use conservation of angular momentum as no external force is acting on the system.
So we can write :
$I_1w_1\ =\ I_2w_2$
$w_2 = \frac{I_1w_1}{I_2}= \frac{I(40)}{\frac{2}{5}I}$
$w_2 =\ 100\ rev/min$
Answer:
The final and initial velocities are given below :
$E_f\ =\ \frac{1}{2}I_2w_2^2$ and $E_i\ =\ \frac{1}{2}I_1w_1^2$
Taking the ratio of both, we get,
$\frac{E_f}{E_i}\ =\ \frac{\frac{1}{2}I_2w_2^2}{\frac{1}{2}I_1w_1^2}$
or $\frac{E_f}{E_i}=\ \frac{2}{5}\times \frac{100\times 100}{40\times40}$
or $\frac{E_f}{E_i}=\ 2.5$
Thu,s the final energy is 2.5 times the initial energy.
The increase in energy is due to the internal energy of the boy.
Answer:
The moment of inertia is given by :
$I\ =\ mr^2$
or $I=\ 3\times (0.4)^2\ =\ 0.48\ Kg\ m^2$
And the torque is given by :
$\tau \ =\ r\times F=\ 0.4\times 30\ =\ 12\ Nm$
Also, $\tau\ =\ I\alpha$
So $\alpha \ =\ \frac{\tau }{I}\ =\ \frac{12}{0.48}\ =\ 25\ rad/s^{-2}$
And the linear acceleration is $a\ =\ \alpha r\ =\ 0.4\times 25\ =\ 10\ m/s^{-2}$
Answer:
The relation between power and torque is given by :
$P\ =\ \tau \omega$
or $P=\ 180\times 200\ =\ 36000\ W$
Hence, the required power is 36 KW.
Answer:
Let the mass per unit area of the disc be $\sigma$.
So total mass $=\ \pi r^2\sigma\ =\ m$
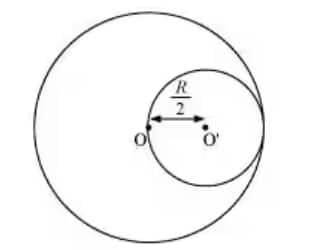
Mass of the smaller disc $=\ \pi \left ( \frac{r}{2} \right )^2\sigma\ =\ \frac{m}{4}$
Now, since the disc is removed, we can assume that part to have negative mass with respect to the initial condition.
So, the centre of mass of the disc is given by the formula :
$x\ = \frac{m_1r_1\ +\ m_2r_2}{m_1\ +\ m_2}$
Or $x=\ \frac{m\times 0\ -\ \frac{m}{4}\times \frac{r}{2}}{m\ -\ \frac{m}{4}}$
Or, $x=\ \frac{-r}{6}$
Hence, the centre of mass is shifted $\frac{r}{6}$ leftward from point O.
Answer:
The centre of mass of the meter stick is at 50 cm.
Let the mass of the meter stick be m.
Now, according to the situation given in the question, we will use the rotational equilibrium condition at the centre point of the meter stick.
$10g(45 - 12)\ -\ mg(50 - 45)\ =\ 0$
or $m\ =\ \frac{10\times 33}{5}\ =\ 66\ g$
Thus, the mass of the meter stick is 66 g.
Answer:
We are given the moment of inertia and the velocity of the molecule.
Let the mass of an oxygen molecule be m.
So the mass of each oxygen atom is given by: $\frac{m}{2}$
Moment of inertia is :
$I\ =\ \frac{m}{2}r^2\ +\ \frac{m}{2}r^2\ =\ mr^2$
or $r\ =\ \sqrt{\frac{I}{m}}$
or $r\ =\ \sqrt{\frac{1.94\times 10^{-46}}{5.36\times 10^{-26}}}\ =\ 0.60\times 10^{-10}\ m$
We are given that :
$E_{rot}\ =\ \frac{2}{3}E_{tra}$
or $\frac{1}{2}I\omega ^2\ =\ \frac{2}{3}\times \frac{1}{2}mv^2$
or $\omega \ =\ \sqrt{\frac{2}{3}}\times \frac{v}{r}$
or $\omega=\ 6.80\times 10^{12}\ rad/s$
System of Particles and Rotational Motion NCERT Solutions: Higher Order Thinking Skills (HOTS) Questions
The Higher Order Thinking Skills (HOTS) questions of Class XII Physics Chapter 6: System of Particles and Rotational Motion are developed in such a way that they enhance theoretical knowledge, as well as assess the application of learning. These questions can be much more than simple problem-solving ones, and invite the students to analyse, evaluate and apply concepts of rotational motion and centre of mass to new and complicated scenarios, which are perfect to practice a competitive exam such as JEE.
Question 1) A solid sphere of mass $M$ and radius $R$ is rolling without slipping with a velocity $v_0$ on a horizontal surface. It encounters an inclined plane making an angle $\theta$ with the horizontal. Assuming no energy loss due to friction, find the maximum height $h$ the sphere will reach before coming to rest.
1) $
\frac{5 v_0^2}{6 q_2}
$
2) $
\frac{3 v_0^2}{4 g}
$
3) $
\frac{7 v_0^2}{10 g}
$
4) $
\frac{v_0^2}{2 g}
$
Answer:
For a rolling solid sphere, the total kinetic energy is the sum of translational and rotational kinetic energy:
$
E_{\text {total }}=K E_{\text {translational }}+K E_{\text {rotational }} \\$
$K E_{\text {total }}=\frac{1}{2} M v_0^2+\frac{1}{2} I \omega^2
$
For a solid sphere, the moment of inertia about its centre is:
$
I=\frac{2}{5} M R^2
$
Using the rolling without slipping condition, $v_0=R \omega$, so:
$
\omega=\frac{v_0}{R}
$
Substituting $I$ and $\omega$ :
$
\begin{aligned}
K E_{\text {rotational }} & =\frac{1}{2} \times \frac{2}{5} M R^2 \times\left(\frac{v_0}{R}\right)^2 \\
& =\frac{1}{5} M v_0^2
\end{aligned}
$
So, the total kinetic energy:
$
K E_{\text {total }}=\frac{1}{2} M v_0^2+\frac{1}{5} M v_0^2 \\$
$K E_{\text {total }}=\frac{5}{10} M v_0^2+\frac{2}{10} M v_0^2=\frac{7}{10} M v_0^2
$
At maximum height, all kinetic energy converts into gravitational potential energy:
$
P E=M g h
$
Equating energy:
$
\begin{gathered}
\frac{7}{10} M v_0^2=M g h \\
h=\frac{7 v_0^2}{10 g}
\end{gathered}
$
Hence, the answer is option (3).
Question 2) A rod starts rotating with angular velocity $\omega_o$, but due to viscous force, its angular speed starts decreasing with variable retardation: $\alpha=-c \omega$. Find out the angle traversed by the rod as a function of time.
1) $
\theta=2 \frac{\omega_0}{c}\left[1-e^{-c t}\right]
$
2) $
\theta=\frac{\omega_0}{c}\left[1-e^{-c t}\right]
$
3) $
\theta=\frac{\omega_0}{2 c}\left[1-e^{-c t}\right]
$
4) $
\theta=\frac{\omega_0}{3 c}\left[1-e^{-c t}\right]
$
Answer:
We know
$
\begin{aligned}
& \alpha=-c \omega \\
& \frac{d \omega}{d t}=-c \omega \\
& \Rightarrow \int_{a_0}^\omega \frac{d \omega}{\omega}=-\int_0^t c d t \\
& \ln \frac{\omega}{\omega_0}=-c t \\
& \Rightarrow \omega=\omega_0 e^{-c t} \\
& \Rightarrow \quad \frac{d \theta}{d t}=\omega_0 e^{-c t} \\
& \Rightarrow \int_0^\theta d \theta=\omega_0 \int_0^t e^{-c t} d t \\
& \Rightarrow \quad \theta=\frac{\omega_0}{c}\left[1-e^{-c t}\right]
\end{aligned}
$
Hence, the answer is option (2).
Question 3) A wedge of mass M=2kg carries two blocks A and B, as shown in the figure. Block A lies on a smooth-incline surface of the wedge inclined at an angle $\theta$ to the horizontal. B lies inside a horizontal groove made in the wedge. The two blocks have m=1kg each and are connected by a light string. Length of the groove is $l$=2m as shown. The entire system is released from rest. What is the distance travelled by the wedge (in m) on the smooth horizontal surface by the time block B comes out of the groove?
Answer:
Let the displacement of the wedge be $x$ towards the right. Displacement of $B=(x-1)$ towards right.
Displacement of A w.r.t wedge (on the incline) is $l$.
$\therefore$ Displacement of A in horizontal direction $=l \cos \theta+x$
The COM of the entire system suffers no displacement in the horizontal direction.
$
\begin{aligned}
& \therefore \Delta x_{\mathrm{COM}}=0 \\
& \Rightarrow m_1 \Delta x_1+m_2 \Delta x_2+m_3 \Delta x_3=0 \\
& \Rightarrow M \cdot x+m(x-l)+m(l \cos \theta+x)=0 \\
& \Rightarrow x=\frac{m l(1-\cos \theta)}{M+2 m}
\end{aligned}
$
Now, putting $\mathrm{m}=1 \mathrm{~kg}, \mathrm{M}=2 \mathrm{kgI}=2 \mathrm{~m}$ and $\theta=60^{\circ}$ in (i), we get
$
\begin{aligned}
& x=\frac{1 \times 2\left(1-\cos 60^{\circ}\right)}{2+2 \times 1} \\
& x=0.25 \mathrm{~m}
\end{aligned}
$
Hence, the answer is 0.25.
Question 4)
A sphere is released on a smooth inclined plane from the top. When it moves down, its angular momentum is:
1) Conserved about every point
2) Conserved about the point of contact only
3) Conserved about the centre of the sphere only
4) Conserved about any point on a line parallel to the inclined plane and passing through the centre of the ball.
Answer:
As the inclined plane is smooth, the sphere can never roll; rather, it will just slip down. Hence, the angular momentum remains conserved at any point on a line parallel to the inclined plane and passing through the centre of the ball.
Hence, the answer is option (4).
Question 5) A square plate of mass $m$ and length $l$ is rotated with angular velocity $w$ with a vertical axis passing through its centre, and it is kept on a rough surface. It takes ' $t_0$ ' time to stop because of uniform friction. Now if we hinge it at the corner & give the same angular velocity, in $k t_0$ time it will take to stop, find $k$.
Answer:
The torque by friction will be $\tau$ = Cμmgl and moment of inertia will be,$I=k m l^2$
$\tau$= Iα
Hence, angular acceleration will be
$\alpha=\frac{C \mu g}{k}\left(\frac{1}{l}\right)$
$\Rightarrow \alpha$ is inversely proportional to $l$
Now, as it is hinged at one corner, we can assumea plate of double-sided length
Now this is again the central axis, the value of angular acceleration will be half.
Hence, it will take $2t_0$ time to stop.
Hence, the answer is 2.
Class 11 Physics Chapter 6 - System of Particles and Rotational Motion: Topics
In Class 11 Physics Chapter 6 - System of Particles and Rotational Motion, the topics that are covered deal with centre of mass, motion of a system of particles, torque, angular velocity, angular momentum and rotational dynamics. These topics constitute the basis of learning complex physical systems and are of great value in board exams and competitive exams such as JEE and NEET.
6.1 Introduction
6.1.1 What Kind Of Motion Can A Rigid Body Have?
6.2 Centre Of Mass
6.3 Motion Of the Centre Of Mass
6.4 Linear Momentum Of A System Of Particles
6.5 Vector Product Of Two Vectors
6.6 Angular Velocity And Its Relation With Linear Velocity
6.6.1 Angular Acceleration
6.7 Torque And Angular Momentum
6.7.1 Moment Of Force (Torque)
6.7.2 Angular Momentum Of A Particle
6.8 Equilibrium Of A Rigid Body
6.8.2 Centre Of Gravity
6.9 Moment Of Inertia
6.10 Kinematics Of Rotational Motion About A Fixed Axis
6.11 Dynamics Of Rotational Motion About A Fixed Axis
6.12 Angular Momentum In Case Of Rotation About A Fixed Axis
6.12.1 Conservation Of Angular Momentum
System of Particles and Rotational Motion NCERT Solutions: Key Formulas
System of Particles and Rotational Motion class 11 question answers: Key Formulas include important equations related to centre of mass, torque, moment of inertia, angular momentum, and rotational kinetic energy. These formulas act as quick revision tools and help students solve numerical problems efficiently in exams like CBSE, JEE, and NEET.
1. Centre of mass
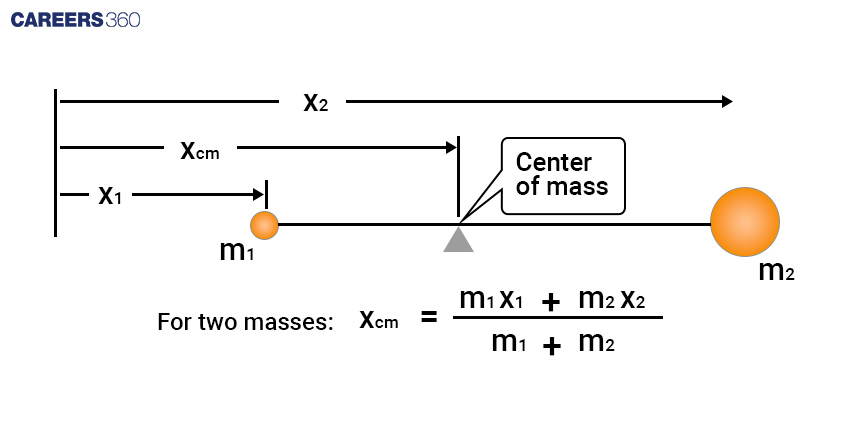
For a system of particles: $\vec{R}_{\mathrm{COM}}=\frac{\sum m_i \vec{r}_i}{\sum m_i}$
2. Motion of COM
$M=\sum m_i \\$
$\vec{v}_{\mathrm{cm}}=\frac{\sum m_i \vec{v}_i}{M}$
$\vec{p}_{\mathrm{cm}}=M \vec{v}_{\mathrm{cm}}$
$\vec{a}_{\mathrm{cm}}=\frac{\vec{F}_{\mathrm{ext}}}{M}$
3. Angular Velocity & Linear Velocity
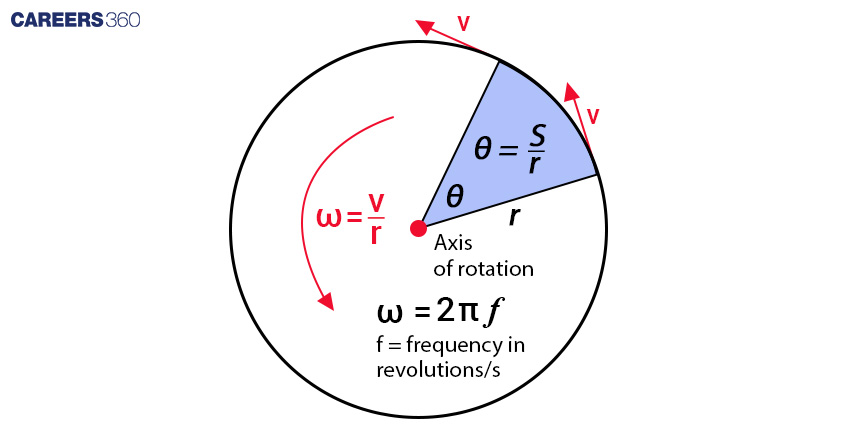
Average angular velocity =∆θ/∆t
Instantaneous angular velocity, ω=dθ/dt
4. Moment of Inertia (MI)
$\begin{aligned} & I=\sum m_i r_i^2 \text { (Discrete system) } \\ & I=\int r^2 d m \text { (Continuous body) }\end{aligned}$
5. Moment of Inertia of a few useful configurations
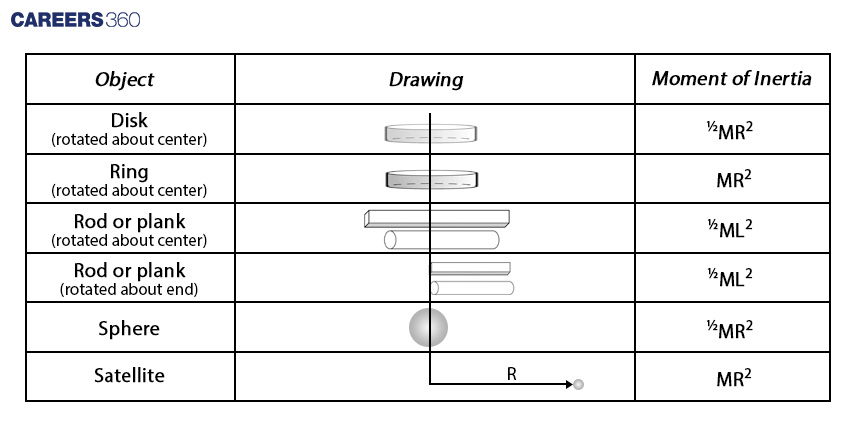
6. Torque (Moment of Force)
$\vec{\tau}=\vec{r} \times \vec{F}=r F \sin \theta$
7. Angular Momentum
$
\vec{L}=\vec{r} \times \vec{p}=m \vec{r} \times \vec{v}
$
For a rotating body:
$
L=I \omega
$
8. Torque-Angular Acceleration Relation
$\tau=I \alpha$
9. Rotational Kinetic Energy
$K \cdot E_{\cdot \mathrm{rot}}=\frac{1}{2} I \omega^2$
10. Angular Equations of Motion (Uniform Angular Acceleration)
$\begin{aligned} & \omega=\omega_0+\alpha t \\ & \theta=\omega_0 t+\frac{1}{2} \alpha t^2 \\ & \omega^2=\omega_0^2+2 \alpha \theta\end{aligned}$
Approach to Solve Questions of Class 11 Physics Chapter 6 - System of Particles and Rotational Motion
In Physics, Chapter 11, System of Particles and Rotational Motion, Chapter 6 is concerned with the motion of rigid bodies, torque, angular momentum and moment of inertia. This chapter requires conceptual clarity and practice in problem-solving methods to address the questions effectively in this chapter. The systematic approach can be used to make sure that there are no inaccuracies in derivations, numericals, and applications.
- It is always good to start by noting that the chapter assumes that the bodies are rigid (no deformation). This makes the problems of torque and rotational motion easier.
- When solving, separate linear motion (using Newton's laws) and rotational motion ($using torque = I\alpha$). They should only be combined when necessary.
- Appropriate rules of vectors should be applied to answer questions on torque, angular momentum and cross products. Practice right-hand rule applications for direction.
- The theorems which are commonly applied in numerical questions are the parallel axis and the perpendicular axis theorems. Use them directly in practice in order to save time during exams.
- In the problem of particle systems, find the COM first. Simplification can then be made on the motion of the entire system by taking the translation + rotation of a system about the COM.
- Derivations such as the correlation between torque and angular momentum, kinetic energy in rotation and rolling motion are common exam problems to be prepared for.
- Comparing rotational motion to real-life examples such as wheels, flywheels, ceiling fans, or gyroscopes can be beneficial when it comes to writing a better response to an explanation.
Importance of NCERT Solutions for Class 11 Physics Chapter 6: System of Particles and Rotational Motion
NCERT Solutions of Class 11 Physics Chapter 6: System of Particles and Rotational Motion is necessary to learn how bodies of large size move and rotate due to the influence of forces. This chapter goes beyond the motion of point particles and introduces new ideas that describe phenomena of rotation in the real world.
- Helps students understand the motion of a system of particles and how individual motions combine to produce overall motion.
- Elaborates about fundamental terms like centre of mass, torque, angular momentum, as well as moment of inertia, in a systematic and easy-to-understand manner.
- Establishes a solid foundation of more advanced topics such as rigid body dynamics, rotational equilibrium and gravitation.
- Keeps a significant role in board exams of CBSE, as most of the numerical and conceptual questions in the exams revolve around rotational motion.
- Highly important for competitive exams like JEE and NEET, where rotational mechanics is a frequently tested topic.
- Develops analytical and problem-solving ability by practicing numericals that involve the concepts of torque, angular momentum, and rotational energy.
- Helps students connect the concepts of physics to things they see in real life (rolling things, turning objects, and balancing systems).
- Allows the correct use of equations in various physical conditions of rotation and equilibrium.
What Students Learn from NCERT Solutions for Class 11 Physics Chapter 6: System of Particles and Rotational Motion?
Students are introduced to a more realistic perception of what the motion is with the help of the chapter System of Particles and Rotational Motion that describes the movement of objects with size and shape under the influence of forces. Through the NCERT Solutions of Class 11 Physics Chapter 6, students can study complex motions of rotation, balance and a combination of forces in an orderly manner and in a clear manner.
- Study the application of the concept of the centre of mass in the analysis of the motion of a system of particles.
- Learn the concept of rotational motion, angular displacement, angular velocity and angular acceleration.
- Learn the significance of important quantities like torque, angular momentum and moment of inertia and their physical importance.
- Study the application of the laws of Newton to the rotation of rigid bodies.
- Understand the conditions for rotational equilibrium and stability of bodies.
- Study the concepts of rotational kinetic energy and angular momentum conservation.
- Develop strong problem-solving and analytical skills through step-by-step numerical solutions.
- Prepare effectively for CBSE board exams and competitive exams such as JEE and NEET.
What Extra Should Students Study Beyond NCERT for JEE/NEET
To crack JEE, one must get out of NCERT and must practice higher-level conceptual problems of torque, rotational motion of Chapter 6: System of Particles and Rotational Motion and rolling motion. Answering difficult questions and practising past year JEE questions will enable you to brush through the depth of knowledge needed to crack competitive exams.
Also, Check NCERT Books and NCERT Syllabus here
NCERT Solutions for Class 11 Physics Chapter-Wise
The NCERT Solutions to Class 11 Physics are available in a chapter-wise format to provide inexpensive, step-by-step solutions to each chapter. The links are useful in revising major concepts, doing numerical problems, and preparing a sound base for exams such as CBSE, JEE, and NEET. All solutions are designed by professionals according to the new syllabus.
NCERT solutions for class 11 Subject-wise
Frequently Asked Questions (FAQs)
It is about constraint on the motion of rigid bodies, rotation about a fixed axis and concepts such as torque, moment of inertia and angular momentum.
By assuming rigidity, it eliminates complications of deformation hence making the analysis easy.
Linear motion is the movement in a straight direction and rotational is the turning around an axis.
Yes it bears the same role in rotational motion as mass does in linear motion.
The most common example includes rotating wheels, ceiling fans, spinning tops, and rotating planets.
- Identify the given data (mass, velocity, torque, etc.).
- Apply relevant formulas (e.g., I=mr2 for moment of inertia).
- Solve step by step, keeping track of units and dimensions.
- Use the principle of conservation of momentum and energy where applicable.
The solutions describe the centre of mass using some very simple examples and stepwise computations, which are easier to visualise and use in numerical problems.
These solutions are perfect to learn on your own without further instructions because of the detailed explanations and the structure of the solutions.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters


