Linear Inequalities Class 11th Notes - Free NCERT Class 11 Maths Chapter 6 notes - Download PDF

Linear Inequalities Class 11 Notes PDF download: Free PDF Download

Download PDF

Students who wish to access the Linear Inequalities Class 11 Maths notes can click on the link below to download the entire notes in PDF.

Linear Inequalities Class 11 Notes

Careers360 experts have curated these Linear Inequalities Class 11 Notes to help students revise quickly and confidently.

Linear Inequalities

A linear inequality is defined as an expression where any two values are compared by the inequality symbol, such as < > ≤ ≥

Let us take an example.

Ram has Rs. 120 and wants to buy some bats and balls. The cost of one register is Rs. 40, and that of a pen is Rs. 20. In this case, if x denotes the number of bats and y, the number of balls that Ram buys, then the total amount spent by her is Rs. (40x + 20y), and we have

40x + 20y ≤ 120

A statement involving the symbols ' $>$ ', ' $<$ ', ' $\geq$ ', ' $\leq$ ' is called an inequality. For example $5>3, x \leq 4, x+y \geq 9$.
(i) Inequalities that do not involve variables are called numerical inequalities. For example, $3< 8,5\geq2$.
(ii) Inequalities that involve variables are called literal inequalities. For example, $x>3, y \leq 5, x-y \geq 0$.
(iii) An inequality may contain more than one variable, and it can be linear, quadratic, cubic, etc. For example, $3 x-2<0$ is a linear inequality in one variable, $2 x+3 y \geq 4$ is a linear inequality in two variables, and $x^2+3 x+2<0$ is a quadratic inequality in one variable.
(iv) Inequalities involving the symbol ' $>$ ' or ' $<$ ' are called strict inequalities. For example, $3 x-y>5, x<3$.
(v) Inequalities involving the symbol ' $\geq$ ' or ' $\leq$ ' are called slack inequalities. For example, $3 x-y \geq 5, x \leq 5$.

Solution of an inequality

(i) The value(s) of the variable(s) which make the inequality a true statement are called its solutions. The set of all solutions of an inequality is called the solution set of the inequality. For example, $x-1 \geq 0$ has an infinite number of solutions, as all real values greater than or equal to one make it a true statement. The inequality $x^2+1<0$ has no solution in $\mathbf{R}$ as no real value of $x$ makes it a true statement.

To solve an inequality, we can
(i) Add (or subtract) the same quantity to (from) both sides without changing the sign of the inequality.
(ii) Multiply (or divide) both sides by the same positive quantity without changing the sign of the inequality. However, if both sides of inequality are multiplied (or divided) by the same negative quantity, the sign of inequality is reversed, i.e., ' $>$ ' changes into ' $<$ ' and vice versa.

Representation of the solution of a linear inequality in one variable on a number line

To represent the solution of a linear inequality in one variable on a number line, we use the following conventions:
(i) If the inequality involves ' $\geq$ ' or ' $\leq$ ', we draw a filled circle $(\bullet)$ on the number line to indicate that the number corresponding to the filled circle is included in the solution set.
(ii) If the inequality involves ' $>$ ' or ' $<$ ', we draw an open circle (O) on the number line to indicate that the number corresponding to the open circle is excluded from the solution set.

Graphical representation of the solution of a linear inequality

(a) To represent the solution of a linear inequality in one or two variables graphically in a plane, we proceed as follows:
(i) If the inequality involves ' $\geq$ ' or ' $\leq$ ', we draw the graph of the line as a thick line to indicate that the points on this line are included in the solution set.
(ii) If the inequality involves ' $>$ ' or ' $<$ ', we draw the graph of the line as a dotted line to indicate that the points on the line are excluded from the solution set.

(b) Solution of a linear inequality in one variable can be represented on the number line as well as in the plane, but the solution of a linear inequality in two variables of the type $a x+b y>c, a x+b y \geq c, a x+b y<c$
or $a x+b y \leq c(a \neq 0, b \neq 0)$ can be represented in the plane only.

(c) Two or more inequalities taken together comprise a system of inequalities, and the solutions of the system of inequalities are the solutions common to all the inequalities comprising the system.

Algebraic Solutions Of Linear Inequalities In One Variable And Their Graphical Representation

Equal numbers may be subtracted from or added to both sides of an inequality without affecting the inequality sign.

Example:

Solve 5x – 3 < 3x +1

when (i) x is an integer

(ii) x is a real number.

Solution:

We have,

5x –3 < 3x + 1

or 5x –3 + 3 < 3x +1 +3 (Rule 1)

or 5x < 3x +4

or 5x – 3x < 3x + 4 – 3x (Rule 1)

or 2x < 4 or x < 2 (Rule 2)

When x is an integer, the solutions of the given inequality are:

– 4, – 3, – 2, – 1, 0, 1

When x is a real number, the solutions of the inequality are given by x < 2, i.e., all real numbers x which are less than 2.

Therefore, the solution set of the inequality is x ∈ (– ∞, 2).

Graphical Solution of Linear Inequalities in Two Variables

We know that a line divides the Cartesian plane into two parts known as half-planes.

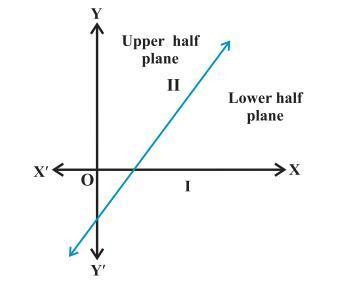
• The region consisting of all the solutions of an inequality is called the solution region.

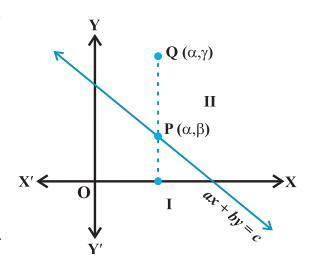
• If inequality is of the type ax + by ≥ c or ax + by ≤ c, then the points on the line ax + by = c, are also included in the solution region. So draw a dark line in the solution region.

• If inequality is of the form ax + by > c or ax + by < c, then the points on the line ax + by = c, are not to be included in the solution region. So draw a broken or dotted line in the solution region.

This is all about this chapter.

Linear Inequalities: Previous Year Question and Answer

Given below are selected previous year question answers for NCERT Class 11 Maths Chapter 5 Linear Inequalities, collected from various examinations.

Question 1:

Solve for x, the inequalities in $\left | x -1 \right |\leq 5,\left | x \right |\geq 2$

Solution:
$\left | x-1 \right |\leq 5........(given)$
(i) Now, there will be two cases –
$x-1 \leq 5,$
Adding 1 on both sides, we get,
$x \leq 6$
(ii) $-\left (x-1 \right ) \leq 5$
i.e., $-x+1 \leq 5$
Subtract 1 from both sides, and we will get,
$-x \leq 4$ i.e $x \geq -4$
Now, from (i) & (ii), we get,
$-4 \leq x\leq 6.........(a)$
& $\left | x \right |\geq 2$'
Thus, $x \geq 2$ & $-x \geq 2$
Thus $x \leq -2$
i.e $x \epsilon(-4,-2] \cup[2,6]$

Question 2:

A company manufactures cassettes. Its cost and revenue functions are C(x) = 26,000 + 30x and R(x) = 43x, respectively, where x is the number of cassettes produced and sold in a week. How many cassettes must be sold by the company to realise some profit?

Solution:
Given: Revenue, R(x) = 43x
Cost, C(x) = 26,000 + 30x,
Where ‘x’ is the no. of cassettes.
Requirement: profit > 0
We know that,
Profit = revenue – cost
= 43x – 26000 – 30x > 0
= 13x – 26000 > 0
= 13x > 26000
= x > 2000
Therefore, 2000 more cassettes should be sold by the company to realise the profit.

Question 3:

The longest side of a triangle is twice the shortest side, and the third side is 2 cm longer than the shortest side. If the perimeter of the triangle is more than 166 cm, then find the minimum length of the shortest side.

Solution:

Let us assume that the length of the shortest side of the triangle is ‘x’ cm
Thus, length of the largest side = 2x …. (given)
& length of the third side = (x + 2) cm …. (given)
Now, we know that,
The perimeter of a triangle = the sum of all three sides
= x + 2x + x + 2
= 4x + 2 cm
Now, it is given that the perimeter of the triangle is more than 166 cm.
Thus, $4x+2\geq 166$
$4x\geq 164$
Thus, $x\geq 41$
Therefore, the minimum length of the shortest side should be = 41 cm.

Importance of NCERT Class 11 Math Chapter 5 Notes

Class 11 Linear inequalities notes will help to understand the formulas, statements, and rules in detail. Also, Class 11 Math chapter 5 notes contain previous year’s questions and the NCERT textbook PDF.

• NCERT problems are very important to perform well in exams. Students must try to solve all the NCERT problems, including miscellaneous exercises, and if needed, refer to the NCERT Solutions for Class 11 Maths Chapter 5 Linear Inequalities
• Students are advised to go through the NCERT Class 11 Maths Chapter 5 Notes before solving the questions.
• To boost your exam preparation as well as for quick revision, these NCERT notes are very useful.

NCERT Class 11 Maths Notes – Chapter-Wise Links

We at Careers360 compiled all the NCERT class 11 Maths notes in one place for easy student reference. The following links will allow you to access them.

Subject-Wise NCERT Exemplar Solutions

After finishing the textbook exercises, students can use the following links to check the NCERT exemplar solutions for a better understanding of the concepts.

• NCERT Exemplar Class 11 Solutions
• NCERT Exemplar Class 11 Maths
• NCERT Exemplar Class 11 Physics
• NCERT Exemplar Class 11 Chemistry
• NCERT Exemplar Class 11 Biology

Subject-Wise NCERT Solutions

Students can also check these well-structured, subject-wise solutions.

• NCERT Solutions for Class 11 Mathematics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 11 Biology

NCERT syllabus and NCERT books

Before the start of a new academic year, students should refer to the latest syllabus to determine the chapters they’ll be studying. Below are the updated syllabus links, along with some recommended reference books.

• NCERT Books Class 11 Maths
• NCERT Syllabus Class 11 Maths
• NCERT Books Class 11
• NCERT Syllabus Class 11