Permutation And Combinations Class 11th Notes - Free NCERT Class 11 Maths Chapter 7 notes - Download PDF

Permutations and Combinations Class 11 Notes: Free PDF Download

Use the link below to download the Permutations and Combinations Class 11 Notes PDF for free. After that, you can view the PDF anytime you desire without internet access. It is very useful for revision and last-minute studies.

Download PDF

NCERT Class 11 Maths Chapter 6 Notes: Permutations and Combinations

Permutations and Combinations are mathematical techniques used to count the number of ways to arrange or select items. Permutations focus on arrangements where order matters, while Combinations deal with selections where order doesn’t matter. These concepts are essential in probability, statistics, and real-life decision-making problems.

Fundamental Principle of Counting

The fundamental principle of counting is a rule used to find the total number of outcomes possible in a given situation. The fundamental principle of counting can be classified into two types.

Multiplication Rule

If a certain work W can be completed by doing 2 tasks, first doing task A AND then doing task B. A can be done in m ways and, following that, B can be done in n ways, then the number of ways of doing the work W is (m x n) ways.

For example, let's say a person wants to travel from Noida to Gurgaon, and he has to travel via New Delhi. It is given that the person can travel from Noida to New Delhi in 3 different ways and from New Delhi to Gurgaon in 5 different ways.

So, in this case, to complete his work (reach Gurgaon) he has to do two tasks one after the other, first traveling from Noida to New Delhi (task A) AND then from New Delhi to Gurgaon (task B), as he has 3 different ways of reaching New Delhi (doing task A), and he has 5 different ways to reach Gurgaon from New Delhi (doing task B), so in that way, he has a total of 3×5 = 15 different ways to reach Gurgaon from Noida.

Addition Rule

If work W can be completed by doing task A OR task B, and A can be done in m ways and B can be done in n ways (and both cannot occur simultaneously: in this case we call tasks A and B as mutually exclusive), then work W can be done in (m + n) ways.

For example, let’s say that a person can travel from New Delhi to Noida in 3 different types of buses, and 2 different types of trains, so, he can complete the work of going from New Delhi to Noida in 3 + 2 = 5 ways (As work can be completed by going by bus (A) OR by going by train (B))

Permutation

The definition refers to several possible ways of arranging or ordering a set of numbers.

There are two types of permutations.

1. Linear Permutation

2. Circular Permutation

Linear Permutation

This is defined as when some things are arranged linearly. Like the arrangement of books, pens and many more.

The formula to compute problems goes by: ${ }^n P_r$

Consider the following example:

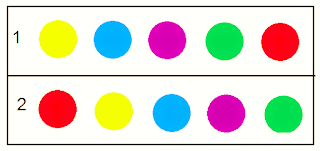
The above example represents a group of five different coloured balls arranged in two different orders in a straight line. Here, the starting and ending positions of the balls are different at each order.

Circular Permutation

This is defined as when something is arranged in a circular manner. Like the arrangement of chairs at a round table or the arrangement of beads in a necklace.
$P_n=n-1$

Consider the following example:

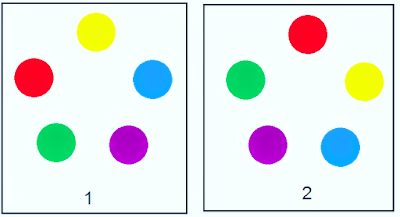
In the figure above, the five balls are arranged in two different orders in the circular form. Both the permutations look different, but they are the same. Because every ball has the same coloured ball to its right and left.

Combination

It is defined as a selection of objects without regard to order.

Now, the formula for finding the number of combinations of n different objects taken r at a time, denoted by ${ }^n C_r$.

$
{ }^n C_r=\frac{n!}{r!(n-r)!}
$

Ex: Choosing 3 pens from the set of 10.
Then,
$
{ }^{10} C_3=\frac{10!}{3!(10-3)!}=120
$

The relationship between Permutation and Combination is:
$
{ }^n C_r=\frac{{ }^n P_r}{r!}
$

Permutations Vs Combinations

Always remember, in an arrangement, the order is always important. Whereas, in Combination, the order is not important.

Consider the following examples-
1. Selecting a team of 11 from 16 players - Selection.
Drawing a batting line-up of 11 from 16 players - Arrangement.

2. Selecting 3 students out of 10 students who will receive scholarships of the same value - Selection.
Selecting 3 students out of 10 students who will receive scholarships of Rs. 500, Rs. 1000, and Rs. 2000 - Arrangement

Permutations and Combinations: Previous Year Question and Answer

Given below are some previous year question answers of various examinations from the NCERT class 11 chapter 6, Permutations and Combinations:

Question 1: The number of natural numbers, between 212 and 999, such that the sum of their digits is 15, is_______________.

Solution:
We are given the range of natural numbers from 212 to 999 and are asked to find how many of these numbers have a digit sum equal to 15.
Let a 3-digit number be represented as $ xyz$, where:
$ x \in \{2, 3, ..., 9\} $ (since the number must be greater than 212)
$ y, z \in \{0, 1, ..., 9\} $
The digit sum condition is $ x + y + z = 15 $
We analyse this by fixing values of $ x $ from 2 to 9 and counting the number of integer solutions to $ y + z = 15-x$, under the constraint $ 0 \leq y, z \leq 9 $.
Let’s compute valid $ (y, z) $ pairs for each $ x $:
$ x = 2 \Rightarrow y + z = 13 \Rightarrow \text{valid pairs: } (4,9), (5,8), (6,7), (7,6), (8,5), (9,4) \Rightarrow 6 \text{ solutions} $
$ x = 3 \Rightarrow y + z = 12 \Rightarrow \text{pairs: } (3,9), (4,8), ..., (9,3) \Rightarrow 7 \text{ solutions} $
$ x = 4 \Rightarrow y + z = 11 \Rightarrow \text{pairs: } (2,9), (3,8), ..., (9,2) \Rightarrow 8 \text{ solutions} $
$ x = 5 \Rightarrow y + z = 10 \Rightarrow \text{pairs: } (1,9), (2,8), ..., (9,1) \Rightarrow 9 \text{ solutions} $
$ x = 6 \Rightarrow y + z = 9 \Rightarrow \text{pairs: } (0,9), (1,8), ..., (9,0) \Rightarrow 10 \text{ solutions} $
$ x = 7 \Rightarrow y + z = 8 \Rightarrow \text{pairs: } (0,8), (1,7), ..., (8,0) \Rightarrow 9 \text{ solutions} $
$ x = 8 \Rightarrow y + z = 7 \Rightarrow \text{pairs: } (0,7), (1,6), ..., (7,0) \Rightarrow 8 \text{ solutions} $
$ x = 9 \Rightarrow y + z = 6 \Rightarrow \text{pairs: } (0,6), (1,5), ..., (6,0) \Rightarrow 7 \text{ solutions}$
Now summing the valid cases:
$6 + 7 + 8 + 9 + 10 + 9 + 8 + 7 = 64$
Hence, the correct answer is $64$.

Question 2: Let S be the set of all the words that can be formed by arranging all the letters of GARDEN. From the set S, one word is selected at random. The probability that the selected word will NOT have vowels in alphabetical order is:

Solution:
We are given the word "GARDEN" which consists of 6 distinct letters: G, A, R, D, E, N.
The total number of words that can be formed by arranging all these letters is:
$\text{Total number of arrangements} = 6! = 720$
We are interested in finding the probability that the selected word does NOT have vowels in alphabetical order.
The vowels in "GARDEN" are A and E.
We define "vowels in alphabetical order" to mean A appears before E in the arrangement.
Let’s calculate the number of arrangements where A comes before E.
Since all letters are distinct, and exactly two of them are vowels (A and E), in half of the total arrangements, A will come before E, and in the other half, E will come before A.
So, the number of arrangements where A comes before E:
$\frac{720}{2} = 360$
Thus, the number of arrangements where vowels are not in alphabetical order (i.e., E before A) is:
$720 - 360 = 360$
So, the required probability is:
$\frac{\text{Number of unfavorable cases}}{\text{Total cases}} = \frac{360}{720} = \frac{1}{2}$
Hence, the correct answer is $\frac{1}{2}$.

Question 3: Several functions $f:\{1,2, \ldots, 100\} \rightarrow\{0,1\}$, that assign 1 to exactly one of the positive integers less than or equal to 98, are equal to___________.

Solution:
Given:
$ f: \{1, 2, \ldots, 100\} \to \{0,1\} $
$ f(i) = 1 $ for exactly one $ i \in \{1, 2, \ldots, 98\} $
For all other $ j \neq i $ in $\{1, \ldots, 98\}$, $ f(j) = 0 $
No restriction on $ f(99) $ and $ f(100) $, they can be 0 or 1 independently.
Step 1: Choose the unique position for 1 among first 98 integers
Number of ways:
$\binom{98}{1} = 98$
Step 2: Values for $ f(99) $ and $ f(100) $
Each can be either 0 or 1, independently:
$2 \times 2 = 4 \text{ ways}.$
Step 3: Total number of such functions
$98 \times 4 = 392.$
Hence, the correct answer is 392.

Importance of NCERT Class 11 Math Chapter 6 Notes

NCERT Class 11 Maths chapter 6 notes can be an essential learning tool if students use them wisely. The important aspects of these notes are as follows:

• These notes will clarify the concepts of Permutations and combinations. Students will understand when the order matters and when it doesn't.
• A good number of questions come from this chapter in class 11 board exams as well as in exams like JEE Main, NDA, and CUET.
• Students can use this note for quick revision of the important concepts and formulas.
• These notes will improve students' logical thinking and analytical skills.
• Completing these notes will boost the confidence of the students and create a positive vibe, which is a necessity before an exam.

NCERT Class 11 Notes Chapter Wise

All the links to chapter-wise notes for NCERT class 11 maths are given below:

Subject-Wise NCERT Exemplar Solutions

Students can check these NCERT exemplar links for further practice purposes.

• NCERT Exemplar Class 11 Solutions
• NCERT Exemplar Class 11 Maths
• NCERT Exemplar Class 11 Physics
• NCERT Exemplar Class 11 Chemistry
• NCERT Exemplar Class 11 Biology

Subject-Wise NCERT Solutions

After checking the Mathematics solutions, students can also check the solutions of other subjects. These solutions are well-structured and well-explained.

• NCERT Solutions for Class 11 Mathematics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 11 Biology

NCERT Books and Syllabus

Students need to be aware of the latest CBSE syllabus. Also, an extra reference book always proved handy. Here are some links that will help students with the above two causes.

• NCERT Book for Class 11
• NCERT Syllabus for Class 11