NCERT Solutions for Class 11 Maths Chapter 6 Linear Inequalities

Q: What are important topics of the chapter Linear Inequalities ?

Inequalities class 11 includes the important topics such as Basic concept of inequalities, algebraic solutions of linear inequalities in one variable and their graphical representation, graphical solution of linear inequalities in two variables, and solution of system of linear inequalities in two variables. students should practice these concepts to get good a hold of the concepts discussed in class 11 chapter 6 .

Q: Explain the steps to plot a graph of linear inequality covered in NCERT Solutions for Class 11 Maths Chapter 6.

The steps to plot a graph of a linear inequality covered in linear inequalities class 11 ncert solutions are as follows: Write the inequality in the form of a linear equation Solve the equation for y Identify the boundary line Choose a test point Substitute the test point Shade the region Identify the solution set Label the graph Students can find NCERT solutions for class 11 maths by clicking on the link.

Q: List out the number of exercises present in NCERT solutions for class 11 maths chapter 6.

The linear inequalities class 11 solutions includes there three exercises and one miscellaneous exercise. Exercise 6.1 – 26 Questions Exercise 6.2 – 10 Questions Exercise 6.3 – 15 Questions Miscellaneous Exercise – 14 Questions

Q: Which is the official website of NCERT ?

NCERT official is the official website of the NCERT where you can get NCERT textbooks and syllabus from class 1 to 12.

NCERT Solutions for Class 11 Maths Chapter 6 Linear Inequalities

Edited By Ramraj Saini | Updated on Sep 23, 2023 06:01 PM IST

Linear Inequalities Class 11 Questions And Answers

NCERT Solutions for Class 11 Maths Chapter 6 Linear Inequalities are provided here. These NCERT So lutions are created by expert team at Careers360 keeping in mind of latest syllabus of CBSE 2023-24. In earlier classes, you have studied equations of one variable and two variables and have solved many problems based on this. In this article, you will get linear inequalities class 11 NCERT solutions. Class 11 Mathematics NCERT book will help you understand the concepts in a much easier way. Here you will get NCERT solutions for class 11 also.

JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy

Suggested: JEE Main: high scoring chapters | Past 10 year's papers

This Story also Contains

Linear Inequalities Class 11 Questions And Answers
Linear Inequalities Class 11 Questions And Answers PDF Free Download
Linear Inequalities Class 11 Solutions - Important Formulae And Points
Linear Inequalities Class 11 NCERT Solutions (Intext Questions and Exercise)
Linear Inequality Example
NCERT Solutions For Class 11 Mathematics - Chapter Wise
NCERT Solutions For Class 11- Subject Wise

NCERT Solutions for Class 11 Maths Chapter 6 Linear Inequalities

Many real life problems can be solved by converting a problem into a mathematical equation but some problems like the height of all the members in your family is less than 180 cm, auditorium can occupy at most 120 tables or chairs or both can't be converted into equations. Statements which involve sign ‘’ '>' (greater than), ‘≤’ (less than or equal) and ≥ (greater than or equal), '<' (less than) are known as inequalities. T he concept of inequality is used in formulating the constraints. In NCERT solutions for class 11 maths chapter 6 linear inequalities you will understand questions based on inequalities in one variable and two variables.

Linear Inequalities Class 11 Questions And Answers PDF Free Download

Download PDF

Linear Inequalities Class 11 Solutions - Important Formulae And Points

Inequation (Inequality):

An inequation or inequality is a statement involving variables and the sign of inequality like >, <, ≥, or ≤.

Symbols used in inequalities:

The symbol < means less than.

The symbol > means greater than.

The symbol < with a bar underneath ≤ means less than or equal to.

The symbol > with a bar underneath ≥ means greater than or equal to.

The symbol ≠ means the quantities on the left and right sides are not equal to.

Algebraic Solutions for Linear Inequalities in One Variable:

Linear inequalities involve expressions with variables and inequality symbols like <, >, ≤, or ≥.

The solution to a linear inequality can be determined using algebraic methods.

Important rules to follow when solving linear inequalities:

Rule 1: Don’t change the sign of an inequality by adding or subtracting the same integer on both sides of an equation.
Rule 2: Add or subtract the same positive integer from both sides of an inequality equation.

Graphical Representation of Linear Inequalities:

Linear inequalities can also be represented graphically on a number line.

For example, x > 3 represents all real numbers greater than 3, which can be shaded on the number line to the right of 3.

Similarly, x ≤ -2 represents all real numbers less than or equal to -2, which can be shaded on the number line to the left of -2.

Free download NCERT Solutions for Class 11 Maths Chapter 6 Linear Inequalities for CBSE Exam.

Linear Inequalities Class 11 NCERT Solutions (Intext Questions and Exercise)

Class 11 maths chapter 6 question answer - Exercise 6.1

Question:1(i) Solve $24x < 100$ , when
$x$ i s a natural number.

Answer:

Given : $24x < 100$

$\Rightarrow$ $24x < 100$

Divide by 24 from both sides

$\Rightarrow \, \, \, \frac{24}{24}x< \frac{100}{24}$

$\Rightarrow \, \, \, x< \frac{25}{6}$

$\Rightarrow \, \, \, x< 4.167$

$x$ i s a natural number which is less than 4.167.

Hence, values of x can be $\left \{ 1,2,3,4 \right \}$

Question:1(ii) Solve $24x< 100$ , when

$x$ is an integer.

Answer:

Given : $24x < 100$

$\Rightarrow$ $24x < 100$

Divide by 24 from both sides

$\Rightarrow \, \, \, \frac{24}{24}x< \frac{100}{24}$

$\Rightarrow \, \, \, x< \frac{25}{6}$

$\Rightarrow \, \, \, x< 4.167$

$x$ i s are integers which are less than 4.167.

Hence, values of x can be $\left \{..........-3,-2,-1,0, 1,2,3,4 \right \}$

Question:2(i) Solve $-12x>30$ , when
x is a natural number.

Answer:

Given : $-12x>30$

$\Rightarrow$ $-12x>30$

Divide by -12 from both side

$\Rightarrow \, \, \, \frac{-12}{-12}x< \frac{30}{-12}$

$\Rightarrow \, \, \, x< \frac{30}{-12}$

$\Rightarrow \, \, \, x< -2.5$

$x$ i s a natural number which is less than - 2.5.

Hence, the values of x do not exist for given inequality.

Question:2(ii) Solve $- 12x > 30$ , when

$x$ is an integer.

Answer:

Given : $-12x>30$

$\Rightarrow$ $-12x>30$

Divide by -12 from both side

$\Rightarrow \, \, \, \frac{-12}{-12}x< \frac{30}{-12}$

$\Rightarrow \, \, \, x< \frac{30}{-12}$

$\Rightarrow \, \, \, x< -2.5$

$x$ are integers less than - 2.5 .

Hence, values of x can be $\left \{ .............,-6,-5,-4,-3 \right \}$

Question:3(i) Solve $5x - 3 < 7$ , when

$x$ is an integer.

Answer:

Given : $5x - 3 < 7$

$\Rightarrow$ $5x - 3 < 7$

$\Rightarrow \, \, \, 5x< 10$

Divide by 5 from both sides

$\Rightarrow \, \, \, \frac{5}{5}x< \frac{10}{5}$

$\Rightarrow \, \, \, x< 2$

$x$ are integers less than 2

Hence, values of x can be $\left \{.........-3,-2-1,0,1,\right \}$

Question:3(ii) Solve $5x - 3 < 7$ , when

$x$ is a real number.

Answer:

Given : $5x - 3 < 7$

$\Rightarrow$ $5x - 3 < 7$

$\Rightarrow \, \, \, 5x< 10$

Divide by 5 from both sides

$\Rightarrow \, \, \, \frac{5}{5}x< \frac{10}{5}$

$\Rightarrow \, \, \, x< 2$

$x$ are real numbers less than 2

i.e. $x\in (-\infty ,2)$

Question:4(i) Solve $3x + 8 >2$ , when
x is an integer.

Answer:

Given : $3x + 8 >2$

$\Rightarrow$ $3x + 8 >2$

$\Rightarrow \, \, \, 3x> -6$

Divide by 3 from both sides

$\Rightarrow \, \, \, \frac{3}{3}x> \frac{-6}{3}$

$\Rightarrow \, \, \, x> - 2$

$x$ are integers greater than -2

Hence, the values of x can be $\left \{-1,0,1,2,3,4...............\right \}$ .

Question:4(ii) Solve $3x + 8 >2$ , when ) $x$ is a real number.

Answer:

Given : $3x + 8 >2$

$\Rightarrow$ $3x + 8 >2$

$\Rightarrow \, \, \, 3x> -6$

Divide by 3 from both side

$\Rightarrow \, \, \, \frac{3}{3}x> \frac{-6}{3}$

$\Rightarrow \, \, \, x> - 2$

$x$ are real numbers greater than -2

Hence , values of x can be as $x\in (-2,\infty )$

Question:5 Solve the inequality for real $x$ . $4x + 3 < 5x + 7$

Answer:

Given : $4x + 3 < 5x + 7$

$\Rightarrow$ $4x + 3 < 5x + 7$

$\Rightarrow \, \, \, 4x-5x< 7-3$

$\Rightarrow \, \, \, x> -4$

$x$ are real numbers greater than -4.

Hence, values of x can be as $x\in (-4 ,\infty )$

Question:6 Solve the inequality for real $x$ $3x - 7 > 5x -1$

Answer:

Given : $3x - 7 > 5x -1$

$\Rightarrow$ $3x - 7 > 5x -1$

$\Rightarrow \, \, \, -2x> 6$

$\Rightarrow \, \, \, x< \frac{6}{-2}$

$\Rightarrow \, \, \, x< -3$

$x$ are real numbers less than -3.

Hence, values of x can be $x\in (-\infty ,-3)$

Question:7 Solve the inequality for real $x$ . $3(x-1) \leq 2(x-3)$

Answer:

Given : $3(x-1) \leq 2(x-3)$

$\Rightarrow$ $3(x-1) \leq 2(x-3)$

$\Rightarrow \, \, \, 3x-3\leq 2x-6$

$\Rightarrow \, \, \, 3x-2x\leq -6+3$

$\Rightarrow \, \, \, x\leq -3$

$x$ are real numbers less than equal to -3

Hence , values of x can be as , $x\in (-\infty ,-3]$

Question:8 Solve the inequality for real $x$ $3(2- x) \geq 2(1-x)$

Answer:

Given : $3(2- x) \geq 2(1-x)$

$\Rightarrow$ $3(2- x) \geq 2(1-x)$

$\Rightarrow \, \, \, 6-3x\geq 2-2x$

$\Rightarrow \, \, \, 6-2\geq 3x-2x$

$\Rightarrow \, \, \, 4\geq x$

$x$ are real numbers less than equal to 4

Hence, values of x can be as $x\in (-\infty ,4]$

Question:9 Solve the inequality for real $x$ $x + \frac{x}{2} + \frac{x}{3} < 11$

Answer:

Given : $x + \frac{x}{2} + \frac{x}{3} < 11$

$\Rightarrow$ $x + \frac{x}{2} + \frac{x}{3} < 11$

$\Rightarrow \, \, \, x(1+\frac{1}{2}+\frac{1}{3})< 11$

$\Rightarrow \, \, \, x(\frac{11}{6})< 11$

$\Rightarrow \, \, \, 11 x< 11\times 6$

$\Rightarrow \, \, \, x< 6$

$x$ are real numbers less than 6

Hence, values of x can be as $x\in (-\infty ,6)$

Question:10 Solve the inequality for real $x$ . $\frac{x}{3} > \frac{x}{2} + 1$

Answer:

Given : $\frac{x}{3} > \frac{x}{2} + 1$

$\Rightarrow$ $\frac{x}{3} > \frac{x}{2} + 1$

$\Rightarrow \, \, \, \frac{x}{3}-\frac{x}{2}> 1$

$\Rightarrow \, \, \,x (\frac{1}{3}-\frac{1}{2})> 1$

$\Rightarrow \, \, \,x (-\frac{1}{6})> 1$

$\Rightarrow \, \, \, -x > 6$

$\Rightarrow \, \, \, x< -6$

$x$ are real numbers less than -6

Hence, values of x can be as $x\in (-\infty ,-6)$

Question:11 Solve the inequality for real $x$ $\frac{3(x-2)}{5} \leq \frac{5(2-x)}{3}$

Answer:

Given : $\frac{3(x-2)}{5} \leq \frac{5(2-x)}{3}$

$\Rightarrow$ $\frac{3(x-2)}{5} \leq \frac{5(2-x)}{3}$

$\Rightarrow \, \, \, 9(x-2)\leq 25(2-x)$

$\Rightarrow \, \, \, 9x-18\leq 50-25x$

$\Rightarrow \, \, \, 9x+25x\leq 50+18$

$\Rightarrow \, \, \, 34x\leq 68$

$\Rightarrow \, \, \, x\leq 2$

$x$ are real numbers less than equal to 2.

Hence, values of x can be as $x\in (-\infty ,2]$

Question:12 Solve the inequality for real $x$ $\frac{1}{2}\left(\frac{3x}{5} + 4 \right ) \geq \frac{1}{3}(x - 6)$

Answer:

Given : $\frac{1}{2}\left(\frac{3x}{5} + 4 \right ) \geq \frac{1}{3}(x - 6)$

$\Rightarrow$ $\frac{1}{2}\left(\frac{3x}{5} + 4 \right ) \geq \frac{1}{3}(x - 6)$

$\Rightarrow \, \, 3\left(\frac{3x}{5} + 4 \right ) \geq 2(x - 6)$

$\Rightarrow \, \, \frac{9x}{5} + 12 \geq 2x-12$

$\Rightarrow \, \, 12+12 \geq 2x-\frac{9x}{5}$

$\Rightarrow \, \, 24 \geq \frac{x}{5}$

$\Rightarrow \, \, 120 \geq x$

$x$ are real numbers less than equal to 120.

Hence, values of x can be as $x\in (-\infty,120 ]$ .

Question:13 Solve the inequality for real $x$ $2(2x + 3) - 10 < 6(x-2)$

Answer:

Given : $2(2x + 3) - 10 < 6(x-2)$

$\Rightarrow$ $2(2x + 3) - 10 < 6(x-2)$

$\Rightarrow \, \, \, 4x+6-10 < 6x-12$

$\Rightarrow \, \, \, 6-10+12 < 6x-4x$

$\Rightarrow \, \, \, 8 < 2x$

$\Rightarrow \, \, \, 4 < x$

$x$ are real numbers greater than 4

Hence , values of x can be as $x\in (4,\infty )$

Question:14 Solve the inequality for real $x$ $37 - (3x + 5) \geq 9x - 8(x-3)$

Answer:

Given : $37 - (3x + 5) \geq 9x - 8(x-3)$

$\Rightarrow$ $37 - (3x + 5) \geq 9x - 8(x-3)$

$\Rightarrow \, \, \, 37 - 3x - 5 \geq 9x - 8x+24$

$\Rightarrow \, \, \, 32 - 3x \geq x+24$

$\Rightarrow \, \, \, 32 - 24 \geq x+3x$

$\Rightarrow \, \, \, 8 \geq 4x$

$\Rightarrow \, \, \, 2\geq x$

$x$ are real numbers less than equal to 2.

Hence , values of x can be as $x\in (-\infty ,2]$

Question:15 Solve the inequality for real x $\frac{x}{4}< \frac{(5x-2)}{3} - \frac{(7x-3)}{5}$

Answer:

Given : $\frac{x}{4}< \frac{(5x-2)}{3} - \frac{(7x-3)}{5}$

$\Rightarrow$ $\frac{x}{4}< \frac{(5x-2)}{3} - \frac{(7x-3)}{5}$

$\Rightarrow \, \, \, \, 15x< 20(5x-2)-12(7x-3)$

$\Rightarrow \, \, \, \, 15x< 100x-40-84x+36$

$\Rightarrow \, \, \, \, 15x< 16x-4$

$\Rightarrow \, \, \, \, 4< x$

$x$ are real numbers greater than 4.

Hence, values of x can be as $x\in (4,\infty)$

Question:16 Solve the inequality for real $x$ $\frac{(2x - 1)}{3} \geq \frac{3x-2}{4} - \frac{(2-x)}{5}$

Answer:

Given : $\frac{(2x - 1)}{3} \geq \frac{3x-2}{4} - \frac{(2-x)}{5}$

$\Rightarrow$ $\frac{(2x - 1)}{3} \geq \frac{3x-2}{4} - \frac{(2-x)}{5}$

$\Rightarrow \, \, \, 20(2x - 1) \geq 15(3x-2) - 12(2-x)$

$\Rightarrow \, \, \, 40x - 20 \geq 45x-30 - 24+12x$

$\Rightarrow \, \, \, 30+24 - 20 \geq 45x-40x+12x$

$\Rightarrow \, \, \, 34 \geq 17x$

$\Rightarrow \, \, \, 2 \geq x$

$x$ are real numbers less than equal 2.

Hence, values of x can be as $x\in (-\infty,2 ]$ .

Question:17 Solve the inequality and show the graph of the solution on number line $3x - 2 < 2x + 1$

Answer:

Given : $3x - 2 < 2x + 1$

$\Rightarrow$ $3x - 2 < 2x + 1$

$\Rightarrow \, \, \, 3x - 2x< 2 + 1$

$\Rightarrow \, \, \, x< 3$

$x$ are real numbers less than 3

Hence, values of x can be as $x\in (-\infty ,3)$

The graphical representation of solutions of the given inequality is as :

1635762263704

Question:18 Solve the inequality and show the graph of the solution on number line $5x - 3 \geq 3x -5$

Answer:

Given : $5x - 3 \geq 3x -5$

$\Rightarrow$ $5x - 3 \geq 3x -5$

$\Rightarrow \, \, \, 5x - 3x \geq 3 -5$

$\Rightarrow \, \, \, 2x \geq -2$

$\Rightarrow \, \, \, x \geq -1$

$x$ are real numbers greater than equal to -1.

Hence, values of x can be as $x\in [-1,\infty )$

The graphical representation of solutions of the given inequality is as :

1635762285990

Question:19 Solve the inequality and show the graph of the solution on number line $3(1-x) < 2 (x +4)$

Answer:

Given : $3(1-x) < 2 (x +4)$

$\Rightarrow$ $3(1-x) < 2 (x +4)$

$\Rightarrow \, \, \, 3- 3x< 2x + 8$

$\Rightarrow \, \, \, 3- 8< 2x + 3x$

$\Rightarrow \, \, \, -5< 5 x$

$\Rightarrow \, \, \, -1< x$

$x$ are real numbers greater than -1

Hence, values of x can be as $x\in (-1,\infty )$

The graphical representation of solutions of given inequality is as :

1635762322180

Question:20 Solve the inequality and show the graph of the solution on number line $\frac{x}{2} \geq \frac{(5x-2)}{3} - \frac{(7x-3)}{5}$

Answer:

Given : $\frac{x}{2} \geq \frac{(5x-2)}{3} - \frac{(7x-3)}{5}$

$\Rightarrow$ $\frac{x}{2} \geq \frac{(5x-2)}{3} - \frac{(7x-3)}{5}$

$\Rightarrow \, \, \, 15x \geq 10(5x-2) - 6(7x-3)$

$\Rightarrow \, \, \, 15x \geq 50x-20 - 42x+18$

$\Rightarrow \, \, \, 15x+42x-50x \geq 18-20$

$\Rightarrow \, \, \, 7x \geq -2$

$\Rightarrow \, \, \, x \geq \frac{-2}{7}$

$x$ are real numbers greater than equal to $= \frac{-2}{7}$

Hence, values of x can be as $x\in (-\frac{2}{7},\infty )$

The graphical representation of solutions of the given inequality is as :

1635762357828

Question:21 Ravi obtained 70 and 75 marks in first two unit test. Find the minimum marks he should get in the third test to have an average of at least 60 marks.

Answer:

Let x be marks obtained by Ravi in the third test.

The student should have an average of at least 60 marks.

$\therefore \, \, \, \frac{70+75+x}{3}\geq 60$

$\, \, \, 145+x\geq 180$

$x\geq 180-145$

$x\geq 35$

the student should have minimum marks of 35 to have an average of 60

Question:22 To receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94 and 95, find minimum marks that Sunita must obtain in fifth examination to get grade ‘A’ in the course.

Answer:

Sunita’s marks in the first four examinations are 87, 92, 94 and 95.

Let x be marks obtained in the fifth examination.

To receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations.

$\therefore \, \, \, \frac{87+92+94+95+x}{5}\geq 90$

$\Rightarrow \, \, \, \frac{368+x}{5}\geq 90$

$\Rightarrow \, \, \, 368+x\geq 450$

$\Rightarrow \, \, \, x\geq 450-368$

$\Rightarrow \, \, \, x\geq 82$

Thus, Sunita must obtain 82 in the fifth examination to get grade ‘A’ in the course.

Question:23 Find all pairs of consecutive odd positive integers both of which are smaller than 10 such that their sum is more than 11.

Answer:

Let x be smaller of two consecutive odd positive integers. Then the other integer is x+2.

Both integers are smaller than 10.

$\therefore \, \, \, x+2< 10$

$\Rightarrow \, \, \, \, x< 10-2$

$\Rightarrow \, \, \, \, x< 8$

Sum of both integers is more than 11.

$\therefore \, \, \, x+(x+2)> 11$

$\Rightarrow \, \, \, (2x+2)> 11$

$\Rightarrow \, \, \, 2x> 11-2$

$\Rightarrow \, \, \, 2x> 9$

$\Rightarrow \, \, \, x> \frac{9}{2}$

$\Rightarrow \, \, \, x> 4.5$

We conclude $\, \, \, \, x< 8$ and $\, \, \, x> 4.5$ and x is odd integer number.

x can be 5,7.

The two pairs of consecutive odd positive integers are $(5,7)\, \, \, and\, \, \, (7,9)$ .

Question:24 Find all pairs of consecutive even positive integers, both of which are larger than 5 such that their sum is less than 23.

Answer:

Let x be smaller of two consecutive even positive integers. Then the other integer is x+2.

Both integers are larger than 5.

$\therefore \, \, \, x> 5$

Sum of both integers is less than 23.

$\therefore \, \, \, x+(x+2)< 23$

$\Rightarrow \, \, \, (2x+2)< 23$

$\Rightarrow \, \, \, 2x< 23-2$

$\Rightarrow \, \, \, 2x< 21$

$\Rightarrow \, \, \, x< \frac{21}{2}$

$\Rightarrow \, \, \, x< 10.5$

We conclude $\, \, \, \, x< 10.5$ and $\, \, \, x> 5$ and x is even integer number.

x can be 6,8,10.

The pairs of consecutive even positive integers are $(6,8),(8,10),(10,12)$ .

Question:25 The longest side of a triangle is 3 times the shortest side and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side.

Answer:

Let the length of the smallest side be x cm.

Then largest side = 3x cm.

Third side = 3x-2 cm.

Given: The perimeter of the triangle is at least 61 cm.

$\therefore\, \, \, x+3x+(3x-2)\geq 61$

$\Rightarrow \, \, \, 7x-2\geq 61$

$\Rightarrow \, \, \, 7x\geq 61+2$

$\Rightarrow \, \, \, 7x\geq 63$

$\Rightarrow \, \, \, x\geq \frac{63}{7}$

$\Rightarrow \, \, \, x\geq 9$

Minimum length of the shortest side is 9 cm.

Question:26 A man wants to cut three lengths from a single piece of board of length 91cm. The second length is to be 3cm longer than the shortest and the third length is to be twice as long as the shortest. What are the possible lengths of the shortest board if the third piece is to be at least 5cm longer than the second?

[ Hint : If x is the length of the shortest board, then $x$ , $(x + 3)$ and $2x$ are the lengths of the second and third piece, respectively. Thus, $x + (x + 3) + 2x \leq 91$ and $2x \geq (x + 3) + 5$ ].

Answer:

Let x is the length of the shortest board,

then $(x + 3)$ and $2x$ are the lengths of the second and third piece, respectively.

The man wants to cut three lengths from a single piece of board of length 91cm.

Thus, $x + (x + 3) + 2x \leq 91$

$4x+3\leq 91$

$\Rightarrow \, \, \, \, 4x\leq 91-3$

$\Rightarrow \, \, \, \, 4x\leq 88$

$\Rightarrow \, \, \, \, x\leq \frac{88}{4}$

$\Rightarrow \, \, \, \, x\leq 22$

if the third piece is to be at least 5cm longer than the second, than

$2x \geq (x + 3) + 5$

$\Rightarrow \, \, \, \, 2x\geq x+8$

$\Rightarrow \, \, \, \, 2x-x\geq 8$

$\Rightarrow \, \, \, \, x\geq 8$

We conclude that $\, \, \, \, x\geq 8$ and $\, \, \, \, x\leq 22$ .

Thus , $8\leq x\leq 22$ .

Hence, the length of the shortest board is greater than equal to 8 cm and less than equal to 22 cm.

Class 11 maths chapter 6 question answer - Exercise: 6.2

Question:1 Solve the following inequality graphically in two-dimensional plane:

$x + y < 5$

Answer:

Graphical representation of $x+y=5$ is given in the graph below.

The line $x+y=5$ divides plot in two half planes.

Select a point (not on line $x+y=5$ ) which lie in one of the half planes, to determine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

$1+2< 5$ i.e. $3< 5$ , which is true.

Therefore, half plane (above the line) is not a solution region of given inequality i.e. $x + y < 5$ .

Also, the point on the line does not satisfy the inequality.

Thus, the solution to this inequality is half plane below the line $x+y=5$ excluding points on this line represented by the green part.

This can be represented as follows:

1635762532191

Question:2 Solve the following inequality graphically in two-dimensional plane: $2x + y \geq 6$

Answer:

$2x + y \geq 6$

Graphical representation of $2x+y=6$ is given in the graph below.

The line $2x+y=6$ divides plot in two half-planes.

Select a point (not on the line $2x+y=6$ ) which lie in one of the half-planes, to determine whether the point satisfies the inequality.

Let there be a point $(3,2)$

We observe

$6+2\geq 6$ i.e. $8\geq 6$ , which is true.

Therefore, half plane II is not a solution region of given inequality i.e. $2x + y \geq 6$

Also, the point on the line does satisfy the inequality.

Thus, the solution to this inequality is the half plane I, above the line $2x+y=6$ including points on this line , represented by green colour.

This can be represented as follows:

1635762558839

Question:3 Solve the following inequality graphically in two-dimensional plane: $3x + 4y \leq 12$

Answer:

$3x + 4y \leq 12$

Graphical representation of $3x + 4y = 12$ is given in the graph below.

The line $3x + 4y = 12$ divides plot into two half-planes.

Select a point (not on the line $3x + 4y = 12$ ) which lie in one of the half-planes, to determine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

$1+2\leq 12$ i.e. $3\leq 12$ , which is true.

Therefore, the half plane I(above the line) is not a solution region of given inequality i.e. $3x + 4y \leq 12$ .

Also, the point on the line does satisfy the inequality.

Thus, the solution to this inequality is half plane II (below the line $3x + 4y = 12$ ) including points on this line, represented by green colour.

This can be represented as follows:

1635762572337

Question:4 Solve the following inequality graphically in two-dimensional plane: $y + 8 \geq 2x$

Answer:

$y + 8 \geq 2x$

Graphical representation of $y + 8 = 2x$ is given in the graph below.

The line $y + 8 = 2x$ divides plot in two half-planes.

Select a point (not on the line $y + 8 = 2x$ ) which lie in one of the half-planes, to determine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

$2+8\geq 2\times 1$ i.e. $10\geq 2$ , which is true.

Therefore, half plane II is not solution region of given inequality i.e. $y + 8 \geq 2x$ .

Also, the point on the line does satisfy the inequality.

Thus, the solution to this inequality is the half plane I including points on this line, represented by green colour.

This can be represented as follows:

1635762587304

Question:5 Solve the following inequality graphically in two-dimensional plane: $x - y \leq 2$

Answer:

$x - y \leq 2$

Graphical representation of $x - y =2$ is given in the graph below.

The line $x - y =2$ divides plot in two half planes.

Select a point (not on the line $x - y =2$ ) which lie in one of the half-planes, to determine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

$1-2\leq 2$ i.e. $-1\leq 2$ , which is true.

Therefore, half plane Ii is not solution region of given inequality i.e. $x - y \leq 2$ .

Also, the point on the line does satisfy the inequality.

Thus, the solution to this inequality is the half plane I including points on this line, represented by green colour

This can be represented as follows:

1635762601555

Question:6 Solve the following inequality graphically in two-dimensional plane: $2x - 3y > 6$

Answer:

$2x - 3y > 6$

Graphical representation of $2x - 3y = 6$ is given in the graph below.

The line $2x - 3y = 6$ divides plot in two half planes.

Select a point (not on the line $2x - 3y = 6$ )which lie in one of the half-planes, to determine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

$2-6> 6$ i.e. $-4 > 6$ , which is false .

Therefore, half plane I is not solution region of given inequality i.e. $2x - 3y > 6$ .

Also point on line does not satisfy the inequality.

Thus, the solution to this inequality is half plane II excluding points on this line, represented by green colour.

This can be represented as follows:

1635762622339

Question:7 Solve the following inequality graphically in two-dimensional plane: $-3x + 2y \geq -6$

Answer:

$-3x + 2y \geq -6$

Graphical representation of $-3x + 2y = -6$ is given in the graph below.

The line $-3x + 2y = -6$ divides plot in two half planes.

Select a point (not on the line $-3x + 2y = -6$ ) which lie in one of the half planes, to determine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

$-3+4\geq -6$ i.e. $1\geq -6$ , which is true.

Therefore, half plane II is not solution region of given inequality i.e. $-3x + 2y \geq -6$ .

Also, the point on the line does satisfy the inequality.

Thus, the solution to this inequality is the half plane I including points on this line, represented by green colour

This can be represented as follows:

1635762636448

Question:8 Solve the following inequality graphically in two-dimensional plane: $3y - 5x < 30$

Answer:

$3y - 5x < 30$

Graphical representation of $3y - 5x =30$ is given in graph below.

The line $3y - 5x =30$ divides plot in two half planes.

Select a point (not on the line $3y - 5x =30$ ) which lie in one of the half plane , to detemine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

$6-5< 30$ i.e. $1< 30$ , which is true.

Therefore, half plane II is not solution region of given inequality i.e. $3y - 5x < 30$ .

Also point on the line does not satisfy the inequality.

Thus, solution to this inequality is half plane I excluding points on this line, represented by green colour.

This can be represented as follows:

1635762649943

Question:9 Solve the following inequality graphically in two-dimensional plane: $y < -2$

Answer:

$y < -2$

Graphical representation of $y=-2$ is given in graph below.

The line $y < -2$ divides plot in two half planes.

Select a point (not on the line $y < -2$ ) which lie in one of the half plane , to detemine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

i.e. $2< -2$ , which is false.

Therefore, the half plane I is not a solution region of given inequality i.e. $y < -2$ .

Also, the point on the line does not satisfy the inequality.

Thus, the solution to this inequality is half plane II excluding points on this line, represented by green colour.

This can be represented as follows:

1635762675271

Question:10 Solve the following inequality graphically in two-dimensional plane: $x > - 3$

Answer:

$x > - 3$

Graphical representation of $x=-3$ is given in the graph below.

The line $x=-3$ divides plot into two half-planes.

Select a point (not on the line $x=-3$ ) which lie in one of the half-planes, to determine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

i.e. $1> -3$ , which is true.

Therefore, half plane II is not a solution region of given inequality i.e. $x > - 3$ .

Also, the point on the line does not satisfy the inequality.

Thus, the solution to this inequality is the half plane I excluding points on this line.

This can be represented as follows:

1635762691903

Class 11 maths chapter 6 question answer - Exercise 6.3

Question:1 Solve the following system of inequalities graphically:

$x \geq 3,\ y\geq 2$

Answer:

$x \geq 3,\ y\geq 2$

Graphical representation of $x=3$ and $y=2$ is given in the graph below.

The line $x=3$ and $y=2$ divides plot in four regions i.e.I,II,III,IV.

For $x \geq 3$ ,

The solution to this inequality is region II and III including points on this line because points on the line also satisfy the inequality.

For $y \geq 2$ ,

The solution to this inequality is region IV and III including points on this line because points on the line also satisfy the inequality.

Hence, solution to $x \geq 3,\ y\geq 2$ is common region of graph i.e. region III.

Thus, solution of $x \geq 3,\ y\geq 2$ is region III.

This can be represented as follows:

1654687280859

The below green colour represents the solution

1654687281313

Question:2 Solve the following system of inequalities graphically: $3x +2y \leq 12,\ x \geq 1, \ y\geq 2$

Answer:

$3x +2y \leq 12,\ x \geq 1, \ y\geq 2$

Graphical representation of $x=1 \, \, ,3x+2y=12$ and $y=2$ is given in graph below.

For $x \geq 1$ ,

The solution to this inequality is region on right hand side of line $(x=1)$ including points on this line because points on the line also satisfy the inequality.

For $y \geq 2$ ,

The solution to this inequality is region above the line $(y=2)$ including points on this line because points on the line also satisfy the inequality.

For $3x+2y\leq 12$

The solution to this inequality is region below the line $(3x+2y= 12)$ including points on this line because points on the line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure including points on the respective lines.

This can be represented as follows:

1635762856044

Question:3 Solve the following system of inequalities graphically: $2x +y \geq 6, 3x +4y\leq 12$

Answer:

$2x +y \geq 6, 3x +4y\leq 12$

Graphical representation of $2x +y =6\, \, and\, \, 3x +4y=12$ is given in the graph below.

For $2x +y \geq 6$ ,

The solution to this inequality is region above line $(2x +y =6)$ including points on this line because points on the line also satisfy the inequality.

For $3x +4y\leq 12$ ,

The solution to this inequality is region below the line $( 3x +4y= 12)$ including points on this line because points on the line also satisfy the inequality.

Hence, the solution to these linear inequalities is the shaded region(ABC) as shown in figure including points on the respective lines.

This can be represented as follows:

1635762935162

Question:4 Solve the following system of inequalities graphically: $x + y \geq 4, 2x - y <0$

Answer:

$x + y \geq 4, 2x - y <0$

Graphical representation of $x +y =4\, \, and\, \, 2x -y=0$ is given in the graph below.

For $x + y \geq 4,$ ,

The solution to this inequality is region above line $(x +y =4)$ including points on this line because points on the line also satisfy the inequality.

For $2x - y <0$ ,

The solution to this inequality is half plane corresponding to the line $( 2x -y=0)$ containing point $(1,0)$ excluding points on this line because points on the line does not satisfy the inequality.

Hence, the solution to these linear inequalities is the shaded region as shown in figure including points on line $(x +y =4)$ and excluding points on the line $( 2x -y=0)$ .

This can be represented as follows:

1635763100696

Question:5 Solve the following system of inequalities graphically: $2x - y > 1, \ x -2y < -1$

Answer:

$2x - y > 1, \ x -2y < -1$

Graphical representation of $x -2y =-1\, \, and\, \, 2x -y=1$ is given in graph below.

For $2x - y > 1,$

The solution to this inequality is region below line $( 2x -y=1)$ excluding points on this line because points on line does not satisfy the inequality.

For $\ x -2y < -1$ ,

The solution to this inequality is region above the line $(x -2y =-1)$ excluding points on this line because points on line does not satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure excluding points on the lines.

This can be represented as follows:

1635763130508

Question:6 Solve the following system of inequalities graphically: $x + y \leq 6, x + y \geq 4$

Answer:

$x + y \leq 6, x + y \geq 4$

Graphical representation of $x + y = 6,\, \, and\, \, \, x + y = 4$ is given in the graph below.

For $x + y \leq 6,$

The solution to this inequality is region below line $( x+y=6)$ in cluding points on this line because points on the line also satisfy the inequality.

For $x + y \geq 4$ ,

The solution to this inequality is region above the line $( x+y=4)$ including points on this line because points on the line also satisfy the inequality.

Hence, the solution to these linear inequalities is shaded region as shown in figure including points on the lines.

This can be represented as follows:

1635763165801

Question:7 Solve the following system of inequalities graphically: $2x + y \geq 8 , x + 2y \geq 10$

Answer:

$2x + y \geq 8 , x + 2y \geq 10$

Graphical representation of $2x + y = 8\, \, and\, \, x + 2y =10$ is given in graph below.

For $2x + y \geq 8 ,$

The solution to this inequality is region above line $(2x + y = 8)$ including points on this line because points on line also satisfy the inequality.

For $x + 2y \geq 10$ ,

The solution to this inequality is region above the line $( x + 2y =10)$ including points on this line because points on line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure including points on the lines.

This can be represented as follows:

1635763179656

Question:8 Solve the following system of inequalities graphically: $x + y \leq 9, y > x, x\geq 0$

Answer:

$x + y \leq 9, y > x, x\geq 0$

Graphical representation of $x+y=9,x=y$ and $x=0$ is given in graph below.

For $x + y \leq 9$ ,

The solution to this inequality is region below line $(x+y=9)$ including points on this line because points on line also satisfy the inequality.

For $y > x$ ,

The solution to this inequality represents half plane corresponding to the line $(x=y)$ containing point $(0,1)$ excluding points on this line because points on line does not satisfy the inequality.

For $x\geq 0$ ,

The solution to this inequality is region on right hand side of the line $(x=0)$ including points on this line because points on line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure.

This can be represented as follows:

1635763196635

Question:9 Solve the following system of inequalities graphically: $5x+4y\leq20, \ x\geq 1, \ y\geq 2$

Answer:

$5x+4y\leq20, \ x\geq 1, \ y\geq 2$

Graphical representation of $\, ,5x+4y=20,\, \, \, x=1\, \, and \, \, y=2$ is given in graph below.

For $5x+4y\leq20,$ ,

The solution to this inequality is region below the line $(5x+4y=20)$ including points on this line because points on line also satisfy the inequality.

For $\ x\geq 1,$ ,

The solution to this inequality is region right hand side of the line $(x=1)$ including points on this line because points on line also satisfy the inequality.

For $\ y\geq 2,$

The solution to this inequality is region above the line $(y=2)$ including points on this line because points on line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure including points on the respective lines.

This can be represented as follows:

1635763228699

Question:10 Solve the following system of inequalities graphically: $3x + 4y \leq 60,\ x + 3y \leq 30, \ x \geq 0, \ y\geq 0$

Answer:

$3x + 4y \leq 60,\ x + 3y \leq 30, \ x \geq 0, \ y\geq 0$

Graphical representation of $3x+4y=60 \, \, ,x+3y=30\, \, \, ,x=0\, \, and\, \, y=0$ is given in graph below.

For $3x + 4y \leq 60$ ,

The solution to this inequality is region below the line $(3x+4y=60)$ including points on this line because points on line also satisfy the inequality.

For $\ x + 3y \leq 30$ ,

The solution to this inequality is region below the line $(x+3y=30)$ including points on this line because points on line also satisfy the inequality.

For $\ x \geq 0,$

The solution to this inequality is region right hand side of the line $(x=0)$ including points on this line because points on line also satisfy the inequality.

For $\ y \geq 0,$

The solution to this inequality is region above the line $(y=0)$ including points on this line because points on line also satisfy the inequality.

Hence, the solution to these linear inequalities is shaded region as shown in figure including points on the respective lines.

This can be represented as follows:

1635763315671

Question:11 Solve the following system of inequalities graphically: $2x +y \geq 4, \ x + y \leq 3, \ 2x - 3y \leq 6$

Answer:

$2x +y \geq 4, \ x + y \leq 3, \ 2x - 3y \leq 6$

Graphical representation of $2x+y=4 \, \, ,x+y=3$ and $2x-3y=6$ is given in graph below.

For $2x +y \geq 4,$ ,

The solution to this inequality is region above the line $(2x+y=4)$ including points on this line because points on line also satisfy the inequality.

For $\ x + y \leq 3,$ ,

The solution to this inequality is region below the line $(x+y=3)$ including points on this line because points on line also satisfy the inequality.

For $\ 2x - 3y \leq 6,$

The solution to this inequality is region above the line $(2x-3y= 6)$ including points on this line because points on line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure including points on the respective lines.

This can be represented as follows:

1635763400655

Question:12 Solve the following system of inequalities graphically: $x -2y \leq 3, 3x + 4y \geq 12, x \geq 0, y\geq 1$

Answer:

$x -2y \leq 3, 3x + 4y \geq 12, x \geq 0, y\geq 1$

Graphical representation of $x-2y=3 \, \, ,3x+4y=12\, \, \, ,x=0\, \, and\, \, y=1$ is given in graph below.

For $x -2y \leq 3$ ,

The solution to this inequality is region above the line $(x-2y=3)$ including points on this line because points on line also satisfy the inequality.

For $3x + 4y \geq 12$ ,

The solution to this inequality is region above the line $(3x+4y=12)$ including points on this line because points on line also satisfy the inequality.

For $\ x \geq 0,$

The solution to this inequality is region right hand side of the line $(x=0)$ including points on this line because points on line also satisfy the inequality.

For $\ y \geq 1,$

The solution to this inequality is region above the line $(y=1)$ including points on this line because points on line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure including points on the respective lines.

This can be represented as follows:

1635763420814

Question:13 Solve the following system of inequalities graphically: $4x + 3y \leq 60,\ y\geq 2x,\ x\geq 3,\ x,y\geq 0$

Answer:

$4x + 3y \leq 60,\ y\geq 2x,\ x\geq 3,\ x,y\geq 0$

Graphical representation of $4x+3y=60 \, \, ,y=2x\, \, \,,x=3\, \, ,x=0\, \, and\, \, y=0$ is given in graph below.

For $4x + 3y \leq 60,$

The solution to this inequality is region below the line $(4x+3y=60)$ including points on this line because points on the line also satisfy the inequality.

For $y\geq 2x$ ,

The solution to this inequality is region above the line $(y=2x)$ including points on this line because points on the line also satisfy the inequality.

For $x\geq 3$ ,

The solution to this inequality is region right hand side of the line $(x=3)$ including points on this line because points on the line also satisfy the inequality.

For $\ x \geq 0,$

The solution to this inequality is region right hand side of the line $(x=0)$ including points on this line because points on the line also satisfy the inequality.

For $\ y \geq 0,$

The solution to this inequality is region above the line $(y=0)$ including points on this line because points on line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure including points on the respective lines.

This can be represented as follows:

1635763491115

Question:14 Solve the following system of inequality graphically: $3x + 2y \leq 150, \ x +4y \leq 80,\ x\leq 15 \ y\geq 0, \ x\geq 0$

Answer:

$3x + 2y \leq 150, \ x +4y \leq 80,\ x\leq 15 \ y\geq 0, \ x\geq 0$

Graphical representation of $3x+2y=150 \, \, ,x+4y=80\, \, \,,x=15\, \, ,x=0\, \, and\, \, y=0$ is given in graph below.

For $3x + 2y \leq 150,$

The solution to this inequality is region below the line $(3x+2y=150)$ including points on this line because points on the line also satisfy the inequality.

For $x+4y\leq 80$ ,

The solution to this inequality is region below the line $(x+4y=80)$ including points on this line because points on the line also satisfy the inequality.

For $x\leq 15$ ,

The solution to this inequality is region left hand side of the line $(x=15)$ including points on this line because points on the line also satisfy the inequality.

For $\ x \geq 0,$

The solution to this inequality is region right hand side of the line $(x=0)$ including points on this line because points on the line also satisfy the inequality.

For $\ y \geq 0,$

The solution to this inequality is region above the line $(y=0)$ including points on this line because points on line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure including points on the respective lines.

This can be represented as follows:

1635763512601

Question:15 Solve the following system of inequality graphically: $x+2y \leq 10, \ x +y \geq 1, \ x-y\leq 0, x\geq 0, \ y\geq 0$

Answer:

$x+2y \leq 10, \ x +y \geq 1, \ x-y\leq 0, x\geq 0, \ y\geq 0$

Graphical representation of $x+2y=10 \, \, ,x+y=1\, \, \,,x-y=0\, \, ,x=0\, \, and\, \, y=0$ is given in graph below.

For $x+2y \leq 10,$

The solution to this inequality is region below the line $(x+2y=10)$ including points on this line because points on line also satisfy the inequality.

For $\ x +y \geq 1,$ ,

The solution to this inequality is region above the line $(x+y=1)$ including points on this line because points on line also satisfy the inequality.

For $\ x-y\leq 0,$ ,

The solution to this inequality is region above the line $(x-y=0)$ including points on this line because points on line also satisfy the inequality.

For $\ x \geq 0,$

The solution to this inequality is region right hand side of the line $(x=0)$ including points on this line because points on line also satisfy the inequality.

For $\ y \geq 0,$

The solution to this inequality is region above the line $(y=0)$ including points on this line because points on line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure including points on the respective lines.

This can be represented as follows:

1635763543684

Linear inequalities equations ncert solutions - Miscellaneous Exercise

Question:1 Solve the inequality $2\leq 3x-4\leq5$

Answer:

Given : $2\leq 3x-4\leq5$

$2\leq 3x-4\leq5$

$\Rightarrow\, \, 2+4\leq 3x\leq 5+4$

$\Rightarrow\, \, 6\leq 3x\leq 9$

$\Rightarrow\, \, \frac{6}{3}\leq x\leq \frac{9}{3}$

$\Rightarrow\, \, 2\leq x\leq 3$

Thus, all the real numbers greater than equal to 2 and less than equal to 3 are solutions to this inequality.

Solution set is $\left \[2,3 \right \]$

Question:2 Solve the inequality $6 \leq -3(2x - 4) < 12$

Answer:

Given $6 \leq -3(2x - 4) < 12$

$6 \leq -3(2x - 4) < 12$

$\Rightarrow\, \ \frac{6}{3}\leq -(2x-4)< \frac{12}{3}$

$\Rightarrow\, \ -2\geq (2x-4)> -4$

$\Rightarrow\, \ -2+4\geq 2x> -4+4$

$\Rightarrow\, \ 2\geq 2x> 0$

$\Rightarrow\, \ 1\geq x> 0$

Solution set is $(01]$

Question:3 Solve the inequality $-3 \leq 4 - \frac{7x}{2}\leq 18$

Answer:

Given $-3 \leq 4 - \frac{7x}{2}\leq 18$

$\Rightarrow \, \, -3 \leq 4 - \frac{7x}{2}\leq 18$

$\Rightarrow \, \, -3-4 \leq - \frac{7x}{2}\leq 18-4$

$\Rightarrow \, \, -7 \leq - \frac{7x}{2}\leq 14$

$\Rightarrow \, \, 7 \geq \frac{7x}{2} \geq -14$

$\Rightarrow \, \, 7\times 2 \geq 7x\geq -14\times 2$

$\Rightarrow \, \, 14 \geq 7x \geq -28$

$\Rightarrow \, \, \frac{14}{7} \geq x \geq \frac{-28}{7}$

$\Rightarrow \, \, 2 \geq x \geq -4$

Solution set is $[-4,2]$

Question:4 Solve the inequality $-15 < \frac{3(x-2)}{5} \leq 0$

Answer:

Given The inequality

$-15 < \frac{3(x-2)}{5} \leq 0$

$\Rightarrow\, \ -15\times 5< 3(x-2)\leq 0\times 5$

$\Rightarrow\, \ -75< 3(x-2)\leq 0$

$\Rightarrow\, \ \frac{-75}{3}< (x-2)\leq \frac{0}{3}$

$\Rightarrow\, \ -25< (x-2)\leq 0$

$\Rightarrow\, \ -25+2< x\leq 0+2$

$\Rightarrow\, \ -23< x\leq 2$

The solution set is $(-23,2]$

Question:5 Solve the inequality $-12<4-\frac{3x}{-5} \leq 2$

Answer:

Given the inequality

$-12<4-\frac{3x}{-5} \leq 2$

$\Rightarrow\, \, -12-4< -\frac{3x}{-5}\leq 2-4$

$\Rightarrow\, \, -16< -\frac{3x}{-5}\leq -2$

$\Rightarrow\, \, -16< \frac{3x}{5}\leq -2$

$\Rightarrow\, \, -16\times 5< 3x\leq -2\times 5$

$\Rightarrow\, \, -80< 3x\leq -10$

$\Rightarrow\, \, \frac{-80}{3}< 3x\leq \frac{-10}{3}$

Solution set is $(\frac{-80}{3}, \frac{-10}{3}]$

Question:6 Solve the inequality $7 \leq \frac{(3x+ 11)}{2}\leq 11$

Answer:

Given the linear inequality

$7 \leq \frac{(3x+ 11)}{2}\leq 11$

$\Rightarrow \, \, 7\times 2 \leq (3x+ 11)\leq 11\times 2$

$\Rightarrow \, \, 14 \leq (3x+ 11)\leq 22$

$\Rightarrow \, \, 14-11 \leq (3x)\leq 22-11$

$\Rightarrow \, \, 3 \leq 3x\leq 11$

$\Rightarrow \, \, 1 \leq x\leq \frac{11}{3}$

The solution set of the given inequality is $[1,\frac{11}{3}]$

Question:7 Solve the inequality and represent the solution graphically on number line. $5x + 1 > -24,\ 5x - 1 <24$

Answer:

Given : $5x + 1 > -24,\ 5x - 1 <24$

$5x + 1 > -24\, \, \, \, \, \, \, and\, \, \, \, \, \, \ 5x - 1 <24$

$\Rightarrow 5x > -24-1\, \, \, \, \, \, \, and\, \, \, \, \, \, \ 5x <24+1$

$\Rightarrow 5x > -25\, \, \, \, \, \, \, and\, \, \, \, \, \, \ 5x <25$

$\Rightarrow x > \frac{-25}{5}\, \, \, \, \, \, \, and\, \, \, \, \, \, \ x <\frac{25}{5}$

$\Rightarrow x > -5\, \, \, \, \, \, \, and\, \, \, \, \, \, \ x <5$

$(-5,5)$

The solution graphically on the number line is as shown :

1635763658335

Question:8 Solve the inequality and represent the solution graphically on number line. $2(x-1)<x+5,\ 3(x+2)> 2 -x$

Answer:

Given : $2(x-1)<x+5,\ 3(x+2)> 2 -x$

$2(x-1)<x+5\, \, \, \, and\, \, \, \, \, \ 3(x+2)> 2 -x$

$\Rightarrow \, \, 2x-2<x+5\, \, \, \, and\, \, \, \, \, \ 3x+6> 2 -x$

$\Rightarrow \, \, 2x-x<2+5\, \, \, \, and\, \, \, \, \, \ 3x+x> 2 -6$

$\Rightarrow \, \, x<7\, \, \, \, and\, \, \, \, \, \ 4x> -4$

$\Rightarrow \, \, x<7\, \, \, \, and\, \, \, \, \, \ x> -1$

$(-1,7)$

The solution graphically on the number line is as shown :

1635763681053

Question:9 Solve the inequality and represent the solution graphically on number line. $3x - 7 > 2(x-6),\ 6-x > 11 - 2x$

Answer:

Given : $3x - 7 > 2(x-6),\ 6-x > 11 - 2x$

$3x - 7 > 2(x-6)\, \, \, \, and\, \, \, \, \, \ 6-x > 11 - 2x$

$\Rightarrow \, \, 3x - 7 > 2x-12\, \, \, \, and\, \, \, \, \, \ 6-x > 11 - 2x$

$\Rightarrow \, \, 3x - 2x >7-12\, \, \, \, and\, \, \, \, \, \ 2x-x > 11 - 6$

$\Rightarrow \, \, x >-5\, \, \, \, and\, \, \, \, \, \ x > 5$

$x\in (5,\infty )$

The solution graphically on the number line is as shown :

1635763701201

Question:10 Solve the inequality and represent the solution graphically on number line.

$5(2x-7)-3(2x+3)\leq 0,\quad 2x + 19 \leq 6x +47$

Answer:

Given : $5(2x-7)-3(2x+3)\leq 0,\quad 2x + 19 \leq 6x +47$

$5(2x-7)-3(2x+3)\leq 0\, \, \, \, \, and\, \, \, \, \, \, \, \quad 2x + 19 \leq 6x +47$

$\Rightarrow \, \, 10x-35-6x-9\leq 0\, \, \, \, \, and\, \, \, \, \, \, \, \quad 2x -6x\leq 47-19$

$\Rightarrow \, \, 4x-44\leq 0\, \, \, \, \, and\, \, \, \, \, \, \, \quad -4x\leq 28$

$\Rightarrow \, \, 4x\leq 44\, \, \, \, \, and\, \, \, \, \, \, \, \quad 4x\geq - 28$

$\Rightarrow \, \, x\leq 11\, \, \, \, \, and\, \, \, \, \, \, \, \quad x\geq - 7$

$x\in [-7,11]$

The solution graphically on the number line is as shown :

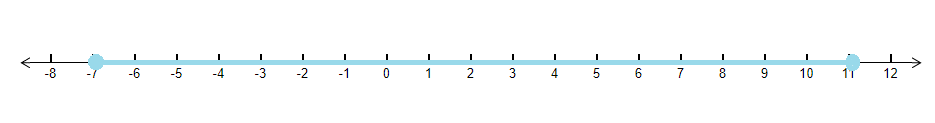
1635763730673

Question:11 A solution is to be kept between 68° F and 77° F. What is the range in temperature in degree Celsius (C) if the Celsius / Fahrenheit (F) conversion formula is given by $F = \frac{9}{5}C + 32$

Answer:

Since the solution is to be kept between 68° F and 77° F.

$68< F< 77$

Putting the value of $F = \frac{9}{5}C + 32$ , we have

$\Rightarrow \, \, \, 68< \frac{9}{5}C + 32< 77$

$\Rightarrow \, \, \, 68-32< \frac{9}{5}C < 77-32$

$\Rightarrow \, \, \, 36< \frac{9}{5}C < 45$

$\Rightarrow \, \, \, 36\times 5< 9C < 45\times 5$

$\Rightarrow \, \, \, 180< 9C < 225$

$\Rightarrow \, \, \, \frac{180}{9}< C < \frac{225}{9}$

$\Rightarrow \, \, \, 20< C < 25$

the range in temperature in degree Celsius (C) is between 20 to 25.

Question:12 A solution of 8% boric acid is to be diluted by adding a 2% boric acid solution to it. The resulting mixture is to be more than 4% but less than 6% boric acid. If we have 640 litres of the 8% solution, how many litres of the 2% solution will have to be added?

Answer:

Let x litres of 2% boric acid solution is required to be added.

Total mixture = (x+640) litres

The resulting mixture is to be more than 4% but less than 6% boric acid.

$\therefore \, 2\%x+8\%\, of\, 640> 4\%\, of\, (640+x)$ and $2\%x+8\%\, of\, 640< 6\%\, of\, (x+640)$

$\Rightarrow \, 2\%x+8\%\, of\, 640> 4\%\, of\, (640+x)$ and $2\%x+8\%\, of\, 640< 6\%\, of\, (x+640)$

$\Rightarrow \, \frac{2}{100}x+(\frac{8}{100}) 640> \frac{4}{100} (640+x)$ $\Rightarrow \, \frac{2}{100}x+(\frac{8}{100}) 640< \frac{6}{100} (640+x)$

$\Rightarrow \, 2x+5120> 4x+2560$ $\Rightarrow \, 2x+5120< 6x+3840$

$\Rightarrow \, 5120-2560> 4x-2x$ $\Rightarrow \, 5120-3840< 6x-2x$

$\Rightarrow \, 2560> 2x$ $\Rightarrow \, 1280< 4x$

$\Rightarrow \, 1280> x$ $\Rightarrow \, 320< x$

Thus, the number of litres 2% of boric acid solution that is to be added will have to be more than 320 and less than 1280 litres.

Question:13 How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?

Answer:

Let x litres of water is required to be added.

Total mixture = (x+1125) litres

It is evident that amount of acid contained in the resulting mixture is 45% of 1125 litres.

The resulting mixture contain more than 25 % but less than 30% acid.

$\therefore \, 30\%\, of\, (1125+x) > 45\%\, of\, (1125)$ and $25\%\, of\, (1125+x)< 45\%\, of\, 1125$

$\Rightarrow \, 30\%\, of\, (1125+x) > 45\%\, of\, (1125)$ and $25\%\, of\, (1125+x)< 45\%\, of\, 1125$

$\Rightarrow \, \frac{30}{100}(1125+x)> \frac{45}{100} (1125)$ $\Rightarrow \, (\frac{25}{100}) (1125+x)< \frac{45}{100} (1125)$

$\Rightarrow \, 30\times 1125+30x> 45\times (1125)$ $\Rightarrow \, 25 (1125+x)< 45(1125)$

$\Rightarrow \, 30x> (45-30)\times (1125)$ $\Rightarrow \, 25 x< (45-25)1125$

$\Rightarrow \, 30x> (15)\times (1125)$ $\Rightarrow \, 25 x< (20)1125$

$\Rightarrow \, x> \frac{15\times 1125}{30}$ $\Rightarrow \, x< \frac{20\times 1125}{25}$

$\Rightarrow \, x> 562.5$ $\Rightarrow \, x< 900$

Thus, the number of litres water that is to be added will have to be more than 562.5 and less than 900 litres.

Question:14 IQ of a person is given by the formula $IQ= \frac{MA}{CA}\times 100$ where MA is mental age and CA is chronological age. If $80\leq IQ\leq140$ for a group of 12 years old children, find the range of their mental age.

Answer:

Given that group of 12 years old children.

$80\leq IQ\leq140$

For a group of 12 years old children, CA =12 years

$IQ= \frac{MA}{CA}\times 100$

Putting the value of IQ, we obtain

$80\leq IQ\leq140$

$\Rightarrow \, \, 80\leq \frac{MA}{CA}\times 100\leq140$

$\Rightarrow \, \, 80\leq \frac{MA}{12}\times 100\leq140$

$\Rightarrow \, \, 80\times 12\leq MA\times 100\leq140\times 12$

$\Rightarrow \, \, \frac{80\times 12}{100}\leq MA\leq \frac{140\times 12}{100}$

$\Rightarrow \, \, 9.6\leq MA\leq 16.8$

Thus, the range of mental age of the group of 12 years old children is $\, \, 9.6\leq MA\leq 16.8$

Class 11 maths chapter 6 NCERT solutions - Symmary

Definition of Inequality: An inequality is a statement that two values are not equal. In mathematics, inequalities are used to compare values and to represent constraints in real-world problems.

Linear Inequalities: Linear inequalities are a type of inequality where the variables appear only in the first degree, that is, raised to the power of 1.

Solving Linear Inequalities: The process of finding all the possible values of the variable that satisfy a given linear inequality is called solving the inequality. In this chapter, various methods of solving linear inequalities are discussed.

Graphical Representation: Graphical representation is an important tool to visualize the solution of a linear inequality. The chapter 6 class 11 maths discusses how to plot linear inequalities on a coordinate plane.

Solution of System of Linear Inequalities: The NCERT solution for class 11 maths chapter 6 also discusses the solution of a system of linear inequalities, which involves finding the region on the coordinate plane that satisfies all the inequalities in the system.

Application in Real-World Problems: Linear inequalities are widely used in real-world problems, such as optimizing production, minimizing costs, and maximizing profits. The chapter provides various examples of real-world problems that can be solved using linear inequalities.

Linear Inequality Example

A manufacturing unit makes two models p and q of a product. Each piece of p requires 9 labour hours for fabricating and 1 labour hour for finishing. Each piece of q requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available are 180 and 30 respectively. The manufacturing unit makes a profit of Rs 8000 on each piece of p and Rs 12000 on each piece of Model q. Formulate this problem in linear equalities to maximize the profit.

The above problem can be formulated using linear inequalities and can be solved using linear programming which you will study in NCERT solutions for class 11 maths chapter 6 linear inequalities.

The above problem is formulated as follows.

Let x is the number of pieces of Model p and y is the number of pieces of Model q

We have to maximize the profit Z= 8000x+12000y subjected to the following constraints

$\\9x+12y\leq 180 \(fabricating \ constraint)\\x+3y\leq 30\ (finishing\ constraint)$

Linear Inequalities Exercise Wise Solutions

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

NCERT Solutions For Class 11 Mathematics - Chapter Wise

chapter-1	Sets
chapter-2	Relations and Functions
chapter-3	Trigonometric Functions
chapter-4	Principle of Mathematical Induction
chapter-5	Complex Numbers and Quadratic equations
chapter-6	Linear Inequalities
chapter-7	Permutation and Combinations
chapter-8	Binomial Theorem
chapter-9	Sequences and Series
chapter-10	Straight Lines
chapter-11	Conic Section
chapter-12	Three Dimensional Geometry
chapter-13	Limits and Derivatives
chapter-14	Mathematical Reasoning
chapter-15	Statistics
chapter-16	Probability

Key Features Of Linear Inequalities Class 11 Maths NCERT Chapter

Conceptual Clarity: The chapter begins by introducing the basic concepts of linear inequalities, ensuring that students understand the fundamental principles.

Real-Life Applications: Linear inequalities are explained with reference to real-life scenarios, helping students relate mathematical concepts to practical situations.

Inequality Notations: The chapter covers different types of inequality notations, such as "less than," "greater than," "less than or equal to," and "greater than or equal to".

NCERT Solutions For Class 11- Subject Wise

Benefits of NCERT Solutions

Linear inequalities equations ncert solutions will build your fundamentals which will be helpful in solving many real-life problems like maximizing the profit, minimizing the expenditure, allocating the resources with given constraints.
As all the above class 11 maths ch 6 question answer are prepared and explained in a step-by-step manner with the help of the graphs, it can be understood and visualize the problem easily.
NCERT solutions for maths chapter 6 class 11 will some innovative ways of solving the problems which become very important to solve some specific problems in an easy way.
This ch 6 maths class 11 also useful in the prediction of future events based on the past data which is the fundamentals of machine learning

NCERT Books and NCERT Syllabus

Happy Reading !!!

Frequently Asked Questions (FAQs)

1. What are important topics of the chapter Linear Inequalities ?

Inequalities class 11 includes the important topics such as Basic concept of inequalities, algebraic solutions of linear inequalities in one variable and their graphical representation, graphical solution of linear inequalities in two variables, and solution of system of linear inequalities in two variables. students should practice these concepts to get good a hold of the concepts discussed in class 11 chapter 6.

2. Explain the steps to plot a graph of linear inequality covered in NCERT Solutions for Class 11 Maths Chapter 6.

The steps to plot a graph of a linear inequality covered in linear inequalities class 11 ncert solutions are as follows:

Write the inequality in the form of a linear equation
Solve the equation for y
Identify the boundary line
Choose a test point
Substitute the test point
Shade the region
Identify the solution set
Label the graph

Students can find NCERT solutions for class 11 maths by clicking on the link.

3. List out the number of exercises present in NCERT solutions for class 11 maths chapter 6.

The linear inequalities class 11 solutions includes there three exercises and one miscellaneous exercise.

Exercise 6.1 – 26 Questions
Exercise 6.2 – 10 Questions
Exercise 6.3 – 15 Questions
Miscellaneous Exercise – 14 Questions

4. Which is the official website of NCERT ?

NCERT official is the official website of the NCERT where you can get NCERT textbooks and syllabus from class 1 to 12.

Also Read

NCERT Class 11 Chemistry Chapter 4 Notes Chemical Bonding and Molecular Structure - Download PDF

Hydrogen Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 9 Notes - Download PDF

The S-Block Elements Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 10 Notes - Download PDF

The P-Block Elements Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 11 Notes - Download PDF

Environmental Chemistry Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 14 Notes - Download PDF

NCERT Class 11 Chemistry Chapter 3 Notes - Download PDF

NCERT Solutions for Class 11 Physics Chapter 6 Work Energy and Power

NCERT Solutions for Class 11 Chemistry Chapter 5 States of Matter

NCERT Class 11 Physics Chapter 5 Notes Laws of Motion - Download PDF

NCERT Class 11 Physics Chapter 3 Notes Motion in a straight Line - Download PDF

NCERT Solutions for Exercise 10.1 Class 11 Maths Chapter 10 - Straight Lines

NCERT Solutions for Miscellaneous Exercise Chapter 16 Class 11 - Probability

NCERT Exemplar Class 11 Maths Solutions Chapter 12 Introduction to Three Dimensional Geometry

NCERT Exemplar Class 11 Maths Solutions Chapter 10 Straight Lines

NCERT Exemplar Class 11 Maths Solutions Chapter 6 Linear Inequalities

NCERT Exemplar Class 11 Maths Solutions Chapter 16 Probability

NCERT Exemplar Class 11 Maths Solutions Chapter 14 Mathematical Reasoning

NCERT Exemplar Class 11 Maths Solutions Chapter 7 Permutations and Combinations

Articles

How to Make APAAR ID via DigiLocker and School: A Complete Guide

Dec 17, 2024

Sainik School Entrance Exam 2025: Application, Exam Date, How to Apply, Syllabus

Dec 17, 2024

MVPP Scholarship Exam 2024: Mukhyamantri Vigyan Pratibha Pariksha Registration, Exam Date

Dec 16, 2024

Silverzone ISSO Answer Key 2024-25: Download PDF

Dec 16, 2024

Silverzone IOEL Answer Key 2024 – Download International Olympiad of English Language Solutions

Dec 16, 2024

Silverzone Olympiad IOM Answer Key 2024-25: Qualifying Marks, Score

Dec 16, 2024

Silverzone STEM Olympiad Answer Key 2024-25: Check Answer Key for all Classes

Dec 16, 2024

Silverzone ABHO Answer Key 2024 | Download Akhil Bhartiya Hindi Olympiad Solutions

Dec 16, 2024

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Eligibility Criteria

Application Process

Exam Pattern

Gujarat Board Higher Secondary School Certificate

Late Fee Application Date:13 December,2024 - 22 December,2024

Exam Pattern

Result

Admit Card

Madhya Pradesh State Open School 10th Examination

Admit Card Date:13 December,2024 - 31 December,2024

Admit Card

Result

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Class 11 Maths Chapter 6 Linear Inequalities

Linear Inequalities Class 11 Questions And Answers

Linear Inequalities Class 11 Questions And Answers PDF Free Download

Linear Inequalities Class 11 Solutions - Important Formulae And Points

Linear Inequalities Class 11 NCERT Solutions (Intext Questions and Exercise)

Class 11 maths chapter 6 NCERT solutions - Symmary

Linear Inequality Example

Linear Inequalities Exercise Wise Solutions

NCERT Solutions For Class 11 Mathematics - Chapter Wise

Key Features Of Linear Inequalities Class 11 Maths NCERT Chapter

NCERT Solutions For Class 11- Subject Wise

Benefits of NCERT Solutions

NCERT Books and NCERT Syllabus

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

Bihar Open Board 10th Examination

Bihar Open Board 12th Examination

National Means Cum-Merit Scholarship

Gujarat Board Higher Secondary School Certificate

Madhya Pradesh State Open School 10th Examination

Popular Questions

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

JEE Main Important Mathematics Formulas

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

Schools By Medium

By Ownership

By City

By State

NVS

JNVST

Download Careers360 App

All this at the convenience of your phone

Scan and download the app