• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Exercise 6.1 Class 11 Maths Chapter 6 - Linear Inequalities

NCERT Solutions for Exercise 6.1 Class 11 Maths Chapter 6 - Linear Inequalities

Edited By Vishal kumar | Updated on Nov 06, 2023 12:01 PM IST

NCERT Solutions for Class 11 Maths Chapter 6 - Linear Inequalities Exercise 6.1- Download Free PDF

NCERT Solutions for Class 11 Maths Chapter 6: Linear Inequalities Exercise 6.1- NCERT Solutions for Exercise 6.1 Class 11 Maths Chapter 6 is the very first exercise of the chapter Linear Inequalities. The NCERT has covered linear equations in the lower classes. The concepts of linear inequalities are introduced in the NCERT Class 11 Maths book and these concepts are important in solving problems in various fields like economics, optimisation problems, statistics, mathematics etc. Class 11 maths ex 6.1 gives practice problems on solving inequalities in one variable. Also, NCERT solutions for exercise 6.1 Class 11 Maths chapter 6 covers forming an inequality in one variable and solving them.

JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy

Suggested: JEE Main: high scoring chapters | Past 10 year's papers

This Story also Contains
  1. NCERT Solutions for Class 11 Maths Chapter 6 - Linear Inequalities Exercise 6.1- Download Free PDF
  2. Access Linear Inequalities Class 11 Chapter 6- Exercise: 6.1
  3. More About NCERT Solutions for Class 11 Maths Chapter 6 Exercise 6.1
  4. Key Features of NCERT 11th Class Maths Exercise 6.1 Answers
  5. NCERT Solutions of Class 11 Subject Wise
  6. Subject Wise NCERT Exampler Solutions
NCERT Solutions for Exercise 6.1 Class 11 Maths Chapter 6 - Linear Inequalities
NCERT Solutions for Exercise 6.1 Class 11 Maths Chapter 6 - Linear Inequalities

NCERT book Class 11 Maths chapter 6 exercise 6.1 mainly deals with solutions of inequalities in one variable. A few more exercises are coming after NCERT syllabus 11th class maths exercise 6.1 answers. Those are listed below, which are prepared by subject matter experts at Careers360. They are presented in a straightforward language that is easy to comprehend. Additionally, these resources are available in PDF format, enabling students to access them at their convenience, free of cost, and without requiring an internet connection.

Linear Inequalities Exercise 6.2

Linear Inequalities Exercise 6.3

Linear Inequalities Miscellaneous Exercise

**As per the new CBSE Syllabus for 2023-24, this chapter has been assigned a different number, and it is now referred to as Chapter 5.

Download the PDF of NCERT Solutions for Class 11 Maths Chapter 6 – Linear Inequalities Exercise 6.1

Download PDF


Access Linear Inequalities Class 11 Chapter 6- Exercise: 6.1

Question:1(i) Solve 24x < 100 , when
x i s a natural number.

Answer:

Given : 24x < 100

\Rightarrow 24x < 100

Divide by 24 from both sides

\Rightarrow \, \, \, \frac{24}{24}x< \frac{100}{24}

\Rightarrow \, \, \, x< \frac{25}{6}

\Rightarrow \, \, \, x< 4.167

x i s a natural number which is less than 4.167.

Hence, values of x can be \left \{ 1,2,3,4 \right \}

Question:1(ii) Solve 24x< 100 , when

x is an integer.

Answer:

Given : 24x < 100

\Rightarrow 24x < 100

Divide by 24 from both sides

\Rightarrow \, \, \, \frac{24}{24}x< \frac{100}{24}

\Rightarrow \, \, \, x< \frac{25}{6}

\Rightarrow \, \, \, x< 4.167

x i s are integers which are less than 4.167.

Hence, values of x can be \left \{..........-3,-2,-1,0, 1,2,3,4 \right \}

Question:2(i) Solve -12x>30 , when
x is a natural number.

Answer:

Given : -12x>30

\Rightarrow -12x>30

Divide by -12 from both side

\Rightarrow \, \, \, \frac{-12}{-12}x< \frac{30}{-12}

\Rightarrow \, \, \, x< \frac{30}{-12}

\Rightarrow \, \, \, x< -2.5

x i s a natural number which is less than - 2.5.

Hence, the values of x do not exist for given inequality.

Question:2(ii) Solve - 12x > 30 , when

x is an integer.

Answer:

Given : -12x>30

\Rightarrow -12x>30

Divide by -12 from both side

\Rightarrow \, \, \, \frac{-12}{-12}x< \frac{30}{-12}

\Rightarrow \, \, \, x< \frac{30}{-12}

\Rightarrow \, \, \, x< -2.5

x are integers less than - 2.5 .

Hence, values of x can be \left \{ .............,-6,-5,-4,-3 \right \}

Question:3(i) Solve 5x - 3 < 7 , when

x is an integer.

Answer:

Given : 5x - 3 < 7

\Rightarrow 5x - 3 < 7

\Rightarrow \, \, \, 5x< 10

Divide by 5 from both sides

\Rightarrow \, \, \, \frac{5}{5}x< \frac{10}{5}

\Rightarrow \, \, \, x< 2

x are integers less than 2

Hence, values of x can be \left \{.........-3,-2-1,0,1,\right \}

Question:3(ii) Solve 5x - 3 < 7 , when

x is a real number.

Answer:

Given : 5x - 3 < 7

\Rightarrow 5x - 3 < 7

\Rightarrow \, \, \, 5x< 10

Divide by 5 from both sides

\Rightarrow \, \, \, \frac{5}{5}x< \frac{10}{5}

\Rightarrow \, \, \, x< 2

x are real numbers less than 2

i.e. x\in (-\infty ,2)

Question:4(i) Solve 3x + 8 >2 , when
x is an integer.

Answer:

Given : 3x + 8 >2

\Rightarrow 3x + 8 >2

\Rightarrow \, \, \, 3x> -6

Divide by 3 from both sides

\Rightarrow \, \, \, \frac{3}{3}x> \frac{-6}{3}

\Rightarrow \, \, \, x> - 2

x are integers greater than -2

Hence, the values of x can be \left \{-1,0,1,2,3,4...............\right \} .

Question:4(ii) Solve 3x + 8 >2 , when ) x is a real number.

Answer:

Given : 3x + 8 >2

\Rightarrow 3x + 8 >2

\Rightarrow \, \, \, 3x> -6

Divide by 3 from both side

\Rightarrow \, \, \, \frac{3}{3}x> \frac{-6}{3}

\Rightarrow \, \, \, x> - 2

x are real numbers greater than -2

Hence , values of x can be as x\in (-2,\infty )

Question:5 Solve the inequality for real x . 4x + 3 < 5x + 7

Answer:

Given : 4x + 3 < 5x + 7

\Rightarrow4x + 3 < 5x + 7

\Rightarrow \, \, \, 4x-5x< 7-3

\Rightarrow \, \, \, x> -4

x are real numbers greater than -4.

Hence, values of x can be as x\in (-4 ,\infty )

Question:6 Solve the inequality for real x 3x - 7 > 5x -1

Answer:

Given : 3x - 7 > 5x -1

\Rightarrow3x - 7 > 5x -1

\Rightarrow \, \, \, -2x> 6

\Rightarrow \, \, \, x< \frac{6}{-2}

\Rightarrow \, \, \, x< -3

x are real numbers less than -3.

Hence, values of x can be x\in (-\infty ,-3)

Question:7 Solve the inequality for real x . 3(x-1) \leq 2(x-3)

Answer:

Given : 3(x-1) \leq 2(x-3)

\Rightarrow3(x-1) \leq 2(x-3)

\Rightarrow \, \, \, 3x-3\leq 2x-6

\Rightarrow \, \, \, 3x-2x\leq -6+3

\Rightarrow \, \, \, x\leq -3

x are real numbers less than equal to -3

Hence , values of x can be as , x\in (-\infty ,-3]

Question:8 Solve the inequality for real x 3(2- x) \geq 2(1-x)

Answer:

Given : 3(2- x) \geq 2(1-x)

\Rightarrow3(2- x) \geq 2(1-x)

\Rightarrow \, \, \, 6-3x\geq 2-2x

\Rightarrow \, \, \, 6-2\geq 3x-2x

\Rightarrow \, \, \, 4\geq x

x are real numbers less than equal to 4

Hence, values of x can be as x\in (-\infty ,4]

Question:9 Solve the inequality for real x x + \frac{x}{2} + \frac{x}{3} < 11

Answer:

Given : x + \frac{x}{2} + \frac{x}{3} < 11

\Rightarrowx + \frac{x}{2} + \frac{x}{3} < 11

\Rightarrow \, \, \, x(1+\frac{1}{2}+\frac{1}{3})< 11

\Rightarrow \, \, \, x(\frac{11}{6})< 11

\Rightarrow \, \, \, 11 x< 11\times 6

\Rightarrow \, \, \, x< 6

x are real numbers less than 6

Hence, values of x can be as x\in (-\infty ,6)

Question:10 Solve the inequality for real x . \frac{x}{3} > \frac{x}{2} + 1

Answer:

Given : \frac{x}{3} > \frac{x}{2} + 1

\Rightarrow\frac{x}{3} > \frac{x}{2} + 1

\Rightarrow \, \, \, \frac{x}{3}-\frac{x}{2}> 1

\Rightarrow \, \, \,x (\frac{1}{3}-\frac{1}{2})> 1

\Rightarrow \, \, \,x (-\frac{1}{6})> 1

\Rightarrow \, \, \, -x > 6

\Rightarrow \, \, \, x< -6

x are real numbers less than -6

Hence, values of x can be as x\in (-\infty ,-6)

Question:11 Solve the inequality for real x \frac{3(x-2)}{5} \leq \frac{5(2-x)}{3}

Answer:

Given : \frac{3(x-2)}{5} \leq \frac{5(2-x)}{3}

\Rightarrow\frac{3(x-2)}{5} \leq \frac{5(2-x)}{3}

\Rightarrow \, \, \, 9(x-2)\leq 25(2-x)

\Rightarrow \, \, \, 9x-18\leq 50-25x

\Rightarrow \, \, \, 9x+25x\leq 50+18

\Rightarrow \, \, \, 34x\leq 68

\Rightarrow \, \, \, x\leq 2

x are real numbers less than equal to 2.

Hence, values of x can be as x\in (-\infty ,2]

Question:12 Solve the inequality for real x \frac{1}{2}\left(\frac{3x}{5} + 4 \right ) \geq \frac{1}{3}(x - 6)

Answer:

Given : \frac{1}{2}\left(\frac{3x}{5} + 4 \right ) \geq \frac{1}{3}(x - 6)

\Rightarrow\frac{1}{2}\left(\frac{3x}{5} + 4 \right ) \geq \frac{1}{3}(x - 6)

\Rightarrow \, \, 3\left(\frac{3x}{5} + 4 \right ) \geq 2(x - 6)

\Rightarrow \, \, \frac{9x}{5} + 12 \geq 2x-12

\Rightarrow \, \, 12+12 \geq 2x-\frac{9x}{5}

\Rightarrow \, \, 24 \geq \frac{x}{5}

\Rightarrow \, \, 120 \geq x

x are real numbers less than equal to 120.

Hence, values of x can be as x\in (-\infty,120 ] .

Question:13 Solve the inequality for real x 2(2x + 3) - 10 < 6(x-2)

Answer:

Given : 2(2x + 3) - 10 < 6(x-2)

\Rightarrow2(2x + 3) - 10 < 6(x-2)

\Rightarrow \, \, \, 4x+6-10 < 6x-12

\Rightarrow \, \, \, 6-10+12 < 6x-4x

\Rightarrow \, \, \, 8 < 2x

\Rightarrow \, \, \, 4 < x

x are real numbers greater than 4

Hence , values of x can be as x\in (4,\infty )

Question:14 Solve the inequality for real x 37 - (3x + 5) \geq 9x - 8(x-3)

Answer:

Given : 37 - (3x + 5) \geq 9x - 8(x-3)

\Rightarrow37 - (3x + 5) \geq 9x - 8(x-3)

\Rightarrow \, \, \, 37 - 3x - 5 \geq 9x - 8x+24

\Rightarrow \, \, \, 32 - 3x \geq x+24

\Rightarrow \, \, \, 32 - 24 \geq x+3x

\Rightarrow \, \, \, 8 \geq 4x

\Rightarrow \, \, \, 2\geq x

x are real numbers less than equal to 2.

Hence , values of x can be as x\in (-\infty ,2]

Question:15 Solve the inequality for real x \frac{x}{4}< \frac{(5x-2)}{3} - \frac{(7x-3)}{5}

Answer:

Given : \frac{x}{4}< \frac{(5x-2)}{3} - \frac{(7x-3)}{5}

\Rightarrow \frac{x}{4}< \frac{(5x-2)}{3} - \frac{(7x-3)}{5}

\Rightarrow \, \, \, \, 15x< 20(5x-2)-12(7x-3)

\Rightarrow \, \, \, \, 15x< 100x-40-84x+36

\Rightarrow \, \, \, \, 15x< 16x-4

\Rightarrow \, \, \, \, 4< x

x are real numbers greater than 4.

Hence, values of x can be as x\in (4,\infty)

Question:16 Solve the inequality for real x \frac{(2x - 1)}{3} \geq \frac{3x-2}{4} - \frac{(2-x)}{5}

Answer:

Given : \frac{(2x - 1)}{3} \geq \frac{3x-2}{4} - \frac{(2-x)}{5}

\Rightarrow\frac{(2x - 1)}{3} \geq \frac{3x-2}{4} - \frac{(2-x)}{5}

\Rightarrow \, \, \, 20(2x - 1) \geq 15(3x-2) - 12(2-x)

\Rightarrow \, \, \, 40x - 20 \geq 45x-30 - 24+12x

\Rightarrow \, \, \, 30+24 - 20 \geq 45x-40x+12x

\Rightarrow \, \, \, 34 \geq 17x

\Rightarrow \, \, \, 2 \geq x

x are real numbers less than equal 2.

Hence, values of x can be as x\in (-\infty,2 ] .

Question:17 Solve the inequality and show the graph of the solution on number line 3x - 2 < 2x + 1

Answer:

Given : 3x - 2 < 2x + 1

\Rightarrow3x - 2 < 2x + 1

\Rightarrow \, \, \, 3x - 2x< 2 + 1

\Rightarrow \, \, \, x< 3

x are real numbers less than 3

Hence, values of x can be as x\in (-\infty ,3)

The graphical representation of solutions of the given inequality is as :

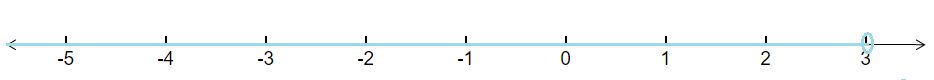
1635762263704

Question:18 Solve the inequality and show the graph of the solution on number line 5x - 3 \geq 3x -5

Answer:

Given : 5x - 3 \geq 3x -5

\Rightarrow5x - 3 \geq 3x -5

\Rightarrow \, \, \, 5x - 3x \geq 3 -5

\Rightarrow \, \, \, 2x \geq -2

\Rightarrow \, \, \, x \geq -1

x are real numbers greater than equal to -1.

Hence, values of x can be as x\in [-1,\infty )

The graphical representation of solutions of the given inequality is as :

1635762285990

Question:19 Solve the inequality and show the graph of the solution on number line 3(1-x) < 2 (x +4)

Answer:

Given : 3(1-x) < 2 (x +4)

\Rightarrow3(1-x) < 2 (x +4)

\Rightarrow \, \, \, 3- 3x< 2x + 8

\Rightarrow \, \, \, 3- 8< 2x + 3x

\Rightarrow \, \, \, -5< 5 x

\Rightarrow \, \, \, -1< x

x are real numbers greater than -1

Hence, values of x can be as x\in (-1,\infty )

The graphical representation of solutions of given inequality is as :

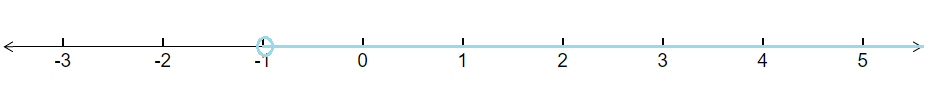
1635762322180

Question:20 Solve the inequality and show the graph of the solution on number line \frac{x}{2} \geq \frac{(5x-2)}{3} - \frac{(7x-3)}{5}

Answer:

Given : \frac{x}{2} \geq \frac{(5x-2)}{3} - \frac{(7x-3)}{5}

\Rightarrow\frac{x}{2} \geq \frac{(5x-2)}{3} - \frac{(7x-3)}{5}

\Rightarrow \, \, \, 15x \geq 10(5x-2) - 6(7x-3)

\Rightarrow \, \, \, 15x \geq 50x-20 - 42x+18

\Rightarrow \, \, \, 15x+42x-50x \geq 18-20

\Rightarrow \, \, \, 7x \geq -2

\Rightarrow \, \, \, x \geq \frac{-2}{7}

x are real numbers greater than equal to = \frac{-2}{7}

Hence, values of x can be as x\in (-\frac{2}{7},\infty )

The graphical representation of solutions of the given inequality is as :

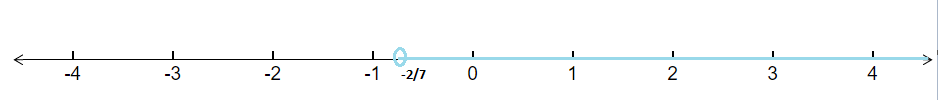
1635762357828

Question:21 Ravi obtained 70 and 75 marks in first two unit test. Find the minimum marks he should get in the third test to have an average of at least 60 marks.

Answer:

Let x be marks obtained by Ravi in the third test.

The student should have an average of at least 60 marks.

\therefore \, \, \, \frac{70+75+x}{3}\geq 60

\, \, \, 145+x\geq 180

x\geq 180-145

x\geq 35

the student should have minimum marks of 35 to have an average of 60

Question:22 To receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94 and 95, find minimum marks that Sunita must obtain in fifth examination to get grade ‘A’ in the course.

Answer:

Sunita’s marks in the first four examinations are 87, 92, 94 and 95.

Let x be marks obtained in the fifth examination.

To receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations.

\therefore \, \, \, \frac{87+92+94+95+x}{5}\geq 90

\Rightarrow \, \, \, \frac{368+x}{5}\geq 90

\Rightarrow \, \, \, 368+x\geq 450

\Rightarrow \, \, \, x\geq 450-368

\Rightarrow \, \, \, x\geq 82

Thus, Sunita must obtain 82 in the fifth examination to get grade ‘A’ in the course.

Question:23 Find all pairs of consecutive odd positive integers both of which are smaller than 10 such that their sum is more than 11.

Answer:

Let x be smaller of two consecutive odd positive integers. Then the other integer is x+2.

Both integers are smaller than 10.

\therefore \, \, \, x+2< 10

\Rightarrow \, \, \, \, x< 10-2

\Rightarrow \, \, \, \, x< 8

Sum of both integers is more than 11.

\therefore \, \, \, x+(x+2)> 11

\Rightarrow \, \, \, (2x+2)> 11

\Rightarrow \, \, \, 2x> 11-2

\Rightarrow \, \, \, 2x> 9

\Rightarrow \, \, \, x> \frac{9}{2}

\Rightarrow \, \, \, x> 4.5

We conclude \, \, \, \, x< 8 and \, \, \, x> 4.5 and x is odd integer number.

x can be 5,7.

The two pairs of consecutive odd positive integers are (5,7)\, \, \, and\, \, \, (7,9) .

Question:24 Find all pairs of consecutive even positive integers, both of which are larger than 5 such that their sum is less than 23.

Answer:

Let x be smaller of two consecutive even positive integers. Then the other integer is x+2.

Both integers are larger than 5.

\therefore \, \, \, x> 5

Sum of both integers is less than 23.

\therefore \, \, \, x+(x+2)< 23

\Rightarrow \, \, \, (2x+2)< 23

\Rightarrow \, \, \, 2x< 23-2

\Rightarrow \, \, \, 2x< 21

\Rightarrow \, \, \, x< \frac{21}{2}

\Rightarrow \, \, \, x< 10.5

We conclude \, \, \, \, x< 10.5 and \, \, \, x> 5 and x is even integer number.

x can be 6,8,10.

The pairs of consecutive even positive integers are (6,8),(8,10),(10,12) .

Question:25 The longest side of a triangle is 3 times the shortest side and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side.

Answer:

Let the length of the smallest side be x cm.

Then largest side = 3x cm.

Third side = 3x-2 cm.

Given: The perimeter of the triangle is at least 61 cm.

\therefore\, \, \, x+3x+(3x-2)\geq 61

\Rightarrow \, \, \, 7x-2\geq 61

\Rightarrow \, \, \, 7x\geq 61+2

\Rightarrow \, \, \, 7x\geq 63

\Rightarrow \, \, \, x\geq \frac{63}{7}

\Rightarrow \, \, \, x\geq 9

Minimum length of the shortest side is 9 cm.

Question:26 A man wants to cut three lengths from a single piece of board of length 91cm. The second length is to be 3cm longer than the shortest and the third length is to be twice as long as the shortest. What are the possible lengths of the shortest board if the third piece is to be at least 5cm longer than the second?

[ Hint : If x is the length of the shortest board, then x , (x + 3) and 2x are the lengths of the second and third piece, respectively. Thus, x + (x + 3) + 2x \leq 91 and 2x \geq (x + 3) + 5 ].

Answer:

Let x is the length of the shortest board,

then (x + 3) and 2x are the lengths of the second and third piece, respectively.

The man wants to cut three lengths from a single piece of board of length 91cm.

Thus, x + (x + 3) + 2x \leq 91

4x+3\leq 91

\Rightarrow \, \, \, \, 4x\leq 91-3

\Rightarrow \, \, \, \, 4x\leq 88

\Rightarrow \, \, \, \, x\leq \frac{88}{4}

\Rightarrow \, \, \, \, x\leq 22

if the third piece is to be at least 5cm longer than the second, than

2x \geq (x + 3) + 5

\Rightarrow \, \, \, \, 2x\geq x+8

\Rightarrow \, \, \, \, 2x-x\geq 8

\Rightarrow \, \, \, \, x\geq 8

We conclude that \, \, \, \, x\geq 8 and \, \, \, \, x\leq 22 .

Thus , 8\leq x\leq 22 .

Hence, the length of the shortest board is greater than equal to 8 cm and less than equal to 22 cm.

More About NCERT Solutions for Class 11 Maths Chapter 6 Exercise 6.1

A total of twenty-six practice problems are given in the Class 11 Maths ch 6 ex 6.1. Solutions to exercise 6.1 Class 11 Maths are written in detail in this page for NCERT solutions for Class 11 Maths chapter 6 exercise 6.1. Questions 21 to 26 of 11th class maths exercise 6.1 answers are to form Linear Inequalities in one variable from the given statements. After Class 11th Maths chapter 6 exercise 6.1 linear inequalities in two variables are introduced in the NCERT book.

Also Read| Linear Inequalities Class 11th Notes

Benefits of NCERT Solutions for Class 11 Maths Chapter 6 Exercise 6.1

  • The NCERT syllabus Class 11 chapter Linear Inequalities gives an insight into the basic concepts of linear inequalities and the exercise 6.1 Class 11 Maths gives practice questions on this.

  • NCERT Solutions for Class 11 Maths chapter 6 exercise 6.1 give an idea of forming linear inequalities in one variable and solving them.

Key Features of NCERT 11th Class Maths Exercise 6.1 Answers

  1. Step-by-step explanations: Detailed, step-by-step ex 6.1 class 11 solutions for each problem to help students understand the concepts and problem-solving techniques.

  2. Clarity and accuracy: Clear and precise presentation, ensuring students can confidently prepare for their exams and improve their understanding.

  3. Variety of practice problems: Class 11 maths ex 6.1 typically includes a range of practice problems to help students reinforce their knowledge and problem-solving skills.

  4. Accessibility: These class 11 ex 6.1 solutions are often available for free, making them easily accessible to students.

  5. Format options: PDF versions of the solutions may be provided, allowing students to download and use them conveniently, both online and offline.

JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

Also See-

NCERT Solutions of Class 11 Subject Wise

Subject Wise NCERT Exampler Solutions

Frequently Asked Questions (FAQs)

1. Give an example of numerical inequality.

3<5 represents a numerical inequality

2. Write some examples of literal inequalities

x<5, y>2 etc...

3. Can you write a double inequality?

Yes, an example for double inequality is 3<5<7

4. List two inequalities in one variable

2x+3<0

2x+3>0

5. Write two inequalities in two variable

3x+4y>7

5x-2y<3

6. Write a quadratic inequality in one variable

2x^2+2x-2>0

7. Whether quadratic inequalities are solved in the exercise 6.1 Class 11 Maths

No, the NCERT solutions for Class 11 Maths chapter 6 exercise 6.1 deal with linear inequalities in one variable.

8. Give examples of strict inequalities

2x+3<0

5x+2y<0

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 10th examination

Application Date:21 November,2024 - 20 December,2024

National Institute of Open Schooling 12th Examination

Application Date:21 November,2024 - 20 December,2024

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

West Bengal Board 12th Examination

Exam Date:02 December,2024 - 20 December,2024

Gujarat Board Secondary School Certificate Examination

Late Fee Application Date:11 December,2024 - 20 December,2024

View All School Exams
Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
CBSE files police complaint against two Delhi schools for submitting fake land certificates
Several Delhi schools receive bomb threat; fifth incident in nine days
Schools, colleges in Delhi NCR to switch to hybrid mode in view of air pollution
‘Take action’ on 22,298 unrecognised schools in UDISE Plus by March: Education ministry to states
Shiv Nadar School concludes 'Anandam 2024'; celebrating art, creativity in digital age
Jaipur: 10 students hospitalised after suspected gas leak at Mahesh Nagar coaching institute
Student not allowed to enter classroom without removing tilak from forehead in Rishikesh
Back to top