NCERT Solutions for Miscellaneous Exercise Chapter 6 Class 11

Q: What is question number 11 of NCERT solutions for Class 11 Maths chapter 6 miscellaneous exercise?

It’s about finding the range of temperature in degrees Celsius. Given the range of Fahrenheit.

Q: Give the solutions of 3x-6≥0

The solution is 3x≥6 Or x ≥ 2. The solution is the right-hand side of the line x=2 including the points on the line. The graphical representation is given in the NCERT Class 11 Maths book chapter 6 example 10.

Q: How many exercises are solved in NCERT syllabus chapter 6 Class 11?

4 exercises are discussed in NCERT Class 11 Maths chapter 6

Q: How many questions are solved in the Class 11 Maths chapter 6 miscellaneous exercise solutions?

Fourteen questions are solved in Linear Inequality Class 11 NCERT Maths chapter 6 miscellaneous exercise

NCERT Solutions for Miscellaneous Exercise Chapter 6 Class 11 - Linear Inequalities

Edited By Vishal kumar | Updated on Nov 16, 2023 12:38 PM IST

NCERT Solutions for Class 11 Maths Chapter 6: Linear Inequalities Miscellaneous Exercise- Download Free PDF

NCERT solutions for Class 11 Maths Chapter 6 miscellaneous exercises are the solutions to the practice questions given at the end of the chapter. The Class 11 Maths Chapter 6 miscellaneous exercise solutions cover all the topics of the chapter linear inequalities. The questions based on all other three exercises of the chapter are discussed in the Class 11 Maths chapter 6 miscellaneous solutions. Miscellaneous exercise Chapter 6 Class 11 gives more practice questions of the concepts discussed in the chapter linear inequalities.

JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy

Suggested: JEE Main: high scoring chapters | Past 10 year's papers

This Story also Contains

NCERT Solutions for Class 11 Maths Chapter 6: Linear Inequalities Miscellaneous Exercise- Download Free PDF
Download the PDF of NCERT Solutions for Class 11 Maths Chapter 6 – Linear Inequalities Miscellaneous Exercise
Access Linear Inequalities Class 11 NCERT Maths- Miscellaneous Exercise
More About NCERT Solutions for Class 11 Maths Chapter 6 Miscellaneous Exercises
Benefits of NCERT Solutions for Class 11 Maths Chapter 6 Miscellaneous Exercises
Topics Covered in Miscellaneous Exercise Class 11 Chapter 6
Key Features of Class 11 Maths ch 6 Miscellaneous Exercise Solutions
NCERT Solutions of Class 11 Subject Wise
Subject Wise NCERT Exampler Solutions

The class 11 chapter 6 maths miscellaneous solutions provided by subject experts at Careers360 are presented in a clear and easily understandable language. They are crafted in a step-by-step format, ensuring simplicity and clarity for students. Additionally, PDF versions of the class 11 maths ch 6 miscellaneous exercise solutions are available, allowing students to choose the format that suits their preferences and comfort. The other exercises discussed in the NCERT book chapter linear inequalities are discussed below.

**In the CBSE Syllabus for 2023-24, miscellaneous exercise class 11 chapter 6 has been renumbered as Chapter 5.

Download the PDF of NCERT Solutions for Class 11 Maths Chapter 6 – Linear Inequalities Miscellaneous Exercise

Download PDF

Access Linear Inequalities Class 11 NCERT Maths- Miscellaneous Exercise

Question:1 Solve the inequality $2\leq 3x-4\leq5$

Answer:

Given : $2\leq 3x-4\leq5$

$2\leq 3x-4\leq5$

$\Rightarrow\, \, 2+4\leq 3x\leq 5+4$

$\Rightarrow\, \, 6\leq 3x\leq 9$

$\Rightarrow\, \, \frac{6}{3}\leq x\leq \frac{9}{3}$

$\Rightarrow\, \, 2\leq x\leq 3$

Thus, all the real numbers greater than equal to 2 and less than equal to 3 are solutions to this inequality.

Solution set is $\left \[2,3 \right \]$

Question:2 Solve the inequality $6 \leq -3(2x - 4) < 12$

Answer:

Given $6 \leq -3(2x - 4) < 12$

$6 \leq -3(2x - 4) < 12$

$\Rightarrow\, \ \frac{6}{3}\leq -(2x-4)< \frac{12}{3}$

$\Rightarrow\, \ -2\geq (2x-4)> -4$

$\Rightarrow\, \ -2+4\geq 2x> -4+4$

$\Rightarrow\, \ 2\geq 2x> 0$

$\Rightarrow\, \ 1\geq x> 0$

Solution set is $(01]$

Question:3 Solve the inequality $-3 \leq 4 - \frac{7x}{2}\leq 18$

Answer:

Given $-3 \leq 4 - \frac{7x}{2}\leq 18$

$\Rightarrow \, \, -3 \leq 4 - \frac{7x}{2}\leq 18$

$\Rightarrow \, \, -3-4 \leq - \frac{7x}{2}\leq 18-4$

$\Rightarrow \, \, -7 \leq - \frac{7x}{2}\leq 14$

$\Rightarrow \, \, 7 \geq \frac{7x}{2} \geq -14$

$\Rightarrow \, \, 7\times 2 \geq 7x\geq -14\times 2$

$\Rightarrow \, \, 14 \geq 7x \geq -28$

$\Rightarrow \, \, \frac{14}{7} \geq x \geq \frac{-28}{7}$

$\Rightarrow \, \, 2 \geq x \geq -4$

Solution set is $[-4,2]$

Question:4 Solve the inequality $-15 < \frac{3(x-2)}{5} \leq 0$

Answer:

Given The inequality

$-15 < \frac{3(x-2)}{5} \leq 0$

$\Rightarrow\, \ -15\times 5< 3(x-2)\leq 0\times 5$

$\Rightarrow\, \ -75< 3(x-2)\leq 0$

$\Rightarrow\, \ \frac{-75}{3}< (x-2)\leq \frac{0}{3}$

$\Rightarrow\, \ -25< (x-2)\leq 0$

$\Rightarrow\, \ -25+2< x\leq 0+2$

$\Rightarrow\, \ -23< x\leq 2$

The solution set is $(-23,2]$

Question:5 Solve the inequality $-12<4-\frac{3x}{-5} \leq 2$

Answer:

Given the inequality

$-12<4-\frac{3x}{-5} \leq 2$

$\Rightarrow\, \, -12-4< -\frac{3x}{-5}\leq 2-4$

$\Rightarrow\, \, -16< -\frac{3x}{-5}\leq -2$

$\Rightarrow\, \, -16< \frac{3x}{5}\leq -2$

$\Rightarrow\, \, -16\times 5< 3x\leq -2\times 5$

$\Rightarrow\, \, -80< 3x\leq -10$

$\Rightarrow\, \, \frac{-80}{3}< 3x\leq \frac{-10}{3}$

Solution set is $(\frac{-80}{3}, \frac{-10}{3}]$

Question:6 Solve the inequality $7 \leq \frac{(3x+ 11)}{2}\leq 11$

Answer:

Given the linear inequality

$7 \leq \frac{(3x+ 11)}{2}\leq 11$

$\Rightarrow \, \, 7\times 2 \leq (3x+ 11)\leq 11\times 2$

$\Rightarrow \, \, 14 \leq (3x+ 11)\leq 22$

$\Rightarrow \, \, 14-11 \leq (3x)\leq 22-11$

$\Rightarrow \, \, 3 \leq 3x\leq 11$

$\Rightarrow \, \, 1 \leq x\leq \frac{11}{3}$

The solution set of the given inequality is $[1,\frac{11}{3}]$

Question:7 Solve the inequality and represent the solution graphically on number line. $5x + 1 > -24,\ 5x - 1 <24$

Answer:

Given : $5x + 1 > -24,\ 5x - 1 <24$

$5x + 1 > -24\, \, \, \, \, \, \, and\, \, \, \, \, \, \ 5x - 1 <24$

$\Rightarrow 5x > -24-1\, \, \, \, \, \, \, and\, \, \, \, \, \, \ 5x <24+1$

$\Rightarrow 5x > -25\, \, \, \, \, \, \, and\, \, \, \, \, \, \ 5x <25$

$\Rightarrow x > \frac{-25}{5}\, \, \, \, \, \, \, and\, \, \, \, \, \, \ x <\frac{25}{5}$

$\Rightarrow x > -5\, \, \, \, \, \, \, and\, \, \, \, \, \, \ x <5$

$(-5,5)$

The solution graphically on the number line is as shown :

1635763658335

Question:8 Solve the inequality and represent the solution graphically on number line. $2(x-1)<x+5,\ 3(x+2)> 2 -x$

Answer:

Given : $2(x-1)<x+5,\ 3(x+2)> 2 -x$

$2(x-1)<x+5\, \, \, \, and\, \, \, \, \, \ 3(x+2)> 2 -x$

$\Rightarrow \, \, 2x-2<x+5\, \, \, \, and\, \, \, \, \, \ 3x+6> 2 -x$

$\Rightarrow \, \, 2x-x<2+5\, \, \, \, and\, \, \, \, \, \ 3x+x> 2 -6$

$\Rightarrow \, \, x<7\, \, \, \, and\, \, \, \, \, \ 4x> -4$

$\Rightarrow \, \, x<7\, \, \, \, and\, \, \, \, \, \ x> -1$

$(-1,7)$

The solution graphically on the number line is as shown :

1635763681053

Question:9 Solve the inequality and represent the solution graphically on number line. $3x - 7 > 2(x-6),\ 6-x > 11 - 2x$

Answer:

Given : $3x - 7 > 2(x-6),\ 6-x > 11 - 2x$

$3x - 7 > 2(x-6)\, \, \, \, and\, \, \, \, \, \ 6-x > 11 - 2x$

$\Rightarrow \, \, 3x - 7 > 2x-12\, \, \, \, and\, \, \, \, \, \ 6-x > 11 - 2x$

$\Rightarrow \, \, 3x - 2x >7-12\, \, \, \, and\, \, \, \, \, \ 2x-x > 11 - 6$

$\Rightarrow \, \, x >-5\, \, \, \, and\, \, \, \, \, \ x > 5$

$x\in (5,\infty )$

The solution graphically on the number line is as shown :

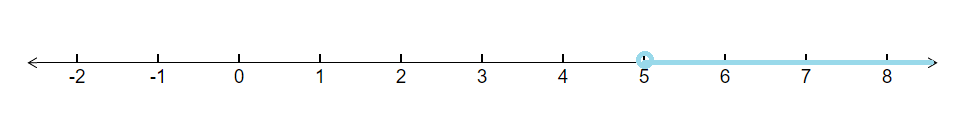
1635763701201

Question:10 Solve the inequality and represent the solution graphically on number line.

$5(2x-7)-3(2x+3)\leq 0,\quad 2x + 19 \leq 6x +47$

Answer:

Given : $5(2x-7)-3(2x+3)\leq 0,\quad 2x + 19 \leq 6x +47$

$5(2x-7)-3(2x+3)\leq 0\, \, \, \, \, and\, \, \, \, \, \, \, \quad 2x + 19 \leq 6x +47$

$\Rightarrow \, \, 10x-35-6x-9\leq 0\, \, \, \, \, and\, \, \, \, \, \, \, \quad 2x -6x\leq 47-19$

$\Rightarrow \, \, 4x-44\leq 0\, \, \, \, \, and\, \, \, \, \, \, \, \quad -4x\leq 28$

$\Rightarrow \, \, 4x\leq 44\, \, \, \, \, and\, \, \, \, \, \, \, \quad 4x\geq - 28$

$\Rightarrow \, \, x\leq 11\, \, \, \, \, and\, \, \, \, \, \, \, \quad x\geq - 7$

$x\in [-7,11]$

The solution graphically on the number line is as shown :

1635763730673

Question:11 A solution is to be kept between 68° F and 77° F. What is the range in temperature in degree Celsius (C) if the Celsius / Fahrenheit (F) conversion formula is given by $F = \frac{9}{5}C + 32$

Answer:

Since the solution is to be kept between 68° F and 77° F.

$68< F< 77$

Putting the value of $F = \frac{9}{5}C + 32$ , we have

$\Rightarrow \, \, \, 68< \frac{9}{5}C + 32< 77$

$\Rightarrow \, \, \, 68-32< \frac{9}{5}C < 77-32$

$\Rightarrow \, \, \, 36< \frac{9}{5}C < 45$

$\Rightarrow \, \, \, 36\times 5< 9C < 45\times 5$

$\Rightarrow \, \, \, 180< 9C < 225$

$\Rightarrow \, \, \, \frac{180}{9}< C < \frac{225}{9}$

$\Rightarrow \, \, \, 20< C < 25$

the range in temperature in degree Celsius (C) is between 20 to 25.

Question:12 A solution of 8% boric acid is to be diluted by adding a 2% boric acid solution to it. The resulting mixture is to be more than 4% but less than 6% boric acid. If we have 640 litres of the 8% solution, how many litres of the 2% solution will have to be added?

Answer:

Let x litres of 2% boric acid solution is required to be added.

Total mixture = (x+640) litres

The resulting mixture is to be more than 4% but less than 6% boric acid.

$\therefore \, 2\%x+8\%\, of\, 640> 4\%\, of\, (640+x)$ and $2\%x+8\%\, of\, 640< 6\%\, of\, (x+640)$

$\Rightarrow \, 2\%x+8\%\, of\, 640> 4\%\, of\, (640+x)$ and $2\%x+8\%\, of\, 640< 6\%\, of\, (x+640)$

$\Rightarrow \, \frac{2}{100}x+(\frac{8}{100}) 640> \frac{4}{100} (640+x)$ $\Rightarrow \, \frac{2}{100}x+(\frac{8}{100}) 640< \frac{6}{100} (640+x)$

$\Rightarrow \, 2x+5120> 4x+2560$ $\Rightarrow \, 2x+5120< 6x+3840$

$\Rightarrow \, 5120-2560> 4x-2x$ $\Rightarrow \, 5120-3840< 6x-2x$

$\Rightarrow \, 2560> 2x$ $\Rightarrow \, 1280< 4x$

$\Rightarrow \, 1280> x$ $\Rightarrow \, 320< x$

Thus, the number of litres 2% of boric acid solution that is to be added will have to be more than 320 and less than 1280 litres.

Question:13 How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?

Answer:

Let x litres of water is required to be added.

Total mixture = (x+1125) litres

It is evident that amount of acid contained in the resulting mixture is 45% of 1125 litres.

The resulting mixture contain more than 25 % but less than 30% acid.

$\therefore \, 30\%\, of\, (1125+x) > 45\%\, of\, (1125)$ and $25\%\, of\, (1125+x)< 45\%\, of\, 1125$

$\Rightarrow \, 30\%\, of\, (1125+x) > 45\%\, of\, (1125)$ and $25\%\, of\, (1125+x)< 45\%\, of\, 1125$

$\Rightarrow \, \frac{30}{100}(1125+x)> \frac{45}{100} (1125)$ $\Rightarrow \, (\frac{25}{100}) (1125+x)< \frac{45}{100} (1125)$

$\Rightarrow \, 30\times 1125+30x> 45\times (1125)$ $\Rightarrow \, 25 (1125+x)< 45(1125)$

$\Rightarrow \, 30x> (45-30)\times (1125)$ $\Rightarrow \, 25 x< (45-25)1125$

$\Rightarrow \, 30x> (15)\times (1125)$ $\Rightarrow \, 25 x< (20)1125$

$\Rightarrow \, x> \frac{15\times 1125}{30}$ $\Rightarrow \, x< \frac{20\times 1125}{25}$

$\Rightarrow \, x> 562.5$ $\Rightarrow \, x< 900$

Thus, the number of litres water that is to be added will have to be more than 562.5 and less than 900 litres.

Question:14 IQ of a person is given by the formula $IQ= \frac{MA}{CA}\times 100$ where MA is mental age and CA is chronological age. If $80\leq IQ\leq140$ for a group of 12 years old children, find the range of their mental age.

Answer:

Given that group of 12 years old children.

$80\leq IQ\leq140$

For a group of 12 years old children, CA =12 years

$IQ= \frac{MA}{CA}\times 100$

Putting the value of IQ, we obtain

$80\leq IQ\leq140$

$\Rightarrow \, \, 80\leq \frac{MA}{CA}\times 100\leq140$

$\Rightarrow \, \, 80\leq \frac{MA}{12}\times 100\leq140$

$\Rightarrow \, \, 80\times 12\leq MA\times 100\leq140\times 12$

$\Rightarrow \, \, \frac{80\times 12}{100}\leq MA\leq \frac{140\times 12}{100}$

$\Rightarrow \, \, 9.6\leq MA\leq 16.8$

Thus, the range of mental age of the group of 12 years old children is $\, \, 9.6\leq MA\leq 16.8$

Benefits of NCERT Solutions for Class 11 Maths Chapter 6 Miscellaneous Exercises

Students can practice all the questions of miscellaneous exercise chapter 6 Class 11 to revise the chapter.
All the questions in the Class 11 Maths Chapter 6 miscellaneous exercise solutions are equally important and students should solve the first three exercises prior to NCERT solutions for Class 11 Maths Chapter 6 miscellaneous exercise.

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

Topics Covered in Miscellaneous Exercise Class 11 Chapter 6

The Miscellaneous Exercise in NCERT Solutions for Class 11 Maths Chapter 6 - Linear Inequalities covers key topics such as:

Introduction to Linear Inequalities
Inequalities
Algebraic Solutions of Linear Inequalities in One Variable and Their Graphical Representation

The class 11 chapter 6 miscellaneous exercise solutions align with the latest CBSE guidelines, offering students a comprehensive approach to mastering the subject. Regular practice with these questions not only follows CBSE recommendations but also boosts students' confidence, making it essential for those aiming for high scores in the Maths board examination. Regular and thorough practice of NCERT Solutions for Class 11 Maths is crucial for success.

Key Features of Class 11 Maths ch 6 Miscellaneous Exercise Solutions

Comprehensive Coverage: Class 11 Chapter 6 maths miscellaneous solutions address all the miscellaneous exercise problems in Chapter 6, ensuring comprehensive coverage of the topics.
CBSE Guidelines: The class 11 maths miscellaneous exercise chapter 6 solution are designed in accordance with the latest CBSE guidelines, ensuring relevance to the prescribed curriculum.
Clarity and Accuracy: Class 11 maths ch 6 miscellaneous exercise solutions are presented with clarity and accuracy to facilitate better understanding for students.
Step-by-Step Approach: Each problem is solved in a step-by-step manner, providing a clear and logical progression to aid in better comprehension.
Graphical Representation: Class 11 Chapter 6 miscellaneous exercise solutions include graphical representations where applicable, helping students visualize concepts and solutions.
Relevance to Board Examination: The Class 11 chapter 6 maths miscellaneous solutions are tailored to help students prepare effectively for the Class 11 Maths board examination, aligning with the exam pattern and question types.
Accessible PDF Format: The solutions are available in a PDF format, offering convenience for students to use them according to their preferences and ease of access.

Also see-

NCERT Solutions of Class 11 Subject Wise

Subject Wise NCERT Exampler Solutions

Frequently Asked Questions (FAQs)

1. What is the relation between degree Celsius (C) and Fahrenheit (F)?

F=9C/5+32

2. What is question number 11 of NCERT solutions for Class 11 Maths chapter 6 miscellaneous exercise?

It’s about finding the range of temperature in degrees Celsius. Given the range of Fahrenheit.

3. What is the solution of 3x-6=0?

3x-6=0

3x=6

x=2

4. Give the solutions of 3x-6≥0

The solution is 3x≥6

Or x ≥ 2. The solution is the right-hand side of the line x=2 including the points on the line. The graphical representation is given in the NCERT Class 11 Maths book chapter 6 example 10.

5. What is the difference between the solutions of x ≥ 2 and x>2?

Both inequalities have solutions to the right of the line x=2. For x ≥ 2 points on the line x=2 are included and for x>2 points on the linex=2 are excluded.

6. How can you represent x>120 and x<300 as a double inequality?

120<x<300

7. How many exercises are solved in NCERT syllabus chapter 6 Class 11?

4 exercises are discussed in NCERT Class 11 Maths chapter 6

8. How many questions are solved in the Class 11 Maths chapter 6 miscellaneous exercise solutions?

Fourteen questions are solved in Linear Inequality Class 11 NCERT Maths chapter 6 miscellaneous exercise

Also Read

NCERT Class 11 Chemistry Chapter 4 Notes Chemical Bonding and Molecular Structure - Download PDF

Hydrogen Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 9 Notes - Download PDF

The S-Block Elements Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 10 Notes - Download PDF

The P-Block Elements Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 11 Notes - Download PDF

Environmental Chemistry Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 14 Notes - Download PDF

NCERT Class 11 Chemistry Chapter 3 Notes - Download PDF

NCERT Solutions for Class 11 Physics Chapter 6 Work Energy and Power

NCERT Solutions for Class 11 Chemistry Chapter 5 States of Matter

NCERT Class 11 Physics Chapter 5 Notes Laws of Motion - Download PDF

NCERT Class 11 Physics Chapter 3 Notes Motion in a straight Line - Download PDF

NCERT Solutions for Exercise 10.1 Class 11 Maths Chapter 10 - Straight Lines

NCERT Solutions for Miscellaneous Exercise Chapter 16 Class 11 - Probability

NCERT Exemplar Class 11 Maths Solutions Chapter 12 Introduction to Three Dimensional Geometry

NCERT Exemplar Class 11 Maths Solutions Chapter 10 Straight Lines

NCERT Exemplar Class 11 Maths Solutions Chapter 6 Linear Inequalities

NCERT Exemplar Class 11 Maths Solutions Chapter 16 Probability

NCERT Exemplar Class 11 Maths Solutions Chapter 14 Mathematical Reasoning

NCERT Exemplar Class 11 Maths Solutions Chapter 7 Permutations and Combinations

Articles

How to Make APAAR ID via DigiLocker and School: A Complete Guide

Dec 17, 2024

Sainik School Entrance Exam 2025: Application, Exam Date, How to Apply, Syllabus

Dec 17, 2024

MVPP Scholarship Exam 2024: Mukhyamantri Vigyan Pratibha Pariksha Registration, Exam Date

Dec 16, 2024

Silverzone ISSO Answer Key 2024-25: Download PDF

Dec 16, 2024

Silverzone IOEL Answer Key 2024 – Download International Olympiad of English Language Solutions

Dec 16, 2024

Silverzone Olympiad IOM Answer Key 2024-25: Qualifying Marks, Score

Dec 16, 2024

Silverzone STEM Olympiad Answer Key 2024-25: Check Answer Key for all Classes

Dec 16, 2024

Silverzone ABHO Answer Key 2024 | Download Akhil Bhartiya Hindi Olympiad Solutions

Dec 16, 2024

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Eligibility Criteria

Application Process

Exam Pattern

Gujarat Board Higher Secondary School Certificate

Late Fee Application Date:13 December,2024 - 22 December,2024

Exam Pattern

Result

Admit Card

Madhya Pradesh State Open School 10th Examination

Admit Card Date:13 December,2024 - 31 December,2024

Admit Card

Result

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Miscellaneous Exercise Chapter 6 Class 11 - Linear Inequalities

NCERT Solutions for Class 11 Maths Chapter 6: Linear Inequalities Miscellaneous Exercise- Download Free PDF

Download the PDF of NCERT Solutions for Class 11 Maths Chapter 6 – Linear Inequalities Miscellaneous Exercise

Access Linear Inequalities Class 11 NCERT Maths- Miscellaneous Exercise

More About NCERT Solutions for Class 11 Maths Chapter 6 Miscellaneous Exercises

Benefits of NCERT Solutions for Class 11 Maths Chapter 6 Miscellaneous Exercises

Topics Covered in Miscellaneous Exercise Class 11 Chapter 6

Key Features of Class 11 Maths ch 6 Miscellaneous Exercise Solutions

NCERT Solutions of Class 11 Subject Wise

Subject Wise NCERT Exampler Solutions

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

Bihar Open Board 10th Examination

Bihar Open Board 12th Examination

National Means Cum-Merit Scholarship

Gujarat Board Higher Secondary School Certificate

Madhya Pradesh State Open School 10th Examination

Popular Questions

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

JEE Main Important Mathematics Formulas

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

Schools By Medium

By Ownership

By City

By State

NVS

JNVST

Download Careers360 App

All this at the convenience of your phone

Scan and download the app