NCERT Solutions for Exercise 6.2 Class 11 Maths Chapter 6

Q: What is the difference between x less than n and x less than or equal to n on the number line?

For x<n there will be a circle on the number n and for x less than or equal to n there will be a dark circle on the number n.

Q: What topic is covered in exercise 6.2 Class 11 Maths?

Linear inequalities in one variable, their formation and solution

Q: Solve 30x<90

30x<90 divide both sides with 30, then we get x<30; which is the required solution and can be represented graphically by a dark line left to the number 30 and a circle on 30(i.e without including 30) on a number line

Q: Solve -30x<90

Divide both sides with 30 -x<30 Multiply both sides by -1 (the inequality sign get reversed) x>-30 is the solution. This can be represented on a number line by a dark line to the right of -30 with a circle on -30

NCERT Solutions for Exercise 6.2 Class 11 Maths Chapter 6 - Linear Inequalities

Edited By Vishal kumar | Updated on Nov 06, 2023 01:34 PM IST

NCERT Solutions for Class 11 Maths Chapter 6: Linear Inequalities Exercise 6.2- Download Free PDF

NCERT Solutions for Class 11 Maths Chapter 6: Linear Inequalities Exercise 6.2- NCERT solutions for exercise 6.2 Class 11 Maths Chapter 6 discusses questions from the topic of graphical solutions of linear inequalities in two variables. Exercise 6.2 Class 11 Maths questions related to linear inequalities in two-dimensional planes graphically. One example of the question type is given in the NCERT solutions for Class 11 Maths chapter 6 exercise 6.2 is “solve graphically; x+2y<5. The concepts of solution region, solution set, identification of half-plane etc can be practised through Class 11 Maths chapter 6 exercise 6.2. The questions in NCERT syllabus Class 11th Maths chapter 6 exercise 6.2 are single two-variable inequalities. The system of inequalities in 2 variables is discussed in the session after Class 11 Maths Chapter 6 Exercise 6.2.

JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy

Suggested: JEE Main: high scoring chapters | Past 10 year's papers

This Story also Contains

NCERT Solutions for Class 11 Maths Chapter 6: Linear Inequalities Exercise 6.2- Download Free PDF
Access Linear Inequalities Class 11 Chapter 6 Exercise 6.2
More About NCERT Solutions for Class 11 Maths Chapter 6 Exercise 6.2
Benefits of NCERT Solutions for Class 11 Maths Chapter 6 Exercise 6.2
Key Features of NCERT 11th Class Maths Exercise 6.2 Answers
NCERT Solutions of Class 11 Subject Wise
Subject Wise NCERT Exampler Solutions

NCERT Solutions for Exercise 6.2 Class 11 Maths Chapter 6 - Linear Inequalities

The following practice exercises are also discussed in the NCERT book chapter linear inequalities along with exercise 6.2 Class 11 Maths which are developed by subject matter experts. They are presented in an easy-to-understand language, and each question is explained in comprehensive detail. In addition to text solutions, PDF versions are also available, enabling students to use them according to their convenience, without requiring an internet connection, and all of this is provided free of charge.

**As per the new CBSE Syllabus for 2023-24, this chapter has been assigned a different number, and it is now referred to as Chapter 5.

Download the PDF of NCERT Solutions for Class 11 Maths Chapter 6 – Linear Inequalities Exercise 6.2

Download PDF

Access Linear Inequalities Class 11 Chapter 6 Exercise 6.2

Question:1 Solve the following inequality graphically in two-dimensional plane:

$x + y < 5$

Answer:

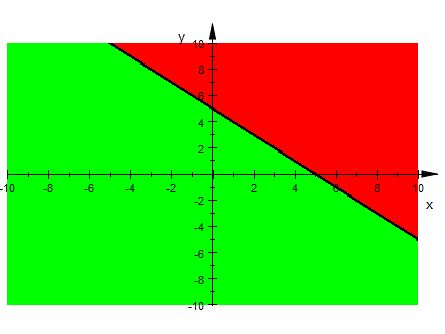
Graphical representation of $x+y=5$ is given in the graph below.

The line $x+y=5$ divides plot in two half planes.

Select a point (not on line $x+y=5$ ) which lie in one of the half planes, to determine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

$1+2< 5$ i.e. $3< 5$ , which is true.

Therefore, half plane (above the line) is not a solution region of given inequality i.e. $x + y < 5$ .

Also, the point on the line does not satisfy the inequality.

Thus, the solution to this inequality is half plane below the line $x+y=5$ excluding points on this line represented by the green part.

This can be represented as follows:

1635762532191

Question:2 Solve the following inequality graphically in two-dimensional plane: $2x + y \geq 6$

Answer:

$2x + y \geq 6$

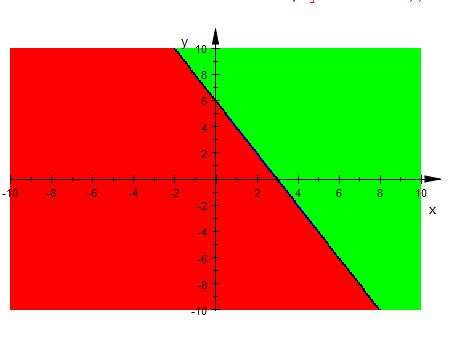
Graphical representation of $2x+y=6$ is given in the graph below.

The line $2x+y=6$ divides plot in two half-planes.

Select a point (not on the line $2x+y=6$ ) which lie in one of the half-planes, to determine whether the point satisfies the inequality.

Let there be a point $(3,2)$

We observe

$6+2\geq 6$ i.e. $8\geq 6$ , which is true.

Therefore, half plane II is not a solution region of given inequality i.e. $2x + y \geq 6$

Also, the point on the line does satisfy the inequality.

Thus, the solution to this inequality is the half plane I, above the line $2x+y=6$ including points on this line , represented by green colour.

This can be represented as follows:

1635762558839

Question:3 Solve the following inequality graphically in two-dimensional plane: $3x + 4y \leq 12$

Answer:

$3x + 4y \leq 12$

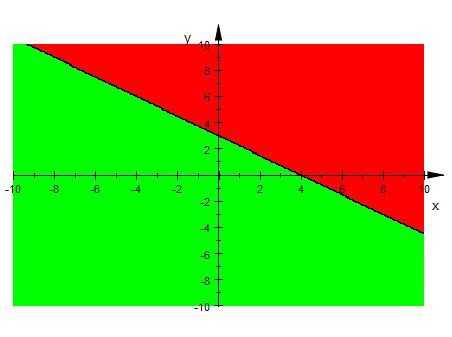
Graphical representation of $3x + 4y = 12$ is given in the graph below.

The line $3x + 4y = 12$ divides plot into two half-planes.

Select a point (not on the line $3x + 4y = 12$ ) which lie in one of the half-planes, to determine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

$1+2\leq 12$ i.e. $3\leq 12$ , which is true.

Therefore, the half plane I(above the line) is not a solution region of given inequality i.e. $3x + 4y \leq 12$ .

Also, the point on the line does satisfy the inequality.

Thus, the solution to this inequality is half plane II (below the line $3x + 4y = 12$ ) including points on this line, represented by green colour.

This can be represented as follows:

1635762572337

Question:4 Solve the following inequality graphically in two-dimensional plane: $y + 8 \geq 2x$

Answer:

$y + 8 \geq 2x$

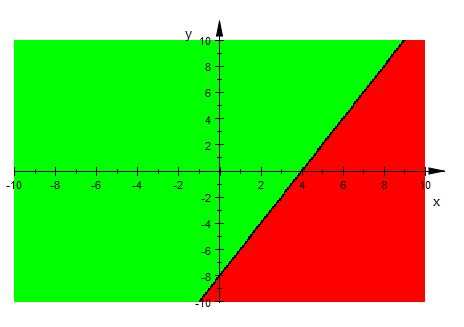
Graphical representation of $y + 8 = 2x$ is given in the graph below.

The line $y + 8 = 2x$ divides plot in two half-planes.

Select a point (not on the line $y + 8 = 2x$ ) which lie in one of the half-planes, to determine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

$2+8\geq 2\times 1$ i.e. $10\geq 2$ , which is true.

Therefore, half plane II is not solution region of given inequality i.e. $y + 8 \geq 2x$ .

Also, the point on the line does satisfy the inequality.

Thus, the solution to this inequality is the half plane I including points on this line, represented by green colour.

This can be represented as follows:

1635762587304

Question:5 Solve the following inequality graphically in two-dimensional plane: $x - y \leq 2$

Answer:

$x - y \leq 2$

Graphical representation of $x - y =2$ is given in the graph below.

The line $x - y =2$ divides plot in two half planes.

Select a point (not on the line $x - y =2$ ) which lie in one of the half-planes, to determine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

$1-2\leq 2$ i.e. $-1\leq 2$ , which is true.

Therefore, half plane Ii is not solution region of given inequality i.e. $x - y \leq 2$ .

Also, the point on the line does satisfy the inequality.

Thus, the solution to this inequality is the half plane I including points on this line, represented by green colour

This can be represented as follows:

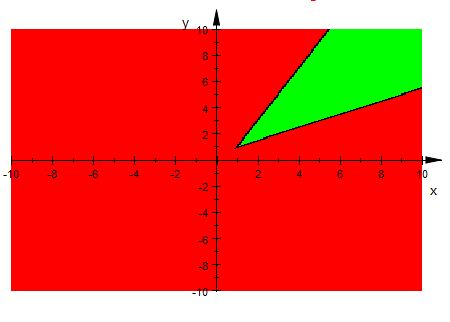
1635762601555

Question:6 Solve the following inequality graphically in two-dimensional plane: $2x - 3y > 6$

Answer:

$2x - 3y > 6$

Graphical representation of $2x - 3y = 6$ is given in the graph below.

The line $2x - 3y = 6$ divides plot in two half planes.

Select a point (not on the line $2x - 3y = 6$ )which lie in one of the half-planes, to determine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

$2-6> 6$ i.e. $-4 > 6$ , which is false .

Therefore, half plane I is not solution region of given inequality i.e. $2x - 3y > 6$ .

Also point on line does not satisfy the inequality.

Thus, the solution to this inequality is half plane II excluding points on this line, represented by green colour.

This can be represented as follows:

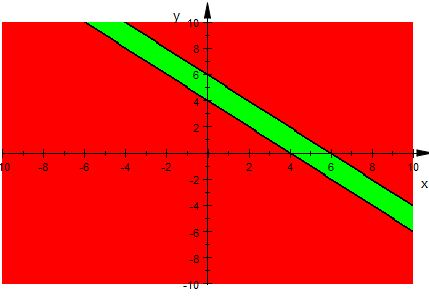
1635762622339

Question:7 Solve the following inequality graphically in two-dimensional plane: $-3x + 2y \geq -6$

Answer:

$-3x + 2y \geq -6$

Graphical representation of $-3x + 2y = -6$ is given in the graph below.

The line $-3x + 2y = -6$ divides plot in two half planes.

Select a point (not on the line $-3x + 2y = -6$ ) which lie in one of the half planes, to determine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

$-3+4\geq -6$ i.e. $1\geq -6$ , which is true.

Therefore, half plane II is not solution region of given inequality i.e. $-3x + 2y \geq -6$ .

Also, the point on the line does satisfy the inequality.

Thus, the solution to this inequality is the half plane I including points on this line, represented by green colour

This can be represented as follows:

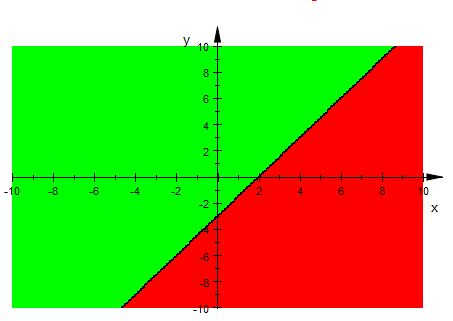
1635762636448

Question:8 Solve the following inequality graphically in two-dimensional plane: $3y - 5x < 30$

Answer:

$3y - 5x < 30$

Graphical representation of $3y - 5x =30$ is given in graph below.

The line $3y - 5x =30$ divides plot in two half planes.

Select a point (not on the line $3y - 5x =30$ ) which lie in one of the half plane , to detemine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

$6-5< 30$ i.e. $1< 30$ , which is true.

Therefore, half plane II is not solution region of given inequality i.e. $3y - 5x < 30$ .

Also point on the line does not satisfy the inequality.

Thus, solution to this inequality is half plane I excluding points on this line, represented by green colour.

This can be represented as follows:

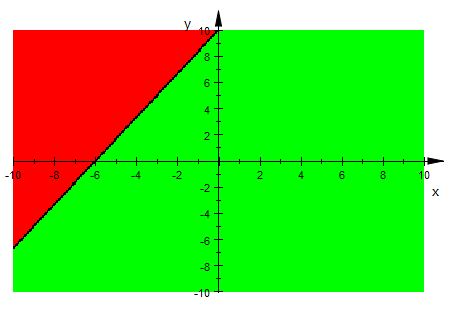
1635762649943

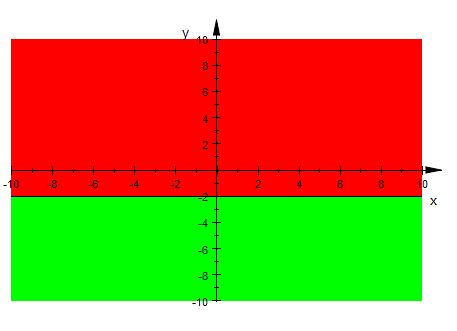
Question:9 Solve the following inequality graphically in two-dimensional plane: $y < -2$

Answer:

$y < -2$

Graphical representation of $y=-2$ is given in graph below.

The line $y < -2$ divides plot in two half planes.

Select a point (not on the line $y < -2$ ) which lie in one of the half plane , to detemine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

i.e. $2< -2$ , which is false.

Therefore, the half plane I is not a solution region of given inequality i.e. $y < -2$ .

Also, the point on the line does not satisfy the inequality.

Thus, the solution to this inequality is half plane II excluding points on this line, represented by green colour.

This can be represented as follows:

1635762675271

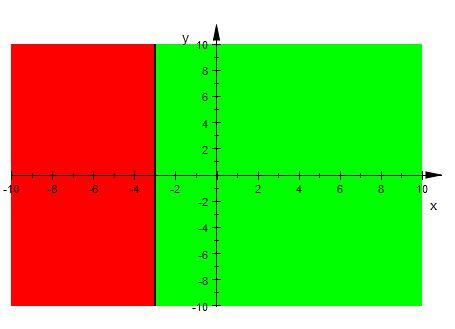
Question:10 Solve the following inequality graphically in two-dimensional plane: $x > - 3$

Answer:

$x > - 3$

Graphical representation of $x=-3$ is given in the graph below.

The line $x=-3$ divides plot into two half-planes.

Select a point (not on the line $x=-3$ ) which lie in one of the half-planes, to determine whether the point satisfies the inequality.

Let there be a point $(1,2)$

We observe

i.e. $1> -3$ , which is true.

Therefore, half plane II is not a solution region of given inequality i.e. $x > - 3$ .

Also, the point on the line does not satisfy the inequality.

Thus, the solution to this inequality is the half plane I excluding points on this line.

This can be represented as follows:

1635762691903

Benefits of NCERT Solutions for Class 11 Maths Chapter 6 Exercise 6.2

The questions in exercise 6.2 Class 11 Maths help to understand the graphical method of solving linear inequalities in two variables.
Also, students can expect questions from Class 11 Maths Chapter 6 exercise 6.2 for their final exams

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

Key Features of NCERT 11th Class Maths Exercise 6.2 Answers

Step-by-step solutions: Detailed, step-by-step explanations for each 11th class maths exercise 6.2 answers to facilitate an understanding of mathematical concepts and problem-solving techniques.
Clarity and accuracy: Ex 6.2 class 11 solutions are presented clearly and accurately, helping students prepare for exams with confidence and improve their comprehension.
Curriculum alignment: Class 11 maths ex 6.2 solutions closely adhere to the NCERT curriculum, covering topics and concepts as per the official syllabus.
Accessibility: These class 11 ex 6.2 solutions are often available for free, making them easily accessible to students.
Format options: PDF versions of the class 11 maths chapter 6 exercise 6.2 is provided, allowing students to download and use them conveniently, both online and offline.

Also see-

NCERT Solutions of Class 11 Subject Wise

Subject Wise NCERT Exampler Solutions

Frequently Asked Questions (FAQs)

1. Mention the number of exercises solved in the Class 11 NCERT Maths chapter linear inequalities

4 exercises are solved including the miscellaneous exercises.

2. How many questions are discussed in the NCERT solutions for Class 11 Maths chapter 6 exercise 6.2?

Ten questions.

3. What is the solution region?

The area which contains all the solutions of inequality is called the solution region.

4. What happens when both sides of an inequality are multiplied by a negative number?

The inequality is reversed.

5. What is the difference between x less than n and x less than or equal to n on the number line?

For x<n there will be a circle on the number n and for x less than or equal to n there will be a dark circle on the number n.

6. What topic is covered in exercise 6.2 Class 11 Maths?

Linear inequalities in one variable, their formation and solution

7. Solve 30x<90

30x<90

divide both sides with 30, then we get

x<30; which is the required solution and can be represented graphically by a dark line left to the number 30 and a circle on 30(i.e without including 30) on a number line

8. Solve -30x<90

Divide both sides with 30

-x<30

Multiply both sides by -1 (the inequality sign get reversed)

x>-30 is the solution. This can be represented on a number line by a dark line to the right of -30 with a circle on -30

Also Read

NCERT Class 11 Chemistry Chapter 4 Notes Chemical Bonding and Molecular Structure - Download PDF

Hydrogen Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 9 Notes - Download PDF

The S-Block Elements Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 10 Notes - Download PDF

The P-Block Elements Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 11 Notes - Download PDF

Environmental Chemistry Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 14 Notes - Download PDF

NCERT Class 11 Chemistry Chapter 3 Notes - Download PDF

NCERT Solutions for Class 11 Physics Chapter 6 Work Energy and Power

NCERT Solutions for Class 11 Chemistry Chapter 5 States of Matter

NCERT Class 11 Physics Chapter 5 Notes Laws of Motion - Download PDF

NCERT Class 11 Physics Chapter 3 Notes Motion in a straight Line - Download PDF

NCERT Solutions for Exercise 10.1 Class 11 Maths Chapter 10 - Straight Lines

NCERT Solutions for Miscellaneous Exercise Chapter 16 Class 11 - Probability

NCERT Exemplar Class 11 Maths Solutions Chapter 12 Introduction to Three Dimensional Geometry

NCERT Exemplar Class 11 Maths Solutions Chapter 10 Straight Lines

NCERT Exemplar Class 11 Maths Solutions Chapter 6 Linear Inequalities

NCERT Exemplar Class 11 Maths Solutions Chapter 16 Probability

NCERT Exemplar Class 11 Maths Solutions Chapter 14 Mathematical Reasoning

NCERT Exemplar Class 11 Maths Solutions Chapter 7 Permutations and Combinations

Articles

AMU Class 1 Admission 2025: Application Process, Eligibility & Key Dates

Dec 30, 2024

Jamia Millia Islamia School Admission 2025: Application Process, Eligibility & Dates

Dec 30, 2024

SoSE Delhi School Admission 2025: All You Need to Know About Eligibility, Dates & Process

Dec 30, 2024

DBSE Result 2025, Check Delhi Board 10th, 12th Result

Dec 30, 2024

NMMS Chhattisgarh Result 2024-25: Check Merit List, Cut Off Marks

Dec 28, 2024

CBSE Scholarship 2024-25: Check CBSE Scholarships for Class 10, 12

Dec 27, 2024

HOS 12th Date Sheet 2025 - Haryana Open School Class 12 Exam Schedule

Dec 27, 2024

AMU School Admission 2025 - Know Application Process, Eligibility & Important Dates

Dec 27, 2024

Upcoming School Exams

Madhya Pradesh State Open School 12th Examination

Admit Card Date:13 December,2024 - 06 January,2025

Admit Card

Result

All India Sainik Schools Entrance Examination

Application Date:24 December,2024 - 13 January,2025

Exam Pattern

Answer Key

Result

Telangana State Board of Intermediate Education Examination

Late Fee Application Date:25 December,2024 - 02 January,2025

Exam Pattern

Mock Test

Admit Card

Telangana Intermediate 1st Year Examination

Late Fee Application Date:25 December,2024 - 02 January,2025

Admit Card

Question Paper

Result

National Means Cum-Merit Scholarship

Application Date:27 December,2024 - 09 January,2025

Eligibility Criteria

Application Process

Exam Pattern

View All School Exams

Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms^-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×10⁷J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 ms⁻² :

Option 1)

2.45×10⁻³ kg

Option 2)

6.45×10⁻³ kg

Option 3)

9.89×10⁻³ kg

Option 4)

12.89×10⁻³ kg

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

A particle is projected at 60⁰ to the horizontal with a kinetic energy $K$ . The kinetic energy at the highest point

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

In the reaction,

$2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

How many moles of magnesium phosphate, $Mg_{3}(PO_{4})_{2}$ will contain 0.25 mole of oxygen atoms?

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

With increase of temperature, which of these changes?

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol^-1) is

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t²) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m² , the number of rotations made by the pulley before its direction of motion if reversed, is