NCERT Solutions for Exercise 6.3 Class 11 Maths Chapter 6

Q: Give an application of linear inequalities?

In solving linear programming problems, linear inequalities are used.

Q: How many questions are solved in the exercise 6.3 Class 11 Maths?

15 questions are solved in the NCERT solutions for Class 11 Maths chapter 6 exercise 6.3

Q: Why do we solve Class 11 Maths chapter 6 exercise 6.3?

To get an exposure to the concepts of solving a system of linear inequalities in two variables using the graphical method

Q: What is the importance of NCERT Class 11 Maths exercises?

As far as mathematics is concerned it is a subject that requires a good amount of practice. And the NCERT exercise helps for the same.

NCERT Solutions for Exercise 6.3 Class 11 Maths Chapter 6 - Linear Inequalities

Edited By Vishal kumar | Updated on Nov 07, 2023 06:48 AM IST

NCERT Solutions for Class 11 Maths Chapter 6: Linear Inequalities Exercise 6.3- Download Free PDF

NCERT Solutions for Class 11 Maths Chapter 6: Linear Inequalities Exercise 6.3- In the section before exercise 6.3 Class 11 Maths, the NCERT presented the topics of linear inequalities in one and two variables and their graphical solutions. In NCERT solutions for exercise 6.3 Class 11 Maths chapter 6 the questions related to the system of two-variable linear inequalities is discussed. Solving the Class 11 Maths chapter 6 exercise 6.3 will give a good idea of the concepts discussed before Class 11th Maths chapter 6 exercise 6.3. Before practising the NCERT solutions for Class 11 Maths Chapter 6 Exercise 6.3 it's better to go through the solved examples given in the NCERT book prior to Class 11 Maths chapter 6 exercise 6.3.

JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy

Suggested: JEE Main: high scoring chapters | Past 10 year's papers

This Story also Contains

NCERT Solutions for Class 11 Maths Chapter 6: Linear Inequalities Exercise 6.3- Download Free PDF
Access Linear Inequalities Class 11 Chapter 6-Exercise: 6.3
Question:1 Solve the following system of inequalities graphically:
More About NCERT Solutions for Class 11 Maths Chapter 6 Exercise 6.3
Benefits of NCERT Solutions for Class 11 Maths Chapter 6 Exercise 6.3
Key Features of NCERT 11th Class Maths Exercise 6.3 Answers
NCERT Solutions of Class 11 Subject Wise
Subject Wise NCERT Exampler Solutions

NCERT Solutions for Exercise 6.3 Class 11 Maths Chapter 6 - Linear Inequalities

11th class maths exercise 6.3 answers are written by subject experts at Careers360 in great detail and step-by-step, ensuring that students can easily understand them. In addition to the text solutions of ex 6.3 class 11, PDF versions of the solutions are also available for students, and they are provided free of charge. This allows students to access and use them anytime and anywhere. The following exercises are also listed in the NCERT syllabus for Class 11 Mathematics.

**As per the new CBSE Syllabus for 2023-24, this chapter has been assigned a different number, and it is now referred to as Chapter 5.

Download the PDF of NCERT Solutions for Class 11 Maths Chapter 6 – Linear Inequalities Exercise 6.3

Download PDF

Access Linear Inequalities Class 11 Chapter 6-Exercise: 6.3

Question:1 Solve the following system of inequalities graphically:

$x \geq 3,\ y\geq 2$

Answer:

$x \geq 3,\ y\geq 2$

Graphical representation of $x=3$ and $y=2$ is given in the graph below.

The line $x=3$ and $y=2$ divides plot in four regions i.e.I,II,III,IV.

For $x \geq 3$ ,

The solution to this inequality is region II and III including points on this line because points on the line also satisfy the inequality.

For $y \geq 2$ ,

The solution to this inequality is region IV and III including points on this line because points on the line also satisfy the inequality.

Hence, solution to $x \geq 3,\ y\geq 2$ is common region of graph i.e. region III.

Thus, solution of $x \geq 3,\ y\geq 2$ is region III.

This can be represented as follows:

The below green colour represents the solution

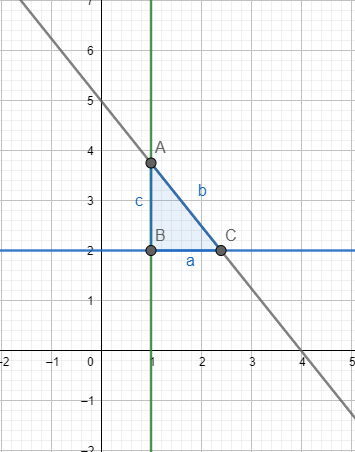
Question:2 Solve the following system of inequalities graphically: $3x +2y \leq 12,\ x \geq 1, \ y\geq 2$

Answer:

$3x +2y \leq 12,\ x \geq 1, \ y\geq 2$

Graphical representation of $x=1 \, \, ,3x+2y=12$ and $y=2$ is given in graph below.

For $x \geq 1$ ,

The solution to this inequality is region on right hand side of line $(x=1)$ including points on this line because points on the line also satisfy the inequality.

For $y \geq 2$ ,

The solution to this inequality is region above the line $(y=2)$ including points on this line because points on the line also satisfy the inequality.

For $3x+2y\leq 12$

The solution to this inequality is region below the line $(3x+2y= 12)$ including points on this line because points on the line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure including points on the respective lines.

This can be represented as follows:

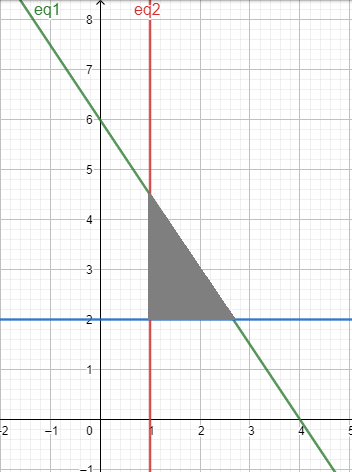
1635762856044

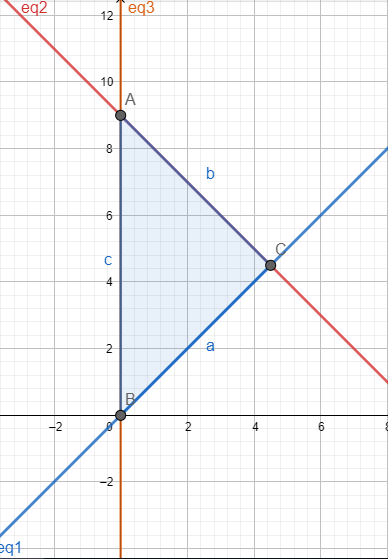
Question:3 Solve the following system of inequalities graphically: $2x +y \geq 6, 3x +4y\leq 12$

Answer:

$2x +y \geq 6, 3x +4y\leq 12$

Graphical representation of $2x +y =6\, \, and\, \, 3x +4y=12$ is given in the graph below.

For $2x +y \geq 6$ ,

The solution to this inequality is region above line $(2x +y =6)$ including points on this line because points on the line also satisfy the inequality.

For $3x +4y\leq 12$ ,

The solution to this inequality is region below the line $( 3x +4y= 12)$ including points on this line because points on the line also satisfy the inequality.

Hence, the solution to these linear inequalities is the shaded region(ABC) as shown in figure including points on the respective lines.

This can be represented as follows:

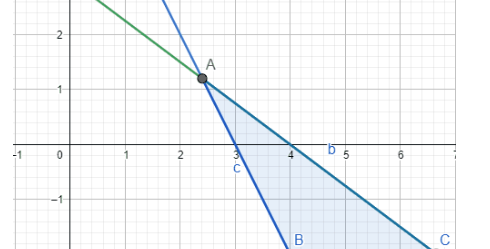
1635762935162

Question:4 Solve the following system of inequalities graphically: $x + y \geq 4, 2x - y <0$

Answer:

$x + y \geq 4, 2x - y <0$

Graphical representation of $x +y =4\, \, and\, \, 2x -y=0$ is given in the graph below.

For $x + y \geq 4,$ ,

The solution to this inequality is region above line $(x +y =4)$ including points on this line because points on the line also satisfy the inequality.

For $2x - y <0$ ,

The solution to this inequality is half plane corresponding to the line $( 2x -y=0)$ containing point $(1,0)$ excluding points on this line because points on the line does not satisfy the inequality.

Hence, the solution to these linear inequalities is the shaded region as shown in figure including points on line $(x +y =4)$ and excluding points on the line $( 2x -y=0)$ .

This can be represented as follows:

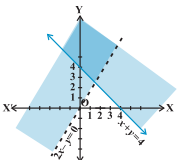
1635763100696

Question:5 Solve the following system of inequalities graphically: $2x - y > 1, \ x -2y < -1$

Answer:

$2x - y > 1, \ x -2y < -1$

Graphical representation of $x -2y =-1\, \, and\, \, 2x -y=1$ is given in graph below.

For $2x - y > 1,$

The solution to this inequality is region below line $( 2x -y=1)$ excluding points on this line because points on line does not satisfy the inequality.

For $\ x -2y < -1$ ,

The solution to this inequality is region above the line $(x -2y =-1)$ excluding points on this line because points on line does not satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure excluding points on the lines.

This can be represented as follows:

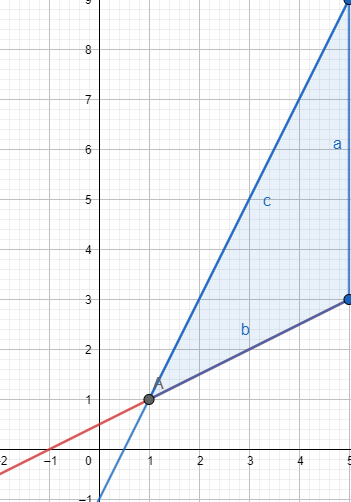
1635763130508

Question:6 Solve the following system of inequalities graphically: $x + y \leq 6, x + y \geq 4$

Answer:

$x + y \leq 6, x + y \geq 4$

Graphical representation of $x + y = 6,\, \, and\, \, \, x + y = 4$ is given in the graph below.

For $x + y \leq 6,$

The solution to this inequality is region below line $( x+y=6)$ in cluding points on this line because points on the line also satisfy the inequality.

For $x + y \geq 4$ ,

The solution to this inequality is region above the line $( x+y=4)$ including points on this line because points on the line also satisfy the inequality.

Hence, the solution to these linear inequalities is shaded region as shown in figure including points on the lines.

This can be represented as follows:

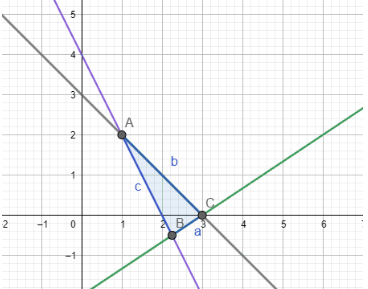
1635763165801

Question:7 Solve the following system of inequalities graphically: $2x + y \geq 8 , x + 2y \geq 10$

Answer:

$2x + y \geq 8 , x + 2y \geq 10$

Graphical representation of $2x + y = 8\, \, and\, \, x + 2y =10$ is given in graph below.

For $2x + y \geq 8 ,$

The solution to this inequality is region above line $(2x + y = 8)$ including points on this line because points on line also satisfy the inequality.

For $x + 2y \geq 10$ ,

The solution to this inequality is region above the line $( x + 2y =10)$ including points on this line because points on line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure including points on the lines.

This can be represented as follows:

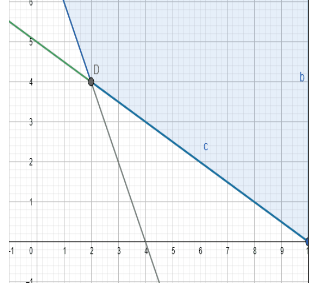
1635763179656

Question:8 Solve the following system of inequalities graphically: $x + y \leq 9, y > x, x\geq 0$

Answer:

$x + y \leq 9, y > x, x\geq 0$

Graphical representation of $x+y=9,x=y$ and $x=0$ is given in graph below.

For $x + y \leq 9$ ,

The solution to this inequality is region below line $(x+y=9)$ including points on this line because points on line also satisfy the inequality.

For $y > x$ ,

The solution to this inequality represents half plane corresponding to the line $(x=y)$ containing point $(0,1)$ excluding points on this line because points on line does not satisfy the inequality.

For $x\geq 0$ ,

The solution to this inequality is region on right hand side of the line $(x=0)$ including points on this line because points on line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure.

This can be represented as follows:

1635763196635

Question:9 Solve the following system of inequalities graphically: $5x+4y\leq20, \ x\geq 1, \ y\geq 2$

Answer:

$5x+4y\leq20, \ x\geq 1, \ y\geq 2$

Graphical representation of $\, ,5x+4y=20,\, \, \, x=1\, \, and \, \, y=2$ is given in graph below.

For $5x+4y\leq20,$ ,

The solution to this inequality is region below the line $(5x+4y=20)$ including points on this line because points on line also satisfy the inequality.

For $\ x\geq 1,$ ,

The solution to this inequality is region right hand side of the line $(x=1)$ including points on this line because points on line also satisfy the inequality.

For $\ y\geq 2,$

The solution to this inequality is region above the line $(y=2)$ including points on this line because points on line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure including points on the respective lines.

This can be represented as follows:

1635763228699

Question:10 Solve the following system of inequalities graphically: $3x + 4y \leq 60,\ x + 3y \leq 30, \ x \geq 0, \ y\geq 0$

Answer:

$3x + 4y \leq 60,\ x + 3y \leq 30, \ x \geq 0, \ y\geq 0$

Graphical representation of $3x+4y=60 \, \, ,x+3y=30\, \, \, ,x=0\, \, and\, \, y=0$ is given in graph below.

For $3x + 4y \leq 60$ ,

The solution to this inequality is region below the line $(3x+4y=60)$ including points on this line because points on line also satisfy the inequality.

For $\ x + 3y \leq 30$ ,

The solution to this inequality is region below the line $(x+3y=30)$ including points on this line because points on line also satisfy the inequality.

For $\ x \geq 0,$

The solution to this inequality is region right hand side of the line $(x=0)$ including points on this line because points on line also satisfy the inequality.

For $\ y \geq 0,$

The solution to this inequality is region above the line $(y=0)$ including points on this line because points on line also satisfy the inequality.

Hence, the solution to these linear inequalities is shaded region as shown in figure including points on the respective lines.

This can be represented as follows:

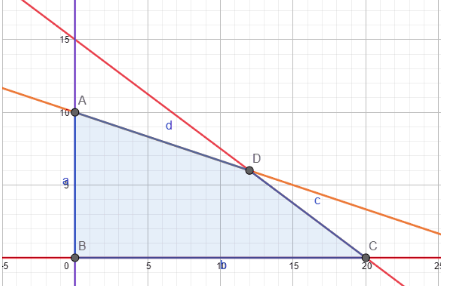
1635763315671

Question:11 Solve the following system of inequalities graphically: $2x +y \geq 4, \ x + y \leq 3, \ 2x - 3y \leq 6$

Answer:

$2x +y \geq 4, \ x + y \leq 3, \ 2x - 3y \leq 6$

Graphical representation of $2x+y=4 \, \, ,x+y=3$ and $2x-3y=6$ is given in graph below.

For $2x +y \geq 4,$ ,

The solution to this inequality is region above the line $(2x+y=4)$ including points on this line because points on line also satisfy the inequality.

For $\ x + y \leq 3,$ ,

The solution to this inequality is region below the line $(x+y=3)$ including points on this line because points on line also satisfy the inequality.

For $\ 2x - 3y \leq 6,$

The solution to this inequality is region above the line $(2x-3y= 6)$ including points on this line because points on line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure including points on the respective lines.

This can be represented as follows:

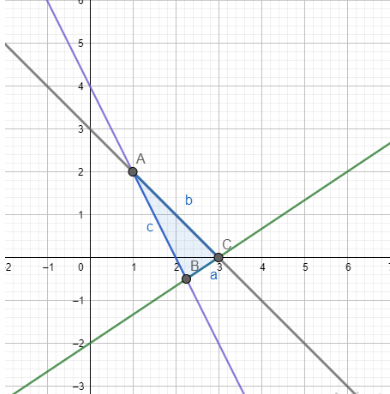
1655375979301

Question:12 Solve the following system of inequalities graphically: $x -2y \leq 3, 3x + 4y \geq 12, x \geq 0, y\geq 1$

Answer:

$x -2y \leq 3, 3x + 4y \geq 12, x \geq 0, y\geq 1$

Graphical representation of $x-2y=3 \, \, ,3x+4y=12\, \, \, ,x=0\, \, and\, \, y=1$ is given in graph below.

For $x -2y \leq 3$ ,

The solution to this inequality is region above the line $(x-2y=3)$ including points on this line because points on line also satisfy the inequality.

For $3x + 4y \geq 12$ ,

The solution to this inequality is region above the line $(3x+4y=12)$ including points on this line because points on line also satisfy the inequality.

For $\ x \geq 0,$

The solution to this inequality is region right hand side of the line $(x=0)$ including points on this line because points on line also satisfy the inequality.

For $\ y \geq 1,$

The solution to this inequality is region above the line $(y=1)$ including points on this line because points on line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure including points on the respective lines.

This can be represented as follows:

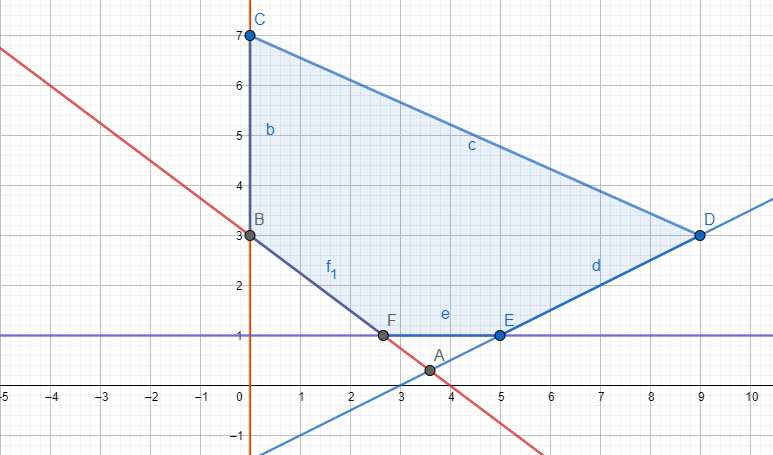
1635763420814

Question:13 Solve the following system of inequalities graphically: $4x + 3y \leq 60,\ y\geq 2x,\ x\geq 3,\ x,y\geq 0$

Answer:

$4x + 3y \leq 60,\ y\geq 2x,\ x\geq 3,\ x,y\geq 0$

Graphical representation of $4x+3y=60 \, \, ,y=2x\, \, \,,x=3\, \, ,x=0\, \, and\, \, y=0$ is given in graph below.

For $4x + 3y \leq 60,$

The solution to this inequality is region below the line $(4x+3y=60)$ including points on this line because points on the line also satisfy the inequality.

For $y\geq 2x$ ,

The solution to this inequality is region above the line $(y=2x)$ including points on this line because points on the line also satisfy the inequality.

For $x\geq 3$ ,

The solution to this inequality is region right hand side of the line $(x=3)$ including points on this line because points on the line also satisfy the inequality.

For $\ x \geq 0,$

The solution to this inequality is region right hand side of the line $(x=0)$ including points on this line because points on the line also satisfy the inequality.

For $\ y \geq 0,$

The solution to this inequality is region above the line $(y=0)$ including points on this line because points on line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure including points on the respective lines.

This can be represented as follows:

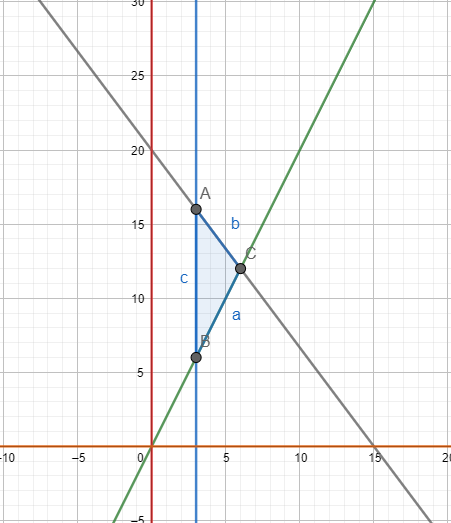
1635763491115

Question:14 Solve the following system of inequality graphically: $3x + 2y \leq 150, \ x +4y \leq 80,\ x\leq 15 \ y\geq 0, \ x\geq 0$

Answer:

$3x + 2y \leq 150, \ x +4y \leq 80,\ x\leq 15 \ y\geq 0, \ x\geq 0$

Graphical representation of $3x+2y=150 \, \, ,x+4y=80\, \, \,,x=15\, \, ,x=0\, \, and\, \, y=0$ is given in graph below.

For $3x + 2y \leq 150,$

The solution to this inequality is region below the line $(3x+2y=150)$ including points on this line because points on the line also satisfy the inequality.

For $x+4y\leq 80$ ,

The solution to this inequality is region below the line $(x+4y=80)$ including points on this line because points on the line also satisfy the inequality.

For $x\leq 15$ ,

The solution to this inequality is region left hand side of the line $(x=15)$ including points on this line because points on the line also satisfy the inequality.

For $\ x \geq 0,$

The solution to this inequality is region right hand side of the line $(x=0)$ including points on this line because points on the line also satisfy the inequality.

For $\ y \geq 0,$

The solution to this inequality is region above the line $(y=0)$ including points on this line because points on line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure including points on the respective lines.

This can be represented as follows:

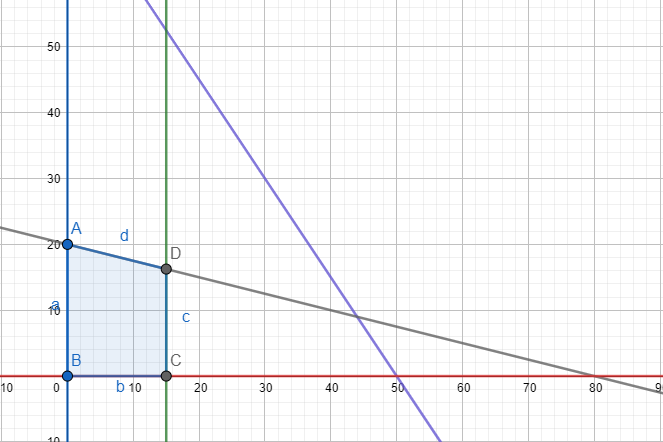
1635763512601

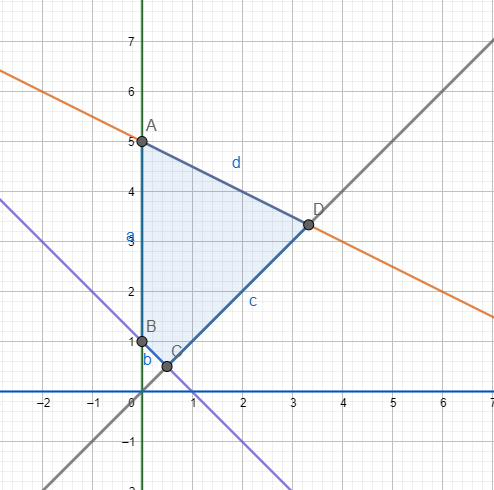
Question:15 Solve the following system of inequality graphically: $x+2y \leq 10, \ x +y \geq 1, \ x-y\leq 0, x\geq 0, \ y\geq 0$

Answer:

$x+2y \leq 10, \ x +y \geq 1, \ x-y\leq 0, x\geq 0, \ y\geq 0$

Graphical representation of $x+2y=10 \, \, ,x+y=1\, \, \,,x-y=0\, \, ,x=0\, \, and\, \, y=0$ is given in graph below.

For $x+2y \leq 10,$

The solution to this inequality is region below the line $(x+2y=10)$ including points on this line because points on line also satisfy the inequality.

For $\ x +y \geq 1,$ ,

The solution to this inequality is region above the line $(x+y=1)$ including points on this line because points on line also satisfy the inequality.

For $\ x-y\leq 0,$ ,

The solution to this inequality is region above the line $(x-y=0)$ including points on this line because points on line also satisfy the inequality.

For $\ x \geq 0,$

The solution to this inequality is region right hand side of the line $(x=0)$ including points on this line because points on line also satisfy the inequality.

For $\ y \geq 0,$

The solution to this inequality is region above the line $(y=0)$ including points on this line because points on line also satisfy the inequality.

Hence, solution to these linear inequalities is shaded region as shown in figure including points on the respective lines.

This can be represented as follows:

1635763543684

Benefits of NCERT Solutions for Class 11 Maths Chapter 6 Exercise 6.3

The content covered in exercise 6.3 Class 11 Maths is helpful in revising the concepts discussed in the chapter.
Practising problems is important for maths subjects. And the Class 11 Maths chapter 6 exercise 6.3 helps for the same.

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

Key Features of NCERT 11th Class Maths Exercise 6.3 Answers

Comprehensive Coverage: The class 11 maths ex 6.3 answers provided cover all the exercises and problems in Chapter 6, Exercise 6.3 of the NCERT 11th Class Mathematics textbook.
Step-by-Step Solutions: The class 11 ex 6.3 answers are presented in a step-by-step format, making it easier for students to follow and understand the solution process.
Clarity and Accuracy: The class 11 maths chapter 6 exercise 6.3 solutions are written with clarity and accuracy, ensuring that students can grasp the concepts and methods required to solve mathematical problems.
Use of Proper Notation: The 11th class maths exercise 6.3 answers use appropriate mathematical notations and terminology, helping students become familiar with the language of mathematics.
Free Access: The ex 6.3 class 11 answers are typically made available for free, allowing students to access them without any cost, making it a valuable resource for self-study.
Supplementary Learning: These class 11 maths ex 6.3 answers can be used as a supplementary learning resource to reinforce classroom learning and aid in exam preparation.
Homework and Practice: Students can use these answers to check their work, practice problem-solving, and improve their overall performance in mathematics.

Also see-

NCERT Solutions of Class 11 Subject Wise

Subject Wise NCERT Exampler Solutions

Frequently Asked Questions (FAQs)

1. Give examples of linear inequalities?

2x>5

2x+3y>5

2. Give examples for a system of linear inequalities

X>0,y>2

2x+y.6, 3x+y<12

3. The quadrant that represents both x and y coordinate greater than or equal to zero is………?

The first quadrant

4. Give an application of linear inequalities?

In solving linear programming problems, linear inequalities are used.

5. How many questions are solved in the exercise 6.3 Class 11 Maths?

15 questions are solved in the NCERT solutions for Class 11 Maths chapter 6 exercise 6.3

6. What method is used to solve the linear inequalities given in the Class 11 Maths chapter 6 exercise 6.3?

Graphical method

7. Why do we solve Class 11 Maths chapter 6 exercise 6.3?

To get an exposure to the concepts of solving a system of linear inequalities in two variables using the graphical method

8. What is the importance of NCERT Class 11 Maths exercises?

As far as mathematics is concerned it is a subject that requires a good amount of practice. And the NCERT exercise helps for the same.

Also Read

NCERT Class 11 Chemistry Chapter 4 Notes Chemical Bonding and Molecular Structure - Download PDF

Hydrogen Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 9 Notes - Download PDF

The S-Block Elements Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 10 Notes - Download PDF

The P-Block Elements Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 11 Notes - Download PDF

Environmental Chemistry Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 14 Notes - Download PDF

NCERT Class 11 Chemistry Chapter 3 Notes - Download PDF

NCERT Solutions for Class 11 Physics Chapter 6 Work Energy and Power

NCERT Solutions for Class 11 Chemistry Chapter 5 States of Matter

NCERT Class 11 Physics Chapter 5 Notes Laws of Motion - Download PDF

NCERT Class 11 Physics Chapter 3 Notes Motion in a straight Line - Download PDF

NCERT Solutions for Exercise 10.1 Class 11 Maths Chapter 10 - Straight Lines

NCERT Solutions for Miscellaneous Exercise Chapter 16 Class 11 - Probability

NCERT Exemplar Class 11 Maths Solutions Chapter 12 Introduction to Three Dimensional Geometry

NCERT Exemplar Class 11 Maths Solutions Chapter 10 Straight Lines

NCERT Exemplar Class 11 Maths Solutions Chapter 6 Linear Inequalities

NCERT Exemplar Class 11 Maths Solutions Chapter 16 Probability

NCERT Exemplar Class 11 Maths Solutions Chapter 14 Mathematical Reasoning

NCERT Exemplar Class 11 Maths Solutions Chapter 7 Permutations and Combinations

Articles

How to Make APAAR ID via DigiLocker and School: A Complete Guide

Dec 17, 2024

Sainik School Entrance Exam 2025: Application, Exam Date, How to Apply, Syllabus

Dec 17, 2024

MVPP Scholarship Exam 2024: Mukhyamantri Vigyan Pratibha Pariksha Registration, Exam Date

Dec 16, 2024

Silverzone ISSO Answer Key 2024-25: Download PDF

Dec 16, 2024

Silverzone IOEL Answer Key 2024 – Download International Olympiad of English Language Solutions

Dec 16, 2024

Silverzone Olympiad IOM Answer Key 2024-25: Qualifying Marks, Score

Dec 16, 2024

Silverzone STEM Olympiad Answer Key 2024-25: Check Answer Key for all Classes

Dec 16, 2024

Silverzone ABHO Answer Key 2024 | Download Akhil Bhartiya Hindi Olympiad Solutions

Dec 16, 2024

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Eligibility Criteria

Application Process

Exam Pattern

Gujarat Board Higher Secondary School Certificate

Late Fee Application Date:13 December,2024 - 22 December,2024

Exam Pattern

Result

Admit Card

Madhya Pradesh State Open School 10th Examination

Admit Card Date:13 December,2024 - 31 December,2024

Admit Card

Result

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Exercise 6.3 Class 11 Maths Chapter 6 - Linear Inequalities

NCERT Solutions for Class 11 Maths Chapter 6: Linear Inequalities Exercise 6.3- Download Free PDF

Download the PDF of NCERT Solutions for Class 11 Maths Chapter 6 – Linear Inequalities Exercise 6.3

Access Linear Inequalities Class 11 Chapter 6-Exercise: 6.3

Question:1 Solve the following system of inequalities graphically:

More About NCERT Solutions for Class 11 Maths Chapter 6 Exercise 6.3

Benefits of NCERT Solutions for Class 11 Maths Chapter 6 Exercise 6.3

Key Features of NCERT 11th Class Maths Exercise 6.3 Answers

NCERT Solutions of Class 11 Subject Wise

Subject Wise NCERT Exampler Solutions

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

Bihar Open Board 10th Examination

Bihar Open Board 12th Examination

National Means Cum-Merit Scholarship

Gujarat Board Higher Secondary School Certificate

Madhya Pradesh State Open School 10th Examination

Popular Questions

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

JEE Main Important Mathematics Formulas

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

Schools By Medium

By Ownership

By City

By State

NVS

JNVST

Download Careers360 App

All this at the convenience of your phone

Scan and download the app