NCERT Exemplar Class 11 Maths Solutions Chapter 6 Linear Inequalities

Question 2

Solve for x, the inequalities in $\frac{\left | x-2 \right | -1}{\left | x-2 \right | -2}\leq 0$

Answer:

Given: $\frac{\left |x-2 \right |-1}{\left |x-2 \right |-2}\leq 0$
Now, let us assume that,
y = |x-2|
Thus, $\frac{ y-1}{y-2}\leq 0$
if $y< 1$,
$y-1<0$ & $y-2<0 $, & thus ,
$y-\frac 1 y-2> 0,$ viz. Not needed
now,
if $1\leq y< 2,$
$y-1\geq 0$ & $y-2< 0,$
& hence,
$y-\frac 1 y-2< 0$… thus, we get the answer we need.
Now, $1\leq y< 2,$
Thus, $1\leq \left | x-2 \right |< 2$
Now, from this, we will get 2 cases, which are-
$1\leq x-2< 2= 3\leq x< 4$
& $1\leq -\left (x-2 \right )< 2= 1\leq -x+2< 2$
On multiplying each term by -1, we get,
$-2\leq x-2< -1$
Now, we’ll add 2 to each term, and we get,
$0\leq x< 1$
Therefore, $\left [ 0,1 \right ]\upsilon \left [ 3,4 \right ]$

Question 3

Solve for x the inequalities in $\frac{1}{\left | x \right |-3}\leq \frac{1}{2}$

Answer:

Given: $\frac{1}{\left | x \right |-3}\leq \frac{1}{2}$
From this, we get,
$\frac{1}{\left | x \right |-3}- \frac{1}{2}\leq 0$
$\frac{1}{\left | x \right |-3}- \frac{1}{2}\leq 0$
$\\\frac{2-|x|+3}{2(|x|-3)} \leq 0 \\\\ \frac{5-|x|}{|x|-3} \leq 0$
Thus, we get,
$5-\left | x \right |\leq 0$ & $\left | x \right |-3\geq 0$ or $5-\left | x \right |\geq 0$ & $\left | x \right |-3< 0$
Thus $\left | x \right |\geq 5$ & $\left | x \right | > 3$ or $\left | x \right | \leq 5$ & $\left | x \right | < 3$
Thus,
$x \epsilon \left ( -\infty , -5 \right ]$ or $\left [ 5, -\infty \right )$ or $x \epsilon \left ( -3, 3 \right )$
Therefore,
$x \epsilon \left ( -\infty , -5 \right ] \upsilon \left ( -3,3 \right ) \upsilon \left [5,\infty \right )$

Question 4

Solve for x, the inequalities in $\left | x -1 \right |\leq 5,\left | x \right |\geq 2$

Answer:

$\left | x-1 \right |\leq 5........(given)$
(i) Now, there will be two cases –
$x-1 \leq 5,$
Adding 1 on both sides, we get,
$x \leq 6$
(ii) $-\left (x-1 \right ) \leq 5$
i.e., $-x+1 \leq 5$
Subtract 1 from both sides, we will get,
$-x \leq 4$ i.e $x \geq -4$
Now, from (i) & (ii), we get,
$-4 \leq x\leq 6.........(a)$
& $\left | x \right |\geq 2$'
Thus, $x \geq 2$ & $-x \geq 2$
Thus $x \leq -2$
i.e $x \epsilon(-4,-2] \cup[2,6]$

Question 5

Solve for x, the inequalities in $-5\leq \frac{2-3x}{4}\leq 9$

Answer:

Given $-5\leq \frac{2-3x}{4}\leq 9$
On multiplying all the terms by 4, we get,
$-20\leq 2-3x\leq 36$
Now, add -2 to each term,
$-22\leq -3x\leq 34$
And now, divide each term by 3,
$-\frac{22}{3}\leq -x\leq \frac{34}{3}$
Now, we will multiply each term by -1 to invert the inequality. We get,
$-\frac{34}{3}\leq x\leq \frac{22}{3}$

Question 6

Solve for x, the inequalities in $4x+3\geq 2x+17, 3x-5< -2$

Answer:

$4x+3\geq 2x+17 .......$ given
Thus, $4x-2x\geq 17-3$
Thus $2x\geq 14$
Thus $x\geq 7$ .........(i)
Now,
$3x-5< -2$............. given
Thus $x< 1$.........(ii)
Therefore, x has no solution as eq. (i) & eq. (ii) cannot be possible simultaneously.

Question 7

A company manufactures cassettes. Its cost and revenue functions are C(x) = 26,000 + 30x and R(x) = 43x, respectively, where x is the number of cassettes produced and sold in a week. How many cassettes must be sold by the company to realise some profit?

Answer:

Given: Revenue, R(x) = 43x
Cost, C(x) = 26,000 + 30x,
Where ‘x’ is the no. of cassettes.
Requirement: profit > 0
Solution: We know that,
Profit = revenue – cost
⇒ 43x – 26000 – 30x > 0
⇒ 13x – 26000 > 0
⇒ 13x > 26000
⇒ x > 2000
Therefore, 2000 more cassettes should be sold by the company to realise the profit.

Question 8

The water acidity in a pool is considered normal when the average pH reading of three daily measurements is between 8.2 and 8.5. If the first two pH readings are 8.48 and 8.35, find the range of pH values for the third reading that will result in the acidity level being normal.

Answer:

Given: First reading = 8.48
Second reading = 8.35
To find: Third reading
Solution:
Let ‘x’ be the third reading,
Now, the average pH should be between 8.2 & 8.5
Average pH = (8.48 + 8.35 + x)/3
Thus,
8.2 < (8.48 + 8.35 + x)/3 < 8.5
On multiplying each term by 3, we get,
24.6 < 16.83 + x < 25.5
Now, subtracting 16.83 from each term, we get,
7.77 < x < 8.67
Therefore, the third reading should be between 7.77 & 8.67.

Question 9

A solution of 9% acid is to be diluted by adding 3% acid solution to it. The resulting mixture is to be more than 5% but less than 7% acid. If there are 460 litres of the 9% solution, how many litres of the 3% solution will have to be added?

Answer:

Let us assume that ‘x’ litres of 3% solution are added to 460 L of 9% solution.
Thus, total solution = (460 + x)L
& total acid content in resulting solution = (460 × 9/100 + x × 3/100)
= (41.4 + 0.03x) %
Now, according to the question,
The resulting mixture we get should be less than 7% acidic & more than 5% acidic
Thus, we get,
5% of (460 + x) < 41.4 + 0.03x < 7% 0f (460 + x)
= 23 + 0.05x < 41.4 + 0.03x < 32.2 + 0.07x
Now,
23 + 0.05x < 41.4 + 0.03x & 41.4 + 0.03x < 32.2 + 0.07x
= 0.02x < 18.4 & 0.04x > 9.2
Thus, 2x < 1840 & 4x > 920
= 230 < x < 920
Therefore, the solution between 230 l & 920 l should be added.

Question 10:

A solution is to be kept between 40°C and 45°C. What is the range of temperature in degrees Fahrenheit, if the conversion formula is $F=\frac{9}{5}C+32$

Answer:

Given: The solution should be kept between 40°C & 45°C
Now, let C be the temp in Celsius & F be the temp in Fahrenheit.
Thus, 40 < C < 45
On multiplying each term by $\frac 95$,
72 < $\frac 95$ C < 81
Now, add 32 to each term,
104 < $\frac 95$ C + 32 < 113
Thus, 104 < F < 113
Therefore, F, i.e., temp in Fahrenheit, should be between 104°F & 113°F.

Question 11

The longest side of a triangle is twice the shortest side and the third side is 2 cm longer than the shortest side. If the perimeter of the triangle is more than 166 cm then find the minimum length of the shortest side.

Answer:

Let us assume that the length of the shortest side of the triangle is ‘x’ cm
Thus, length of the largest side = 2x …. (given)
& length of the third side = (x + 2) cm …. (given)
Now, we know that,
The perimeter of a triangle = sum of all three sides
= x + 2x + x + 2
= 4x + 2 cm
Now, it is given that the perimeter of the triangle is more than 166 cm,
Thus, $4x+2\geq 166$
$4x\geq 164$
Thus,$x\geq 41$
Therefore, the minimum length of the shortest side should be = 41 cm.

Question 12

In drilling the world’s deepest hole, it was found that the temperature T in degrees Celsius, x km below the earth’s surface was given by T = 30 + 25 (x – 3), 3 ≤ x ≤ 15. At what depth will the temperature be between 155°C and 205°C?

Answer:

Given:
T = 30 + 25 (x – 3), $3 \leq x\leq 15$
Where, T = temperature
x = depth inside Earth
It is also given that T should be between 155? C & 205? C
Thus,
155 < T < 205
155 < 30 + 25 (x – 3) < 205
155 < 30 + 25x – 75 < 205
155 < 25x – 45 < 205
Now, we will add 45 to each term,
We get,
200 < 25x < 250
Now, on dividing each term by 25, we get,
8 < x < 10
Therefore, at a depth of 8-10 km, temperature varies from 1550C to 2050C.

Question 13

Solve the following system of inequalities $\frac{2x+1}{7x-1}> 5,\frac{x+7}{x-8}>2$

Answer:

Given: $2x+\frac 17x-1 > 5$
$\frac{(2x+1)}{(7x - 1)} – 5 > 0$ …….. (on subtracting 5 from both the sides)
$\frac{(2x + 1 – 35x + 5)}{(7x – 1)} > 0$
$\frac{(6 – 33x)}{(7x – 1) }>0$
Now, either the numerator or the denominator should be greater than 0, or both should be less than 0 for the above fraction to be greater than 0; thus,
$6 – 33x > 0$ & $7x – 1 > 0$
$33x <6$ & $7x > 1$
X < $\frac {2}{11}$ & x > $\frac 17$
i.e., $\frac 17$ < x < $\frac {2}{11}$ ……. (i)
Or,
$6 – 33x < 0$ & $7x – 1 < 0$
$33x > 6$ & $7x < 1$
X > $\frac {2}{11}$ & x < $\frac 17$
i.e., $\frac {2}{11}$ < x < $\frac 17$ ….. viz. impossible
Now,
$\frac{(x + 7)}{(x – 8)} > 2$ …… (given)
$\frac{(x + 7)}{(x – 8 )}– 2 > 0$ …… (subtracting both sides by 2)
$\frac{(x +7 – 2x + 16)}{(x – 8)}> 0$
$\frac{(23 – x)}{(x – 8) }> 0$
Now, either the numerator or the denominator should be greater than 0, or both should be less than 0 for the above fraction to be greater than 0; thus,
$23 – x > 0$ & $x – 8 > 0$
$X < 23$ & $x > 8$
i.e., $8 < x < 23$ …….. (ii)
Or,
$23 – x > 0$ & $8 > 0$
$X > 23$ & $x < 8$
i.e., $23 < x < 8$ ….. viz. impossible
Therefore, from (i) & (ii), we can say that there is no solution satisfying both inequalities. Thus, the system has no solution.

Question 14

Find the linear inequalities for which the shaded region in the given figure is the solution set
.

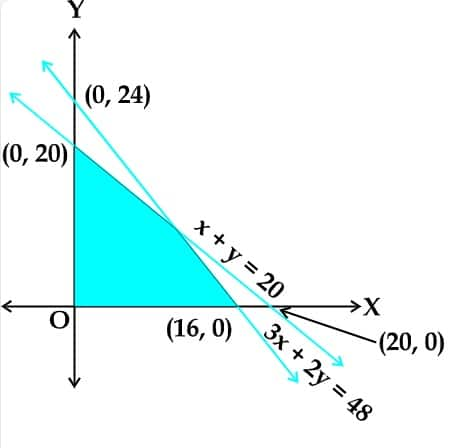
Answer:

Let us consider, 3x + 2y = 48
Now, from the graph, we can say that the constraint $3x+2y\leq 48$ is satisfied since the shaded region and the origin are on the same side of the line
Now, we will consider,
x + y = 20
The graph, we can say that the constraint $x+y\leq 20$ is satisfied since the shaded region & the origin are on the same side of the line
We know that,
In the first quadrant shaded region is $x\geq 0$ & $y\geq 0$ ,
Thus, the linear inequalities will be,
$3x+2y\leq 48$
$⇒x+y\leq 20$
$⇒x\geq 0$
$⇒y\geq 0$

Question 15

Find the linear inequalities for which the shaded region in the given figure is the solution set.

Answer:

Let us consider,
$x + y = 8$,
Now, from the graph, we can say that the constraint $x+y\leq 8$ is satisfied since the shaded region and the origin are on the same side of the line.
Now, let us consider, $x + y = 4$,
Here, the constraint $x+y\geq 0$ is not satisfied since the origin is on the opposite side of the shaded region.
Thus, the required constraint is $x+y\geq 4$
Now, we know that,
The shaded region in the first quadrant is $x\geq 0$ &$y\geq 0$
& shaded region below the line y = 5 & left to the line x = 5 is
$y\leq 0$ & $x\geq 0$
Therefore, the linear inequalities are,
$x+y\leq 8$
$x+y\geq 4$
$x\geq 0$
&$y\geq 0$
$x\leq 5$& $y\leq 5$

Question 16

Show that the following system of linear inequalities has no solution $x+2y\leq 3, 3x+4y\geq 12, x\geq 0, y\geq 1$

Answer:

Given: $x+2y\leq 3$ Line: x + 2y = 3

Now, (0,0) doesn't satisfy $3x+4y\geq 12$,
Thus, the region is not towards the origin
The region is to the right of the y-axis; thus,
$x\geq 0$
& Region is above the line x = 1, thus,
$y\geq 1$
Thus, the graph can be plotted as,

Therefore, the system has no common region as a solution.

Question 17

Solve the following system of linear inequalities $3x+2y\geq 24, 3x+y\leq 15, x> 4$

Answer:

Let us find the common region of all by plotting each inequality.
Given: 3x + 2y ≥ 24
Thus, for line,
3x + 2y = 24

Now, we know that (0,0) does not satisfy 3x + 2y ≥ 24
Thus, the region is away from the origin.
Now, 3x + y ≤ 15 … (given)
Thus, for line,
3x + y = 15

Now, here (0,0) satisfies 3x + y ≤ 15
Thus, the region is towards the origin.
Now, x ≥ 4 implies that the region is to the right of the line x = 4

Therefore, the above system has no common region as a solution.

Question 18

Show that the solution set of the following system of linear inequalities is an unbounded region $2x+y \geq 8, x+2y\geq 10, x\geq 0, y\geq 0$

Answer:

Let us find the common region of all by plotting each inequality.
2x + y ≥ 8 …… (given)
Thus, for line,
2x + y = 8

Now, we know that (0,0) does not satisfy 2x + y ≥ 8
Thus, the region is away from the origin.
Now, x + 2y ≥ 10 …… (given)
Thus, for line,
x + 2y = 10

Now, we know that (0,0) does not satisfy x + 2y ≥ 10
Thus, the region is away from the origin.
Also, x ≥ 0 & y ≥ 0 implies that the region is in the first quadrant
Thus, the graph will be -

Hence, from the graph, it is clear that the shaded region is unbounded.

Question 19

If $x< 5$, then
A. $-x< -5$
B. $-x\leq -5$
C. $-x> -5$
D. $-x\geq -5$

Answer:

From what’s given : x < 5,
…….. (sinc, multiplication or division by -ve no. Inverts the inequality sign)
Thus, -x > -5.

Question 20

Given that x, y, and b are real numbers and $x< y,b< 0$, then.
A. $\frac{x}{b}< \frac{y}{b}$
B. $\frac{x}{b}\leq \frac{y}{b}$
C. $\frac{x}{b}> \frac{y}{b}$
D.$\frac{x}{b}\geq \frac{y}{b}$

Answer:

x < y ….. (given)
Also, b < 0 ….. (given)
Now, we know that,
Multiplication or division by -ve no. Inverts the inequality sign
Thus, $\frac{x}{b}> \frac{y}{b}$

Question 21

If $3x + 17 < -13$ then
A. $x\epsilon \left ( 10,\infty \right )$
B.$x\epsilon \left ( 10,\infty \right )$
C.$x\epsilon \left ( -\infty,10 \right )$
D.$x\epsilon \left ( -10,10 \right )$

Answer:

Given: 3x + 17 < -13
Now, we will subtract both sides by 17, we get,
-3x < -30
Now, we know that,
Multiplication or division by -ve no. Inverts the inequality sign
Thus, x > 10
Thus, x ∈ (10,$\infty$)

Question 22

If x is a real number and $\left | x \right | < 3$ then
A. $x\geq 3$
B. $-3< x< 3$
C.$x\leq -3$
D. $-3\leq x\leq 3$

Answer:

Given: |x|< 3
Thus, there will be two cases,
x < 3 …… (i)
& x > -3 ….. (ii)
Thus, -3 < x < 3 …….. [From (i) & (ii)]

Question 23

x and b are real numbers. If $b> 0$ and $\left |x \right |> b$ then
A. $x\epsilon \left ( -b,\infty \right )$
B. $x\epsilon \left ( -\infty,b \right )$
C. $x\epsilon \left ( -b,b \right )$
D.$x\epsilon \left ( -\infty .-b \right ) \upsilon \left ( b,\infty \right )$

Answer:

Given: |x|> b
Thus, there will be 2 cases,
x > b → x (b,∞) …….. (i)
& -x > b → x < -b
Thus, x $\epsilon$ (-∞, -b) ……… (ii)
Therefore,
x $\epsilon$(-∞, -b) U (b,∞)

Question 24

If $\left | x-1 \right |> 5$ then
A. $x\epsilon \left ( -4,6 \right )$
B. $x\epsilon \left [ -4,6 \right ]$
C.$x\epsilon \left [ -\infty ,-4 \right )\upsilon \left ( 6,\infty \right )$
D. $x\epsilon \left [ -\infty ,-4 \right )\upsilon \left [ 6,\infty \right )$

Answer:

Given: |x-1|> 5
Thus, there will be two cases,
(x-1) > 5, x > 6 → x $\epsilon$ (6,∞) …….. (i)
& -(x-1) > 5 → -x + 1 > 5 → -x > 4
i.e., x < -4
x $\epsilon$ (-∞, -4) …… (ii)
Therefore, x $\epsilon$ (-∞, -4) U (6,∞)

Question 25

IF $\left | x+2 \right |\leq 9$ then
A. $x\epsilon \left ( -7,11 \right )$
B. $x\epsilon \left ( -11,7 \right )$
C. $x\epsilon \left ( -\infty ,-7 \right ) \upsilon \left ( 11,\infty \right )$
D. $x\epsilon \left ( -\infty ,-7 \right ) \upsilon \left [ 11,\infty \right )$

Answer:

Given: $\left | x-2 \right |\leq 9$Thus, there will be two cases,
(x+2) ≤ 9 → x ≤ 7
Thus, x $\epsilon$ (-∞,7) …….. (i)
& -(x+2) ≤ 9 → -x-2 ≤ 9 → -x ≤ 11 → x ≥ -11
Thus, x $\epsilon$ [-11, ∞] …….. (ii)
Therefore, x $\epsilon$ [-11,7] ………. [From (i) & (ii)]

Question 26

The inequality represented in the following graph is

A. $\left | x \right |< 5$
B.$\left | x \right |\leq 5$

C. $\left | x \right |> 5$
D. $\left | x \right |\geq 5$

Answer:

(a) |x|< 5
Thus, there will be two cases,
x < 5 …… (i)
& -x < 5
→ x > -5 …… (ii)

Therefore, -5 < x < 5 …….. [From (i) & (ii)]

Question 27

The solution to linear inequality in variable x is represented on a number line. Choose the correct answer from the given four options in each of the

A. $x \epsilon \left ( -\infty ,5 \right )$
B. $x \epsilon \left ( -\infty ,5 \right ]$
C. $x \epsilon \left [5 , \infty \right )$
D. $x \epsilon \left (5 , \infty \right )$

Answer:

Here, x > 5, I.e., x $\epsilon$ (5,∞),
Since excluding 5, the above graph represents all values of x greater than 5.

Question 28

The solution of a linear inequality in variable x is represented on a number line. Choose the correct answer from the given four options in each of the

A. $x\epsilon \left ( \frac{9}{2},\infty \right )$
B. $x\epsilon \left [ \frac{9}{2},\infty \right )$
C. $x\epsilon \left [ -\infty, \frac{9}{2} \right )$
D.$x\epsilon \left ( -\infty, \frac{9}{2} \right ]$

Answer:

All the values of x greater than $\frac 92$, including $\frac 92$, are represented by the above graph.
Thus, x ≥ $\frac 92$
Therefore, x $\epsilon$($\frac 92$,∞)

Question 29

The solution of a linear inequality in variable x is represented on a number line. Choose the correct answer from the given four options in each of the

A. $x\epsilon \left (-\infty, \frac{7}{2} \right )$
B. $x\epsilon \left (-\infty, \frac{7}{2} \right ]$
C. $x\epsilon \left [-\infty, \frac{7}{2} \right )$
D.$x\epsilon \left ( \frac{7}{2} , \infty \right )$

Answer:

All the values of x less than $\frac 72$, excluding $\frac 72$, are represented by the above graph.
Thus, x < $\frac 72$
Therefore, x $\epsilon$ (-∞,$\frac 72$)

Question 30

A. $x\epsilon \left ( -\infty ,-2 \right )$
B. $x\epsilon \left ( -\infty ,-2 \right ]$
C. $x\epsilon \left ( -2, \infty \right ]$
D.$x\epsilon \left [ -2, \infty \right )$

Answer:

All the values of x less than -2, including -2, are represented by the above graph,
Thus, x ≤ 2,
Therefore, x $\epsilon$(-∞,-2)

The solution of a linear inequality in variable x is represented on a number line. Choose the correct answer from the given four options in each of the A. B. C. D.

Question 31

State which of the following statements is True or False

(i) If x < y and b < 0, then $\frac{x}{y}< \frac{y}{b}$
(ii) If xy > 0, then x > 0 and y < 0
(iii) If xy > 0, then x < 0 and y < 0
(iv) If xy < 0, then x < 0 and y < 0
(v) If x < –5 and x < –2, then x ∈ (– ∞, – 5)
(vi) If x < –5 and x > 2, then x ∈ (– 5, 2)
(vii) If x > –2 and x < 9, then x ∈ (– 2, 9)
(viii) If |x| > 5, then x ∈ (– ∞, – 5) ∪ [5, ∞)
(ix) If |x| ≤ 4, then x ∈ [– 4, 4]
(x) Graph of x < 3 is

(xi) Graph of x ≥ 0 is


(xii) Graph of y ≤ 0 is

(xiii) Solution set of x ≥ 0 and y ≤ 0 is

(xiv) Solution set of x ≥ 0 and y ≤ 1 is


(xv) Solution set of x + y ≥ 0 is

Answer:

(i) It is False.
x < y, b<0 ……. (given)
Multiplication or division by -ve no. Inverts the inequality sign
Thus, x/b > y/b

(ii) It is False.
If xy > 0, then,
Either x >0 & y > 0,
Or x < 0 & y < 0.

(iii) It is True.
If xy > 0, then,
Either x >0 & y > 0,
Or x < 0 & y < 0.

(iv) It is False.
If xy < 0, then,
Either x < 0 & y > 0,
Or x > 0 & y < 0

(v) It is True.
We know that,
x < -5 → x $\epsilon$ (-∞,-5) ………. (i)
& x < -2 → x $\epsilon$ (-∞,-2) ………. (ii)
Thus, x$\epsilon$ (-∞,-5) ………… [By taking the intersection of (i) & (ii)]

(vi) It is False.
We know that,
x < -5 → x $\epsilon$ (-∞,-5) ………. (i)
& x < 2 → x $\epsilon$ (∞,2) ………. (ii)
Therefore, x has no common solution ……… [From (i) & (ii)]

(vii) It is True.
x > -2 → x $\epsilon$ (-∞,-2) ………. (i)
& x < 9 x $\epsilon$ (-∞,9) ………. (ii)
Therefore, x $\epsilon$ (-2,9) ……… [From (i) & (ii)]

(viii) It is True.
|x|< 5
Thus, there will be two cases,
x > 5 → x $\epsilon$ (5,∞) …… (i)
& -x > 5 → x < -5
→ x $\epsilon$ ( -∞,-2) …… (ii)
x $\epsilon$ (-∞,-5) U (5,∞) ……. [From (i) & (ii)]

(ix) It is True.
|x| ≤ 4,
Thus, there will be two cases,
x ≤ 4 → x $\epsilon$ (-∞,4) …….. (i)
& -x ≤4, x ≥ -4 → x $\epsilon$ [-4,∞] ……. (ii)
Therefore, x $\epsilon$ [-4,4] …….. [From (i) & (ii)]

(x) It is True.
Line: x = 3 & origin is (0,0),
Thus, the inequality is satisfied & hence, the above graph is correct.

(xi) It is True.
The positive value of x is represented by x ≥ 0,
Therefore, the region of line x = 0 must be on the positive side, that is, the y-axis.

(xii) It is False.
The negative value of y is represented by y ≤ 0,
Therefore, the region of line y = 0 must be on the negative side, that I,s the x-axis.

(xiii) It is False.
The shaded region is the first quadrant & the 4th quadrant is represented by x ≥ 0 & y ≤ 0.

(xiv) It is False.
The region on the left side of the y-axis is implied by x ≥ 0 & the region below the line y = 1 is implied by y ≤ 1.

(xv) It is True
The inequality is satisfied if we take any point above the line x + y = 0, say (3,2)
Thus, x+y ≥ 0
….…..(since, 3 + 2 = 5 > 0)
Therefore, the region should be above the line x+y = 0

Question 32

Fill in the blanks of the following:
(i) If – 4x ≥ 12, then x ... – 3.
(ii) If -3x/4 ≤ –3, then x…..4.
(iii) If $\frac{2}{x+2}$> 0, then x …. –2.
(iv) If x > –5, then 4x ... –20.
(v) If x > y and z < 0, then – xz ... – yz.
(vi) If p > 0 and q < 0, then p – q ... p.
(vii) If |x+ 2|> 5, then x ... – 7 or x ... 3.
(viii) If – 2x + 1 ≥ 9, then x ... – 4.
Answer:

(i) -4x ≥ 12
-x ≥ 3 ……….. (Dividing by 4)
Now, we will invert the equation by taking negative signs on both sides, we get,
x ≤ 3
(ii) -3/4 x ≤ -3
Thus, -3x ≤ -12 …… (On multiplying by 4)
Now, we will invert the equation by taking negative signs on both sides, and we get,
3x ≤ 12 I.e., x ≤ 4.
(iii) 2/x+2 > 0
For the above to be greater than 0,
x+2 > 0 i.e., x > -2
(iv) x > -5
I.e., 4x > -20 …….. (on multiplying by 4)
(v) x > y
z is negative, since z < 0
Now, we will invert the equation by taking negative signs on both sides, and we get,
Thus, -xz > - yz
(vi) q < 0
Now, we will invert the equation by taking negative signs on both sides, and we get,
-q > 0
p - q > p ….. (adding p on both sides)
(vii) |x+2|> 5
Thus, there will be two cases,
X+2 > 5 & -(x+2)<5
X>3 & -x-2 <5
X > 3 & -x > 7
X > 3 & x < -7
(viii) -2x + 1 ≥ 0
-2x ≥ 8 …… (on adding -1 to both sides)
Now, we will invert the equation by taking negative signs on both sides, and we get,
Thus, x ≤ -4.