NCERT Solutions for Class 11 Maths Chapter 1 Sets
Sets are the foundation of modern mathematics. Collecting and Segregating things is a fundamental task that we all use in our day-to-day lives to organise things. In mathematics, we also use the process of collecting and segregating elements in a well-defined manner, and this process is known as a set. Sets are well-defined collections of objects, and they can be classified into different types based on their elements or characteristics, including finite, infinite, empty, singleton, equal, and universal sets. NCERT Solutions for Class 11 Maths also emphasise Intervals as subsets of the real numbers (R), the Universal Set, Venn Diagrams, and operations on Sets, such as Union, Intersection, Difference, and Complement. Many toppers rely on NCERT Solutions because they are designed in accordance with the latest syllabus.
This Story also Contains
- Sets Class 11 Questions And Answers PDF Free Download
- NCERT Solutions for Class 11 Maths Chapter 1 Sets: Exercises
- Sets Class 11 NCERT Solutions: Exercise-wise
- Class 11 Maths NCERT Chapter 1 Sets: Extra Question
- Sets Class 11 Chapter 1: Topics
- Set Class 11 Solutions – Important Notes
- Approach to Solve Questions of Sets Class 11
- What Extra Should Students Study Beyond NCERT for JEE?
- Why are Class 11 Maths Chapter 1 Sets question answers important?
- NCERT Class 11 Maths Solutions - Chapter Wise
Understanding sets is like learning the alphabet of higher mathematics. This article provides clear and step-by-step solutions to exercise problems in the NCERT Class 11 Mathematics textbook. These NCERT Solutions for Class 11 are designed by Subject Matter Experts according to the latest NCERT syllabus, ensuring that students grasp the concepts effectively. Students can also refer to the NCERT notes, which will help them understand the idea more clearly. Find everything in one place – NCERT Books, Solutions, Syllabus, and Exemplar Problems with Solutions – in this NCERT article.
Sets Class 11 Questions And Answers PDF Free Download
To make maths learning easier, Careers360 experts have created these NCERT Solutions for Class 11 Maths Chapter 1. A downloadable PDF is available — click the link below to access it.
NCERT Solutions for Class 11 Maths Chapter 1 Sets: Exercises
NCERT Class 11 Maths Chapter 1 Sets question answers with detailed explanations are provided below.
|
Sets Class 11 Question Answers |
Question 1 (i): Which of the following are sets? justify your answer
The collection of all the months of a year beginning with the letter J.
Answer:
The months starting with the letter J are:
January
June
July
Hence, this is a collection of well-defined objects, so it is a set.
Question 1 (ii): Which of the following are sets? justify your answer
The collection of the ten most talented writers of India.
Answer:
The ten most talented writers may vary depending on the criteria used to determine talent.
Hence, this is not well-defined, so it cannot be a set.
Question 1 (iii): Which of the following are sets? justify your answer
A team of eleven of the best cricket batsmen in the world.
Answer:
The eleven most talented cricketers may be different depending on the criteria for determining the talent of a player.
Hence, this is not well defined, so it is not a set.
Question 1 (iv): Which of the following are sets? justify your answer
The collection of all the boys in your class.
Answer:
The collection of boys in a class is well-defined and known.
A group of well-defined objects is a set.
Hence, it is a set.
Question 1 (v): Which of the following are sets? justify your answer
The collection of all natural numbers is less than 100.
Answer:
Natural numbers less than 100 have a defined and known collection of numbers.
that is S= {1,2,3............99}
Hence, it is a set.
Question 1 (vi): Which of the following are sets? Justify your answer
A collection of novels written by the writer Munshi Prem Chand.
Answer:
The collection of novels written by Munshi Prem Chand is well-defined and known.
Hence, it is a set.
Question 1 (vii): Which of the following are sets? Justify your answer
The collection of all even integers.
Answer:
The collection of even integers is well-defined because we can get even integers till infinity. that is
Hence, it is a set.
Question 1 (viii): Which of the following are sets? Justify your answer
The collection of questions in this Chapter.
Answer:
The collection of questions in a chapter is well-defined and known.
Hence, it is a set.
Question 1 (ix): Which of the following are sets? Justify your answer
A collection of the most dangerous animals in the world.
Answer:
A Collection of the most dangerous animals is not well defined because the criteria for defining the dangerousness of any animal can vary.
Hence, it is not a set.
Question 2: Let $A = \left \{ 1,2,3,4,5,6 \right \}$.Insert the appropriate symbol $\in$ or $\notin$ in the blank space:
(ii) 8_____A
(iii) 0_____A
(iv) 4_____A
(v) 2_____A
(vi) 10____A
Answer:
A = $\left \{1,2,3,4,5,6 \right \}$, the elements which lie in this set belong to this set, and others do not belong.
(i) 5 $\in$ A
(ii) 8 $\notin$ A
(iii) 0 $\notin$ A
(iv) 4 $\in$ A
(v) 2 $\in$ A
(vi) 10 $\notin$ A
Question 3(i): Write the following sets in roster form
$ \text {(i)} A=\{x: x \text { is an integer and }-3 \leq x<7\}$
Answer:
Elements of this set are: -3, -1, 0, 1, 2, 1,0,1,2,3,4,5,6.
Hence, this can be written as:
A = $\left \{ -3,-2,-1,0,1,2,3,4,5,6 \right \}$
Question 3 (ii): Write the following sets in roster form
$\left ( ii \right )B= \left \{ x:x\, is \, a\, natural\, number\, less\, than\, 6 \right \}$
Answer:
Natural numbers less than 6 are 1,2,3,4,5.
This can be written as:
$B = \left \{1,2,3,4,5 \right \}$
Question 3(iii): Write the following sets in roster form
C = {x: x is a two-digit natural number such that the sum of its digits is 8}
Answer:
The two-digit numbers having a sum equal to 8 are, and 17,26,35,44,53,62,71,80.
This can be written as:
$C= \left \{17,26,35,44,53,62,71,80 \right \}$
Question 3 (iv): Write the following sets in roster form
D = {x: x is a prime number which is a divisor of 60}
Answer:
$60= 2\times 2\times 3\times 5$
Prime numbers which are divisors of 60 are 2, 3, and 5.
This can be written as:
$D= \left \{ 2,3,5 \right \}$
Question 3(v): Write the following sets in roster form
E = The set of all letters in the word TRIGONOMETRY.
Answer:
Letters of the word TRIGONOMETRY are: T, R, I, G, N, O, M, E, Y.
This can be written as:
E = {T, R, I, G, N, O, M, E, Y}
Question 3 (vi): Write the following sets in roster form
F = The set of all letters in the word BETTER.
Answer:
The set of letters of the word BETTER are: {B, E, T, R}
This can be written as:
F = {B, E, T, R}
Question 4 (i): Write the following sets in the set builder form
{3, 6, 9, 12}
Answer:
A = {3,6,9,12}
This can be written as: $\left \{3,6,9,12 \right \}= \left \{ x:x= 3n,n\in N\, \, and\,\, 1\leq n\leq 4 \right \}$
Question 4(ii): Write the following sets in the set builder form
{2,4,8,16,32}
Answer:
$2 = 2^{1}$
$4 = 2^{2}$
$8= 2^{3}$
$16 = 2^{4}$
$32 = 2^{5}$
$\left \{ 2,4,8,16,32 \right \}$ can be written as $\left \{ x:x= 2^{n},n\in N and 1\leq n\leq 5 \right \}.$
Question 4 (iii): Write the following sets in the set builder form:
{5, 25, 125, 625}
Answer:
$5= 5^{1}$
$25= 5^{2}$
$125= 5^{3}$
$625= 5^{4}$
$\left \{5,25,125,625 \right \}$ can be written as $\left \{ x:x= 5^{n},n\in N and 1\leq n\leq 4 \right \}$
Question 4 (iv): Write the following sets in the set builder form:
{2, 4, 6,...}
Answer:
This is a set of all even natural numbers.
{2,4,6....} can be written as {x: x is an even natural number}
Question 4 (v): Write the following sets in the set builder form :
{1,4,9, . . .,100}
Answer:
$1= 1^{2}$
$4= 2^{2}$
$9= 3^{2}$
.
.
.
$100= 10^{2}$
$\left \{ 1,4,9.....100 \right \}$ can be written as $\left \{ x:x= n^{2} ,n\in N and \, 1\leq n\leq 10\right \}$
Question 5(i): List all the elements of the following sets:
A = {x: x is an odd natural number}.
Answer:
A = { x : x is an odd natural number } = {1,3,5,7,9,11,13.............}
Question 5 (ii): List all the elements of the following sets:
B= { x : x is an integer, $\frac{-1}{2} < x< \frac{9}{2}$ }
Answer:
Integers between $-\frac{1}{2}< x< \frac{9}{2}$ are 0,1,2,3,4.
Hence, B = {0,1,2,3,4}
Question 5 (iii): List all the elements of the following sets:
C = {x : x is an integer, $x^{2}\leq 4$ }
Answer:
$\left (-2 \right)^{2}= 4$
$\left (-1 \right)^{2}= 1$
$\left (0 \right)^{2}= 0$
$\left ( 1\right )^{2}= 1$
$\left ( 2\right )^{2}= 4$
Integers whose square is less than or equal to 4 are: -2,-1,0,1,2.
Hence, it can be written as c = {-2, -1,0,1,2}.
Question 5 (iv): List all the elements of the following sets:
D = {x: x is a letter in the word “LOYAL”}
Answer:
LOYAL has the letters L, O, Y, A.
D = {x: x is a letter in the word “LOYAL”} can be written as {L, O, Y, A}.
Question 5 (v): List all the elements of the following sets:
E = {x: x is a month of a year not having 31 days}
Answer:
The months that do not have 31 days are:
February
April
June
September
November
It can be written as {February, April, June, September, November}
Question 5 (vi): List all the elements of the following sets :
F = {x: x is a consonant in the English alphabet which precedes k }.
Answer:
The consonants in English which precede K are: B, C, D, F, G, H, J
Hence, F = {B, C, D, F, G, H, J}.
(i) {1, 2, 3, 6} (a) {x: x is a prime number and a divisor of 6}
(ii) {2, 3} (b) {x: x is an odd natural number less than 10}
(iii) {M, A, T, H, E, I, C, S} (c) {x: x is a natural number and a divisor of 6}
(iv) {1, 3, 5, 7, 9} (d) {x: x is a letter of the word MATHEMATICS}.
Answer:
(i) 1,2,3,6, all are natural numbers and also divisors of 6.
Hence, (i) matches with (c)
(ii) 2,3 are prime numbers and are divisors of 6.
Hence, (ii) matches with (a).
(iii) M, A, T, H, E, I, C, S are letters of the word "MATHEMATICS".
Hence, (iii) matches with (d).
(iv) 1,3,5,7,9 are odd natural numbers less than 10.
Hence, (iv) matches with (b).
|
Sets Class 11 Question Answers |
Question 1(i): Which of the following are examples of the null set :
Set of odd natural numbers divisible by 2
Answer:
No odd number is divisible by 2.
Hence, this is a null set.
Question 1(ii): Which of the following are examples of the null set :
Set of even prime numbers.
Answer:
Even prime number = 2.
Hence, it is not a null set.
Question 1(iii): Which of the following are examples of the null set:
{ x : x is a natural numbers, $x< 5$ and $x> 7$ }
Answer:
No number exists which is less than 5 and more than 7.
Hence, this is a null set.
Question 1(iv): Which of the following are examples of the null set :
{y: y is a point common to any two parallel lines}
Answer:
Parallel lines do not intersect, so they do not have any common points.
Hence, it is a null set.
Question 2: Which of the following sets are finite or infinite:
(i) The set of months of a year
(ii) {1, 2, 3, . . .}
(iii) {1, 2, 3, . . .99, 100}
(iv) The set of positive integers greater than 100.
(v) The set of prime numbers less than 99
Answer:
(i) The number of months in a year is 12 and finite.
Hence, this set is finite.
(ii) {1,2,3,4.......} and so on, this does not have any limit.
Hence, this is an infinite set.
(iii) {1,2,3,4,5......100} has finite numbers.
Hence, this is a finite set.
(iv) Positive integers greater than 100 have no limit.
Hence, it is an infinite set.
(v) Prime numbers less than 99 are finite, known numbers.
Hence, it is a finite set.
Question 3: State whether each of the following sets is finite or infinite:
(i) The set of lines which are parallel to the x-axis
(ii) The set of letters in the English alphabet
(iii) The set of numbers which are multiples of 5
(iv) The set of animals living on the earth
(v) The set of circles passing through the origin (0,0)
Answer:
(i) Lines parallel to the x-axis are infinite.
Hence, it is an infinite set.
(ii) Letters in the English alphabet are 26 finite letters.
Hence, it is a finite set.
(iii) Numbers which are multiples of 5 have no limit; they are infinite.
Hence, it is an infinite set.
(iv) Animals living on earth are finite, though the number is very high.
Hence, it is a finite set.
(v) There is an infinite number of circles which pass through the origin.
Hence, it is an infinite set.
Question 4(i): In the following, state whether A = B or not:
A = {a, b, c, d} B = {d, c, b, a}
Answer:
Given
A = {a, b, c, d}
B = {d, c, b, a}
Comparing the elements of set A and set B, we conclude that all the elements of A and all the elements of B are equal.
Hence, A = B.
Question 4(ii): In the following, state whether A = B or not:
A = {4, 8, 12, 16} B = {8, 4, 16, 18}
Answer:
12 belongs to A, but 12 does not belong to B
12 $\in$ A but 12 $\notin$ B.
Hence, A $\neq$ B.
Question 4(iii): In the following, state whether A = B or not:
A = {2, 4, 6, 8, 10} B = {x: x is positive even integer and $x \leq 10$}
Answer:
Positive even integers less than or equal to 10 are, and 2,4,6,8,10.
So, B = {2,4,6,8,10} which is equal to A = {2,4,6,8,10}
Hence, A = B.
Question 4(iv): In the following, state whether A = B or not:
A = {x: x is a multiple of 10}, B = {10, 15, 20, 25, 30, . . .}
Answer:
Multiples of 10 are 10,20,30,40, ........ till infinity.
So, A = {10,20,30,40, .........}
B = {10,15,20,25,30........}
Comparing elements of A and B, we conclude that elements of A and B are not equal.
Hence, A $\neq$ B.
Question 5(i): Are the following pairs of sets equal? Give reasons.
A = {2, 3}, B = {x: x is solution of $x^{2}$ + 5x + 6 = 0}
Answer:
As given,
A = {2,3}
And,
$x^{2}+5x+6= 0$
$x\left (x+3 \right) + 2\left (x+3 \right) = 0$
(x+2)(x+3)=0
x = -2 and -3
B = {-2, -3}
Comparing elements of A and B, we conclude that elements of A and B are not equal.
Hence, A $\neq$ B.
Question 5(ii): Are the following pairs of sets equal? Give reasons.
A = {x: x is a letter in the word FOLLOW}
B = {y: y is a letter in the word WOLF}
Answer:
Letters of the word FOLLOW are F, OL, and W.
SO, A = {F, O, L, W}
Letters of the word WOLF are W, O, L, and F.
So, B = {W, O, L, F}
Comparing A and B, we conclude that the elements of A are equal to the elements of B.
Hence, A=B.
Question 6: From the sets given below, select equal sets :
A = {2, 4, 8, 12}, B = {1, 2, 3, 4}, C = {4, 8, 12, 14}, D = {3, 1, 4, 2}
E = {–1, 1}, F = {0, a}, G = {1, –1}, H = {0, 1}
Answer:
Compare the elements of A, B, C, D, E, F, G, and H.
8 $\in$ A but $8\notin B,8\in C,8\notin D,8\notin E,8\notin F,8\notin G,8\notin H$
Now, 2 $\in$ A but 2 $\notin$ C.
Hence, A $\neq$ B, A $\neq$ C, A $\neq$ D, A $\neq$ E, A $\neq$ F, A $\neq$ G, A $\neq$ H.
3 $\in$ B,3 $\in$ D but 3 $\notin$ C,3 $\notin$ E,3 $\notin$ F,3 $\notin$ G,3 $\notin$ H.
Hence,B $\neq$ C,B $\neq$ E,B $\neq$ F,B $\neq$ G,B $\neq$ H.
Similarly, comparing other elements of all sets, we conclude that elements of B and D are equal, and elements of E and G are equal.
Hence, B = D and E = G.
|
Sets Class 11 Question Answers |
Question 1: Make correct statements by filling in the symbols $\subset$ or $\not\subset$ in the blank spaces :
(i) { 2, 3, 4 } _____ { 1, 2, 3, 4,5 }
(ii) { a, b, c }______ { b, c, d }
(iii) {x : x is a student of Class XI of your school}______{x : x student of your school}
(iv) {x: x is a circle in the plane} ______{x: x is a circle in the same plane with radius 1 unit}
(v) {x : x is a triangle in a plane} ______ {x : x is a rectangle in the plane}
(vi) {x : x is an equilateral triangle in a plane} ______{x : x is a triangle in the same plane}
(vii) {x : x is an even natural number} _____ {x : x is an integer}
Answer:
A set A is said to be a subset of a set B if every element of A is also an element of B.
(i). All elements {2,3,4} are also elements of {1,2,3,4,5} .
So, {2,3,4} $\subset$ {1,2,3,4,5}.
(ii) All elements { a, b, c } are not elements of{ b, c, d }.
Hence, { a, b, c } $\not\subset$ { b, c, d }.
(iii) Students of class XI are also students of your school.
Hence,{x : x is a student of Class XI of your school} $\subset$ {x : x student of your school}
(iv). Here, {x: x is a circle in the plane} $\not\subset$ {x: x is a circle in the same plane with radius 1 unit}: since a circle in the plane can have any radius
(v). Triangles and rectangles are two different shapes.
Hence,{x : x is a triangle in a plane} $\not\subset$ {x : x is a rectangle in the plane}
(vi) Equilateral triangles are part of all types of triangles.
So,{x : x is an equilateral triangle in a plane} $\subset$ {x : x is a triangle in the same plane}
(vii). Even natural numbers are part of all integers.
Hence, {x : x is an even natural number} $\subset$ {x : x is an integer}
Question 2: Examine whether the following statements are true or false:
(i) { a, b } $\not\subset$ { b, c, a }
(ii) { a, e } $\subset$ { x : x is a vowel in the English alphabet}
(iii) { 1, 2, 3 } $\subset$ { 1, 3, 5 }
(iv) { a } $\subset$ { a, b, c }
(v) { a } $\in$ { a, b, c }
(vi) { x : x is an even natural number less than 6} $\subset$ { x : x is a natural number which divides 36}
Answer:
(i) All elements of { a, b } lie in { b, c, a }.So,{ a, b } $\subset$ { b, c, a }.
Hence, it is false.
(ii) All elements of { a, e } lie in {a,e,i,o,u}.
Hence, the statement is true.
(iii) All elements of { 1, 2, 3 } are not present in { 1, 3, 5 }.
Hence, the statement given is false.
(iv) Element of { a } lie in { a, b, c }.
Hence, the statement is true.
(v). { a } $\subset$ { a, b, c }
So, the statement is false.
(vi) All elements {2,4,} lies in {1,2,3,4,6,9,12,18,36}.
Hence, the statement is true.
Question 3(i): Let A = { 1, 2, { 3, 4 }, 5 }. Which of the following statements are incorrect and why?
{3, 4} $\subset$ A
Answer:
3 $\in$ {3,4} but 3 $\notin$ {1,2,{3,4},5}.
SO, {3, 4} $\not \subset$ A
Hence, the statement is incorrect.
Question 3(ii): Let A = { 1, 2, { 3, 4 }, 5 }. Which of the following statements are incorrect and why?
{3, 4} $\in$ A
Answer:
{3, 4} is an element of A.
So, {3, 4} $\in$ A.
Hence, the statement is correct.
Question 3(iii): Let A = { 1, 2, { 3, 4 }, 5 }. Which of the following statements are incorrect and why?
{{3, 4}} $\subset$ A
Answer:
Here,
{ 3, 4 } $\in$ { 1, 2, { 3, 4 }, 5 }
and { 3, 4 } $\in$ {{3, 4}}
So, {{3, 4}} $\subset$ A.
Hence, the statement is correct.
Question 3(iv): Let A = { 1, 2, { 3, 4 }, 5 }. Which of the following statements are incorrect and why?
1 $\in$ A
Answer:
Given, 1 is element of { 1, 2, { 3, 4 }, 5 }.
So,1 $\in$ A.
Hence, the statement is correct.
Question 3(v): Let A = { 1, 2, { 3, 4 }, 5 }. Which of the following statements are incorrect and why?
1 $\subset$ A
Answer:
Here, 1 is an element of set A = { 1, 2, { 3, 4 }, 5 }. So, elements of set A cannot be a subset of set A.
1 $\not\subset$ { 1, 2, { 3, 4 }, 5 }.
Hence, the statement given is incorrect.
Question 3(vi): Let A = { 1, 2, { 3, 4 }, 5 }. Which of the following statements are incorrect and why?
{1,2,5} $\subset$ A
Answer:
All elements of {1,2,5} are present in { 1, 2, { 3, 4 }, 5 }.
So, {1,2,5} $\subset$ { 1, 2, { 3, 4 }, 5 }.
Hence, the statement given is correct.
Question 3(vii): Let A = { 1, 2, { 3, 4 }, 5 }. Which of the following statements are incorrect and why?
{1,2,5} $\in$ A
Answer:
Here,{1,2,5} is not an element of { 1, 2, { 3, 4 }, 5 }.
So,{1,2,5} $\notin$ A .
Hence, the statement is incorrect.
Question 3(viii): Let A = { 1, 2, { 3, 4 }, 5 }. Which of the following statements are incorrect and why?
{1,2,3} $\subset$ A
Answer:
Here, 3 $\in$ {1,2,3}
but 3 $\notin$ { 1, 2, { 3, 4 }, 5 }.
So, {1,2,3} $\not \subset$ A
Hence, the given statement is incorrect.
Question 3(ix): Let A = { 1, 2, { 3, 4 }, 5 }. Which of the following statements are incorrect and why?
Answer:
$\phi$ is not an element of { 1, 2, { 3, 4 }, 5 }.
So, $\phi \notin A$ .
Hence, the above statement is incorrect.
Question 3(x): Let A = { 1, 2, { 3, 4 }, 5 }. Which of the following statements are incorrect and why?
Answer:
$\phi$ is a subset of all sets.
Hence, the above statement is correct.
Question 3(xi): Let A = { 1, 2, { 3, 4 }, 5 }. Which of the following statements are incorrect and why?
$\left \{ \phi \right \} \subset A$
Answer:
$\phi$ $\subset$ { 1, 2, { 3, 4 }, 5 }. but $\phi$ is not an element of { 1, 2, { 3, 4 }, 5 }.
$\left \{ \phi \right \} \not\subset A$
Hence, the above statement is incorrect.
Question 4(i): Write down all the subsets of the following sets
{a}
Answer:
Subsets of $\left \{ a \right \} = \phi \, and \left \{ a \right \}$ .
Question 4 (ii): Write down all the subsets of the following sets:
{a, b}
Answer:
Subsets of $\left \{ a,b \right \}\ are \ \phi , \left \{ a \right \},\left \{ b \right \} and \left \{ a,b \right \}$ . Thus, the given set has 4 subsets
Question 4 (iii): Write down all the subsets of the following sets:
{1,2,3}
Answer:
Subsets of
$\left \{ 1,2,3 \right \} = \left \{ 1 \right \},\left \{ 2 \right \},\left \{ 3 \right \},\phi ,\left \{ 1,2 \right \},\left \{ 2,3 \right \},\left \{ 3,1 \right \},\left \{ 1,2,3 \right \}$
Question 4 (iv): Write down all the subsets of the following sets:
Answer:
Subset of $\phi$ is $\phi$ only.
The subset of a null set is the null set itself.
Question 5: Write the following as intervals :
(i) {x : x $\in$ R, – 4 $<$ x $\leq$ 6}
(ii) {x : x $\in$ R, – 12 $<$ x $<$ –10}
(iii) {x : x $\in$ R, 0 $\leq$ x $<$ 7}
(iv) {x : x $\in$ R, 3 $\leq$ x $\leq$ 4}
Answer:
The following can be written in the interval as :
(i) {x : x $\in$ R, – 4 $<$ x $\leq$ 6} $= \left ( -4 ,6 \right ]$
(ii) {x : x $\in$ R, – 12 $<$ x $<$ –10} $= \left ( -12,-10 \right )$
(iii) {x : x $\in$ R, 0 $\leq$ x $<$ 7}=[0,7)
(iv) (iv) {x : x $\in$ R, 3 $\leq$ x $\leq$ 4} $=\left [ 3,4 \right ]$
Question 6: Write the following intervals in set-builder form :
(i) (– 3, 0)
(ii) [6, 12]
(iii) (6, 12]
(iv) [–23, 5)
Answer:
The given intervals can be written in set builder form as :
(i) (– 3, 0) $= \left \{ x:x\in R, -3< x< 0 \right \}$
(ii) [6 , 12] $= \left \{ x:x\in R, 6\leq x\leq 12\right \}$
(iii) (6, 12] $= \left \{ x:x\in R, 6< x\leq 12\right \}$
(iv) [–23, 5) $= \left \{ x:x\in R, -23 \leq x< 5\right \}$
Question 7: What universal set(s) would you propose for each of the following :
(i) The set of right triangles.
(ii) The set of isosceles triangles.
Answer:
(i) The universal set for a set of right-angle triangles can be a set of polygons or a set of all triangles.
(ii) The universal set for a set of isosceles angle triangles can be a set of polygons.
Question 8 should be added.
|
Sets Class 11 Question Answers |
Question 1(i): Find the union of each of the following pairs of sets :
X = {1, 3, 5} Y = {1, 2, 3}
Answer:
Union of X and Y is X $\cup$ Y = {1,2,3,5}
Question 1 (ii): Find the union of each of the following pairs of sets :
A = [ a, e, i, o, u} B = {a, b, c}
Answer:
Union of A and B is A $\cup$ B = {a, b, c, e, i, o, u}.
Question 1 (iii): Find the union of each of the following pairs of sets :
A = {x : x is a natural number and multiple of 3}, B = {x : x is a natural number less than 6}
Answer:
Here,
A = {3,6,9,12,15,18, ............}
B = {1,2,3,4,5,6}
The Union of A and B is A $\cup$ B.
A $\cup$ B = {1,2,3,4,5,6,9,12,15........}
Question 1 (iv): Find the union of each of the following pairs of sets :
A = {x: x is a natural number and 1 $<$ x $\leq$ 6}
B = {x: x is a natural number and 6 $<$ x $<$ 10}
Answer:
Here,
A = {2,3,4,5,6}
B = {7,8,9}
A $\cup$ B = {2,3,4,5,6,7,8,9}
or it can be written as A $\cup$ B = {x : x is a natural number and 1 $<$ x $<$ 10 }
Question 1 (v): Find the union of each of the following pairs of sets :
A = {1, 2, 3} B = $\phi$
Answer:
Here,
A union B is A $\cup$ B.
A $\cup$ B = {1,2,3}
Question 2: Let A = { a, b }, B = {a, b, c}. Is A $\subset$ B ? What is A $\cup$ B?
Answer:
Here,
We can see elements of A lie in set B.
Hence, A $\subset$ B.
And, A $\cup$ B = {a,b,c} = B
Question 3: If A and B are two sets such that A $\subset$ B, then what is A $\cup$ B?
Answer:
If A is a subset of B, then A $\cup$ B will be set B.
Question 4(i): If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8 }and D = { 7, 8, 9, 10 }; find
$A \cup B$
Answer:
Here,
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
The union of the set can be written as follows
A $\cup$ B = {1,2,3,4,5,6}
Question 4(ii): If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8 }and D = { 7, 8, 9, 10 }; find
$A \cup C$
Answer:
Here,
A = {1, 2, 3, 4}
C = {5, 6, 7, 8}
The union can be written as follows
A $\cup$ C = {1,2,3,4,5,6,7,8}
Question 4(iii): If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8 }and D = { 7, 8, 9, 10 }; find
B $\cup$ C
Answer:
Here,
B = {3, 4, 5, 6},
C = {5, 6, 7, 8}
The union of the given sets are
B $\cup$ C = {3,4,5,6,7,8}
Question 4(iv): If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8 }and D = { 7, 8, 9, 10 }; find
B $\cup$ D
Answer:
Here,
B = {3, 4, 5, 6}
D = {7, 8, 9, 10}
B $\cup$ D = {3,4,5,6,7,8,9,10}
Question 4(v): If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8 }and D = { 7, 8, 9, 10 }; find
A $\cup$ B $\cup$ C
Answer:
Here,
A = {1, 2, 3, 4},
B = {3, 4, 5, 6},
C = {5, 6, 7, 8}
The union can be written as
A $\cup$ B $\cup$ C = {1,2,3,4,5,6,7,8}
Question 4(vi): If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8 }and D = { 7, 8, 9, 10 }; find
A $\cup$ B $\cup$ D
Answer:
Here,
A = {1, 2, 3, 4},
B = {3, 4, 5, 6}
D = {7, 8, 9, 10}
The union can be written as
A $\cup$ B $\cup$ D = {1,2,3,4,5,6,7,8,9,10}
Question 4(vii): If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8 }and D = { 7, 8, 9, 10 }; find
B $\cup$ C $\cup$ D
Answer:
Here, B = {3, 4, 5, 6},
C = {5, 6, 7, 8 } and
D = { 7, 8, 9, 10 }
The union can be written as
B $\cup$ C $\cup$ D = {3,4,5,6,7,8,9,10}
Question 5: Find the intersection of each pair of sets of question 1 above
(i) X = {1, 3, 5} Y = {1, 2, 3}
(ii) A = [ a, e, i, o, u} B = {a, b, c}
(iii) A = {x : x is a natural number and multiple of 3} B = {x : x is a natural number less than 6}
(iv) A = {x : x is a natural number and 1 $<$ x $\leq$ 6 } B = {x : x is a natural number and 6 $<$ x $<$ 10 }
Answer:
(i) X = {1, 3, 5} Y = {1, 2, 3}
X $\cap$ Y = {1,3}
(ii) A = [ a, e, i, o, u} B = {a, b, c}
A $\cap$ B = {a}
(iii) A = {x : x is a natural number and multiple of 3} B = {x : x is a natural number less than 6}
A = {3,6,9,12,15.......} B = {1,2,3,4,5}
A $\cap$ B = {3}
(iv)A = {x : x is a natural number and 1 $<$ x $\leq$ 6 } B = {x : x is a natural number and 6 $<$ x $<$ 10 }
A = {2,3,4,5,6} B = {7,8,9}
A $\cap$ B = $\phi$
(v) A = {1, 2, 3}, B = $\phi$
A $\cap$ B = $\phi$
Question 6: If A = { 3, 5, 7, 9, 11 }, B = {7, 9, 11, 13}, C = {11, 13, 15}and D = {15, 17}; find
(i) A $\cap$ B (ii) B $\cap$ C
(iii) A $\cap$ C $\cap$ D (iv) A $\cap$ C
(v) B $\cap$ D (vi) A $\cap$ (B $\cup$ C)
(vii) A $\cap$ D (viii) A $\cap$ (B $\cup$ D)
(ix) ( A $\cap$ B ) $\cap$ ( B $\cup$ C )
(x) ( A $\cup$ D) $\cap$ ( B $\cup$ C)
Answer:
Here, A = { 3, 5, 7, 9, 11 }, B = {7, 9, 11, 13}, C = {11, 13, 15} and D = {15, 17}
(i) A $\cap$ B = {7,9,11} (vi) A $\cap$ (B $\cup$ C) = {7,9,11}
(ii) B $\cap$ C = { 11,13} (vii) A $\cap$ D = $\phi$
(iii) A $\cap$ C $\cap$ D = $\phi$ (viii) A $\cap$ (B $\cup$ D) = {7,9,11}
(iv) A $\cap$ C = { 11 } (ix) ( A $\cap$ B ) $\cap$ ( B $\cup$ C ) = {7,9,11}
(v) B $\cap$ D = $\phi$ (x) ( A $\cup$ D) $\cap$ ( B $\cup$ C) = {7,9,11,15}
(i) A $\cap$ B
(ii) A $\cap$ C
(iii) A $\cap$ D
(iv) B $\cap$ C
(v) B $\cap$ D
(vi) C $\cap$ D
Answer:
Here, A = {1,2,3,4,5,6...........}
B = {2,4,6,8,10...........}
C = {1,3,5,7,9,11,...........}
D = {2,3,5,7,11,13,17,......}
(i) A $\cap$ B = {2,4,6,8,10........} = B
(ii) A $\cap$ C = {1,3,5,7,9.........} = C
(iii) A $\cap$ D = {2,3,5,7,11,13.............} = D
(iv) B $\cap$ C = $\phi$
(v) B $\cap$ D = {2}
(vi) C $\cap$ D = {3,5,7,11,13,..........} = $\left ( x:x \, is\, \, odd\, \, \, prime \, \, number \right )$
Question 8(i): Which of the following pairs of sets are disjoint
{1, 2, 3, 4} and {x : x is a natural number and 4 $\leq$ x $\leq$ 6 }
Answer:
Here, {1, 2, 3, 4} and {4,5,6}
{1, 2, 3, 4} $\cap$ {4,5,6} = {4}
Hence, it is not a disjoint set.
Question 8(ii): Which of the following pairs of sets are disjoint
{ a, e, i, o, u } and { c, d, e, f }
Answer:
Here, { a, e, i, o, u } and { c, d, e, f }
{ a, e, i, o, u } $\cap$ { c, d, e, f } = {e}
Hence, it is not a disjoint set.
Question 8(iii): Which of the following pairs of sets are disjoint
{x : x is an even integer } and {x : x is an odd integer}
Answer:
Here, {x : x is an even integer } and {x : x is an odd integer}
{2,4,6,8,10,..........} and {1,3,5,7,9,11,.....}
{2,4,6,8,10,..........} $\cap$ {1,3,5,7,9,11,.....} = $\phi$
Hence, it is a disjoint set.
(i) A – B (ii) A – C (iii) A – D (iv) B – A (v) C – A (vi) D – A
(vii) B – C (viii) B – D (ix) C – B (x) D – B (xi) C – D (xii) D – C
Answer:
A = {3, 6, 9, 12, 15, 18, 21}, B = { 4, 8, 12, 16, 20 }, C = { 2, 4, 6, 8, 10, 12, 14, 16 }, D = {5, 10, 15, 20 }
The given operations are done as follows
(i) A – B = {3,6,9,15,18,21} (vii) B – C = {20}
(ii) A – C = {3,9,15,18,21} (viii) B – D = {4,8,12,16}
(iii) A – D = {3,6,9,12,18,21} (ix) C – B = {2,6,10,14}
(iv) B – A = {4,8,16,20} (x) D – B = {5,10,15}
(v) C – A = {2,4,8,10,14,16} (xi) C – D = {2,4,6,8,12,14,16}
(vi) D – A = {5,10,20} (xii) D – C = {5,15,20}
Question 10: If X= { a, b, c, d } and Y = { f, b, d, g}, find
(i) X – Y
(ii) Y – X
(iii) X $\cap$ Y
Answer:
X= { a, b, c, d } and Y = { f, b, d, g}
(i) X – Y = {a,c}
(ii) Y – X = {f,g}
(iii) X $\cap$ Y = {b,d}
Question 11: If R is the set of real numbers and Q is the set of rational numbers, then what is R – Q?
Answer:
R = set of real numbers.
Q = set of rational numbers.
R - Q = set of irrational numbers.
Question 12 (i): State whether each of the following statements is true or false. Justify your answer.
{ 2, 3, 4, 5 } and { 3, 6} are disjoint sets.
Answer:
Here,
{ 2, 3, 4, 5 } and { 3, 6}
{ 2, 3, 4, 5 } $\cap$ { 3, 6} = {3}
Hence, these are not disjoint sets.
So, false.
Question 12 (ii): State whether each of the following statements about the three dimensions is true or false. Justify your answer.
{ a, e, i, o, u } and { a, b, c, d }are disjoint sets
Answer:
Here, { a, e, i, o, u } and { a, b, c, d }
{ a, e, i, o, u } $\cap$ { a, b, c, d } = {a}
Hence, these are not disjoint sets.
So, the statement is false.
Question 12 (iii): State whether each of the following statements is true or false. Justify your answer.
{ 2, 6, 10, 14 } and { 3, 7, 11, 15} are disjoint sets.
Answer:
Here,
{ 2, 6, 10, 14 } and { 3, 7, 11, 15}
{ 2, 6, 10, 14 } $\cap$ { 3, 7, 11, 15} = $\phi$
Hence, these are disjoint sets.
So, given the statement is true.
Question 12 (iv): State whether each of the following statements is true or false. Justify your answer.
{ 2, 6, 10 } and { 3, 7, 11} are disjoint sets.
Answer:
Here,
{ 2, 6, 10 } and { 3, 7, 11}
{ 2, 6, 10 } $\cap$ { 3, 7, 11} = $\phi$
Hence, these are disjoint sets.
So, the statement is true.
|
Sets Class 11 Question Answers |
Question 1: Let U = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }, A = { 1, 2, 3, 4}, B = { 2, 4, 6, 8 } and C = { 3, 4, 5, 6 }. Find
(i) A′
(ii) B′
(iii) (A $\cup$ C)′
(iv) (A $\cup$ B)′
(v) (A')'
(vi) (B – C)'
Answer:
U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = { 1, 2, 3, 4}, B = { 2, 4, 6, 8 } and C = { 3, 4, 5, 6 }
(i) A′ = U - A = {5,6,7,8,9}
(ii) B′ = U - B = {1,3,5,7,9}
(iii) A $\cup$ C = {1,2,3,4,5,6}
(A $\cup$ C)′ = U - (A $\cup$ C) = {7,8,9}
(iv) (A $\cup$ B) = {1,2,3,4,6,8}
(A $\cup$ B)′ = U - (A $\cup$ B) = {5,7,9}
(v) (A')' = A = { 1, 2, 3, 4}
(vi) (B – C) = {2,8}
(B – C)' = U - (B – C) = {1,3,4,5,6,7,9}
Question 2: If U = { a, b, c, d, e, f, g, h}, find the complements of the following sets :
(i) A = {a, b, c}
(ii) B = {d, e, f, g}
(iii) C = {a, c, e, g}
(iv) D = { f, g, h, a}
Answer:
U = { a, b, c, d, e, f, g, h}
(i) A = {a, b, c}
A' = U - A = {d,e,f,g,h}
(ii) B = {d, e, f, g}
B' = U - B = {a,b,c,h}
(iii) C = {a, c, e, g}
C' = U - C = {b,d,f,h}
(iv) D = { f, g, h, a}
D' = U - D = {b,c,d,e}
Question 3: Taking the set of natural numbers as the universal set, write down the complements of the following sets:
(i) {x : x is an even natural number}
(ii) { x : x is an odd natural number }
(iii) {x : x is a positive multiple of 3}
(iv) { x : x is a prime number }
(v) {x: x is a natural number divisible by 3 and 5}
Answer:
Universal set = U = {1,2,3,4,5,6,7....................}
(i) {x : x is an even natural number} = {2,4,6,8,..........}
{x : x is an even natural number}'= U - {x : x is an even natural number} = {1,3,5,7,9,..........} = {x : x is an odd natural number}
(ii) { x : x is an odd natural number }' = U - { x : x is an odd natural number } = {x : x is an even natural number}
(iii) {x : x is a positive multiple of 3}' = U - {x : x is a positive multiple of 3} = {x : x , x $\in$ N and is not a positive multiple of 3}
(iv) { x : x is a prime number }' = U - { x : x is a prime number } = { x : x is a positive composite number and 1 }
(v) {x : x is a natural number divisible by 3 and 5}' = U - {x : x is a natural number divisible by 3 and 5} = {x : x is a natural number not divisible by 3 or 5}
Question 3: Taking the set of natural numbers as the universal set, write down the complements of the following sets:
(vi) { x : x is a perfect square }
(vii) { x : x is a perfect cube}
(viii) { x : x + 5 $=$ 8 }
(ix) { x : 2x + 5 $=$ 9}
(x) { x : x $\geq$ 7 }
(xi) { x : x $\in$ N and 2x + 1 $>$ 10 }
Answer:
Universal set = U = {1,2,3,4,5,6,7,8.............}
(vi) { x : x is a perfect square }' = U - { x : x is a perfect square } = { x : x $\in$ N and x is not a perfect square }
(vii) { x : x is a perfect cube}' = U - { x : x is a perfect cube} = { x : x $\in$ N and x is not a perfect cube}
(viii) { x : x + 5 $=$ 8 }' = U - { x : x + 5 $=$ 8 } = U - {3} = { x : x $\in$ N and x $\neq$ 3 }
(ix) { x : 2x + 5 $=$ 9}' = U - { x : 2x + 5 $=$ 9} = U -{2} = { x : x $\in$ N and x $\neq$ 2}
(x) { x : x $\geq$ 7 }' = U - { x : x $\geq$ 7 } = { x : x $\in$ N and x $<$ 7}
(xi) { x : x $\in$ N and 2x + 1 $>$ 10 }' = U - { x : x $\in$ N and x $>$ 9/2 } = { x : x $\in$ N and x $\leq$ 9/2 }
Question 4: If U = {1, 2, 3, 4, 5, 6, 7, 8, 9 }, A = {2, 4, 6, 8} and B = { 2, 3, 5, 7}. Verify that
(i) (A $\cup$ B)′ = A′ $\cap$ B′
(ii) (A $\cap$ B)′ = A′ $\cup$ B′
Answer:
U = {1, 2, 3, 4, 5, 6, 7, 8, 9 }, A = {2, 4, 6, 8} and B = { 2, 3, 5, 7}
(i) (A $\cup$ B)′ = A′ $\cap$ B′
L.H.S = (A $\cup$ B)′ = U - (A $\cup$ B) = {1,9}
R.H.S = A′ $\cap$ B′ = {1,3,5,7,9} $\cap$ {1,4,6,8,9} = {1,9}
L.H.S = R.H.S
Hence, the statement is true.
(ii) (A $\cap$ B)′ = A′ $\cup$ B′
L.H.S = U - (A $\cap$ B) ={1,3,4,5,6,7,8,9}
R.H.S = A′ $\cup$ B′ = {1,3,5,7,9} $\cup$ {1,4,6,8,9} = {1,3,4,5,6,7,8,9}
L.H.S = R.H.S
Hence, the statement is true.
Question 5: Draw an appropriate Venn diagram for each of the following :
(i) (A ∪ B)′
(ii) A′ \cap B′
(iii) (A \cap B)′
(iv) A′ ∪ B′
Answer:
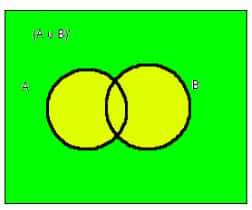
(i) $(A\cup B)’$
$(A\cup B)$ is in the yellow colour
$(A\cup B)’$ is in green colour.
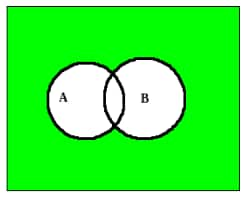
ii) $A′ \cap B′$ is represented by the green colour in the figure below.
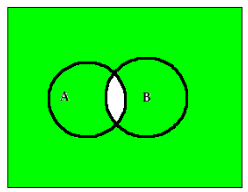
iii) $(A \cap B)′$ is represented by green colour in the diagram below, and white colour represents $(A \cap B)$
iv) $A’\cup B’$
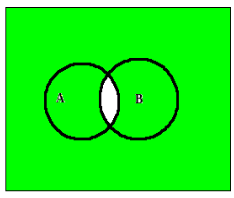
The green colour represents $A’\cup B’$.
Answer:
$A'$ is the set of all triangles whose angle is $60^\circ$, in other words, $A'$ is the set of all equilateral triangles.
Question 7: Fill in the blanks to make each of the following a true statement :
(i) A $\cup$ A′ $=$ $\cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot$
(ii) $\phi '$ $\cap$ A $=$ $\cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot$
(iii) A $\cap$ A′ $=$ $\cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot$
(iv) U′ $\cap$ A $=$ $\cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot$
Answer:
The following are the answers to the questions
(i) A $\cup$ A′ $=$ U
(ii) $\phi$ ′ $\cap$ A $=$ A
(iii) A $\cap$ A′ $=$ $\phi$
(iv) U′ $\cap$ A $=$ $\phi$
|
Sets Class 11 Question Answers |
Question 1: Decide, among the following sets, which sets are subsets of one another:
A = { x : x $\in$ R and x satisfy $x^{2}$ – 8x + 12 = 0 }, B = { 2, 4, 6 },
C = { 2, 4, 6, 8,...}, D = { 6 }.
Answer:
Solution of this equation are $x^{2}$ – 8x + 12 = 0
( x - 2 ) ( x - 6 ) = 0
X = 2,6
$\therefore$ A = { 2,6 }
B = { 2, 4, 6 }
C = { 2, 4, 6, 8, . . . }
D = { 6 }
From the sets given above, we can conclude that A $\subset$ B, A $\subset$ C, D $\subset$ A, D $\subset$ B, D $\subset$ C, B $\subset$ C.
Hence, we can say that D $\subset$ A $\subset$ B $\subset$ C
Question 2(i): In each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example.
If x $\in$ A and A $\in$ B , then x $\in$ B
Answer:
The given statement is false,
example: Let A = { 2,4 }
B = { 1,{2,4},5}
x be 2.
then, 2 $\in$ { 2,4 } = x $\in$ A and { 2,4 } $\in$ { 1,{2,4},5} = A $\in$ B
But 2 $\notin$ { 1,{2,4},5} i.e. x $\notin$ B
Question 2(ii): In each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example.
If A $\subset$ B and B $\in$ C , then A $\in$ C
Answer:
The given statement is false,
Let, A = {1}
B = {1,2,3}
C = {0, {1,2,3},4}
Here, {1} $\subset$ {1,2,3} = A $\subset$ B and {1,2,3} $\in$ {0,{1,2,3},4} = B $\in$ C
But, {1} $\notin$ {0,{1,2,3},4} = A $\notin$ C
Question 2(iii): In each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example.
If A $\subset$ B and B $\subset$ C , then A $\subset$ C
Answer:
Let A ⊂ B and B ⊂ C
There is an element x such that
Let, x $\in$ A
$\Rightarrow$ x $\in$ B (Because A $\subset$ B)
$\Rightarrow$ x $\in$ C (Because B $\subset$ C)
Hence, the statement is true that A $\subset$ C.
Question 2(iv): In each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example.
If A $\not\subset$ B and B $\not\subset$ C, then A $\not\subset$ C
Answer:
The given statement is false
Let, A = {1,2}
B = {3,4,5}
C = {1,2,6,7,8}
Here, {1,2} $\not\subset$ {3,4,5} = A $\not\subset$ B and {3,4,5} $\not\subset$ {1,2,6,7,8} = B $\not\subset$ C
But, {1,2} $\subset$ {1,2,6,7,8} = A $\subset$ C
Question 2 (v): In each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example.
If x $\in$ A and A $\not\subset$ B , then x $\in$ B
Answer:
The given statement is false,
Let x be 2
A = {1,2,3}
B = {4,5,6,7}
Here, 2 $\in$ {1,2,3} = x $\in$ A and {1,2,3} $\not \subset$ {4,5,6,7} = A $\not \subset$ B
But, 2 $\notin$ {4,5,6,7} implies x $\notin$ B
Question 2 (vi): In each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example.
If A $\subset$ B and x $\notin$ B, then x $\notin$ A
Answer:
The given statement is true,
Let, A $\subset$ B and x $\notin$ B
Suppose, x $\in$ A
Then, x $\in$ B , which is contradiction to x $\notin$ B
Hence, x $\notin$ A.
Question 3: Let A, B, and C be the sets such that A $\cup$ B = A $\cup$ C and A $\cap$ B = A $\cap$ C. Show that B = C.
Answer:
Let A, B, and C be the sets such that A $\cup$ B = A $\cup$ C and A $\cap$ B = A $\cap$ C
To prove: B = C.
A $\cup$ B = A + B - A $\cap$ B = A $\cup$ C = A + C - A $\cap$ C
A + B - A $\cap$ B = A + C - A $\cap$ C
B - A $\cap$ B = C - A $\cap$ C ( since A $\cap$ B = A $\cap$ C )
B = C
Hence, it is proved that B = C.
Question 4: Show that the following four conditions are equivalent :
(i) A $\subset$ B (ii) A – B = $\phi$ (iii) A $\cup$ B = B (iv) A $\cap$ B = A
Answer:
First, we need to show A $\subset$ B $\Leftrightarrow$ A – B = $\phi$
Let A $\subset$ B
To prove: A – B = $\phi$
Suppose A – B $\neq \phi$
this means, x $\in$ A and x $\not =$ B , which is not possible as A $\subset$ B .
So, A – B = $\phi$.
Hence, A $\subset$ B $\implies$ A – B = $\phi$ .
Now, let A – B = $\phi$
(i). To prove: A $\subset$ B
Suppose, x $\in$ A
A – B = $\phi$ so x $\in$ B
Since, x $\in$ A and x $\in$ B and A – B = $\phi$ so A $\subset$ B
Hence, A $\subset$ B $\Leftrightarrow$ A – B = $\phi$.
Let A $\subset$ B
(ii). To prove: A $\cup$ B = B
We can say B $\subset$ A $\cup$ B
Suppose, x $\in$ A $\cup$ B
means x $\in$ A or x $\in$ B
If x $\in$ A
since A $\subset$ B so x $\in$ B
Hence, A $\cup$ B = B
and If x $\in$ B then also A $\cup$ B = B.
Now, let A $\cup$ B = B
(iii). To prove: A $\subset$ B
Suppose: x $\in$ A
A $\subset$ A $\cup$ B so x $\in$ A $\cup$ B
A $\cup$ B = B so x $\in$ B
Hence, A $\subset$ B
Also, A $\subset$ B $\Leftrightarrow$ A $\cup$ B = B
(iv). Now, we need to show A $\subset$ B $\Leftrightarrow$ A $\cap$ B = A
Let A $\subset$ B
To prove: A $\cap$ B = A
Suppose: x $\in$ A
We know A $\cap$ B $\subset$ A
x $\in$ A $\cap$ B Also, A $\subset$ A $\cap$ B
Hence, A $\cap$ B = A
Let A $\cap$ B = A
To prove: A $\subset$ B
Suppose: x $\in$ A
x $\in$ A $\cap$ B (replacing A by A $\cap$ B)
x $\in$ A and x $\in$ B
$\therefore$ A $\subset$ B
A $\subset$ B $\Leftrightarrow$ A $\cap$ B = A
Question 5: Show that if A $\subset$ B, then C – B $\subset$ C – A.
Answer:
Given, A $\subset$ B
To prove: C – B $\subset$ C – A
Let, x $\in$ C - B means x $\in$ C but x $\notin$ B
A $\subset$ B so x $\in$ C but x $\notin$ A i.e. x $\in$ C - A
Hence, C – B $\subset$ C – A
Question 6: Show that for any sets A and B,
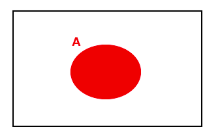
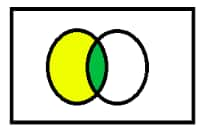
A = ( A $\cap$ B ) $\cup$ ( A – B ) and A $\cup$ ( B – A ) = ( A $\cup$ B )
Answer:
A = ( A $\cap$ B ) $\cup$ ( A – B )
L.H.S = A = Red coloured area
R.H.S = ( A $\cap$ B ) $\cup$ ( A – B )
( A $\cap$ B ) = green coloured
( A – B ) = yellow coloured
( A $\cap$ B ) $\cup$ ( A – B ) = coloured part
Hence, L.H.S = R.H.S = Coloured part
A $\cup$ ( B – A ) = ( A $\cup$ B )
A = sky blue coloured
( B – A )=pink coloured
L.H.S = A $\cup$ ( B – A ) = sky blue coloured + pink coloured
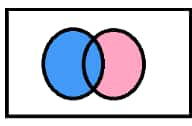
R.H.S = ( A $\cup$ B ) = brown coloured part
L.H.S = R.H.S = Coloured part
Question 7(i): Using properties of sets, show that
A $\cup$ ( A $\cap$ B ) = A
Answer:
(i) A $\cup$ ( A $\cap$ B ) = A
We know that A $\subset$ A
and A $\cap$ B $\subset$ A
A $\cup$ ( A $\cap$ B ) $\subset$ A
and also , A $\subset$ A $\cup$ ( A $\cap$ B )
Hence, A $\cup$ ( A $\cap$ B ) = A
Question 7(ii): Using properties of sets, show that
A $\cap$ ( A $\cup$ B ) = A
Answer:
This can be solved as follows
(ii) A $\cap$ ( A $\cup$ B ) = A
A $\cap$ ( A $\cup$ B ) = (A $\cap$ A) $\cup$ ( A $\cap$ B )
A $\cap$ ( A $\cup$ B ) = A $\cup$ ( A $\cap$ B ) { A $\cup$ ( A $\cap$ B ) = A proved in 9(i)}
A $\cap$ ( A $\cup$ B ) = A
Question 8: Show that A $\cap$ B = A $\cap$ C need not imply B = C.
Answer:
Let, A = {0,1,2}
B = {1,2,3}
C = {1,2,3,4,5}
Given, A $\cap$ B = A $\cap$ C
L.H.S : A $\cap$ B = {1,2}
R.H.S : A $\cap$ C = {1,2}
and here {1,2,3} $\not =$ {1,2,3,4,5} = B $\not =$ C.
Hence, A $\cap$ B = A $\cap$ C need not imply B = C.
Answer:
Given, A $\cap$ X $=$ B $\cap$ X $=$ $\phi$ and A $\cup$ X $=$ B $\cup$ X
To prove: A = B
A = A $\cap$ (A $\cup$ X) (A $\cap$ X $=$ B $\cap$ X)
= A $\cap$ (B $\cup$ X)
= (A $\cap$ B) $\cup$ (A $\cap$ X)
= (A $\cap$ B) $\cup$ $\phi$ (A $\cap$ X $=$ $\phi$ )
= (A $\cap$ B)
B = B $\cap$ (B $\cup$ X) (A $\cap$ X $=$ B $\cap$ X)
= B $\cap$ (A $\cup$ X)
= (B $\cap$ A) $\cup$ (B $\cap$ X)
= (B $\cap$ A) $\cup$ $\phi$ (B $\cap$ X $=$ $\phi$ )
= (B $\cap$ A)
We know that (A $\cap$ B) = (B $\cap$ A) = A = B
Hence, A = B
Answer:
Given, A $\cap$ B, B $\cap$ C and A $\cap$ C are non-empty sets
To prove: A $\cap$ B $\cap$ C $=$ $\phi$
Let A = {1,2}
B = {1,3}
C = {3,2}
Here, A $\cap$ B = {1}
B $\cap$ C = {3}
A $\cap$ C = {2}
and A $\cap$ B $\cap$ C $=$ $\phi$
Sets Class 11 NCERT Solutions: Exercise-wise
Exercise-wise NCERT Solutions of Sets Class 11 Maths Chapter 1 are provided in the links below.
- NCERT Solutions for Class 11 Maths Chapter 1 Sets Exercise 1.1
- NCERT Solutions for Class 11 Maths Chapter 1 Sets Exercise 1.2
- NCERT Solutions for Class 11 Maths Chapter 1 Sets Exercise 1.3
- NCERT Solutions for Class 11 Maths Chapter 1 Sets Exercise 1.4
- NCERT Solutions for Class 11 Maths Chapter 1 Sets Exercise 1.5
- NCERT Solutions for Class 11 Maths Chapter 1 Sets Miscellaneous Exercise
Class 11 Maths NCERT Chapter 1 Sets: Extra Question
Question: Let $A=\{1,6,11,16, \ldots\}$ and $B=\{9,16,23,30, \ldots\}$ be the sets consisting of the first 2025 terms of two arithmetic progressions. Then $n(A \cup B)$ is:
Solution:
We have the sets in AP,
$\begin{aligned}
& A=\{1,6,11,16,21,26,31,36,41,46,51,56,61, \\
& 66,71,76,81,86,91, \ldots \ldots\} \\
& B=\{9,16,23,30,37,44,51,58,65,72,79,86, \\
& 93,100, \ldots \ldots\} \\
& A \cap B=\{16,51,86, \ldots .\}
\end{aligned}$
$\text { For set } A \Rightarrow \mathrm{T}_{2025}=1+(2025-1)(5)=10121$
$\text { For set B} \Rightarrow \mathrm{T}_{2025}=9+(2025-1)(7)=14177$
$\text { So, for }(A \cap B) \Rightarrow T_n=16+(n-1)(35) \leq 10121$
$(\mathrm{n}-1) \leq \frac{10121-16}{35}=288.71$
$\mathrm{n} \leq 289.71 \Rightarrow \mathrm{n}=289$
$\therefore \mathrm{n}(\mathrm{~A} \cup \mathrm{~B})=\mathrm{n}(\mathrm{~A})+\mathrm{n}(\mathrm{~B})-\mathrm{n}(\mathrm{~A} \cap \mathrm{~B})$
$=2025+2025-289=3761$
Hence, the correct answer is 3761.
Sets Class 11 Chapter 1: Topics
Students will explore the following topics in NCERT Class 11 Maths Chapter 1 Sets:
- Introduction
- Sets and Their Representations
- Empty Set
- Finite and Infinite Sets
- Equal Sets
- Subsets
- Universal Set
- Venn Diagram
- Operations on Sets
- Complement of a Set
Set Class 11 Solutions – Important Notes
Careers360 has prepared these Class 11 Sets Notes to make your revision smoother and faster. Additionally, these notes will help students to understand the Sets class 11 solutions and solve them on their own from next time.
Set:
A set is a well-defined collection of objects. It can be represented in 2 forms, i.e. Set Builder and Roaster forms.
Examples of sets:
$\mathbf{N}$: the set of all natural numbers
$\mathbf{Z}$: the set of all integers
$\mathbf{Q}$: the set of all rational numbers
$\mathbf{R}$: the set of real numbers
$\mathbf{Z}^{+}$: the set of positive integers
$\mathbf{Q}^{+}$: the set of positive rational numbers, and
$\mathbf{R}^{+}$: the set of positive real numbers.
Type of Sets:
Empty Set or Null Set: It has no elements present in it. Example: $A=\{ \}$ is a null set.
Finite Set: It has a limited number of elements. Example: $A=\{1,2,3,4,6,8,9\}$
Infinite Set: It has an infinite number of elements. Example: $A=\{x: x$ is the set of all Complex numbers $\}$
Equal Set: Two sets which have the same members. Example: $A=\{1,2,8\}$ and $B=\{2,8,1\}$ : Set $A=\operatorname{Set} B$
Subsets: $A$ set ' $A$ ' is said to be a subset of $B$ if each element of $A$ is also an element of B. Example: $A=\{1,2,4\}, B=\{1,2,3,4,5,6\}$, then $A \subseteq B$
Universal Set: A set which consists of all elements of other sets present in a Venn diagram. Example: $A=\{1,3\}, B=\{2,3\}$, The universal set here will be, $U=\{1,2,3\}$
Intervals:
An interval is a set of real numbers that includes all numbers between two specified endpoints, between one endpoint and infinity, or between negative infinity and one endpoint.
Types Of Intervals
Open Interval: An interval that does not include its endpoints. It's represented using parentheses () in interval notation.
Closed Interval: An interval that includes its endpoints. It's represented using square brackets [] in interval notation.
Half-Open/Half-Closed Interval: An interval that includes one endpoint but not the other. It's represented using a combination of parentheses and square brackets.
Important Formulae
Union of Sets $(A\cup B): A\cup B$
Intersection of Sets $(A\cap B): A\cap B$
Complement of a Set $(A'): A'$
De Morgan’s Theorem:
De Morgan’s Theorems state the relationship between union and intersection in set theory and Boolean algebra. The two theorems are:
First Theorem:
$(A\cup B)' = A’\cap B'$
Second Theorem:
$(A\cap B)' = A’\cup B'$
Set Cardinality with Intersection:
$n (A\cup B) = n(A) + n(B)$
$n (A\cup B) = n(A) + n(B) - n(A\cap B)$
Other Set Formulas:
$A - A = \phi$
$B - A = B\cap A'$
$B - A = B - (A\cap B)$
$(A - B) = A$ if $A\cap B = \phi$
$(A - B) \cap C = (A\cap C) - (B\cap C)$
$A \triangle B = (A-B)\cup (B-A)$
$n(A\cup B\cup C) = n(A) + n(B) + n(C) - n(B\cap C) - n(A\cap B) - n(A\cap C) + n(A\cap B\cap C)$
$n(A - B) = n(A\cup B) - n(B)$
$n(A - B) = n(A) - n(A\cap B)$
$n(A') = n(U) - n(A)$
$n(U) = n(A) + n(B) - n(A\cap B)$
$n((A\cup B)') = n(U) + n(A\cap B) - n(A) - n(B)$
Approach to Solve Questions of Sets Class 11
Using these approaches, students can tackle the Sets Class 11 Chapter 1 Question Answers with greater confidence.
- Know Set Types: Identify empty set, singleton, finite/infinite, subset, universal set, and power set.
- Use Correct Signs: Aware of symbols such as ∈, ⊂, ∪, ∩, and ′ (complement).
- Utilise Venn Diagrams: Utilise them in solving problems dealing with union, intersection, and complement.
- Use Set Identities: Use standard formulas like A$\cup$B = n(A) + n(B) − n(A$\cap$B) to solve counting problems.
- Learn the Complement Properly: Keep in mind that A′ = U − A; specify the universal set in such problems.
- Change the word Problems to Sets: Define the sets clearly from the given situation before solving.
- Prove Identities: To prove identities, suppose x ∈ LHS and show x ∈ RHS, or vice versa.
- Solve NCERT & Exemplar Problems: Practice various types of questions, including MCQs and proofs.
What Extra Should Students Study Beyond NCERT for JEE?
Here is a comparison list of the concepts in Sets that are covered in JEE and NCERT, to help students understand what extra they need to study beyond the NCERT for JEE:
Why are Class 11 Maths Chapter 1 Sets question answers important?
This chapter on Sets is the starting point of higher mathematics. It helps us understand how to group and organise objects logically. We will see this idea being used in almost every topic that comes later. These Class 11 Maths chapter 1 Sets question answers make these ideas clear and easy to practice. Here are some more points on why these question answers are important:
- It helps us understand the language of maths, as sets form the base for many concepts like relations and functions.
- Students learn to represent and compare groups of numbers or objects using symbols and Venn diagrams.
- This chapter builds logical thinking and reasoning skills useful in problem-solving.
- Studying Class 11 Maths chapter 1 Sets question answers helps us score well now and also understand advanced topics in Class 12 and college-level maths.
NCERT Class 11 Maths Solutions - Chapter Wise
Given below is the chapter-wise list of the NCERT Class 11 Maths solutions with their respective links:
Also, read,
- NCERT Exemplar Class 11 Maths Solutions Chapter 1 Sets
- NCERT Notes Class 11 Maths Solutions Chapter 1 Sets
NCERT Class 11 Solutions - Subject Wise
Check out the NCERT Class 11 solutions for different subjects below. Click on the links to view the complete solutions.
- NCERT solutions for class 11 biology
- NCERT solutions for class 11 chemistry
- NCERT Solutions for Class 11 Physics
NCERT Books and NCERT Syllabus
Access the latest NCERT books and updated syllabus for class 11 through the links below.
Frequently Asked Questions (FAQs)
A set A is a subset of B if every element of A is also in B. It is written as A ⊆ B.
The main operations are:
Union (A ∪ B): all elements from A and B
Intersection (A ∩ B): common elements in A and B
Difference (A − B): elements in A but not in B
Complement (A′): elements not in A (with respect to a universal set)
A set can be represented in two ways:
Roster form: listing all elements, e.g., A = {1, 2, 3, 4}
Set-builder form: describing a property, e.g., A = {x | x is a natural number less than 5}.
A finite set has a limited, countable number of elements, while an infinite set has an unlimited, uncountable number of elements.
In NCERT Class 11 Maths, the basic operations on sets include union, intersection, difference, and complement.
In Class 11 Maths Chapter 1 (Sets), De Morgan's Laws provide a relationship between the complement of the union and intersection of sets, stating that the complement of the union is the intersection of the complements, and vice versa.
In Class 11 Maths, to find the union of sets, combine all unique elements from both sets, while for intersection, find the elements common to both sets.
In Class 11 Maths Chapter 1 on Sets, you'll learn about finite and infinite sets, empty sets, equal sets, subsets, and the power set.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
