• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Exemplar Class 11 Maths Solutions Chapter 1 Sets

NCERT Exemplar Class 11 Maths Solutions Chapter 1 Sets

Edited By Ravindra Pindel | Updated on Sep 12, 2022 04:38 PM IST

NCERT Exemplar Class 11 Maths solutions chapter 1 Sets deals with a variety of definitions and terms related to a set which was first introduced by Georg Cantor which serves a very important part at each, and every branch of mathematics in present times. The chapter has its reach in various different topics such as geometry, trigonometry, sequence, etc., which makes it even more vital to be understood. With the help of NCERT Exemplar Class 11 Maths chapter 1 solutions, students will be able to understand the application of sets. NCERT Exemplar solutions Class 11 Maths chapter 1 also helps in identifying whether a collection could be termed as a set or not. The essential rules like a set is denoted by a capital letter, its members or objects are represented by small letters, and the terms and objects of the collection should be synonymous, are also explained.

JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy

Suggested: JEE Main: high scoring chapters | Past 10 year's papers

This Story also Contains
  1. NCERT Exemplar Class 11 Maths Solutions Chapter 1: Short Answer Type
  2. NCERT Exemplar Class 11 Maths Solutions Chapter 1: Long Answer Type
  3. NCERT Exemplar Class 11 Maths Solutions Chapter 1: Objective Type
  4. Important Notes To Follow While Studying NCERT Exemplar Class 11 Maths Solutions Chapter 1 Sets
  5. Main Subtopics of NCERT Exemplar Class 11 Maths Solutions Chapter 1
  6. What will the students learn in NCERT Exemplar Class 11 Maths Solutions Chapter 1?
  7. NCERT Solutions for Class 11 Mathematics Chapters
  8. Important Topics To Cover in NCERT Exemplar Class 11 Maths Solutions Chapter 1 Sets

NCERT Exemplar Class 11 Maths Solutions Chapter 1: Short Answer Type

Question:

  1. Write the following sets in the roaster form:

(i) A = \left \{ x : x \epsilon R, 2x + 11 = 15 \right \}
(ii) B = \left \{ x | x^{2} = x, x \epsilon R \right \}
(iii) C = \left \{ x | x is a positive factor of a prime number p\left \ \right \}

Answer:

(i) Given that A = \left \{ x : x \epsilon R, 2x + 11 = 15 \right \}

2x + 11 = 15

2x = 4

2x = 4

x = 2 ; Hence , A =\left \{ 2 \right \}

(ii) Given that B = \left \{ x | x^{2} = x, x \epsilon R \right \}

x^{2} = x

x^{2} - x = 0

x(x-1) = 0

x = 0 ,x = 1 ; Hence B = (0,1)

(iii) Given that C = \left \{ x | x is a positive factor of a prime number p\left \ \right \}

So , the positive factors of prime number P are 1 and P . Hence , C= \left \{ 1,P \right \}

Question:

Write the following sets in the roaster form:
(i) D = \left \{ t | t^{3} = t,t\epsilon R\right \}
(ii) E = \left \{ w |\frac{w-2}{w+3} =3 ,w\epsilon R\right \}
(iii) F = \left \{ x | x^{4} - 5x^{2} +6 =0 ,x\epsilon R\right \}

Answer:

(i) Given that D = \left \{ t | t^{3} = t,t\epsilon R\right \}
t^{3} = t
t\left ( t^{2}-1 \right ) = 0
t\left ( t-1 \right )\left ( t+1 \right ) = 0
(ii) Given that E = \left \{ w |\frac{w-2}{w+3} =3 ,w\epsilon R\right \}
\frac{w-2}{w+3} =3
3w +9 = w-2
2w=-11
w=-\frac{11}{2}
Hence , E=\left \{ -\frac{11}{2} \right \}
(iii) Given that F = \left \{ x | x^{4} - 5x^{2} +6 =0 ,x\epsilon R\right \}
x^{4} - 5x^{2} +6 =0
\left ( x^{2} -2 \right ) \left ( x^{2}-3 \right ) = 0
x^{2} -2 =0 , x^{2}-3 = 0
x = \pm \sqrt{2} , and , x=\pm \sqrt{3}
Hence F = -\sqrt{2} , +\sqrt{2} , -\sqrt{3} , +\sqrt{3}

Question:

Write the following sets in the roaster form:

  1. A = \{x : x \in R,\ 2x + 11 = 15\}

  2. B = \{x : x^2 = x, x\in R\}

  3. C = \{x : x\text{ is a positive factor of a prime number }p\}

Answer:

(i) Given that: A = \{x : x \in R,\ 2x + 11 = 15\}
\begin{aligned}2x + 11 &= 15 \\ 2x & = 4 \\ x & = 2\end{aligned}
Hence, A = \{2\}
(ii) Given that B = \{x : x^2 = x, x\in R\}
\begin{aligned}x^2 &= x \\ x^2 - x& = 0 \\ x(x-1)&=0 \\ \therefore x =0 & \ x = 1 \end{aligned}
Hence, B = \{0,1\}
(iii) Given that C = \{x : x\text{ is a positive factor of a prime number }p\}
So the positive factors of prime number p are 1 and p. Hence C = \{1,p\}

Question:

Write the following sets in the roaster form:

  1. D = \left\{t : t^3 = t, t\in R \right \}

  2. E = \left\{w:\frac{w-2}{w+3} = 3, w\in R \right \}

  3. F= \left\{x:x^4 -5x^2 + 6= 0, x\in R \right \}

Answer:

(i) Given that D = \left\{t : t^3 = t, t\in R \right \}
\begin{aligned}t^3 &= t \\ t^3 - t &= 0 \\ t(t-1)(t+1)&= 0 \\ t &= -1,0,1\end{aligned}
hence, D = \left\{-1,0,1 \right \}
(ii) Given that E = \left\{w:\frac{w-2}{w+3} = 3, w\in R \right \}
\begin{aligned}\frac{w-2}{w+3} &= 3\\ 3w + 9 &= w-2 \\ 2w &= -11 \\ w& = -\frac{11}{2} \end{aligned}
Hence, E = \left\{\frac{-11}{2} \right \}
(iii) Given that F= \left\{x:x^4 -5x^2 + 6= 0, x\in R \right \}
\begin{aligned} x^4 - 5x^2 + 6 &= 0 \\ (x^2-2)(x^2-3)&=0\end{aligned}
x = \pm\sqrt2 and x = \pm\sqrt3
Hence, F = \left\{-\sqrt{2}, + \sqrt{2}, -\sqrt{3}, + \sqrt{3}\right\}

Question:

If Y = \{x : x\text{ is a positive factor of the number }2^{p - 1} (2^p - 1)\text{, where }2^p - 1\text{ is a prime number} \}. Write Y in the roaster form.

Answer:

Given that
Y = \{x : x\text{ is a positive factor of the no. }2^{p - 1} (2^p - 1)\text{, where }2^p - 1\text{ is a prime number} \}
The factors of 2^{p-1} are 1,2,2^2, 2^3,...,2^{p-1}
The factors of 2^p -1 are 1 and 2^p -1
Hence, Y = \left\{1,2,2^2,2^3,...,2^{p-1},2^{p}-1\right\}

Question:

State which of the following statements are true and which are false. Justify your answer.
(i) 35 \in \{x : x\text{ has exactly four positive factors}\}
(ii) 128 \in \{y :\text{ the sum of all the positive factors of }y\text{ is }2y\}
(iii) 3 \notin \{x : x^4 - 5x^3 + 2x^2 - 112x + 6 = 0\}
(iv) 496 \notin \{y :\text{ the sum of all the positive factors of }y\text{ is }2y\}

Answer:

(i) Given that: 35 \in \{x : x\text{ has exactly four positive factors}\}
Factors of 35 are 1, 5, 7, 35.
Hence, true
(ii) Given that: 128 \in \{y :\text{ the sum of all the positive factors of }y\text{ is }2y\}
Factors of 128 are 1,2,4,8,16,32,64,128
sum of all factors 255 \neq 2\times 128
hence statement is false.
(iii) Given that: 3 \notin \{x : x^4 - 5x^3 + 2x^2 - 112x + 6 = 0\}
x^4 - 5x^3 + 2x^2 -112x + 6 = 0
Put x = 3
- 366 = 0 which is not true, So 3 is not an element of the set
Hence, statement is true
(iv) Given that: 496 \notin \{y :\text{ the sum of all the positive factors of }y\text{ is }2y\}
The positive factors of 496 are 1,2,4,8,16, 31, 62, 124, 248, and 496
The sum of all positive factors is 992 = 2\times 496 which is true, so the 496 is element of the set . Hence the statement is false.

Question:

Given L = \{1, 2, 3, 4\},\ M = \{3, 4, 5, 6\} and N = \{1, 3, 5\}. Verify that L - (M\cup N) = (L-M) \cap (L-N).

Answer:

Given that L = \{1, 2, 3, 4\},\ M = \{3, 4, 5, 6\} and N = \{1, 3, 5\}.
Now,
\begin{aligned} LHS = L - (M\cup N) &= \{1,2,3,4\} - (\{3,4,5,6\} \cup \{1,3,5\}) \\ & = \{1,2,3,4\} - \{1,3,4,5,6\} = \{2\} \end{aligned}
\begin{aligned} RHS& = (L-M)\cap (L-N) \\ (L-M) &= \{1,2,3,4\} - \{3,4,5,6\} = \{1,2\} \\ (L-N) &= \{1,2,3,4\} - \{1,3,5\} = \{2,4\} \\ (L-M) & \cap (L-N) = \{1,2\} \cap \{2,4\} = \{2\} \\ LHS & = RHS\end{aligned}

Question:

If A and B are subsets of the universal set U, then show that
(i) A ⊂ A ∪ B
(ii) A ⊂ B ⇔ A ∪ B = B
(iii) (A ∩ B) ⊂ A

Answer:

(i) Given that A \subset U and B \subset U
To prove: A \subset A\cup B we have to show that if x\in A; x\in A\cup B
Let x\in A\Rightarrow x\in A \ or x\in B \Rightarrow x\in A\cup B
hence, A \subset A\cup B
(ii) A\subset B then let x\in A\cup B
\Rightarrow x \in A \ or \ x\in B
\Rightarrow x \in B
A\cup B \subset B \qquad\qquad (i)
But B \subset A\cup B \qquad\qquad (ii)
From (i) and (ii) we get A\cup B = B
Now if A\cup B = B, then
let y\in A \Rightarrowy\in A\cup B \Rightarrow y\in B
Hence, A \subset B
Thus, A \subset B \Rightarrow A\cup B = B
iii)
\begin{array}{l} \text { Let } x \in A \cap B \\ \quad x \in A \text { and } x \in B \\ \quad x \in A \\ \text { Hence, } A \cap B \subset A \end{array}

Question:

Given that N = {1, 2, 3,…, 100}. Then write
(i) the subset of N whose elements are even numbers.
(ii) the subset of N whose element are perfect square numbers.

Answer:

N = {1,2,3,4……100}

  1. Required subset whose elements are even = {2,4, 6,8…..,100}

  2. Required subset whose elements are perfect squares = {1,4,9 ,16,25,36,49,64,81,100}

Question:

If X = {1, 2, 3}, if n represents any member of X, write the following sets containing all numbers represented by:
(i) 4n
(ii) n + 6
(iii) \frac{n}{2}
(iv) n – 1

Answer:

Given that X = \{1,2,3\}
(i) \{4n | n\in X\} = \{4,8,12\}
(ii) \{n + 6\ |\ n\in X\} = \{7,8,9\}
(iii) \left\{\frac{n}{2} \ | \ x\in X \right \} = \left\{\frac{1}{2},1,\frac{3}{2} \right \}
(iv) \left\{(n-1)\ | \ x\in X \right \} = \left\{0,1,2 \right \}

Question:

If Y = {1, 2, 3,…, 10}, and a represents any element of Y, write the following sets, containing all the elements satisfying the given conditions.
(i) a\in Y but a^2\notin Y
(ii) a + 1 = 6, a\in Y
(iii) a is less than 6 and a\in Y

Answer:

Given that: Y = {1, 2, 3,…, 10}
(i) \{a \ | \ a\in Y \text{ but }a^2\notin Y\} = \{4,5,6,7,8,9,10\}
(ii) \{a \ | \ a + 1 = 6,\ a\in Y \} = \{5\}
(iii) \{a \ | \ a < 6\text{ and } a\in Y \} = \{1,2,3,4,5\}

Question:

A, B and C are subsets of Universal Set U. If A = {2, 4, 6, 8, 12, 20}, B = {3, 6, 9, 12, 15}, C = {5, 10, 15, 20} and U is the set of all whole numbers, draw a Venn diagram showing the relation of U, A, B and C.

Answer:

NUS5nMyxM1vZKu4YnNO6_c-EmwE8NAbIFrMmegYy_qaHJ4bAdqTEslpsVR0gbv9806EDtdtA3kQE2ZMwsEohO8_EZBGScnOBYlsYRKp18v-ystpmHNgKDTh9scs163z9cPp_SiN1MCCTO4YCUg
Given that: A, B and C are the subsets of a universal set U.
Where A= {2,4,6,8,12,20}
B = {3, 6,9, 12, 15}
And C = {5, 10, 15, 20}

Question:

Let U be the set of all boys and girls in a school, G be the set of all girls in the school, B be the set of all boys in the school, and S be the set of all students in the school who take swimming. Some, but not all, students in the school take swimming. Draw a Venn diagram showing one of the possible interrelationships among sets U, G, B and S.

Answer:

Given that U: Set of all boys and girls
G = Set of girls
B = Set of boys
S = Set of all students who take swimming
_UsVPbXvI1ig8tIFivf7vy0slQJ40HHc3DFx9zITEd-9tI7MlrUwdIXj2f26lCuaWAuCsk5odeOGFCFC5aA3YnWVo3a7f50S0pAoKqrS4AdAs5smUERQZlg2PT5EXF8IwLPiY7ut9XxEbg8pzg

Question:

For all sets A, B and C, show that (A - B) \cap (A - C) = A - (B \cup C)

Answer:

Let x\in (A- B)\cap (A - C)
\\\Rightarrow x\in (A-B) \text{ and } x\in (A-C) \\\Rightarrow x\in A \text{ and } (x\notin B\text{ and } x\notin C) \\\Rightarrow x\in A \text{ and } (x\notin B\cup C)
So, (A - B) \cap (A - C) \subset A - (B \cup C)\qquad \qquad (i)
Let y\in A-(B\cup C)
y \in A - (B\cup C)\\ \Rightarrow y\in A\text{ and } (y\notin B\cup C) \\ \Rightarrow y \in A\text{ and } y\notin B \quad \text{and}\quad y\in A\text{ and }y\notin C\\ \Rightarrow y\in (A-B)\text{ and } y\in(A-C)\\ \Rightarrow y \in (A-B)\cap (A-C)
So, A - (B \cup C) \subset (A - B) \cap (A - C) \qquad \qquad (ii)
From (i) and (ii), we get,
(A - B) \cap (A - C) = A - (B \cup C)

Question:

For all sets A and B, (A-B)\cup (A\cap B) = A

Answer:

\begin{aligned}LHS &= (A-B)\cup (A\cap B) \\ &= [(A-B)\cup A]\cap [(A-B)\cup B] \\ &=A\cap (A\cup B) = A = RHS \end{aligned}

Question:

For all sets A, B and C, A – (B – C) = (A – B) – C

Answer:

Let us use the following Venn diagram to solve this question
Step 1: - B - C
o6Ev1CrJSEnfLpz4GHtlOgZyxiwT3Q4e-VfPFbZkGdAZ3S_-g4HcoIyrTPI2sNk_aCfBkBC8Yo-idwmLcfmGsHAY56HE4nGNvvkfk2C4b7hODkGzZm3X1dPec5Tq6fwfIskmT7gz1fb2eA1ooQ
Step 2: - A-(B-C)
Il1JMjuW9Ob8iibrdM1FllDsBgD5LWAyYd7W335Qe8Fr1n1Ur4xuPWOQiWAyDzVucF_8jcpZYz8gP6yJCzuUyav90Be3LG--gIsvv0oZFnN9eqOEn836U0-1Bc4QC1y9PSWVfs__SOg9JKwyPA
Step 3: - A-B
JExL0NLAa3vWuIxCpPSJNyOLj3jZljEN0cp2TYTbdrlq4dyqm1JmwE6oazuFfMEYQaspUduHnWei2sOChK6QRnO-q2lPdMLb9gFql3UtfHSr8OADnRZJXZ80FTRAHCiHX5v1_DhAhqXVPow-4w
Step 4: - (A-B)-C
2A6gv2vK_uPgV-l1gpk-dMO0sYRPiIdLtlysMQKx3q7lxHARIej2N8M0ltz6Hw9UbflAVpePKVLDELqpKPERvY4mFRETSBxpmSw_pseWP1YTmv2TBOPU0zjM3fTHgoTgi9cZxy-uv10yeFTlQw
As steps 2 and 4 are inequal, hence, the statement given is not true.

Question:

For all sets A, B and C, if A ⊂ B, then A ∩ C ⊂ B ∩ C

Answer:

Suppose A\subset B,
Let x\in A \cap C
\\x\in A \text{ and }x\in C\\ x\in B \text{ and }x\in C\\ x\in B\cap C\\ \therefore A\cap C \subset B\cap C
Hence the given statement is true.

Question:

For all sets A, B and C, if A ⊂ B, then A ∪ C ⊂ B ∪ C

Answer:

Suppose A\subset B,
Let x\in A \cup C
\\x\in A \text{ or }x\in C\\ x\in B \text{ or }x\in C\\ x\in B\cup C\\ \therefore A\cup C \subset B\cup C
Hence the given statement is true.

Question:

For all sets A, B and C, if A ⊂ C and B ⊂ C, then A ∪ B ⊂ C

Answer:

Suppose A \subset C, B\subset C.
Let x\in A\cup B
\\ x\in A \text{ and } x\in B \\ x\in C \text{ and } x\in C \quad [A\subset C\text{ and }B\subset C] \\ \Rightarrow x\in C\Rightarrow A\cup B \subset C
hence the given statement is true

Question:

For all sets A and B, A ∪ (B – A) = A ∪ B

Answer:

\begin{aligned} A\cup (B-A)& = A\cup (B\cap A')\\ &=(A\cup B)\cap (A\cup A') &[\text{Distributive law}]\\ &=(A\cup B)\cap U&[A\cup A' = U] \\ &=A\cup B = RHS\end{aligned}
Hence the given statement is true.

Question:

For all sets A and B, A – (A – B) = A ∩ B

Answer:

\begin{aligned} LHS & = A - (A-B) = A - (A\cap B') &\quad & [A-B= A\cap B'] \\ & = A\cap (A\cap B')' = A\cap [A'\cup(B')'] & \quad & [(A\cap B)' = A'\cup B']\\ & = A\cap (A'\cup B) \\ & = (A\cap A')\cup (A\cap B) = P \cup (A\cap B) & \quad &\text{Where } P = (A\cap A') \\ & = A\cap B = RHS\end{aligned}]
Hence, the given statement is proved.

Question:

For all sets A and B, A – (A ∩ B) = A – B

Answer:

\begin{aligned} LHS &= A-(A\cup B) = A\cap (A\cup B)' &\quad&[A - B = A\cup B']\\ &= A\cap (A'\cup B') &\quad& [(A\cap B)' = A' \cup B'] \\ &= (A\cap A') \cup (A\cap B) \\ &= P \ \cup (A-B) && [P=(A\cap A')\text{ and } A-B = A\cap B'] \\ & = (A-B) = R.H.S \end{aligned}

Question:

For all sets A and B, (A ∪ B) – B = A – B

Answer:

\begin{aligned} LHS &= (A\cup B) - B = (A\cup B )\cap B' &\quad& [A-B = A\cap B'] \\ & = (A\cap B')\cup (B\cap B') \\ & = (A-B)\cup P && [ P = (A\cap A')\text{ and }A - B = A\cap B'] \\ & = (A-B) = RHS\end{aligned}

Question:

Let
T = \left\{x \ | \ \frac{x+5}{x-7} - 5 = \frac{4x-40}{13-x} \right \}
Is T an empty set? Justify your answer.

Answer:

Given: T = \left\{x \ | \ \frac{x+5}{x-7} - 5 = \frac{4x-40}{13-x} \right \}
\begin{aligned}\Rightarrow& & \frac{x+5}{x-7}- 5 &= \frac{4x-40}{13-x} \\ && \frac{(x+5)-5(x-7)}{x-7} & = \frac{4x-40}{13-x} \\ \Rightarrow && \frac{x + 5 - 5x + 35}{x-7} & = \frac{4x-40}{13-x} \\ \Rightarrow & & -4(x-10)(13-x) &= 4( x -10)(x-7) \\ \Rightarrow & & -4(x-10) (13-x + x -7) & = 0 \\ \Rightarrow & & -4(x - 10)6 &= 0 \\ \Rightarrow & & -24(x-10) &=0 \\ \Rightarrow & & x - 10 &= 0 \\ \Rightarrow & & x = 10& \text{ or }T = \{10\}\end{aligned}
Hence T is not an empty set.

NCERT Exemplar Class 11 Maths Solutions Chapter 1: Long Answer Type

Question:

Let A, B and C be sets. Then show that A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

Answer:

Let x\in A\cap (B\cup C)
\begin{aligned} \Rightarrow & x\in A \text{ and } x\in (B\cup C) \\ \Rightarrow & x\in A \text{ and } x\in B\text{ or }x\in C \\ \Rightarrow & x\in A \text{ and } x\in B\text{ or }x\in A \text{ and } x\in C \\ \Rightarrow & x\in(A\cap B)\text{ or } x\in (A\cap C) \\ \Rightarrow & x\in (A\cap B)\cup (A\cap C) \\ \therefore & A\cap (B\cup C) \subset \ (A\cap B)\cup (A\cap C) & -(i) \end{aligned}
Let y\in (A\cap B)\cup (A\cap C)
\begin{aligned} \Rightarrow & y\in (A\cap B)\cup(A\cap C) \\ \Rightarrow & y \in (A\cap B)\text{ or }y\in (A\cap C) \\ \Rightarrow & y\in A\text{ and } y\in B\text{ or }y\in A\text{ and } y\in C\\ \Rightarrow &y \in A\text{ and }(y \in B\text{ or }y\in C) \\ \Rightarrow &y \in A\text{ and }(y \in B\cup C )\\ \Rightarrow &y \in A\cap(B\cup C ) \\\therefore & \ (A\cap B)\cup (A\cap C)\subset A\cap (B\cup C) & -(ii)\end{aligned}
From and (i) and (ii)
A\cap (B\cup C) =(A\cap B)\cup (A\cap C)

Question:

Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed
(i) in English and Mathematics but not in Science
(ii) in Mathematics and Science but not in English
(iii) in Mathematics only
(iv) in more than one subject only

Answer:

Let the set of students who passed in mathematics be M, the set of students who passed in English be E and set of students who passed in science be S.
screenshot_20200908_233624
Then n(U)=100, n(M)=12, n(S)=8,
n(E\cap M)=6, n(M\cap S)=7, n(E\cap S)=4 and n(E\cap M\cap S)=4
According to the Venn diagram
n(E\cap M\cap S)=4; e = 4
n(E\cap M)=6; d + e= 6; d = 2
n(M\cap S)=7; e + f= 7; f = 3
n(E\cap S)=4; b + e= 4; b= 0
n(E)=15; a + b + d + e= 15; a= 9
n(M)=12; d + e + f+g= 12; g= 3
n(S)=8; b + e + f + c= 8; c= 1
Thus, number of students who passed in English and mathematics but not in science = d= 2
Number of students who passed in Science and mathematics but not in English = f=3
Number of students who passed in mathematics only = g =3
Number of students who passed in more than one subject = b+ e+ d +f =0+4+2+3 =9

Question:

In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Find the number of students who play neither?

Answer:

Let C be the set of students who play cricket and T the set of students who play tennis.
Total number of students = 60 ⇒n(U)=60
Number of students who play cricket = 25 \Rightarrow n(C)=25
Number of students who play tennis = 20 \Rightarrow n(T)=20
Number of students who play both the games = 10 \Rightarrow n(C\cap T) = 10
Number of students who play any one game= n (C \cup T ) =n(C ) +n(T) - nC\cap T = 25+20=10 =35
Number of students who play neither = n(U) - n(C \cup T) = 60-35 = 25

Question:

In a town of 10,000 families it was found that 40% families buy newspaper A, 20% families buy newspaper B, 10% families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three newspapers. Find
(a) The number of families which buy newspaper A only.
(b) The number of families which buy none of A, B and C

Answer:

Let A be a set of families which buy newspaper A, B be the set of families which buy newspaper B and C be the set of families which buy newspaper C
n(U) = 10000, n(A) = 40\%, n(B) = 20\%,n(c) = 10\%, n(A\cap B) = 5\%, n(B\cap C) = 3\%, n(A\cap C) = 4\% and n(A\cap B\cap C) = 2\%
Number of families which buy newspaper A only = n(A) - n(A\cap B) - n(A\cap C) +n(A\cap B\cap C)
= 10000 \times (\frac{40}{100} - \frac{5}{100} - \frac{4}{100} +\frac{2}{100}) = 10000\times \frac{33}{100} = 3300 \ \text{families}
Number of families which buy none of A, B and C =n(U) - n(A\cup B\cup C)
\small =n(U) - [n(A) + n(B) + n(C) - n(A\cap B) - n(B\cap C) - n(A\cap C) + n (A\cap B\cap C)]
\small = [100 - (40 + 20 + 10 - 5-3-4+2)]\times 10000
\small = \frac{40}{100}\times 10000 = 4000 \ families

Question:

In a survey of 200 students of a school, it was found that 120 study Mathematics, 90 study Physics and 70 study Chemistry, 40 study Mathematics and Physics, 30 study Physics and Chemistry, 50 study Chemistry and Mathematics and 20 none of these subjects. Find the number of students who study all the three subjects.

Answer:

Let the set of students who study mathematics be M, the set of students who study physics be P and set of students who study chemistry be C.
N(U) =200, n(M)=120, n(P)=90, n(C)=70, n(MP) = 40, n(P\cap C) = 30, n(C\cap M) = 50 and
n(M' \cap P' \cap C') = 20
n(U) - n(M'\cap P' \cap C') = n(M\cup P \cup C) = 200-20 = 180
n(M \cup P \cup C) = n(M) + n(P) + n(C) - n(M\cap P) - n(P\cap C)- n(C\cap M) + n(M\cap P\cap C)
180 = 120 + 90 + 7 - 40-30-50 + n(M\cap P \cap C)
180 -40 = n(M\cap P \cap C) = 20
Hence, the number of students who study all 3 subjects = 20

Question:

In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15
French and English = 09, English and Sanskrit = 4
French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study
(i) French only
(ii) English only
(iii) Sanskrit only
(iv) English and Sanskrit but not French
(v) French and Sanskrit but not English
(vi) French and English but not Sanskrit
(vii) at least one of the three languages
(viii) none of the three languages

Answer:

Let F be the set of students who study French, E be the set of students who study English and S be the set of students who study Sanskrit
n(U) = 5, n(F) = 17, n(E) = 13, n (S) = 15, n(F\cap E) = 9, n(E\cap S) = 5 and n(F\cap E\cap S) = 3
\begin{aligned} n(F\cap E\cap S) = 3&\Rightarrow e = 3\\ n(F\cap E) = 9&\Rightarrow b + e = 9&\Rightarrow b = 6 \\ n(F\cap S) = 5 &\Rightarrow d + e = 5 &\Rightarrow d = 2 \\ n(F) = 17 &\Rightarrow a + b +d + e = 17&\Rightarrow a = 6\\n(E) = 13&\Rightarrow b + c + e +f = 13&\Rightarrow c = 3\\ n(S) = 15 &\Rightarrow d + e + f + g = 15&\Rightarrow g = 9\end{aligned}
Number of students who study French only =a =6
Number of students who study English only =c =3
Number of students who study Sanskrit only =g =9
Number of students who study English and Sanskrit but not French =f =1
Number of students who study French and Sanskrit but not English =d =2
Number of students who study French and English but not Sanskrit =b = 6
Number of students who study at least one of the three languages = a+b+c+d+e+f+g =6+6+3+2+3+1+9 =30
Number of students who study none of the three languages = 50-30=20

NCERT Exemplar Class 11 Maths Solutions Chapter 1: Objective Type

Question:

Suppose A_1, A_2, ..., A_{30} are thirty sets each having 5 elements and B_1, B_2, ..., B_{n} are n sets each with 3 elements, let
\bigcup_{i=1}^{30} A_i = \bigcup_{j=1}^{n}B_j = S
and each element of S belongs to exactly 10 of the Ai’s and exactly 9 of the B,’S. then n is equal to
A. 15
B. 3
C. 45
D. 35

Answer:

Number of elements in

\begin{aligned}A_1\cup A_2\cup A_3\cup...\cup A_{30} = 30\times 5 = 150\\ (\text{when repetition is allowed}) \end{aligned}
However, each element is repeated 10 times.
n(S) = 30 \times \frac{5}{10} = \frac{150}{10} = 15\quad (i)
Number of elements in B_1\cup B_2\cup B_3\cup...\cup B_n = 3n \ (\text{When repetition is not allowed})
But each element is repeated 09 times
n(S) = \frac{3n}{9} = \frac{n}{3}
From (i) and (ii) we get \frac{n}{3} = 15; n = 45. hence, the correct option is (c)

Question:

Two finite sets have m and n elements. The number of subsets of the first set is 112 more than that of the second set. The values of m and n are, respectively, (a) 4,7 (b) 7,4 (c) 4,4 (d) 7, 7
Answer:

According to the question we have,
\\2^m -2^n = 112 \\ \quad 2^n(2^{m-n} - 1) = 2^4\times 7\\ 2^n = 2^4 \text{ and } 2^{m-n} -1 = 7\\ n = 4\text{ and } 2^{m-n} = 1+7 = 8 = 2^3 \\ n+4\text{ and } m-n = 3 \\ m = 7

Question:

The set (A ∩ B′)′ ∪ (B ∩ C) is equal to
A. A′∪ B ∪ C
B. A′ ∪ B
C. A′ ∪ C′
D. A′ ∩ B

Answer:

The answer is option B.
We know that
\begin{aligned} (A\cap B)' &= A'\cup B' &\quad& [\text{De Morgan's Law}] \\ (A\cap B)'\cup (B\cap C) &= \left[A'\cup B' \right ]\cup(B\cap C)\\ & =(A'\cup B)\cup (B\cap C) && [(B')' = B] \\ &= A'\cup B\end{aligned}

Question:

Let F1 be the set of parallelograms, F2 the set of rectangles, F3 the set of rhombuses, F4 the set of squares and F5 the set of trapeziums in a plane. Then F1may be equal to
(a) F2 ∩F3
(b) F3 ∩F4
(c) F2 u Fs
(d) F2 ∪ F3 ∪ F4 ∪ F1

Answer:

The answer is the option (d). Rectangles, rhombus and square in a plane is a parallelogram but trapezium is not
F_1 = F_2\cup F_3 \cup F_4 \cup F_1
Hence, (d) is correct

Question:

Let S = set of points inside the square, T = the set of points inside the triangle and C = the set of points inside the circle. If the triangle and circle intersect each other and are contained in a square. Then

(A) S ∩ T ∩ C = φ
(B) S ∪ T ∪ C = C
(C) S ∪ T ∪ C = S
(D) S ∪ T = S ∩ C

Answer:

The answer is the option (c)
eNo4Wx4JzhA5KCNib-zK6L8FxDgacEqdsUlwd6KMrPYT_J_O1wY7_tmHCcnqBhInAN4vGs9hQgyS1-RqLdMoBoz0oqAi8doSW7uJBdc7viYHqG_D5zjQ3iswUk_ant9pnseHFSd4EZvqOa5qEQ
From the above Venn diagram
S\cup T\cup C = S
Hence, the correct option is (C)

Question:

Let R be set of points inside a rectangle of sides a and b (a, b > 1) with two sides along the positive direction of x-axis and y-axis. Then
A. R = \left\{(x,y) : 0 \leq x\leq a, 0\leq y\leq b\right\}
B. R = \left\{(x,y) : 0 \leq x< a, 0\leq y\leq b\right\}
C.R = \left\{(x,y) : 0 \leq x< a, 0< y< b\right\}
D. R = \left\{(x,y) : 0 < x< a, 0< y< b\right\}

Answer:

The answer is the option (d)
R be set of points inside a rectangle of sides a and b (a, b > 1) with two sides along the positive direction of x-axis and y-axis
R = \left\{(x,y) : 0 < x< a, 0< y< b\right\}
Hence, the correct option is (d)

Question:

In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Then, the number of students who play neither is
(a) 0 (b) 25 (c) 35 (d) 45

Answer:

The answer is the option (b).
Let C be the set of students who play cricket and T the set of students who play tennis.
Total number of students = 60 ⇒n(U)=60
Number of students who play cricket = 25 \Rightarrow n(C)=25
Number of students who play tennis = 20 \Rightarrow n(T)=20
Number of students who play both the games = 10 \Rightarrow n(C\cap T) = 10
Number of students who play any one game= n (C \cup T ) =n(C ) +n(T) - nC\cap T = 25+20=10 =35
Number of students who play neither = n(U) - n(C \cup T) = 60-35 = 25

Question:

In a town of 840 persons, 450 persons read Hindi, 300 read English and 200 read both. Then the number of persons who read neither is
(a) 210 (b) 290 (c) 180 (d) 260

Answer:

The answer is the option (b)
Total number of persons in a town = 840 \Rightarrow n(U) = 840
Number of students who read Hindi = 450 \Rightarrow n(H) = 450
Number of students who play English = 300 \Rightarrow n(E) = 300
Number of students who read both = 200 \Rightarrow n(H\cap E) = 200
\begin{aligned} n(H\cup E) = n(H) + n(E) - n(H\cap E) &= 450+300 - 200 = 550 \\ n(H'\cap E') = n(U) - n(H\cup E) &= 840 - 550 = 290\end{aligned}

Question:

If X = \{8^n-7n - 1 : n\in N\}} and Y = \{49n-49 : n\in N\}. Then
(A) X\subset Y (B) Y\subset X (C) X = Y (D) X\cap Y = \phi

Answer:

The answer is the option (a).
Given that X = \{8^n-7n - 1 : n\in N\} = \{0, 49, 490,...\}
And Y = \{49n-49 : n\in N\} = \{0, 49, 98,...\}
Here, it is clear that every element belonging to the X is also present in Y.
X\subset Y. Hence, the correct option is (A).

Question:

A survey shows that 63% of the people watch a News Channel whereas 76% watch another channel. If x% of the people watch both channel, then
(A) x = 35 (B) x = 63 (C) 39 \leq x \leq 69 (D) x = 39

Answer:

Let p% of people watch a channel and q% of people watch another channel
n(p\cap q) = x\% \text{ and }n(p\cup q) \leq 100
So, n(p\cup q) \geq n(p) + n(q) - n(p\cap q)
100 \geq 63 + 76 - x
x \geq 39
Now n(p) = 63.
n(p\cap q) \leq n(p)
x \leq 63
So, 39 \leq x \leq 63
Hence, the correct option is (C).

Question:

If sets A and B are defined as A = \left\{(x,y):y= \frac{1}{x}, 0\neq x\in R \right \} B= \left\{(x,y):y= -x, x\in R \right \}, then
(A) A ∩ B = A (B) A ∩ B = B (C) A ∩ B = φ (D) A ∪ B = A

Answer:

The answer is option (c). Given that A = \left\{(x,y):y= \frac{1}{x}, 0\neq x\in R \right \} and B= \left\{(x,y):y= -x, x\in R \right \}
So, y = \frac{1}{x} and y = - x
\frac{1}{x} \neq - x
A\cap B = \phi
Thus, option C is correct.

Question:

If A and B are two sets, then A ∩ (A ∪ B) equals
(A) A (B) B (C) \phi (D) (A ∪ B)

Answer:

The answer is the option (a). Let x\in A\cap (A\cup B)
\begin{aligned} \Rightarrow x\in A&\text{ and }x\in (A\cup B) \\ \Rightarrow x\in A &\text{ and } (x\in A \text{ or } x\in B) \\ \Rightarrow (x\in A &\text{ and } x\in A)\text{ or } (x\in A\text{ and } x\in B \\ \Rightarrow x\in A &\text{ or } x\in A\cap B\end{aligned}
Hence A is correct.

Question:

If A = {1, 3, 5, 7, 9, 11, 13, 15, 17} B = {2, 4, ... , 18} and N the set of natural numbers is the universal set, then A′ ∪ (A ∪ B) ∩ B′) is
(A) φ (B) N (C) A (D) B

Answer:

The answer is the option (b).
Given that A ={1,3,5,7,9,11,13,15,17}
B = {2,4,6………..,18}
U=N={1,2,3,4,5,……..}
\begin{aligned}A'\cup (A\cup B)\cap B' &= A'\cup [(A\cap B')\cup (B\cap B')] \\ & = A'\cup (A\cap B')\cup \phi&[A\cap A' = \phi] \\ &= A'\cup(A\cap B') \\ & = (A'\cup A) \cap (A'\cup B') \\ &=N\cup (A'\cup B')\\& = A'\cup B' \\ & = (A\cap B)' = \phi ' = N\end{aligned}

Question:

Let S = {x | x is a positive multiple of 3 less than 100} P = {x | x is a prime number less than 20}. Then n(S) + n(P) is
(A) 34 (B) 41 (C) 33 (D) 30

Answer:

The answer is the option (b).
Given that: S={x| x is a positive multiple of 3 < 100}
S = {3, 6, 9, 12, 15, 18 …..99}
n(S) = 33
T = { x| x is a prime number < 20}
T = {2, 3, 5, 7, 11, 13, 17, 19}
n(T) = 8
So, n(S) + n(T) = 33+8 =41
Hence, (b) is correct.

Question:

If X and Y are two sets and X′ denotes the complement of X, then X ∩ (X ∪ Y)′ is equal to
(A) X (B) Y (C) φ (D) X ∩ Y

Answer:

The answer is option (c)
Let

\begin{aligned} x \in X\cap (X\cup Y)' \\ x\in X\cap (X'\cap Y') \\ x\in (X\cap X')\cap (X\cap Y')\\x\ x\in \phi \cap (X\cap Y')\\x\in\phi\end{aligned}

Question:

The set \{x\in R: 1 \leq x < 2\} can be written as ______________.

Answer:

The set \{x\in R: 1 \leq x < 2\} can be written as [1,2)

Question:

WhenA = \phi, then number of elements in P(A) is ______________.

Answer:

WhenA = \phi, then number of elements in P(A) is 1
Here A = \phi, n(A) = 0
\begin{aligned} n[P(A)] &= 2^{n(A)} \\ &= 2^0 \\ &= 1\end{aligned}

Question:

If A and B are finite sets such that A ⊂ B, then n (A ∪ B) = ______________.

Answer:

Since, 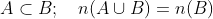A\subset B; \quad n(A\cup B) = n(B)

Question:

If A and B are any two sets, then A – B is equal to

Answer:

3hYgVkSk4n3t8ZnXc6bEbNQC-fAYtr4rwy0HDG6Xme9DYbxfgMi3cvnOFD17IUa7z2TV1mI56nUJjpKDswZK_-2LRlqbUZC2WJb7_uecje4yQm0F7Ja4ZUs9OkMzGInBoDooYS_0V2QooXbY8Q
From the Venn diagram
A - B = A\cap B'

Question:

Power set of the set A = {1, 2} is ______________.

Answer:

\text{Power set of }A = P(A) = \{\{1\}, \{2\}, \{1,2\},\phi\}

Question:

Given the sets A = {1, 3, 5}. B = {2, 4, 6} and C = {0, 2, 4, 6, 8}. Then the universal set of all the three sets A, B and C can be ______________.

Answer:

Given that A = {1,3,5}, B= {2,4,6} and C = {0,2,4,6,8}
Universal set of all given sets is U = {0, 1, 2, 3, 4, 5, 6, 8}

Question:

If U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {1, 2, 3, 5}, B = {2, 4, 6, 7} and C = {2, 3, 4, 8}. Then
(i) (B ∪ C)′ is ______________. (ii)(C – A)′ is ______________.

Answer:

Given that: U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {1, 2, 3, 5}, B ={2, 4, 6, 7} and C = {2, 3, 4, 8}

  1. (B\cup C)' = \{2,3,4,6,7,8\}' = \{1,5,9,10\}

  2. (C-A)' = \{1,2,3,5,6,7,9,10\}

Question:

For all sets A and B, A – (A ∩ B) is equal to ______________.

Answer:

Since A - B = A\cap B'
A - (A\cap B) = A\cap B'

Question:

If A is any set, then A ⊂ A

Answer:

Every set is a subset of itself. Hence, true.

Question:

Given that M = {1, 2, 3, 4, 5, 6, 7, 8, 9} and if B = {1, 2, 3, 4, 5, 6, 7, 8, 9}, then B\not\subset M

Answer:

M = {1, 2, 3, 4, 5, 6, 7, 8, 9}
And B = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Since B and M has same elements
M = B, So, B \not\subset M is false

Question:

The sets {1, 2, 3, 4} and {3, 4, 5, 6} are equal.

Answer:

The two sets do not contain same elements. Hence, false.

Question:

Q \cup Z = Q, where Q is the set of rational numbers and Z is the set of integers.

Answer:

Since every integer is a rational number
\therefore Z\subset Q\Rightarrow Q \cup Z = Q
Hence true

Question:

Let sets R and T be defined as
R = \{x\in Z : x \text{ is divisible by 2}\}
T = \{x\in Z : x \text{ is divisible by 6}\}
Then T ⊂ R

Answer:

R = {………….., -8, -6, -4, -2, 0, 2, 4, 6, 8,…..}
And T= {……., -18, -12, -6, 0 , 6, 12, 18,…….}
Since every element of T is present in R. So, T\subset R
Hence, the statement is true.

Question:

GivenA = \{0,1,2\}, B = \{x\in R:0\leq x \leq 2\}. Then A = B.

Answer:

Here A = { 0, 1, 2} B is a set having all real numbers from 0 to 2.
So, A\neq B
Hence, the given statement is False.


Question:

Match the following sets for all sets A, B and C

  1. ((A' \cup B') - A)' (a) A - B

  2. [B'\cup (B'-A')]' (b) A

  3. (A_B) - (B-C) (c) B

  4. (A-B)\cap(C-B) (d) (A\times B)\cap(C\times B)

  5. A\times (B\cap C) (e) (A\times B) \cup (A\times C)

  6. A\times (B\cup C) (f) (A\cap C)-B


Answer:

(I)
\begin{aligned} ((A' \cup B') - A)' &= [A'\cup B'\cap A]'& [\text{As }A-B = A\cap B'] \\ &= [A\cap B)'\cap A']' \\ &=[(A\cap B)']'\cup(A')' &[\text{As }(A')' =A] \\ &=(A\cup B)\cup A \\ &=A \end{aligned}
(II)
\begin{aligned} {[B'\cup (B'-A')]'} &=[B'\cup (B'\cap A')]' \\ &=(B')'\cap (B'\cap A')'\\ & = B\cap (B\cup A) \\ & = B \end{aligned}

(iii)
\begin{aligned} (A-B)-(B- C) &= (A\cap B')- (B\cap C') \\ & = (A\cap B') \cap (B\cap C')' \\ & = (A\cap B')\cap (B' \cap C) \\ & = [A\cap (B'\cap C)]\cap [B'\cap(B'\cap C)] \\ &=[A\cap (B'\cap C)]\cap B' \\ &= (A\cap B')\cap B' \\ &= (A\cap B')\\ &= A - B\end{aligned}
(iv)
\begin{aligned} (A-B)\cap (C- B) &= (A\cap B')\cap(C\cap B') \\ & = (A\cap C)\cap B' \\ &= (A\cap C)- B\end{aligned}
(v) A\times (B\cap C) = (A\times B)\cap (A\times C)
(vi) A\times (B\cup C) = (A\times B)\cup (A\times C)
So (i) – b , (ii) – c, (iii) – a, (iv) – (f), (v) - (d), (vi) – (e)

Important Notes To Follow While Studying NCERT Exemplar Class 11 Maths Solutions Chapter 1 Sets

Sets are basically defined as a collection of objects belonging to a particular field or are of the same kind in a defined manner and could be differentiated from others for all at the same time or in the same sense.

For example- a group of days in a week will be the same for everyone, so, it is considered a set whereas a group of top ten favourite musicians in the world would be different for everyone as everyone has different choices, so this collection or group is not a set.

NCERT Exemplar Class 11 Maths chapter 1 solutions provided here for the NCERT books are very useful for Board exams as well as the JEE Main exams. Students can use NCERT Exemplar Class 11 Maths solutions chapter 1 PDF download for offline learning.

Main Subtopics of NCERT Exemplar Class 11 Maths Solutions Chapter 1

The topics included in the chapter are mentioned below:

  • 1.1 Introduction
  • 1.2 Sets and their Representations
  • 1.3 The Empty Set
  • 1.4 Finite and Infinite Sets
  • 1.5 Equal Sets
  • 1.6 Subsets
  • 1.6.1 Subsets of a set of real numbers
  • 1.6.2 Intervals as subsets of R
  • 1.7 Power Set
  • 1.8 Universal Set
  • 1.9 Venn Diagrams
  • 1.10 Operations on Sets
  • 1.10.1 Union of sets
  • 1.10.2 Intersection of sets
  • 1.10.3 Difference of sets
  • 1.11 Complement of a Set
  • 1.12 Practical Problems on Union and Intersection of Two Sets

What will the students learn in NCERT Exemplar Class 11 Maths Solutions Chapter 1?

With NCERT Exemplar Class 11 Maths chapter 1 solutions, the students will learn about forming sets through a roaster and set builder method. This will help in various life situations to form combinations or groups of things belonging to the same category or are related to one another with a well-defined purpose. They also have wide application in mathematics for different subjects and are used in every field of mathematics in some or the other way. It also has its application in different programming languages and economic analysis, which will enable students to relate its use to real life. NCERT Exemplar Class 11 Maths solutions chapter 1 will also teach discipline to students through organizing and categorizing different things for better daily needs.

NCERT Solutions for Class 11 Mathematics Chapters

Important Topics To Cover in NCERT Exemplar Class 11 Maths Solutions Chapter 1 Sets

· Class 11 Maths NCERT Exemplar solutions Chapter 1 also provides two different methods for the representation of sets, i.e. roster or tabular form and set builder form both of which use different representations for displaying a set. The roster of the tabular method shows elements in a form, as A = {a, e, w, o, u}, but the same set in set-builder form will be represented as A = {a : a is a vowel in English language} which depicts that the element an of set A is a vowel of English language.

· NCERT Exemplar solutions for class 11 Maths chapter 1 also defines different types of the set such as empty set not having any member elements, finite set, having fixed/countable elements, infinite set, having uncountable member elements, equal sets have identical elements, power set, universal set, and subsets.

· NCERT Exemplar Class 11 Maths solutions chapter 1 also covers Venn diagrams and its application in different operations of the set, including union, intersection, and difference along with their detailed properties.

Check Chapter-Wise NCERT Solutions of Book

NCERT Exemplar Class 11 Solutions

Read more NCERT Solution subject wise -

JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

Also, read NCERT Notes subject wise -

Also Check NCERT Books and NCERT Syllabus here:

Frequently Asked Questions (FAQs)

1. Which topics are covered in this chapter?

The chapter of sets covers everything related to sets like the types, the subsets, the Venn diagrams and practical problems related to sets.

2. Can these solutions be helpful for competitive exams?

Yes, these questions and NCERT Exemplar Class 11 Maths solutions chapter 1 are helpful for those who are preparing for engineering and other entrance exams.

3. How to make the most of these solutions?

These NCERT exemplar Class 11 Maths chapter 1 solutions can be used while practising the questions from the NCERT book. These solutions can also be a reference for checking the answers.

4. How many questions are solved in these solutions?

Our team has solved every exercise question that is present in the main exercise and also the ones in the additional questions. 

Also Read

Articles

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 January,2025

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 January,2025

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Gujarat Board Higher Secondary School Certificate

Late Fee Application Date:13 December,2024 - 22 December,2024

Madhya Pradesh State Open School 10th Examination

Admit Card Date:13 December,2024 - 31 December,2024

View All School Exams
Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
Kerala Class 7 student bitten by snake in classroom; Govt orders probe
Haryana schools to remain shut today in view of ex-CM Chautala's demise
Odisha: 14-year-old student stabs classmate in school; motive unknown
Class 10 student dies by suicide; parents allege harassment from teachers, peers
Winter vacation for Delhi schools from January 1 to 15; DoE issues guidelines for remedial class
Several Delhi schools receive bomb-threat mail, no suspicious items found
CBSE conducts surprise inspections at 29 schools; most violated board’s affiliation by-laws
Back to top