NCERT Solutions for Class 11 Maths Chapter 8 Sequences and Series

Edited By Komal Miglani | Updated on Jun 07, 2025 09:01 AM IST

Imagine you decided to save 10 rupees each day for a new bicycle, then you have 10 rupees on day 1, 20 rupees on day 2, and by the end of the month, you will have nearly 300 rupees. Also, in 1 year, you will have close to 3650 rupees, which is a decent amount for a bicycle. Here, you can notice a pattern in your savings: 10, 20, 30, ...., 300, ...., 3650. In our everyday lives, we can see many patterns where sequences and series play an important role. In the sequences and series chapter of class 11 mathematics, you will learn how some numbers follow a particular order, i.e. a sequence and the sum of their terms, i.e. a series, behaves. The main purpose of this NCERT Solutions for Class 11, sequence and series article is to help students build a clear and strong conceptual foundation.

JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy

Suggested: JEE Main: high scoring chapters | Past 10 year's papers

This Story also Contains

NCERT Solution for Class 11 Maths Chapter 8 Solutions: Download PDF
Sequences And Series Class 11 Solutions: Important Formulae
NCERT Solutions for Class 11 Maths Chapter 8: Exercise Questions
Class 11 Maths NCERT Chapter 8: Extra Question
What Extra Should Students Study Beyond the NCERT for JEE?
NCERT Solutions for Class 11 Maths: Chapter Wise

NCERT Solutions for Class 11 Maths Chapter 8 Sequences and Series

This article on NCERT solutions for class 11 Maths Chapter 8 Sequences and Series offers clear and step-by-step solutions for the exercise problems given in the NCERT book. Careers360 Subject Matter Experts, with years of experience in the field, created these class 11 Sequences and Series solutions. They followed the latest CBSE syllabus, ensuring students effectively grasp the basic concepts. For syllabus, notes, and PDF, refer to this link: NCERT.

NCERT Solution for Class 11 Maths Chapter 8 Solutions: Download PDF

Students who wish to access the Class 11 Maths Chapter 8 NCERT Solutions can click on the link below to download the complete solution in PDF.

Download PDF

Sequences And Series Class 11 Solutions: Important Formulae

Progression: A sequence whose terms follow certain patterns is known as a progression.

Geometric Progression (GP):

A sequence in which the ratio of two consecutive terms is constant is called a geometric progression (GP).

The constant ratio is called the common ratio (r), i.e., $r = \frac{a_{n + 1}}{a_{n}}$ , for all n > 1.

The general term or nth term of GP is $a_{n} = a r^{(n - 1)}$ .

The nth term of a GP from the end: $a_{n} = \frac{1}{r^{n - 1}}$ , where $l$ is the last term.

If a, b, and c are three consecutive terms of a GP, then $b^{2} = a c$ .

Geometric Mean (GM):

If a, G, and b are in a GP, then G is called the geometric mean of a and b and is given by $G = \sqrt{a b}$ .

If a, G1, G2, G3, …, Gn, b are in GP, then G1, G2, G3, …, Gn are in GMs between a and b.

The common ratio r is given as: $r = {(\frac{b}{a})}^{\frac{1}{n + 1}}$ .

The GM of a1, a2, a3,…, an is given by: $GM = {(a_{1} \cdot a_{2} \cdot a_{3} \dots a_{n})}^{\frac{1}{n}}$ .

Product of n GMs is $G_{1} \times G_{2} \times G_{3} \times \dots \times G_{n} = G_{n} = (a b)^{\frac{n}{2}}$ .

Relationship between A.M. and G.M.

$A . M . = \frac{a + b}{2} and G . M . = \sqrt{a b}$
Thus, we have

$\begin{aligned} A . M . - G . M . & = \frac{a + b}{2} - \sqrt{a b} = \frac{a + b - 2 \sqrt{a b}}{2} \\ = \frac{(\sqrt{a} - \sqrt{b})^{2}}{2} \geq 0 \end{aligned}$

Thus, we get the relationship $A . M . \geq G . M .$ always.

NCERT Solutions for Class 11 Maths Chapter 8: Exercise Questions

Sequences and Series class 11 questions and answers: Exercise: 8.1
Page number: 138-139
Total Questions: 14

Question 1: Write the first five terms of each of the sequences in Exercises 1 to 6 whose nth terms are:

$a_{n} = n (n + 2)$

Answer:

Given : $a_{n} = n (n + 2)$

$a_{1} = 1 (1 + 2) = 3$

$a_{2} = 2 (2 + 2) = 8$

$a_{3} = 3 (3 + 2) = 15$

$a_{4} = 4 (4 + 2) = 24$

$a_{5} = 5 (5 + 2) = 35$

Therefore, the required number of terms = 3, 8, 15, 24, 35

Question 2: Write the first five terms of each of the sequences in Exercises 1 to 6 whose terms are:

$a_{n} = \frac{n}{n + 1}$

Answer:

Given : $a_{n} = \frac{n}{n + 1}$

$a_{1} = \frac{1}{1 + 1} = \frac{1}{2}$

$a_{2} = \frac{2}{2 + 1} = \frac{2}{3}$

$a_{3} = \frac{3}{3 + 1} = \frac{3}{4}$

$a_{4} = \frac{4}{4 + 1} = \frac{4}{5}$

$a_{5} = \frac{5}{5 + 1} = \frac{5}{6}$

Therefore, the required number of terms $\frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}$

Question 3: Write the first five terms of each of the sequences in Exercises 1 to 6 whose terms are:

$a_{n} = 2^{n}$

Answer:

Given : $a_{n} = 2^{n}$

$a_{1} = 2^{1} = 2$

$a_{2} = 2^{2} = 4$

$a_{3} = 2^{3} = 8$

$a_{4} = 2^{4} = 16$

$a_{5} = 2^{5} = 32$

Therefore, the required number of terms $= 2, 4, 8, 16, 32.$

Question 4: Write the first five terms of each of the sequences in Exercises 1 to 6 whose nth terms are:

$a_{n} = \frac{2 n - 3}{6}$

Answer:

Given : $a_{n} = \frac{2 n - 3}{6}$

$a_{1} = \frac{2 \times 1 - 3}{6} = \frac{- 1}{6}$

$a_{2} = \frac{2 \times 2 - 3}{6} = \frac{1}{6}$

$a_{3} = \frac{2 \times 3 - 3}{6} = \frac{3}{6} = \frac{1}{2}$

$a_{4} = \frac{2 \times 4 - 3}{6} = \frac{5}{6}$

$a_{5} = \frac{2 \times 5 - 3}{6} = \frac{7}{6}$

Therefore, the required number of terms $= \frac{- 1}{6}, \frac{1}{6}, \frac{1}{2}, \frac{5}{6}, \frac{7}{6}$

Question 5: Write the first five terms of each of the sequences in Exercises 1 to 6 whose nth terms are:

$a_{n} = (- 1)^{n - 1} 5^{n + 1}$

Answer:

Given : $a_{n} = (- 1)^{n - 1} 5^{n + 1}$

$a_{1} = (- 1)^{1 - 1} 5^{1 + 1} = (- 1)^{0} {.5}^{2} = 25$

$a_{2} = (- 1)^{2 - 1} 5^{2 + 1} = (- 1)^{1} {.5}^{3} = - 125$

$a_{3} = (- 1)^{3 - 1} 5^{3 + 1} = (- 1)^{2} {.5}^{4} = 625$

$a_{4} = (- 1)^{4 - 1} 5^{4 + 1} = (- 1)^{3} {.5}^{5} = - 3125$

$a_{5} = (- 1)^{5 - 1} 5^{5 + 1} = (- 1)^{4} {.5}^{6} = 15625$

Therefore, the required number of terms $= 25, - 125, 625, - 3125, 15625$

Question 6: Write the first five terms of each of the sequences in Exercises 1 to 6 whose nth terms are:

$a_{n} = n \frac{n^{2} + 5}{4}$

Answer:

Given : $a_{n} = n \frac{n^{2} + 5}{4}$

$a_{1} = 1. \frac{1^{2} + 5}{4} = \frac{6}{4} = \frac{3}{2}$

$a_{2} = 2. \frac{2^{2} + 5}{4} = \frac{18}{4} = \frac{9}{2}$

$a_{3} = 3. \frac{3^{2} + 5}{4} = \frac{42}{4} = \frac{21}{2}$

$a_{4} = 4. \frac{4^{2} + 5}{4} = \frac{84}{4} = 21$

$a_{5} = 5. \frac{5^{2} + 5}{4} = \frac{150}{4} = \frac{75}{2}$

Therefore, the required number of terms $= \frac{3}{2}, \frac{9}{2}, \frac{21}{2}, 21, \frac{75}{2}$

Question 7: Find the indicated terms in each of the sequences in Exercises 7 to 10 whose nth terms are:

$a_{n} = 4 n - 3; a_{17}, a_{24}$

Answer:

$a_{n} = 4 n - 3$

Put $n = 17,$

$a_{17} = 4 \times 17 - 3 = 68 - 3 = 65$

Put n = 24,

$a_{24} = 4 \times 24 - 3 = 96 - 3 = 93$

Hence, we have $a_{17} = 65$ and $a_{24} = 93.$

Question 8: Find the indicated terms in each of the sequences in Exercises 7 to 10 whose nth terms are:

$a_{n} = \frac{n^{2}}{2^{n}}; a_{7}$

Answer:

Given : $a_{n} = \frac{n^{2}}{2^{n}}$

Put n=7,

$a_{7} = \frac{7^{2}}{2^{7}} = \frac{49}{128}$

Hence, we have $a_{7} = \frac{49}{128}$

Question 9: Find the indicated terms in each of the sequences in Exercises 7 to 10 whose nth terms are:

$a_{n} = (- 1)^{n - 1} n^{3}, a_{9}$

Answer:

Given : $a_{n} = (- 1)^{n - 1} n^{3}$

Put n = 9,

$a_{9} = (- 1)^{9 - 1} 9^{3} = (1) . (729) = 729$

The value of $a_{9} = 729$

Question 10: Find the indicated terms in each of the sequences in Exercises 7 to 10 whose nth terms are:

$a_{n} = \frac{n (n - 2)}{n + 3}; a_{20}$

Answer:

Given : $a_{n} = \frac{n (n - 2)}{n + 3}$

Put n = 20,

$a_{20} = \frac{20 (20 - 2)}{20 + 3} = \frac{360}{23}$

Hence, value of $a_{20} = \frac{360}{23}$

Question 11: Write the first five terms of each of the sequences in Exercises 11 to 13 and obtain the corresponding series:

$a_{1} = 3, a_{n} = 3 a_{n - 1} + 2 f o r a l l n > 1$

Answer:

Given : $a_{1} = 3, a_{n} = 3 a_{n - 1} + 2 f o r a l l n > 1$

$a_{2} = 3 a_{2 - 1} + 2 = 3 a_{1} + 2 = 3 (3) + 2 = 11$

$a_{3} = 3 a_{3 - 1} + 2 = 3 a_{2} + 2 = 3 (11) + 2 = 35$

$a_{4} = 3 a_{4 - 1} + 2 = 3 a_{3} + 2 = 3 (35) + 2 = 107$

$a_{5} = 3 a_{5 - 1} + 2 = 3 a_{4} + 2 = 3 (107) + 2 = 323$

Hence, the five terms of the series are $3, 11, 35, 107, 323$

Series $= 3 + 11 + 35 + 107 + 323 + . . . . . . . . . . . . . . .$

Question 12: Write the first five terms of each of the sequences in Exercises 11 to 13 and obtain the corresponding series:

$a_{1} = - 1, a_{n} = \frac{a_{n - 1}}{n}, n \geq 2$

Answer:

Given : $a_{1} = - 1, a_{n} = \frac{a_{n - 1}}{n}, n \geq 2$

$a_{2} = \frac{a_{2 - 1}}{2} = \frac{a_{1}}{2} = \frac{- 1}{2}$

$a_{3} = \frac{a_{3 - 1}}{3} = \frac{a_{2}}{3} = \frac{- 1}{6}$

$a_{4} = \frac{a_{4 - 1}}{4} = \frac{a_{3}}{4} = \frac{- 1}{24}$

$a_{5} = \frac{a_{5 - 1}}{5} = \frac{a_{4}}{5} = \frac{- 1}{120}$

Hence, five terms of series are $- 1, \frac{- 1}{2}, \frac{- 1}{- 6}, \frac{- 1}{24}, \frac{- 1}{120}$

Series

$= - 1 + \frac{- 1}{2} + \frac{- 1}{- 6} + \frac{- 1}{24} + \frac{- 1}{120} . . . . . . . . . . . . . . . . . . . . . . . . .$

Question 13: Write the first five terms of each of the sequences in Exercises 11 to 13 and obtain the corresponding series: $a_{1} = a_{2} = 2, a_{n} = a_{n - 1} - 1, n > 2$

Answer:

Given : $a_{1} = a_{2} = 2, a_{n} = a_{n - 1} - 1, n > 2$

$a_{3} = a_{3 - 1} - 1 = a_{2} - 1 = 2 - 1 = 1$

$a_{4} = a_{4 - 1} - 1 = a_{3} - 1 = 1 - 1 = 0$

$a_{5} = a_{5 - 1} - 1 = a_{4} - 1 = 0 - 1 = - 1$

Hence, the five terms of the series are $2, 2, 1, 0, - 1$

Series $= 2 + 2 + 1 + 0 + (- 1) + . . . . . . . . . . . . . . . . . .$

Question 14: The Fibonacci sequence is defined by $1 = a_{1} = a_{2} a n d a_{n} = a_{n - 1} + a_{n - 2}, n > 2$

Find $\frac{a_{n + 1}}{a_{n}}$ , for n = 1, 2, 3, 4, 5

Answer:

Given: The Fibonacci sequence is defined by $1 = a_{1} = a_{2} a n d a_{n} = a_{n - 1} + a_{n - 2}, n > 2$

$a_{3} = a_{3 - 1} + a_{3 - 2} = a_{2} + a_{1} = 1 + 1 = 2$

$a_{4} = a_{4 - 1} + a_{4 - 2} = a_{3} + a_{2} = 2 + 1 = 3$

$a_{5} = a_{5 - 1} + a_{5 - 2} = a_{4} + a_{3} = 3 + 2 = 5$

$a_{6} = a_{6 - 1} + a_{6 - 2} = a_{5} + a_{4} = 5 + 3 = 8$

$F o r n = 1, \frac{a_{n + 1}}{a_{n}} = \frac{a_{1 + 1}}{a_{1}} = \frac{a_{2}}{a_{1}} = \frac{1}{1} = 1$

$F o r n = 2, \frac{a_{n + 1}}{a_{n}} = \frac{a_{2 + 1}}{a_{2}} = \frac{a_{3}}{a_{2}} = \frac{2}{1} = 2$

$F o r n = 3, \frac{a_{n + 1}}{a_{n}} = \frac{a_{3 + 1}}{a_{3}} = \frac{a_{4}}{a_{3}} = \frac{3}{2}$

$F o r n = 4, \frac{a_{n + 1}}{a_{n}} = \frac{a_{4 + 1}}{a_{4}} = \frac{a_{5}}{a_{4}} = \frac{5}{3}$

$F o r n = 5, \frac{a_{n + 1}}{a_{n}} = \frac{a_{5 + 1}}{a_{5}} = \frac{a_{6}}{a_{5}} = \frac{8}{5}$

Sequences and Series class 11 questions and answers: Exercise: 8.2
Page number: 145-147
Total Questions: 32

Question 1: Find the $20^{t h}$ and $n^{t h}$ terms of the G.P. $\frac{5}{2}, \frac{5}{4}, \frac{5}{8}, . . . .$

Answer:

G.P :

$\frac{5}{2}, \frac{5}{4}, \frac{5}{8}, . . . .$

first term = a

$a = \frac{5}{2}$

common ratio = r

$r = \frac{\frac{5}{4}}{\frac{5}{2}} = \frac{1}{2}$

$a_{n} = a . r^{n - 1}$

$\Rightarrow$ $a_{20} = \frac{5}{2} . (\frac{1}{2})^{20 - 1}$

$\Rightarrow$ $a_{20} = \frac{5}{2} . (\frac{1}{2^{19}})$

$\Rightarrow$ $a_{20} = \frac{5}{2^{20}}$

$a_{n} = a . r^{n - 1}$

$\Rightarrow$ $a_{n} = \frac{5}{2} . {(\frac{1}{2})}^{n - 1}$

$\Rightarrow$ $a_{n} = \frac{5}{2} . \frac{1}{2^{n - 1}}$

$\Rightarrow$ $a_{n} = \frac{5}{2^{n}}$ the nth term of G.P

Question 2: Find the $12^{t h}$ term of a G.P. whose $8^{t h}$ term is 192 and the common ratio is 2.

Answer:

First term = a

common ratio = r = 2

$8^{t h}$ term is 192

$a_{n} = a . r^{n - 1}$

$\Rightarrow$ $a_{8} = a . (2)^{8 - 1}$

$\Rightarrow$ $192 = a . (2)^{7}$

$\Rightarrow$ $a = \frac{2^{6} .3}{2^{7}}$

$\Rightarrow$ $a = \frac{3}{2}$

$a_{n} = a . r^{n - 1}$

$\Rightarrow$ $a_{12} = \frac{3}{2} . (2)^{12 - 1}$

$\Rightarrow$ $a_{12} = \frac{3}{2} . (2)^{11}$

$\Rightarrow$ $a_{12} = 3. (2)^{10}$

$\Rightarrow$ $a_{12} = 3072$ is the $12^{t h}$ term of a G.P.

Question 3: The $5^{t h}, 8^{t h} a n d n d 11^{t h}$ terms of a G.P. are p, q, and s, respectively. Show that $q^{2} = p s$

Answer:

To prove : $q^{2} = p s$

Let first term and common ratio = r

$a_{5} = a . r^{4} = p . . . . . . . . . . . . . . . . . . (1)$

$a_{8} = a . r^{7} = q . . . . . . . . . . . . . . . . . . (2)$

$a_{11} = a . r^{10} = s . . . . . . . . . . . . . . . . . . (3)$

Dividing equation 2 by 1, we have

$\frac{a . r^{7}}{a . r^{4}} = \frac{q}{p}$

$\Rightarrow r^{3} = \frac{q}{p}$

Dividing equation 3 by 2, we have

$\frac{a . r^{10}}{a . r^{7}} = \frac{s}{q}$

$\Rightarrow r^{3} = \frac{s}{q}$

Equating values of $r^{3}$ , we have

$\frac{q}{p} = \frac{s}{q}$

$\Rightarrow q^{2} = p s$

Hence proved.

Question 4: The $4^{t h}$ term of a G.P. is the square of its second term, and the first term is -3. Determine its $7^{t h}$ term.

Answer:

First term =a= -3

$4^{t h}$ term of a G.P. is the square of its second term

$\Rightarrow a_{4} = (a_{2})^{2}$

$\Rightarrow a . r^{4 - 1} = (a . r^{2 - 1})^{2}$

$\Rightarrow a . r^{3} = a^{2} . r^{2}$

$\Rightarrow r = a = - 3$

$a_{7} = a . r^{7 - 1}$

$\Rightarrow a_{7} = (- 3) . (- 3)^{6}$

$\Rightarrow a_{7} = (- 3)^{7} = - 2187$

Thus, the seventh term is -2187.

Question 5: Which term of the following sequences:

(a) $2, 2 \sqrt{2}, 4 ., . . . . i s 128 ?$

(b) Which term of the following sequences: $\sqrt{3}, 3, 3 \sqrt{3}, . . . i s 729 ?$

Answer:

(a) Given : $G P = 2, 2 \sqrt{2}, 4 ., . . . . . . . . . . . .$

$a = 2 a n d r = \frac{2 \sqrt{2}}{2} = \sqrt{2}$

nth term is given as 128.

$a_{n} = a . r^{n - 1}$

$\Rightarrow 128 = 2. (\sqrt{2})^{n - 1}$

$\Rightarrow 64 = (\sqrt{2})^{n - 1}$

$\Rightarrow 2^{6} = (\sqrt{2})^{n - 1}$

$\Rightarrow {\sqrt{2}}^{12} = (\sqrt{2})^{n - 1}$

$\Rightarrow n - 1 = 12$

$\Rightarrow n = 12 + 1 = 13$

The 13th term is 128.

(b) Given : $G P = \sqrt{3}, 3, 3 \sqrt{3}, . . . . . . . .$

$a = \sqrt{3} a n d r = \frac{3}{\sqrt{3}} = \sqrt{3}$

n The term is given as 729.

$a_{n} = a . r^{n - 1}$

$\Rightarrow 729 = \sqrt{3} . (\sqrt{3})^{n - 1}$

$\Rightarrow 729 = (\sqrt{3})^{n}$

$\Rightarrow (\sqrt{3})^{12} = (\sqrt{3})^{n}$

$\Rightarrow n = 12$

The 12th term is 729.

$a = \frac{1}{3} a n d r = \frac{\frac{1}{9}}{\frac{1}{3}} = \frac{1}{3}$

nth term is given as $\frac{1}{19683}$

$a_{n} = a . r^{n - 1}$

$\Rightarrow \frac{1}{19683} = \frac{1}{3} . (\frac{1}{3})^{n - 1}$

$\Rightarrow \frac{1}{19683} = \frac{1}{3^{n}}$

$\Rightarrow \frac{1}{3^{9}} = \frac{1}{3^{n}}$

$\Rightarrow n = 9$

Thus, n = 9.

Question 6: For what values of x, the numbers $- \frac{2}{7}, x, - \frac{7}{2}$ are in G.P.?

Answer:

$G P = - \frac{2}{7}, x, - \frac{7}{2}$

Common ratio = r.

$r = \frac{x}{\frac{- 2}{7}} = \frac{\frac{- 7}{2}}{x}$

$\Rightarrow x^{2} = 1$

$\Rightarrow x = \pm 1$

Thus, for $x = \pm 1$ , the numbers will be in GP.

Question 7: Find the sum of the indicated number of terms in each of the geometric progressions in 0.15, 0.015, 0.0015, ... 20 terms.

Answer:

Geometric progressions are 0.15, 0.015, 0.0015, ... .....

a = 0.15 , r = 0.1 , n = 20

$S_{n} = \frac{a (1 - r^{n})}{1 - r}$

$\Rightarrow$ $S_{20} = \frac{0.15 (1 - (0.1)^{20})}{1 - 0.1}$

$\Rightarrow$ $S_{20} = \frac{0.15 (1 - (0.1)^{20})}{0.9}$

$\Rightarrow$ $S_{20} = \frac{0.15}{0.9} (1 - (0.1)^{20})$

$\Rightarrow$ $S_{20} = \frac{15}{90} (1 - (0.1)^{20})$

$\Rightarrow$ $S_{20} = \frac{1}{6} (1 - {0.1}^{20})$

Question 8: Find the sum to the indicated number of terms in each of the geometric progressions in $\sqrt{7}, \sqrt{21}, 3 \sqrt{7}, . . . . n t e r m s$

Answer:

$G P = \sqrt{7}, \sqrt{21}, 3 \sqrt{7}, . . . . . . . . . . . . . . .$

$a = \sqrt{7} a n d r = \frac{\sqrt{21}}{\sqrt{7}} = \sqrt{3}$

$S_{n} = \frac{a (1 - r^{n})}{1 - r}$

$\Rightarrow$ $S_{n} = \frac{\sqrt{7} (1 - {\sqrt{3}}^{n})}{1 - \sqrt{3}}$

$\Rightarrow$ $S_{n} = \frac{\sqrt{7} (1 - {\sqrt{3}}^{n})}{1 - \sqrt{3}} \times \frac{1 + \sqrt{3}}{1 + \sqrt{3}}$

$\Rightarrow$ $S_{n} = \frac{\sqrt{7} (1 - {\sqrt{3}}^{n})}{1 - 3} (1 + \sqrt{3})$

$\Rightarrow$ $S_{n} = \frac{\sqrt{7} (1 - {\sqrt{3}}^{n})}{- 2} (1 + \sqrt{3})$

$\Rightarrow$ $S_{n} = \frac{\sqrt{7} (1 + \sqrt{3})}{2} ({\sqrt{3}}^{n} - 1)$

Question 9: Find the sum to the indicated number of terms in each of the geometric progressions in $- a, a^{,} - a^{3}, . . . n t e r m s (i f a \neq - 1)$

Answer:

The sum to the indicated number of terms in each of the geometric progressions is:

$G P = 1, - a, a^{2}, - a^{3}, . . . . . . . . . . . . .$

$a = 1 a n d r = - a$

$S_{n} = \frac{a (1 - r^{n})}{1 - r}$

$\Rightarrow$ $S_{n} = \frac{1 (1 - (- a)^{n})}{1 - (- a)}$

$\Rightarrow$ $S_{n} = \frac{1 (1 - (- a)^{n})}{1 + a}$

$\Rightarrow$ $S_{n} = \frac{1 - (- a)^{n}}{1 + a}$

Question 10: Find the sum to the indicated number of terms in each of the geometric progressions in $x^{3}, x^{5}, x^{7} . . . n t e r m s (i f x \neq \pm 1)$

Answer:

$G P = x^{3}, x^{5}, x^{7} . . . . . . . . . . . . . . . . . . . . .$

$a = x^{3} a n d r = \frac{x^{5}}{x^{3}} = x^{2}$

$S_{n} = \frac{a (1 - r^{n})}{1 - r}$

$\Rightarrow$ $S_{n} = \frac{x^{3} (1 - (x^{2})^{n})}{1 - x^{2}}$

Question 11: Evaluate $\sum_{k = 1}^{11} (2 + 3^{k})$

Answer:

Given :

$\sum_{k = 1}^{11} (2 + 3^{k})$

$\Rightarrow$ $\sum_{k = 1}^{11} (2 + 3^{k}) = \sum_{k = 1}^{11} 2 + \sum_{k = 1}^{11} 3^{k}$

$= 22 + \sum_{k = 1}^{11} 3^{k} . . . . . . . . . . . . . . . (1)$

$\Rightarrow$ $\sum_{k = 1}^{11} 3^{k} = 3^{1} + 3^{2} + 3^{3} + . . . . . . . . . . . . . . . . . . . {.3}^{11}$

These terms form GP with a = 3 and r = 3.

$S_{n} = \frac{a (1 - r^{n})}{1 - r}$

$\Rightarrow$ $S_{n} = \frac{3 (1 - 3^{11})}{1 - 3}$

$\Rightarrow$ $S_{n} = \frac{3 (1 - 3^{11})}{- 2}$

$\Rightarrow$ $S_{n} = \frac{3 (3^{11} - 1)}{2}$ $= \sum_{k = 1}^{11} 3^{k}$

$\Rightarrow$ $\sum_{k = 1}^{11} (2 + 3^{k})$ $= 22 + \frac{3 (3^{11} - 1)}{2}$

Question 12: The sum of the first three terms of a G.P. is $\frac{39}{10}$ and their product is 1. Find the common ratio and the terms.

Answer:

Given: The sum of the first three terms of a G.P. is $\frac{39}{10}$ and their product is 1.

Let three terms be $\frac{a}{r}, a, a r$ .

$S_{n} = \frac{a (1 - r^{n})}{1 - r}$

$S_{3} = \frac{a (1 - r^{3})}{1 - r} = \frac{39}{10}$

$\frac{a}{r} + a + a r = \frac{39}{10} . . . . . . . . .1$

The product of 3 terms is 1.

$\frac{a}{r} \times a \times a r = 1$

$\Rightarrow a^{3} = 1$

$\Rightarrow a = 1$

Put the value of an in equation 1,

$\frac{1}{r} + 1 + r = \frac{39}{10}$

$10 (1 + r + r^{2}) = 39 (r)$

$\Rightarrow 10 r^{2} - 29 r + 10 = 0$

$\Rightarrow 10 r^{2} - 25 r - 4 r + 10 = 0$

$\Rightarrow 5 r (2 r - 5) - 2 (2 r - 5) = 0$

$\Rightarrow (2 r - 5) (5 r - 2) = 0$

$\Rightarrow r = \frac{5}{2}, r = \frac{2}{5}$

The three terms of AP are $\frac{5}{2}, 1, \frac{2}{5}$ .

Question 13: How many terms of G.P. $3, 3 ^ 2 3 ^ 3 … are needed to give the sum 120?

Answer:

G.P.= $3, 3^{2}, 3^{3}$ , …............

Sum = 120

These terms are GP with a = 3 and r = 3.

$S_{n} = \frac{a (1 - r^{n})}{1 - r}$

$\Rightarrow$ $120 = \frac{3 (1 - 3^{n})}{1 - 3}$

$\Rightarrow$ $120 \times \frac{- 2}{3} = (1 - 3^{n})$

$\Rightarrow$ $- 80 = (1 - 3^{n})$

$\Rightarrow 3^{n} = 1 + 80 = 81$

$\Rightarrow 3^{n} = 81$

$\Rightarrow 3^{n} = 3^{4}$

$\Rightarrow n = 4$

Hence, we have a value of n as 4 to get a sum of 120.

Question 14: The sum of the first three terms of a G.P. is 16 and the sum of the next three terms is 128. Determine the first term, the common ratio, and the sum to n terms of the G.P.

Answer:

Let GP be $a, a r, a r^{2}, a r^{3}, a r^{4}, a r^{5}, a r^{6} . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .$

Given: The sum of the first three terms of a G.P. is 16

$a + a r + a r^{2} = 16$

$\Rightarrow a (1 + r + r^{2}) = 16. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (1)$

Given: the sum of the next three terms is 128.

$a r^{3} + a r^{4} + a r^{5} = 128$

$\Rightarrow a r^{3} (1 + r + r^{2}) = 128. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (2)$

Dividing equation (2) by (1), we have

$\Rightarrow \frac{a r^{3} (1 + r + r^{2})}{a (1 + r + r^{2})} = \frac{128}{16}$

$\Rightarrow r^{3} = 8$

$\Rightarrow r^{3} = 2^{3}$

$\Rightarrow r = 2$

Putting the value of r =2 in equation 1, we have

$\Rightarrow a (1 + 2 + 2^{2}) = 16$

$\Rightarrow a (7) = 16$

$\Rightarrow a = \frac{16}{7}$

$S_{n} = \frac{a (1 - r^{n})}{1 - r}$

$S_{n} = \frac{\frac{16}{7} (1 - 2^{n})}{1 - 2}$

$S_{n} = \frac{16}{7} (2^{n} - 1)$

Question 15: Given a G.P. with a = 729 and $7^{t h}$ term 64, determine $s_{7}$

Answer:

Given a G.P. with a = 729 and $7^{t h}$ term 64.

$a_{n} = a . r^{n - 1}$

$\Rightarrow 64 = 729. r^{7 - 1}$

$\Rightarrow r^{6} = \frac{64}{729}$

$\Rightarrow r^{6} = {(\frac{2}{3})}^{6}$

$\Rightarrow r = \frac{2}{3}$

$S_{n} = \frac{a (1 - r^{n})}{1 - r}$

$S_{7} = \frac{729 (1 - {(\frac{2}{3})}^{7})}{1 - \frac{2}{3}}$

$S_{7} = \frac{729 (1 - {(\frac{2}{3})}^{7})}{\frac{1}{3}}$

$S_{7} = 3 \times 729 (\frac{3^{7} - 2^{7}}{3^{7}})$

$S_{7} = (3^{7} - 2^{7})$

$S_{7} = 2187 - 128$

$S_{7} = 2059$

Question 16: Find a G.P. for which the sum of the first two terms is – 4 and the fifth term is 4 times the third term

Answer:

Given the sum of the first two terms is – 4 and the fifth term is 4 times the third term

Let the first term be a and the common ratio be r

$a_{5} = 4. a_{3}$

$\Rightarrow a . r^{5 - 1} = 4. a . r^{3 - 1}$

$\Rightarrow a . r^{4} = 4. a . r^{2}$

$\Rightarrow r^{2} = 4$

$\Rightarrow r = \pm 2$

If r = 2, then

$S_{n} = \frac{a (1 - r^{n})}{1 - r}$

$\Rightarrow \frac{a (1 - 2^{2})}{1 - 2} = - 4$

$\Rightarrow \frac{a (1 - 4)}{- 1} = - 4$

$\Rightarrow a (- 3) = 4$

$\Rightarrow a = \frac{- 4}{3}$

If r = - 2, then

$S_{n} = \frac{a (1 - r^{n})}{1 - r}$

$\Rightarrow \frac{a (1 - (- 2)^{2})}{1 - (- 2)} = - 4$

$\Rightarrow \frac{a (1 - 4)}{3} = - 4$

$\Rightarrow a (- 3) = - 12$

$\Rightarrow a = \frac{- 12}{- 3} = 4$

Thus, required GP is $\frac{- 4}{3}, \frac{- 8}{3}, \frac{- 16}{3}, . . . . . . . . .$ or $4, - 8, - 16, - 32, . . . . . . . . . .$ .

Question 17: If the $4^{t h}, 10^{t h}, 16^{t h}$ terms of a G.P. are x, y and z, respectively. Prove that x,y, and z are in G.P.

Answer:

Let x,y, and z be in G.P.

Let first term and common ratio = r

$a_{4} = a . r^{3} = x . . . . . . . . . . . . . . . . . . (1)$

$a_{10} = a . r^{9} = y . . . . . . . . . . . . . . . . . . (2)$

$a_{16} = a . r^{15} = z . . . . . . . . . . . . . . . . . . (3)$

Dividing equation 2 by 1, we have

$\frac{a . r^{9}}{a . r^{3}} = \frac{y}{x}$

$\Rightarrow r^{4} = \frac{y}{x}$

Dividing equation 3 by 2, we have

$\frac{a . r^{15}}{a . r^{9}} = \frac{z}{y}$

$\Rightarrow r^{4} = \frac{z}{y}$

Equating values of $r^{4}$ , we have

$\frac{y}{x} = \frac{z}{y}$

Thus, x, y, z are in GP.

Question 18: Find the sum to n terms of the sequence, 8, 88, 888, 8888….

Answer:

8, 88, 888, 8888… is not a GP.

It can be changed in GP by writing terms such s

$\Rightarrow$ $S_{n} = 8 + 88 + 888 + 8888 + . . . . . . . . . . . . .$ to n terms

$\Rightarrow$ $S_{n} = \frac{8}{9} [9 + 99 + 999 + 9999 + . . . . . . . . . . . . . . . .]$

$\Rightarrow$ $S_{n} = \frac{8}{9} [(10 - 1) + (10^{2} - 1) + (10^{3} - 1) + (10^{4} - 1) + . . . . . . . . . . . . . . . .]$

$\Rightarrow$ $S_{n} = \frac{8}{9} [(10 + 10^{2} + 10^{3} + . . . . . . . .) - (1 + 1 + 1. . . . . . . . . . . . . . . . . . . . .)]$

$\Rightarrow$ $S_{n} = \frac{8}{9} [\frac{10 (10^{n} - 1)}{10 - 1} - (n)]$

$\Rightarrow$ $S_{n} = \frac{8}{9} [\frac{10 (10^{n} - 1)}{9} - (n)]$

$\Rightarrow$ $S_{n} = \frac{80}{81} (10^{n} - 1) - \frac{8 n}{9}$

Question 19: Find the sum of the products of the corresponding terms of the sequences 2, 4, 8, 16, 32 and 128, 32, 8, 2,1/2

Answer:

$R e q u i r e d s u m = 2 \times 128 + 4 \times 32 + 8 \times 8 + 16 \times 2 + 32 \times \frac{1}{2}$

$R e q u i r e d s u m = 64 [4 + 2 + 1 + \frac{1}{2} + \frac{1}{2^{2}}]$

Here, $4, 2, 1, \frac{1}{2}, \frac{1}{2^{2}}$ is a GP.

first term = a = 4

common ratio =r

$r = \frac{1}{2}$

$S_{n} = \frac{a (1 - r^{n})}{1 - r}$

$\Rightarrow$ $S_{5} = \frac{4 (1 - {(\frac{1}{2})}^{5})}{1 - \frac{1}{2}}$

$\Rightarrow$ $S_{5} = \frac{4 (1 - {(\frac{1}{2})}^{5})}{\frac{1}{2}}$

$\Rightarrow$ $S_{5} = 8 (1 - (\frac{1}{32}))$

$\Rightarrow$ $S_{5} = 8 (\frac{31}{32})$

$\Rightarrow$ $S_{5} = \frac{31}{4}$

$R e q u i r e d s u m = 64 [\frac{31}{4}]$

$R e q u i r e d s u m = 16 \times 31 = 496$

Question 20: Show that the products of the corresponding terms of the sequences $a, a r, a r^{,} . . . a r^{n - 1} a n d A, A R, A R^{2} . . . . A R^{n - 1}$ form a G.P, and find the common ratio.

Answer:

To prove : $a A, a r A R, a r^{2} A R^{2}, . . . . . . . . . . . . . . . . . . .$ is a GP.

$\frac{s e c o n d t e r m}{f i r s t t e r m} = \frac{a r A R}{a A} = r R$

$\frac{t h i r d t e r m}{s e c o n d t e r m} = \frac{a r^{2} A R^{2}}{a r A R} = r R$

Thus, the above sequence is a GP with a common ratio of rR.

Question 21: Find four numbers forming a geometric progression in which the third term is greater than the first term by 9, and the second term is greater than the $4^{t h}$ by 18.

Answer:

Let the first term be a and the common ratio be r.

$a_{1} = a, a_{2} = a r, a_{3} = a r^{2}, a_{4} = a r^{3}$

Given: the third term is greater than the first term by 9, and the second term is greater than the $4^{t h}$ by 18.

$a_{3} = a_{1} + 9$

$\Rightarrow a r^{2} = a + 9$

$\Rightarrow a (r^{2} - 1) = 9. . . . . . . . . . . . . . . . .1$

$a_{2} = a_{4} + 18$

$\Rightarrow a r = a r^{3} + 18$

$\Rightarrow a r (1 - r^{2}) = 18. . . . . . . . . . . . . . . . . . . . . .2$

By dividing equation 2 by 1 we get

$\frac{a r (1 - r^{2})}{- a (1 - r^{2})} = \frac{18}{9}$

$\Rightarrow r = - 2$

Putting the value of r, we get

$4 a = a + 9$

$\Rightarrow 4 a - a = 9$

$\Rightarrow 3 a = 9$

$\Rightarrow a = 3$

Thus, four terms of GP are $3, - 6, 12, - 24.$

Question 22: If the $p^{t h} q^{t h}, r^{t h}$ terms of a G.P. are a, b and c, respectively. Prove that $a^{q - r} b^{r - p} C^{p - q} = 1$

Answer:

To prove : $a^{q - r} b^{r - p} C^{p - q} = 1$

Let A be the first term and R be the common ratio.

According to the given information, we have

$a_{p} = A . R^{p - 1} = a$

$a_{q} = A . R^{q - 1} = b$

$a_{r} = A . R^{r - 1} = c$

L.H.S : $a^{q - r} b^{r - p} C^{p - q}$

$\Rightarrow$ $A^{q - r} . R^{(q - r) (p - 1)} . A^{r - p} . R^{(r - p) (q - 1)} . A^{p - q} . R^{(p - q) (r - 1)}$

$\Rightarrow$ $A^{q - r + r - p + p - q} . R^{(q p - r p - q + r) + (r q - p q + p - r) + (p r - p - q r + q)}$

$\Rightarrow$ $A^{0} . R^{0} = 1$ =RHS

Thus, LHS = RHS.

Hence proved.

Question 23: If the first and the nth terms of a G.P. are a and b, respectively, and if P is the product of n terms, prove that $P^2 = ( ab)^n.

Answer:

Given First term =a and n th term = b.

Common ratio = r.

To prove : $P^{2} = (a b)^{n}$

Then , $G P = a, a r, a r^{2}, a r^{3}, a r^{4}, . . . . . . . . . . . . . . . . . . . . . . . . . .$

$a_{n} = a . r^{n - 1} = b . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1$

P = product of n terms

$\Rightarrow$ $P = (a) . (a r) . (a r^{2}) . (a r^{3}) . . . . . . . . . . . . . . (a r^{n - 1})$

$\Rightarrow$ $P = (a . a . a . . . . . . . . . . . . . . . a) ((1) . (r) . (r^{2}) . (r^{3}) . . . . . . . . . . . . . . (r^{n - 1}))$

$\Rightarrow$ $P = (a^{n}) (r^{1 + 2 + . . . . . . . . . (n - 1)}) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2$

Here, $1 + 2 + . . . . . . . . . (n - 1)$ is aananP.

$∴ s u m = \frac{n}{2} [2 a + (n - 1) d]$

$\Rightarrow$ $\frac{n - 1}{2} [2 (1) + (n - 1 - 1) 1]$

$\Rightarrow$ $\frac{n - 1}{2} [2 + n - 2]$

$\Rightarrow$ $\frac{n - 1}{2} [n]$

$\Rightarrow$ $\frac{n (n - 1)}{2}$

Put in equation (2),

$P = (a^{n}) (r^{\frac{n (n - 1)}{2}})$

$\Rightarrow$ $P^{2} = (a^{2 n}) (r^{n (n - 1)})$

$\Rightarrow$ $P^{2} = (a . a . r^{(n - 1)})^{n}$

$\Rightarrow$ $P^{2} = (a . b)^{n}$

Hence proved.

Question 24: Show that the ratio of the sum of the first n terms of a G.P. to the sum of terms from $(n + 1)^{t h} t o (2 n)^{t h}$ term is $\frac{1}{r^{n}}$

Answer:

Let the first term =a and common ratio = r.

$s u m o f n t e r m s = \frac{a (1 - r^{n})}{1 - r}$

Since there are n terms from (n+1) to 2n term.

The sum of terms from (n+1) to 2n.

$S_{n} = \frac{a_{(n + 1)} (1 - r^{n})}{1 - r}$

$a_{(n + 1)} = a . r^{n + 1 - 1} = a r^{n}$

Thus, the required ratio = $\frac{a (1 - r^{n})}{1 - r} \times \frac{1 - r}{a r^{n} (1 - r^{n})}$

$= \frac{1}{r^{n}}$

Thus, the common ratio of the sum of the first n terms of a G.P. to the sum of terms from $(n + 1)^{t h} t o (2 n)^{t h}$ term is $\frac{1}{r^{n}}$ .

Question 25: If a, b, c, and d are in G.P. show that $(a^{2} + b^{2} + c^{2}) (b^{2} + c^{2} + d^{2}) = (a b + b c + c d)^{2} .$

Answer:

If a, b, c, and d are in G.P.

$b c = a d . . . . . . . . . . . . . . . . . . . . (1)$

$b^{2} = a c . . . . . . . . . . . . . . . . . . . . (2)$

$c^{2} = b d . . . . . . . . . . . . . . . . . . . . (3)$

To prove : $(a^{2} + b^{2} + c^{2}) (b^{2} + c^{2} + d^{2}) = (a b + b c + c d)^{2} .$

RHS : $(a b + b c + c d)^{2} .$

$\Rightarrow$ $(a b + a d + c d)^{2} .$

$\Rightarrow$ $(a b + d (a + c))^{2} .$

$\Rightarrow$ $a^{2} b^{2} + d^{2} (a + c)^{2} + 2 (a b) (d (a + c))$

$\Rightarrow$ $a^{2} b^{2} + d^{2} (a^{2} + c^{2} + 2 a c) + 2 a^{2} b d + 2 b c d$

Using equation (1) and (2),

$\Rightarrow$ $a^{2} b^{2} + 2 a^{2} c^{2} + 2 b^{2} c^{2} + d^{2} a^{2} + 2 d^{2} b^{2} + d^{2} c^{2}$

$\Rightarrow$ $a^{2} b^{2} + a^{2} c^{2} + a^{2} c^{2} + b^{2} c^{2} + b^{2} c^{2} + d^{2} a^{2} + d^{2} b^{2} + d^{2} b^{2} + d^{2} c^{2}$

$\Rightarrow$ $a^{2} b^{2} + a^{2} c^{2} + a^{2} d^{2} + b^{2} . b^{2} + b^{2} c^{2} + b^{2} d^{2} + c^{2} b^{2} + c^{2} . c^{2} + d^{2} c^{2}$

$\Rightarrow$ $a^{2} (b^{2} + c^{2} + d^{2}) + b^{2} (b^{2} + c^{2} + d^{2}) + c^{2} (b^{2} + c^{2} + d^{2})$

$\Rightarrow$ $(b^{2} + c^{2} + d^{2}) (a^{2} + b^{2} + c^{2})$ = LHS

Hence proved.

Question 26: Insert two numbers between 3 and 81 so that the resulting sequence is G.P.

Answer:

Let A, and B be two numbers between 3 and 81 such that series 3, A, B, and 81 form a GP.

Let a=first term and common ratio =r.

$∴ a_{4} = a . r^{4 - 1}$

$\Rightarrow$ $81 = 3. r^{3}$

$\Rightarrow$ $27 = r^{3}$

$\Rightarrow$ $r = 3$

For $r = 3$ ,

$A = a r = (3) (3) = 9$

$B = a r^{2} = (3) (3)^{2} = 27$

The required numbers are 9,27.

Question 27: Find the value of n so that $\frac{a^{n + 1} + b^{n + 1}}{a^{n} + b^{n}}$ may be the geometric mean between a and b.

Answer:

M of a and b is $\sqrt{a b} .$

Given :

$\frac{a^{n + 1} + b^{n + 1}}{a^{n} + b^{n}} = \sqrt{a b}$

Squaring both sides

${(\frac{a^{n + 1} + b^{n + 1}}{a^{n} + b^{n}})}^{2} = a b$

${(a^{n + 1} + b^{n + 1})^{2} = (a^{n} + b^{n})}^{2} a b$

$\Rightarrow (a^{2 n + 2} + b^{2 n + 2} + 2. a^{n + 1} . b^{n + 1}) = (a^{2 n} + b^{2 n} + 2. a^{n} . b^{n}) a b$

$\Rightarrow (a^{2 n + 2} + b^{2 n + 2} + 2. a^{n + 1} . b^{n + 1}) = (a^{2 n + 1} . b + a . b^{2 n + 1} + 2. a^{n + 1} . b^{n + 1})$

$\Rightarrow (a^{2 n + 2} + b^{2 n + 2}) = (a^{2 n + 1} . b + a . b^{2 n + 1})$

$\Rightarrow a^{2 n + 1} (a - b) = b^{2 n + 1} (a - b)$

$\Rightarrow a^{2 n + 1} = b^{2 n + 1}$

$\Rightarrow {(\frac{a}{b})}^{2 n + 1} = 1$

$\Rightarrow {(\frac{a}{b})}^{2 n + 1} = 1 = {(\frac{a}{b})}^{0}$

$\Rightarrow 2 n + 1 = 0$

$\Rightarrow 2 n = - 1$

$\Rightarrow n = \frac{- 1}{2}$

Question 28: The sum of two numbers is 6 times their geometric mean, showing numbers are in the ratio $(3 + 2 \sqrt{2}) : (3 - 2 \sqrt{2})$

Answer:

Let there be two numbers a and b

Geometric mean $= \sqrt{a b}$

According to the given condition,

$a + b = 6 \sqrt{a b}$

$\Rightarrow$ $(a + b)^{2} = 36 (a b)$ .............................................................(1)

Also, $(a - b)^{2} = (a + b)^{2} - 4 a b = 36 a b - 4 a b = 32 a b$

$(a - b) = \sqrt{32} \sqrt{a b}$

$\Rightarrow$ $(a - b) = 4 \sqrt{2} \sqrt{a b}$ .......................................................(2)

From (1) and (2), we get

$2 a = (6 + 4 \sqrt{2}) \sqrt{a b}$

$\Rightarrow$ $a = (3 + 2 \sqrt{2}) \sqrt{a b}$

Putting the value of 'a' in (1),

$\Rightarrow$ $b = 6 \sqrt{a b} - (3 + 2 \sqrt{2}) \sqrt{a b}$

$\Rightarrow$ $b = (3 - 2 \sqrt{2}) \sqrt{a b}$

$\Rightarrow$ $\frac{a}{b} = \frac{(3 + 2 \sqrt{2}) \sqrt{a b}}{(3 - 2 \sqrt{2}) \sqrt{a b}}$

$\Rightarrow$ $\frac{a}{b} = \frac{(3 + 2 \sqrt{2})}{(3 - 2 \sqrt{2})}$

Thus, the ratio is $(3 + 2 \sqrt{2}) : (3 - 2 \sqrt{2})$ .

Question 29: If A and G are A.M. and G.M., respectively between two positive numbers, prove that the numbers are $A \pm \sqrt{(A + G) (A - G)}$

Answer:

If A and Garee A.M. and G.M., respectively between two positive numbers,
Two numberarebe a and b.

$A M = A = \frac{a + b}{2}$

$\Rightarrow a + b = 2 A$ ...................................................................1

$G M = G = \sqrt{a b}$

$\Rightarrow a b = G^{2}$ ...........................................................................2

We know $(a - b)^{2} = (a + b)^{2} - 4 a b$

Put values from equation 1 and 2,

$(a - b)^{2} = 4 A^{2} - 4 G^{2}$

$\Rightarrow$ $(a - b)^{2} = 4 (A^{2} - G^{2})$

$\Rightarrow$ $(a - b)^{2} = 4 (A + G) (A - G)$

$\Rightarrow$ $(a - b) = 4 \sqrt{(A + G) (A - G)}$ ..................................................................3

From 1 and 3, we have

$2 a = 2 A + 2 \sqrt{(A + G) (A - G)}$

$\Rightarrow a = A + \sqrt{(A + G) (A - G)}$

Put the value of an in equation 1, and we get

$b = 2 A - A - \sqrt{(A + G) (A - G)}$

$\Rightarrow b = A - \sqrt{(A + G) (A - G)}$

Thus, numbers are $A \pm \sqrt{(A + G) (A - G)}$ .

Question 30: The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of the 2nd hour, 4th hour, and nth hour?

Answer:

The number of bacteria in a certain culture doubles every hour. It forms GP.

Given a = 30 and r = 2.

$a_{3} = a . r^{3 - 1} = 30 (2)^{2} = 120$

$a_{5} = a . r^{5 - 1} = 30 (2)^{4} = 480$

$a_{n} +_{1} = a . r^{n + 1 - 1} = 30 (2)^{n}$

Thus, bacteria present at the end of the 2nd hour, 4th hour, r, and nth hour are 120,480 and $30 (2)^{n}$ respectively.

Question 31: What will R50 amount to in 10 years after its deposit in a bank that pays an annual interest rate of 10% compounded annually?

Answer:

Given: The Bank pays an annual interest rate of 10% compounded annually.

Rs 500 amounts are deposited in the bank.

At the end of the first year, the amount

$= 500 (1 + \frac{1}{10}) = 500 (1.1)$

At the end of the second year, the amount $= 500 (1.1) (1.1)$

At the end of the third year, the amount $= 500 (1.1) (1.1) (1.1)$

At the end of 10 years, the amount $= 500 (1.1) (1.1) (1.1) . . . . . . . . (10 t i m e s)$

$= 500 (1.1)^{10}$

Thus, at the end of 10 years, amount $= R s . 500 (1.1)^{10}$ .

Question 32: If A.M. and G.M. of roots of a quadratic equation are 8 and 5, respectively, then obtain the quadratic equation

Answer:

Let the roots of the quadratic equation be a and b.

According to the given conditions,

$A M = \frac{a + b}{2} = 8$

$\Rightarrow (a + b) = 16$

$G M = \sqrt{a b} = 5$

$\Rightarrow a b = 25$

We know that $x^{2} - x (s u m o f r o o t s) + (p r o d u c t o f r o o t s) = 0$

$\Rightarrow$ $x^{2} - x (16) + (25) = 0$

$\Rightarrow$ $x^{2} - 16 x + 25 = 0$

Thus, the quadratic equation = $x^{2} - 16 x + 25 = 0$

Sequences and Series class 11 NCERT solutions: Miscellaneous Exercise
Page number: 147-148
Total Questions: 18

Question 1: If f is a function satisfying f (x +y) = f(x) f(y) for all x, y $ϵ$ N such that f(1) = 3 and

$\sum_{x = 1}^{n} f (x) = 120$ , find the value of n.

Answer:

Given : f (x +y) = f(x) f(y) for all x, y $ϵ$ N such that f(1) = 3

$f (1) = 3$

Taking $x = y = 1$ , we have

$f (1 + 1) = f (2) = f (1) * f (1) = 3 * 3 = 9$

$\Rightarrow f (1 + 1 + 1) = f (1 + 2) = f (1) * f (2) = 3 * 9 = 27$

$\Rightarrow f (1 + 1 + 1 + 1) = f (1 + 3) = f (1) * f (3) = 3 * 27 = 81$

$f (1), f (2), f (3), f (4) . . . . . . . . . . . . . . . . . . . . .$ is $3, 9, 27, 81, . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .$ forms a GP with first term=3 and common ratio = 3.

$\sum_{x = 1}^{n} f (x) = 120 = S_{n}$

$S_{n} = \frac{a (1 - r^{n})}{1 - r}$

$\Rightarrow$ $120 = \frac{3 (1 - 3^{n})}{1 - 3}$

$\Rightarrow$ $40 = \frac{(1 - 3^{n})}{- 2}$

$\Rightarrow$ $- 80 = (1 - 3^{n})$

$\Rightarrow$ $- 80 - 1 = (- 3^{n})$

$\Rightarrow$ $- 81 = (- 3^{n})$

$\Rightarrow$ $3^{n} = 81$

Therefore, $n = 4$

Thus, the value of n is 4.

Question 2: The sum of some terms of G.P. is 315 whose first term and the common ratio are 5 and 2, respectively. Find the last term and the number of terms.

Answer:

Let the sum of some terms of G.P. is 315 whose first term and the common ratio are 5 and 2

$S_{n} = \frac{a (1 - r^{n})}{1 - r}$

$\Rightarrow$ $315 = \frac{5 (1 - 2^{n})}{1 - 2}$

$\Rightarrow$ $63 = \frac{(1 - 2^{n})}{- 1}$

$\Rightarrow$ $- 63 = (1 - 2^{n})$

$\Rightarrow$ $- 63 - 1 = (- 2^{n})$

$\Rightarrow$ $- 64 = (- 2^{n})$

$\Rightarrow$ $2^{n} = 64$

Therefore, $n = 6$

Thus, the value of n is 6.

Last term of GP = 6th term 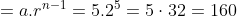$=a.r^{n-1}=5.2^5=5\cdot32=160$

The last term of GP =160

Question 3: The first term of a G.P. is 1. The sum of the third term and fifth term is 90. Find the common ratio of G.P.

Answer:

Given: The first term of a G.P. is 1. The sum of the third term and fifth term is 90.

$a = 1$

$a_{3} = a . r^{2} = r^{2}$ $a_{5} = a . r^{4} = r^{4}$

$∴ r^{2} + r^{4} = 90$

$∴ r^{4} + r^{2} - 90 = 0$

$\Rightarrow r^{2} = \frac{- 1 \pm \sqrt{1 + 360}}{2}$

$\Rightarrow$ $r^{2} = \frac{- 1 \pm \sqrt{361}}{2}$

$\Rightarrow$ $r^{2} = - 10 o r 9$

$\Rightarrow$ $r = \pm 3$

Thus, the common ratio of GP is $\pm 3$ .

Question 4: The sum of three numbers in G.P. is 56. If we subtract 1, 7, 2and 1 from these numbers in that order, we obtain an arithmetic progression. Find the numbers.

Answer:

Let three terms of GP be $a, a r, a r^{2} .$

Then, we have $a + a r + a r^{2} = 56$

$a (1 + r + r^{2}) = 56$ ...............................................1

$a - 1, a r - 7, a r^{2} - 21$ from an AP.

$∴ a r - 7 - (a - 1) = a r^{2} - 21 - (a r - 7)$

$a r - 7 - a + 1 = a r^{2} - 21 - a r + 7$

$a r - 6 - a = a r^{2} - 14 - a r$

$\Rightarrow a r^{2} - 2 a r + a = 8$

$\Rightarrow a r^{2} - a r - a r + a = 8$
$\Rightarrow a (r^{2} - 2 r + 1) = 8$

$\Rightarrow a (r^{2} - 1)^{2} = 8$ ....................................................................2

From equation 1 and 2, we get

$\Rightarrow 7 (r^{2} - 2 r + 1) = 1 + r + r^{2}$

$\Rightarrow 7 r^{2} - 14 r + 7 - 1 - r - r^{2} = 0$

$\Rightarrow 6 r^{2} - 15 r + 6 = 0$

$\Rightarrow 2 r^{2} - 5 r + 2 = 0$

$\Rightarrow 2 r^{2} - 4 r - r + 2 = 0$

$\Rightarrow 2 r (r - 2) - 1 (r - 2) = 0$

$\Rightarrow (r - 2) (2 r - 1) = 0$

$\Rightarrow r = 2, r = \frac{1}{2}$

If r = 2, GP = 8,16,32

If r=0.2, GP= 32,16,8.

Thus, the numbers required are 8,16,32.

Question 5: A G.P. consists of an even number of terms. If the sum of all the terms is 5 times the sum of terms occupying odd places, then find its common ratio.

Answer:

Let GP be $A_{1}, A_{2}, A_{3}, . . . . . . . . . . . . . . . . . . . A_{2 n}$

Number of terms = 2n

According to the given condition,

$(A_{1},A_{2},A_{3},...................A_{2n})=5(A_{1},A_{3},...................A_{2n-1})$

$\Rightarrow (A_{1},A_{2},A_{3},...................A_{2n})-5(A_{1},A_{3},...................A_{2n-1})=0$

$\Rightarrow (A_{2},A_{4},A_{6},...................A_{2n})=4(A_{1},A_{3},...................A_{2n-1})$

Lettheme be GP as $a, a r, a r^{2}, . . . . . . . . . . . . . . . . . .$

$\Rightarrow \frac{a r (r^{n} - 1)}{r - 1} = \frac{4. a (r^{n} - 1)}{r - 1}$

$\Rightarrow a r = 4 a$

$\Rightarrow r = 4$

Thus, the common ratio is 4.

Question 6: If $\frac{a + b x}{a - b x} = \frac{b + c x}{b - c x} = \frac{c + d x}{c - d x} (x \neq 0)$ then show that a, b, c and d are in G.P.

Answer:

Given :

$\frac{a + b x}{a - b x} = \frac{b + c x}{b - c x} = \frac{c + d x}{c - d x} (x \neq 0)$

Takin,

$\frac{a + b x}{a - b x} = \frac{b + c x}{b - c x}$

$\Rightarrow (a + b x) (b - c x) = (b + c x) (a - b x)$

$\Rightarrow a b + b^{2} x - b c x^{2} - a c x) = b a - b^{2} x + a c x - b c x^{2}$

$\Rightarrow 2 b^{2} x = 2 a c x$

$\Rightarrow b^{2} = a c$

$\Rightarrow \frac{b}{a} = \frac{c}{b} . . . . . . . . . . . . . . . . . .1$

Taking,

$\frac{b + c x}{b - c x} = \frac{c + d x}{c - d x}$

$\Rightarrow (b + c x) (c - d x) = (c + d x) (b - c x)$

$\Rightarrow b c - b d x + c^{2} x - c d x^{2} = b c - c^{2} x + b d x - c d x^{2}$

$\Rightarrow 2 b d x = 2 c^{2} x$

$\Rightarrow b d = c^{2}$

$\Rightarrow \frac{d}{c} = \frac{c}{b} . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2$

From equation 1 and 2, we have

$\Rightarrow \frac{d}{c} = \frac{c}{b} = \frac{b}{a}$

Thus, a,b,c,d and are in GP.

Question 7: Let S be the sum, P the product, and R the sum of reciprocals of n terms in a G.P. Prove that $P^{2} R^{n} = S^{n}$

Answer:

Let there be a GP $= a, a r, a r^{2}, a r^{3}, . . . . . . . . . . . . . . . . . . . .$

According to the given information,

$S = \frac{a (r^{n} - 1)}{r - 1}$

$P = a^{n} \times r^{(1 + 2 + . . . . . . . . . . . . . . . . . . . n - 1)}$

$\Rightarrow P = a^{n} \times r^{\frac{n (n - 1)}{2}}$

$R = \frac{1}{a} + \frac{1}{a r} + \frac{1}{a r^{2}} + . . . . . . . . . . . . . . . . . . \frac{1}{a r^{n - 1}}$

$\Rightarrow R = \frac{r^{n - 1} + r^{n - 2} + r^{n - 3} + . . . . . . . . . . . . . . r + 1}{a . r^{n - 1}}$

$\Rightarrow R = \frac{1}{a . r^{n - 1}} \times \frac{1 (r^{n} - 1)}{r - 1}$

$\Rightarrow R = \frac{(r^{n} - 1)}{a . r^{n - 1} . (r - 1)}$

To prove : $P^{2} R^{n} = S^{n}$

LHS : $P^{2} R^{n}$

$= a^{2 n} . r^{n (n - 1)} \frac{(r^{n} - 1)^{n}}{a^{n} . r^{n (n - 1)} . (r - 1)^{n}}$

$= a^{n} \frac{(r^{n} - 1)^{n}}{(r - 1)^{n}}$

$= {(\frac{a (r^{n} - 1)}{(r - 1)})}^{n}$

$= S^{n} = R H S$

Hence proved.

Question 8: If a, b, c, d are in G.P, prove that $(a^{n} + b^{n}), (b^{n} + c^{n}), (c^{n} + d^{n})$ are in G.P.

Answer:

Given: a, b, c, d are in G.P.

To prove: $(a^{n} + b^{n}), (b^{n} + c^{n}), (c^{n} + d^{n})$ are in G.P.

Then we can write,

$b^{2} = a c . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1$

$c^{2} = b d . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2$

$a d = b c . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3$

Let $(a^{n} + b^{n}), (b^{n} + c^{n}), (c^{n} + d^{n})$ be in GP.

$(b^{n} + c^{n})^{2} = (a^{n} + b^{n}) (c^{n} + d^{n})$

LHS: $(b^{n} + c^{n})^{2}$

$(b^{n} + c^{n})^{2} = b^{2 n} + c^{2 n} + 2 b^{n} c^{n}$

$(b^{n} + c^{n})^{2} = (b^{2})^{n} + (c^{2})^{n} + 2 b^{n} c^{n}$

$= (a c)^{n} + (b d)^{n} + 2 b^{n} c^{n}$

$= a^{n} c^{n} + b^{n} c^{n} + a^{n} d^{n} + b^{n} d^{n}$

$= c^{n} (a^{n} + b^{n}) + d^{n} (a^{n} + b^{n})$

$= (a^{n} + b^{n}) (c^{n} + d^{n}) = R H S$

Hence proved.

Thus, $(a^{n} + b^{n}), (b^{n} + c^{n}), (c^{n} + d^{n})$ are in GP

Question 9: If a and b are the roots of $x^{2} - 3 x + p = 0$ and c, d are roots of $x^{2} - 12 x + q = 0$ , where a, b, c, d form a G.P. Prove that (q + p) : (q – p) = 17:15.

Answer:

Given: a and b are the roots of $x^{2} - 3 x + p = 0$

Then, $a + b = 3 a n d a b = p . . . . . . . . . . . . . . . . . . . . . .1$

Also, c, d are roots of $x^{2} - 12 x + q = 0$

$c + d = 12 a n d c d = q . . . . . . . . . . . . . . . . . . . . . .2$

Given: a, b, c, d form a G.P

Let, $a = x, b = x r, c = x r^{2}, d = x r^{3}$

From 1 and 2, we get

$x + x r = 3$ and $x r^{2} + x r^{3} = 12$

$\Rightarrow x (1 + r) = 3$ $x r^{2} (1 + r) = 12$

On dividing them,

$\frac{x r^{2} (1 + r)}{x (1 + r)} = \frac{12}{3}$

$\Rightarrow r^{2} = 4$

$\Rightarrow r = \pm 2$

When , r = 2,

$x = \frac{3}{1 + 2} = 1$

When, r = -2,

$x = \frac{3}{1 - 2} = - 3$

Case (1) when r=2 and x=1,

$a b = x^{2} r = 2 a n d c d = x^{2} r^{5} = 32$

$∴ \frac{q + p}{q - p} = \frac{32 + 2}{32 - 2} = \frac{34}{30} = \frac{17}{15}$

i.e. (q + p) : (q – p) = 17:15.

Case (2) when r = -2 and x = -3,

$a b = x^{2} r = - 18 a n d c d = x^{2} r^{5} = - 288$

$∴ \frac{q + p}{q - p} = \frac{- 288 - 18}{- 288 + 18} = \frac{- 305}{- 270} = \frac{17}{15}$

i.e. (q + p) : (q – p) = 17 : 15.

Question 10: The ratio of the A.M. and G.M. of two positive numbers a and b, is m n. Show that $a : b = (m + \sqrt{m^{2} - n^{2}}) : (m - \sqrt{m^{2} - n^{2}})$

Answer:

Let two numbers be a and b.

$A M = \frac{a + b}{2} a n d G M = \sqrt{a b}$

According to the given condition,

$\frac{a + b}{2 \sqrt{a b}} = \frac{m}{n}$

$\Rightarrow \frac{(a + b)^{2}}{4 a b} = \frac{m^{2}}{n^{2}}$

$\Rightarrow (a + b)^{2} = \frac{4 a b . m^{2}}{n^{2}}$

$\Rightarrow (a + b) = \frac{2 \sqrt{a b} . m}{n}$ ...................................................................1

$(a - b)^{2} = (a + b)^{2} - 4 a b$

We get,

$(a - b)^{2} = (\frac{4 a b m^{2}}{n^{2}}) - 4 a b$

$(a - b)^{2} = (\frac{4 a b m^{2} - 4 a b n^{2}}{n^{2}})$

$\Rightarrow (a - b)^{2} = (\frac{4 a b (m^{2} - n^{2})}{n^{2}})$

$\Rightarrow (a - b) = (\frac{2 \sqrt{a b} \sqrt{(m^{2} - n^{2})}}{n})$ .....................................................2

From 1 and 2, we get

$2 a = (\frac{2 \sqrt{a b}}{n}) (m + \sqrt{(m^{2} - n^{2})})$

$\Rightarrow a = (\frac{\sqrt{a b}}{n}) (m + \sqrt{(m^{2} - n^{2})})$

Putting the value of an ann equation 1, we have

$b = (\frac{2. \sqrt{a b}}{n}) m - (\frac{\sqrt{a b}}{n}) (m + \sqrt{(m^{2} - n^{2})})$

$\Rightarrow b = (\frac{\sqrt{a b}}{n}) m - (\frac{\sqrt{a b}}{n}) (\sqrt{(m^{2} - n^{2})})$

$= (\frac{\sqrt{a b}}{n}) (m - \sqrt{(m^{2} - n^{2})})$

$∴ a : b = \frac{a}{b} = \frac{(\frac{\sqrt{a b}}{n}) (m + \sqrt{(m^{2} - n^{2})})}{(\frac{\sqrt{a b}}{n}) (m - \sqrt{(m^{2} - n^{2})})}$

$= \frac{(m + \sqrt{(m^{2} - n^{2})})}{(m - \sqrt{(m^{2} - n^{2})})}$

$a : b = (m + \sqrt{(m^{2} - n^{2})}) : (m - \sqrt{(m^{2} - n^{2})})$

Question 11: Find the sum of the following series up to n terms:

(i) $5 + 55 + 555 + . . . .$

(ii) .6 +. 66 +. 666+…

Answer:

(i) $5 + 55 + 555 + . . . .$ is not a GP.

It can be changed in GP by writing terms such s

$S_{n} = 5 + 55 + 555 + . . . .$ to n terms

$S_{n} = \frac{5}{9} [9 + 99 + 999 + 9999 + . . . . . . . . . . . . . . . .]$

$S_{n} = \frac{5}{9} [(10 - 1) + (10^{2} - 1) + (10^{3} - 1) + (10^{4} - 1) + . . . . . . . . . . . . . . . .]$

$S_{n} = \frac{5}{9} [(10 + 10^{2} + 10^{3} + . . . . . . . .) - (1 + 1 + 1. . . . . . . . . . . . . . . . . . . . .)]$

$S_{n} = \frac{5}{9} [\frac{10 (10^{n} - 1)}{10 - 1} - (n)]$

$S_{n} = \frac{5}{9} [\frac{10 (10^{n} - 1)}{9} - (n)]$

$S_{n} = \frac{50}{81} [(10^{n} - 1)] - \frac{5 n}{9}$

Thus, the sum is

$S_{n} = \frac{50}{81} [(10^{n} - 1)] - \frac{5 n}{9}$

(ii) The sum of 0.6 +0. 66 + 0. 666+….................

It can be written as

$S_{n} = 0.6 + 0.66 + 0.666 + . . . . . . . . . . . . . . . . . . . . . . . . . .$ to n terms

$\Rightarrow S_{n} = 6 [0.1 + 0.11 + 0.111 + 0.1111 + . . . . . . . . . . . . . . . .]$

$\Rightarrow S_{n} = \frac{6}{9} [0.9 + 0.99 + 0.999 + 0.9999 + . . . . . . . . . . . . . . . .]$

$\Rightarrow S_{n} = \frac{6}{9} [(1 - \frac{1}{10}) + (1 - \frac{1}{10^{2}}) + (1 - \frac{1}{10^{3}}) + (1 - \frac{1}{10^{4}}) + . . . . . . . . . . . . . . . .]$

$\Rightarrow S_{n} = \frac{2}{3} [(1 + 1 + 1. . . . . . . . . . . . . . . . . . . . . n t e r m s) - \frac{1}{10} (1 + \frac{1}{10} + \frac{1}{10^{2}} + . . . . . . . . . . . . . . . . . . . n t e r m s)]$

$\Rightarrow S_{n} = \frac{2}{3} [n - \frac{\frac{1}{10} ({\frac{1}{10}}^{n} - 1)}{\frac{1}{10} - 1}]$

$\Rightarrow S_{n} = \frac{2 n}{3} - \frac{2}{30} [\frac{10 (1 - 10^{- n})}{9}]$

$\Rightarrow S_{n} = \frac{2 n}{3} - \frac{2}{27} (1 - 10^{- n})$

Question 12: Find the 20th term of the series $2 \times 4 + 4 \times 6 + \times 6 \times 8 + . . . . + n$ terms.

Answer:

The series = $2 \times 4 + 4 \times 6 + \times 6 \times 8 + . . . . + n$

$∴ n^{t h} t e r m = a_{n} = 2 n (2 n + 2) = 4 n^{2} + 4 n$

$∴ a_{20} = 2 (20) [2 (20) + 2]$

$= 40 [40 + 2]$

$= 40 [42]$

$= 1680$

Thus, the 20th term of the series is 1680

Question 13: A farmer buys a used tractor for Rs 12000. He pays Rs 6000 cash and agrees to pay the balance in annual installments of Rs 500 plus 12% interest on the unpaid amount. How much will the tractor cost him?

Answer:

Given Farmer pays Rs 6000 cash.

Therefore, unpaid amount = 12000-6000=Rs. 6000

According to the condition, interest paid annually is

12% of 6000,12% of 5500,12% of 5000,......................12% of 500.

Thus, the total interest to be paid

$= 12 % o f 6000 + 12 % o f 5500 + . . . . . . . . . . . . .12 % o f 500$

$= 12 % o f (6000 + 5500 + . . . . . . . . . . . . . + 500)$

$= 12 % o f (500 + 1000 + . . . . . . . . . . . . . + 6000)$

Here, $500, 1000, . . . . . . . . . . . . .5500, 6000$ is a AP with first term =a=500 and common difference =d = 500

We know that $a_{n} = a + (n - 1) d$

$\Rightarrow 6000 = 500 + (n - 1) 500$

$\Rightarrow 5500 = (n - 1) 500$

$\Rightarrow 11 = (n - 1)$

$\Rightarrow n = 11 + 1 = 12$

The sum of AP:

$S_{12} = \frac{12}{2} [2 (500) + (12 - 1) 500]$

$\Rightarrow S_{12} = 6 [1000 + 5500]$

$= 6 [6500]$

$= 39000$

Thus, interest to be paid :

$= 12 % o f (500 + 1000 + . . . . . . . . . . . . . + 6000)$

$= 12 % o f (39000)$

$= R s . 4680$

Thus, cost of tractor = Rs. 12000+ Rs. 4680 = Rs. 16680

Question 14: Shamshad Ali buys a scooter for Rs 22000. He pays Rs 4000 cash and agrees to pay the balance in an annual installment of Rs 1000 plus 10% interest on the unpaid amount. How much will the scooter cost him?

Answer:

Given: Shamshad Ali buys a scooter for Rs 22000.

Therefore, the unpaid amount = 22000-4000=Rs. 18000

According to the given condition, interest paid annually is

10% of 18000,10% of 17000,10% of 16000,......................10% of 1000.

Thus, the total interest to be paid

$= 10 % o f 18000 + 10 % o f 17000 + . . . . . . . . . . . . .10 % o f 1000$

$= 10 % o f (18000 + 17000 + . . . . . . . . . . . . . + 1000)$

$= 10 % o f (1000 + 2000 + . . . . . . . . . . . . . + 18000)$

Here, $1000, 2000, . . . . . . . . . . . . .17000, 18000$ is a AP with first term =a=1000 and common difference =d = 1000

We know that $a_{n} = a + (n - 1) d$

$\Rightarrow 18000 = 1000 + (n - 1) 1000$

$\Rightarrow 17000 = (n - 1) 1000$

$\Rightarrow 17 = (n - 1)$

$\Rightarrow n = 17 + 1 = 18$

The sum of AP:

$S_{18} = \frac{18}{2} [2 (1000) + (18 - 1) 1000]$

$= 9 [2000 + 17000]$

$= 9 [19000]$

$= 171000$

Thus, interest to be paid :

$= 10 % o f (1000 + 2000 + . . . . . . . . . . . . . + 18000)$

$= 10 % o f (171000)$

$= R s . 17100$

Thus, cost of tractor = Rs. 22000 + Rs. 17100 = Rs. 39100

Question 15: A person writes a letter to four of his friends. He asks each one of them to copy the letter and mail it to four different persons with the instruction that they move the chain similarly. Assuming that the chain is not broken and that it costs 50 paise to mail one letter. Find the amount spent on the postage when the 8th set of letters is mailed.

Answer:

The number of letters mailed from a GP: $4, 4^{2}, 4^{3}, . . . . . . . . . . . . {.4}^{8}$

First term = a=4

Common ratio=r=4

Number of terms = 8

We know that the sum of GP is

$S_{n} = \frac{a (r^{n} - 1)}{r - 1}$

$= \frac{4 (4^{8} - 1)}{4 - 1}$

$= \frac{4 (65536 - 1)}{3}$

$= \frac{4 (65535)}{3}$

$= 87380$

Costs to mail one letter are 50 paise.

Cost of mailing 87380 letters

$= R s . 87380 \times \frac{50}{100}$

$= R s . 43690$

Thus, the amount spent when the 8th set of the letter is mailed is Rs. 43690.

Question 16: A man deposited Rs 10000 in a bank at the rate of 5% simple interest annually. Find the amount in 1the 5th year since he deposited the amount and also calculate the total amount after 20 years.

Answer:

Given: A man deposited Rs 10000 in a bank at the rate of 5% simple interest annually.

$= \frac{5}{100} \times 10000 = R s .500$

$∴$ Interest in fifteen year 10000+ 14 times Rs. 500

$∴$ Amount in 15 th year $= R s . 10000 + 14 \times 500$

$= R s . 10000 + 7000$

$= R s . 17000$

$∴$ Amount in 20 th year $= R s . 10000 + 20 \times 500$

$= R s . 10000 + 10000$

$= R s . 20000$

Question 17: A manufacturer reckons that the value of a machine, which costs him Rs. 15625, will depreciate each year by 20%. Find the estimated value at the end of 5 years.

Answer:

Cost of machine = Rs. 15625

Machines depreciate each year by 20%.

Therefore, its value every year is 80% of the original cost i.e. $\frac{4}{5}$ of the original cost.

$∴$ Value at the end of 5 years

$= 15625 \times \frac{4}{5} \times \frac{4}{5} \times \frac{4}{5} \times \frac{4}{5} \times \frac{4}{5}$

$= 5120$

Thus, the value of the machine at the end of 5 years is Rs. 5120

Question 18: 150 workers were engaged to finish a job in a certain number of days. 4 workers dropped out on the second day, 4 more workers dropped out on the third day, and so on.

Answer:

Let x be the number of days in which 150 workers finish the work.

According to the given information, we have

$150 x = 150 + 146 + 142 + . . . . . . . . . . . . (x + 8) t e r m s$

Series $150 x = 150 + 146 + 142 + . . . . . . . . . . . . (x + 8) t e r m s$ is a AP

First term=a=150

Common difference= -4

Number of terms = x+8

$\Rightarrow 150 x = \frac{x + 8}{2} [2 (150) + (x + 8 - 1) (- 4)]$

$\Rightarrow 300 x = x + 8 [300 - 4 x - 28]$

$\Rightarrow 300 x = 300 x - 4 x^{2} - 28 x + 2400 - 32 x + 224$

$\Rightarrow x^{2} + 15 x - 544 = 0$

$\Rightarrow x^{2} + 32 x - 17 x - 544 = 0$

$\Rightarrow x (x + 32) - 17 (x + 32) = 0$

$\Rightarrow (x + 32) (x - 17) = 0$

$\Rightarrow x = - 32, 17$

Since x cannot be negative so x=17.

Thus, in 17 days 150 workers finish the work.

Thus, the required number of days = 17+8=25 days.

Class 11 Maths NCERT Chapter 8: Extra Question

Question: If $t_{n}$ denotes the $n^{th}$ term of the series $2 + 3 + 6 + 11 + 18 + \dots$ then $t_{50}$ is___.

Solution:
$\begin{aligned} S_{n} = 2 + 3 + 6 + 11 + 18 + \dots + t_{50} (Using method of difference) \\ S_{n} = 0 + 2 + 3 + 6 + 11 + 18 + \dots + t_{50} \\ \Rightarrow S_{n} - S_{n} = (2 - 0) + (3 - 2) + (6 - 3) + (11 - 6) + (18 - 11) + \dots - t_{50} \\ \Rightarrow t_{50} = 2 + [1 + 3 + 5 + 7 + \dots upto 49 terms] \\ \Rightarrow t_{50} = 2 + \frac{49}{2} [2 + (49 - 1) 2] \\ \Rightarrow t_{50} = 2 + 49^{2} = 2403 \end{aligned}$
Hence, the correct answer is 2403.

What Extra Should Students Study Beyond the NCERT for JEE?

Concept Name	JEE	NCERT
Sequence And Series	✅	✅
Arithmetic Progression	✅	✅
Sum of n Terms of an AP	✅	✅
Arithmetic Mean in AP	✅	✅
Geometric Progression	✅	✅
Geometric Mean In GP	✅	✅
Sum To n Terms Of a GP	✅	✅
Harmonic Progression	✅
Harmonic Mean in HP	✅
Relation between A.M., G.M. and H.M.	✅	✅
Arithmetico Geometric Series	✅
Sum of an Infinite Arithmetic Geometric Series	✅
SUMMATION FORMULA	✅
Sum of Common Series	✅
If the differences of successive terms of a series are in A.P.and G.P	✅
Method of Difference	✅
Sum to n Terms of Special Series	✅
Application of AM-GM Inequality	✅

NCERT Solutions for Class 11 Maths: Chapter Wise

NCERT Solutions for Class 11 Mathematics Chapter 1: Sets

NCERT Solutions for Class 11 Mathematics Chapter 2: Relations and Functions

NCERT Solutions for Class 11 Mathematics Chapter 3: Trigonometric Functions

NCERT Solutions for Class 11 Mathematics Chapter 4: Complex Numbers and Quadratic Equations

NCERT Solutions for Class 11 Mathematics Chapter 5: Linear Inequalities

NCERT Solutions for Class 11 Mathematics Chapter 6: Permutations and Combinations

NCERT Solutions for Class 11 Mathematics Chapter 7: Binomial Theorem

NCERT Solutions for Class 11 Mathematics Chapter 8: Sequences and Series

NCERT Solutions for Class 11 Mathematics Chapter 9: Straight Lines

NCERT Solutions for Class 11 Mathematics Chapter 10: Conic Sections

NCERT Solutions for Class 11 Mathematics Chapter 11: Introduction to Three-Dimensional Geometry

NCERT Solutions for Class 11 Mathematics Chapter 12: Limits and Derivatives

NCERT Solutions for Class 11 Mathematics Chapter 13: Statistics

NCERT Solutions for Class 11 Mathematics Chapter 14: Probability

NCERT solutions for class 11- Subject-wise

Given below are some useful links for NCERT books and the NCERT syllabus for class 10:

NCERT Books and NCERT Syllabus

Here are the subject-wise links for the NCERT solutions of class 10:

Frequently Asked Questions (FAQs)

1. What are the important topics covered in NCERT Class 11 Maths Chapter 8?

Chapter 8 of Class 11 Maths focuses on sequences and series, which includes Arithmetic Progression (AP) and Geometric Progression (GP). It covers the nth term of an AP and GP, the sum of the first n terms of both AP and GP and the concept of Arithmetic Mean and Geometric Mean. Understanding the relationship between terms in these progressions, as well as the formulas to find the sum and nth terms, are key parts of this chapter.

2. How to find the sum of an arithmetic progression (AP) in Class 11 Maths?

The sum of the first n terms of an arithmetic progression (AP) can be calculated using the formula Sn=n2(2a+(n−1)⋅d), where a is the first term, d is the common difference, and n is the number of terms. This formula helps in finding the total sum of terms when you know the starting term and the common difference between consecutive terms.

3. What is the formula for the nth term of a geometric progression (GP)?

The nth term of a geometric progression (GP) is given by the formula Tn=a⋅rn−1, where a is the first term and r is the common ratio. This formula allows you to find any term in the sequence when you know the first term and the common ratio.

4. What is the difference between arithmetic and geometric sequences?

The key difference between arithmetic and geometric sequences lies in how the terms are generated. In an Arithmetic Progression (AP), the difference between any two consecutive terms is constant, referred to as the common difference. In contrast, a Geometric Progression (GP) is defined by a constant ratio between consecutive terms, known as the common ratio. These differences in structure give rise to different formulas and methods for calculating terms and sums in each sequence.

5. How to find the sum of an infinite geometric series?

The sum of an infinite geometric series, provided the common ratio r satisfies |r|<1, is calculated using the formula S∞=a1−r, where a is the first term and r is the common ratio. This formula helps in finding the sum of an infinite series when the terms approach zero and the series converges, which is a key concept in both mathematics and real-world applications.

Also Read

NCERT Solutions for Class 11 Maths Chapter 7 Binomial Theorem

NCERT Solutions for Class 11 Chemistry Chapter 3 Classification of Elements and Periodicity in Properties

NCERT Solutions for Class 11 Chemistry Chapter 1 Some Basic Concepts of Chemistry

NCERT Solutions for Class 11 Chemistry Chapter 2 Structure of Atom

NCERT Solutions for Class 11 Maths Chapter 4 - Complex Numbers and Quadratic Equations

NCERT Solutions for Class 11 Maths Chapter 2 Relations And Functions

Some basic concepts of Chemistry Class 11th Notes - Free NCERT Class 11 Chemistry Chapter 1 Notes - Download PDF

NCERT Class 11 Biology Chapter 13 Notes Photosynthesis In Higher Plants - Download PDF Notes

NCERT Class 11 Biology Chapter 14 Notes Respiration In Plants - Download PDF Notes

NCERT Class 11 Biology Chapter 15 Notes Plant Growth And Development- Download PDF Notes

NCERT Class 11 Biology Chapter 22 Notes Chemical Coordination And Integration- Download PDF Notes

NCERT Class 11 Biology Chapter 21 Notes Neural Control And Coordination- Download PDF Notes

NCERT Exemplar Class 11 Chemistry Solutions Chapter 9 Hydrogen

NCERT Exemplar Class 11 Chemistry Solutions Chapter 8 Redox Reactions

NCERT Exemplar Class 11 Chemistry Solutions Chapter 2 Structure of Atom

NCERT Exemplar Class 11 Solutions - Subject Wise Problems with Solutions

NCERT Exemplar Class 11 Biology Solutions Chapter 1 The Living World

NCERT Exemplar Class 11 Biology Solutions Chapter 21 Neural Control and Coordination

NCERT Books for class 11 Maths 2025-26: Download Free PDF

NCERT Book for class 11 Biology 2025-26: Download Free PDF

NCERT Books for Class 11 Physics 2025-26: Download PDF

NCERT Books for Class 11 Chemistry 2025-26: Download Free PDF

NCERT Books for Class 11 English 2025-26: Download Free PDF

NCERT Books for class 11 Hindi 2025-26: Download Free PDF

NCERT Syllabus for Class 11 Physics 2025-26 - Download Latest Syllabus Pdf

Articles

JoSAA 2025: Number of Seats Increased for IITs, NITs

Jun 20, 2025

SAMS Odisha +2 Admission 2025 – Dates, Eligibility, and Application Process

Jun 20, 2025

UP Scholarships for General Category Students: Eligibility & Application Guide

Jun 19, 2025

Tamil Nadu BSc Nursing Admission 2025: Fees, Eligibility Criteria, Application, Top Colleges

Jun 19, 2025

JAC Delhi Merit List 2025 – Download and Check College wise Cut offs

Jun 18, 2025

IOQM Admit Card 2025: Download Indian Olympiad Qualifier in Mathematics Hall Ticket

Jun 18, 2025

DU LLB Counselling 2025 (Started) – First Allotment (Out), Documents, Admission Process

Jun 18, 2025

Silverzone ITHO Olympiad 2025 – Exam Date, Syllabus, Eligibility & Results

Jun 17, 2025

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:16 May,2025 - 30 June,2025

Result

Admit Card

Bihar Open Board 12th Examination

Application Date:16 May,2025 - 30 June,2025

Result

Admit Card

National Institute of Open Schooling 10th examination

Application Date:24 May,2025 - 23 June,2025

Result

Admit Card

Mock Test

National Institute of Open Schooling 12th Examination

Application Date:24 May,2025 - 23 June,2025

Result

Mock Test

Admit Card

Chattisgarh State Open School 12th Examination

Application Date:01 June,2025 - 30 June,2025

Result

Admit Card

View All School Exams

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

Exams

Top Schools

Products & Resources

NCERT Study Material

Exams

Colleges

Predictors

Resources

Exams

Colleges & Courses

Predictors

Resources

Exams

Colleges

Predictors

Resources

Exams

Colleges

Predictors & E-Books

Resources

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Exams

Resources

Top Courses & Careers

Colleges

Exams

Colleges

Resources

Quick Links

Exams

Colleges

Resources

Exams

Colleges

Resources

Diploma Colleges

Exams

Resources

Upcoming Events

Other Exams

Exams

Colleges

Top Countries

Resources

Exams

Colleges

Upcoming Events

Resources

Engineering Preparation

Medical Preparation

Law Preparation

MBA Preparation

Top Streams

Specializations

Resources

Top Providers

NCERT Solutions for Class 11 Maths Chapter 8 Sequences and Series

NCERT Solution for Class 11 Maths Chapter 8 Solutions: Download PDF

Sequences And Series Class 11 Solutions: Important Formulae

NCERT Solutions for Class 11 Maths Chapter 8: Exercise Questions

Class 11 Maths NCERT Chapter 8: Extra Question

What Extra Should Students Study Beyond the NCERT for JEE?

NCERT Solutions for Class 11 Maths: Chapter Wise

NCERT solutions for class 11- Subject-wise

NCERT Books and NCERT Syllabus

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

Bihar Open Board 10th Examination

Bihar Open Board 12th Examination

National Institute of Open Schooling 10th examination

National Institute of Open Schooling 12th Examination

Chattisgarh State Open School 12th Examination