Along with NCERT Solutions for Class 11 Chemistry Chapter 1 Some Basic Concepts of Chemistry, solutions for all other chapters are also provided for comprehensive preparation. These NCERT Solutions are prepared as per the latest syllabus and exam pattern.
NCERT Solutions for Class 11 Chemistry Chapter 1 Some Basic Concepts of Chemistry
Do you know what matter is made of, how scientists measure substances that are too small to see, and what makes chemical reactions follow the same proportions every time? The answer to all these questions lies in some basic concepts of chemistry ncert solutions . This chapter is like the ABCs of Chemistry where you get to know what matter is made of, how atoms and molecules interact, and why every tiny calculation in chemistry counts. From the air we breathe, the food we eat, the water we drink, or the medicines we use, everything is made up of chemicals. NCERT Solutions for Class 11 Chemistry Chapter 1 Some Basic Concepts of Chemistry are all about the science of molecules and their transformation.
This Story also Contains
- NCERT Solution for Class 11 Chemistry Chapter 1: Download PDF
- NCERT Solutions for Class 11 Chemistry Chapter 1- (Exercise Questions)
- Class 11 Chemistry NCERT Chapter 1: Higher Order Thinking Skills (HOTS) Questions
- Approach to Solve Questions of Class 11 Chemistry Chapter 1
- Topics and Subtopics Covered in the NCERT Textbook Class 11 Chemistry Chapter 1
- What Extra Should Students Study Beyond the NCERT for JEE/NEET?
- NCERT Class 11 Chemistry Chapter 1 Some Basic Concepts of Chemistry: Important Formulas
- What Students Learn from NCERT Solutions for Class 11 Chemistry Chapter 1
- NCERT Solutions for Class 11 Chemistry Chapter-Wise

The NCERT Solutions for Class 11 Chemistry help students develop analytical and problem solving abilities of students. These solutions of NCERT are designed by subject experts to provide easy and comprehensive explanations of every question. In this article, you will get an effective approach for solving questions and some higher order thinking skills (HOTS) questions that are beyond memorization and promote conceptual understanding, improve analytical thinking, enhance application skills.
NCERT Solution for Class 11 Chemistry Chapter 1: Download PDF
Students can download the NCERT Solutions for Class 11 Chemistry Chapter 1 Some Basic Concepts of Chemistry pdf from the icon given below. These solutions are designed to help you understand the fundamental concepts and solve textbook questions with ease.
NCERT Solutions for Class 11 Chemistry Chapter 1- (Exercise Questions)
Given below the class 11 chemistry chapter 1 some basic concepts of chemistry question answer. These solutions of NCERT cover all important questions from the chapter and provide clear, explanations. They help students strengthen their understanding of basic chemistry concepts and prepare effectively for exams.
Question 1.1 Calculate the molar mass of the following:
Answer :
The molar mass of Water $(H_{2}O)$ is:
$= 2\times Atomic\ mass\ of\ hydrogen\ + \ Atomic\ mass\ of\ oxygen$
$= 2\times(1.008\ u) + 16.00\ u$
$= 18.02\ u$
Question 1.1 Calculate the molar mass of the following:
(ii) $\mathrm{CO}_2$
Answer :
The molar mass of Carbon dioxide $CO_{2}$ is:
$= 1\times Atomic\ mass\ of\ carbon\ + \ 2\times Atomic\ mass\ of\ oxygen$
$= 1\times(12.011\ u) + 2\times (16.00\ u)$
$= 44.011\ u$
Question 1.1 Calculate the molar mass of the following:
(iii) $\mathrm{CH}_4$
Answer :
The molar mass of Methane $CH_{4}$ is:
$= 1\times Atomic\ mass\ of\ carbon\ + \ 4\times Atomic\ mass\ of\ hydrogen$
$= 1\times(12.011\ u) + 4\times (1.008\ u)$
$= 16.043\ u$
Question 1.2 Calculate the mass per cent of different elements present in sodium sulphate (Na2SO4).
Answer :
The different elements present in sodium sulphate are:
Sodium (Na), Sulphur (S), and Oxygen (O).
The molar mass of sodium sulphate $Na_{2}SO_{4}$ ; $= (2\times Atomic\ mass\ of\ Na) + (1\times Atomic\ mass\ of\ S) + (4\times Atomic\ mass\ of\ O)$
$= 2\times (23.0\ u) + (32.066\ u) + 4\times (16.00\ u)$
$= 142.066\ u$
So, the mass percentage of an element in a compound is given by,
$= \frac{Mass\ of\ element\ in\ the\ compound}{Molar\ mass\ of\ the\ compound} \times 100$
Therefore,
The mass per cent of Sodium (Na):
$=\frac{46.0\ u}{142.066\ u} \times 100$
$=32.379\%$
$\approx 32.4\%$
The mass per cent of Sulphur (S):
$=\frac{32.066\ u}{142.066\ u} \times 100$
$= 22.57 \%$
$\approx 22.6\%$
The mass per cent of Oxygen (O):
$=\frac{64.0\ u}{142.066\ u} \times 100$
$= 45.049 \%$
$\approx 45.0\%$
Question 1.3 Determine the empirical formula of an oxide of iron, which has 69.9% iron and 30.1% dioxygen by mass.
Answer :
Given there is an oxide of iron which has $69.9\%$ iron and $30.1\%$ dioxygen by mass:
Relative moles of iron in iron oxide:
$= \frac{\%\ of\ iron\ by\ mass}{Atomic\ mass\ of\ iron}$
$= \frac{69.9}{55.85} = 1.25$
Relative moles of oxygen in iron oxide:
$= \frac{\%\ of\ oxygen\ by\ mass}{Atomic\ mass\ of\ oxygen}$
$= \frac{30.1}{16.00} = 1.88$
The simplest molar ratio of iron to oxygen:
$\Rightarrow 1.25:1.88$ $\Rightarrow 1:1.5$ $\Rightarrow 2:3$
Therefore, the empirical formula of the iron oxide is $Fe_{2}O_{3}$ .
Question 1.4 Calculate the amount of carbon dioxide that could be produced when
(i) 1 mole of carbon is burnt in the air.
Answer :
When carbon is burnt in the air:
The chemical equation for this reaction is:
$C_{(s)}+O_{2(g)} \rightarrow CO_{2(g)}$
Here 1 mole of carbon (solid) weighing 12g is burnt in 1 mole of Dioxygen (gas) weighing 32g to produce 1 mole of carbon dioxide (gas) weighing 44g.
Question 1.4 Calculate the amount of carbon dioxide that could be produced when
(ii) 1 mole of carbon is burnt in 16 g of dioxygen.
Answer :
When carbon is burnt in 16 g of dioxygen:
The chemical equation for this reaction is:
$C_{(s)}+O_{2(g)} \rightarrow CO_{2(g)}$
Here, oxygen acts as a limiting reagent as only 16g of dioxygen is available.
Hence, it will react with 0.5 mole of carbon to give 22g of carbon dioxide.
Question 1.4 Calculate the amount of carbon dioxide that could be produced when
(iii) 2 moles of carbon are burnt in 16 g of dioxygen.
Answer :
When 2 moles of carbon is burnt in 16 g of dioxygen:
The chemical equation for this reaction is:
$C_{(s)}+O_{2(g)} \rightarrow CO_{2(g)}$
Here, oxygen acts as a limiting reagent as only 16g of dioxygen is available.
Thus, 16g of dioxygen will react with 0.5 mole of carbon to give 22g of carbon dioxide.
Answer :
$0.375$ molar aqueous solution would contain $0.375$ moles of $CH_{3}COONa$ dissolved in $1000mL$ of solvent.
So, we have to calculate for $500mL$ solution of $CH_{3}COONa$ .
Therefore the number of moles of sodium acetate in $500mL$ will be:
$= \frac{0.375}{1000}\times 500$
$=0.1875\ mole$
Given Molar mass of sodium acetate: $82.0245\ g\ mol^{-1}$
So, the required mass of sodium acetate $= (82.0245\ g\ mol^{-1})\times (0.1875\ mole)$
$= 15.38\ grams$
Answer :
Given the mass percentage of nitric acid is $69\%$ .
That means 69 grams of nitric acid are present in 100 grams of nitric acid solution.
The molar mass of nitric acid $HNO_{3}$ is $1+14+ 3\times (16) = 63g\ mol^{-1}$ .
So, the number of moles in 69g of Nitric acid:
$= \frac{69}{63}\ moles = 1.095\ moles$
and volume of 100g of the nitric acid solution:
$=\frac{100}{1.41}mL = 70.92mL = 0.07092\ L$
Therefore, the concentration of Nitric acid in moles per litre is:
$= \frac{1.095}{0.07092} = 15.44\ M$
Question 1.7 How much copper can be obtained from 100 g of copper sulphate (CuSO4 )?
Answer :
Given that 100g of Copper sulphate $CuSO_{4}$ ;
1 mole of $CuSO_{4}$ contains 1 mole of copper.
Molar Mass of Copper sulphate is:
$= 63.5 + 32.00 + 4\times 16.00 = 159.5g$
Now, $159.5g$ of copper sulphate contains $63.5g$ of copper.
So, $100g$ of copper sulphate will contain copper content:
$=\frac{63.5}{159.5}\times 100 = 39.81g$
Answer :
Given that the mass percentage of iron is $69.9\%$ and the mass percentage of oxygen is $30.1\%$
The atomic mass of iron $= 55.85\ u$ .
The atomic mass of oxygen $=16.00\ u$ .
So, the relative moles of iron in iron oxide will be:
$=\frac{mass\ of\ iron\ by\ mass}{Atomic\ mass\ of\ iron}$
$= \frac{69.9}{55.85} = 1.25$
And relative moles of oxygen in iron oxide will be:
$=\frac{mass\ of\ oxygen \ by\ mass}{Atomic\ mass\ of\ oxygen}$
$= \frac{30.01}{16.00} = 1.88$
Hence the simplest molar ratio:
$=\frac{1.25}{1.88}$ or $\Rightarrow 1:1.5 = 2:3$
Therefore, the empirical formula of iron oxide will be $Fe_{2}O_{3}$ .
Now, calculating the molar mass of $Fe_{2}O_{3}$ :
$=(2\times 55.85) + (3\times16.00) = 159.7g\ mol^{-1}$ .
Hence it is matching with the given molar mass of the oxide.
Question 1.9 Calculate the atomic mass (average) of chlorine using the following data:

Answer:
To calculate the average atomic mass of chlorine:
Given the fractional natural abundance of $_{}^{35}\textrm{Cl}$ with $34.9689\ u$ molar mass is $75.77\%$ and that of $_{}^{37}\textrm{Cl}$ with $36.9659\ u$ molar mass is $24.23\%$ .
Therefore we have,
Average Atomic mass of Chlorine:
$= \left ( 0.7577\times34.9689\ u \right ) + \left ( 0.2423\times36.9659\ u \right )$
$= 26.4959\ u + 8.9568\ u = 35.4527\ u$
Question 1.10 In three moles of ethane (C2H6), calculate the following:
(i) Number of moles of carbon atoms.
Answer:
Given there are three moles of Ethane $C_{2}H_{6}$ ;
So, 1 mole of $C_{2}H_{6}$ contains 2 moles of carbon atoms.
Therefore, 3 moles of $C_{2}H_{6}$ contains 6 moles of carbon atoms.
Question 1.10 In three moles of ethane (C2H6), calculate the following:
(ii) Number of moles of hydrogen atoms.
Answer :
Given there are three moles of Ethane $C_{2}H_{6}$ ;
So, 1 mole of $C_{2}H_{6}$ contains 6 moles of hydrogen atoms.
Therefore, 3 moles of $C_{2}H_{6}$ contains 18 moles of hydrogen atoms.
Question 1.10 In three moles of ethane (C2 H6), calculate the following:
(iii) Number of molecules of ethane.
Answer :
Given there are three moles of Ethane $C_{2}H_{6}$ ;
So, 1 mole of $C_{2}H_{6}$ contains $6.02\times 10^{23}$ molecules of ethane.
Therefore, 3 moles of $C_{2}H_{6}$ contains $3\times6.02\times 10^{23} = 18.06\times10^{23}$ molecules of ethane.
Question 1.11 What is the concentration of sugar (C12H22O11) in mol L-1 if its 20 g are dissolved in enough water to make a final volume up to 2L?
Answer :
The molar mass of sugar $C_{12}H_{22}O_{11}$ is:
$= (12\times12)+ (1\times 22)+(11\times16) = 342g\ mol^{-1}$ .
The number of moles of sugar in 20g of sugar will be:
$= \frac{20}{342} = 0.0585\ mole$
and given the volume of the solution after dissolving enough water is 2L .
$Molar\ concentration = \frac{Moles\ of\ solute}{Volume\ of\ solution\ in\ 1L}$
$= \frac{0.0585mol}{2L} = 0.0293mol\ L^{-1} = 0.0293\ M$
Question 1.12 If the density of methanol is 0.793 kg L-1 , what is its volume needed for making 2.5 L of its 0.25 M solution?
Answer :
Given that the density of methanol $CH_{3}OH$ is $0.793 Kg\ L^{-1}$ .
So, the number of moles present in the methanol per litre will be or the Molarity of the solution will be :
$= \frac{0.793Kg\ L^{-1}}{0.032Kg\ mol^{-1}} = 24.78\ mol\ L^{-1}$
Now, to make 2.5L of its 0.25M solution:
We will apply the formula: $M_{1}V_{1} (for\ given\ solution) = M_{2}V_{2} (for\ solution\ to\ be\ prepared)$
$24.78\times V_{1} =0.25\times 2.5L$
$V_{1} = 0.02522L\ or\ 25.22\ mL$ .
Hence $25.22\ mL$ volume will be required for making 2.5L of methanol 0.25M solution.
Answer :
The pressure is as given is force per unit area of the surface.
$Pressure = \frac{Force}{Area}$
Given to calculate the pressure exerted by the air on sea water, if the mass of air at sea level is $1034\ g\ cm^{-2}$ .
The force with which the air is exerting on the surface is:
$= \frac{1034g\times9.8ms^{-2}}{cm^2}\times\frac{1kg}{1000g}\times\frac{100cm}{1m} = 1.01332\times10^5\ N$
Now,
as $1 Pascal = 1N\ m^{-2}$
Therefore, $1.01332 \times 10^5 \mathrm{~N}^{-2}=1.01332 \times 10^5 \mathrm{~Pa}$
Question 1.14 What is the SI unit of mass? How is it defined?
Answer :
The SI unit of mass is Kilogram (Kg).
It is defined as the mass of platinum-iridium (Pt-Ir) cylinder that is stored in an air-tight jar at the International Bureau of Weigh and Measures in France.
Question 1.15 Match the following prefixes with their multiples:
Prefixes Multiples
| Prefixes | Multiples |
| (i) micro | 106 |
| (ii) deca | 109 |
| (iii) mega | 10-6 |
| (iv) giga | 10 -15 |
| (v) femto | 10 |
Answer :
Matched items are given in below table:
|
Prefixes |
Multiples |
|
(i) micro |
$10^{-6}$ |
|
(ii) Deca |
$10$ |
|
(iii) Mega |
$10^6$ |
|
(iv) Giga |
$10^9$ |
|
(v) femto |
$10^{-15}$ |
Question 1.16 What do you mean by significant figures?
Answer :
Significant figures are meaningful digits that are known with certainty including the last digit whose value is uncertain.
For example: if we write a result as 56.923 Kg, we say the 56.92 is certain and 3 is uncertain and the uncertainty would be $\pm 1$ in the last digit. Here we also include the last uncertain digit in the significant figures.
(i) Express this in per cent by mass.
Answer :
1ppm means 1 parts in million $(10^6)$ parts.
So, in percentage by mass:
We have,
$Percentage\ by\ mass = \frac{15}{10^6}\times 100 = 15\times10^{-4}$
$= 1.5\times10^{-3}\%$
(ii) Determine the molality of chloroform in the water sample .
Answer :
The molarity of chloroform sample in water will be:
$= \frac{number\ of\ moles\ present}{Volume\ of\ solution\ in\ L}$
The molar mass of Chloroform $CHCl_{3}$ :
$= 12+1+(3\times35.5) = 118.5g\ mol^{-1}$
So we have calculated in the previous part that percentage by mass of chloroform is $1.5\times10^{-3}$ .
Hence in 100g sample, there will be $1.5\times10^{-3}g$ of chloroform.
Therefore, 1000g (1Kg) of the sample will contain choroform $= 1.5\times10^{-2}g$ .
$= \frac{1.5\times10^{-2}}{118.65\ mol} = 1.266\times 10^{-4}\ mol$
Therefore, the molarity of chloroform in the water sample is $1.266\times 10^{-4}\ M$ .
Question 1.18 Express the following in the scientific notation:
(i) 0.0048
Answer :
The scientific notation of $0.0048$ will be $4.8\times 10^{-3}$ .
Question 1.18 Express the following in the scientific notation:
(ii) 234,000
Answer :
The scientific notation of $234,000$ will be $2.34\times10^5$ .
Question 1.18 Express the following in the scientific notation:
(iii) 8008
Answer :
The scientific notation of $8008$ will be $8.008\times 10^3$ .
Question 1.18 Express the following in the scientific notation:
(iv) 500.0
Answer :
The scientific notation of $500.0$ will be $5.000\times10^2$ .
Question 1.18 Express the following in the scientific notation:
(v) 6.0012
Answer :
The scientific notation of $6.0012$ will be $6.0012\times10^0$
Question 1.19 How many significant figures are present in the following?
(i) 0.0025
Answer :
There are 2 significant digits because all non-zero digits are in a number are significant and the zeros written to the left of the first non-zero digit in a number are non-significant.
Question 1.19 How many significant figures are present in the following?
(ii) 208
Answer :
There are 3 significant digits because all non-zero digits are in a number are significant and the zeros between two non-zero digits are always significant.
Question 1.19 How many significant figures are present in the following?
(iii) 5005
Answer :
There are 4 significant digits because all non-zero digits are in a number are significant and the zeros between two non-zero digits are always significant.
Question 1.19 How many significant figures are present in the following?
(iv) 126,000
Answer :
There are 3 significant digits because all non-zero digits are in a number are significant and the terminal zeros are not significant if there is no decimal point.
Question 1.19 How many significant figures are present in the following?
(v) 500.0
Answer :
There are 4 significant digits because the zeros written to the left of the first non-zero digit in a number are non-significant and all zeros placed to the right of a decimal point in a number are significant.
Question 1.19 How many significant figures are present in the following?
(vi) 2.0034
Answer :
There are 5 significant digits because all zeros placed to the right of a decimal point in a number are significant.
Question 1.20 Round up the following upto three significant figures:
(i) 34.216
Answer :
After round upto three significant figures:
Answer - $34.2$
Question 1.20 Round up the following upto three significant figures:
(ii) 10.4107
Answer :
After round upto three significant figures:
Answer - $10.4$ .
Question 1.20 Round up the following upto three significant figures:
(iii) 0.04597
Answer :
After round up to three significant figures:
Here the rightmost digit to be removed is more than 5 i.e., 7, then the preceding number is increased by one. So we get $0.0460$ .
Answer - $0.0460$
Question 1.20 Round up the following upto three significant figures:
(iv) 2808
Answer :
After round upto three significant figures:
Here the rightmost digit to be removed is more than 5 i.e., 8, then the preceding number is increased by one. So we get $2810$ .
Answer - $2810$
Answer :
Here if we fix the mass of dinitrogen at 14g, then the masses of dioxygen that will combine with the fixed mass of dinitrogen are 16g, 32g, 32g, and 80g.
The masses of dioxygen bear a whole number ratio of 1:2:2:5.
Hence, the given experimental data obeys the Law of Multiple Proportional .
The law given by Dalton states that "if two elements can combine to form more than one compound, the masses of one element that combine with a fixed mass of the other element, are in the ratio of small whole numbers".
Question 1.21 The following data are obtained when dinitrogen and dioxygen react together to form different compounds:
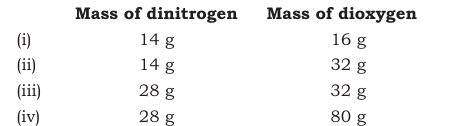
(b) Fill in the blanks in the following conversions:
(i) 1 km = ...................... mm = ...................... pm
(ii) 1 mg = ...................... kg = ...................... ng
(iii) 1 mL = ...................... L = ...................... dm3
Answer :
(i) As we know in
$1km = 1000m$
$1m = 1000mm$ .
or $1 km = 1000\times1000 mm =10^6 mm$
And $1pm = 1\times10^{-12}m$
or $1km = 10^{15} pm$
Therefore we have,
$1 km = 10^6 mm =10^{15} pm$
(ii) As we know in
$1kg = 1000g$
or $1g = 1000mg$ .
or $1 kg = 1000\times1000 mg$
or $1mg = \frac{1}{10^6} kg=10^{-6}kg$
And $1 ng = 10^{-9}g$
or $1ng = 10^{-9}\times1000mg$
or $1ng = 10^{-6}mg$
or $1 mg =10^6ng$ .
Therefore we have,
$1 mg = 10^{-6} kg =10^{6} ng$ .
(iii) As we know in
$1L= 1000mL$
or $1mL =\frac{1}{1000}L = 10^{-3}L$
or $1dm = 0.1 m \Rightarrow 1dm = 10cm$
or $1cm = 0.1dm$
And $1 m L=1 \mathrm{~cm}^3$
or we can write it as:
$1mL = \frac{1dm}{10cm}\times\frac{1dm}{10cm}\times\frac{1dm}{10cm}$
And $1mL = 10^{-3}dm^3$
Therefore we have,
$1mL = 10^{-3}L =10^{-3}dm^3$
Question 1.22 If the speed of light is $3.0 \times 10^8 m s^{-1}$ , calculate the distance covered by light in 2.00 ns.
Answer :
Given the speed of light to be $3.0 \times 10^8 m s^{-1}$ , so the distance covered by light in 2.00 ns. will be:
$Distance = Speed\times Time$
$Distance = (3.0\times10^{8}ms^{-1})\times(2.00\times10^{-9}sec) = 6.00\times10^{-1}m = 0.600m$
Therefore, the light will travel 0.600 metres in 2 nano seconds.
Question 1.23 In a reaction
$A + B_2 \rightarrow AB_2$
Identify the limiting reagent, if any, in the following reaction mixtures.
(i) 300 atoms of A + 200 molecules of B
Answer :
Here according to the reaction 1 atom of A reacts with 1 molecule of B.
Therefore, 200 molecules of atoms of B will react with 200 atoms of A, thereby left with 100 atoms of A unreacted.
Hence, B is the limiting reagent in this reaction.
Question 1.23 In a reaction
$A + B_2 \rightarrow AB_2$
Identify the limiting reagent, if any, in the following reaction mixtures.
(ii) 2 mol A + 3 mol B
Answer :
Here according to the reaction 1 atom of A reacts with 1 molecule of B.
Therefore, 2 mol of A atoms will react with only 2 mol of B molecules, thereby left with 1 mole of B unreacted.
Hence, A is the limiting reagent in this reaction.
Question 1.23 In a reaction
$A + B_2 \rightarrow AB_2$
Identify the limiting reagent, if any, in the following reaction mixtures.
(iii) 100 atoms of A + 100 molecules of B
Answer :
Here, according to the reaction 1 atom of A reacts with 1 molecule of B.
Therefore, all 100 atoms of A will react with 100 molecules of B, so the reaction is stoichiometric and there is no limiting reagent .
Hence, there is no limiting reagent in this reaction.
Question 1.23 In a reaction
$A + B_2 \rightarrow AB_2$
Identify the limiting reagent, if any, in the following reaction mixtures.
(iv) 5 mol A + 2.5 mol B
Answer :
Here, according to the reaction 1 atom of A reacts with 1 molecule of B.
Therefore, 2.5 moles of B molecules will react with only 2.5 moles of A atoms, thereby left with 2.5 moles of A unreacted.
Hence, B limiting reagent in this reaction.
Question 1.23 In a reaction
$A + B_2 \rightarrow AB_2$
Identify the limiting reagent, if any, in the following reaction mixtures.
(v) 2.5 mol A + 5 mol B
Answer :
Here according to the reaction 1 atom of A reacts with 1 molecule of B.
Therefore, 2.5 moles of A atoms will react with only 2.5 moles of B molecules, thereby left with 2.5 moles of B unreacted.
Hence, A limiting reagent in this reaction.
(i) Calculate the mass of ammonia produced if 2.00 × 10 3 g dinitrogen reacts with 1.00 ×103 g of dihydrogen.
Answer :
Given that if $2.00\times10^3g$ of dinitrogen reacts with $1.00\times10^3g$ of dihydrogen.
From the reaction we have:
1 mole of dinitrogen weighing 28g reacts with 3 moles of dihydrogen weighing 6g to give 2 moles of ammonia weighing 34g.
Therefore, $2.00\times10^3g$ of $N_{2}$ will react with $H_{2}$ $= \frac{6}{28}\times200g = 428.6g$ .
Thus, here $N_{2}$ is the limiting reagent while $H_{2}$ is in excess.
So, $28g$ of $N_{2}$ produces $34g$ of $NH_{3}$ .
Therefore, $2.00\times10^3g$ of $N_{2}$ will produce $= \frac{34}{28}\times 2000g = 2428.57g$ of $NH_{3}$ .
(ii) Will any of the two reactants remain unreacted?
Answer :
As from the previous part we have:
$N_{2}$ is the limiting reagent and $H_{2}$ is the excess reagent.
Hence, $H_{2}$ will remain unreacted.
(iii) If yes, which one and what would be its mass?
Answer :
Yes , $H_{2}$ will remain unreacted.
And the mass of dihydrogen left unreacted will be $=1000g-428.6g = 571.4g$ .
Question 1.25 How are 0.50 mol Na2CO3 and 0.50 M Na2CO3 different?
Answer :
Calculating the molar mass of $Na_{2}CO_{3}$ :
$= (2\times23)+12.00+(3\times16) = 106g\ mol^{-1}$
Therefore,
$0.50\ mol$ of $Na_{2}CO_{3}$ means:
$0.50\times106g = 53g$
whereas,
$0.50 M$ $Na_{2}CO_{3}$ means:
$0.50\ mol$ of $Na_{2}CO_{3}$ or $53g$ of $Na_{2}CO_{3}$ are present in 1litre of the solution.
Question 1.26 If 10 volumes of dihydrogen gas reacts with five volumes of dioxygen gas, how many volumes of water vapour would be produced?
Answer : For the given situation we have the reaction:
$2H_{2}(g)+O_{2}(g)\rightarrow2H_{2}O(g)$
Here, 2 volumes of dihydrogen gas react with 1 volume of dioxygen to produce 2 volumes of water vapour.
So, if 10 volumes of dihydrogen gas react with 5 volume of dioxygen then it will produce ( $2\times5 = 10$ volumes of water vapour.
Question 1.27 Convert the following into basic units:
(i) 28.7 pm
Answer :
To convert 28.7 pm into the basic units:
As $1pm = 10^{-12}m$ .
$\therefore$ $28.7\ pm = 28.7\times10^{-12}m = 2.87\times10^{-11}m$
Question 1.27 Convert the following into basic units:
(ii) 15.15 pm
Answer :
To convert 15.15 pm into the basic units:
As $1pm = 10^{-12}m$ .
$\therefore$ $15.15\ pm = 15.15\times10^{-12}m = 1.515\times10^{-11}m$
Question 1.27 Convert the following into basic units:
(iii) 25365 mg
Answer :
To convert 25365 mg into basic unit:
As $1mg = 10^{-3}g$ .
$\therefore$ $25365\ mg = 2.5365\times10^4\times10^{-3}g$
Now, as
$1 g= 10^{-3} kg$
$2.5365\times10g = 2.5365\times10\times10^{-3} kg$
$\therefore 25365\ mg = 2.5365\times 10^{-2}kg$
Answer :
Calculating and then comparing for each:
(i) 1 g of Au will contain:
$= \frac{1}{197}\ mol= \frac{1}{197}\times6.022\times10^{23}\ atoms.$
(ii) 1 g of Na will contain:
$= \frac{1}{23}\ mol= \frac{1}{23}\times6.022\times10^{23}\ atoms.$
(iii) 1 g of Li will contain:
$= \frac{1}{7}\ mol= \frac{1}{7}\times6.022\times10^{23}\ atoms.$
(iv) 1 g of Cl 2 will contain:
$= \frac{1}{71}\ mol= \frac{1}{71}\times6.022\times10^{23}\ atoms.$
Clearly, we can compare and say that the number of atoms in 1g of Li has the largest.
Question 1.29 Calculate the molarity of a solution of ethanol in water, in which the mole fraction of ethanol is 0.040 (assume the density of water to be one) .
Answer :
Given that the mole fraction of ethanol in water is $0.040$ .
$Mole\ fraction\ of\ ethanol\ = \frac{Number\ of\ moles\ of\ ethanol}{Total\ number\ of\ moles\ of\ solution}$
$\Rightarrow X_{ethanol} = \frac{n_{ethanol}}{n_{water}+n_{ethanol}} = 0.040$
To find the molarity we must have to find the number of moles of ethanol present in 1litre of solution.
Assuming the density of water to be $1 kg\ m^3$ .
Therefore, water is approximately equal to 1Litre.
The number of moles in 1L of water:
$= \frac{1000g}{18g}\ mol^{-1} = 55.55\ moles$
So, substituting in place of $n_{water} = 55.55$ in above equation we get,
$\Rightarrow X_{ethanol} = \frac{n_{ethanol}}{55.55+n_{ethanol}} = 0.040$
$\Rightarrow 0.96\times n_{ethanol} = 55.55\times0.040$
$n_{ethanol} = 2.31\ mol$
So, $2.31\ moles$ are present in 1L of solution.
Hence, the molarity of the solution is $2.31\ M$
Question 1.30 What will be the mass of one 12 C atom in g?
Answer :
As we know the mass of 1 mole of $_{}^{12}C\textrm{}$ atoms or $6.022\times10^{23}$ number of atoms is 12grams . Hence, the mass of one $_{}^{12}C\textrm{}$ atom will be: $\Rightarrow \frac{12}{6.022\times10^{23}g} = 1.9927\times10^{-23}g$
Question 1.31 How many significant figures should be present in the answer of the following calculation?
(i) $\frac{0.02856\times 298.12\times 0.112}{0.5785}$
Answer :
To find the number of significant figures that would be present in the answer, we will be finding the least precise term, having the least significant figures.
Here, the least precise term is 0.112 having only 3 significant digits.
Therefore, there will be 3 significant figures in the calculated answer.
Question 1.31 How many significant figures should be present in the answer of the following calculation?
(ii) $5\times 5.364$
Answer :
Here, $5.364$ is having 4 significant digits.
Therefore, after multiplying by 5 the answer would also have the same 4 significant figures .
Question 1.31 How many significant figures should be present in the answer of the following calculation?
(iii) 0.0125 + 0.7864 + 0.0215
Answer :
Here, the least number of decimal places in each term is four.
Therefore, the calculation would also have the same 4 significant figures .
Question 1.32 Use the data given in the following table to calculate the molar mass of naturally occuring argon isotopes:
|
Isotope |
Isotopic molar mass |
Abundance |
|
36 Ar |
35.96755 g mol -1 |
0.337% |
|
38 Ar |
37.96272 g mol -1 |
0.063% |
|
40 Ar |
39.9624 g mol -1 |
99.600% |
Answer :
For different isotopes of argon, we have given their naturally occurring abundances.
So, to calculate the molar mass:
Multiply the isotopic molar mass with their abundance to get the molar mass, and then add all of them to get,
$\therefore Molar\ Mass\ of Argon = \sum m_{i}A_{i}$
$= (35.96755\times0.337)+ (37.96272\times0.063)+(39.9624\times99.600)$
$= 39.948g\ mol^{-1}$
Question 1.33 Calculate the number of atoms
(i) 52 moles of Ar
Answer :
As 1 mole of air contains $6.022\times10^{23}$ atoms.
Therefore, 52 moles of Ar will contain $52\times6.022\times10^{23}$ atoms.
$\Rightarrow 3.131\times10^{25}\ atoms$ .
Question 1.33 Calculate the number of atoms
(ii) 52 u of He.
Answer :
As 1 atom of He weights 4 u.
Hence the number of atoms of He present in 52 u will be:
$=\frac{52\ u}{4\ u} = 13\ atoms$
Question 1.33 Calculate the number of atoms
(iii) 52 g of He.
Answer :
As 1 mole of He weights 4g and contains $6.022\times10^{23}$ atoms.
Therefore, $52g$ will contain $\frac{52}{4}moles = 13\ moles$ .
Hence, the number of atoms will be $13\times6.022\times10^{23}\ atoms$ .
$\Rightarrow 7.8286\times10^{24}\ atoms$ .
(i) empirical formula
Answer :
The amount of carbon in $3.38 g$ of $CO_{2}$ :
$= \frac{12}{44}\times3.38g = 0.9218g$
The amount of hydrogen in $0.690g$ of $H_{2}O$ :
$= \frac{2}{18}\times0.690g = 0.0767g$
The compound contains only C and H,
Therefore, the total mass of the compound will be:
$= 0.9218+0.0767 = 0.9985g$
Now, the percentage of Carbon in the compound:
$= (\frac{0.9218}{0.9985})\times100 = 92.32$
and the percentage of Hydrogen in the compound:
$= (\frac{0.0767}{0.9985})\times100 = 7.68$
Now, the empirical formula,
Moles of carbon in the compound:
$= \frac{92.32}{12} = 7.69$
Moles of hydrogen in the compound:
$= \frac{7.68}{1} = 7.68$
So, the simplest molar ratio will be $= 7.69:7.68 = 1:1$
Therefore, the empirical formula is $CH$ .
(ii) molar mass of the gas
Answer :
Weight of 10 Litres of the gas at S.T.P. is $11.6g$
The weight of 22.4 Litres of gas at S.T.P. will be:
$= \frac{11.6g}{10.0L}\times22.4L$
$= 25.984\ g\ mol^{-1}$
$\approx 26\ g\ mol^{-1}$
Question 1.34 A welding fuel gas contains carbon and hydrogen only. Burning a small sample of it in oxygen gives 3.38 g carbon dioxide, 0.690 g of water and no other products. A volume of 10.0 L (measured at STP) of this welding gas is found to weigh 11.6 g. Calculate
(iii) molecular formula.
Answer :
As we know the empirical formula from the previous part is $CH$ .
The mass of empirical formula $CH$ $= 12+1 =13$ .
Therefore,
$n = \frac{Molecular\ Mass}{Empirical\ Formula}$
$\Rightarrow \frac{26}{13} =2$
Therefore, Molecular formula is $C_{2}H_{2}$ .
Question 1.35 Calcium carbonate reacts with aqueous HCl to give CaCl2 and CO2 according to the reaction,
$CaCO_3 (s) + 2 HCl (aq) \rightarrow CaCl_2 (aq) + CO_2 (g) + H_2 O(l)$
What mass of CaCO3 is required to react completely with 25 mL of 0.75 M HCl?
Answer :
$0.75M$ $HCl$ contains $0.75\ mole$ in $1000mL$ of solution.
Or, $0.75\times36.5g = 24.375g$ of $HCl$ in $1000mL$ solution.
Therefore,
Mass of $HCl$ in $25mL$ of $0.75M\ HCl$ :
$= \frac{24.375}{1000}\times25 g = 0.6844g$
so, from the given chemical equation,
$CaCO_3 (s) + 2 HCl (aq) \rightarrow CaCl_2 (aq) + CO_2 (g) + H_2 O(l)$
1 mole of $CaCO_{3}(s)$ i.e., $100g$ reacts with 2 moles of $HCl(aq)$ i.e., $73g$ .
Therefore, $0.6844g$ $HCl$ reacts completely with $CaCO_{3}$ to give:
$=\frac{100}{73}\times 0.6844g = 0.938 g$
Question 1.36 Chlorine is prepared in the laboratory by treating manganese dioxide (MnO2 ) with aqueous hydrochloric acid according to the reaction
$4 HCl (aq) + MnO_2 (s) \rightarrow 2H_2 O (l) + MnCl_2 (aq) + Cl_2 (g)$
How many grams of HCl react with 5.0 g of manganese dioxide?
Answer :
Molar mass of $MnO_{2}$ is $55+32 g = 87g$ .
Here from the reaction 1 mole of $MnO_{2}$ reacts with 4 moles of $HCl$ ,
i.e., $4\times36.5g =146g$ of $HCl$ .
Therefore, $5.0 g$ of $MnO_{2}$ will react with $HCl$ :
$= \frac{146}{87}\times5.0g = 8.40g.$
Class 11 Chemistry NCERT Chapter 1: Higher Order Thinking Skills (HOTS) Questions
Some higher-order thinking skills questions based on class 11 chemistry chapter 1 some basic concepts of chemistry solutions are given below. These (HOTS) questions will help you think deeper.
Question 1. An unknown organic compound containing ‘amine’ as the functional group produces nitrogen gas on treatment with nitrous acid. On exhaustive methylation with methyl iodide, it forms a quaternary salt that contains 59.07% iodine. Evaluate the molecular mass of the quaternary salt and the number of carbon atoms in the unknown organic compound. Given, the atomic mass of $I=127 \mathrm{~g}$
(If the molecular mass of the quaternary salt is 123 g and the number of carbon atoms in the unknown organic compound is 4, report your answer as 123.04).
Answer:
The evolution of nitrogen upon treatment of the organic compound with nitrous acid suggests that the compound is a primary amine.
Now, 59.07 of iodine is present in 100 g of compound.
$\Rightarrow$ 127 g of iodine will be present in $\frac{100 \times 127}{59.07}=215 \mathrm{~g}$ of compound.
Thus, the molecular mass of quaternary salt =215 g.
Now, the quarternary ammonium salt is $R N\left(\mathrm{CH}_3\right)_3 I$
Mass balance gives,
R+14+45+127 = 215
Thus , R = 29
Therefore, R is C2H5
Thus, the unknown organic compound is ethanamine, which contains two carbon atoms.
Hence, the answer is (215).
Question 2. Among $10^{-9} \mathrm{~g}$ (each) of the following elements, which one will have the highest number of atoms?
Element : $\mathrm{Pb}, \mathrm{Po}, \mathrm{Pr}$ and Pt
(1) Po
(2) Pr
(3) Pb
(4) Pt
Answer:
$\text { No. of atoms }=\frac{\text { Mass}}{\text { MolarMas }(\mathrm{g} / \mathrm{mol})} \times \mathrm{N}_{\mathrm{A}}$
From this formula, it's clear that for a given mass, the element with the smallest molar mass will have the greatest number of atoms, as it appears in the denominator.
$\mathrm{M}_{\mathrm{P}_{\mathrm{o}}}=209$
$\mathrm{M}_{\mathrm{pr}}=141$
$\mathrm{M}_{\mathrm{Pb}}=207$
$\mathrm{M}_{\mathrm{Pt}}=195$
Pr has the lowest molar mass ( $M_{\mathrm{Pr}}=141 \mathrm{~g} / \mathrm{mol}$ ), $10^{-9}$ grams of Pr will contain the highest number of atoms compared to the other elements listed.
Hence, the correct answer is option (2).
Question 3: On combustion 0.210 g of an organic compound containing $\mathrm{C}, \mathrm{H}$ and O gave $0.127 \mathrm{~g} \mathrm{H}_2 \mathrm{O}$ and $0.307 \mathrm{~g} \mathrm{CO}_2$. The percentages of hydrogen and oxygen in the given organic compound respectively are:
(1) $53.41,39.6$
(2) $6.72,53.41$
(3) $7.55,43.85$
(4) $6.72,39.87$
Answer:
Mass of organic compound $=0.210 \mathrm{~g}$
Mass of water formed $=0.127 \mathrm{~g}$
Mass of $\mathrm{CO}_2$ formed $=0.307 \mathrm{~g}$
Mass of hydrogen $=\frac{0.127 \times 2}{18}=0.014 \mathrm{~g}$
Percentage of hydrogen $=\frac{0.014 \times 100}{0.210}=6.72 \%$
Mass of carbon $=\frac{0.307 \times 12}{44}=0.084 \mathrm{~g}$
Percentage of carbon $=\frac{0.084 \times 100}{0.210}=39.87 \%$
Percentage of oxygen $= 100- (39.87 + 6.72) = 53.41 \%$
Hence, the correct answer is option (2).
Question 4. An organic compound weighing 500 mg , produced 220 mg of $\mathrm{CO}_2$. on complete combustion. The percentage composition of carbon in the compound is________%. (nearest integer)
(Given molar mass in $\mathrm{g} \mathrm{mol}^{-1}$ of $\mathrm{C}: 12, \mathrm{O}: 16$ )
Answer:
Organic compound $\xrightarrow[\Delta]{\mathrm{CuO}} \mathrm{CO}_2+\mathrm{H}_2 \mathrm{O}$
$\mathrm{n}_{\mathrm{CO}_2}=\frac{220 \times 10^{-3}}{44}=5 \times 10^{-3}$ moles
$\mathrm{m}_{\mathrm{C}}=5 \times 10^{-3} \times 12$
$\%$ m carbon $=\frac{5 \times 10^{-3} \times 12}{500 \times 10^{-3}} \times 100=12 \%$
Hence, the answer is 12.
Question 5. Fortification of food with iron is done using $\mathrm{FeSO}_4 \cdot 7 \mathrm{H}_2 \mathrm{O}$. The mass in grams of the $\mathrm{FeSO}_4 \cdot 7 \mathrm{H}_2 \mathrm{O}$ required to achieve 12 ppm of iron in 150 kg of wheat is _________ (Nearest integer)
[Given : Molar mass of $\mathrm{Fe}, \mathrm{S}$ and O respectively are 56,32 and $\left.16 \mathrm{~g} \mathrm{~mol}^{-1}\right]$
Answer:
Let mass of iron = w g
$\begin{aligned}
& \Rightarrow \frac{\mathrm{w}}{150 \times 10^3} \times 10^6=12 \\
& \Rightarrow \mathrm{w}=150 \times 12 \times 10^{-3}=1.8 \mathrm{gm}
\end{aligned}$
Let mass of $\mathrm{FeSO}_4 \cdot 7 \mathrm{H}_2 \mathrm{O}=\mathrm{w}_1 \mathrm{gm}$
$\begin{aligned} & \Rightarrow \text { Moles of } \mathrm{Fe}=\frac{1.8}{56}=\left(\frac{\mathrm{w}_1}{56+96+7 \times 18}\right) \\ & \Rightarrow \mathrm{w}_1=8.935 \mathrm{gm}\end{aligned}$
Hence, the answer is 8.935gm
Question 6. Match the LIST-I with LIST-II
| LIST-I | LIST-II | ||
| A. | Carbocation | I. | Species that can supply a pair of electrons. |
| B. | C-Free radical | II. | Species that can receive a pair of electrons. |
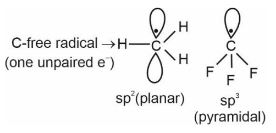
| C. | Nucleophile | III. | $\mathrm{sp}^2$ hybridized carbon with empty p-orbital. |
| D. | Electrophile | IV. | $\mathrm{sp}^2 / \mathrm{sp}^3$ hybridized carbon with one unpaired electron. |
Choose the correct answer from the options given below :
(1) A-IV, B-II, C-III, D-I
(2) A-II, B-III, C-I, D-IV
(3) A-III, B-IV, C-II, D-I
(4) A-III, B-IV, C-I, D-II
Answer:
Carbocation $\Rightarrow$ 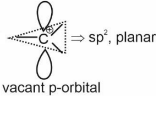
Nucleophile $\Rightarrow \mathrm{e}^{-}$rich species like anions etc.
$\Rightarrow$ can supply a pair of electrons
Electrophile $\Rightarrow \mathrm{e}^{-}$deficient species $\Rightarrow$ can receive
a pair of electrons.
Hence, the correct answer is option (4).
Question 7: Phosphorus and oxygen are heated together in a closed vessel to form $\mathrm{P}_2 \mathrm{O}_3$ and $\mathrm{P}_2 \mathrm{O}_5$ in a molar ratio of 2 : 1 respectively. The mass of oxygen taken is three times the mass of phosphorus. Assuming phosphorus reacts in its monoatomic form and that the limiting reactant is completely consumed, answer the following:
(1) Oxygen is the excess reactant and 76.8% (by mass) of it remains unreacted.
(2) Phosphorus is the excess reactant and 33.3% (by mass) of it remains unreacted.
(3) Oxygen is the limiting reactant and both oxides are formed completely.
(4) Both reactants are completely consumed.
Answer:
Formation of oxides in molar ratio :
$\mathrm{P}_2 \mathrm{O}_3: \mathrm{P}_2 \mathrm{O}_5=2: 1$
Mass of O taken =3×mass of P
$\begin{aligned} & 2 \mathrm{P}+3 \mathrm{O}_2 \rightarrow \mathrm{P}_2 \mathrm{O}_3 \\ & 4 \mathrm{P}+5 \mathrm{O}_2 \rightarrow \mathrm{P}_2 \mathrm{O}_5\end{aligned}$
Moles of Oxides formed
$\begin{aligned} & P_2 O_3=2 \mathrm{~mol} \\ & P_2 O_5=1 \mathrm{~mol}\end{aligned}$
For 2mol $\mathrm{P}_2 \mathrm{O}_3$
1mol needs 2P
Hence, 2mol needs 4P
And For 1mol $\mathrm{P}_2 \mathrm{O}_5$:
1mol needs 4P
Total P used = 4+4=8 mol
For 2mol $\mathrm{P}_2 \mathrm{O}_3$:1 mol needs $3 / 2 \mathrm{O}_2$
hence, 2 mol needs $3 \mathrm{O}_2$
For $1 \mathrm{~mol} \mathrm{P}_2 \mathrm{O}_5$ needs $5 / 2 \mathrm{O}_2$
Mass of P used $=8 \times 31=248 g$
Mass of O consumed $=5.5 \times 32=136 \mathrm{~g}$
Mass of $\mathrm{O}_2$ taken $=3 \times$ mass of $\mathrm{P}=3 \times 248=744 \mathrm{~g}$
Oxygen is excess;
Unreacted O = O taken-O consumed=744 g-176 g =568 g excess
$\%$ excess $02=744 / 568 \times 100=76.3 \%$
Hence, the correct answer is option (1)
Question 8: x mg of $\mathrm{Mg}(\mathrm{OH})_2($ molar mass $=58)$ is required to be dissolved in 1.0 L of water to produce a pH of 10.0 at 298 K . The value of x is ______ mg. (Nearest integer)
(Given : $\mathrm{Mg}(\mathrm{OH})_2$ is assumed to dissociate completely in $\mathrm{H}_2 \mathrm{O}$ )
Answer:
$\begin{aligned}
& \mathrm{pH}=10 \\
& \mathrm{pOH}=4 \\
& {\left[\mathrm{OH}^{-}\right]=10^{-4}}
\end{aligned}$
no. of moles of $\mathrm{OH}^{-}=10^{-4}$
$\begin{aligned}
& \text { no. of moles of } \mathrm{Mg}(\mathrm{OH})_2=\frac{10^{-4}}{2}=5 \times 10^{-5} \\
& \begin{aligned}
\text { mass of } \mathrm{Mg}(\mathrm{OH})_2 & (x)= moles \times molar mass \\
&5 \times 10^{-5} \times 58 \times 10^3 \mathrm{mg} \\
& =2.9 ~mg
\end{aligned}
\end{aligned}$
Hence, the answer is 2.9
Approach to Solve Questions of Class 11 Chemistry Chapter 1
To solve some basic concepts of chemistry class 11 question answer, it is important to follow a systematic approach. Given below the approaches to solve these questions effectively.
1. While solving questions from this chapter students are guided to first understand the basic concepts like SI Units & Measurements, Significant figures, Scientific notation, Dimensional analysis, and Laws of Chemical Combination.
2. Students must practice formulas like Atomic Mass and number of moles, Mole & Avogadro’s Number, Percentage Composition like Empirical Formula & Molecular Formula, and Stoichiometry.
3. Practice is the key to success; students must practice maximum questions from some basic concepts of chemistry ncert solutions
- Conversions of mass into moles and moles into the number of particles, empirical & Molecular formulas, finding % composition, converting % to grams, etc
- Find the moles of each element, determine the simplest ratio, which is the empirical formula, and use the particular molecular mass to find the actual formula.
- Stoichiometric Problems like using balanced equations, applying mole ratios, and identifying limiting reagents.
4. Given below are some important topics from class 11 chemistry chapter 1 some basic concepts of chemistry question answer that are asked in exams so students must practice them to score good marks
- Density & Molar Volume for gases, use 1 mole = 22.4 L at STP.
- Molarity (M) = Moles of solute / Volume of solution (L)
- Molality (m) = Moles of solute / Mass of solvent (kg)
- Mole Fraction (χ) = Moles of component / Total moles
- Percentage Purity: (Mass of pure substance / Total mass) × 100.
5. Practice NCERT Solutions for Class 11, as these questions are asked directly in boards and other competitive exams. For revision students can follow Class 11 Some Basic Concepts of Chemistry Notes. While solving questions, students must take care of a few basic points like, converting the units where required, and significant figures must be thoroughly checked.
NCERT Books and NCERT Syllabus
Topics and Subtopics Covered in the NCERT Textbook Class 11 Chemistry Chapter 1
Given below all the topics and subtopics covered in some basic concepts of chemistry class 11 question answer. These NCERT Solutions for Class 11 will help students quickly see what is included in the chapter and plan their studies in an organised way.
1.1 Importance of Chemistry
1.2 Nature of Matter
1.2.1 States of Matter
1.2.2. Classification of Matter
1.3 Properties of Matter and their Measurement
1.3.1 Physical and chemical properties
1.3.2 Measurement of physical properties
1.3.3 The International System of Units (SI)
1.3.4 Mass and Weight
1.3.5 Volume
1.3.6 Density
1.3.7 Temperature
1.4 Uncertainty in Measurement
1.4.1 Scientific Notation
1.4.2 Significant Figures
1.4.3 Dimensional Analysis
1.5 Laws of Chemical Combinations
1.5.1 Law of Conservation of Mass
1.5.2 Law of Definite Proportions
1.5.3 Law of Multiple Proportions
1.5.4 Gay Lussac's Law of Gaseous Volumes
1.5.5 Avogadro's Law
1.6 Dalton’s Atomic Theory
1.7 Atomic and Molecular Masses
1.7.1 Atomic Mass
1.7.2 Average Atomic Mass
1.7.3 Molecular Mass
1.7.4 Formula Mass
1.8 Mole Concept and Molar Masses
1.9 Percentage Composition
1.9.1 Empirical Formula for Molecular Formula
1.10 Stoichiometry and Stoichiometric Calculations
1.10.1 Limiting Reagent
1.10.2 Reactions in Solutions
What Extra Should Students Study Beyond the NCERT for JEE/NEET?
Beyond class 11 chemistry some basic concepts of chemistry question answer students need to focus on important concepts, theories, and their limitations according to the table given below. The table shows a comparison between topics that are included in the JEE syllabus and topics that are given in the NCERT textbook:
NCERT Class 11 Chemistry Chapter 1 Some Basic Concepts of Chemistry: Important Formulas
Some important formulas from the some basic concepts of chemistry ncert solutions are given below. These formulas are essential for solving numerical problems and understanding core concepts in the chapter.
1. The mass percent of an element
$\\Mass\:percent\:of\: an\: element =\frac{Mass \:of\:that\:element\:in \:the\:compound\times 100}{molar \:mass\:of\:the\:compound}$
2. Mass percent
$\\Mass\:percent =\frac{Mass \:of\:solute\times 100}{mass\:of\:solution}\\$
3. Mole fraction
$\\Mole\: fraction \:of \:A =\frac{No. \:of\:moles\:of\:A}{No.\:of\:moles\:of\:solutions}=\frac{n_A}{n_A+n_B}$
4. Molarity(M)
$\\M =\frac{No. \:of\:moles\:of\:solute}{Volume\:of\:solution\:in\:litres}$
5. Molality(m)
$\\m =\frac{No. \:of\:moles\:of\:solute}{Mass\:of\:solvent\:in\:Kg}$
NCERT Solutions for Class 11
What Students Learn from NCERT Solutions for Class 11 Chemistry Chapter 1
These some basic concepts of chemistry ncert solutions introduces students to the chemistry and their relationships. These solutions build the foundation for understanding how substances combine and react in definite proportions.These solutions also help students practice questions and prepare well for exams
- Students can easily understand the laws of chemical combination using these solutions.
- Fundamental concepts of chemistry like atoms, molecules, and molar mass are explained here very well.
- They learn about the mole concept and Avogadro number, which help in relating the amount of substance to the number of particles.
- In these class 11 chemistry some basic concepts of chemistry question answer stoichiometric calculations and chemical equations are explained very well.
- Methods to calculate empirical and molecular formulas are explained here.
NCERT Solutions for Class 11 Chemistry Chapter-Wise
Frequently Asked Questions (FAQs)
Chapter 1 of Class 11 Chemistry NCERT is titled Some Basic Concepts of Chemistry. It covers fundamental topics such as the laws of chemical combination, atomic and molecular masses, mole concept, Avogadro’s number, and stoichiometric calculations.
To prepare for Class 11 Chemistry, start by thoroughly reading the NCERT textbook to understand all concepts clearly. Make concise notes of important definitions, formulas, and reactions for quick revision. Solve all in-text and exercise questions to strengthen problem-solving skills, and regularly revise the topics.
This chapter covers several key laws, including the Law of Conservation of Mass, which states that mass cannot be created or destroyed in a chemical reaction, and the Law of Definite Proportions, which posits that a chemical compound always contains its constituent elements in a fixed ratio.
Stoichiometry is used to calculate the quantities of reactants and products in a chemical reaction. By using balanced chemical equations, stoichiometry allows chemists to predict how much of each substance is needed or produced.
An empirical formula represents the simplest whole-number ratio of elements in a compound, while the molecular formula shows the actual number of atoms of each element in a molecule.
NCERT solutions for Class 11 Chemistry help students by providing clear, step-by-step explanations of all textbook questions. They make complex concepts easier to understand, assist in solving numerical problems, and serve as a reliable resource for exam preparation and quick revision.
Some Basic Concepts of Chemistry is Chapter 1 of the Class 11 Chemistry textbook. It introduces fundamental ideas such as the laws of chemical combination, atoms and molecules, molar mass, the mole concept, Avogadro’s number, and stoichiometric calculations, forming the foundation for all further studies in chemistry.
The mole concept is crucial in chemistry because it provides a bridge between the atomic and macroscopic worlds. By using moles, chemists can count particles (atoms, molecules, ions) in a sample by weighing it, which simplifies calculations involving chemical reactions, stoichiometry, and concentrations.
To calculate the molar mass of a compound, you need to sum the atomic masses of all the atoms in the compound's chemical formula. This information can typically be found on the periodic table.
Avogadro's number, 6.022 x 10²³, is significant because it defines the number of particles in one mole of a substance. This concept allows for easy conversion between the mass of a substance and the number of atoms or molecules it contains, facilitating calculations in chemical reactions.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters