NCERT Solutions for Class 11 Maths Chapter 3 Trigonometric Functions

Q: How to solve trigonometric equations in Class 11 Maths Chapter 3?

To solve trigonometric equations in Class 11 Maths Chapter 3, express the given terms in basic trigonometric functions like sin, cos, and tan, then try to apply proper trigonometric identities and use simplification.

Q: What are the key formulas of Trigonometric Functions in NCERT Class 11?

The key formulas of Trigonometric Functions in NCERT Class 11 are: $1) \cos^2x+\sin^2x=1$ $2) 1+\tan^2x =\sec^2x$ $3)1+\cot^2x =\operatorname{cosec}^2x$ $4)\cos (2n\pi + x)= \cos x$ $5)\sin (2n\pi + x) = \sin x$ $6) \sin (-x) = -\sin x$ $7) \cos (-x)= \cos x$ $8)\cos (x + y) = \cos x \cos y - \sin x \sin y$ $9)\cos (x - y) = \cos x \cos y + \sin x \sin y$ $10)\sin (x + y) = \sin x \cos y + \cos x \sin y$ $11)\sin (x - y) = \sin x \cos y - \cos x \sin y$ $12) \tan(x+y)=\frac{\tan x+\tan y}{1-\tan x\tan y}$ $13) \tan(x-y)=\frac{\tan x-\tan y}{1+\tan x\tan y}$ $14) \cot(x+y)=\frac{\cot x\cot y-1}{\cot x+\cot y}$ $15) \cot(x-y)=\frac{1+\cot x\cot y}{\cot y-\cot x}$

Q: How to find the general solution of a trigonometric equation?

To find the general solution of a trigonometric equation, use the following standard equations: $\sin \theta=\sin \alpha \Rightarrow \theta=n \pi+(-1)^n \alpha, n \in \mathbb{Z}$ $\cos \theta=\cos \alpha \Rightarrow \theta=2 n \pi \pm \alpha, n \in \mathbb{Z}$ $\tan \theta=\tan \alpha \Rightarrow \theta=n \pi+\alpha, n \in \mathbb{Z}$

Q: What are the domain and range of trigonometric functions in Class 11?

In class 11 chapter 3 trigonometric functions, a domain basically denotes the input values and range denotes the output values. For example: The domain of $\sin\theta$ and $\cos\theta$ is $(-\infty,\infty)$ and range is (–1, 1).

Q: How to derive the sine and cosine function graphs?

To derive the sine and cosine function graphs, plot $y=\sin\theta$ and $y=\cos\theta$ for the values of $\theta$ like 0°, 30°, 60°, 90°, 180°, etc.. The sine graph starts at (0, 0) and goes up to 1 at 90°, drops to –1 at 270°, and comes to 0 again at 360° then repeats.

NCERT Solutions for Class 11 Maths Chapter 3 Trigonometric Functions

Edited By Komal Miglani | Updated on Jun 19, 2025 09:54 PM IST

Have you ever wondered how engineers design huge buildings, how sailors and pilots navigate their journey, or how shadows change their length throughout the day? You can find all these answers in trigonometry, a fascinating branch of mathematics. In class 11 Maths NCERT chapter 3, trigonometric functions, contains the advanced concepts of trigonometry like radian measure, relation between degree and radian, sign of trigonometric functions, graphs of trigonometric functions, domain and range of trigonometric functions, and trigonometric functions of the sum and difference of two angles. Understanding these concepts will make students more efficient in solving problems involving height, distance, and angles. NCERT solutions of class 11 of trigonometric functions will also build a strong foundation for more advanced trigonometric concepts, which have many practical, real-life applications like construction, navigation, architecture, etc.

JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy

Suggested: JEE Main: high scoring chapters | Past 10 year's papers

This Story also Contains

NCERT Solution for Class 11 Maths Chapter 3 Solutions: Download PDF
Trigonometric Functions Class 11 NCERT Solutions (Exercises)
Class 11 Maths NCERT Chapter 3: Extra Question
Trigonometric Functions Class 11 Chapter 3: Topics
Trigonometric Functions Class 11 Solutions: Important Formulae
Approach to Solve Questions of Trigonometric Functions Class 11
What Extra Should Students Study Beyond NCERT for JEE?
NCERT Solutions for Class 11 Mathematics - Chapter Wise

NCERT Solutions for Class 11 Maths Chapter 3 Trigonometric Functions

This article on NCERT solutions for class 11 Maths Chapter 3 Trigonometric Functions offers clear and step-by-step solutions for the exercise problems in the NCERT Class 11 Maths Book. Students requiring trigonometric functions class 11 solutions will find this article useful. It covers all the important Class 11 Maths Chapter 3 question answers and concepts of trigonometric functions. According to the latest CBSE syllabus, the experienced Subject Matter Experts of Careers360 have curated these trigonometric functions class 11 NCERT solutions, ensuring that students can grasp the basic concepts effectively. For syllabus, notes, and PDF, refer to this link: NCERT

NCERT Solution for Class 11 Maths Chapter 3 Solutions: Download PDF

Download PDF

Trigonometric Functions Class 11 NCERT Solutions (Exercises)

NCERT Trigonometric Functions Class 11 Solutions: Exercise: 3.1

Page Number: 48-49

Total Questions: 7

Question 1: Find the radian measures corresponding to the following degree measures:

(i) $25^{\circ}$
(ii) $- 47^{\circ}$ $30^{'}$
(iii) $240^{\circ}$
(iv) $520^{\circ}$

Answer:

It is solved using the relation between degree and radian
(i) $25^{\circ}$
We know that $180^{\circ}$ = $π$ radian
So, $1^{\circ} = \frac{π}{180}$ radian
$25^{\circ} = \frac{π}{180} \times 25$ radian $= \frac{5 π}{36}$ radian

(ii) $- 47^{\circ} 30^{'}$
We know that
$- 47^{\circ} 30^{'} = - 47 {\frac{1}{2}}^{\circ} = - {\frac{95}{2}}^{\circ}$
Now, we know that $180^{\circ} = π \Rightarrow 1^{\circ} = \frac{π}{180}$ radian
So, $- {\frac{95}{2}}^{\circ} = \frac{π}{180} \times (- \frac{95}{2})$ radian $= \frac{- 19 π}{72}$ radian

(iii) $240^{\circ}$
We know that
$180^{\circ} = π \Rightarrow 1^{\circ} = \frac{π}{180}$ radian
So, $240^{\circ} = \frac{π}{180} \times 240 = \frac{4 π}{3}$ radian

(iv) $520^{\circ}$
We know that
$180^{\circ} = π \Rightarrow 1^{\circ} = \frac{π}{180}$ radian
So, $520^{\circ} = \frac{π}{180} \times 520$ radian $= \frac{26 π}{9}$ radian

Question 2: Find the degree measures corresponding to the following radian measures. (Use $π = \frac{22}{7}$ )

$(i) \frac{11}{16}$
$(i i) - 4$
$(i i i) \frac{5 π}{3}$
$(i v) \frac{7 π}{6}$

Answer:

(i) $\frac{11}{16}$
We know that
$π$ radian $= 180^{\circ} \Rightarrow 1 r a d i a n = {\frac{180}{π}}^{\circ}$
So, $\frac{11}{16} r a d i a n = \frac{180}{π} \times {\frac{11}{16}}^{\circ}$ (we need to take $π = \frac{22}{7}$ )
$\frac{11}{16} r a d i a n = \frac{180 \times 7}{22} \times {\frac{11}{16}}^{\circ} = {\frac{315}{8}}^{\circ}$
(we use $1^{\circ} = 60^{'}$ and 1' = 60'')
Here 1' represents 1 minute and 60" represents 60 seconds
Now,
${\frac{315}{8}}^{\circ} = 39 {\frac{3}{8}}^{\circ} = 39^{\circ} + {\frac{3 \times 60}{8}}^{'} = 39^{\circ} + 22^{'} + {\frac{1}{2}}^{'} = 39^{\circ} + 22^{'} + 30^{″} = {\frac{315}{8}}^{\circ} = 39^{\circ} 22^{'} 30^{″}$

(ii) $- 4$
We know that
$π$ radian $= 180^{\circ} \Rightarrow 1 r a d i a n = {\frac{180}{π}}^{\circ}$ (we need to take $π = \frac{22}{7}$ )
So, $- 4 r a d i a n = \frac{- 4 \times 180}{π} = \frac{- 4 \times 180 \times 7}{22} = - {\frac{2520}{11}}^{\circ}$
(we use $1^{\circ} = 60^{'}$ and 1' = 60'')
$\Rightarrow {\frac{- 2520}{11}}^{\circ} = - 229 {\frac{1}{11}}^{\circ} = - 229^{\circ} + {\frac{1 \times 60}{11}}^{'} = - 229^{\circ} + 5^{'} + {\frac{5}{11}}^{'} = - 229^{\circ} + 5^{'} + 27^{″} = - 229^{\circ} 5^{'} 27^{″}$

(iii) $\frac{5 π}{3}$
We know that
$π$ radian $= 180^{\circ} \Rightarrow 1 r a d i a n = {\frac{180}{π}}^{\circ}$ (we need to take $π = \frac{22}{7}$ )
So, $\frac{5 π}{3} r a d i a n = \frac{180}{π} \times {\frac{5 π}{3}}^{\circ} = 300^{\circ}$

(iv) $\frac{7 π}{6}$
We know that
$π$ radian $= 180^{\circ} \Rightarrow 1 r a d i a n = {\frac{180}{π}}^{\circ}$ (we need to take $π = \frac{22}{7}$ )
So, $\frac{7 π}{6} r a d i a n = \frac{180}{π} \times \frac{7 π}{6} = 210^{\circ}$

Question 3: A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?

Answer:
Number of revolutions made by the wheel in 1 minute = 360
$∴$ Number of revolutions made by the wheel in 1 second = $\frac{360}{60} = 6$
( $∵$ 1 minute = 60 seconds)
In one revolution, the wheel will cover $2 π$ radian
So, in 6 revolutions it will cover = $6 \times 2 π = 12 π$ radian
$∴$ In 1 the second wheel will turn $12 π$ radian.

Question 4: Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm (use $π = \frac{22}{7}$ )

Answer:
We know that
$l = r θ$ ( where $l$ is the length of the arc, $r$ is the radius of the circle and $θ$ is the angle subtended)
here $r$ = 100 cm
and $l$ = 22 cm
Now,
$θ = \frac{l}{r} = \frac{22}{100}$ radian
We know that
$π r a d i a n = 180^{\circ}$
So, 1 radian = ${\frac{180}{π}}^{\circ}$
$∴ \frac{22}{100} r a d i a n = \frac{180}{π} \times {\frac{22}{100}}^{\circ} = \frac{180 \times 7}{22} \times \frac{22}{100} = {\frac{63}{5}}^{\circ}$
So, ${\frac{63}{5}}^{\circ} = 12 {\frac{3}{5}}^{\circ} = 12^{\circ} + {\frac{3 \times 60}{5}}^{'} = 12^{\circ} + 36^{'} = 12^{\circ} 36^{'}$
Thus, the angle subtended at the centre of a circle $θ = 12^{\circ} 36^{'}$ .

Question 5: In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.

Answer:
Given: radius ( $r$ ) of circle = $\frac{D i a m e t e r}{2} = \frac{40}{2} = 20$ cm
length of chord = 20 cm
We know that
$θ = \frac{l}{r}$ ( $r$ = 20 cm , $l$ = ? , $θ$ = ?)
Now,
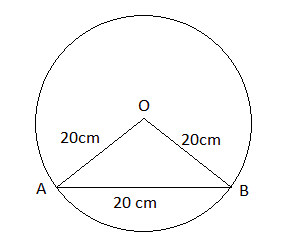
1654678632225
AB is the chord of length 20 cm and OA and OB are radii of circle i.e. 20 cm each
The angle subtended by OA and OB at centre = $θ$
$∵$ OA = OB = AB
$∴$ $Δ$ OAB is equilateral triangle
So, each angle is $60^{\circ}$
$∴$ $θ = 60^{\circ}$ $= \frac{π}{3}$ radian
Now, we have $θ$ and $r$
So, $l = r θ = 20 \times \frac{π}{3} = \frac{20 π}{3}$
$∴$ the length of the minor arc of the chord ( $l$ ) = $\frac{20 π}{3}$ cm.

Question 6: If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii.

Answer:
Given: $θ_{1} = 60^{\circ}, θ_{2} = 75^{\circ}$ and $l_{1} = l_{2}$
We need to find the ratio of their radii $\frac{r_{1}}{r_{2}}$
We know that arc length $l = r θ$
So, $l_{1} = r_{1} θ_{1}$ and $l_{2} = r_{2} θ_{2}$
Now, $l_{1} = l_{2}$
So, $\frac{r_{1}}{r_{2}} = \frac{θ_{2}}{θ_{1}} = \frac{75}{60} = \frac{5}{4}$ , which is the ratio of their radii.

Question 7: Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
(i) 10 cm
(ii) 15 cm
(iii) 21 cm

Answer:
(i) We know that
$l = r θ$
Now,
$r$ = 75 cm
$l$ = 10 cm
So,
$θ = \frac{l}{r} = \frac{10}{75} = \frac{2}{15}$ radian

(ii) We know that
$l = r θ$
Now,
$r$ = 75 cm
$l$ = 15 cm
So,
$θ = \frac{l}{r} = \frac{15}{75} = \frac{1}{5}$ radian

(iii) We know that
$l = r θ$
Now,
$r$ = 75 cm
$l$ = 21 cm
So,
$θ = \frac{l}{r} = \frac{21}{75} = \frac{7}{25}$ radian

NCERT Trigonometric Functions Class 11 Solutions: Exercise: 3.2

Page Number: 57

Total Questions: 10

Question 1: Find the values of other five trigonometric functions as $\cos x = - \frac{1}{2}$ , $x$ lies in third quadrant.

Answer:
$\cos x = - \frac{1}{2}$
$∵ \sec x = \frac{1}{\cos x} = \frac{1}{- \frac{1}{2}} = - 2$
$x$ lies in III quadrants. Therefore sec x is negative
$\sin^{2} x + \cos^{2} x = 1 \Rightarrow \sin^{2} x = 1 - \cos^{2} x$
$\Rightarrow \sin^{2} x = 1 - {(- \frac{1}{2})}^{2} \Rightarrow \sin^{2} x = 1 - \frac{1}{4} = \frac{3}{4} \Rightarrow \sin x = \sqrt{\frac{3}{4}} = \pm \frac{\sqrt{3}}{2}$
$x$ lies in III quadrants. Therefore sin x is negative
$∴ \sin x = - \frac{\sqrt{3}}{2}$
$∵ c o s e c x = \frac{1}{\sin x} = \frac{1}{- \frac{\sqrt{3}}{2}} = - \frac{2}{\sqrt{3}}$
$x$ lies in III quadrants. Therefore cosec x is negative
$\tan x = \frac{\sin x}{\cos x} = \frac{- \frac{\sqrt{3}}{2}}{- \frac{1}{2}} = \sqrt{3}$
$x$ lies in III quadrants. Therefore tan x is positive
$\cot x = \frac{1}{\tan x} = \frac{1}{\sqrt{3}}$
$x$ lies in III quadrants. Therefore cot x is positive.

Question 2: Find the values of other five trigonometric functions as $\sin x = \frac{3}{5}$ , $x$ lies in second quadrant.

Answer:
$\sin x = \frac{3}{5}$
$c o s e c x = \frac{1}{\sin x} = \frac{1}{\frac{3}{5}} = \frac{5}{3}$
$x$ lies in the second quadrant. Therefore cosec x is positive
$\sin^{2} x + \cos^{2} x = 1 \Rightarrow \cos^{2} x = 1 - \sin^{2} x$
$\Rightarrow \cos^{2} x = 1 - {(\frac{3}{5})}^{2} \Rightarrow \cos^{2} x = 1 - \frac{9}{25} = \frac{16}{25} \Rightarrow \cos x = \sqrt{\frac{16}{25}} = \pm \frac{4}{5}$
$x$ lies in the second quadrant. Therefore cos x is negative
$∴ \cos x = - \frac{4}{5}$
$\sec x = \frac{1}{\cos x} = \frac{1}{- \frac{4}{5}} = - \frac{5}{4}$
$x$ lies in the second quadrant. Therefore sec x is negative
$\tan x = \frac{\sin x}{\cos x} = \frac{\frac{3}{5}}{- \frac{4}{5}} = - \frac{3}{4}$
$x$ lies in the second quadrant. Therefore tan x is negative
$\cot x = \frac{1}{\tan x} = \frac{1}{- \frac{3}{4}} = - \frac{4}{3}$
$x$ lies in the second quadrant. Therefore cot x is negative.

Question 3: Find the values of other five trigonometric functions as $\cot x = \frac{3}{4}$ , $x$ lies in third quadrant.

Answer:
$\cot x = \frac{3}{4}$
$\tan x = \frac{1}{\cot x} = \frac{1}{\frac{3}{4}} = \frac{4}{3}$
$1 + \tan^{2} x = \sec^{2} x \Rightarrow 1 + \frac{4^{2}}{3^{2}} = \sec^{2} x \Rightarrow 1 + \frac{16}{9} = \sec^{2} x \Rightarrow \frac{25}{9} = \sec^{2} x$
$\Rightarrow \sec x = \sqrt{\frac{25}{9}} = \pm \frac{5}{3}$
$x$ lies in x lies in third quadrant. therefore sec x is negative
$\sec x = - \frac{5}{3}$
$\cos x = \frac{1}{\sec x} = \frac{1}{- \frac{5}{3}} = - \frac{3}{5}$
$\sin^{2} x + \cos^{2} x = 1 \Rightarrow \sin^{2} x = 1 - \cos^{2} x$
$\Rightarrow \sin^{2} x = 1 - {(- \frac{3}{5})}^{2} \Rightarrow \sin^{2} x = 1 - \frac{9}{25} \Rightarrow \sin^{2} x = \frac{16}{25} \Rightarrow \sin x = \sqrt{\frac{16}{25}} = \pm \frac{4}{5}$
$x$ lies in third quadrant. Therefore sin x is negative
$\sin x = - \frac{4}{5}$
$c o s e c x = \frac{1}{\csc} = \frac{1}{- \frac{4}{5}} = - \frac{5}{4}$ .

Question 4: Find the values of other five trigonometric functions as $\sec x = \frac{13}{5}$ , $x$ lies in fourth quadrant.

Answer:
$\sec x = \frac{13}{5}$
$\cos x = \frac{1}{\sec x} = \frac{1}{\frac{13}{5}} = \frac{5}{13}$
$\sin^{2} x + \cos^{2} x = 1 \Rightarrow \sin^{2} x = 1 - \cos^{2} x$
$\Rightarrow \sin^{2} x = 1 - (\frac{5}{13})^{2} \Rightarrow \sin^{2} x = 1 - \frac{25}{169} = \frac{144}{169} \Rightarrow \sin x = \sqrt{\frac{144}{169}} = \pm \frac{12}{13}$
$x$ lies in fourth quadrant. Therefore $\sin x$ is negative.
$\sin x = - \frac{12}{13}$
$\csc x = \frac{1}{\sin x} = \frac{1}{- \frac{12}{13}} = - \frac{13}{12}$
$\tan x = \frac{\sin x}{\cos x} = \frac{- \frac{12}{13}}{\frac{5}{13}} = - \frac{12}{5}$
$\cot x = \frac{1}{\tan x} = \frac{1}{- \frac{12}{5}} = - \frac{5}{12}$ .

Question 5: Find the values of the other five trigonometric functions as $\tan x = - \frac{5}{12}$ , $x$ lies in second quadrant.

Answer:
$\tan x = - \frac{5}{12}$
$\cot x = \frac{1}{\tan x} = \frac{1}{- \frac{5}{12}} = - \frac{12}{5}$
$1 + \tan^{2} x = \sec^{2} x \Rightarrow 1 + {(- \frac{5}{12})}^{2} = \sec^{2} x \Rightarrow 1 + \frac{25}{144} = \sec^{2} x \Rightarrow \frac{169}{144} = \sec^{2} x$
$\Rightarrow \sec x = \sqrt{\frac{169}{144}} = \pm \frac{13}{12}$
$x$ lies in second quadrant. Therefore the value of $\sec x$ is negative
$\sec x = - \frac{13}{12}$
$\cos x = \frac{1}{\sec x} = \frac{1}{- \frac{13}{12}} = - \frac{12}{13}$
$\sin^{2} x + \cos^{2} x = 1 \Rightarrow \sin^{2} x = 1 - \cos^{2} x$
$\Rightarrow \sin^{2} x = 1 - {(- \frac{12}{13})}^{2} \Rightarrow \sin^{2} x = 1 - \frac{144}{169} \Rightarrow \sin^{2} x = \frac{25}{169} \Rightarrow \sin x = \sqrt{\frac{25}{169}} = \pm \frac{5}{13}$
$x$ lies in the second quadrant.
Therefore the value of $\sin x$ is positive.
$\sin x = \frac{5}{13}$
$\csc = \frac{1}{\sin x} = \frac{1}{\frac{5}{13}} = \frac{13}{5}$ .

Question 6: Find the values of the trigonometric functions $\sin 765^{\circ}$

Answer:
We know that values of $\sin x$ repeat after an interval of $2 π$ or $360^{\circ}$
$\sin 765^{\circ} = \sin (2 \times 360^{\circ} + 45^{\circ}) = \sin 45^{\circ} = \frac{1}{\sqrt{2}}$ .

Question 7: Find the values of the trigonometric functions $c o s e c (- 1410^{\circ})$

Answer:
We know that value of $cosec x$ repeats after an interval of $2 π$ or $360^{\circ}$ .
$cosec (- 1410^{\circ}) = cosec (360^{\circ} \times 4 + (- 1410^{\circ})) = cosec 30^{\circ} = 2$

Question 8: Find the values of the trigonometric functions $\tan \frac{19 π}{3}$

Answer:
We know that $\tan x$ repeats after an interval of $π$ or 180 $^{\circ}$ .
$\tan (\frac{19 π}{3}) = \tan (6 π + \frac{π}{3}) = \tan \frac{π}{3} = \tan 60^{\circ} = \sqrt{3}$

Question 9: Find the values of the trigonometric functions $\sin (- \frac{11 π}{3})$

Answer:
We know that $\sin x$ repeats after an interval of $2 π$ or $360^{\circ}$
$\sin (- \frac{11 π}{3}) = \sin (4 π + (- \frac{11 π}{3})) = \sin \frac{π}{3} = \frac{\sqrt{3}}{2}$

Question 10: Find the values of the trigonometric functions $\cot (- \frac{15 π}{4})$

Answer:
We know that $\cot x$ repeats after an interval of $π$ or 180 $^{\circ}$ .
$\cot (- \frac{15 π}{4}) = \cot (4 π + (- \frac{15 π}{4})) = \cot (\frac{π}{4}) = 1$

NCERT Trigonometric Functions Class 11 Solutions: Exercise: 3.3

Page Number: 67-68

Total Questions: 25

Question 1: Prove that $\sin^{2} (\frac{π}{6}) + \cos^{2} (\frac{π}{3}) - \tan^{2} (\frac{π}{4}) = - \frac{1}{2}$

Answer:
We know the values of sin 30°, cos 60°, and tan 45°.
$\sin (\frac{π}{6}) = (\frac{1}{2}), \cos (\frac{π}{3}) = (\frac{1}{2}), \tan (\frac{π}{4}) = 1$
L.H.S. $= \sin^{2} \frac{π}{6} + \cos^{2} \frac{π}{3} - \tan^{2} \frac{π}{4} =$ ${(\frac{1}{2})}^{2} + {(\frac{1}{2})}^{2} - 1^{2}$
$= \frac{1}{4} + \frac{1}{4} - 1 = - \frac{1}{2} =$ R.H.S.

Question 2: Prove that $2 \sin^{2} (\frac{π}{6}) + {cosec}^{2} (\frac{7 π}{6}) \cos^{2} \frac{π}{3} = \frac{3}{2}$

Answer:
$\sin \frac{π}{6} = \frac{1}{2}, cosec \frac{7 π}{6} = cosec (π + \frac{π}{6}) = - cosec \frac{π}{6} = - 2, \cos \frac{π}{3} = \frac{1}{2}$
L.H.S. = $2 \sin^{2} \frac{π}{6} + {cosec}^{2} \frac{7 π}{6} \cos^{2} \frac{π}{3} = 2 {(\frac{1}{2})}^{2} + {(- 2)}^{2} {(\frac{1}{2})}^{2} = 2 \times \frac{1}{4} + 4 \times \frac{1}{4} = \frac{1}{2} + 1 = \frac{3}{2}$
= R.H.S.

Question 3: Prove that $\cot^{2} (\frac{π}{6}) + \csc (\frac{5 π}{6}) + 3 \tan^{2} (\frac{π}{6}) = 6$

Answer:
We know the values of cot 30°, tan 30°, and cosec 30°.
$\cot \frac{π}{6} = \sqrt{3}, cosec \frac{5 π}{6} = cosec (π - \frac{π}{6}) = cosec \frac{π}{6} = 2, \tan \frac{π}{6} = \frac{1}{\sqrt{3}}$
L.H.S. $= \cot^{2} \frac{π}{6} + cosec \frac{5 π}{6} + 3 \tan^{2} \frac{π}{6} = {(\sqrt{3})}^{2} + 2 + 3 \times {(\frac{1}{\sqrt{3}})}^{2} = 3 + 2 + 1 = 6 =$ R.H.S.

Question 4: Prove that $2 \sin^{2} (\frac{3 π}{4}) + 2 \cos^{2} (\frac{π}{4}) + 2 \sec^{2} (\frac{π}{3}) = 10$

Answer:
$\sin \frac{3 π}{4} = \sin (π - \frac{π}{4}) = \sin \frac{π}{4} = \frac{1}{\sqrt{2}}, \cos \frac{π}{4} = \frac{1}{\sqrt{2}}, \sec \frac{π}{3} = 2$
Using the above values
L.H.S. $= 2 \sin^{2} \frac{3 π}{4} + 2 \cos^{2} \frac{π}{4} + 2 \sec^{2} \frac{π}{3} = 2 \times {(\frac{1}{\sqrt{2}})}^{2} + 2 \times {(\frac{1}{\sqrt{2}})}^{2} + 2 {(2)}^{2} \Rightarrow 1 + 1 + 8 = 10 =$ R.H.S.

Question 5(i): Find the value of $(i) \sin 75^{\circ}$

Answer:
$\sin 75^{\circ} = \sin (45^{\circ} + 30^{\circ})$
We know that
$\sin (x + y) = \sin x \cos y + \cos x \sin y$
Using this idendity
$\sin 75^{\circ} = \sin (45^{\circ} + 30^{\circ}) = \sin 45^{\circ} \cos 30^{\circ} + \cos 45^{\circ} \sin 30^{\circ}$
$= \frac{1}{\sqrt{2}} \times \frac{\sqrt{3}}{2} + \frac{1}{\sqrt{2}} \times \frac{1}{2} \Rightarrow \frac{\sqrt{3}}{2 \sqrt{2}} + \frac{1}{2 \sqrt{2}} = \frac{\sqrt{3} + 1}{2 \sqrt{2}}$

Question 5 (ii): Find the value of
$(i i) \tan 15^{\circ}$

Answer:
$\tan 15^{\circ} = \tan (45^{\circ} - 30^{\circ})$
We know that,
$[\tan (x - y) = \frac{\tan x - \tan y}{1 + \tan x \tan y}]$
By using this we can write,
$\tan (45^{\circ} - 30^{\circ}) = \frac{\tan 45^{\circ} - t a n 30^{\circ}}{1 + \tan 45^{\circ} \tan 30^{\circ}} = \frac{1 - \frac{1}{\sqrt{3}}}{1 + 1 (\frac{1}{\sqrt{3}})} = \frac{\frac{\sqrt{3} - 1}{\sqrt{3}}}{\frac{\sqrt{3} + 1}{\sqrt{3}}} = \frac{\sqrt{3} - 1}{\sqrt{3} + 1}$
$= \frac{{(\sqrt{3} - 1)}^{2}}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \frac{3 + 1 - 2 \sqrt{3}}{{(\sqrt{3})}^{2} - {(1)}^{2}} \Rightarrow \frac{4 - 2 \sqrt{3}}{3 - 1} = \frac{2 (2 - \sqrt{3})}{2} = 2 - \sqrt{3}$

Question 6: Prove the following: $\cos (\frac{π}{4} - x) \cos (\frac{π}{4} - y) - \sin (\frac{π}{4} - x) \sin (\frac{π}{4} - y) = \sin (x + y)$

Answer:
$\cos (\frac{π}{4} - x) \cos (\frac{π}{4} - y) - \sin (\frac{π}{4} - x) \sin (\frac{π}{4} - y)$
Multiply and divide by 2 both cos and sin functions
We get,
$\frac{1}{2} [2 \cos (\frac{π}{4} - x) \cos (\frac{π}{4} - y)] + \frac{1}{2} [- 2 \sin (\frac{π}{4} - x) \sin (\frac{π}{4} - y)]$
Now, we know that
2cosAcosB = cos(A+B) + cos(A-B) --------(i)
-2sinAsinB = cos(A+B) - cos(A-B) ----------(ii)
We use these two identities
In our question A = $(\frac{π}{4} - x)$
B = $(\frac{π}{4} - y)$
So,
$\frac{1}{2} [\cos {(\frac{π}{4} - x) + (\frac{π}{4} - y)} + \cos {(\frac{π}{4} - x) - (\frac{π}{4} - y)}] + \frac{1}{2} [\cos {(\frac{π}{4} - x) + (\frac{π}{4} - y)} - \cos {(\frac{π}{4} - x) + (\frac{π}{4} - y)}]$
$= 2 \times \frac{1}{2} [\cos {(\frac{π}{4} - x) + (\frac{π}{4} - y)}]$
$= \cos [\frac{π}{2} - (x + y)]$
As we know that
$(\cos (\frac{π}{2} - A) = \sin A)$
By using this
$= \cos [\frac{π}{2} - (x + y)]$ $= \sin (x + y) =$ R.H.S.

Question 7: Prove the following $\frac{\tan (\frac{π}{4} + x)}{\tan (\frac{π}{4} - x)} = {(\frac{1 + \tan x}{1 - \tan x})}^{2}$

Answer:
As we know that
$(\tan (A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B})$ and $\tan (A - B) = \frac{\tan A - \tan B}{1 + \tan A \tan B}$
So, by using these identities
L.H.S. $= \frac{\tan (\frac{π}{4} + x)}{\tan (\frac{π}{4} - x)} = \frac{\frac{\tan \frac{π}{4} + \tan x}{1 - \tan \frac{π}{4} \tan x}}{\frac{\tan \frac{π}{4} - \tan x}{1 + \tan \frac{π}{4} \tan x}} = \frac{\frac{1 + \tan x}{1 - \tan x}}{\frac{1 - \tan x}{1 + \tan x}} = {(\frac{1 + \tan x}{1 - \tan x})}^{2} =$ R.H.S.

Question 8: Prove the following $\frac{\cos (π + x) \cos (- x)}{\sin (π - x) \cos (\frac{π}{2} + x)} = \cot^{2} x$

Answer:
As we know,
$\cos (π + x) = - \cos x$ , $\sin (π - x) = \sin x$ , $\cos (\frac{π}{2} + x) = - \sin x$ and $\cos (- x) = \cos x$
By using these our equation simplify to
$\frac{\cos x \times - \cos x}{\sin x \times - \sin x} = \frac{- \cos^{2} x}{- \sin^{2} x} = \cot^{2} x$ $(∵ \cot x = \frac{\cos x}{\sin x}) =$ R.H.S.

Question 9: Prove the following $\cos (\frac{3 π}{2} + x) \cos (2 π + x) [\cot (\frac{3 π}{2} - x) + \cot (2 π + x)] = 1$

Answer:
We know that
$\cos (\frac{3 π}{2} + x) = \sin x, \cos (2 π + x) = \cos x, \cot (\frac{3 π}{2} - x) = \tan x, \cot (2 π + x) = \cot x$
So, by using these our equation simplifies to
$\cos (\frac{3 π}{2} + x) \cos (2 π + x) [\cot (\frac{3 π}{2} - x) + \cot (2 π + x)]$
$= \sin x \cos x [\tan x + \cot x] = \sin x \cos x [\frac{\sin x}{\cos x} + \frac{\cos x}{\sin x}]$
$= \sin x \cos x [\frac{\sin^{2} x + \cos^{2} x}{\sin x \cos x}] = \sin^{2} x + \cos^{2} x = 1 =$ R.H.S.

Question 10: Prove the following $\sin (n + 1) x \sin (n + 2) x + \cos (n + 1) x \cos (n + 2) x = \cos x$

Answer:
Multiply and divide by 2
$= \frac{2 \sin (n + 1) x \sin (n + 2) x + 2 \cos (n + 1) x \cos (n + 2) x}{2}$
Now by using identities
–2sinAsinB = cos(A+B) – cos(A–B)
2cosAcosB = cos(A+B) + cos(A–B)
Now, $\frac{{- (\cos (2 n + 3) x - \cos (- x)) + (\cos (2 n + 3) + \cos (- x))}}{2} (∵ \cos (- x) = \cos x)$
$= \frac{2 \cos x}{2} = \cos x =$ R.H.S.

Question 11: Prove the following $\cos (\frac{3 π}{4} + x) - \cos (\frac{3 π}{4} - x) = - \sqrt{2} \sin x$

Answer:
We know that
[ cos(A+B) - cos (A-B) = -2sinAsinB ]
By using this identity
$\cos (\frac{3 π}{4} + x) - \cos (\frac{3 π}{4} - x) = - 2 \sin \frac{3 π}{4} \sin x = - 2 \times \frac{1}{\sqrt{2}} \sin x = - \sqrt{2} \sin x =$ R.H.S.

Question 12: Prove the following $\sin^{2} 6 x - \sin^{2} 4 x = \sin 2 x \sin 10 x$

Answer:
We know that
$a^{2} - b^{2} = (a + b) (a - b)$
So, $\sin^{2} 6 x - \sin^{2} 4 x = (\sin 6 x + \sin 4 x) (\sin 6 x - \sin 4 x)$
Now, we know that
$\sin A + \sin B = 2 \sin (\frac{A + B}{2}) \cos (\frac{A - B}{2}), \sin A - \sin B = 2 \cos (\frac{A + B}{2}) \sin (\frac{A - B}{2})$
By using these identities
sin6x + sin4x = 2sin5x cosx
sin6x - sin4x = 2cos5x sinx
$\Rightarrow \sin^{2} 6 x - \sin^{2} 4 x = (2 \cos 5 x \sin 5 x) (2 \sin x \cos x)$
Now,
2sinAcosB = sin(A+B) + sin(A-B)
2cosAsinB = sin(A+B) - sin(A-B)
by using these identities
2cos5x sin5x = sin10x - 0
2sinx cosx = sin2x + 0
So, $\sin^{2} 6 x - \sin^{2} 4 x = \sin 2 x \sin 10 x$

Question 13: Prove the following $\cos^{2} 2 x - \cos^{2} 6 x = \sin 4 x \sin 8 x$

Answer:
As we know that
$a^{2} - b^{2} = (a - b) (a + b)$
$∴ \cos^{2} 2 x - \cos^{2} 6 x = (\cos 2 x - \cos 6 x) (\cos 2 x + \cos 6 x)$
Now, $\cos A - \cos B = - 2 \sin (\frac{A + B}{2}) \sin (\frac{A - B}{2}) \cos A + \cos B = 2 \cos (\frac{A + B}{2}) \cos (\frac{A - B}{2})$
By using these identities
cos2x - cos6x = -2sin(4x)sin(-2x) = 2sin4xsin2x ( $∵$ sin(-x) = -sin x and cos(-x) = cosx)
cos2x + cos 6x = 2cos4xcos(-2x) = 2cos4xcos2x
So our equation becomes
$(\cos 2 x - \cos 6 x) (\cos 2 x + \cos 6 x) = (2 \sin 4 x \sin 2 x) (2 \cos 4 x \cos 2 x) = (2 \sin 2 x \cos 2 x) (2 \sin 4 x \cos 4 x)$
$= \sin 4 x \sin 8 x =$ R.H.S.

Question 14: Prove the following $\sin 2 x + 2 \sin 4 x + \sin 6 x = 4 \cos^{2} x \sin 4 x$

Answer:
We know that
$\sin A + \sin B = 2 \sin (\frac{A + B}{2}) \cos (\frac{A - B}{2})$
We are using this identity
sin2x + 2sin4x + sin6x = (sin2x + sin6x) + 2sin4x
sin2x + sin6x = 2sin4xcos(-2x) = 2sin4xcos(2x) ( $∵$ cos(-x) = cos x)
So, our equation becomes
sin2x + 2sin4x + sin6x = 2sin4xcos(2x) + 2sin4x
Now, take the 2sin4x common
sin2x + 2sin4x + sin6x = 2sin4x(cos2x +1) ( $∵ \cos 2 x = 2 \cos^{2} x - 1$ )
= $2 \sin 4 x (2 \cos^{2} x - 1$ +1 )
= $2 \sin 4 x (2 \cos^{2} x$ )
= $4 \sin 4 x \cos^{2} x =$ R.H.S.

Question 15: Prove the following $\cot 4 x (\sin 5 x + \sin 3 x) = \cot x (\sin 5 x - \sin 3 x)$

Answer:
We know that
$\sin x + \sin y = 2 \sin (\frac{x + y}{2}) \cos (\frac{x - y}{2})$
By using this , we get
sin5x + sin3x = 2sin4xcosx
$\frac{\cos 4 x}{\sin 4 x} (2 \sin 4 x \cos x) = 2 \cos 4 x \cos x$
Now multiply and divide by sin x
$\frac{2 \cos 4 x \cos x \sin x}{\sin x} = \cot x (2 \cos 4 x \sin x) (∵ \frac{\cos x}{s i n x} = \cot x)$
Now we know that
$2 \cos x \sin y = \sin (x + y) - \sin (x - y)$
By using this our equation becomes
$= \cot x (\sin 5 x - \sin 3 x) =$ R.H.S.

Question 16: Prove the following $\frac{\cos 9 x - \cos 5 x}{\sin 17 x - \sin 3 x} = - \frac{\sin 2 x}{\cos 10 x}$

Answer:
As we know that
$\cos x - \cos y = - 2 \sin \frac{x + y}{2} \sin \frac{x - y}{2}, \cos 9 x - \cos 5 x = - 2 \sin 7 x \sin 2 x$
$\sin x - \sin y = 2 \cos \frac{x + y}{2} \sin \frac{x - y}{2}, \sin 17 x - \sin 3 x = 2 \cos 10 x \sin 7 x$
Now, $\frac{\cos 9 x - \cos 5 x}{\sin 17 x - \sin 3 x} = \frac{- 2 \sin 7 x \sin 2 x}{2 \cos 10 x \sin 7 x} = - \frac{\sin 2 x}{\cos 10 x} =$ R.H.S.

Question 17: Prove the following $\frac{\sin 5 x + \sin 3 x}{\cos 5 x + \cos 3 x} = \tan 4 x$

Answer:
We know that
$\sin A + \sin B = 2 \sin \frac{A + B}{2} \cos \frac{A - B}{2}$ and $\cos A + \cos B = 2 \cos \frac{A + B}{2} \cos \frac{A - B}{2}$
We use these identities
$\sin 5 x + \sin 3 x = 2 \sin 4 x \cos x, \cos 5 x + \cos 3 x = 2 \cos 4 x \cos x$
Now, $\frac{\sin 5 x + \sin 3 x}{\cos 5 x + \cos 3 x} = \frac{2 \sin 4 x \cos x}{2 \cos 4 x \cos x} = \frac{\sin 4 x}{\cos 4 x} = \tan 4 x =$ R.H.S.

Question 18: Prove the following $\frac{\sin x - \sin y}{\cos x + \cos y} = \tan \frac{(x - y)}{2}$

Answer:
We know that
$\sin x - \sin y = 2 \cos \frac{x + y}{2} \sin \frac{x - y}{2}$ and $\cos x + \cos y = 2 \cos \frac{x + y}{2} \cos \frac{x - y}{2}$
We use these identities
$\frac{\sin x - \sin y}{\cos x + \cos y} = \frac{2 \cos \frac{x + y}{2} \sin \frac{x - y}{2}}{2 \cos \frac{x + y}{2} \cos \frac{x - y}{2}} = \frac{\sin \frac{x - y}{2}}{\cos \frac{x - y}{2}} = \tan \frac{x - y}{2} =$ R.H.S.

Question 19: Prove the following $\frac{\sin x + \sin 3 x}{\cos x + \cos 3 x} = \tan 2 x$

Answer:
We know that
$\sin x + \sin y = 2 \sin \frac{x + y}{2} \cos \frac{x - y}{2}$
$\cos x + \cos y = 2 \cos \frac{x + y}{2} \cos \frac{x - y}{2}$
We use these equations,
$\sin x + \sin 3 x = 2 \sin 2 x \cos (- x) = 2 \sin 2 x \cos x (∵ \cos (- x) = \cos x)$
$\cos x + \cos 3 x = 2 \cos 2 x \cos (- x) = 2 \cos 2 x \cos x (∵ \cos (- x) = \cos x)$
Now, $\frac{\sin x + \sin 3 x}{\cos x + \cos 3 x} = \frac{2 \sin 2 x \cos x}{2 \cos 2 x \cos x} = \frac{\sin 2 x}{\cos 2 x} = \tan 2 x =$ R.H.S.

Question 20: Prove the following $\frac{\sin x - \sin 3 x}{\sin^{2} x - \cos^{2} x} = 2 \sin x$

Answer:
We know that
$\sin 3 x = 3 \sin x - 4 \sin^{3} x, \cos^{2} x - \sin^{2} x = \cos 2 x$ and $\cos 2 x = 1 - 2 \sin^{2} x$
We use these identities
$\sin x - \sin 3 x = \sin x - (3 \sin x - 4 \sin^{3} x) = 4 \sin^{3} x - 2 \sin x = 2 \sin x (2 \sin^{2} x - 1)$
$\sin^{2} x - \cos^{2} x = \sin^{2} x - (1 - \sin^{2} x) = 2 \sin^{2} x - 1$
Now, $\frac{\sin x - \sin 3 x}{\sin^{2} - \cos^{2} x} = \frac{2 \sin x (2 \sin^{2} x - 1)}{2 \sin^{2} x - 1} = 2 \sin x =$ R.H.S.

Question 21: Prove the following $\frac{\cos 4 x + \cos 3 x + \cos 2 x}{\sin 4 x + \sin 3 x + \sin 2 x} = \cot 3 x$

Answer:
We know that
$\cos x + \cos y = 2 \cos \frac{x + y}{2} \cos \frac{x - y}{2}$ and $\sin x + \sin y = 2 \sin \frac{x + y}{2} \cos \frac{x - y}{2}$
We use these identities
$\frac{(\cos 4 x + \cos 2 x) + \cos 3 x}{(\sin 4 x + \sin 2 x) + \sin 3 x} = \frac{2 \cos 3 x \cos x + \cos 3 x}{2 \sin 3 x \cos x + \sin 3 x} = \frac{2 \cos 3 x (\cos x + 1)}{2 \sin 3 x (\cos x + 1)} = \cot 3 x =$ R.H.S.

Question 22: prove the following $\cot x \cot 2 x - \cot 2 x \cot 3 x - \cot 3 x \cot x = 1$

Answer:
L.H.S.
= $\cot x \cot 2 x - \cot 3 x (\cot 2 x - \cot x)$
Now we can write $\cot 3 x = \cot (2 x + x)$
⇒ $\cot (a + b) = \frac{\cot a \cot b - 1}{\cot a + \cot b}$
So, $\cot x \cot 2 x - \frac{\cot 2 x \cot x - 1}{\cot 2 x + \cot x} (\cot 2 x + \cot x)$
= $\cot x \cot 2 x - (\cot 2 x \cot x - 1)$
= $\cot x \cot 2 x - \cot 2 x \cot x + 1 = 1 =$ R.H.S.

Question 23: Prove that $\tan 4 x = \frac{4 \tan x (1 - \tan^{2} x)}{1 - 6 \tan^{2} x + \tan^{4} x}$

Answer:
We know that
$\tan 2 A = \frac{2 \tan A}{1 - \tan^{2} A}$
and we can write tan 4x = tan 2(2x)
So, $\tan 4 x = \frac{2 \tan 2 x}{1 - \tan^{2} 2 x}$ = $\frac{2 (\frac{2 \tan x}{1 - \tan^{2} x})}{1 - (\frac{2 \tan x}{1 - \tan^{2} x})^{2}}$
= $\frac{2 (2 \tan x) (1 - \tan^{2} x)}{(1 - \tan x)^{2} - (4 \tan^{2} x)}$
= $\frac{(4 \tan x) (1 - \tan^{2} x)}{(1)^{2} + (\tan^{2} x)^{2} - 2 \tan^{2} x - (4 \tan^{2} x)}$
= $\frac{(4 \tan x) (1 - \tan^{2} x)}{1^{2} + \tan^{4} x - 6 \tan^{2} x}$ = R.H.S.

Question 24: Prove the following $\cos 4 x = 1 - 8 \sin^{2} x \cos^{2} x$

Answer:

We know that
$\cos 2 x = 1 - 2 \sin^{2} x$
We use this in our problem
$\cos 4 x = \cos 2 (2 x)$
= $1 - 2 \sin^{2} 2 x$
= $1 - 2 (2 \sin x \cos x)^{2}$ $(∵ \sin 2 x = 2 \sin x \cos x)$
= $1 - 8 \sin^{2} x \cos^{2} x =$ R.H.S.

Question 25: Prove the following $\cos 6 x = 32 \cos^{6} x - 48 \cos^{4} x + 18 \cos^{2} x - 1$

Answer:
We know that
$\cos 3 x = 4 \cos^{3} x - 3 \cos x$
We use this in our problem
we can write $\cos 6 x$ as $\cos 3 (2 x)$
$\cos 3 (2 x) = 4 \cos^{3} 2 x - 3 \cos 2 x$
= $4 (2 \cos^{2} x - 1)^{3} - 3 (2 \cos^{2} x - 1) (∵ \cos 2 x = 2 \cos^{2} x - 1)$
= $4 [(2 \cos^{2} x)^{3} - (1)^{3} - 3 (2 \cos^{2} x)^{2} (1) + 3 (2 \cos^{2} x) (1)^{2}] - 6 \cos^{2} x + 3 [(a - b)^{3} = a^{3} - b^{3} - 3 a^{2} b + 3 a b^{2}]$
= $32 \cos^{6} x - 4 - 48 \cos^{4} x + 24 \cos^{2} x - 6 \cos^{2} x + 3$
= $32 \cos^{6} x - 48 \cos^{4} x + 18 \cos^{2} x - 1 =$ R.H.S.

NCERT Trigonometric Functions Class 11 Solutions: Miscellaneous Exercise

Page Number: 71-72

Total Questions: 10

Question 1: Prove that $2 \cos \frac{π}{13} \cos \frac{9 π}{13} + \cos \frac{3 π}{13} + \cos \frac{5 π}{13} = 0$

Answer:
We know that
cos A+ cos B = $2 \cos (\frac{A + B}{2}) \cos (\frac{A - B}{2})$
we use this in our problem
$2 \cos \frac{π}{13} \cos \frac{9 π}{13} + 2 \cos \frac{(\frac{3 π}{13} + \frac{5 π}{13})}{2} \cos \frac{(\frac{3 π}{13} - \frac{5 π}{13})}{2}$
= $2 \cos \frac{π}{13} \cos \frac{9 π}{13} + 2 \cos \frac{4 π}{13} \cos \frac{- π}{13}$ ( we know that cos(-x) = cos x )
= $2 \cos \frac{π}{13} \cos \frac{9 π}{13} + 2 \cos \frac{4 π}{13} \cos \frac{π}{13}$
= $2 \cos \frac{π}{13} (\cos \frac{9 π}{13} + \cos \frac{4 π}{13})$
again use the above identity
= $2 \cos \frac{π}{13} (2 \cos (\frac{\frac{9 π}{13} + \frac{4 π}{13}}{2}) \cos (\frac{\frac{9 π}{13} - \frac{4 π}{13}}{2})$
= $2 \cos \frac{π}{13} 2 \cos \frac{π}{2} \cos \frac{5 π}{26}$
we know that $\cos \frac{π}{2}$ = 0
So, $2 \cos \frac{π}{13} 2 \cos \frac{π}{2} \cos \frac{5 π}{26}$ = 0 = R.H.S.

Question 2: Prove that $(\sin 3 x + \sin x) \sin x + (\cos 3 x - \cos x) \cos x = 0$

Answer:
We know that
$\sin 3 x = 3 \sin x - 4 \sin^{3} x$ and $\cos 3 x = 4 \cos^{3} x - 3 \cos x$
We use this in our problem
$(\sin 3 x + \sin x) \sin x + (\cos 3 x - \cos x) \cos x$
= $(3 \sin x - 4 \sin^{3} x + \sin x) \sin x$ + $(4 \cos^{3} x - 3 \cos x - \cos x) \cos x$
= (4sinx - 4 $\sin^{3} x$ )sin x + (4 $\cos^{3} x$ - 4cos x)cos x
Now take the 4sinx common from 1st term and -4cosx from 2nd term
= 4 $\sin^{2} x$ (1 - $\sin^{2} x$ ) - 4 $\cos^{2} x$ (1 - $\cos^{2} x$ )
= 4 $\sin^{2} x$ $\cos^{2} x$ - 4 $\cos^{2} x$ $\sin^{2} x$ ( $∵ \cos^{2} x = 1 - \sin^{2} x$ and $\sin^{2} x = 1 - \cos^{2} x$ )
= 0 = R.H.S.

Question 3: Prove that $(\cos x + \cos y)^{2} + (\sin x - \sin y)^{2} = 4 \cos^{2} (\frac{x + y}{2})$

Answer:
We know that $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ and $(a - b)^{2} = a^{2} - 2 a b + b^{2}$
We use these two in our problem
$(\sin x - \sin y)^{2} = \sin^{2} x - 2 \sin x \sin y + \sin^{2} y$ and $(\cos x + \cos y)^{2} = \cos^{2} x + 2 \cos x \cos y + \cos^{2} y$
$(\cos x + \cos y)^{2} + (\sin x - \sin y)^{2}$ = $\cos^{2} x + 2 \cos x \cos y + \cos^{2} y$ + $\sin^{2} x - 2 \sin x \sin y + \sin^{2} y$
= 1 + 2 cos x cos y + 1 - 2 sin x sin y $(∵ \sin^{2} x + \cos^{2} x = 1 a n d \sin^{2} y + \cos^{2} y = 1)$
= 2 + 2(cos x cos y - sin x sin y)
= 2 + 2cos(x + y)
= 2(1 + cos(x + y) )
Now we can write
$\cos (x + y) = 2 \cos^{2} \frac{(x + y)}{2} - 1$ $(∵ \cos 2 x = 2 \cos^{2} x - 1 \Rightarrow \cos x = 2 \cos^{2} \frac{x}{2} - 1)$
= $2 (1 + 2 \cos^{2} \frac{(x + y)}{2} - 1)$
= $4 \cos^{2} \frac{(x + y)}{2}$
= R.H.S.

Question 4: Prove that $(\cos x - \cos y)^{2} + (\sin x - \sin y)^{2} = 4 \sin^{2} (\frac{x - y}{2})$

Answer:
We know that $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ and $(a - b)^{2} = a^{2} - 2 a b + b^{2}$
We use these two in our problem
$(\sin x - \sin y)^{2} = \sin^{2} x - 2 \sin x \sin y + \sin^{2} y$ and $(\cos x - \cos y)^{2} = \cos^{2} x - 2 \cos x \cos y + \cos^{2} y$
$(\cos x - \cos y)^{2} + (\sin x - \sin y)^{2}$ = $\cos^{2} x - 2 \cos x \cos y + \cos^{2} y$ + $\sin^{2} x - 2 \sin x \sin y + \sin^{2} y$
= 1 - 2cos x cos y + 1 - 2sin x sin y $(∵ \sin^{2} x + \cos^{2} x = 1 a n d \sin^{2} y + \cos^{2} y = 1)$
= 2 - 2(cos x cos y + sin x sin y)
= 2 - 2cos(x - y) $(∵ \cos (x - y) = \cos x \cos y + \sin x \sin y)$
= 2(1 - cos(x - y) )
Now we can write
$\cos (x - y) = 1 - 2 \sin^{2} \frac{(x - y)}{2}$ $(∵ \cos 2 x = 1 - 2 \sin^{2} x \Rightarrow \cos x = 1 - 2 \sin^{2} \frac{x}{2})$
So, $2 (1 - \cos (x - y)) = 2 (1 - (1 - 2 \sin^{2} \frac{(x - y)}{2}))$
= $4 \sin^{2} \frac{(x - y)}{2}$ = R.H.S.

Question 5: Prove that $\sin x + \sin 3 x + \sin 5 x + \sin 7 x = 4 \cos x \cos 2 x \sin 4 x$

Answer:
we know that $\sin A + \sin B = 2 \sin \frac{A + B}{2} \cos \frac{A - B}{2}$
We use this identity in our problem
If we notice we need sin4x in our final result so it is better if we need a combination of sin7x and sin x , sin3x and sin5x to get sin4x.
$(\sin 7 x + \sin x) + (\sin 5 x + \sin 3 x) = 2 \sin \frac{7 x + x}{2} \cos \frac{7 x - x}{2}$ $+ 2 \sin \frac{5 x + 3 x}{2} \cos \frac{5 x - 3 x}{2}$
$=$ $2 \sin 4 x \cos 3 x + 2 \sin 4 x \cos x$
take 2sin4x common
= 2sin4x(cos3x + cosx)
We know that
$\cos A + \cos B = 2 \cos \frac{A + B}{2} \cos \frac{A - B}{2}$
We use this
$\cos 3 x + \cos x = 2 \cos \frac{3 x + x}{2} \cos \frac{3 x - x}{2}$
= $2 \cos 2 x \cos x$
Now 2sin4x(cos3x + cosx) = 2sin4x( $2 \cos 2 x \cos x$ )
= $4 \cos x \cos 2 x \sin 4 x$ = R.H.S.

Question 6: Prove that $\frac{(\sin 7 x + \sin 5 x) + (\sin 9 x + \sin 3 x)}{(\cos 7 x + \cos 5 x) + (\cos 9 x + \cos 3 x)} = \tan 6 x$

Answer:
We know that
$\sin A + \sin B = 2 \sin \frac{A + B}{2} \cos \frac{A - B}{2}$
$\cos A + \cos B = 2 \cos \frac{A + B}{2} \cos \frac{A - B}{2}$
We use these two identities in our problem
sin7x + sin5x = $2 \sin \frac{7 x + 5 x}{2} \cos \frac{7 x - 5 x}{2}$ = $2 \sin 6 x \cos x$
sin 9x + sin 3x = $2 \sin \frac{9 x + 3 x}{2} \cos \frac{9 x - 3 x}{2}$ = $2 \sin 6 x \cos 3 x$
cos 7x + cos5x = $2 \cos \frac{7 x + 5 x}{2} \cos \frac{7 x - 5 x}{2}$ = $2 \cos 6 x \cos x$
cos 9x + cos3x = $2 \cos \frac{9 x + 3 x}{2} \cos \frac{9 x - 3 x}{2}$ = $2 \cos 6 x \cos 3 x$
$\frac{(\sin 7 x + \sin 5 x) + (\sin 9 x + \sin 3 x)}{(\cos 7 x + \cos 5 x) + (\cos 9 x + \cos 3 x)}$ = $\frac{(2 \sin 6 x \cos x) + (2 \sin 6 x \cos 3 x)}{(2 \cos 6 x c o s x) + (2 \cos 6 x \cos 3 x)}$
= $\frac{2 \sin 6 x (\cos x + \cos 3 x)}{2 \cos 6 x (\cos x + \cos 3 x)} = \tan 6 x$ = R.H.S. $(∵ \frac{\sin x}{\cos x} = \tan x)$

Question:7: Prove that $\sin 3 x + \sin 2 x - \sin x = 4 \sin x \cos \frac{x}{2} \cos \frac{3 x}{2}$

Answer:
We know that
$\cos A + \cos B = 2 \cos \frac{A + B}{2} \cos \frac{A - B}{2}$
$\sin A - \sin B = 2 \cos \frac{A + B}{2} \sin \frac{A - B}{2}$
We use these identities
$\sin 3 x - \sin x = 2 \cos \frac{3 x + x}{2} \sin \frac{3 x - x}{2}$
$= 2 \cos 2 x \sin x$
sin2x + $2 \cos 2 x \sin x$ = 2sinx cosx + $2 \cos 2 x \sin x$
take 2 sinx common
$2 \sin x (\cos x + \cos 2 x) = 2 \sin x (2 \cos \frac{2 x + x}{2} \cos \frac{2 x - x}{2})$
$= 2 \sin x (2 \cos \frac{3 x}{2} \cos \frac{x}{2})$
$= 4 \sin x \cos \frac{3 x}{2} \cos \frac{x}{2} =$ R.H.S.

Question 8: Find $\sin \frac{x}{2}, \cos \frac{x}{2}, a n d \tan \frac{x}{2}$ in $\tan x = - \frac{4}{3}$ , x in quadrant II.

Answer:
tan x = $- \frac{4}{3}$
We know that ,
$\sec^{2} x = 1 + \tan^{2} x$
$= 1 + {(- \frac{4}{3})}^{2}$
$= 1 + \frac{16}{9}$ = $\frac{25}{9}$
$\sec x = \sqrt{\frac{25}{9}}$ = $\pm \frac{5}{3}$
x lies in II quadrant thats why sec x is -ve
So, $\sec x = - \frac{5}{3}$
Now, $\cos x = \frac{1}{\sec x}$ = $- \frac{3}{5}$
We know that,
$\cos x = 2 \cos^{2} \frac{x}{2} - 1$ ( $∵ \cos 2 x = 2 \cos^{2} x - 1 \Rightarrow \cos x = 2 \cos^{2} \frac{x}{2} - 1$ )
⇒ $- \frac{3}{5} + 1 = 2$ $\cos^{2} \frac{x}{2}$
⇒ $\frac{- 3 + 5}{5}$ = $2 \cos^{2} \frac{x}{2}$
⇒ $\frac{2}{5}$ = $2 \cos^{2} \frac{x}{2}$
⇒ $\cos^{2} \frac{x}{2}$ = $\frac{1}{5}$
⇒ $\cos \frac{x}{2}$ = $\sqrt{\frac{1}{5}}$ = $\pm \frac{1}{\sqrt{5}}$
x lies in II quadrant so value of $\cos \frac{x}{2}$ is +ve
$\cos \frac{x}{2}$ = $\frac{1}{\sqrt{5}} = \frac{\sqrt{5}}{5}$
we know that
$\cos x = 1 - 2 \sin^{2} \frac{x}{2}$
⇒ $2 \sin^{2} \frac{x}{2}$ = 1 - $(- \frac{3}{5})$ = $\frac{8}{5}$
⇒ $\sin^{2} \frac{x}{2} = \frac{4}{5} = \sin \frac{x}{2} = \sqrt{\frac{4}{5}} = \pm \frac{2}{\sqrt{5}}$
x lies in II quadrant So value of sin x is +ve
$\sin \frac{x}{2} = \frac{2}{\sqrt{} 5} = \frac{2 \sqrt{5}}{5}$
$\tan \frac{x}{2} = \frac{\sin \frac{x}{2}}{\cos \frac{x}{2}} = \frac{\frac{2 \sqrt{5}}{5}}{(\frac{\sqrt{5}}{5})} = 2$

Question 9: Find $\sin \frac{x}{2}, \cos \frac{x}{2}, a n d \tan \frac{x}{2}$ in $\cos x = - \frac{1}{3}$ , x in quadrant III

Answer:
$π < x < \frac{3 π}{2} \Rightarrow \frac{π}{2} < \frac{x}{2} < \frac{3 π}{4}$
We know that
cos x = $2 \cos^{2} \frac{x}{2} - 1$
$2 \cos^{2} \frac{x}{2} =$ cos x + 1 = $(- \frac{1}{3})$ + 1 = $(\frac{- 1 + 3}{3})$ = $\frac{2}{3}$
⇒ $\cos \frac{x}{2} = \sqrt{\frac{1}{3}} = \pm \frac{1}{\sqrt{3}}$
⇒ $\cos \frac{x}{2} = - \frac{1}{\sqrt{3}} = - \frac{\sqrt{3}}{3}$ (As x lies in 3rd quadrant)
we know that
cos x = $1 - 2 \sin^{2} \frac{x}{2}$
⇒ $2 \sin^{2} \frac{x}{2} = 1 - \cos x$ = 1 - $(- \frac{1}{3})$ = $\frac{3 + 1}{3}$ = $\frac{4}{3}$
⇒ $2 \sin^{2} \frac{x}{2} = \frac{4}{3} \Rightarrow \sin^{2} \frac{x}{2} = \frac{2}{3} \Rightarrow \sin \frac{x}{2} = \pm \sqrt{\frac{2}{3}} = \frac{\sqrt{6}}{3}$
Because $\sin \frac{x}{2}$ is +ve in given quadrant
$\tan \frac{x}{2} = \frac{\sin \frac{x}{2}}{\cos \frac{x}{2}} = \frac{\frac{\sqrt{6}}{3}}{\frac{- \sqrt{3}}{3}} = - \sqrt{2}$

Question 10: Find $\sin \frac{x}{2}, \cos \frac{x}{2}, a n d \tan \frac{x}{2}$ in $\sin x = \frac{1}{4}$ ,x in quadrant II

Answer:
$\frac{π}{2} < x < π \Rightarrow \frac{π}{4} < \frac{x}{2} < \frac{π}{2}$ all functions are positive in this range
We know that
$\cos^{2} x = 1 - \sin^{2} x$ = 1 - ${(\frac{1}{4})}^{2}$ = $1 - \frac{1}{16}$ = $\frac{15}{16}$
cos x = $\sqrt{\frac{15}{16}} = \pm \frac{\sqrt{1} 5}{4} = - \frac{\sqrt{1} 5}{4}$ (cos x is -ve in II quadrant)
We know that
cosx = $2 \cos^{2} \frac{x}{2} - 1$
$2 \cos^{2} \frac{x}{2} = \cos x + 1 = - \frac{\sqrt{1} 5}{4} + 1 = \frac{- \sqrt{1} 5 + 4}{4}$
$\cos^{2} \frac{x}{2} = \frac{- \sqrt{1} 5 + 4}{8}$
$\cos \frac{x}{2} = \pm \sqrt{\frac{- \sqrt{1} 5 + 4}{8}} = \frac{\sqrt{- \sqrt{1} 5 + 4}}{2 \sqrt{2}} = \frac{\sqrt{8 - 2 \sqrt{1} 5}}{4}$ (because all functions are posititve in given range)
Similarly,
cos x = $1 - 2 \sin^{2} \frac{x}{2}$
$2 \sin^{2} \frac{x}{2} = 1 - \cos x \Rightarrow 2 \sin^{2} \frac{x}{2} = 1 - (\frac{- \sqrt{1} 5}{4}) = \frac{4 + \sqrt{1} 5}{4}$
$\sin \frac{x}{2} = \pm \sqrt{\frac{\sqrt{1} 5 + 4}{8}} = \frac{\sqrt{\sqrt{1} 5 + 4}}{2 \sqrt{2}} = \frac{\sqrt{8 + 2 \sqrt{1} 5}}{4}$ (because all functions are posititve in given range)
$\tan \frac{x}{2} = \frac{\sin \frac{x}{2}}{\cos \frac{x}{2}} = \frac{\frac{\sqrt{8 + 2 \sqrt{1} 5}}{4}}{\frac{\sqrt{8 - 2 \sqrt{1} 5}}{4}} = \frac{8 + 2 \sqrt{1} 5}{\sqrt{64 - 15 \times 4}} = \frac{8 + 2 \sqrt{1} 5}{\sqrt{4}} = 4 + \sqrt{1} 5$

Also, read,

Class 11 Maths NCERT Chapter 3: Extra Question

Question:
The solution of $\frac{\sqrt{3} + 1}{\sin x} + \frac{\sqrt{3} - 1}{\cos x} = 4 \sqrt{2}$ in the interval $(0, \frac{π}{2})$ is:

Solution:

$\begin{aligned} \frac{\sqrt{3} + 1}{\sin x} + \frac{\sqrt{3} - 1}{\cos x} = 4 \sqrt{2} \\ \Rightarrow & (\frac{\sqrt{3} + 1}{2 \sqrt{2}}) \frac{1}{\sin x} + (\frac{\sqrt{3} - 1}{2 \sqrt{2}}) \frac{1}{\cos x} = 2 \\ \Rightarrow & \frac{\cos \frac{π}{12}}{\sin x} + \frac{\sin \frac{π}{12}}{\cos x} = 2 \\ \Rightarrow & \cos (x - \frac{π}{12}) = \sin 2 x \\ \Rightarrow \sin (\frac{π}{2} - (x - \frac{π}{12})) = \sin 2 x \\ \Rightarrow & \frac{π}{2} - (x - \frac{π}{12}) = n π + (- 1)^{n} 2 x \\ \Rightarrow x = \frac{7 π}{36}, \frac{5 π}{12} \end{aligned}$

Hence, the correct answer is $\frac{7 π}{36}, \frac{5 π}{12}$ .

Trigonometric Functions Class 11 Chapter 3: Topics

The topics discussed in the NCERT Solutions for class 11, chapter 3, Trigonometric Functions are:

Introduction
Angles
Trigonometric Functions
Trigonometric Functions of the Sum and Difference of Two Angles

Trigonometric Functions Class 11 Solutions: Important Formulae

Angle Conversion:

Radian Measure = $\frac{π}{180}$ × Degree Measure

Degree Measure = $\frac{180}{π}$ × Radian Measure

Trigonometric Ratios:

sin θ = P / H
cos θ = B / H
tan θ = P / B
cosec θ = H / P
sec θ = H / B
cot θ = B / P

Reciprocal Trigonometric Ratios:

sin θ = 1 / cosec θ
cosec θ = 1 / sin θ
cos θ = 1 / sec θ
sec θ = 1 / cos θ
tan θ = 1 / cot θ
cot θ = 1 / tan θ

Trigonometric Ratios of Complementary Angles:

sin (90° – θ) = cos θ
cos (90° – θ) = sin θ
tan (90° – θ) = cot θ
cot (90° – θ) = tan θ
sec (90° – θ) = cosec θ
cosec (90° – θ) = sec θ

Periodic Trigonometric Ratios:

sin(π/2-θ) = cos θ
cos(π/2-θ) = sin θ
sin(π-θ) = sin θ
cos(π-θ) = -cos θ
sin(π+θ) = -sin θ
cos(π+θ) = -cos θ
sin(2π-θ) = -sin θ
cos(2π-θ) = cos θ

Trigonometric Identities:

sin^² θ + cos^² θ = 1
cosec^² θ – cot^² θ = 1
sec^² θ – tan^² θ = 1

Product to Sum Formulas:

sin x sin y = 1/2 [cos(x–y) − cos(x+y)]
cos x cos y = 1/2[cos(x–y) + cos(x+y)]
sin x cos y = 1/2[sin(x+y) + sin(x−y)]
cos x sin y = 1/2[sin(x+y) – sin(x−y)]

Sum to Product Formulas:

sin x + sin y = 2 sin [(x+y)/2] cos [(x-y)/2]
sin x – sin y = 2 cos [(x+y)/2] sin [(x-y)/2]
cos x + cos y = 2 cos [(x+y)/2] cos [(x-y)/2]
cos x – cos y = -2 sin [(x+y)/2] sin [(x-y)/2]

General Trigonometric Formulas:

sin (x+y) = sin x × cos y + cos x × sin y
cos(x+y) = cosx × cosy − sinx × siny
cos(x–y) = cosx × cosy + sinx × siny
sin(x–y) = sinx × cosy − cosx × siny

Sum and Difference Formulas for tan:

tan (x+y) = (tan x + tan y) / (1 − tan x tan y)
tan (x−y) = (tan x − tan y) / (1 + tan x tan y)

Double Angle Formulas for tan:

tan 2θ = (2 tan θ) / (1 - tan²θ)

Triple Angle Formulas for sin, cos, and tan:

sin 3θ = 3sin θ – 4sin^³θ
cos 3θ = 4cos^³θ – 3cos θ
tan 3θ = [3tan θ – tan^³θ] / [1 − 3tan^²θ]

Approach to Solve Questions of Trigonometric Functions Class 11

Here are some approaches that students can use to approach the questions related to trigonometric functions.

Identify the perpendicular, base, and hypotenuse in a right-angled triangle efficiently to find the trigonometric ratios of sine, cosine, tangent, secant, cosecant and cotangent.
Learn the relationship between degrees and radians because this chapter includes many questions requiring conversions between them. Remember that π radians = 180°
Draw a table to understand the values of all the trigonometric ratios of standard angles (0°, 30°, 45°, 60°, 90°) in both degrees and radians.
Use graphs wherever necessary to understand the maximum, minimum values of trigonometric functions over intervals.
Be comfortable with the various trigonometric identities to simplify expressions and master the fundamental identities.
sin²x + cos²x = 1
1 + tan²x = sec²x
1 + cot²x = cosec²x
Practice all the formulas, such as the sine rule, cosine rule, projection rule and areas related to triangles, including their applications.
Memorise the ASTC rule (All, Sine, Tangent, Cosine) to determine the sign of a trigonometric ratio in each quadrant.

What Extra Should Students Study Beyond NCERT for JEE?

Here is a comparison list of the concepts in Trigonometric Functions that are covered in JEE and NCERT, to help students understand what extra they need to study beyond the NCERT for JEE:

Concept Name	JEE	NCERT
Measuring Angles	✅	✅
Trigonometric Ratios	✅	✅
Trigonometric Identities	✅	✅
Sign of Trigonometric Functions	✅	✅
Graphs of General Trigonometric Functions	✅	✅
Trigonometric Ratios of Allied Angles	✅	✅
Trigonometric Ratios of Compound Angles	✅	✅
Sum-to-Product and Product-to-Sum Formulas	✅	❌
Product To Sum Formulas	✅	❌
Double Angle Formulas	✅	❌
Triple Angle Identities	✅	❌
Half Angle Formula	✅	❌
Trigonometric Ratio of Submultiple of an Angle	✅	❌
Trigonometric Ratios of Some Specific Angles	✅	✅
Summation Of Series In Trigonometry	✅	❌
Conditional Trigonometric Identities	✅	❌
Maximum and Minimum value of Trigonometric Function	✅	❌
General Solution of Trigonometric Equations	✅	✅
Simultaneous Trigonometric Equations	✅	❌
Trigonometric Equation using Minimum and Maximum value of Function	✅	❌
Trigonometric Inequality	✅	❌
Law of Sines	✅	❌
Law of Cosines	✅	❌
Law Of Tangents	✅	❌
Projection Formula	✅	❌
Semiperimeter and Half Angle Formulae	✅	❌
Area of Triangle	✅	❌
Circumcircle of a Triangle	✅	❌
In-Circle and In-Centre	✅	❌
Escribed Circle of Triangle	✅	❌
Important Solutions of Triangle Formulas	✅	❌
Height and Distance	✅	❌
Inverse Trigonometric Functions	✅	❌
Domain and Range of Trigonometric Functions	✅	❌
Inverse Functions	✅	❌
Graph of Inverse Trigonometric Function	✅	❌
Trigonometric Ratios of Complementary Angles	✅	✅
Sum and difference of angles in terms of arctan	✅	❌
Multiple Angles	✅	❌

NCERT Solutions for Class 11 Mathematics - Chapter Wise

Given below is the chapter-wise list of the NCERT Class 11 Maths solutions with their respective links:

NCERT Solutions for Class 11 Mathematics Chapter 1: Sets
NCERT Solutions for Class 11 Mathematics Chapter 2: Relations and Functions
NCERT Solutions for Class 11 Mathematics Chapter 3: Trigonometric Functions
NCERT Solutions for Class 11 Mathematics Chapter 4: Complex Numbers and Quadratic Equations
NCERT Solutions for Class 11 Mathematics Chapter 5: Linear Inequalities
NCERT Solutions for Class 11 Mathematics Chapter 6: Permutations and Combinations
NCERT Solutions for Class 11 Mathematics Chapter 7: Binomial Theorem
NCERT Solutions for Class 11 Mathematics Chapter 8: Sequences and Series
NCERT Solutions for Class 11 Mathematics Chapter 9: Straight Lines
NCERT Solutions for Class 11 Mathematics Chapter 10: Conic Sections
NCERT Solutions for Class 11 Mathematics Chapter 11: Introduction to Three-Dimensional Geometry
NCERT Solutions for Class 11 Mathematics Chapter 12: Limits and Derivatives
NCERT Solutions for Class 11 Mathematics Chapter 13: Statistics
NCERT Solutions for Class 11 Mathematics Chapter 14: Probability

Also, read,

NCERT Solutions for Class 11 - Subject Wise

Here are the subject-wise links for the NCERT solutions of class 11:

NCERT Books and NCERT Syllabus

Here are some useful links for NCERT books and the NCERT syllabus for class 11:

Frequently Asked Questions (FAQs)

1. How to solve trigonometric equations in Class 11 Maths Chapter 3?

To solve trigonometric equations in Class 11 Maths Chapter 3, express the given terms in basic trigonometric functions like sin, cos, and tan, then try to apply proper trigonometric identities and use simplification.

2. What are the key formulas of Trigonometric Functions in NCERT Class 11?

The key formulas of Trigonometric Functions in NCERT Class 11 are:

$1) \cos^{2} x + \sin^{2} x = 1$

$2) 1 + \tan^{2} x = \sec^{2} x$

$3) 1 + \cot^{2} x = {cosec}^{2} x$

$4) \cos (2 n π + x) = \cos x$

$5) \sin (2 n π + x) = \sin x$

$6) \sin (- x) = - \sin x$

$7) \cos (- x) = \cos x$

$8) \cos (x + y) = \cos x \cos y - \sin x \sin y$

$9) \cos (x - y) = \cos x \cos y + \sin x \sin y$

$10) \sin (x + y) = \sin x \cos y + \cos x \sin y$

$11) \sin (x - y) = \sin x \cos y - \cos x \sin y$

$12) \tan (x + y) = \frac{\tan x + \tan y}{1 - \tan x \tan y}$

$13) \tan (x - y) = \frac{\tan x - \tan y}{1 + \tan x \tan y}$

$14) \cot (x + y) = \frac{\cot x \cot y - 1}{\cot x + \cot y}$

$15) \cot (x - y) = \frac{1 + \cot x \cot y}{\cot y - \cot x}$

3. How to find the general solution of a trigonometric equation?

To find the general solution of a trigonometric equation, use the following standard equations:

$\sin θ = \sin α \Rightarrow θ = n π + (- 1)^{n} α, n \in Z$

$\cos θ = \cos α \Rightarrow θ = 2 n π \pm α, n \in Z$

$\tan θ = \tan α \Rightarrow θ = n π + α, n \in Z$

4. What are the domain and range of trigonometric functions in Class 11?

In class 11 chapter 3 trigonometric functions, a domain basically denotes the input values and range denotes the output values.

For example: The domain of $\sin θ$ and $\cos θ$ is $(- \infty, \infty)$ and range is (–1, 1).

5. How to derive the sine and cosine function graphs?

To derive the sine and cosine function graphs, plot $y = \sin θ$ and $y = \cos θ$ for the values of $θ$ like 0°, 30°, 60°, 90°, 180°, etc..

The sine graph starts at (0, 0) and goes up to 1 at 90°, drops to –1 at 270°, and comes to 0 again at 360° then repeats.

Also Read

NCERT Class 11 Physics Chapter 4 Motion in a Plane Notes - Download PDF

NCERT Class 11 Physics Notes - Download Chapter-wise PDFs

NCERT Class 11 Chemistry Chapter 13 Notes Hydrocarbons - Download PDF

NCERT Class 11 Physics Chapter 2 Notes Units and Measurement - Download PDF

Oscillations Class 11th Notes - Free NCERT Class 11 Physics Chapter 14 Notes - Download PDF

Waves Class 11th Notes - Free NCERT Class 11 Physics Chapter 15 Notes - Download PDF

NCERT Class 11 Physics Chapter 3 Notes Motion in a straight Line - Download PDF

NCERT Solutions for Class 11 Maths - Download Chapter Wise PDF

NCERT Class 11 Physics Chapter 5 Notes Laws of Motion - Download PDF

NCERT Solutions for Class 11 Physics Chapter 3 Motion in a Plane

NCERT Solutions for Class 11 Physics Chapter 14 Waves

NCERT Solutions for Class 11 Physics Chapter 9 Mechanical Properties Of Fluids

NCERT Books for Class 11 Chemistry 2025-26: Download Free PDF

NCERT Books for Class 11 English 2025-26: Download Free PDF

NCERT Books for class 11 Hindi 2025-26: Download Free PDF

NCERT Book for class 11 Biology 2025-26: Download Free PDF

NCERT Books for Class 11: Free PDF Download All Subjects

NCERT Books for class 11 Maths 2025-26: Download Free PDF

NCERT Exemplar Class 11 Chemistry Solutions Chapter 5 States of Matter

NCERT Exemplar Class 11 Chemistry Solutions Chapter 2 Structure of Atom

NCERT Exemplar Class 11 Chemistry Solutions Chapter 10 The s Block Elements

NCERT Exemplar Class 11 Chemistry Solutions Chapter 9 Hydrogen

NCERT Exemplar Class 11 Chemistry Solutions Chapter 8 Redox Reactions

NCERT Exemplar Class 11 Solutions - Subject Wise Problems with Solutions

NCERT Syllabus for Class 11 Physics 2025-26 - Download Latest Syllabus Pdf

Articles

MVPP Result 2025 – Mukhyamantri Vigyan Pratibha Pariksha Merit List

Jul 09, 2025

JAC Delhi Merit List 2025 – Download and Check College wise Cut offs

Jul 08, 2025

Simultala Awasiya Vidyalaya Admission 2025-27: Class 6, Class 9 & Class 11

Jul 07, 2025

UPTAC Counselling 2025: Registration (Started), Date, Seat Allotment, Choice Filling, Document Verification

Jul 06, 2025

UPTAC Seat Allotment 2025 - Dates, Fee, Seat Acceptance, Reporting

Jul 02, 2025

IAPT Registrations 2025‑26: NSEP, NSEC, NSEB, and NSEA Application & Exam Dates

Jul 01, 2025

NSEP Answer Key 2025‑26: Download Solutions & Question Paper PDF

Mock Test

Result

Exam Pattern

View All School Exams

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

Exams

Top Schools

Products & Resources

NCERT Study Material

Exams

Colleges

Predictors

Resources

Exams

Colleges & Courses

Predictors

Resources

Exams

Colleges

Predictors

Resources

Exams

Colleges

Predictors & E-Books

Resources

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Exams

Resources

Top Courses & Careers

Colleges

Exams

Colleges

Resources

Quick Links

Exams

Colleges

Resources

Exams

Colleges

Resources

Diploma Colleges

Exams

Resources

Upcoming Events

Other Exams

Exams

Colleges

Top Countries

Resources

Exams

Colleges

Upcoming Events

Resources

Engineering Preparation

Medical Preparation

Law Preparation

MBA Preparation

Top Streams

Specializations

Resources

Top Providers

NCERT Solutions for Class 11 Maths Chapter 3 Trigonometric Functions

NCERT Solution for Class 11 Maths Chapter 3 Solutions: Download PDF

Trigonometric Functions Class 11 NCERT Solutions (Exercises)

Class 11 Maths NCERT Chapter 3: Extra Question

Trigonometric Functions Class 11 Chapter 3: Topics

Trigonometric Functions Class 11 Solutions: Important Formulae

Angle Conversion:

Trigonometric Ratios:

Reciprocal Trigonometric Ratios:

Trigonometric Ratios of Complementary Angles:

Periodic Trigonometric Ratios:

Trigonometric Identities:

Product to Sum Formulas:

Sum to Product Formulas:

General Trigonometric Formulas:

Sum and Difference Formulas for tan:

Double Angle Formulas for tan:

Triple Angle Formulas for sin, cos, and tan: