NCERT Solutions for Class 11 Maths Chapter 3 Exercise 3.1 - Trigonometric Functions
Trigonometry is one of the oldest branches of mathematics. It was developed initially to solve the problems based on triangles but now its applicability is far beyond algebra. Trigonometry was widely used by ancient navigators, astronomers, and captains mostly rely on it for navigation. Trigonometry helps in understanding the relationship between angles and the side lengths of the triangles. Exercise 3.1 of NCERT mainly focuses on measurements of angles in degrees and radians.
This Story also Contains
- NCERT Solutions Class 11 maths chapter 3 Exercise 3.1
- Topics covered in Chapter 3 Trigonometric Functions: Exercise 3.1
- NCERT Solutions of Class 11 Subject Wise
- Subject-Wise NCERT Exemplar Solutions
In this exercise, students will learn how to convert angles from degrees to radians and vice versa and how to measure angles. Solutions for Exercise 3.1 are designed systematically and comprehensively that helps students to understand concepts easily. Students can also check NCERT Solutions to get detailed solutions from Class 6 to Class 12 for Science and Maths
NCERT Solutions Class 11 maths chapter 3 Exercise 3.1
Question 1 Find the radian measures corresponding to the following degree measures:
(i) $25 ^\circ$(ii)$-47 ^\circ$ $30'$ (iii) $240^\circ$ (iv) $520^\circ$
Answer:
It is solved using relation between degree and radian
(i) $25^{\circ}$
We know that $180^{\circ}=\pi$ radian
So, $1^{\circ}=\frac{\pi}{180}$ radian
$25^{\circ}=\frac{\pi}{180} \times 25$ radian
$=\frac{5 \pi}{36}$ radian
(ii) $-47^{\circ} 30^{\prime}$
We know that$-47^{\circ} 30^{\prime}=-47 \frac{1}{2}$ degree $=-\frac{95^{\circ}}{2}$
Now, we know that $180^{\circ}=\pi \Rightarrow 1^{\circ}=\frac{\pi}{180}$ radian
So, $-\frac{95^{\circ}}{2}=\frac{\pi}{180} \times\left(-\frac{95}{2}\right)$ radian
$\Rightarrow \frac{-19 \pi}{72}$ radian
(iii) $240^{\circ}$
We know that
$180^{\circ}=\pi \Rightarrow 1^{\circ}=\frac{\pi}{180}$ radian
So, $240^{\circ}=\frac{\pi}{180} \times 240 \Rightarrow \frac{4 \pi}{3}$ radian
(iv) $520^{\circ}$
We know that
$180^{\circ}=\pi \Rightarrow 1^{\circ}=\frac{\pi}{180}$ radian
So, $520^{\circ} \Rightarrow \frac{\pi}{180} \times 520$ radian
$\Rightarrow \frac{26 \pi}{9}$ radian
Answer:
(1) $\frac{11}{16}$
We know that
$\pi$ radian $= 180^\circ \Rightarrow 1 radian = \frac{180}{\pi} degree$
So, $\frac{11}{16} radian = \frac{180}{\pi}\times \frac{11}{16}degree$ (we need to take $\pi = \frac{22}{7}$ )
$\frac{11}{16}radian = \frac{180\times 7}{22}\times \frac{11}{16}degree \Rightarrow \frac{315}{8}degree$
(we use $1^\circ = 60'$ and 1' = 60'')
Here 1' represents 1 minute and 60" represents 60 seconds
Now,
$\frac{315}{8}degree=39\frac{3}{8}degree\\ \\ =39^\circ +\frac{3\times 60}{8}minutes \Rightarrow 39^\circ +22' + \frac{1}{2}minutes \Rightarrow 39^\circ +22' +30''\\ \\ \Rightarrow \frac{315}{8}degree = 39^\circ22'30''$
(ii) -4
We know that
$\pi$ radian $= 180^\circ \Rightarrow 1 radian = \frac{180}{\pi} degree$ (we need to take $\pi = \frac{22}{7}$ )
So, -4 radian = $\frac{-4\times 180}{\pi} \Rightarrow \frac{-4\times 180\times 7}{22} \Rightarrow \frac{-2520}{11}degree$
(we use $1^\circ = 60'$ and 1' = 60'')
$\Rightarrow \frac{-2520}{11}degree = -229\frac{1}{11}degree =-229^\circ + \frac{1\times 60}{11}minutes \\ \\ \Rightarrow -229^\circ + 5' + \frac{5}{11}minutes = -229^\circ +5' +27''\\ \\ -\frac{2520}{11} = -229^\circ5'27''$
(iii) $\frac{5\pi}{3}$
We know that
$\pi$ radian $= 180^\circ \Rightarrow 1 radian = \frac{180}{\pi} degree$ (we need to take $\pi = \frac{22}{7}$ )
So, $\frac{5\pi}{3}radian = \frac{180}{\pi}\times \frac{5\pi}{3}degree = 300^\circ$
(iv) $\frac{7\pi}{6}$
We know that
$\pi$ radian $= 180^\circ \Rightarrow 1 radian = \frac{180}{\pi} degree$ (we need to take $\pi = \frac{22}{7}$ )
So, $\frac{7\pi}{6}radian = \frac{180}{\pi}\times \frac{7\pi}{6} = 210^\circ$
Question:3 A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?
Answer:
Number of revolutions made by the wheel in 1 minute = 360
$\therefore$ Number of revolutions made by the wheel in 1 second = $\frac{360}{60} = 6$
( $\because$ 1 minute = 60 seconds)
In one revolutions wheel will cover $2\pi$ radian
So, in 6 revolutions it will cover = $6\times 2\pi = 12\pi$ radian
$\therefore$ In 1 the second wheel will turn $12\pi$ radian
Answer:
We know that
$l = r\Theta$ ( where l is the length of the arc, r is the radius of the circle and $\Theta$ is the angle subtended)
here r = 100 cm
and l = 22 cm
Now,
$\Theta = \frac{l}{r} = \frac{22}{100}radian$
We know that
$\pi radian = 180^\circ\\ \\So, 1radian = \frac{180}{\pi}degree\\ \\ \therefore \frac{22}{100}radian = \frac{180}{\pi}\times\frac{22}{100}degree\Rightarrow \frac{180\times7}{22}\times\frac{22}{100} = \frac{63}{5}degree \\ \\ So, \\ \\\frac{63}{5}degree = 12\frac{3}{5}degree = 12^\circ + \frac{3\times60}{5}minute = 12^\circ + 36'\\ \\ \therefore \frac{63}{5}degree = 12 ^\circ36'$
So,
Angle subtended at the centre of a circle $\Theta = 12^\circ36'$
Answer:
Given :- radius (r)of circle = $\frac{Diameter}{2} = \frac{40cm}{2} = 20 cm$
length of chord = 20 cm
We know that
$\theta = \frac{l}{r}$ (r = 20cm , l = ? , $\theta$ = ?)
Now,
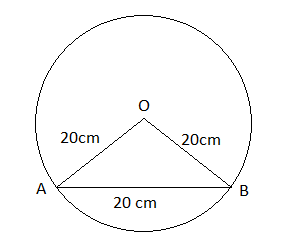 AB is the chord of length 20cm and OA and OB are radii of circle 20 cm each
AB is the chord of length 20cm and OA and OB are radii of circle 20 cm each
The angle subtended by OA and OB at centre = $\theta$
$\because$ OA = OB = AB
$\therefore$ $\Delta$ OAB is equilateral triangle
So, each angle equilateral is $60^\circ$
$\therefore$ $\theta = 60^\circ$ $= \frac{\pi}{3}radian$
Now, we have $\theta$ and r
So,
$l = r\theta = 20\times\frac{\pi}{3}=\frac{20\pi}{3}$
$\therefore$ the length of the minor arc of the chord (l) = $\frac{20\pi}{3}$ cm
Answer:
Given:-
$\theta_1 = 60^\circ\\ \theta_2 = 75^\circ\\$ and $l_1 = l_2$
We need to find the ratio of their radii $\frac{r_1}{r_2} = ?$
We know that arc length $l = r \theta$
So,
$l_1 = r_1 \theta_1\\l_2 = r_2\theta_2$
Now,
$\frac{l_1}{l_2}=\frac{ r_1 \theta_1}{ r_2\theta_2}$ ( $l_1 = l_2$ )
So,
$\frac{ r_1 }{ r_2}= \frac{\theta_2}{\theta_1} = \frac {75}{60} = \frac{5}{4}$ is the ratio of their radii
Question:7 Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
(i) 10 cm
(ii) 15 cm
(iii) 21 cm
Answer:
(i) We know that
$l = r \theta$
Now,
r = 75cm
l = 10cm
So,
$\theta = \frac{l}{r} = \frac{10}{75} = \frac{2}{15}radian$
(ii) We know that
$l = r \theta$
Now,
r = 75cm
l = 15cm
So,
$\theta = \frac{l}{r} = \frac{15}{75} = \frac{1}{5}radian$
(iii) We know that
$l = r \theta$
Now,
r = 75cm
l = 21cm
So,
$\theta = \frac{l}{r} = \frac{21}{75} = \frac{7}{25}radian$
Also read
Trigonometric Functions NCERT Exercise 3.2
Topics covered in Chapter 3 Trigonometric Functions: Exercise 3.1
This Exercise introduces students to angles, measures of degrees and radians. In this exercise, students will find questions that primarily revolve around the following key topics:
Trigonometry: It deals with the relationship between angles and sides of triangles. Trigonometric ratios like sin, cos, tan, cot, sec, and cosec are used to relate angles to sides of triangles.
Angles: An Angle measures the rotation of a line about its initial point. 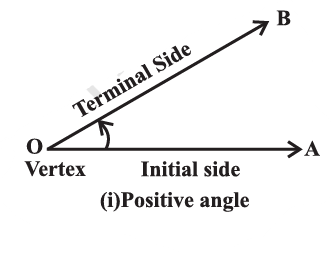
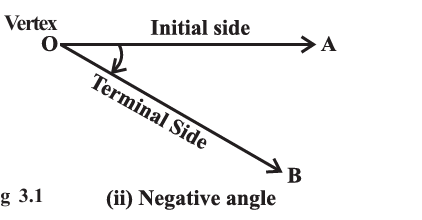

Degree measure: It is the amount of rotation from initial side to the terminal side of the angle. Degree measure is measured in degree.
Complete rotation = 3600
Right angle = 900
Straight angle = 1800
Radian measure: It is the measure of the central angle of a circle that subtends an area which is equal to the length of the radius of the circle. Angle subtended at the centre by an arc of length 1 unit in a unit circle is said to have a measure of 1 radian.
Also Read
NCERT Solutions of Class 11 Subject Wise
Frequently Asked Questions (FAQs)
It can help to save time in the exam but more focus should be on the concepts.
Yes, but in the CBSE examination it is not recommended but it can be used in JEE Main and NEET to save time.
Questions of easy, moderate and a few difficulty level are asked. Most of the questions are of moderate level.
Total 7 questions are discussed in this exercise.
Application of trigonometric functions for finding the arc length, chord length etc. is discussed in this exercise.
Yes, the basics of this chapter are used in the inverse trigonometric functions.
Approx 10 marks questions are asked in the final exams of 11 Class.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
