NCERT Exemplar Class 11 Maths Solutions Chapter 13 Limits and Derivatives

NCERT Exemplar Class 11 Maths Solutions Chapter 13

Question:1

Evaluate $\mathop{\lim}\limits_{x \rightarrow 3}\frac{x^{2}-9}{x-3}$

Answer:

Given $\mathop{\lim }\limits_{x \rightarrow 3}\frac{x^{2}-9}{x-3}=\mathop{\lim }\limits_{x \rightarrow 3}\frac{ \left( x-3 \right) \left( x+3 \right) }{x-3}=\mathop{\lim }\limits_{x \rightarrow 3}x+3=6$

Question:2

Evaluate $\mathop{\lim }\limits\limits_{x \rightarrow 1/2}\frac{4x^{2}-1}{2x-1}$

Answer:

Given that $\mathop{\lim }\limits_{x \rightarrow 1/2}\frac{4x^{2}-1}{2x-1}=\mathop{\lim }\limits_{x \rightarrow 1/2}\frac{ \left( 2x-1 \right) \left( 2x+1 \right) }{2x-1}=\mathop{\lim }\limits_{x \rightarrow 1/2}2x+1=2$

Question:3

Evaluate $\mathop{\lim }\limits_{h \rightarrow 0}\frac{\sqrt{x+h}-\sqrt{x}}{h}$

Answer:

$\mathop{\lim }\limits_{h \rightarrow 0}\frac{\sqrt {x+h}-\sqrt {x}}{h}$

$\\=\mathop{\lim }\limits_{h \rightarrow 0} \frac{\sqrt{x+h}-\sqrt{x}}{h[\sqrt{x+h}+\sqrt{x}]} \times( \sqrt{x+h}+\sqrt{x}) \ $
[Rationalizing the denominator]
$\mathop{\lim }\limits_{h \rightarrow 0}\frac{x+h-x}{h[\sqrt{x+h}+\sqrt{x}]}$ $\\\\=\mathop{\lim }\limits_{h \rightarrow 0} \frac{1}{ \sqrt{x+h}+\sqrt{x}}\\\\$
Put limit
$\\= \frac{1}{ \sqrt{x}+\sqrt{x}}\\\\ =\frac{1}{2\sqrt{x}}$

Question:4

Evaluate: $\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left( x+2 \right) ^{\frac{1}{3}}-2^{\frac{1}{3}}}{x}$

Answer:

Given $\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left( x+2 \right) ^{\frac{1}{3}}-2^{\frac{1}{3}}}{x}~~ \\\\ ~$
Now put x=x-2 limits change from 0 to 2
$\\\\ =\mathop{\lim }\limits_{y \rightarrow 2}\frac{y^{\frac{1}{3}}-2^{\frac{1}{3}}}{y-2}=\frac{1}{3} \left( 2 \right) ^{\frac{1}{3}-1}=\frac{1}{3}2^{-\frac{2}{3}}$ $\left[u \sin g \lim _{x \rightarrow a} \frac{x^{n}-a^{n}}{x-a}=n \cdot a^{n-1}\right]$

Question:5

Evaluate : $\mathop{\lim }\limits_{x \rightarrow 1}\frac{ \left( 1+x \right) ^{6}-1}{ \left( 1+x \right) ^{2}-1}$

Answer:

$\text{Given that }\mathop{\lim }\limits_{x \rightarrow 1}\frac{ \left( 1+x \right) ^{6}-1}{ \left( 1+x \right) ^{2}-1}=\mathop{\lim }\limits_{x \rightarrow 1}\frac{ \left( \left( 1+x \right) ^{2} \right) ^{3}-1}{ \left( 1+x \right) ^{2}-1}$
$\\ =\mathop{\lim }\limits_{x \rightarrow 1}\frac{ \left( \left( 1+x \right) ^{2}-1 \right) \left[ \left( 1+x \right) ^{4}+ \left( 1+x \right) ^{2}+1 \right] }{ \left( 1+x \right) ^{2}-1} \\$

$\\ =\mathop{\lim }\limits_{x \rightarrow 1} \left( 1+x \right) ^{4}+ \left( 1+x \right) ^{2}+1 \\\\ =2^{4}+2^{2}+1=21$

Question:6

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow a}\frac{ \left( 2+x \right) ^{\frac{5}{2}}- \left( 2+a \right) ^{\frac{5}{2}}}{x-a}$

Answer:
Given that $\mathop{\lim }\limits_{x \rightarrow a}\frac{ \left( 2+x \right) ^{\frac{5}{2}}- \left( 2+a \right) ^{\frac{5}{2}}}{x-a}$

$=\mathop{\lim }\limits_{y \rightarrow a+2}\frac{ \left( y \right) ^{\frac{5}{2}}- \left( 2+a \right) ^{\frac{5}{2}}}{y- \left( a+2 \right) }=\frac{5}{2} \left( a+2 \right) ^{\frac{5}{2}-1}=\frac{5}{2} \left( a+2 \right) ^{\frac{3}{2}}$ $\left [\text{using} \lim _{x \rightarrow a} \frac{x^{n}-a^{n}}{x-a}=n \cdot a^{n-1}\right]$

Question:7

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow 1}\frac{x^{4}-\sqrt {x}}{\sqrt {x}-1}$
Answer:

$Given~\mathop{\lim }\limits_{x \rightarrow 1}\frac{x^{4}-\sqrt {x}}{\sqrt {x}-1}=\mathop{\lim }\limits_{x \rightarrow 1}\frac{ \left( x^{4}-\sqrt {x} \right) \left( \sqrt {x}+1 \right) }{ \left( \sqrt {x}-1 \right) \left( \sqrt {x}+1 \right) }$

$\\ =\mathop{\lim }\limits_{x \rightarrow 1}\frac{x^{4}\sqrt {x}+x^{4}-x-\sqrt {x}}{x-1} \\ \\ =\mathop{\lim }\limits_{x \rightarrow 1}\frac{\sqrt {x} \left( x^{4}-1 \right) +x \left( x^{3}-1 \right) }{x-1} \\ $

$\\ =\mathop{\lim }\limits_{x \rightarrow 1}\frac{ \left( x-1 \right) \left( \sqrt {x} \left( x^{3}+x^{2}+x+1 \right) +x \left( x^{2}+x+1 \right) \right) }{x-1} \\$

$ \\ =\mathop{\lim }\limits_{x \rightarrow 1}\sqrt {x} \left( x^{3}+x^{2}+x+1 \right) +x \left( x^{2}+x+1 \right) \\ \\ =1 *4+1 *3=7 \\ \\$

Question:8

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow 2}\frac{x^{2}-4}{\sqrt {3x-2}-\sqrt {x+2} }$

Answer:

Given $\mathop{\lim }\limits_{x \rightarrow 2}\frac{x^{2}-4}{\sqrt {3x-2}-\sqrt {x+2}}=\mathop{\lim }\limits_{x \rightarrow 2}\frac{x^{2}-4}{ \left( \sqrt {3x-2}-\sqrt {x+2} \right) } \times\frac{\sqrt {3x-2}+\sqrt {x+2}}{\sqrt {3x-2}+\sqrt {x+2}} \\$

$ \\ =\mathop{\lim }\limits_{x \rightarrow 2}\frac{x^{2}-4}{ \left( 3x-2-x-2 \right) } \times \left( \sqrt {3x-2}+\sqrt {x+2} \right) \\ $

$\\ =\mathop{\lim }\limits_{x \rightarrow 2}\frac{ \left( x-2 \right) \left( x+2 \right) }{2 \left( x-2 \right) } \times \left( \sqrt {3x-2}+\sqrt {x+2} \right) \\$

$ \\ =\mathop{\lim }\limits_{x \rightarrow 2}\frac{ \left( x+2 \right) }{2} \times \left( \sqrt {3x-2}+\sqrt {x+2} \right) =\frac{4}{2} \times \left( \sqrt {3 \times2-2}+\sqrt {2+2} \right) =8 \\ \\$

Question:9

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow \sqrt {2}}\frac{x^{2}-4}{x^{2}+3\sqrt {2}x-8} \\$

Answer:

$\begin{aligned} &=\lim _{x \rightarrow \sqrt{2}} \frac{\left(x^{2}-2\right)\left(x^{2}+2\right)}{x^{2}+4 \sqrt{2} x-\sqrt{2} x-8}\\ &=\lim _{x \rightarrow \sqrt{2}} \frac{(x+\sqrt{2})(x-\sqrt{2})\left(x^{2}+2\right)}{x(x+4 \sqrt{2})-\sqrt{2}(x+4 \sqrt{2})}\\ &=\lim _{x \rightarrow \sqrt{2}} \frac{(x+\sqrt{2})(x-\sqrt{2})\left(x^{2}+2\right)}{(x+4 \sqrt{2})(x-\sqrt{2})}\\&=\lim _{x \rightarrow \sqrt{2}} \frac{(x+\sqrt{2})\left(x^{2}+2\right)}{x+4 \sqrt{2}}\\ &\text { Put limit }\\ &=\frac{(\sqrt{2}+\sqrt{2})(2+2)}{\sqrt{2}+4 \sqrt{2}}\\&=\frac{2 \sqrt{2} \times 4}{5 \sqrt{2}}=\frac{8}{5} \end{aligned}$

Question:10

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow 1} \left( \frac{x^{7}-2x^{5}+1}{x^{3}-3x^{2}+2} \right) \\ \\$

Answer:

Let us apply LH rule i.e. L.Hospita's rule to this question

$\\ ~~\mathop{\lim }\limits_{x \rightarrow 1} \left( \frac{x^{7}-2x^{5}+1}{x^{3}-3x^{2}+2} \right) \\ \\ \mathop{\lim }\limits_{x \rightarrow a} \left( \frac{f \left( x \right) }{g \left( x \right) } \right) =\mathop{\lim }\limits_{x \rightarrow a} \left( \frac{f^{'} \left( x \right) }{g^{'} \left( x \right) } \right) \\$

$ \\ \mathop{\lim }\limits_{x \rightarrow 1} \left( \frac{x^{7}-2x^{5}+1}{x^{3}-3x^{2}+2} \right) =\mathop{\lim }\limits_{x \rightarrow 1} \left( \frac{7x^{6}-10x^{4}}{3x^{2}-6x} \right) =\frac{7-10}{3-6}=1 \\ \\$

Question:11

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{\sqrt {1+x^{3}}-\sqrt {1-x^{3}}}{x^{2}} \right) \\ \\$

Answer:

$\text{Given that }\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{\sqrt {1+x^{3}}-\sqrt {1-x^{3}}}{x^{2}} \right) \\ \\$
$\\ =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{\sqrt {1+x^{3}}-\sqrt {1-x^{3}}}{x^{2}} *\frac{\sqrt {1+x^{3}}+\sqrt {1-x^{3}}}{\sqrt {1+x^{3}}+\sqrt {1-x^{3}}} \right) \\$

$ \\ =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{1+x^{3}-1+x^{3}}{x^{2}} *\frac{1}{\sqrt {1+x^{3}}+\sqrt {1-x^{3}}} \right) \\ \\ =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{2x}{\sqrt {1+x^{3}}+\sqrt {1-x^{3}}} \right) =0 \\ \\$

Question:12

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow -3} \left( \frac{x^{3}+27}{x^{5}+243} \right)$

Answer:

$\begin{aligned} &=\lim _{x \rightarrow -3} \frac{\frac{x^{3}+(3)^{3}}{x+3}}{\frac{x^{3}+(3)^{3}}{x+3}} \text { [Dividing the numerator and denominator by } \left.x+3\right]\\ &=\frac{\lim _{x \rightarrow -3}\left(\frac{x^{3}+(3)^{3}}{x+3}\right)}{\lim _{x \rightarrow -3}\left(\frac{x^{3}+(3)^{5}}{x+3}\right)}\left[\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\frac{\lim _{x \rightarrow a} f(x)}{\lim _{x \rightarrow a} g(x)}\right]\\ &=\frac{\lim _{x \rightarrow -3}\left(x^2-3x+9\right)}{\lim _{x \rightarrow -3}\left( x^4 - 3x^3 + 9x^2 - 27x + 81\right)} \\ &=\frac{9+9+9}{81+81+81+81+81}=\frac{3 \times 9}{5 \times 81 }=\frac{1}{5 \times 3}=\frac{1}{15} \end{aligned}$

Question:13

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow \frac{1}{2}} \left( \frac{8x-3}{2x-1}-\frac{4x^{2}+1}{4x^{2}-1} \right) \\$

Answer:

Given $\mathop{\lim }\limits_{x \rightarrow \frac{1}{2}} \left( \frac{8x-3}{2x-1}-\frac{4x^{2}+1}{4x^{2}-1} \right) \\ \\$
$\\=\mathop{\lim }\limits_{x \rightarrow \frac{1}{2}} \left( \left( \frac{1}{2x+1} \right) \times \left( \frac{ \left( 8x-3 \right) \left( 2x+1 \right) -4x^{2}-1}{2x-1} \right) \right) \\ \\ =\mathop{\lim }\limits_{x \rightarrow \frac{1}{2}} \left( \left( \frac{1}{2x+1} \right) \times \left( \frac{12x^{2}+2x-4}{2x-1} \right) \right) \\ \\$

$\\ =\mathop{\lim }\limits_{x \rightarrow \frac{1}{2}} \left( \left( \frac{1}{2x+1} \right) \times \left( \frac{12x^{2}+8x-6x-4}{2x-1} \right) \right) \\ \\ =\mathop{\lim }\limits_{x \rightarrow \frac{1}{2}} \left( \left( \frac{1}{2x+1} \right) \times \left( \frac{ \left( 3x+2 \right) \left( 4x-2 \right) }{2x-1} \right) ~ \right) \\$

$\\ =\mathop{\lim }\limits_{x \rightarrow \frac{1}{2}} \left( \left( \frac{1}{2x+1} \right) \times2 \left( 3x+2 \right) ~ \right) =\frac{1}{2 \times\frac{1}{2}+1} \times2 \times \left( 3 \times\frac{1}{2}+2 \right) =\frac{7}{2} \\ \\$

Question:14

Evaluate: Find ‘n’, if
$\mathop{\lim }\limits_{x \rightarrow 2} \left( \frac{x^{n}-2^{n}}{x-2} \right) =80, n \in N \\ \\$

Answer:

$\\ \text{We know that }\mathop{\lim }\limits_{x \rightarrow 2} \left( \frac{x^{n}-2^{n}}{x-2} \right) =n \left( 2 \right) ^{n-1} \\ $

$\\ \\n \left( 2 \right) ^{n-1}=80 \\ $

$\\ n= 5 \times \left( 2 \right) ^{5-1}=5 \times16=80 \\ \\$

Question:15

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow a} \left( \frac{\sin 3x}{\sin 7x} \right) \\$

Answer:

Given $\mathop{\lim }\limits_{x \rightarrow a} \left( \frac{\sin 3x}{\sin 7x} \right) =\frac{\sin 3a}{\sin 7a} \\ \\$

Question:16

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{\sin ^{2}2x}{\sin ^{2}4x} \right) \\$

Answer:

$Given~\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{\sin ^{2}2x}{\sin ^{2}4x} \right) \\ \\ \\ =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{ \left( \frac{\sin 2x}{2x} *2x \right) ^{2}}{ \left( \frac{\sin 4x}{4x} *4x \right) ^{2}} \right) =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{4}{16} *\frac{ \left( \frac{\sin 2x}{2x} \right) ^{2}}{ \left( \frac{\sin 4x}{4x} \right) ^{2}} \right) =\frac{4}{16}=\frac{1}{4} \\ \\$

Question:17

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{1-\cos 2x}{x^{2}} \right)$

Answer:

Given that
$\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{1-\cos 2x}{x^{2}} \right) =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{2\sin ^{2}x}{x^{2}} \right) =\mathop{\lim }\limits_{x \rightarrow 0} \left( 2 * \left( \frac{\sin x}{x} \right) ^{2} \right) =2 \\ \\$

Question:18

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{2\sin x-\sin 2x}{x^{3}} \right) \\$

Answer:

$\\Given~\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{2\sin x-\sin 2x}{x^{3}} \right) =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{2\sin x \left( 1-\cos x \right) }{x^{3}} \right) =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{2\sin x \left( 2\sin ^{2}\frac{x}{2} \right) }{x^{3}} \right) \\ $

$\\ =\mathop{\lim }\limits_{x \rightarrow 0} \left( 2 *\frac{\sin x}{x} *2 * \left( \frac{\sin \frac{x}{2}}{\frac{x}{2}} \right) ^{2} *\frac{1}{4} \right) =1 \\ \\$

Question:19

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{1-\cos mx}{1-\cos nx} \right) \\$

Answer:

$\\ \text{Given that }\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{1-\cos mx}{1-\cos nx} \right) =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{\sin ^{2}\frac{mx}{2}}{\sin ^{2}\frac{nx}{2}} \right) \\ \\ =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{\frac{\sin ^{2}\frac{mx}{2}}{ \left( \frac{mx}{2} \right) ^{2}} * \left( \frac{mx}{2} \right) ^{2}}{\frac{\sin ^{2}\frac{nx}{2}}{ \left( \frac{nx}{2} \right) ^{2}} * \left( \frac{nx}{2} \right) ^{2}} \right) \\$

$ \\ =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{\frac{\sin ^{2}\frac{mx}{2}}{ \left( \frac{mx}{2} \right) ^{2}} *m^{2}}{\frac{\sin ^{2}\frac{nx}{2}}{ \left( \frac{nx}{2} \right) ^{2}} *n^{2}} \right) =\frac{m^{2}}{n^{2}} \\ \\$

Question:20

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{3}}\frac{\sqrt {1-\cos 6x}}{\sqrt {2} \left( \frac{ \pi }{3}-x \right)}$

Answer:

$\\ \mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{3}}\frac{\sqrt {1-\cos 6x}}{\sqrt {2} \left( \frac{ \pi }{3}-x \right) }~~ \\ \\ ~Here\cos 6x= 1-2\sin ^{2}3x \\ \\$

$\\ =\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{3}}\frac{\sqrt {2\sin ^{2}3x}}{\sqrt {2} \left( \frac{ \pi }{3}-x \right) }=\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{3}}\frac{ \vert \sin 3x \vert }{ \left( \frac{ \pi -3x}{3} \right) }=\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{3}}\frac{ \vert \sin \left( \pi -3x \right) \vert }{ \left( \frac{ \pi -3x}{3} \right) } \\ \\ =\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{3}}3 *\frac{ \vert \sin \left( \pi -3x \right) \vert }{ \pi -3x}=3 *1=3 \\$

Question:21

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}}\frac{\sin x-\cos x}{x-\frac{ \pi }{4} }\\$

Answer:

$\\ \text{Given that }\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}}\frac{\sin x-\cos x}{x-\frac{ \pi }{4}} \\ \\ =\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}}\frac{\sqrt {2} \left( \sin x\cos \frac{ \pi }{4}-\cos x\sin \frac{ \pi }{4} \right) }{x-\frac{ \pi }{4}}=\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}}\frac{\sqrt {2}\sin \left( x-\frac{ \pi }{4} \right) }{x-\frac{ \pi }{4}}= \sqrt {2} \\ \\$

Question:22

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{6}}\frac{\sqrt {3}\sin x-\cos x}{x-\frac{ \pi }{6}} \\$

Answer:

$\\\text{Given that }\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{6}}\frac{\sqrt {3}\sin x-\cos x}{x-\frac{ \pi }{6}}=\\\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{6}}\frac{2 \left( \frac{\sqrt {3}}{2}\sin x-\frac{1}{2}\cos x \right) }{x-\frac{ \pi }{6}}=\\ \mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{6}}\frac{2 \left( \cos \frac{ \pi }{6}\sin x-\sin \frac{ \pi }{6}\cos x \right) }{x-\frac{ \pi }{6}} \\ \\$

$=\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{6}}\frac{2\sin \left( x-\frac{ \pi }{6} \right) }{x-\frac{ \pi }{6}}=2 \\ \\$

Question:23

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow 0}\frac{\sin 2x+3x}{2x+\tan 3x} \\$

Answer:

$\\ \text{Given that }\mathop{\lim }\limits_{x \rightarrow 0}\frac{\sin 2x+3x}{2x+\tan 3x} \\ \\ =\mathop{\lim }\limits_{x \rightarrow 0}\frac{2x *\frac{\sin 2x}{2x}+3x}{2x+3x *\frac{\tan 3x}{3x}} \\ \\ =\mathop{\lim }\limits_{x \rightarrow 0}\frac{x \left( 2 *\frac{\sin 2x}{2x}+3 \right) }{x \left( 2+3 *\frac{\tan 3x}{3x} \right) } \\ \\$

$\\ =\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left( 2 *\frac{\sin 2x}{2x}+3 \right) }{ \left( 2+3 *\frac{\tan 3x}{3x} \right) } \\ \\ =\frac{2+3}{2+3}=\frac{5}{5}=1 \\ \\$

Question:24

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow a}\frac{\sin x-\sin a}{\sqrt {x}-\sqrt {a}} \\$

Answer:

$\\ \text{Given that }\mathop{\lim }\limits_{x \rightarrow a}\frac{\sin x-\sin a}{\sqrt {x}-\sqrt {a}} \\ \\ =\mathop{\lim }\limits_{x \rightarrow a}\frac{ \left( \sin x-\sin a \right) \left( \sqrt {x}+\sqrt {a} \right) }{ \left( \sqrt {x}-\sqrt {a} \right) \left( \sqrt {x}+\sqrt {a} \right) } \\ \\ =\mathop{\lim }\limits_{x \rightarrow a}\frac{ \left( \sin x-\sin a \right) \left( \sqrt {x}+\sqrt {a} \right) }{ \left( x-a \right) } \\ \\$
$\\=\mathop{\lim }\limits_{x \rightarrow a}\frac{ \left( 2\cos \left( \frac{x+a}{2} \right) \sin \left( \frac{x-a}{2} \right) \right) \left( \sqrt {x}+\sqrt {a} \right) }{ \left( x-a \right) } \\ $

$\\ =\mathop{\lim }\limits_{x \rightarrow a}\cos \left( \frac{x+a}{2} \right) \frac{\sin \left( \frac{x-a}{2} \right) }{\frac{x-a}{2}} \left( \sqrt {x}+\sqrt {a} \right) \\ \\ =\cos \left( a \right) *1 * \left( 2\sqrt {a} \right) =2\sqrt {a}\cos a \\ \\$

Question:25

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{6}}\frac{\cot ^{2}x-3}{cosec x-2} \\$

Answer:

$\\ \text{Given that }\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{6}}\frac{\cot ^{2}x-3}{cosec x-2} \\ \\ =\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{6}}\frac{cosec^{2}x-1-3}{cosec x-2} \\$

$ \\ =\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{6}}\frac{cosec^{2}x-1-3}{cosec x-2} \\ \\ =\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{6}}\frac{ \left( cosecx-2 \right) \left( cosecx+2 \right) }{cosec x-2}$

$\\ \\ =\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{6}} \left( cosecx+2 \right) =2+2=4 \\ \\$

Question:26

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left( \sqrt {2}-\sqrt {1+\cos x} \right) }{\sin ^{2}x} \\$

Answer:

$\\ \text{Given that }\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left( \sqrt {2}-\sqrt {1+\cos x} \right) }{\sin ^{2}x} \\ \\ =\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left( \sqrt {2}-\sqrt {1+\cos x} \right) \left( \sqrt {2}+\sqrt {1+\cos x} \right) }{\sin ^{2}x \left( \sqrt {2}+\sqrt {1+\cos x} \right) } \\ $

$\\ =\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left( 2- \left( 1+\cos x \right) \right) }{\sin ^{2}x \left( \sqrt {2}+\sqrt {1+\cos x} \right) } \\ \\ =\mathop{\lim }\limits_{x \rightarrow 0}\frac{1-\cos x}{\sin ^{2}x \left( \sqrt {2}+\sqrt {1+\cos x} \right) } \\ \\$
$\\=\mathop{\lim }\limits_{x \rightarrow 0}\frac{1-\cos x}{ \left( 1-\cos x \right) \left( 1+\cos x \right) \left( \sqrt {2}+\sqrt {1+\cos x} \right) } \\$

$ \\ =\mathop{\lim }\limits_{x \rightarrow 0}\frac{1}{ \left( 1+\cos x \right) \left( \sqrt {2}+\sqrt {1+\cos x} \right) } \\ \\ =\frac{1}{ \left( 1+1 \right) * \left( 2\sqrt {2} \right) }=\frac{1}{4\sqrt {2}} \\ \\$

Question:27

Evaluate:
$\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{\sin x-2\sin 3x+\sin 5x}{x} \right) \\$

Answer:

$. \\ \text{Given that }\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{\sin x-2\sin 3x+\sin 5x}{x} \right) \\$

$ \\ =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{\sin x}{x}-\frac{2\sin 3x}{3x} *3+\frac{\sin 5x}{5x} *5 \right) =1-2 *3+5=0 \\ \\$

Question:28

Evaluate: If
$\\ \mathop{\lim }\limits_{x \rightarrow 1} \left( \frac{x^{4}-1}{x-1} \right) = \mathop{\lim }\limits_{x \rightarrow k} \left( \frac{x^{3}-k^{3}}{x^{2}-k^{2}} \right)$

Answer:

$\\ \text{Given that }$

$\mathop{\lim }\limits_{x \rightarrow 1} \left( \frac{x^{4}-1}{x-1} \right) =4 \left( 1 \right) ^{4-1}=4 \\ \\ \mathop{\lim }\limits_{x \rightarrow k} \left( \frac{x^{3}-k^{3}}{x^{2}-k^{2}} \right)$

$ =\mathop{\lim }\limits_{x \rightarrow k} \left( \frac{ \left( x-k \right) \left( x^{2}+k^{2}+xk \right) }{ \left( x-k \right) \left( x+k \right) } \right) =\mathop{\lim }\limits_{x \rightarrow k} \left( \frac{x^{2}+k^{2}+xk}{x+k} \right) \\=\frac{3k}{2} \\ \\$
$\frac{3k}{2}=4 \\ \\ k=8/3 \\ \\$

Question:29

Differentiate each of the functions w.r.t x in
$\frac{x^{4}+x^{3}+x^{2}+1}{x}$

Answer:

$\\\text{ Let y}=\frac{x^{4}+x^{3}+x^{2}+1}{x} \\ \\ \frac{dy}{dx}=\frac{d \left( x^{3} \right) }{dx}+\frac{d \left( x^{2} \right) }{dx}+\frac{d \left( x \right) }{dx}+\frac{d \left( x^{-1} \right) }{dx} \\$

$ \\ =3x^{2}+2x+1-\frac{1}{x^{2}} \\ \\ =\frac{3x^{4}+2x^{3}+x^{2}-1}{x^{2}} \\ \\$

Question:30

Differentiate each of the functions w.r. to x in
$\left(x+\frac{1}{x}\right)^{3}$

Answer:

Let y= $\left( x+\frac{1}{x} \right) ^{3} \\ \\$

$\\ \frac{dy}{dx}=\frac{d}{dx} \left( x+\frac{1}{x} \right) ^{3}=3 \left( x+\frac{1}{x} \right) ^{2} \left( 1-\frac{1}{x^{2}} \right) \\ $

$\\ =3 \left( x^{2}+2+\frac{1}{x^{2}} \right) \left( 1-\frac{1}{x^{2}} \right) \\$

$ \\ =3 \left( x^{2}+2+\frac{1}{x^{2}}-1-\frac{2}{x^{2}}-\frac{1}{x^{4}} \right) \\$

$ \\ =3x^{2}+3-\frac{3}{x^{2}}-\frac{3}{x^{4}} \\ \\$

Question:31

Differentiate each of the functions w.r. to x in
$(3x + 5) (1 + tan x)$

Answer:

Given that $y= \left( 3x+5 \right) \left( 1+\tan x \right) ~ \\ \\$

Applying product rule of differentiation we get

$\\ \frac{dy}{dx}= \left( 1+\tan x \right) \frac{d}{dx} \left( 3x+5 \right) + \left( 3x+5 \right) \frac{d}{dx} \left( 1+\tan x \right) \\ $

$\\ =3 \left( 1+\tan x \right) + \left( 3x+5 \right) \sec ^{2}x \\ \\$

Question:32

Differentiate each of the functions w.r. to x in
$(sec x - 1) (sec x + 1)$

Answer:

y= $\left( \sec x-1 \right) \left( \sec x+1 \right) =\sec ^{2}x-1=\tan ^{2}x~ \\ \\$

Now applying the concept of chain rule

$\frac{dy}{dx}=\frac{d \left( \tan ^{2}x \right) }{dx}=2\tan x\sec ^{2}x \\ \\$

Question:33

Differentiate each of the functions w.r. to x in
$\frac{3x+4}{5x^{2}-7x+9 }\\$

Answer:

Given that $y=\frac{3x+4}{5x^{2}-7x+9} \\ \\$

Applying division rule of differentiation that is

$\\ \frac{dy}{dx}=\frac{d}{dx} \left( \frac{3x+4}{5x^{2}-7x+9} \right) \\$

$ \\ =\frac{ \left( 5x^{2}-7x+9 \right) \frac{d}{dx} \left( 3x+4 \right) - \left( 3x+4 \right) \frac{d}{dx} \left( 5x^{2}-7x+9 \right) }{ \left( 5x^{2}-7x+9 \right) ^{2}} \\ $

$\\ =\frac{ \left( 5x^{2}-7x+9 \right) \left( 3 \right) - \left( 3x+4 \right) \left( 10x-7 \right) }{ \left( 5x^{2}-7x+9 \right) ^{2}} \\$

$ \\ =-\frac{5 \left( 3x^{2}+8x-11 \right) }{ \left( 5x^{2}-7x+9 \right) ^{2}} \\$
$\\ =\frac{5 \left( 3x+11 \right) \left( 1-x \right) }{ \left( 5x^{2}-7x+9 \right) ^{2}} \\ \\$

Question:34

Differentiate each of the functions w.r. to x in
$\frac{x^{5}-\cos x}{\sin x} \\$
Answer:

Given that $y=\frac{x^{5}-\cos x}{\sin x}=\frac{x^{5}}{\sin x}-\frac{\cos x}{\sin x} \\ \\$

Applying division rule of differentiation that is

$\\ \frac{dy}{dx}=\frac{\sin x\frac{d}{dx} \left( x^{5} \right) -x^{5}\frac{d}{dx} \left( sinx \right) }{\sin ^{2}x}-\frac{d}{dx} \left( \cot x \right) \\ \\ =\frac{5x^{4}\sin x-x^{5}\cos x}{\sin ^{2}x}+\mathrm{cosec} ^{2}x \\ \\$

Question:35

Differentiate each of the functions w.r. to x in
$\frac{x^{2}\cos \frac{ \pi }{4}}{\sin x }$

Answer:

$y=\frac{x^{2}\cos \frac{ \pi }{4}}{\sin x} \\ \\$

Applying division rule of differentiation that is

$\\ \frac{dy}{dx}=\frac{\cos \frac{ \pi }{4} \left( \sin x\frac{d}{dx} \left( x^{2} \right) -x^{2}\frac{d}{dx} \left( \sin x \right) \right) }{\sin ^{2}x} \\ \\ =\frac{1}{\sqrt {2}} \left( \frac{2x\sin x-x^{2}\cos x}{\sin ^{2}x} \right) \\ \\$

Question:36
Differentiate each of the functions w.r. to x in

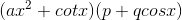
Answer:

Given that $y= \left( ax^{2}+\cot x \right) \left( p+q\cos x \right) ~~~ \\ \\$

Applying the division rule of differentiation that is

$\frac{dy}{dx}= \left( p+q\cos x \right) \frac{d}{dx} \left( ax^{2}+\cot x \right) + \left( ax^{2}+\cot x \right) \frac{d}{dx} \left( p+q\cos x \right) \\ \\$
$= \left( p+q\cos x \right) \left( 2ax-cosec^{2}x \right) + \left( ax^{2}+\cot x \right) \left( -q\sin x \right) \\ \\$

Question:37

Differentiate each of the functions w.r. to x in
$\left( \frac{a+b\sin x}{c+d\cos x} \right)$

Answer:

Given that$y= \left( \frac{a+b\sin x}{c+d\cos x} \right) \\ \\$

Applying division rule of differentiation that is
$\\ \frac{dy}{dt}=\frac{ \left( c+d\cos x \right) \frac{d}{dx} \left( a+b\sin x \right) - \left( a+b\sin x \right) \frac{d}{dx} \left( c+d\cos x \right) }{ \left( c+d\cos x \right) ^{2}} \\ \\ =\frac{b\cos x \left( c+d\cos x \right) - \left( -d\sin x \right) \left( a+b\sin x \right) }{ \left( c+d\cos x \right) ^{2}} \\ \\$

$=\frac{bc\cos x+bd\cos ^{2}x+ad\sin x+bd\sin ^{2}x}{ \left( c+d\cos x \right) ^{2}}=\frac{bd+bc\cos x+ad\sin x}{ \left( c+d\cos x \right) ^{2}} \\ \\$

Question:38

Differentiate each of the functions w.r. to x in

Answer:

Given that
$\\y= \left( \sin x+\cos x \right) ^{2}=\sin ^{2}x+\cos ^{2}x+2\sin x\cos x=1+2\sin x\cos x\\=1+\sin 2x~ \\ \\$
Applying the concept of chain rule
$\frac{dy}{dx}=\frac{d}{dx} \left( 1+\sin 2x \right) =0+2 *\cos 2x=2\cos 2x=2 \left( \cos ^{2}x-\sin ^{2}x \right) \\ \\$

Question:39

Differentiate each of the functions w.r. to x in

Answer:

This question will involve the concept of both chain rule and product rule

Given that $y= \left( 2x-7 \right) ^{2} \left( 3x+5 \right) ^{3}~ \\ \\$

Applying the product rule of differentiation
$\\ \frac{dy}{dx}= \left( 3x+5 \right) ^{3}\frac{d}{dx} \left( 2x-7 \right) ^{2}+ \left( 2x-7 \right) ^{2}\frac{d}{dx} \left( 3x+5 \right) ^{3} \\ $

$\\ = \left( 3x+5 \right) ^{3} *2 * \left( 2x-7 \right) *2+ \left( 2x-7 \right) ^{2} *3 * \left( 3x+5 \right) ^{2} *3 \\$

$ \\ = \left( 2x-7 \right) \left( 3x+5 \right) ^{2} \left[ 4 \left( 3x+5 \right) +9 \left( 2x-7 \right) \right] \\ \\ = \left( 2x-7 \right) \left( 3x+5 \right) ^{2} \left( 30x-43 \right) \\ \\$

Question:40

Differentiate each of the functions w.r. to x in
$x^{2} sinx + cos2x$

Answer:

This question will involve the concept of both chain rule and product rule

$\\Given \: \: that\: \: y=x^{2}\sin x+\cos 2x \\$

$ \\ \frac{dy}{dx}=\frac{d}{dx} \left( x^{2}\sin x \right) +\frac{d}{dx} \left( \cos 2x \right) \\ $

$\\ =\sin x\frac{d}{dx} \left( x^{2} \right) +x^{2}\frac{d}{dx} \left( \sin x \right) +\frac{d}{dx} \left( \cos 2x \right) \\ \\ =2x\sin x+x^{2}\cos x-2\sin 2x \\ \\$

Question:41

Differentiate each of the functions w.r.to x in
$sin ^{3}x cos ^{3}x $

Answer:

The question involves the concept of chain rule

$\\Given\: \: that \: \: y=\sin ^{3}x\cos ^{3}x \\ \\ y=\frac{1}{8} \left( 2\sin x\cos x \right) ^{3}$

$=\frac{1}{8}\sin ^{3}2x \\ \\ \frac{dy}{dx}=\frac{3}{8}\sin ^{2}2x \left( 2\cos 2x \right) =\frac{3}{4}\sin ^{2}2x\cos 2x \\ \\$

Question:42

Differentiate each of the functions w.r. to x in
$\frac{1}{ax^{2}+bx+c}$

Answer:

The question involves the concept of chain rule

$\\ Given\: \: that\: \: y=\frac{1}{ax^{2}+bx+c}= \left( ax^{2}+bx+c \right) ^{-1} \\ $

$\\ \frac{dy}{dx}=-1 \left( ax^{2}+bx+c \right) ^{-2} \left( 2ax+b \right) =-\frac{2ax+b}{ax^{2}+bx+c} \\ \\$

Question:43

Differentiate each of the functions with respect to ‘x’Differentiate using first principle

Answer:

$\\ \text{Let f} \left( x \right) =\cos \left( x^{2}+1 \right) \ldots \ldots .. \left( i \right) \\$

$ \\ f \left( x+ \Delta x \right) =\cos \left( \left( x+ \Delta x \right) ^{2}+1 \right) \ldots \ldots \left( ii \right) \\$

$ \\ \text{ Subtracting equation } \left( i \right) from \: \: equation \left( ii \right) \\$

$ \\ \frac{f \left( x+ \Delta x \right) -f \left( x \right) }{ \Delta x}=\frac{\cos \left( \left( x+ \Delta x \right) ^{2}+1 \right) -\cos \left( x^{2}+1 \right) }{ \Delta x} \\ \\$
$\\ =\mathop{\lim }\limits_{ \Delta x \rightarrow 0}\frac{\cos \left( \left( x+ \Delta x \right) ^{2}+1 \right) -\cos \left( x^{2}+1 \right) }{ \Delta x} \\ $

$\\ =\mathop{\lim }\limits_{ \Delta x \rightarrow 0}\frac{-2\sin \left[ \frac{ \left( x+ \Delta x \right) ^{2}+1-x^{2}-1}{2} \right] \sin \left[ \frac{ \left( x+ \Delta x \right) ^{2}+1+x^{2}+1}{2} \right] }{ \Delta x} \\ \\ =\mathop{\lim }\limits_{ \Delta x \rightarrow 0}\frac{-2\sin \left[ \frac{2x \Delta x+ \left( \Delta x \right) ^{2}}{2} \right] \sin \left[ \frac{2x^{2}+2x \Delta x+2}{2} \right] }{ \Delta x} \\$

$ \\ =\mathop{\lim }\limits_{ \Delta x \rightarrow 0} \left( \frac{2x+ \Delta x}{2} \right) \left( ~\frac{-2\sin \left[ \frac{2x \Delta x+ \left( \Delta x \right) ^{2}}{2} \right] \sin \left[ \frac{2x^{2}+2x \Delta x+2}{2} \right] }{\frac{ \Delta x \left( 2x+ \Delta x \right) }{2}} \right) \\ \\$
$\\ =\mathop{\lim }\limits_{ \Delta x \rightarrow 0} \left( \frac{2x+ \Delta x}{2} \right) \left( -2\sin \left[ \frac{2x^{2}+2x \Delta x+2}{2} \right] \right) \left( ~\frac{\sin \left[ \frac{2x \Delta x+ \left( \Delta x \right) ^{2}}{2} \right] }{\frac{ \Delta x \left( 2x+ \Delta x \right) }{2}} \right) \\$

$ \\ =- \left( \frac{2x+0}{2} \right) \left( 2\sin \left( x^{2}+0+1 \right) \right) \left( 1 \right) =-2x\sin \left( x^{2}+1 \right) \text{is the required answer} \\ \\$

Question:44

Differentiate each of the functions with respect to ‘x’
Differentiate using first principle $\frac{ax+b}{cx+d}$

Answer:

$\\ \text{Let f} \left( x \right) =\frac{ax+b}{cx+d} \ldots .. \left( i \right) \\$

$ \\ f \left( x+ \Delta x \right) =\frac{a \left( x+ \Delta x \right) +b}{c \left( x+ \Delta x \right) +d} \ldots \ldots \left( ii \right) \\$

$ \\ \text{Subtracting equation } \left( i \right) \text{from equation } \left( ii \right) \\ $

$\\ \frac{f \left( x+ \Delta x \right) -f \left( x \right) }{ \Delta x}=\frac{\frac{a \left( x+ \Delta x \right) +b}{c \left( x+ \Delta x \right) +d}-\frac{ax+b}{cx+d}}{ \Delta x}~ \\ \\$
$\\ \text{Taking the limit} \\ \\ f^{'} \left( x \right) =\mathop{\lim }\limits_{ \Delta x \rightarrow 0}\frac{\frac{a \left( x+ \Delta x \right) +b}{c \left( x+ \Delta x \right) +d}-\frac{ax+b}{cx+d}}{ \Delta x} \\ $

$\\ =\mathop{\lim }\limits_{ \Delta x \rightarrow 0}\frac{\frac{ \left( cx+d \right) \left( ax+a \Delta x+b \right) - \left( ax+b \right) \left( cx+c \Delta x+d \right) }{ \left( cx+c \Delta x+d \right) \left( cx+d \right) }}{ \Delta x} \\$

$ \\ =\mathop{\lim }\limits_{ \Delta x \rightarrow 0}\frac{ \left( ad-bc \right) \Delta x}{ \left( cx+c \Delta x+d \right) \left( cx+d \right) \Delta x} \\ \\$

$\\ =\mathop{\lim }\limits_{ \Delta x \rightarrow 0}\frac{ \left( ad-bc \right) }{ \left( cx+c \Delta x+d \right) \left( cx+d \right) }= \frac{ad-bc}{ \left( cx+d \right) ^{2}}\text{ is the required answer} \\ \\$

Question:45

Differentiate each of the functions with respect to ‘x’
Differentiate using first principle $X^{\frac{2}{3}}$

Answer:

$\\ f^{'} \left( x \right) =\mathop{\lim }\limits_{ \Delta x \rightarrow 0}\frac{ \left( x+ \Delta x \right) ^{\frac{2}{3}}-x^{\frac{2}{3}}}{ \Delta x} \\ \\ =\mathop{\lim }\limits_{ \Delta x \rightarrow 0}\frac{x^{\frac{2}{3}} \left[ \left( 1+\frac{ \Delta x}{x} \right) ^{\frac{2}{3}}-1 \right] }{ \Delta x} \\ \\ =\mathop{\lim }\limits_{ \Delta x \rightarrow 0}\frac{x^{\frac{2}{3}} \left[ \left( 1+\frac{2}{3}\frac{ \Delta x}{x}+ \ldots \right) -1 \right] }{ \Delta x} \\ \\$

Expanding by binomial theorem and rejecting the higher powers of $\Delta x \: \: as\: \: \Delta x \rightarrow 0 \\ \\$

$\\ =\mathop{\lim }\limits_{ \Delta x \rightarrow 0}\frac{x^{\frac{2}{3}} \left( \frac{2}{3}\frac{ \Delta x}{x} \right) }{ \Delta x}=\mathop{\lim }\limits_{ \Delta x \rightarrow 0} \left( \frac{2}{3}\frac{x^{\frac{2}{3}}}{x} \right) =\frac{2}{3}x^{-\frac{1}{3}}$

Question:46

Differentiate each of the functions with respect to ‘x’
Differentiate using first principle x cos x.

Answer:

$\\ Given\: \: that\: \: y=x\cos x \ldots . \left( i \right) \\$

$ \\ y+ \Delta y= \left( x+ \Delta x \right) \cos \left( x+ \Delta x \right) \ldots . \left( ii \right) ~ \\ $

$\\ \text{ Subtracting equation } \left( i \right) from equation \left( ii \right) \\ $

$\\ y^{'}=\mathop{\lim }\limits_{ \Delta x \rightarrow 0} \left( \frac{ \left( \left( x+ \Delta x \right) \cos \left( x+ \Delta x \right) -x\cos x \right) }{ \Delta x} \right) \\ \\$

$\\ =\mathop{\lim }\limits_{ \Delta x \rightarrow 0} \left( \frac{x\cos \left( x+ \Delta x \right) -x\cos x}{ \Delta x} \right) +\mathop{\lim }\limits_{ \Delta x \rightarrow 0} \left( \frac{ \Delta x\cos \left( x+ \Delta x \right) }{ \Delta x} \right) \\$

$ \\ =\mathop{\lim }\limits_{ \Delta x \rightarrow 0} \left( \frac{x \left( -2\sin \frac{x+ \Delta x-x}{2}\sin \frac{x+ \Delta x+x}{2} \right) }{ \Delta x} \right) +\mathop{\lim }\limits_{ \Delta x \rightarrow 0}\cos \left( x+ \Delta x \right) \\$

$ \\ =\mathop{\lim }\limits_{ \Delta x \rightarrow 0}\frac{- \left( 2\sin \left( x+\frac{ \Delta x}{2} \right) \sin \left( \frac{ \Delta x}{2} \right) x \right) }{ \Delta x}+\mathop{\lim }\limits_{ \Delta x \rightarrow 0}\cos \left( x+ \Delta x \right) \\ \\$

$\\ =\mathop{\lim }\limits_{ \Delta x \rightarrow 0}-x\sin \left( x+\frac{ \Delta x}{2} \right) \frac{ \left( \sin \left( \frac{ \Delta x}{2} \right) \right) }{\frac{ \Delta x}{2}}+\mathop{\lim }\limits_{ \Delta x \rightarrow 0}\cos \left( x+ \Delta x \right) \\ \\ =-x\sin x+\cos x \\ \\$

Question:47

Evaluate each of the following limits

$\mathop{\lim }\limits_{y \rightarrow 0}\frac{ \left( x+y \right) \sec \left( x+y \right) -x\sec x}{y }$

Answer:

$\\ \text{Given that}$

$\mathop{\lim }\limits_{y \rightarrow 0}\frac{ \left( x+y \right) \sec \left( x+y \right) -x\sec x}{y}=\mathop{\lim }\limits_{y \rightarrow 0} \left( \frac{x\sec \left( x+y \right) -x\sec x}{y}+\frac{y\sec \left( x+y \right) }{y} \right) \\$

$ \\ =\mathop{\lim }\limits_{y \rightarrow 0} \left( \frac{x}{y} \left[ \frac{\cos x-\cos \left( x+y \right) }{\cos x\cos \left( x+y \right) } \right] +\sec \left( x+y \right) \right) \\ $

$\\ =\mathop{\lim }\limits_{y \rightarrow 0} \left( \frac{x}{y} \left[ \frac{-2\sin \left( x+\frac{y}{2} \right) \sin \left( \frac{-y}{2} \right) }{\cos x\cos \left( x+y \right) } \right] +\sec \left( x+y \right) \right) \\ \\$
$\\ =\mathop{\lim }\limits_{y \rightarrow 0} \left( \frac{x\sin \left( x+\frac{y}{2} \right) }{\cos x\cos \left( x+y \right) } \left[ \frac{\sin \left( \frac{y}{2} \right) }{\frac{y}{2}} \right] +\sec \left( x+y \right) \right) \\ \\ =x\sec x\tan x+\sec x \\ \\ =\sec x \left( x\tan x+1 \right) \\ \\$

Question:48

Evaluate each of the following limits
$\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left[ \sin \left( \alpha + \beta \right) x+\sin \left( \alpha - \beta \right) x+\sin 2 \alpha x \right] }{\cos 2 \beta x-\cos 2 \alpha x}x \\$

Answer:

$\\ \mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left[ \sin \left( \alpha + \beta \right) x+\sin \left( \alpha - \beta \right) x+\sin 2 \alpha x \right] }{\cos 2 \beta x-\cos 2 \alpha x}x \\ \\ =\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left[ 2\sin \alpha x\cos \beta x+2\sin \alpha x\cos \alpha x \right] }{ \left[ 2\sin \left( \alpha + \beta \right) x~\sin \left( \alpha - \beta \right) x \right] }x \\$

$ \\ =\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left[ \sin \alpha x \left( \cos \beta x+\cos \alpha x \right) \right] }{ \left[ \sin \left( \alpha + \beta \right) x~\sin \left( \alpha - \beta \right) x \right] }x \\ \\ =\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left[ \sin \alpha x \left( 2\cos \frac{ \left( \alpha + \beta \right) x}{2}\cos \frac{ \left( \alpha - \beta \right) x}{2} \right) \right] }{ \left[ \sin \left( \alpha + \beta \right) x~\sin \left( \alpha - \beta \right) x \right] }x \\$

$ \\$
$\\ =\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left[ \sin \alpha x \right] }{ \left[ 2\sin \frac{ \left( \alpha + \beta \right) x}{2}\sin \frac{ \left( \alpha - \beta \right) x}{2} \right] }x \\$

$ \\ =\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left[ \frac{\sin \alpha x}{ \alpha x} \right] * \alpha x *x}{ \left[ 2 \left( \frac{\sin \frac{ \left( \alpha + \beta \right) x}{2}}{\frac{ \left( \alpha + \beta \right) x}{2}} \right) \left( \frac{\sin \frac{ \left( \alpha - \beta \right) x}{2}}{\frac{ \left( \alpha - \beta \right) x}{2}} \right) *\frac{ \left( \alpha + \beta \right) x}{2} *\frac{ \left( \alpha - \beta \right) x}{2} \right] } \\$

$ \\ =\frac{ \alpha }{2 *\frac{ \left( \alpha + \beta \right) }{2} *\frac{ \left( \alpha - \beta \right) }{2}}=\frac{2 \alpha }{ \alpha ^{2}- \beta ^{2}} \\ \\$

Question:49

Evaluate each of the following limits
$\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}} \left( \frac{\tan ^{3}x-\tan x}{\cos \left( x+\frac{ \pi }{4} \right) } \right)$
Answer:

$\\ \mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}} \left( \frac{\tan ^{3}x-\tan x}{\cos \left( x+\frac{ \pi }{4} \right) } \right) =\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}} \left( \tan x \right) *\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}} \left( \frac{\tan ^{2}x-1}{\cos \left( x+\frac{ \pi }{4} \right) } \right) \\$

$ \\ =1 *\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}} \left( \frac{- \left( 1-\tan x \right) \left( 1+\tan x \right) }{\cos \left( x+\frac{ \pi }{4} \right) } \right) \\$

$ \\ =\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}}- \left( 1+\tan x \right) *\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}} \left( \frac{ \left( 1-\tan x \right) }{\cos \left( x+\frac{ \pi }{4} \right) } \right) \\$

$ \\ =-2\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}} \left( \frac{ \left( \cos x-\sin x \right) }{\cos \left( x+\frac{ \pi }{4} \right) \cos x} \right) \\ \\$
$\\ =-2\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}} \left( \frac{\sqrt {2} \left( \cos \frac{ \pi }{4}\cos x-\sin \frac{ \pi }{4}\sin x \right) }{\cos \left( x+\frac{ \pi }{4} \right) \cos x} \right) \\ $

$\\ =-2\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}} \left( \frac{\sqrt {2} \left( \cos \left( x+\frac{ \pi }{4} \right) \right) }{\cos \left( x+\frac{ \pi }{4} \right) \cos x} \right) =-2\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}} \left( \frac{\sqrt {2}}{\cos x} \right) =-4 \\ \\$

Question:50

Evaluate each of the following limits
$\mathop{\lim }\limits_{x \rightarrow \pi } \left( \frac{1-\sin \frac{x}{2}}{\cos \frac{x}{2} \left( \cos \frac{x}{4}-\sin \frac{x}{4} \right) } \right)$

Answer:

$\\ \mathop{\lim }\limits_{x \rightarrow \pi } \left( \frac{1-\sin \frac{x}{2}}{\cos \frac{x}{2} \left( \cos \frac{x}{4}-\sin \frac{x}{4} \right) } \right) =\mathop{\lim }\limits_{x \rightarrow \pi } \left( \frac{1-\sin \frac{x}{2}}{\cos \frac{x}{2} \left( \cos \frac{x}{4}-\sin \frac{x}{4} \right) } \right) \\$

$ \\ =\mathop{\lim }\limits_{x \rightarrow \pi } \left( \frac{\cos ^{2}\frac{x}{4}+\sin ^{2}\frac{x}{4}-2\sin \frac{x}{4}\cos \frac{x}{4}}{ \left( \cos ^{2}\frac{x}{4}-\sin ^{2}\frac{x}{4} \right) \left( \cos \frac{x}{4}-\sin \frac{x}{4} \right) } \right) \\ \\$
$\\ =\mathop{\lim }\limits_{x \rightarrow \pi } \left( \frac{ \left( \cos \frac{x}{4}-\sin \frac{x}{4} \right) ^{2}}{ \left( \cos ^{2}\frac{x}{4}-\sin ^{2}\frac{x}{4} \right) \left( \cos \frac{x}{4}-\sin \frac{x}{4} \right) } \right) =\mathop{\lim }\limits_{x \rightarrow \pi } \left( \frac{ \left( \cos \frac{x}{4}-\sin \frac{x}{4} \right) }{ \left( \cos ^{2}\frac{x}{4}-\sin ^{2}\frac{x}{4} \right) } \right) \\$

$ \\ =\mathop{\lim }\limits_{x \rightarrow \pi } \left( \frac{1}{ \left( \cos \frac{x}{4}+\sin \frac{x}{4} \right) } \right) =\frac{1}{\frac{1}{\sqrt {2}}+\frac{1}{\sqrt {2}}}=\frac{1}{\sqrt {2}} \\ \\$

Question:51

Evaluate each of the following limits
Show that $\mathop{\lim }\limits_{x \rightarrow 4}\frac{ \vert x-4 \vert }{x-4}$ does not exist.

Answer:

$\\ \mathop{\lim }\limits_{x \rightarrow 4}\frac{ \vert x-4 \vert }{x-4} \\$

$ \\ LHL=\mathop{\lim }\limits_{x \rightarrow \mathop{4}^{-}}\frac{-x+4}{x-4}=-1 \\$

$ \\ RHL=\mathop{\lim }\limits_{x \rightarrow \mathop{4}^{+}}\frac{x-4}{x-4}=1~ \\$

$ \\ LHL \neq RHL \\ \\$

Hence, the limit doesnot exist

Question:52

Let $f \left( x \right) =\frac{k\cos x}{ \pi -2x}$ when $x \neq \frac{\pi}{2}$and
$f(x)=3$ if $\lim _{x \rightarrow \frac{\pi}{2}} f(x)=f\left(\frac{\pi}{2}\right)$ find the value of k.

Answer:

$\\ LHL=\mathop{\lim }\limits_{x \rightarrow \mathop{\frac{ \pi }{2}}^{-}} \left( \frac{k\cos \left( \frac{ \pi }{2}-h \right) }{ \pi -2 \left( \frac{ \pi }{2}-h \right) } \right) =\mathop{\lim }\limits_{h \rightarrow \mathop{0}^{-}} \left( \frac{k\cos \left( \frac{ \pi }{2}-h \right) }{2h} \right) \\ \\ =\mathop{\lim }\limits_{h \rightarrow \mathop{0}^{-}} \left( \frac{k\sin h}{2h} \right) =\frac{k}{2} \\ $

$\\ RHL=\mathop{\lim }\limits_{x \rightarrow \mathop{\frac{ \pi }{2}}^{+}} \left( \frac{k\cos \left( \frac{ \pi }{2}+h \right) }{ \pi -2 \left( \frac{ \pi }{2}+h \right) } \right) =\mathop{\lim }\limits_{h \rightarrow \mathop{0}^{+}} \left( \frac{k\cos \left( \frac{ \pi }{2}+h \right) }{-2h} \right) \\ \\$$\\=\mathop{\lim }\limits_{h \rightarrow \mathop{0}^{-}} \left( \frac{-k\sin h}{-2h} \right) =\frac{k}{2} \\$

$ \\ \mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{2}}f \left( x \right) =\frac{k}{2}=3 \\ \\ k=6 \\ \\$

Question:53

Evaluate each of the following limits
Let $f(x)=\begin{array}{ll} x+2 & x \leq-1 \\ c x^{2} & x>-1 \end{array}$ find ‘c’ if $\lim _{x \rightarrow-1} f(x)$ exists.

Answer:

$\\ LHL=\mathop{\lim }\limits_{x \rightarrow \mathop{-1}^{-}} \left( x+2 \right) =-1+2=1 \\ $

$\\ RHL=\mathop{\lim }\limits_{x \rightarrow \mathop{-1}^{+}}cx^{2}=c \\$

$ \\ LHL=RHL \\$

$ \\ c=1 \\ \\$

Question:54

Choose the correct answer out of 4 options given against each Question
$\mathop{\lim }\limits_{x \rightarrow \pi }\frac{\sin x}{x- \pi }$ is
A. 1
B. 2
C. –1
D. –2

Answer:

$\\ \mathop{\lim }\limits_{x \rightarrow \pi }\frac{\sin x}{x- \pi }=\mathop{\lim }\limits_{x \rightarrow \pi }\frac{\sin \left( \pi -x \right) }{- \left( \pi -x \right) }=-1~ \\ \\ \mathop{\lim }\limits_{x \rightarrow 0}\frac{\sin x}{x}=1~~~ \\ \\ \pi -x \rightarrow 0~~~x \rightarrow \pi \\ \\$

Hence, the answer is option C

Question:55

Choose the correct answer out of 4 options given against each Question
$\mathop{\lim }\limits_{x \rightarrow 0}\frac{x^{2}\cos x}{1-\cos x}~$ is
A. 2
B. $\frac{3}{2}$
C. $\frac{-3}{2}$
D. 1

Answer:

$\\ \mathop{\lim }\limits_{x \rightarrow 0}\frac{x^{2}\cos x}{1-\cos x}=\mathop{\lim }\limits_{x \rightarrow 0}\frac{x^{2}\cos x}{2\sin ^{2}\frac{x}{2}} \\ \\ =\mathop{\lim }\limits_{x \rightarrow 0}\frac{x^{2}\cos x}{\frac{2x^{2}}{4}\frac{\sin ^{2}\frac{x}{2}}{\frac{x^{2}}{4}}}=\mathop{\lim }\limits_{x \rightarrow 0}\frac{\cos x}{\frac{2}{4}\frac{\sin ^{2}\frac{x}{2}}{\frac{x^{2}}{4}}}=2 \\ \\$
Hence, the answer is option A

Question:56

Choose the correct answer out of 4 options given against each Question
$\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left( 1+x \right) ^{n}-1}{x}~$ is
A. n
B. 1
C. –n
D. 0
Answer:

$\\ \mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left( 1+x \right) ^{n}-1}{x}=\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left( 1+x \right) ^{n}-1^{n}}{ \left( 1+x \right) -1}=n \left( 1 \right) ^{n-1}=n \\ \\$
Hence, the answer is option A

Question:57

Choose the correct answer out of 4 options given against each Question
$\mathop{\lim }\limits_{x \rightarrow 1}\frac{x^{m}-1}{x^{n}-1}$ is
A. 1

B. $\frac{m}{n}$
C. $-\frac{m}{n}$
D. $\frac{m^2}{n^2}$

Answer:

$\\ \mathop{\lim }\limits_{x \rightarrow 1}\frac{x^{m}-1}{x^{n}-1} \\ \\ =\mathop{\lim }\limits_{x \rightarrow 1}\frac{\frac{x^{m}-1}{x-1}}{\frac{x^{n}-1}{x-1}}=\frac{m \left( 1 \right) ^{m-1}}{n \left( 1 \right) ^{n-1}}=\frac{m}{n} \\ \\$
Hence, the answer is option B

Question:58

Choose the correct answer out of 4 options given against each Question

$\mathop{\lim }\limits_{ \theta \rightarrow 0} \left( \frac{1-\cos 4 \theta }{1-\cos 6 \theta } \right)$is

A.$\frac{4}{9}$
B.$\frac{1}{2}$
C.$-\frac{1}{2}$
D.$-1$
Answer:

$\\ \mathop{\lim }\limits_{ \theta \rightarrow 0} \left( \frac{1-\cos 4 \theta }{1-\cos 6 \theta } \right) \\ \\ =\mathop{\lim }\limits_{ \theta \rightarrow 0} \left( \frac{2\sin ^{2}2 \theta }{2\sin ^{2}3 \theta } \right) \\ \\ =\mathop{\lim }\limits_{ \theta \rightarrow 0} \left( \frac{\sin 2 \theta }{\sin 3 \theta } \right) ^{2}=\mathop{\lim }\limits_{ \theta \rightarrow 0} \left( \frac{\frac{\sin 2 \theta }{2 \theta } *2 \theta }{ \left( \frac{\sin 3 \theta }{3 \theta } \right) *3 \theta } \right) ^{2}=\frac{4}{9} \\ \\$
Hence, the answer is option A

Question:59

Choose the correct answer out of 4 options given against each Question
$\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{cosec x-\cot x}{x} \right)$ is
A. $-\frac{1}{2}$

B. 1
C. $\frac{1}{2}$
D. –1

Answer:

$\\ \mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{cosec x-\cot x}{x} \right) \\ \\ =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{1-\cos x}{x\sin x} \right) \\ \\ =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{2\sin ^{2}x/2}{2x\sin x/2\cos x/2} \right) \\ \\ =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{\sin x/2}{x\cos x/2} \right) =\frac{1}{2} \\ \\$
Hence, the answer is option C

Question:60

Choose the correct answer out of 4 options given against each Question
$\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{\sin x}{\sqrt {x+1}-\sqrt {1-x}} \right)$ is
A. 2
B. 0
C. 1
D. –1

Answer:

$\\ \mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{\sin x}{\sqrt {x+1}-\sqrt {1-x}} \right) \\ \\ =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{\sin x \left( \sqrt {x+1}+\sqrt {1-x} \right) }{ \left( \sqrt {x+1}-\sqrt {1-x} \right) \left( \sqrt {x+1}+\sqrt {1-x} \right) } \right) \\ $

$\\ =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{\sin x \left( \sqrt {x+1}+\sqrt {1-x} \right) }{ \left( x+1-1+x \right) } \right) \\ \\ =\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{\sin x \left( \sqrt {x+1}+\sqrt {1-x} \right) }{2x} \right) \\ \\ =1 \\ \\$
Hence, the answer is option C

Question:61

Choose the correct answer out of 4 options given against each Question

$\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}} \left( \frac{\sec ^{2}x-2}{\tan x-1} \right)$ is
A. 3
B. 1
C. 0
D. $\sqrt{2}$

Answer:

$\\ \mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}} \left( \frac{\sec ^{2}x-2}{\tan x-1} \right)\\ =\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}} \left( \frac{1+\tan ^{2}x-2}{\tan x-1} \right) \\=\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}} \left( \frac{\tan ^{2}x-1}{\tan x-1} \right)\\ =\mathop{\lim }\limits_{x \rightarrow \frac{ \pi }{4}} \left( \tan x+1 \right)\\ =2 \\ \\$
Hence, the answer is option D

Question:62

Choose the correct answer out of 4 options given against each Question
$\mathop{\lim }\limits_{x \rightarrow 1} \left( \frac{ \left( \sqrt {x}-1 \right) \left( 2x-3 \right) }{2x^{2}+x-3} \right)$ is

A. $\frac{1}{10}$
B. $\frac{-1}{10}$
C. 1
D. None of these

Answer:

$\\ \mathop{\lim }\limits_{x \rightarrow 1} \left( \frac{ \left( \sqrt {x}-1 \right) \left( 2x-3 \right) }{2x^{2}+x-3} \right) \\ \\ =\mathop{\lim }\limits_{x \rightarrow 1} \left( \frac{ \left( \sqrt {x}-1 \right) \left( 2x-3 \right) }{ \left( 2x+3 \right) \left( x-1 \right) } \right) \\$

$ \\ =\mathop{\lim }\limits_{x \rightarrow 1} \left( \frac{ \left( \sqrt {x}-1 \right) \left( 2x-3 \right) }{ \left( 2x+3 \right) \left( \sqrt {x}-1 \right) \left( \sqrt {x}+1 \right) } \right) \\ \\ =\mathop{\lim }\limits_{x \rightarrow 1} \left( \frac{ \left( 2x-3 \right) }{ \left( 2x+3 \right) \left( \sqrt {x}+1 \right) } \right) =-\frac{1}{10} \\ \\$
Hence, the answer is option B

Question:63

Choose the correct answer out of 4 options given against each Question
If $\begin{aligned} f(x)=\frac{\sin [x]}{[x]}, &[x] \neq 0 \\ 0, &[x]=0 \end{aligned}$ where [.] denotes the greatest integer function, then $\lim_{x\rightarrow 0}f(x)$ is equal to
A. 1
B. 0
C. –1
D. None of these
Answer:

$LHL=\mathop{\lim }\limits_{x \rightarrow \mathop{0}^{-}} \left( \frac{\sin \left[ x \right] }{ \left[ x \right] } \right) =\mathop{\lim }\limits_{h \rightarrow \mathop{0}^{-}} \left( \frac{\sin \left[ 0-h \right] }{ \left[ 0-h \right] } \right) =\mathop{\lim }\limits_{h \rightarrow \mathop{0}^{-}} \left( \frac{\sin \left[ -h \right] }{ \left[ -h \right] } \right) \\=\mathop{\lim }\limits_{h \rightarrow \mathop{0}^{-}} \left( \frac{\sin \left( -1 \right) }{-1} \right) =\sin 1 \\ \\$
$RHL=\mathop{\lim }\limits_{x \rightarrow \mathop{0}^{+}} \left( \frac{\sin \left[ x \right] }{ \left[ x \right] } \right) =\mathop{\lim }\limits_{h \rightarrow \mathop{0}^{+}} \left( \frac{\sin \left[ 0+h \right] }{ \left[ 0+h \right] } \right) =\mathop{\lim }\limits_{h \rightarrow \mathop{0}^{+}} \left( \frac{\sin \left[ h \right] }{ \left[ h \right] } \right) =\mathop{\lim }\limits_{h \rightarrow \mathop{0}^{+}} \left( \frac{\sin \left( 0 \right) }{0} \right) \\ \\$
Limit doesn’t exist
Hence, the answer is option D

Question:64

Choose the correct answer out of 4 options given against each Question

$\mathop{\lim }\limits_{x \rightarrow 0} \left( \frac{ \vert \sin x \vert }{x} \right) ~$ is
A. 1
B. –1
C. does not exist
D. None of these

Answer:

$\\ LHL=\mathop{\lim }\limits_{x \rightarrow \mathop{0}^{-}} \left( \frac{ \vert \sin x \vert }{x} \right) =\mathop{\lim }\limits_{h \rightarrow \mathop{0}^{-}} \left( \frac{ \vert \sin \left( 0-h \right) \vert }{ \left( 0-h \right) } \right) =\mathop{\lim }\limits_{h \rightarrow \mathop{0}^{-}} \left( \frac{-\sin \left( -h \right) }{-h} \right) \\=-1 \\ $

$RHL=\mathop{\lim }\limits_{x \rightarrow \mathop{0}^{+}} \left( \frac{ \vert \sin x \vert }{x} \right) =\mathop{\lim }\limits_{h \rightarrow \mathop{0}^{+}} \left( \frac{ \vert \sin \left( 0+h \right) \vert }{ \left( 0+h \right) } \right) =\mathop{\lim }\limits_{h \rightarrow \mathop{0}^{+}} \left( \frac{\sin \left( h \right) }{h} \right) =1 \\ \\$
$\text{ So, limit does}n^{'}\text{t exists} \\ \\ \text{Hence, the answer is option C} \\ \\$

Question:65

Choose the correct answer out of 4 options given against each Question
Let $f(x)=\begin{array}{l} x^{2}-1,0<x<2 \\ 2 x+3,2 \leq x<3 \end{array}$ the quadratic equation whose roots are $\lim _{x \rightarrow 2} f(x) \text { and } \lim _{x \rightarrow 2} f(x)$ is
$\\A. x^{2} - 6x + 9 = 0\\ B. x^{2} -7x + 8 = 0\\ C. x^{2} - 14x + 49 = 0\\ D. x^{2} - 10x + 21 = 0 \\$

Answer:

$\\ LHL=\mathop{\lim }\limits_{x \rightarrow \mathop{2}^{-}}f \left( x \right) =\mathop{\lim }\limits_{x \rightarrow \mathop{2}^{-}} \left( x^{2}-1 \right) =3 \\ $

$\\ RHL=\mathop{\lim }\limits_{x \rightarrow \mathop{2}^{+}}f \left( x \right)$

$ =\mathop{\lim }\limits_{x \rightarrow \mathop{2}^{+}} \left( 2x+3 \right) =7 \\$

$ \\ \text{The quadratic equation whose roots are 3 and 7 are } \left( x-3 \right) \left( x-7 \right)\\ $

$=x^{2}-10x+21 \\ \\$
Hence, the answer is option D

Question:66

Choose the correct answer out of 4 options given against each Question
$\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left( \tan 2x-x \right) }{3x-\sin x}~$ is
A. 2
B. $\frac{1}{2}$
C. $\frac{-1}{2}$
D. $\frac{1}{4}$

Answer:

$\\ \mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left( \tan 2x-x \right) }{3x-\sin x}=\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left( \frac{\tan 2x}{x}-1 \right) }{ \left( 3-\frac{\sin x}{x} \right) }=\mathop{\lim }\limits_{x \rightarrow 0}\frac{ \left( \frac{\text{2 tan}2x}{2x}-1 \right) }{ \left( 3-\frac{\sin x}{x} \right) }=\frac{2-1}{3-1}=\frac{1}{2} \\ \\$
Hence, the answer is option B

Question:67

Choose the correct answer out of 4 options given against each Question
Let f(x) = x – [x], $\in \mathrm{R}, \text { then } \mathrm{f}^{\prime} \frac{1}{2}$ is
A. 3/2
B. 1
C. 0
D. –1

Answer:

$\\ LHD=\mathop{\lim }\limits_{h \rightarrow 0}\frac{ \left( f \left( \frac{1}{2}-h \right) -f \left( \frac{1}{2} \right) \right) }{-h} \\ \\ =\mathop{\lim }\limits_{h \rightarrow 0}\frac{ \left( \left( \frac{1}{2}-h \right) - \left[ \left( \frac{1}{2}-h \right) \right] - \left( \frac{1}{2} \right) + \left[ \frac{1}{2} \right] \right) }{-h}=\mathop{\lim }\limits_{h \rightarrow 0}\frac{-h}{-h}=1 \\ $

$\\ RHD=\mathop{\lim }\limits_{h \rightarrow 0}\frac{ \left( f \left( \frac{1}{2}+h \right) -f \left( \frac{1}{2} \right) \right) }{h} \\ \\ =\mathop{\lim }\limits_{h \rightarrow 0}\frac{ \left( \left( \frac{1}{2}+h \right) - \left[ \left( \frac{1}{2}+h \right) \right] - \left( \frac{1}{2} \right) + \left[ \frac{1}{2} \right] \right) }{h}=\mathop{\lim }\limits_{h \rightarrow 0}\frac{h}{h}=1 \\ \\$
Hence, the answer is option B

Question:68

Choose the correct answer out of 4 options given against each Question
If $If\: \: y=\sqrt {x}+\frac{1}{x}, then \frac{dy}{dx}$ at x = 1 is
A. 1
B. $\frac{1}{2}$
C. $\frac{1}{\sqrt{2}}$
D. 0

Answer:

$\\ y=\sqrt {x}+\frac{1}{x} \\ \\ \frac{dy}{dx}=\frac{1}{2\sqrt {x}}-\frac{1}{x^{2}} \\ $

$\\ \left( \frac{dy}{dx} \right) _{x=1}=\frac{1}{2}-1=-\frac{1}{2} \\ \\$

Hence, the answer is option D

Question:69

Choose the correct answer out of 4 options given against each Question
If $~f \left( x \right) =\frac{x-4}{2\sqrt {x}}$ then f’(1) is
A. $\frac{5}{4}$
B. $\frac{4}{5}$
C. 1
D. 0

Answer:

$\\ f \left( x \right) =\frac{x-4}{2\sqrt {x}} \\$

$ \\ f^{'} \left( x \right) =\frac{1}{2} \left[ \frac{\sqrt {x} *1- \left( x-4 \right) *\frac{1}{2\sqrt {x}}}{x} \right] =\frac{1}{2} \left[ \frac{x+4}{2x^{\frac{3}{2}}} \right] \\$

$ \\ f^{'} \left( 1 \right) =\frac{1}{2} \left[ \frac{1+4}{2 \left( 1 \right) } \right] =\frac{5}{4} \\ \\$
Hence, the answer is option A

Question:70

Choose the correct answer out of 4 options given against each Question

If $y=\frac{1+\frac{1}{x^{2}}}{1-\frac{1}{x^{2}}}$ then $\frac{dy}{dx}$ is
A.$\frac{-4x}{\left(x^{2}-1\right)^{2}}$
B.$\frac {-4 x}{x^{2}-1}$
C.$\frac{1-x^{2}}{4 x}$
D.$\frac{4 x}{x^{2}-1}$

Answer:

$\\y=\frac{1+\frac{1}{x^{2}}}{1-\frac{1}{x^{2}}}=\frac{x^{2}+1}{x^{2}-1} \\$

$ \\ \frac{dy}{dx}=\frac{ \left( x^{2}-1 \right) \left( 2x \right) - \left( x^{2}+1 \right) \left( 2x \right) }{ \left( x^{2}-1 \right) ^{2}}=\frac{ \left( 2x \right) \left( x^{2}-1-x^{2}-1 \right) }{ \left( x^{2}-1 \right) ^{2}}=-\frac{4x}{ \left( x^{2}-1 \right) ^{2}} \\ \\$
Hence, the answer is option A

Question:71

Choose the correct answer out of 4 options given against each Question

If $y=\frac{\sin x+\cos x}{\sin x-\cos x}$ then $\frac{dy}{dx}_{at\: \: x=0}$ is

A. –2
B. 0
C. $\frac{1}{2}$
D. does not exist
Answer:

$\\ y=\frac{\sin x+\cos x}{\sin x-\cos x} \\ \\ \frac{dy}{dx}=\frac{ \left( \sin x-\cos x \right) \left( \cos x-\sin x \right) - \left( \sin x+\cos x \right) \left( \sin x+\cos x \right) }{ \left( \sin x-\cos x \right) ^{2}} \\ $

$\\ =\frac{- \left( \sin ^{2}x+\cos ^{2}x-2\sin x\cos x \right) - \left( \sin ^{2}x+\cos ^{2}x+2\sin x\cos x \right) }{ \left( \sin x-\cos x \right) ^{2}}=-\frac{2}{ \left( \sin x-\cos x \right) ^{2}} \\ $

$\\ \left( \frac{dy}{dx} \right) _{x=0}=-\frac{2}{ \left( -1 \right) ^{2}}=-2 \\ \\$
Hence, the answer is option A

Question:72

Choose the correct answer out of 4 options given against each Question

If $y=\frac{\sin \left( x+9 \right) }{\cos x}$ then $\frac{d y}{d x} \text { at } x=0$ is
A. cos 9
B. sin 9
C. 0
D. 1

Answer:

$\\ y=\frac{\sin \left( x+9 \right) }{\cos x} \\ \\ \frac{dy}{dx}=\frac{\cos x\cos \left( x+9 \right) -\sin \left( x+9 \right) \left( -\sin x \right) }{\cos ^{2}x} \\$

$ \\ =\frac{\cos x\cos \left( x+9 \right) +\sin \left( x+9 \right) \sin x}{\cos ^{2}x} \\$

$ \\ =\frac{\cos \left( x+9-x \right) }{\cos ^{2}x}=\frac{\cos 9}{\cos ^{2}x} \\$

$ \\ \left( \frac{dy}{dx} \right) _{x=0}=\frac{\cos 9}{ \left( 1 \right) ^{2}}=\cos 9 \\ \\$

Hence, the answer is option A

Question:73

Choose the correct answer out of 4 options given against each Question

If $f \left( x \right) =1+x+\frac{x^{2}}{2}+\frac{x^{3}}{3}+ \ldots +\frac{x^{100}}{100}$ then f’(1) is equal to
A. 1/100
B. 100
C. does not exist
D. 0

Answer:

$\\ f \left( x \right) =1+x+\frac{x^{2}}{2}+\frac{x^{3}}{3}+ \ldots +\frac{x^{100}}{100} \\$

$ \\ f^{'} \left( x \right) =0+1+\frac{2x}{2}+\frac{3x^{2}}{3}+ \ldots +\frac{100x^{99}}{100} \\$

$ \\ f^{'} \left( x \right) =0+1+x+x^{2}+ \ldots x^{99} \\$

$ \\ f^{'} \left( 1 \right) =1+1+1+ \ldots +1~~ \left( \text{100 times} \right) =100 \\ \\$

Hence, the answer is option B

Question:74

Choose the correct answer out of 4 options given against each Question

If $f \left( x \right) =\frac{x^{n}-a^{n}}{x-a}$ for some constant ‘a’, then f’(a) is
A. 1
B. 0
C. does not exist
D. 1/2

Answer:

$\\f \left( x \right) =\frac{x^{n}-a^{n}}{x-a} \\ $

$\\ f^{'} \left( x \right) =\frac{ \left( x-a \right) \left( nx^{n-1} \right) - \left( x^{n}-a^{n} \right) \left( 1 \right) }{ \left( x-a \right) ^{2}} \\$

$ \\ f^{'} \left( a \right) =\frac{ \left( a-a \right) \left( na^{n-1} \right) - \left( a^{n}-a^{n} \right) \left( 1 \right) }{ \left( a-a \right) ^{2}}=\frac{0}{0} \\ \\$
Hence, the answer is option B

Question:75

Choose the correct answer out of 4 options given against each Question
If $f(x) = x^{100} + x^{99} + $ \ldots $ x + 1,$, then f’(1) is equal to
A. 5050
B. 5049
C. 5051
D. 50051

Answer:

$\\ f \left( x \right) =x^{100}+x^{99}+ \ldots +x+1 \\ $

$\\ f^{'} \left( x \right) =100x^{99}+99x^{98}+ \ldots +1+0 \\ $

$\\ f^{'} \left( 1 \right) =100+99+98+ \ldots +2+1=\frac{100 *101}{2}=5050 \\ \\$

Hence, the answer is option A

Question:76

Choose the correct answer out of 4 options given against each Question
If $f(x) = 1 - x + x^{2} - x^{3} $ \ldots $ -x^{99} + x^{100}$, then f’(1) is equal to
A. 150
B. –50
C. –150
D. 50

Answer:

$\\ f \left( x \right) =1-x+x^{2}-x^{3}+ \ldots -x^{99}+x^{100} \\ $

$\\ f^{'} \left( x \right) =0-1+2x-3x^{2}+ \ldots -99x^{98}+100x^{99} \\ $

$\\ f^{'} \left( 1 \right) $$=-1+2-3+4- \ldots -99+100 \\ $

$\\ = \left( 2-1 \right) + \left( 4-3 \right) + \left( 6-5 \right) + \ldots \left( 100-99 \right) =1+1+ \ldots +1~~ \left( \text{50 times} \right) =50 \\ \\$
Hence, the answer is option D

Question:77

Fill in the blanks
If $f(x)=\frac{\tan x}{x-\pi}, \lim _{x \rightarrow \pi} f(x)=$

Answer:

$\\ \mathop{\lim }\limits_{x \rightarrow \pi }\frac{\tan x}{x- \pi }=\mathop{\lim }\limits_{x \rightarrow \pi }\frac{-\tan \left( \pi -x \right) }{- \left( \pi -x \right) }=\mathop{\lim }\limits_{ \pi -x \rightarrow 0}\frac{\tan \left( \pi -x \right) }{ \left( \pi -x \right) }=1 \\$

Question:78

Fill in the blanks
$\mathop{\lim }\limits_{x \rightarrow 0}\sin mx\cot \frac{x}{\sqrt {3}}=2$ then m = ________

Answer:

$\\ \mathop{\lim }\limits_{x \rightarrow 0}\sin mx\cot \frac{x}{\sqrt {3}}=2 \\$

$ \\ \mathop{\lim }\limits_{x \rightarrow 0}mx * \left( \frac{\sin mx}{mx} \right) * \left( \frac{\frac{x}{\sqrt {3}}}{\tan \frac{x}{\sqrt {3}}} \right) * \left( \frac{\sqrt{3}}{x} \right) =2 \\ $

$\\ \mathop{\lim }\limits_{x \rightarrow 0}mx * \left( \frac{\sqrt {3}}{x} \right) =2 \\$

$ \\ \sqrt {3}m=2 \\ \\ m=\frac{2}{\sqrt {3}}=\frac{2\sqrt {3}}{3} \\ \\$

Question:79

Fill in the blanks
If $y=1+\frac{x}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+ \ldots$ then $\frac{dy}{dx}=$ ........

Answer:

$\\ y=1+\frac{x}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+ \ldots \\$

$ \\ \frac{dy}{dx}=0+1+\frac{2x}{2!}+\frac{3x^{2}}{3!}+\frac{4x^{3}}{4!}+ \ldots \\ $

$\\ \frac{dy}{dx}=1+\frac{x}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+ \ldots \\ $

$\\ \frac{dy}{dx}=y \\$

Question:80

Fill in the blanks
$\mathop{\lim }\limits_{x \rightarrow \mathop{3}^{+}}\frac{x}{ \left[ x \right] }=$...............

Answer:

$\mathop{\lim }\limits_{x \rightarrow \mathop{3}^{+}}\frac{x}{ \left[ x \right] }=\mathop{\lim }\limits_{h \rightarrow \mathop{0}^{+}}\frac{3+h}{ \left[ 3+h \right] }=\mathop{\lim }\limits_{h \rightarrow \mathop{0}^{+}}\frac{3+h}{3}=\frac{3}{3}=1 \\$