NCERT Class 11 Maths Chapter 1 Notes Sets - Download PDF

Class 11 Sets Notes PDF – Download Free Study Material

Students who wish to access the Sets Class 11 Maths notes can click on the link below to download the entire solution in PDF.

Download PDF

Sets Class 11 Notes

Careers360 has prepared these NCERT Notes Class 11 Maths Chapter 1 Sets to make your revision smoother and faster.

Sets

A set is a well-defined collection of elements. These elements may include numbers, symbols, variables, etc.

We generally represent them using capital letter(A, B, C, D, Z, N etc)

Elements in the sets are represented by small letters(a, b, c, d, e)

Elements of sets are represented using closed brackets { } .

Examples of sets:

• i) set of first n natural numbers: N = 1, 2, 3, 4, 5,.....,n
• ii) set of rational numbers: R.
• iii) set of whole numbers: W.
• iv) set of positive integers: Z+
• v) set of negative integers: Z-

Representation of Sets

We have 2 methods to represent a set:

1. Roster or Tabular Form

In roster form, all the elements of a set are listed; the elements are separated by commas and are enclosed within braces $\{ \}$.

Example: $\{\mathrm{a}, \mathrm{e}, \mathrm{i}, \mathrm{o}, \mathrm{u}\}$ represents the set of all the vowels in the English alphabet in roster form.
In roster form, the order in which the elements are listed is immaterial, i.e. the set of all natural numbers which divide 14 is $\{1,2,7,14\}$ and can also be represented as $\{1,14,7,2\}$.

An element is not generally repeated in the roster form of a set, i.e., all the elements are taken as distinct. For example, the set of letters forming the word 'SCHOOL' is $\{\mathrm{S}, \mathrm{C}, \mathrm{H}, \mathrm{O}, \mathrm{L}\}$ or $\{\mathrm{H}, \mathrm{O}, \mathrm{L}, \mathrm{C}, \mathrm{S} \}$. Here, the order of listing elements has no relevance.

2. Set-Builder Form

In set-builder form, all the elements of a set possess a single common property that is not possessed by any element outside the set. If $Z$ contains all values of $x$ for which the condition $q(x)$ is true, then we write

$
Z=\{x: q(x)\} \text { or } Z=\{x \mid q(x)\}
$
Where ': ' or ' | ' is read as 'such that'
eg. The set $A=\{0,1,8,27,64, \ldots$.$\}$ can be written in Set Builder form as
$\mathrm{A}=\left\{\mathrm{X}^3: \mathrm{X}\right.$ is a non-negative integer $\}$

Types of Sets

Empty set: A set that does not contain any elements and is empty. Such sets are called empty or null, or void sets.

Represented as: { } or ∅

Eg: A={x:1<x,x is a natural number}

So A is an empty set, as we don't have any natural element that is less than 1.

Finite set: A set that is empty or consists of a finite number of elements is called a finite set.
Examples: $\varphi,\{\mathrm{a}\},\{1,2,5,9\},\{\mathrm{x}: \mathrm{x}$ is a person of age more than 18$\}$

Infinite set: A set that has infinite elements is called an infinite set.
Examples:
a set of all the lines passing through a point,
set of all circles in a plane,
set of all points in a plane,
$N, Z, Q, Q ', R$
$\{x: 2<x<2.1\}$

Note: All finite sets can be represented in set-builder form, but infinite sets cannot be represented in set-builder form because they have no fixed pattern.

Singleton set: A set which is having only one element is called a singleton set.
Example: $\{3\},\{b\}$,
$\{\{1,2,3\}\}$ is also a singleton as it has one element, which is a set.
$\{\varphi\}$ is also a singleton set
Note: Empty and singleton sets are finite sets.

Equal sets: Sets where two sets have exactly the same elements.

Represented by the symbol: “ = “

Examples:

i) Let A, B be two sets.

A = set of natural even elements less than 10

A = {2, 4, 6, 8}

B = set of multiples of 2 less than 10 that are natural

B = {2, 4, 6, 8}

Here, A = B. Since every element of A is also an element of B, and vice versa.

ii) A = {1, 2, 3, 4}

B = {1, 3, 2, 1, 4, 1}

Then also A = B, the set elements do not change even if repeated.

The order of the elements also doesn’t matter.

Subset

Any Set that has every element of another set is called a subset.

Representation: A⊂B if a ∈A ⇒ a ∈B

The above representation means that A should have every element of set B, but B need not have every element of A.

Note: Every set is a subset of itself

E.g.: A = {1, 3, 5, 7, 9}

B = {1, 2, 3, 4, 5, 6, 7, 8, 9}

A ⊂ B because every element of A is in B, but not every element of B is in A.

Venn diagram of a subset

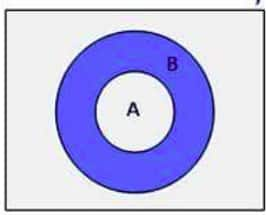
Proper set: If A⊂B and A≠B, then such a set A is called a proper subset of B.

B is called the superset of A.

E.g.: A = {1, 2, 3, 4, 5, 6}

B = {1, 2, 3, 4, 5, 6, 7, 8}

Here A⊂B and A≠B.

So, A is a proper subset of B.

B is a superset of A.

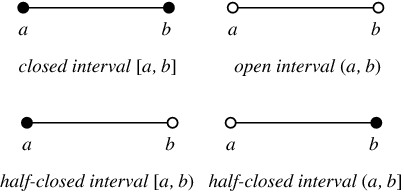
Intervals of subsets

When a,b ∈ real numbers, a<b then,

Set of real numbers: {x: a<x<b} is an open interval, represented as (a, b).

The set that includes endpoints also then such intervals are closed intervals.

{y: a ≤ y ≤ b}, closed interval represented by [a, b].

Eg: (p, q] ⇒ {x: p < x ≤ q}

Here in the set elements include q and exclude p.

Pictorial representation of intervals

Power set: It is a set that is a collection of all subsets, including the null or empty set, and itself denotes a power set.

Represented by p(A).

E.g.: A = {1, 2, 3, 4}

Subsets: ∅, {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1,4}, {2,3}, {2, 4}, {3, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4}

Total subsets:16

Points:

1. First is a null set

2. Next singleton sets(sets with one element}

3. Next, with two elements

4. The set itself

Remember: {1, 2} = {2, 1}

(The order doesn’t matter, so it should be written only once.)

Formula to find a number of subsets

$\mathrm{m}=$ number of elements in set A
Formula: $2^m$
$E g: A=\{1,2,3,4\} \quad t=2^4=16$. We found the same above.

$
A=\{1,2,3,4\}
$

Subsets: ∅, {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4}

Total subsets:16

Universal Set

The set that includes all the elements is called a universal set.

Represented using U.

Venn Diagram:

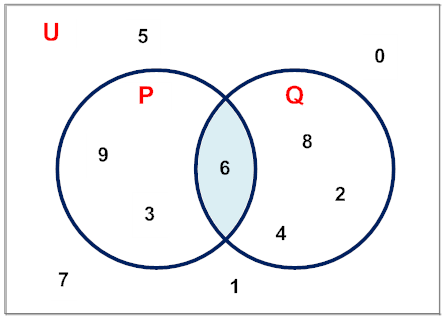
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9} all belong to the universal set.

Operation of Sets

Union of sets: The set contains all the elements of A and B, and repeating elements of both sets A, B are taken only once.

Represented by: ∪

Read as A union B.

Set builder form of union sets:

{y: y∈A or y∈B}

Venn diagram of union:

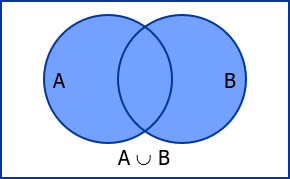
Eg: A = {1, 2, 3, 4, 5} B = {2, 4, 5, 6, 7, 8}

A∪B = {1, 2, 3, 4, 5, 6, 7, 8}

Properties of union

• $A \cup B=B \cup A \quad$ (Commutative Property)
• $(A \cup B) \cup C=A \cup(B \cup C)$ (Associative property)
• $\mathrm{A} \cup \varphi=\mathrm{A}$ (Law of identity element, $\varphi$ is the identity of Null Set)
• $\mathrm{A} \cup \mathrm{A}=\mathrm{A}$ (Idempotent law)
• $U \cup A=U($ Law of $U)$
• If $A$ is a subset of $B$, then $A \cup B=B$

The Intersection of Sets

This set contains the elements that are common to the sets.

Represented as: ∩

Read as A intersection B.

Set builder form of intersection:

{y: y ∈ A and y ∈ B}

Venn diagram of AB:

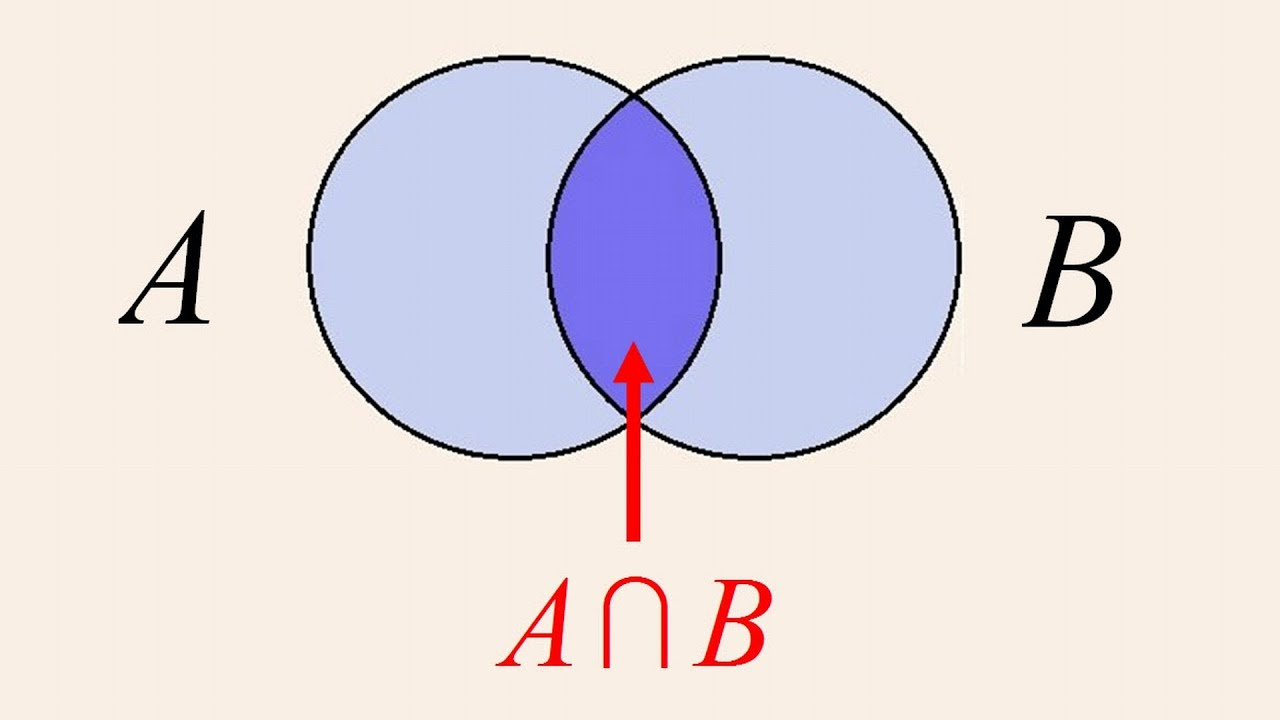
Eg: A = {1, 2, 3, 4, 5, 6} B = (2, 4, 6, 8, 10}

A∩B = {2, 4, 6}

Properties of the intersection

• $\mathrm{A} \cap \mathrm{B}=\mathrm{B} \cap \mathrm{A}$ (Commutative law).
• $(A \cap B) \cap C=A \cap(B \cap C)$ (Associative law).
• $\mathrm{A} \cap \phi=\phi$,
• $\mathrm{A} \cap \mathrm{U}=\mathrm{A}$ (Law of $\phi$ and U$)$.
• $\mathrm{A} \cap \mathrm{A}=\mathrm{A}$ (Idempotent law)
• If $A$ is subset of $B$, then $A \cap B=A$

Difference of Sets:

In the set, the elements belong to A but do not belong to B; such sets are called Differences of sets.

Represented as: A-B

Set builder form: {y: y ∈ A and y ∉ B}

Venn diagram of A - B:

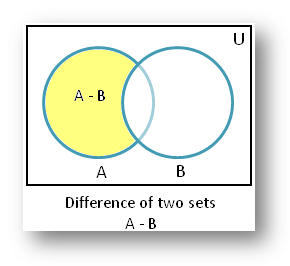
E.g.: A = {1, 2, 3, 4, 5}

B = {2, 3, 4, 8, 9}

A - B = {1, 5}

Here, even though we have {2, 3, 4} in A, as they also belong to B, we also do not include them in A - B.

Complement of a set

The elements other than A that are in the universe come under complementary elements.

Represented by: A’

Set builder form: {y: y ∈ U and y ∉ A}

Venn diagram:

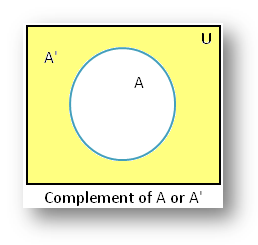
Eg: A = {y: y ∈ U and not divisor of 24}

A’ = {1, 2, 3, 4, 6, 8, 12, 24}

Properties of complement sets

1. A∪A’ = U (complement laws)

2. A∩ A’ = ∅ (complement laws)

3. (A∪B)’ = A’∩B’ (Demorgan’s law)

4. (A∩B)’ = A’∪ B’ (Demorgan’s law)

5. (A’)’ = A (double complement)

6. U’ = ∅ and ∅’= U

De-Morgan’s Laws

1. (A ∪ B)′ = A′ ∩ B′

Let $x$ be any element in $(A \cup B)^{\prime}$

$
x \in(A \cup B)^{\prime} \Leftrightarrow x \notin(A \cup B)
$

$\Leftrightarrow x \notin A$ and $x \notin B$ (As $x$ does not belong to $A \cup B$, it cannot belong to both $A$ and B)
$
\begin{aligned}
& \Leftrightarrow x \in A^{\prime} \text { and } x \in B^{\prime} \\
& \Leftrightarrow x \in\left(A^{\prime} \cap B^{\prime}\right) \\
\therefore x \in(A \cup B)^{\prime} \Leftrightarrow & x \in\left(A^{\prime} \cap B^{\prime}\right)
\end{aligned}
$
So, any element that belongs to $(A \cup B)^{\prime}$ also belongs to $\left(A^{\prime} \cap B^{\prime}\right)$, and vice versa
So, these sets have exactly the same elements.
Hence, they are equal.

2. (A ∩ B)′ = A′ ∪ B′

Let $x$ be any element in $(A \cap B)^{\prime}$

$
x \in(A \cap B)^{\prime} \Leftrightarrow x \notin(A \cap B)
$

$k x \notin A$ or $x \notin B \quad$ (as $x \notin(A \cap B)$, means it is not common in $A$ and $B$, and thus either it is not in $A$ or not in B)

$
\begin{aligned}
& \Leftrightarrow x \in A^{\prime} \text { or } x \in B^{\prime} \\
& \Leftrightarrow x \in\left(A^{\prime} \cup B^{\prime}\right) \\
& \therefore x \in(A \cap B)^{\prime} \Leftrightarrow x \in\left(A^{\prime} \cup B^{\prime}\right)
\end{aligned}
$
So, any element that belongs to $(A \cap B)^{\prime}$ also belongs to $\left(A^{\prime} \cup B^{\prime}\right)$, and vice versa
So, these sets have exactly the same elements.
Hence, they are equal.

Theorems and Proofs

Theorem 1:

n(A∪B) = n(A) + n (B) - n(A∩B)

Proof:

n ( A – B) + n ( A ∩ B ) + n ( B – A )

n(A) - n ( A ∩ B ) + n(B) - n( A ∩ B ) + n( A ∩ B )

n(A) + n(B) - n( A ∩ B )

Hence, it is proved.

Theorem 2: n(A ∪ B ∪ C ) = n ( A ) + n ( B ) + n ( C ) – n ( A ∩ B ) – n ( B ∩ C) – n ( A ∩ C ) + n ( A ∩ B ∩ C )

Proof:

n ( A ∪ B ∪ C ) = n (A) + n ( B ∪ C ) – n [ A ∩ ( B ∪ C ) ]

n (A) + n ( B ) + n ( C ) – n ( B ∩ C ) – n [ A ∩ ( B ∪ C ) ]

n [ A ∩ ( B ∪ C ) ] = n ( A ∩ B ) + n ( A ∩ C ) – n [ ( A ∩ B ) ∩ (A ∩ C)] n ( A ∩ B ) + n ( A ∩ C ) – n (A ∩ B ∩ C)

Similarly for the other two:

Finally, it is proved.

n ( A ∪ B ∪ C ) = n (A) + n ( B ) + n ( C ) – n ( A ∩ B ) – n ( B ∩ C) – n ( A ∩ C ) + n ( A ∩ B ∩ C )

Sets: Previous Year Question and Answer

Given below are selected previous year question answers for NCERT Class 11 Maths Chapter 1 Sets, collected from various examinations.

Question 1:
If A and B are two sets, then A ∩ (A ∪ B) equals:

Solution:
Let $x \in A \cap(A \cup B)$

$
\begin{aligned}
& \Rightarrow x \in A \text { and } x \in(A \cup B) \\
& \Rightarrow x \in A \text { and }(x \in A \text { or } x \in B) \\
& \Rightarrow(x \in A \text { and } x \in A) \text { or }(x \in A \text { and } x \in B \\
& \Rightarrow x \in A \text { or } x \in A \cap B
\end{aligned}
$
Hence, the correct answer is "A".

Question 2:
Two finite sets have m and n elements. The number of subsets of the first set is 112 more than that of the second set. The values of m and n are, respectively:

Solution:
According to the question we have,

$
\begin{aligned}
& 2^m-2^n=112 \\
& 2^n\left(2^{m-n}-1\right)=2^4 \times 7 \\
& 2^n=2^4 \text { and } 2^{m-n}-1=7 \\
& n=4 \text { and } 2^{m-n}=1+7=8=2^3 \\
& n+4 \text { and } m-n=3 \\
& m=7
\end{aligned}
$

Hence, the correct answer is 7 and 4.

Question 3:
If sets A and B are defined as $A = \left\{(x,y):y= \frac{1}{x}, 0\neq x\in R \right \}\prod $ $B= \left\{(x,y):y= -x, x\in R \right \}$, then

Solution:
Given that $A = \left\{(x,y):y= \frac{1}{x}, 0\neq x\in R \right \}$ and $B= \left\{(x,y):y= -x, x\in R \right \}$

So, $y = \frac{1}{x}$ and $y = - x$

$\frac{1}{x} \neq - x$

$A\cap B = \phi$

Hence, the correct answer is "A ∩ B = φ".

NCERT Class 11 Maths Notes – Chapter-Wise Links

We at Careers360 compiled all the NCERT class 11 Maths notes in one place for easy student reference. The following links will allow you to access them.

NCERT Exemplar Solutions Subject-Wise

The following links contain subject-wise NCERT exemplar solutions. These solutions can be used to get acquainted with the concepts and score well in the exam.

• NCERT Exemplar Class 11 Solutions
• NCERT Exemplar Class 11 Maths
• NCERT Exemplar Class 11 Physics
• NCERT Exemplar Class 11 Chemistry
• NCERT Exemplar Class 11 Biology

NCERT Solutions Subject-Wise

The following list contains subject-wise NCERT solutions. These solutions cover all the concepts comprehensively.

• NCERT Solutions for Class 11 Mathematics
• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 11 Biology

NCERT Books and Syllabus

Students can use the following links to check the latest NCERT syllabus and read some reference books.

• NCERT Books Class 11 Maths
• NCERT Syllabus Class 11 Maths
• NCERT Books Class 11
• NCERT Syllabus Class 11