NCERT Exemplar Class 11 Physics solutions Chapter 5 Work Energy and Power

NCERT Exemplar Class 11 Physics Solutions Chapter 6: MCQ I

NCERT Exemplar Class 11 Physics Chapter 6: MCQ I contains correct and well-justified answers to multiple choice questions according to the NCERT Exemplar pattern. The NCERT Exemplar Class 11 Physics Solutions Chapter 6 Work, Energy and Power
are able to assist the students in testing their conceptual knowledge and also in enhancing their accuracy and be ready in facing school exams and also competitive exams such as JEE and NEET.

​Question:6.1

An electron and a proton are moving under the influence of mutual forces. In calculating the change in the kinetic energy of the system during motion, one ignores the magnetic force of one on another.
This is because,
(a) the two magnetic forces are equal and opposite, so they produce no net effect.
(b) the magnetic forces do no work on each particle.
(c) the magnetic forces do equal and opposite (but non-zero) work on each particle.
(d) the magnetic forces are necessarily negligible.

Answer:

The answer is option (b), the magnetic forces do not work on each particle.
The concept used in this question is the work-energy theorem. According to which, net work done = (change in kinetic energy). Final kinetic energy – Initial kinetic energy of the object.

$\sum W=K_f-K_i$
The direction of the magnetic forces will be at an angle of 90 degrees to the motion of the electron and proton under mutual forces. As a result, the magnetic force acts like a centripetal force, which leads the particles to undergo uniform circular motion. Hence, their speed remains constant throughout the motion. Since the speed is constant, the kinetic energy remains the same, and hence the net work done due to the change in kinetic energy by the forces amounts to zero. By the formula, we know that:

$\overrightarrow{F_m}=q \cdot(\vec{v} \times \vec{B})$. , B is the external magnetic field, and v is the velocity of the particle. Hence, we can ignore the magnetic force of one particle on another.

Question:6.2

A proton is kept at rest. A positively charged particle is released from rest at a distance d in its field. Consider two experiments; one in which the charged particles is also a proton and in another, a positron. In the same time t, the work done on the two moving charged particles is
a) same as the same force law is involved in the two experiments
b) less for the case of a positron, as the positron moves away more rapidly and the force on it weakens
c) more for the case of a positron, as the positron moves away a larger distance
d) same as the work done by charged particle on the stationary proton

Answer:

The answer is option (c) more for the case of a positron, as the positron moves away a larger distance
The charges on a proton and a positron are the same, but the mass of a positron is less than that of a proton. Hence, the force between a proton and a positron is the same as that between two protons. But, as the positron has a lower mass, it moves over a larger amount of distance. The change in momentum remains equal for both cases, but the positron, being of lighter weight, moves a larger distance than a proton. Now, work done = force x distance. In our case, the forces are the same, but the positron travels a greater distance, and hence the work done in that case will be more.

Question:6.3

A man squatting on the ground gets straight up and stand. The force of reaction of ground on the man during the process is
a) constant and equal to mg in magnitude
b) constant and greater than mg in magnitude
c) variable but always greater than mg
d) at first greater than mg, and later becomes equal to mg

Answer:

The answer is option (d) at first greater than mg, and later becomes equal to mg.

Question:6.4

A bicyclist comes to a skidding stop in 10 m. During this process, the force on the bicyclist due to the road is 200 N and is directly opposed to the motion. The work done by the cycle on the road is
a) +2000 J
b) -200 J
c) zero
d) -20,000 J

Answer:

The answer is option (c) Zero
Mechanical energy is not conserved here due to the presence of frictional forces. These lead to dissipation of energy. Work done by frictional force$= 200 \times -10 = -2000 J$. Work done by the cycle on the road is zero as the road does not move and covers the distance.

Question:6.5

A body is falling freely under the action of gravity alone in a vacuum. Which of the following quantities remain constant during the fall?
a) kinetic energy
b) potential energy
c) total mechanical energy
d) total linear momentum

Answer:

The answer is option (c) total linear momentum
Under the effect of the conservative forces, for a free-falling body, the potential energy decreases, and the kinetic energy increases continuously. This leads to the total energy (KE + PE) remaining constant.
$E = \frac{1}{2} mv^{2} + mgh$
Velocity is zero at point A, so KE is also zero and Ea = mgH
At point B, $Vb =\sqrt{ 2gh}$
$Eb = \frac{1}{2} m(2gh) + mg(H-h)$
Eb = mgH
At point C,$Vc = \sqrt{2gh}$
$Ec = \frac{1}{2} m(2gH) + mg (0)$
Ec = mgH
Hence, the total mechanical energy remains the same.

Question:6.6

During inelastic collision between two bodies, which of the following quantities always remain conserved?
a) total kinetic energy
b) total mechanical energy
c) total linear momentum
d) speed of each body

Answer:

The answer is option (c) total linear momentum
A collision is inelastic if the kinetic energy pre- and post-collision is not equal.

Question:6.7

Two inclined frictionless tracks, one gradual and the other steep meet at A from where two stones are allowed to slide down from rest, one on each track as shown in Figure.

Which of the following statements is correct?
(a) Both the stones reach the bottom at the same time but not with the same speed.
(b) Both the stones reach the bottom with the same speed and stone I reaches the bottom earlier than stone II.
(c) Both the stones reach the bottom with the same speed and stone II reaches the bottom earlier than stone I.
(d) Both the stones reach the bottom at different times and with different speeds.

Answer:

The answer is option (c). Both the stones reach the bottom with the same speed, and stone II reaches the bottom earlier than stone I.
AB and AC are planes which inclined at angles $\theta _{1}$ and $\theta _{2}$. Friction is absent as the plains are assumed to be smooth, which leads to the conservation of mechanical energy.

For both AB and AC,
$\frac{1}{2} mv^{2} = mgh$ and
$v= \sqrt{2gh}$
Speed is the same for both stones.
Stone I
Acceleration
$a_{1} = g \sin\theta_{1}$
Stone II
Acceleration
$a_{2} = g \sin\theta_{2}$
Now, $\theta_{2} >\theta_{1}$ and hence $a_{2} >a_{1}$. So, stone II reaches faster than stone I.

Question:6.8

The potential energy function for a particle executing linear SHM is given by $\frac{1}{2}kx^{2}$ where k is the force constant of the oscillator (Figure). For k = 0.5N/m, the graph of V(x) versus x is shown in the figure. A particle of total energy E turns back when it reaches $x = \pm xm$ . If V and K indicate the P.E. and K.E., respectively of the particle at $x = \pm xm$, then which of the following is correct?

(a) V = O, K = E
(b) V = E, K = O
(c) V < E, K = O
(d) V = O, K < E.

Answer:

The answer is the option (b) V = E, K = O
Potential energy at any position,
$U = \frac{1}{2} kx^{2}$
Total energy of the mass,
$E = \frac{1}{2} ka^{2}$

Kinetic energy at any position,
$K=E-U = \frac{1}{2} ka^{2}+\frac{1}{2} kx^{2}$
$K= \frac{1}{2} k\left [ a^{2}-x^{2} \right ]$
Now,
$U_{max}= \frac{1}{2} ka^{2}$ at extremes.
U min = 0 {x=0 at mean}
$K_{max}= \frac{1}{2} ka^{2}$ {x=0 at mean}
K min = 0 {extremes}
Hence, $E= \frac{1}{2}ka^{2}$ is constant at all times
When particle is at x = xm (mean), KE =0
So, total energy is $E = PE + 0$ $= \frac{1}{2}kx^{2}$
So, option b is correct.

Question:6.9

Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V as shown in Figure.

If the collision is elastic, which of the following (Figure) is a possible result after the collision?

Answer:

The answer is option (b)
In an elastic collision, the velocities of particles are interchanged while the kinetic energy and total linear momentum are conserved.
Kinetic energy before collision:
$\frac{1}{2} mv^{2} + 0 = \frac{1}{2} mv^{2}$
Option a) Kinetic energy after the collision:
$Ka = \frac{1}{2} (2m) \left ( \frac{v}{2} \right )^{2} = \frac{1}{4} mv^{2}$
Option b) Kinetic energy after the collision:
$Ka = \frac{1}{2} (m) \left ( v\right )^{2} = \frac{1}{2} mv^{2}$
Option c) Kinetic energy after the collision:
$Ka = \frac{1}{2} (3m) \left ( \frac{v}{3}\right )^{2} = \frac{1}{6} mv^{2}$
Option d) Kinetic energy after the collision:
$\\K_{a}=\frac{1}{2}mv^2+\frac{1}{2}m(\frac{v}{2})^2+\frac{1}{2}m(\frac{v}{3})^2\\\\=\frac{49}{72}mv^2$
Hence, option b is correct.

Question:6.10

A body of mass 0.5 kg travels in a straight line with velocity $v = a x^{\frac{3}{2}}$ where $a = 5 m^{\frac{-1}{2}}s^{-1}$. The work done by the net force during its displacement from x = 0 to x = 2 m is
(a) 1.5 J
(b) 50 J
(c) 10 J
(d) 100 J

Answer:

The answer is option (b) 50 J
m = 0.5 kg
$v = a x^{\frac{3}{2}}$
$a = 5 m^{\frac{-1}{2}}s^{-1}$
now, acceleration$= a = \frac{dv}{dt }= v \frac{dv}{dx}$
$= ax^{\frac{3}{2}} \frac{d}{dx} ax^{\frac{3}{2}} = ax^{\frac{3}{2}} \times \frac{3}{2} \times ax^{\frac{1}{2}} = \frac{3}{2} a^{2}x^{2}$
Net force = $ma = m \left (\frac{3}{2} a^{2}x^{2} \right )$
Work done under the variable force
$= \int_{x=0}^{x=2}F.dx = \int_{0}^{2}\frac{3}{2} ma^{2}x^{2} dx$
$= \frac{1}{2}ma^{2} \times 8 = \frac{1}{2} \times (0.5) \times (25) \times 8 = 50 J$

Question:6.11

A body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in Figure correctly shows the displacement-time curve for its motion?

Answer:

The answer is option (b)
$P = F.\frac{ds}{dt} = F. v$= constant
Carrying out dimensional analysis, we get,
[F][v] = constant
$[MLT^{-2}] [LT^{-1}]$= constant
$L^{2}T^{-3}$= constant
$L\propto T^{\frac{3}{2}}$

Question:6.12

Which of the diagrams shown in Figure most closely shows the variation in kinetic energy of the earth as it moves once around the sun in its elliptical orbit?

Answer:

The answer is option (d)
On the path where Earth orbits around the sun, the speed of Earth is maximum when its position is closest to the sun, and the speed of Earth is minimum when it is farther away from the sun. Hence, we can conclude that kinetic energy can never be negative or zero. Hence, the graph in option d is correct.

Question:6.13

Which of the diagrams shown in Figure represents variation of total mechanical energy of a pendulum oscillating in air as function of time?

Answer:

The answer is option (c)
The total mechanical energy of a pendulum decreases continuously when it undergoes oscillatory motion due to the resistance offered by the air. This leads to an exponential decrease in the total mechanical energy of the pendulum. Hence, graph c is correct, which shows an exponential curve between energy and time.

Question:6.14

A mass of 5 kg is moving along a circular path of radius 1 m. If the mass moves with 300 revolutions per minute, its kinetic energy would be
(a) 250 $\pi ^{2}$
(b) 100 $\pi ^{2}$
(c) 5 $\pi ^{2}$
(d) 0

Answer:

The answer is option (a)
m = 5kg, radius = 1m, f = frequency of revolution = 300 rev/min = 300/60 rev/second
angular velocity = $2\pi f = \frac{(300\times 2\times \pi )}{60} = 10\pi$rad/second
now $v = \omega R=10\pi\times1= 10\pi m/s$
kinetic energy
= $\frac{1}{2}mv^{2}$
$= \frac{1}{2}\times 5 \times 10\pi \times 10\pi = 250 \pi^{2} J$

Question:6.15

A raindrop falling from a height h above ground, attains a near terminal velocity when it has fallen through a height $\left (\frac{3}{4} \right )h$. Which of the diagrams shown in Figure correctly shows the change in kinetic and potential energy of the drop during its fall up to the ground?

Answer:

The answer is option (b)
At the height h, the raindrop will have zero kinetic energy and maximum potential energy. As it starts falling down, the PE starts decreasing, and the KE starts increasing proportionately. When we consider zero air resistance, the total mechanical energy remains conserved. However, if we consider air resistance, then there is an up-thrust which opposes the velocity of the droplet falling down, which makes the velocity constant as the time passes, which is known as terminal velocity. This relation is aptly depicted in graph b, and hence it is the correct option.

Question:6.16

In a shotput event an athlete throws the shotput of mass 10 kg with an initial speed of 1m s-1 at $45^{\circ}$ from a height 1.5 m above ground. Assuming air resistance to be negligible and acceleration due to gravity to be 10 m s-2, the kinetic energy of the shotput when it just reaches the ground will be
(a) 2.5 J
(b) 5.0 J
(c) 52.5 J
(d) 155.0 J

Answer:

The answer is option (d) 155.0 J
h = 1.5 m, v = 1 m/s, m = 10 kg, g = 10 ms^-2
The initial energy of the shot put can be calculated as:
$PE + KE = mgh + \frac{1}{2} mv^{2}$
$= 10 \times 10 \times 1.5 + \frac{1}{2} \times 10 \times 1 = 155 J$
From the law of conservation of energy, we can write that,
(PE + KE) initial = (PE + KE) final
Hence, the final kinetic energy of the shotput: KE final + 0 = 155J
Hence, the answer is 155 J

Question:6.17

Which of the diagrams in Figure correctly shows the change in kinetic energy of an iron sphere falling freely in a lake having sufficient depth to impart it a terminal velocity?

Answer:

The answer is option (b)
The velocity of the iron sphere when free-falling in the lake increases as the acceleration due to gravity increases. The up-thrust of the water, however, opposes the motion of the sphere, which makes the velocity constant after some time. Hence, in this case, the velocity increases initially and then becomes constant after some time. So, kinetic energy becomes constant, eventually, which is shown in graph b.

Question:6.18

A cricket ball of mass 150 g moving with a speed of 126 km/h hits at the middle of the bat, held firmly at its position by the batsman. The ball moves straight back to the bowler after hitting the bat.
Assuming that collision between ball and bat is completely elastic and the two remain in contact for 0.001s, the force that the batsman had to apply to hold the bat firmly at its place would be
(a) 10.5 N
(b) 21 N
(c) 1.05 ×104 N
(d) 2.1 × 104 N

Answer:

The answer is option (c)
$m = 150 g = \frac{150}{1000 }= \frac{3}{20} kg, t= 0.001 s$
u =126km/h = 35 m/s
v = -126km/h = -35 m/s
change in momentum = $m(v-u) = \frac{3}{20}(-70) = \frac{-21}{2}$
Force
$= \frac{\frac{-21}{2}}{0.001 } = -1.05 \times 10^{4} N$
The negative sign indicates the opposite direction of the force. Hence, the force exerted by the batman should be 1.05 x 10⁴ N.

NCERT Exemplar Class 11 Physics Solutions Chapter 6: MCQII

NCERT Exemplar Class 11 Physics Chapter 6: MCQII is devoted to solving the assertion-reason and advanced objective-type questions that have clear logic and reasoning. Such NCERT Exemplar Class 11 Physics Solutions Chapter 6 assist students to develop mastery of thinking analytically, to avoid errors in general areas, and to have some confidence in their approach to higher-level MCQs when preparing to take exams and competitive tests.

Question:6.19

A man, of mass m, standing at the bottom of the staircase, of height L climbs it and stands at its top.
(a) Work done by all forces on man is equal to the rise in potential energy mgL.
(b) Work done by all forces on man is zero.
(c) Work done by the gravitational force on man is mgL.
(d) The reaction force from a step does not do work because the point of application of the force does not move while the force exists.

Answer:

The answer is option (b) and (d)
The gravitational force acts in a downward direction. The displacement is labelled L, which is in the upward direction. So, the work done on a man due to the gravitational force amounts to -mgL. Also, the work done to lift the man also amounts to the force in the direction of displacement. Hence, the net force amounts to -mgL+ mgL = 0. Hence, option (b) is correct.
The displacement at the point where the force acts is zero. Hence, the amount of work done by the force is also zero. So, KE =0 and hence option (d) is correct.

Question:6.20

A bullet of mass m fired at $30^{\circ}$ to the horizontal leaves the barrel of the gun with a velocity v. The bullet hits a soft target at a height h above the ground while it is moving downward and emerges out with half the kinetic energy it had before hitting the target.
Which of the following statements are correct in respect of bullet after it emerges out of the target?
(a) The velocity of the bullet will be reduced to half its initial value.
(b) The velocity of the bullet will be more than half of its earlier velocity.
(c) The bullet will continue to move along the same parabolic path.
(d) The bullet will move in a different parabolic path.
(e) The bullet will fall vertically downward after hitting the target.
(f) The internal energy of the particles of the target will increase.

Answer:

The answer is option (b), (d), (f)
If we assume KE1 and KE2 to be the kinetic energy of the bullet pre and post target, then,
$KE_{2} = \frac{1}{2} KE_{1}$
$\frac{1}{2} MV_{2}^{2} =\frac{1}{4} MV_{1}^{2}$
$V_{2}^{2} = \left (\frac{V_{1}}{\sqrt{2}} \right )^{2} = 0.707 V_{1}$
b) $V_{2} = 0.707 V_{1}$
Hence, the velocity of the bullet post it has reached the target is greater than the previous velocity. Hence, option b is the correct choice.
d) the path of the bullet will be parabolic as it has horizontal velocity, and the new parabolic path will have both the components (horizontal and vertical). So, after the target, it will be a new parabolic path and hence option (d) is correct.
f) the internal energy of the particles of the target will increase, and some parts of the kinetic energy will be converted to heat. Hence option f is correct.

Question:6.21

Two blocks $M_{1}$ and $M_{2}$ having equal mass are free to move on a horizontal frictionless surface. $M_{2}$ is attached to a massless spring as shown in Figure. Initially $M_{2}$ is at rest and $M_{1}$ is moving toward M2 with speed v and collides head-on with $M_{2}$.

(a) While spring is fully compressed, all the KE of $M_{1}$ is stored as PE of spring.
(b) While spring is fully compressed the system momentum is not conserved, though final momentum is equal to initial momentum.
(c) If spring is massless, the final state of the $M_{1}$ is state of rest.
(d) If the surface on which the blocks are moving has friction, then the collision cannot be elastic.

Answer:

The answer is option (c)
a) The kinetic energy of $M_{1}$ is not fully transferred to the spring as its potential energy, and hence, option a is incorrect
b) The law of conservation of mass is valid here since the surface is frictionless; hence, option b is incorrect.
c) If we consider the case where the spring is totally massless, then all the kinetic energy of $M_{1}$ gets transferred to $M_{2}$. As a result, m1 comes to rest, and $M_{2}$ acquires a velocity v and starts moving. Hence, option c is correct.
d) Even when the force of friction is not involved, a collision can be inelastic. Hence, we reject option d.

NCERT Exemplar Class 11 Physics Solutions Chapter 6: Very Short Answer

NCERT Exemplar Class 11 Physics Solutions Chapter 6: Very Short Answer provides a concise and exact answer to conceptually based questions. These solutions allow the students to refresh the major formulas and definitions in a short period of time, which is why they are good for last-minute preparation and reinforcing the basic knowledge.

Question:6.22

A rough inclined plane is placed on a cart moving with a constant velocity u on horizontal ground. A block of mass M rests on the incline. Is any work done by force of friction between the block and incline? Is there then a dissipation of energy?

Answer:

The block is in a state of rest on the inclined plane, as shown below.
We have, $f = mg \sin\theta$

Since there is no displacement in the block, the total work done by f as well as the block amounts to zero. So, no dissipation of energy takes place as the work done is also zero.

Question:6.23

Why is electrical power required at all when the elevator is descending? Why should there be a limit on the number of passengers in this case?

Answer:

When the elevator is descending, it is in a condition of free fall due to the force exerted by gravity. But, in order to control the speed of the elevator so that it moves at a uniform speed while descending, power is needed. There is a limit on the number of passengers, as when the number of passengers increases, more power is required to stop the elevator from a condition of free fall. Since the power of the motor system is limited, the number of passengers which can travel at one time also has a limit.

Question:6.24

A body is being raised to a height h from the surface of earth. What is the sign of work done by
(a) applied force
(b) gravitational force?

Answer:

When a body is raised to a height h, the force is applied in this case in the direction of the displacement of the object.
a) so, the sign of the work done by the force is positive here
work done = $\overrightarrow{F}d\overrightarrow{s }=Fds \cos \theta$
As Fds is positive, $\theta =0$
b) The force of gravity always acts in the downward direction. However, the force in our case is being applied in an upward manner. So, the value of $\theta =180$
work done = $\overrightarrow{F}d\overrightarrow{s }=Fds \cos 180=-Fds$. Hence, here the sign is negative.

Question:6.25

Calculate the work done by a car against gravity in moving along a straight horizontal road. The mass of the car is 400 kg and the distance moved is 2m.

Answer:

As we know that work done =$\overrightarrow{ F}d\overrightarrow{s} = Fds \cos \theta$
The value of $\theta =90$ in this case, since the horizontal distance travelled is perpendicular to the force of gravity acting downward.
So, work done = $\overrightarrow{ F}d\overrightarrow{s} = Fds \cos 90=0$
Hence, the car does not do any work against gravity

Question:6.26

A body falls towards earth in air. Will its total mechanical energy be conserved during the fall? Justify.

Answer:

The mechanical energy of a body is not conserved when the body is under a free-fall condition under the force of gravity. The force of air molecules acts against the motion of the body as in the case of free fall, and hence the mechanical energy is not conserved. However, in the case of vacuum as a medium, the free-falling body has no force acting against the motion, and hence the energy is conserved.

Question:6.27

A body is moved along a closed loop. Is the work done in moving the body necessarily zero? If not, state the condition under which work done over a closed path is always zero?

Answer:

Only when the conservative force acts along the body when it moves in a closed loop. The work done can be zero. However, if a non-conservative force acts on the body when it moves in a loop (for example, friction, electrostatic force, etc.), then the work done cannot be zero.

Question:6.28

In an elastic collision of two billiard balls, which of the following quantities remain conserved during the short time of collision of the balls (i.e., when they are in contact).
(a) Kinetic energy.
(b) Total linear momentum?
Give reason for your answer in each case.

Answer:

In the given case of the question, when two balls collide with each other, both the Kinetic energy, as well as the total linear momentum, remain conserved. There is no presence of any non-conservative force like friction, electrostatic force, etc. in this case, and also the balls do not get deformed upon collision; hence, both of them remain conserved. If there is a deformation of the ball, then the kinetic energy is not conserved, but the total energy is conserved.

Question:6.29

Calculate the power of a crane in watts, which lifts a mass of 100 kg to a height of 10 m in 20s.

Answer:

We know from the formula that, the power = work done/ time = $\frac{Fds \cos \theta}{ time}$
F = mgh
$mg = 100 \times 10 = 1000$
h = 10 m
t = 20s
$\theta =0$, as the force and the displacement are in the same direction.
Hence, power = $\frac{1000 \times 10 \cos 0}{20} = 500 watts$

Question:6.30

The average work done by a human heart while it beats once is 0.5J. Calculate the power used by heart if it beats 72 times in a minute.

Answer:

We know from the formula that the power = work done/ time
work done by heart in one beat = 0.5J
work done by heart in 72 beats =$72 \times 0.5 = 36J$
time = 1 minute = 60 seconds
so, power used by the heart = $\frac{36}{60} = 0.6 watts$

Question:6.31

Give example of a situation in which an applied force does not result in a change in kinetic energy.

Answer:

We are aware that work done = $\overrightarrow{F}d\overrightarrow{s} = Fds \cos \theta$
Now, for the value of work done to be zero, $\theta$ has to be equal to 90, since $\cos 90 = 0$
So, the direction between the force and the displacement needs to be at an angle of 90 degrees. Hence, these situations can have work done to be zero. Some examples can be as follows:
i) A body moving in a horizontal direction in a uniform motion. Here, the work done due to gravity is totally zero.
ii) The case when a body is moving in a circular motion, the total work done is zero

Question:6.32

Two bodies of unequal mass are moving in the same direction with equal kinetic energy. The two bodies are brought to rest by applying retarding force of same magnitude. How would the distance moved by them before coming to rest compare?

Answer:

The work-energy theorem states that the change in kinetic energy is equal to the work done by the body. So, we can say that KE = WD.
It is given that$KE_{1} = KE_{2}$
Hence, $WD_{1} = WD_{2}$
So, $F_{1}S_{1} = F_{2}S_{2}$
Since F1 and F2 are equal, $S_{1}$ and $S_{2}$ are also equal.
Hence, irrespective of the mass of the bodies, they travel an equal amount of distance/displacement.

Question:6.33

A bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in Fig. 6.11. What will be the trajectory of the particle if the string is cut at

(a) Point B?
(b) Point C?
(c) Point X?

Answer:

The centripetal force is provided by the string, which moves the object in a circular motion. The tension of the string is balanced by the tangential velocity of the particle. When the string is cut, the centripetal force becomes zero. So, the bob now moves under the influence of gravitational force in the direction of tangential velocity.
a) string cut off at B: tangential velocity in the downward direction, the bob moves along the vertical path under the influence of gravity.
b) string cut off at c: Bob has a horizontal component of velocity, it moves in a parabolic path.
c) string cut off at x: the component of velocity makes an angle θ with the horizontal, the bob reaches a certain height and then adopts a parabolic path.

NCERT Exemplar Class 11 Physics Solutions Chapter 6: Short Answer

Work, Energy and Power Class 11 NCERT Exemplar: Short Answer offers explicit and well-organised answers to the questions, which demand short and yet informative reasoning. These NCERT Exemplar Class 11 Physics Solutions Chapter 6 also assist students to gain conceptual clarity, describe answers well in exams, and enhance their knowledge on the main topics.

Question:6.34

A graph of potential energy V (x) verses x is shown in Figure. A particle of energy E0 is executing motion in it. Draw graph of velocity and kinetic energy versus x for one complete cycle AFA.

Answer:

The graph above is between kinetic energy and x
As we know from the law of conservation of energy,
E = KE + PE
E = KE + V(x)
KE = E - V(x)
The potential energy is maximum at point A,
PE = E0
Hence, KE = E0 -E0 = 0
At point B,
Let $PE = V_b, x = 0$
$KE = E _0- V_{0}$
At point C, PE = 0
$X = x_{1}$
Hence, KE = E - V(x) =E₀ - 0 =E₀
At point D,
$X = x_{2}, KE = E_0$
At point E,
$X = x_{3}, PE = E_0$
Hence, KE = 0
(ii)
The graph is between velocity versus x
Here, KE = -mv
$V = \sqrt{\frac{2K}{M}}$
$V = \sqrt{K}$
Through points A and F, KE = 0
$X_{a} = 0, X_{d} = x_{3}$
At points C and D,
$X_{c} = x_{1}, X_{d} = x_{2}$
KE = E0
Hence $V_{max} = +/- \sqrt{E_0} = V_{0}$
At point B, x = 0 and $KE = E_{1}$
So, $V_{b} = \sqrt{E_{1}} = +/- V$

Question:6.35

A ball of mass m, moving with a speed $2v_{0}$ , collides inelastically (e > 0) with an identical ball at rest. Show that
(a) For head-on collision, both the balls move forward.
(b) For a general collision, the angle between the two velocities of scattered balls is less than $90^{\circ}$.

Answer:

a) We assume V₁ and V₂ to be the velocities of the balls post the collision takes place. As we know from the law of conservation of momentum,
$MV_{0} = MV_{1} + MV_{2}$
From the given, we can infer that,
$2V_{0} = V_{1} + V_{2}$----------(1)
$E = \frac{V_{2} - V_{1}}{ V_{0} + V_{0}}$
Hence, $V_{2} = V_{1} + 2EV_{0}$
$V_{1} = V_{0} (1-e)$
Since e < 1
We can say that the direction of V₁ is the same as V₀, which is positive and in the forward direction.
b)

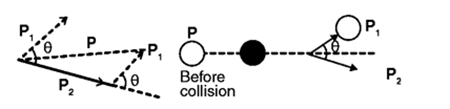
The angle between $p_{1}$ and $p_{2}$ is assumed to be θ
From the law of conservation of momentum, $\overrightarrow{p}= \overrightarrow{p_{1}} + \overrightarrow{p_{2}}$
A portion of kinetic energy is lost as heat when the inelastic collision takes place.
$KE(i) > KE_{1} + KE_{2}$
$\frac{p^{2}}{2m } > \frac{p_{1}^{2}}{2m}+ \frac{p_{2}^{2}}{2m }$
hence,$\overrightarrow{ p}^{2} > \overrightarrow{p}_{1}^{2} + \overrightarrow{ p}_{2}^{2}$
when the angle between $p_{1}$ and $p_{2}$ is lesser than 90 degree, the above equation holds true.

Question:6.36

Consider a one-dimensional motion of a particle with total energy E. There are four regions A, B, C, and D in which the relation between potential energy V, kinetic energy (K) and total energy is as given below:
Region A: V > E
Region B: V < E
Region C: K > E
Region D: V > K
State with reason in each case whether a particle can be found in the given region or not.

Answer:

Total E = V + K --- (1)
K = E - V ---(2)
V = E - K -----(3)
1. Region A: V > E
As V>E
Kinetic energy will be negative according to equation (2)
So, this case is not possible

2. Region B: V < E
If V<E
Then the value of kinetic energy through equation 2 will be positive.
Hence, this case is possible

3.Region C: K > E
In this case, through equation 3, the value of V will become negative.
Hence, this case is not possible.

4.Region D: V > K
This case is possible; hence, the potential energy value can be greater than the value of kinetic energy according to the situation.

Question:6.37

The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in the figure. If the length of the pendulum is 1 m, calculate
a) the height to which Bob A will rise after the collision
b) the speed with which Bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.

Answer:

a) When the bob, which is in motion, collides with the bob at rest, it transfers the momentum and comes to a state of rest. When the position of B is reached by Bob A, kinetic energy is obtained by A as a result of the conversion of potential energy. This happens as the momentum is transferred due to an elastic collision. So, Bob A will not rise.
b)

PE at A₁ is equal to kinetic energy at A₂, which is equal to kinetic energy at B₁
So,
$\frac{1}{2}mv^{2} = mgh$
$V_{b} = \sqrt{2g\times 1} = 4.42 m/s$

Question:6.38

A raindrop of mass 1.00 g falling from a height of 1 km hits the ground with a speed of 50 m/s. Calculate
a) the loss of PE of the drop
b) the gain in KE of the drop
c) is the gain in KE equal to loss of PE? If not why?

Answer:

M = 0.001 kg
H = 1 km, v= 50 m/s, u =0
a) potential energy at the highest point of the drop
$= mgh = 0.001 \times 10 \times 1000m = 10 J$
b) Gain in kinetic energy
$= \frac{1}{2} mv^{2} = \frac{1}{2} \times 0.001 \times 50 \times 50 = 1.25 J$
c) as we can infer, the gain in KE is not equal to the loss in PE as there is some energy lost due to resistance.

Question:6.39

Two pendulums with identical bobs and lengths are suspended from a common support such that in rest position the two bobs are in common. One of the bobs is released after being displaced by 10o so that it collides elastically head-on with the other bob.
a) describe the motion of two bobs
b) draw a graph showing variation in energy of either pendulum with time for$0 \leq t \leq 2T$where T is the period of each pendulum.

Answer:

PE(A) = 0, PE(B) = E, KE(A) = KE(B) = 0
These are the initial values when the bobs are at rest. After this, the bobs are released.
$t=\frac{T}{4}$
When B reaches A, both the bobs collide elastically,
so, KE(A) = 0, KE(B) = E, PE(A) = PE(B)=0
$t=\frac{2T}{4}$
A will reach the highest point or at maximum height. And, B is at its lowest point
KE(A) = 0, KE(B) = 0, PE(A) =E, PE(B)=0

$t=\frac{3T}{4}$
Bob A hits Bob B. Bob A comes to rest, and Bob B starts moving
KE(A) = 0, KE(B) = E, PE(A) =0, PE(B)=0
E_a = 0, E_b = E

$t=\frac{4T}{4}$
B will reach the highest point or at maximum height. And, A is at its lowest point
KE(A) = 0, KE(B) = 0, PE(A) =0, PE(B)=E

Question:6.40

Suppose the average mass of raindrops is $3.0 \times 10^{-5}kg$ and their average terminal velocity 9 m/s. Calculate the energy transferred by rain to each square meter of the surface at a place which receives 100 cm of rain in a year.

Answer:

Rain transfers its kinetic energy to the earth equal to $\frac{1}{2}mv^{2}$
Velocity of rain = 9m/s
Mass = volume/density
$= 1\times 1\times 1000 = 1000kg$
So, total energy transferred by rain fall = $\frac{1}{2} \times 1000 \times 9 \times 9$
= 40500 J

Question:6.41

An engine is attached to a wagon through a shock absorber of length 1.5 m. The system with a total mass of 50,000 kg is moving with a speed of 36 km/h when the brakes are applied to bring it to rest. In the process of the system being brought to rest, the spring of the shock absorber gets compressed by 1.0 m. If 90% of the energy of the wagon is lost due to friction, calculate the spring constant.

Answer:

Kinetic energy is equal to
$\frac{1}{2} mv^{2}$
m = 50,000 kg, v = 10m/s
so, $KE = \frac{1}{2} \times 50000 \times 10\times 10 = 2500000 J$
Now, as we know that 90% of the kinetic energy is lost as a result of the friction brakes. Hence, only 10% of KE is transferred to the spring.
So, the kinetic energy of the spring would be
$\frac{1}{2} kx^{2}$
Here, x = 1m
Hence, K = 500000 J

Question:6.42

An adult weighing 600 N raises the centre of gravity of his body by 0.25 m while taking each step of 1 m length in jogging. If he jogs for 6 km, calculate the energy utilized by him in jogging assuming that there is no energy loss due to friction of ground and air. Assuming that the body of the adult is capable of converting 10% of energy intake in the form of food, calculate the energy equivalents of food that would be required to compensate energy utilized for jogging.

Answer:

Potential energy required by the jogger to raise each step = mgh
mg = 600N, h = 0.25 m
Number of steps travelled in 6 km = 6000
Total Energy for 6000 steps $= 6000 \times 600 \times 0.25$
Jogging utilises 10% of the total energy $= \frac{10}{100}\times 6000 \times 600 \times 0.25$
= 90,000 J

Question:6.43

On complete combustion a litre of petrol gives off heat equivalent to $3\times 10^{7}$ J. In a test drive a car weighing 1200 kg, including the mass of driver, runs 15 km per litre while moving with a uniform speed on a surface and air to be uniform, calculate the force of friction acting on the car during the test drive, if the efficiency of the car engine were 0.5.

Answer:

Car engine’s efficiency = 0.5
So, energy given to the car through petrol of 1 litre $= 0.5 \times 3 \times 10^{7}$
Now, the work done by car is $F \times S = F \times 15000 J$
As we know that the work done by the car is against the force of friction; hence equating both can give us the value of friction.
$F \times 15000 = 0.5 \times 3\times 10^{7}$
F = 1000 N

NCERT Exemplar Class 11 Physics Solutions Chapter 6: Long Answer

Work, Energy and Power Class 11 NCERT Exemplar: Long Answer can be viewed as providing step-by-step answers to descriptive questions, which require a profound explanation and logical derivations. These NCERT Exemplar Class 11 Physics Chapter 6 Solutions assist students to enhance their writing style, conceptual knowledge, and be ready to tackle high-weightage exam-based questions.

Question:6.44

A block of mass 1 kg is pushed up a surface inclined to horizontal at an angle of$30^{\circ}$ by a force of 10 N parallel to the inclined surface. The coefficient of friction between block and the incline is 0.1. If the block is pushed up by 10 m along the incline, calculate
a) work done against gravity
b) work done against force of friction
c) increase in potential energy
d) increase in kinetic energy
e) work done by applied force

Answer:

Mass = 1 kg, $\theta$ = 30, F = 10 N, d = 10m
(a) work done against gravity
= mgh
$\sin 30 = \frac{h}{10}$
$h= \frac{10}{2}=5m$
Work done $= 1 \times 10 \times 5 = 50 J$
(b)
Work done against force of friction $= \mu f.s = \mu mg \cos \theta \times s$
$= 0.1 \times 1 \times 10 \cos 30 \times 10 = 10 \times \frac{\sqrt{3}}{2} = 5 \sqrt{3} Joules$
(c) increase in potential energy
This value is equal to the work done against gravity, which we have calculated above in part a. Hence, the increase in potential energy = 50J
(d) increase in kinetic energy
$\Delta KE$= work done $= -mgh + F_s - f_s$
$= - 50 - 5 \sqrt{3 }+ 10 \times 10 = 50 - 5\sqrt{ 3}$
$= 41.340 J$
(e) work done by applied force.
$= F.S = 10 \times 10 = 100 J$

Question:6.45

A curved surface as shown in the figure. The portion BCD is free of friction. There are three spherical balls of identical radii and masses. Balls are released from one by one from A which is at a slightly greater height than C. with the surface AB, ball 1 has large enough friction to cause rolling down without slipping; ball 2 has small friction and ball 3 has negligible friction.
a) for which balls is total mechanical energy conserved?
b) which ball can reach D?
c) for balls which do not reach D, which of the balls can reach back A?

Answer:

(a) For which ball is total mechanical energy conserved?
For balls 1 and 3, the total mechanical energy is conserved. In the case of ball 1, it rolls down without slipping, and hence no force of friction acts against its motion and no energy is dissipated. In the case of ball 3, it has negligible friction, and hence, there is no loss of energy, which leads to the conservation of mechanical energy.
(b) Which ball (s) can reach D?
Ball 1 slips due to its acquired rotational energy on the frictionless surface. Ball 2 loses its energy due to friction. Hence, it does not reach C.
(c) For balls which do not reach D, which of the balls can reach back A?
As we saw, balls 1 and 2 do not reach C, and hence they also don’t reach D.
Ball 3 has negligible friction and hence can reach D. for balls 1 and 2, no of them can reach back at A.

Question:6.46

A rocket accelerates straight up by ejecting gas downwards. In a small time interval $\Delta t$, it ejects a gas of mass $\Delta m$ at a relative speed u. Calculate KE of the entire system at $t+\Delta t$ and t and show that the device that ejects gas does work $= \left ( \frac{1}{2} \right ) \Delta m u^{2}$ in this time interval.

Answer:

We assume the mass of the rocket at any time to be m.
Let the velocity of the rocket be v
Mass of gas ejected in time t can be Δm
$(KE) _{t+ \Delta t} = \frac{1}{2} ( M- \Delta m) (v + \Delta v)^{2} + \frac{1}{2} \Delta m (v-u)^2$
$= \frac{1}{2} [Mv^{2} + M \Delta v^{2} + 2Mv \Delta v - \Delta mv^{2} - m \Delta v^{2} - 2v \Delta m \Delta v+ \Delta mv^{2}+ \Delta mu^{2} - 2uv \Delta m ]$
When we neglect small terms, we get,
$(KE) = \frac{1}{2} MV^{2}$
$\Delta K = \frac{1}{2} \Delta mu^{2} + v (M \Delta v - u \Delta m)$
In accordance with Newton’s third law,
The reaction upward force on the rocket is equal to the action force by the burning of gases in the downward direction
$M \frac{dv}{dt }= \frac{dm}{dt} |u|$
$M \Delta v = \Delta mu$
Substituting this value, we get,
$K = \frac{1}{2} u^{2} \Delta m$
As we know from the work-energy theorem, $\Delta KE$ = work done
We have, work done = $\frac{1}{2} \Delta m u^{2}$

Question:6.47

Two identical steel cubes(mass 50g, sides 1cm) collide head-on face to face with a speed of 10 cm/s each. Find the maximum compression of each. Young’s modulus for steel$= Y = 2 \times 10^{11} N/m^{2}.$

Answer:

The kinetic energies of the cubes when they collide convert into potential energy.
From Hook's law, we know that stress α strain
Y = stress/strain
$Y=\frac{FL}{A\Delta L}$
$F=\frac{ AY \Delta L}{L} = LY\Delta L$
Work done = $F. \Delta L = LY. \Delta L^{2}$
Kinetic energy
$= 2\left (\frac{1}{2} m v^{2} \right ) = 0.05 \times 0.1 \times 0.1 = 5 \times 10 ^{-4} J$
As WD=KE,
$LY. \Delta L^{2} = 5 \times 10 ^{-4}$
$\Delta L =\sqrt{ 25 \times 0.0001} = 5 \times 10 ^{-7} m$

Question:6.48

A balloon filled with helium rises against gravity increasing its potential energy. The speed of the balloon also increases as it rises. How do you reconcile this with the law of conservation of mechanical energy? You can neglect viscous drag of air and assume that density of air is constant.

Answer:

The net buoyant force in this case = vpg
= vol of air displaced x net density in upward direction x g
= V (p(air) - p(He)) g

If we assume a to be the acceleration in the upward direction,
Ma = V (p(air) - p(He)) g --------- (1)
p(air) - density of air
P(He) - density of helium}
m dv/dt = V (p(air) - p(He)) g
m dv = V (p(air) - p(He)) g. dt
When we integrate both sides,
mv = V (p(air) - p(He)) g. t
v = V/m (p(air) - p(He)) g.t
kinetic energy of the balloon,
$\frac{1}{2}mv^{2} = \frac{1}{2} \frac{V^{2}}{m} (p(air) - p(He))^{2} g^{2}t^{2}$-------------(2)
Let the balloon rise to height h,
a = V/m (p(air) - p(He)) g
$h = ut + \frac{1}{2} at^{2}$
h= V/2m (p(air) - p(He)) gt2 ---------------- (3)
On rearranging the terms from the three equations, we get,
$\frac{1}{2} mv^{2} = {\frac{V}{2m} (p(air) - p(He)) gt^{2}} { V (p(air) - p(He)) g }$
$\frac{1}{2} mv^{2} = V p(air) gh - V p(He)gh$
$\frac{1}{2}mv^{2} + p(He)Vgh = p(air)Vgh$
KE of balloon + PE of balloon = the change in potential energy in air
So, we can conclude that when the balloon goes up, an equal volume of air is displaced downwards. The PE and KE of the balloon keep increasing as the PE of air changes.