Surface Areas and Volumes Class 10th Notes - Free NCERT Class 10 Maths Chapter 13 Notes - Download PDF

Surface Areas and Volumes is an important chapter which helps us understand the concept of the measurement of three-dimensional shapes. The surface area can be distinguished as Lateral surface area (LSA), Curved surface area (CSA) and Total surface area (TSA). In this article, we will discuss the formulas for volume and surface areas of different shapes, such as cuboid, cube, cylinder, cone, frustum, etc. The formulas we study in this chapter are important for solving practical problems related to geometry and real-life applications like construction, packaging, engineering, etc. The main purpose of these NCERT Notes of Surface Areas and Volumes class 10 PDF is to provide students with an efficient study material from which they can revise the entire chapter.

After going through the textbook exercises and solutions, students need a type of study material from which they can recall concepts in a shorter time. Surface Areas and Volumes Class 10 Notes are very useful in this regard. In this article about NCERT Class 10 Maths Notes, everything from definitions and properties to detailed notes, formulas, diagrams, and solved examples is fully covered by our subject matter experts at Careers360 to help the students understand the important concepts and feel confident about their studies. These NCERT Class 10 Maths Chapter 12 Notes are made in accordance with the latest CBSE syllabus while keeping it simple, well-structured and understandable. For the syllabus, solutions, and chapter-wise PDFs, head over to this link: NCERT.

Surface Areas and Volumes Class 10 Notes: Free PDF Download

Use the link below to download the Surface Areas and Volumes Class 10 Notes PDF for free. After that, you can view the PDF anytime you desire without internet access. It is very useful for revision and last-minute studies.

Download PDF

NCERT Class 10 Maths Chapter 12 Notes: Surface Areas and Volumes

Surface area: Surface area can be defined as the measurement of the total area that has been occupied by the object.

Volume: Volume is defined as the measurement of space that is occupied by the object.

Now, let's discuss the basic solid shapes and their respective formula:

Surface Area And Volume of the Cuboid

A cuboid is a three-dimensional shape, also known as a rectangular prism. It has six rectangular faces, eight vertices, and 12 edges.

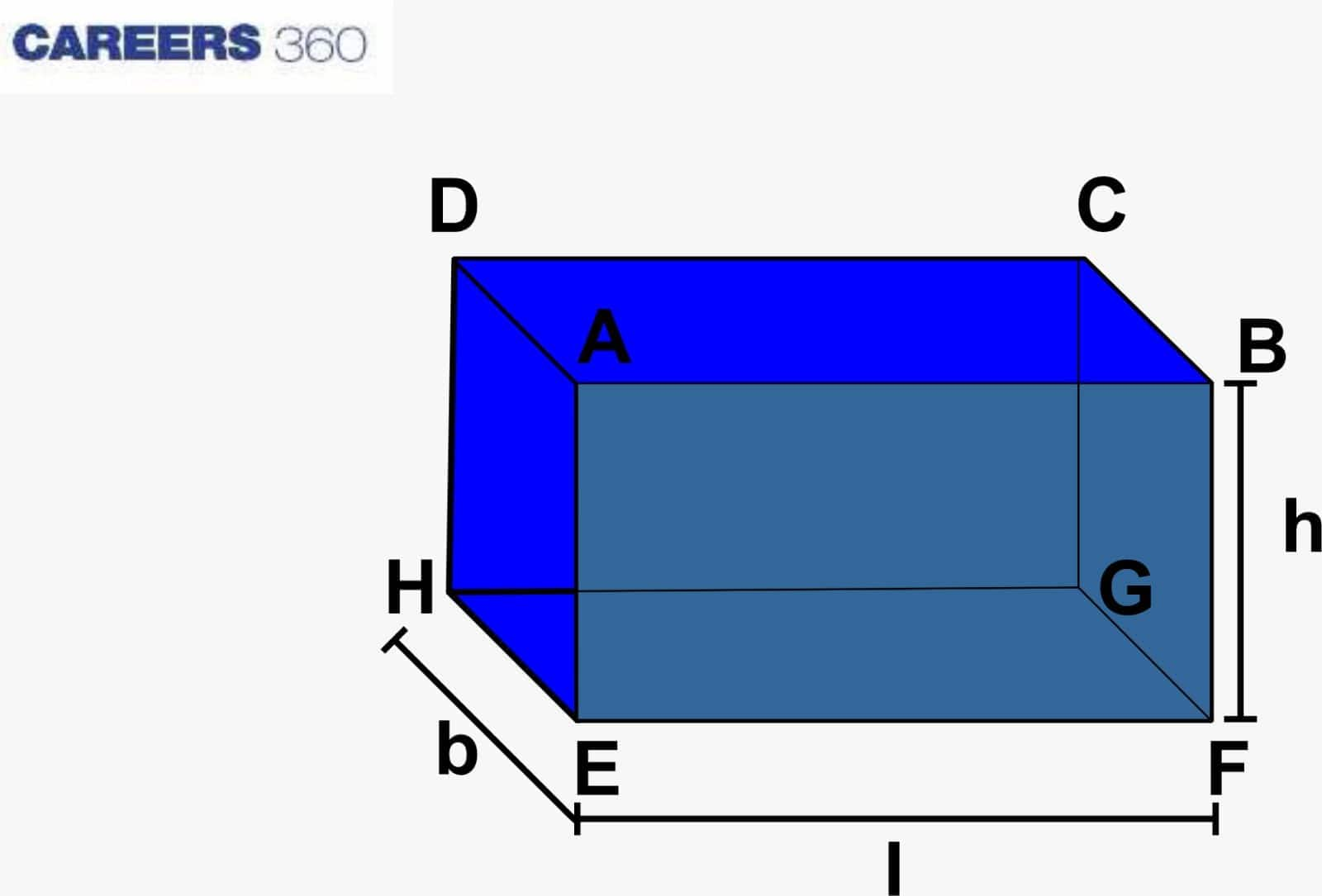
The surface area of a cuboid with the roof.
The total surface area of the cuboid (TSA) = The sum of the areas of all its 6 faces.

The surface area of the cuboid = $2(lb + bh +hl)$ sq. unit.

Here, $l$ denotes the length, $b$ denotes the breadth, and $h$ denotes the height.

The lateral surface area of the Cuboid:
The lateral surface area (LSA) includes all the sides except the top and the bottom faces.

Area of cuboid covering four walls = Area of face AEHD + Area of face BFGC + Area of face ABFE + Area of face DHGC

Lateral Surface Area of the Cuboid = $2(b × h) + 2(l × h)$ = $2h(l + b)$

Length of diagonal of a cuboid =$\sqrt{(l^2 + b^2 + h^2)}$

Volume of a cuboid: The volume of a cuboid is defined as the space occupied between its six rectangular faces. It is given by the product of its dimensions, such as length, breadth and height.

Volume = $l × b × h$ cubic units.

Surface Area and Volume of a Cube

A cube is defined as a three-dimensional solid shape with six square faces, twelve edges and eight vertices.

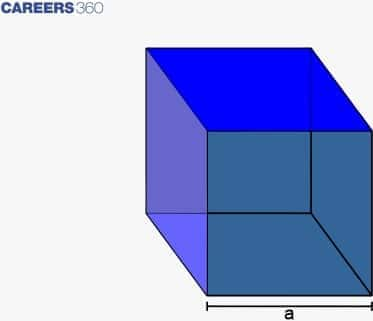
Surface Area of Cube

As we know, all sides of a cube are equal.
So, Length = Breadth = Height = a.

The total surface area of the cube (TSA) = The sum of the areas of all its six faces.

TSA of Cube = 6 × area of Square = $ 6a^2$

The lateral surface area of cube = $2(a × a + a × a)$ = $4a^2$

Diagonal of a cube = $\sqrt3l$

Volume of a Cube

In a cube, all sides are the same or equal. So, the volume of the cube is:

Volume of a cube = Base area × Height

As all dimensions of a cube are the same.

So, Volume = a³

Where a is the length of the edge of the cube.

Surface Area and Volume of a Cylinder

A cylinder is a three-dimensional solid shape having two parallel, congruent bases which are connected by a curved surface at a fixed distance from the centre of the bases. Therefore, it consists of three faces, of which two are circular and one is lateral. Now, based on these dimensions, we can find the surface area and volume of a cylinder.

Surface Area of Cylinder

As shown in the figure below, assume a cylinder of base radius r and height h units. The curved surface of the cylinder, if it were opened along the diameter (d = 2r) of the circular base, can be changed into a rectangle of length $2πr$ and height $h$ units.

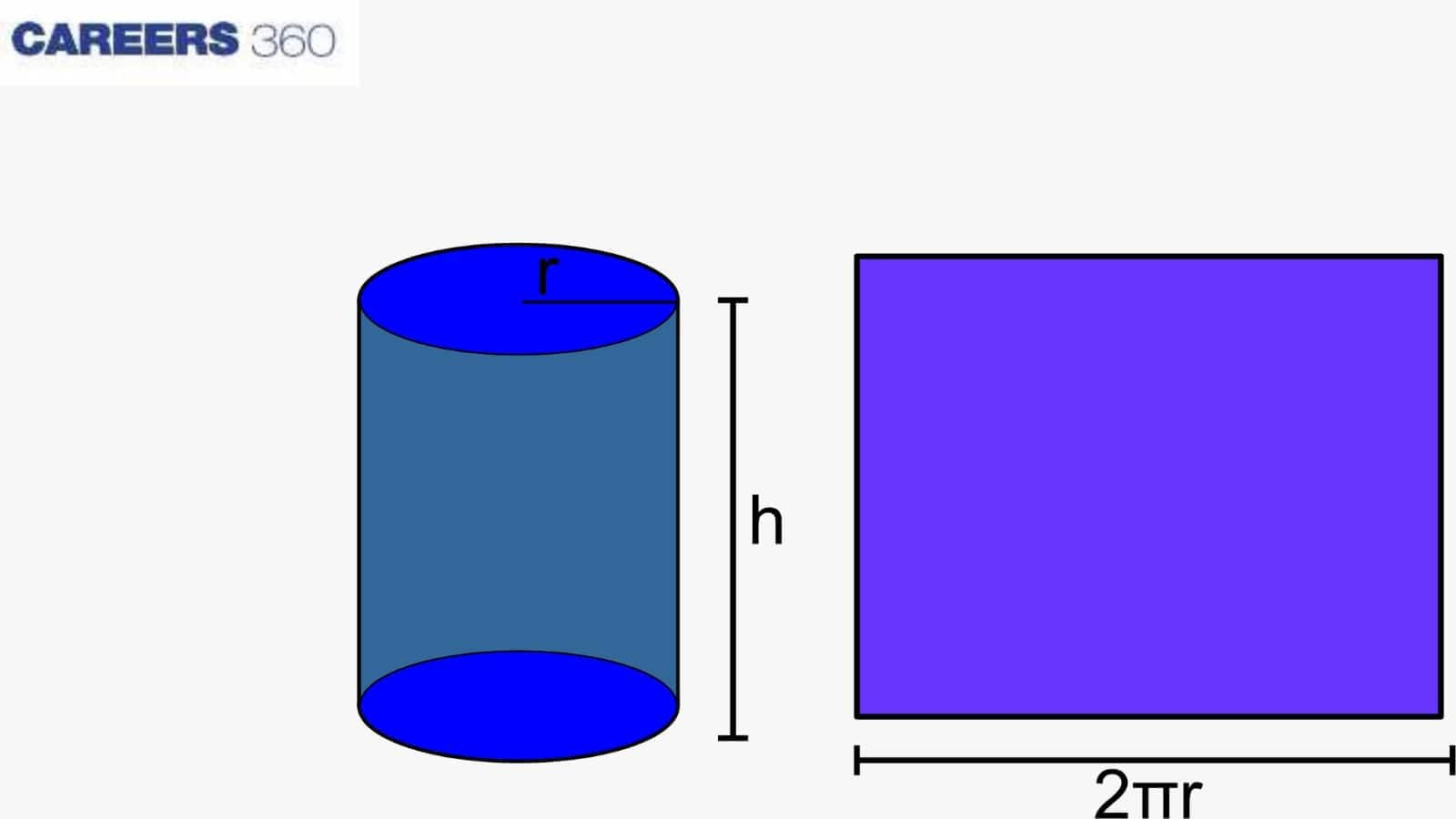
Therefore, the cylinder changes to a rectangle.

CSA of a cylinder of base (where radius = r and height = h) = $2π × r × h$

TSA of a cylinder of base (where radius = r and height = h) = $2π × r × h$ $+$ $2πr^2$ (Area of two circular bases = $2πr^2$)

= $2πr(h + r)$

Volume of a Cylinder

The volume of a cylinder is defined as the amount of space it occupies in a three-dimensional space. It can be calculated as the product of the area of its circular base and its height, as shown below in a diagram.

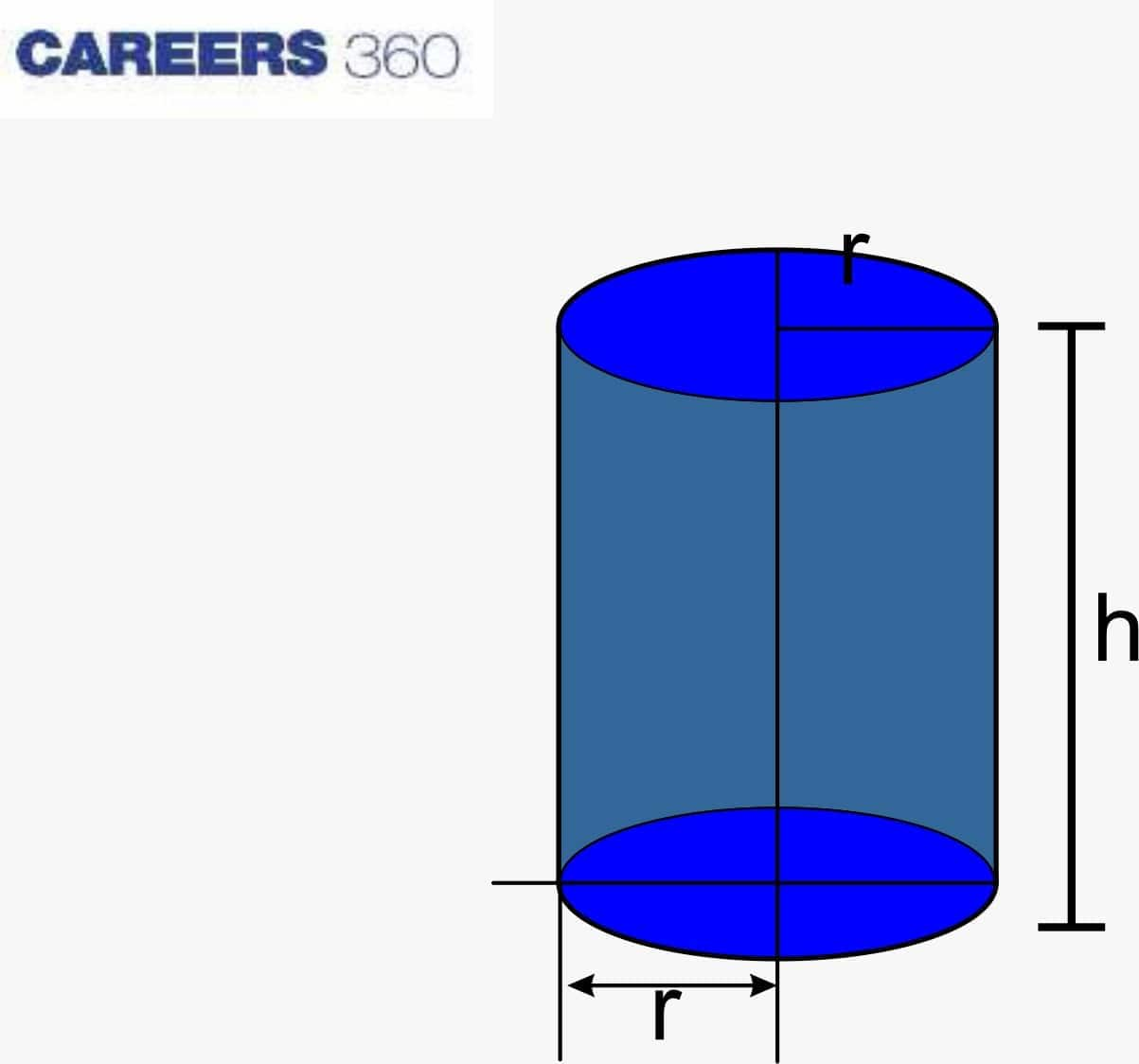
Volume of a Cylinder = $πr^2 × h$ = $πr^2h$

(where r is the radius of the circular base and h is the height of the cylinder.)

Surface Area and Volume of Right Circular Cone

A cone is defined as a three-dimensional geometric shape that consists of a circular base and a curved surface that gradually decreases to a single point called the vertex.

Surface Area of Cone

Let's consider a right circular cone with slant length l, radius r and height h as shown in the diagram.

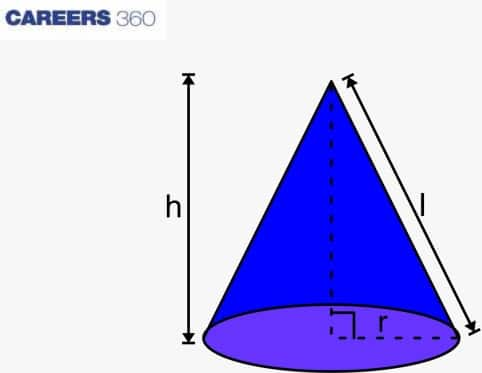
The cone with base radius r and height h

The curved surface area (CSA) of a right circular cone = $πrl$

The total surface area of the cone (TSA) = $πrl + πr^2$ (where, $πr^2$ = Area of a base)
= $πr(l + r)$

Volume of a Right Circular Cone

The volume of a right circular cone is defined as the amount of space it occupies in a three-dimensional space, and the volume of a Right circular cone is equal to one-third that of a cylinder of the same height and base.

The volume of a Right circular cone = $\frac{1}{3}$$πr^2h$

Here, $r$ is the radius of the base and $h$ is the height of the cone.

Surface Area and Volume of Sphere

A solid that is round is known as a sphere. All the points that are located on its surface are equidistant from the center.

Surface Area of Sphere:
As shown in the diagram, let's consider a sphere of radius r.

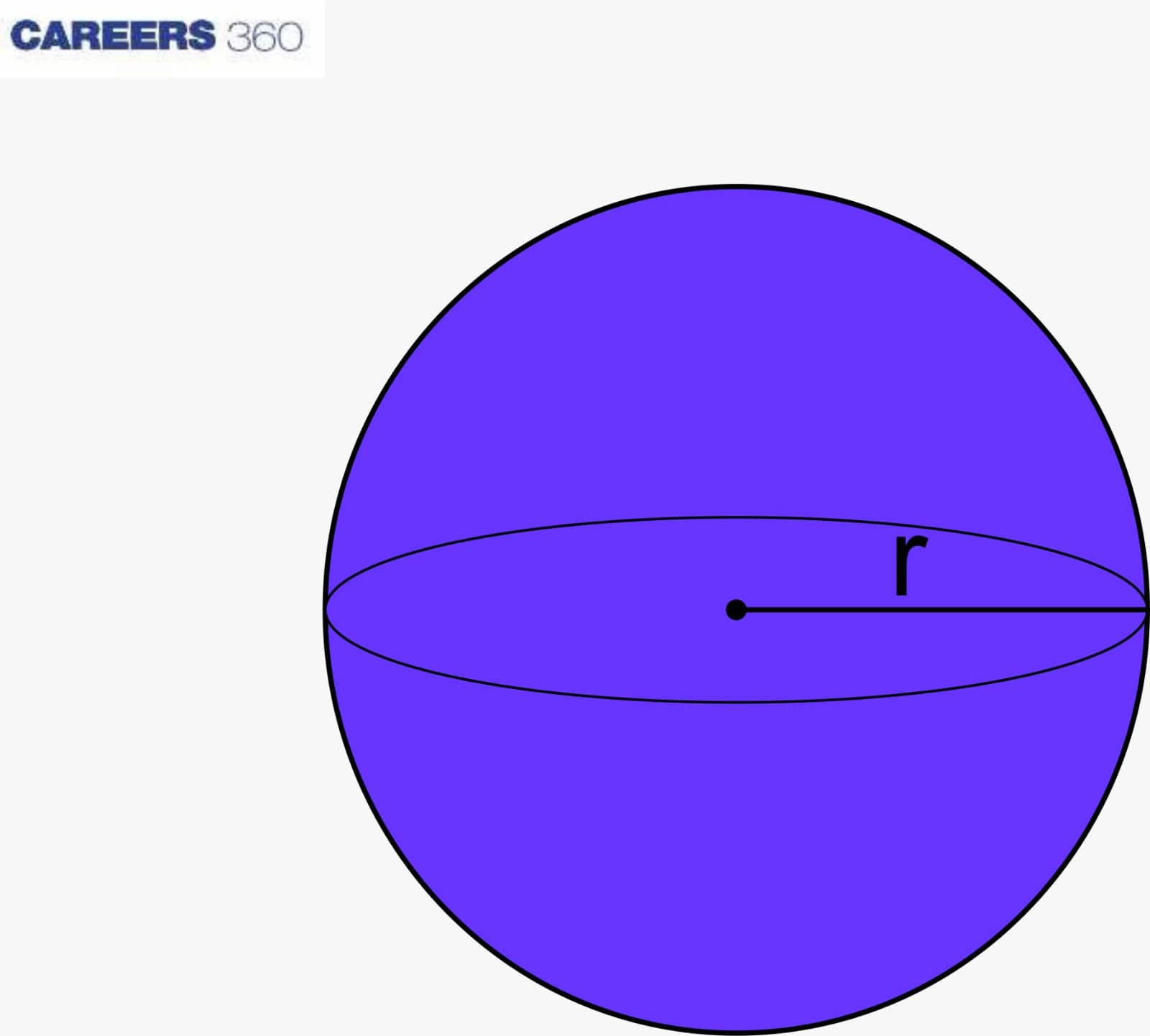
Curved Surface Area (CSA) = Total Surface Area (TSA) = $4πr^2$

Volume of Sphere
The volume of a sphere of radius r = $\frac{4}{3}$ $πr^3$

Surface Area and Volume of a Hemisphere

A hemisphere is defined as one-half of a sphere, which is represented as a 3D shape cut by a plane through its center and has one flat surface, as shown in the figure below.

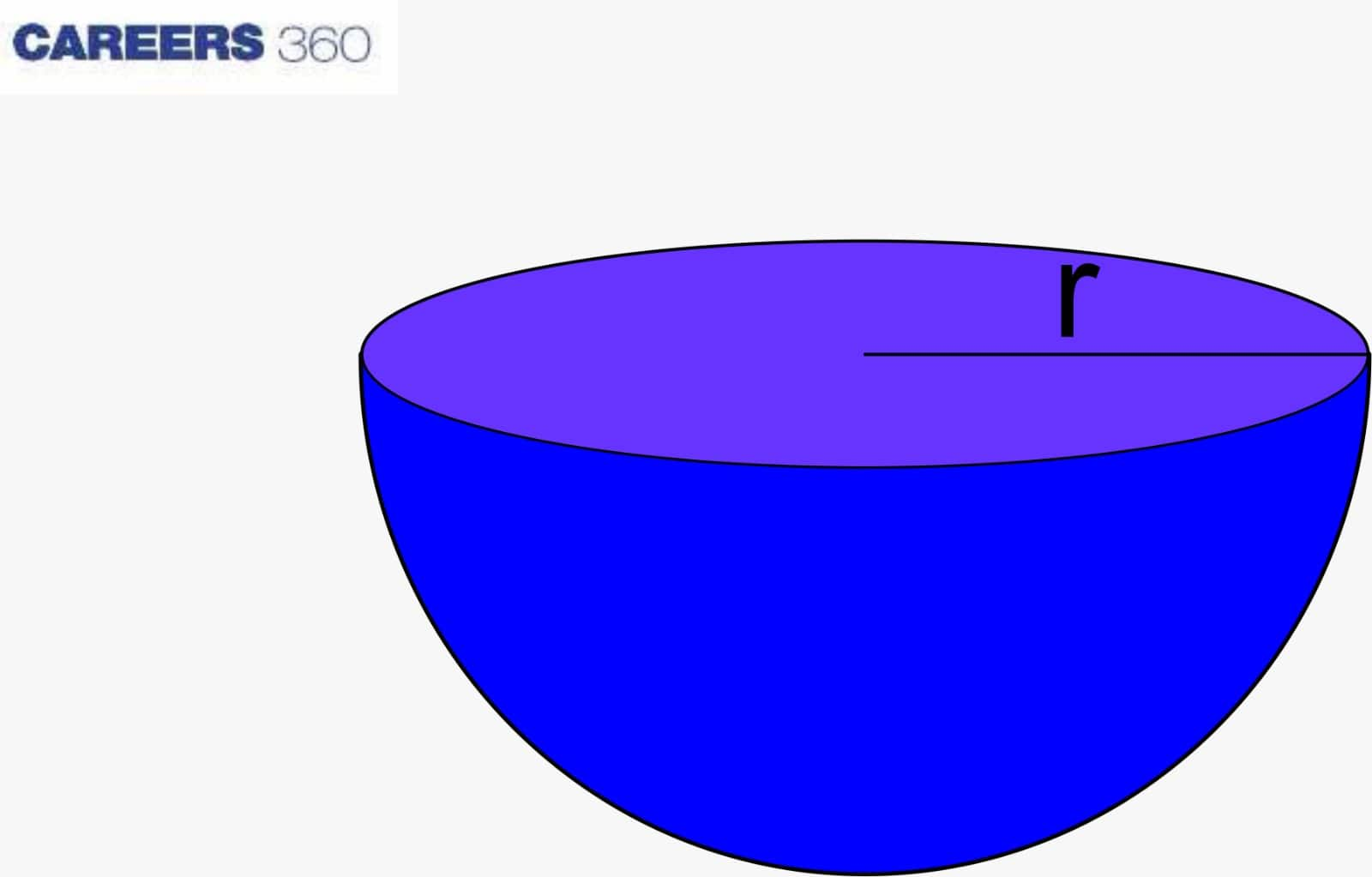
Surface Area of a Hemisphere
As we studied above, the curved surface area (CSA) of a sphere = $4πr^2$.
Half of a sphere is a hemisphere.

Therefore, the Curved Surface Area (CSA) of a hemisphere of radius r = $2πr^2$.

Total Surface Area of hemisphere (TSA) = Curved surface area + Area of the base circle ⇒ $2πr^2$ + $πr^2$

Total Surface Area = $3πr^2$

Volume of Hemisphere
Half of the volume (V) of the sphere is equal to the volume of a hemisphere.

Therefore, the volume of the hemisphere of radius r = $\frac{2}{3}$$πr^3$

Surface Area and Volume of Frustum of a Cone

A plane cutting through a solid creates a new solid form. A cone's frustum, which is created when a plane cuts a cone parallel to its base, is one example of this type of solid. Now let's talk about its volume and surface area.

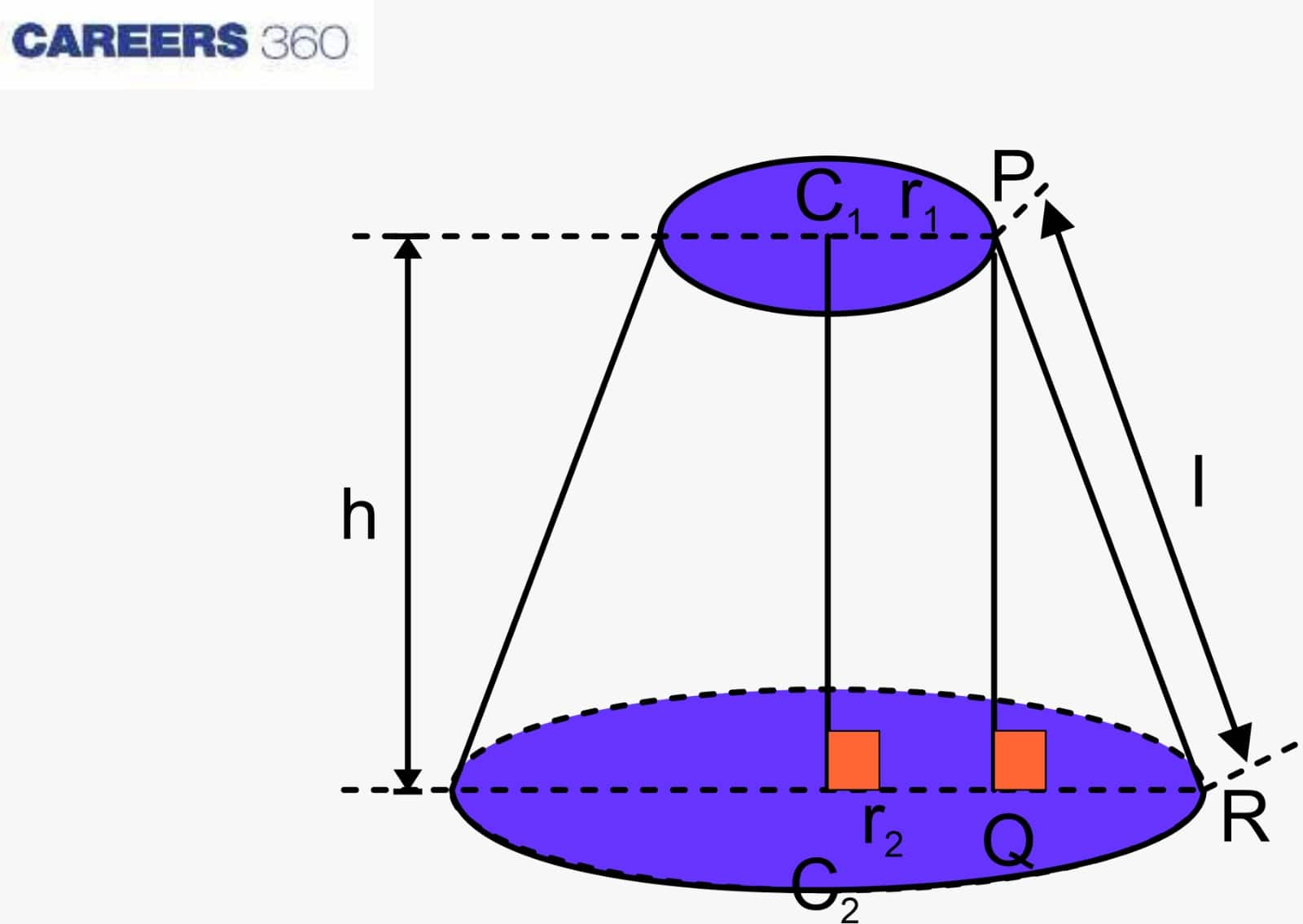
Frustum with radii r1 and r2 and height h
The curved surface area (CSA) of a frustum is $π(r_1+r_2)l$, where $l = \sqrt{h^2+(r_2 – r_1)^2}$.

The total surface area (TSA) of the frustum is the (CSA) + (the areas of the two circular faces) = $π(r_1 + r_2)l + π(r_1^2 + r_2^2)$

Volume of a Frustum
The volume of a frustum of a cone = $\frac{1}{3}πh(r_1^2 + r_2^2 + r_1r2)$

Surface Area and Volume of a Combination of Solids

The combination of solids discusses the forms generated when two different solids are joined together. Thus, the surface area and volume for such shapes will be different from the other fundamental solids.

Surface Area of a Combination of Solids

Complex figures' sections can be dissected and examined as more straightforward, well-known shapes. We can get the necessary area of the unknown figure by calculating the areas of four well-known shapes.

Example: Two cubes with volumes of 125 cm³ each are connected end to end. Determine the final cuboid's surface area.

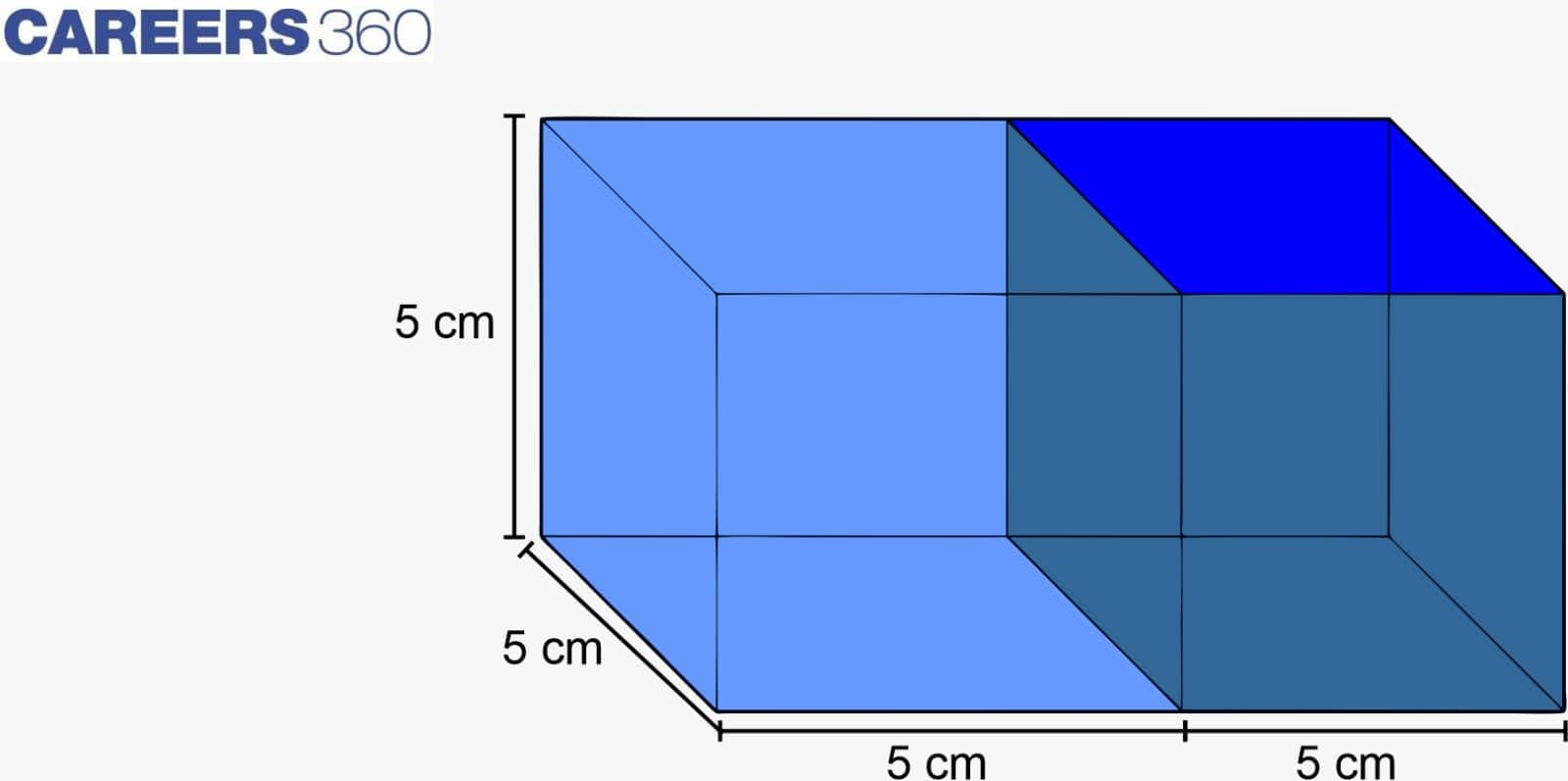
Solution: Length of each cube = $125^\frac{1}{3} $ = $5 cm$
Due to their adjacent joining, these cubes create a cuboid with a length of l = $10 cm$. However, the width and height will stay at $5 cm$.

Now, the combination of 2 equal cubes
Therefore, the new surface area, TSA = $2(lb + bh + lh)$

TSA = $2 (10 × 5 + 5 × 5 + 10 × 5)$

= $2(50 + 25 + 50)$

= $2 × 125$

So, the total surface area (TSA) = $250 cm^2$.

Volume of a Combination of Solids

Visualizing complex objects as a mix of shapes of known solids might simplify their volume.

Example: Daanish operates a business out of a shed that resembles a cuboid with a half-cylinder on top. Determine the amount of air that the shed can contain if its base is 7m by 15m and its cuboidal part is 8m high. Additionally, say that there are 20 workers and that the machinery in the shed takes up 300 m³, with each worker taking up an average of 0.08 m³ of area. How much air is there in the shed, then?

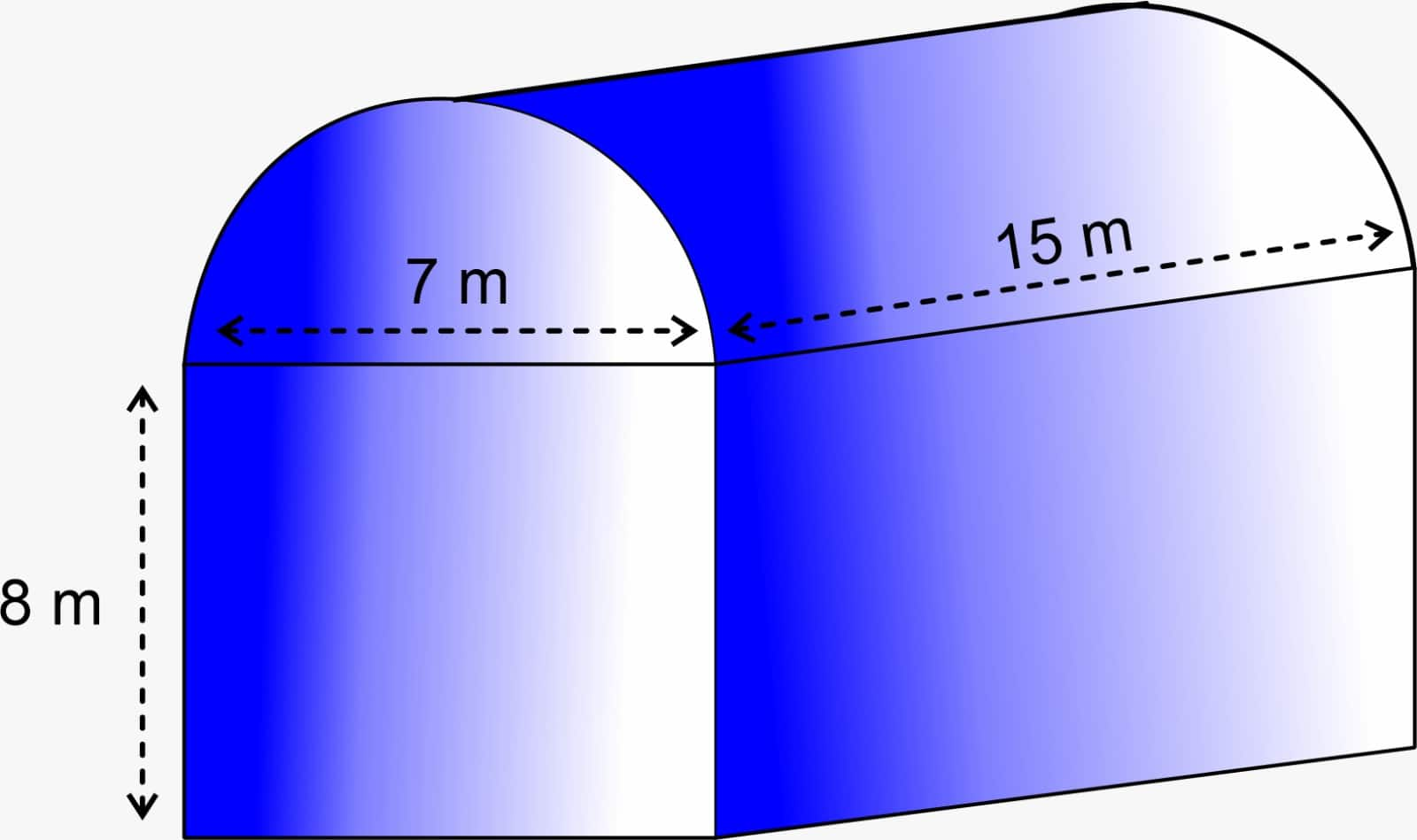
Solution: When no people or equipment are present, the volume of air within the shed is determined by adding the volumes of air inside the cuboid and the half-cylinder.

The cuboid's current dimensions are $15 m$ for length, $7 m$ for width, and $8 m$ for height.

Additionally, the half cylinder has a height of $15 m$ and a diameter of $7 m$.

Therefore, the required volume = volume of the cuboid + $\frac{1}{2}$ volume of the cylinder.

= $[15 × 7 × 8 + \frac{1}{2} × \frac{22}{7} × \frac{7}{2} × \frac{7}{2} × 15] m^3$

= $1128.75 m^3$

Formulas at a Glance:

The students must read the formulas table given below for a quick revision.

Surface Areas and Volumes: Previous Year Question and Answer

Given below are some previous year question answers of various examinations from the NCERT class 10 chapter 12, Surface Areas and Volumes:

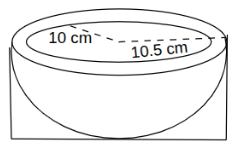
Question 1: A hemispherical bowl is packed in a cuboidal box. The bowl just fits in the box. The inner radius of the bowl is 10 cm. Outer radius of the bowl is 10.5 cm.
Based on the diagram, answer the following question:
The inner surface of the bowl and its thickness are to be painted. Find the area to be painted.

Solution:

Given:

The surface area of a sphere is $4 \pi r^2$

The surface area of a hemisphere is half the surface area of a sphere = $ 2\pi r^2$

The area of a circle is $\pi r^2$

Outer radius of hemisphere $R = 10.5\ \text{cm}$

Inner radius of hemisphere $r = 10\ \text{cm}$

Area to be painted $=2 \pi(r)^2+\pi(\mathrm{R})^2-\pi(r)^2$

$
\begin{aligned}
& =\pi\left(R^2+r^2\right) \\
& =3.14\left((10.5)^2+(10)^2\right) \\
& =3.14(110.25+100) \\
& =660.185 \mathrm{~cm}^2
\end{aligned}
$
Hence, the answer is $ 660.185\mathrm {~cm}^2$.

Question 2: The volume of air in a hollow cylinder is $450 \mathrm{~cm}^3$. A cone of the same height and radius as that of the cylinder is kept inside it. The volume of empty space in the cylinder is:

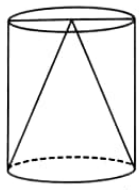
Solution:

Volume of a cone $V_{k}=\frac{1}{3} \pi r^2 h$

where, $r = $ radius of cone

and

$h = $ height of cone

Volume of a cylinder, $V_{c}=\pi r^2 h$

where, $r = $ radius of cylinder

and

$h = $ height of cylinder

We know that, Volume of cone $=\frac{1}{3} \times \text { Volume of cylinder }$

Volume of cylinder $V_c = \pi r^2 h = 450 \mathrm{~cm}^3$

Volume of cone $V_k = \frac{1}{3} \pi r^2 h$

Volume of empty space = $V_c - V_k$

$= \pi r^2 h - \frac{1}{3} \pi r^2 h $

$= \frac{2}{3} \pi r^2 h$

Volume of empty space = $\frac{2}{3} \times 450 = 300 \mathrm{~cm}^3$

Hence, the correct answer is $300 \mathrm{~cm}^3$.

Question 3: Two identical cones are joined as shown in the figure. If the radius of the base is 4 cm and the slant height of the cone is 6 cm, then the height of the solid is:

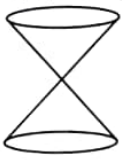
Solution:

Given,

Radius ($r$) of the cone $ = 4$ cm,

Slant height ($l$) of the cone $= 6$ cm.

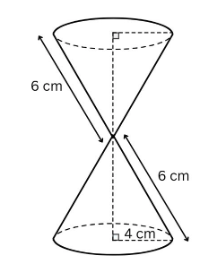
We know that,

Height ($h$) of the cone $= \sqrt{l^2 - r^2} $

$= \sqrt{6^2 - 4^2} $ $\mathrm{cm}$

$= \sqrt{36 - 16} $ $\mathrm{cm}$

$= \sqrt{20}$ $\mathrm{cm}$

$= 2\sqrt{5} $ $\mathrm{cm}$

Thus, the height of the given solid $= 2 h$

Height of the solid $= 2 \times 2\sqrt{5}$ $\mathrm{cm}$

Height of the solid $= 4\sqrt{5}$ $\mathrm{cm}$

Hence, the correct answer is $4\sqrt{5}$ $\mathrm{cm}$.

Class 10 Chapter Wise Notes

All the links to chapter-wise notes for NCERT class 10 maths are given below:

NCERT Exemplar Solutions for Class 10

Students must check the NCERT Exemplar solutions for class 10 of Mathematics and Science Subjects.

• NCERT Exemplar Class 10 Maths solutions

• NCERT Exemplar Class 10 Science solutions

NCERT Solutions for Class 10

Students must check the NCERT solutions for class 10 of Mathematics and Science Subjects.

• NCERT Solutions for Class 10 Maths

• NCERT Solutions for Class 10 Science

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

• NCERT Books for Class 10

• NCERT Syllabus for Class 10