NCERT Exemplar Class 10 Maths Solutions Chapter 12 Surface Areas and Volumes
Upcoming Event
CBSE Class 10th Exam Date:17 Feb' 26 - 17 Feb' 26
NCERT Exemplar Class 10 Maths Solutions chapter 12 discusses the method to determine the surface area and volume of various three-dimensional objects. This chapter helps us to understand how to calculate the area related to covering a solid object and the space it occupies. The concepts we study in this chapter are crucial for solving practical problems related to geometry and real-life applications. These three-dimensional objects can be cones, spheres, or cylinders. In this article, we will deal with many questions such as, 'How do we calculate the surface area and volume of different solids like cubes, cylinders, cones, and spheres?', What are the formulas for surface area and volume?', and 'How do we apply these formulas in different scenarios?' These consist of detailed solutions to study and understand the NCERT class 10 Maths. These NCERT exemplar class 10 Maths chapter 12 solutions are prepared by our skilled subject matter experts.
This Story also Contains
- NCERT Exemplar Solutions Class 10 Maths Chapter 12 Important Topics:
- NCERT Class 10 Exemplar Solutions for Other Subjects:
- NCERT Class 10 Maths Exemplar Solutions for Other Chapters:
- Importance of NCERT Exemplar Class 10 Maths Solutions Chapter 12:
The NCERT Exemplar Class 10 Maths chapter 12 solutions are beneficial for understanding of concepts of surface area and volume due to their comprehensive nature. The CBSE Syllabus Class 10 Maths is the reference for NCERT Exemplar Class 10 Maths solutions chapter 12.
| Class 10 Maths Chapter 12 exemplar solutions Exercise: 12.1 Page number: 138-140 Total questions: 20 |
Question:1
A cylindrical pencil sharpened at one edge is the combination of
(A) a cone and a cylinder (B) frustum of a cone and a cylinder
(C) a hemisphere and a cylinder (D), two cylinders.
(A) A cone –A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex.
A cylinder – A cylinder is a three-dimensional solid that holds two parallel bases joined by a curved surface at a field distance.
Therefore, A cylindrical pencil sharpened at one edge is the combination of a cone and a cylinder.
Question:2
A Surahi is the combination of
(A) a sphere and a cylinder (B) a hemisphere and a cylinder
(C) two hemispheres (D) a cylinder and a cone.
Solution:
(A) A Sphere – The set of all points in three-dimensional space lying at the same distance from a given point.
A cylinder – A cylinder is a three-dimensional solid that has two parallel bases joined by a curved surface at a fixed distance. The neck of Surahi is in the shape of a cylinder, and the bottom forms a shape of sphere.
Question:3
A plumbline (sahul) is the combination of
(A) a cone and a cylinder (B) a hemisphere and a cone
(C) frustum of a cone and a cylinder (D) sphere and cylinder
Question:4
The shape of a glass (tumbler) (see figure) is usually in the form of
(A) a cone (B) frustum of a cone
(C) a cylinder (D) a sphere
Solution
A cone – A cone is a three-dimensional geometrical shape that tapers smoothly from a flat base to a point called the apex or vertex.
(B) Frustum of a cone – It is a portion of a solid that lies between one or two parallel planes cutting it.
(C) A cylinder – A cylinder is a three-dimensional solid that has two parallel bases joined by a curved surface at a fixed distance.
(D) A sphere – The set of all points in three-dimensional space lying the same distance from a given point.
Hence the shape of glass is usually in the form of the frustum of a cone.
Question:5
The shape of a gilli, in the gilli-danda game (See figure), is a combination of
(A) two cylinders (B) a cone and a cylinder
(C) two cones and a cylinder (D) two cylinders and a cone
Question:6
A shuttle cock used for playing badminton has the shape of the combination of
(A) a cylinder and a sphere
(B) a cylinder and a hemisphere
(C) a sphere and a cone
(D) frustum of a cone and a hemisphere
Shuttle cock which is used for playing badminton has the shape of a combination of a frustum of a cone and hemisphere.
Question:7
A cone is cut through a plane parallel to its base and then the cone that is formed on one side of that plane is removed. The new part that is left over on the other side of the plane is called
(A) a frustum of a cone (B) cone
(C) cylinder (D) sphere
Frustum of a cone – It is a portion of a solid that lies between one or two parallel planes cutting it
Question:8
A hollow cube of internal edge 22cm is filled with spherical marbles of diameter 0.5 cm and it is assumed that $\frac{1}{8}$ space of the cube remains unfilled. Then the number of marbles that the cube can accommodate is
(A) 142296 (B) 142396 (C) 142496 (D) 142596
Solution
Diameter of marble = 0.5 cm
Radius $\frac{0.5}{2}=\frac{5}{20}=\frac{1}{4}cm$
Volume of marble $\frac{4\pi r^{3}}{3}=\frac{4}{3}\times \frac{22}{7} \times \frac{1}{4} \times \frac{1}{4} \times \frac{1}{4} =\frac{11}{168}cm^{3}$
Edge of cube = 22 cm
Volume (V) $22 \times 22 \times 22$
Space occupied by marble = total volume $\frac{1}{8}$ part of volume
$=v -\frac{1}{8}v=\frac{7v}{8}$
Number of marble $=\frac{space occupied }{volume of marble}$
$=\frac{7v \times 168 }{8 \times 11}$
$=\frac{7 \times 22\times 22\times 22\times 22\times 168 }{8 \times 11}$
$=142296$
Question:10
A solid piece of iron in the form of a cuboid of dimensions $49cm \times 33cm \times 24cm$, is moulded to form a solid sphere. The radius of the sphere is
(A) 21cm (B) 23cm (C) 25cm (D) 19cm
Solution
Length of cuboid = 49 cm
Breadth of cuboid = 33 cm
Height of cuboid = 24 cm
Volume $=l \times b \times h$
$49 \times 33 \times 24=38808$
We know that volume of sphere $\frac{4}{3}\pi r^{3}$
Also volume of sphere 38808 (given)
$r^{3}=\frac{38808 \times 7 \times 3}{4 \times 22}=\frac{882 \times 7 \times 3}{2}=9261$
$\Rightarrow r^{3}=9261$
$\Rightarrow r=\sqrt[3]{3 \times 3 \times 3 \times 7 \times7 \times 7}$
$\Rightarrow r= 3 \times 7 = 21$
Hence radius of the sphere = 21 cm
Question:11
A mason constructs a wall of dimensions $270cm\times 300cm \times 350cm$ with the bricks each of size $22.5cm \times 11.25cm \times 8.75cm$and it is assumed that $\frac{1}{8}$ space is covered by the mortar. Then the number of bricks used to construct the wall is
(A) 11100 (B) 11200 (C) 11000 (D) 11300
Solution
Length of wall = 270 cm
Breadth = 300 cm
Height = 350 cm
Volume $=l \times b\times h$
$=270\times 300 \times 350= 28350000cm^{3}$
Length of brick = 22.5 cm
Breadth = 11.25 cm
Height = 8.75 cm
Volume $=l \times b\times h$
$= 22.5 \times 11.25 \times 8.75 = 2214.84375cm^{3}$
$\frac{1}{8}$ Space is covered by mortar (given)
Remaining space $=\frac{volume of wall}{8}$
$=\frac{2835000}{8}=3543750cm^{3}$
Surface constructed $= 28350000 - 3543750 = 24806250cm^3$
Number of bricks used $= \frac{ \text{surface contracted}} {\text{volume of brick}}$
$\Rightarrow \frac{24806250}{2214.84375}=11200$
Question:12
Twelve solid spheres of the same size are made by melting a solid metallic cylinder of base diameter 2 cm and height 16 cm. The diameter of each sphere is
(A) 4 cm (B) 3 cm (C) 2 cm (D) 6 cm
Solution
Diameter of metallic cylinder = 2 cm
Radius $=\frac{2}{2}=1cm$
Height = 16cm
Volume $=\pi r^{2}h$
$=\pi\times 1 \times 1 \times 16= 16\pi$
We know that twelve solid spheres are made by melting of solid metallic cylinder
Volume of sphere $=\frac{4}{3}\pi r^{3}$
Hence the volume of 12 spheres $=16 \pi$
$\Rightarrow 12 \times \frac{4}{3}\pi r^{3}=16 \pi$
$\Rightarrow 16\pi r^{3}=16 \pi$
$\Rightarrow r^{3}=1$
$\Rightarrow r=1$
Radius = 1 cm
Diameter $2 \times 1 = 2cm$
Question:13
The radii of the top and bottom of a bucket of slant height 45 cm are 28 cm and 7 cm, respectively. The curved surface area of the bucket is
(A) 4950 cm2 (B) 4951 cm2 (C) 4952 cm2 (D) 4953 cm2
Solution
Slant height of a bucket = 45 cm
Top radius $=r_{1}=28cm$
Bottom radius $=r_{2}=7cm$
Curved surface area of bucket is $=\pi l(r_{1}+r_{2})$
$=\frac{22}{7}\times 45 \times (28+7)$
$=\frac{22}{7}\times 45 \times 35$
$=4950cm^{2}$
Question:14
A medicine-capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of entire capsule is 2 cm. The capacity of the capsule is
(A) 0.36 cm3 (B) 0.35 cm3 (C) 0.34 cm3 (D) 0.33 cm3
Answer:
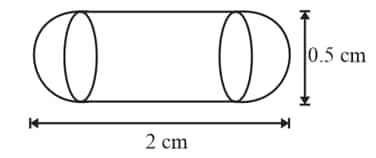
Diameter of hemisphere = 0.5 cm
$Radius$ $=\frac{0.5}{2}=\frac{5}{20}=\frac{1}{4}=0.25cm$
$\text{ Volume of hemisphere }$$=\frac{2}{3}\pi r^{3}$
$= \frac{2}{3}\times\frac{22}{7}\times \frac{1}{4}\times\frac{1}{4}\times \frac{1}{4}=\frac{11}{336}$
$\text{ Volume of two hemispheres}$ $=\frac{2 \times11}{336} =\frac{11}{168}$
Similarly radius of cylinder = 0.25
Height = 2- 0.25 -0.25
= 2- 0.5
=1.5 cm
$Volume$ $= \pi r ^{2}h$
$= \frac{22}{7}\times \frac{1}{4}\times\frac{1}{4}\times\frac{15}{10}\Rightarrow \frac{33}{112}$
The total volume of capsule = volume of two hemispheres + volume of the cylinder
$=\frac{11}{168}+\frac{33}{112}$
$=0.065 +0.294$
= 0.359cm3
=0.36cm3 (approximate)
Question:15
If two solid hemispheres of same base radius r are joined together along their bases, then curved surface area of this new solid is
(A) $4 \pi r^{2}$ (B) $6 \pi r^{2}$ (C) $3 \pi r^{2}$ (D) $8 \pi r^{2}$
The radius of the hemisphere = r
$\text{ Curved surface area}$ $=2 \pi r^{2}$
The curved surface area of two solid hemispheres
$=2 \times 2 \pi r^{2}$
$=4 \pi r^{2}$
Question:16
A right circular cylinder of radius r cm and height h cm (h > 2r) just encloses a sphere of diameter
(A) r cm (B) 2r cm (C) h cm (D) 2h cm
Solution
Here we found that the right circular cylinder of radius r cm and height h cm (h > 2r) can enclose a sphere of radius up to r cm.
$\therefore$ The required sphere is of diameter 2r.
Question:17
During conversion of a solid from one shape to another, the volume of the new shape will
(A) increase (B) decrease
(C) remain unaltered (D) be doubled
Solution
Volume – Volume is defined as the amount of space the object takes up that is the amount of fluid that the container could hold.
During the conversion of a solid from one shape to another, the volume of the new shape remains unchanged.
That is when you convert one solid shape to another then the volume of the original as well as the new solid remains the same.
Question:18
The diameters of the two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of the bucket is
(A) 32.7 litres (B) 33.7 litres (C) 34.7 litres (D) 31.7 litres
Solution
Volume of frustum of cone $=\frac{\pi h}{3} (r_{1}^{2}+ r_{2}^{2}+r_{1}r_{2})$
Diameter of the first end = 44 cm
Radius $(r_{1})=\frac{44}{2}=22cm$
Diameter of the second end = 24 cm
Radius $(r_{2})=\frac{24}{2}=12cm$
Height (h) = 35cm
Volume $=\frac{\pi h}{3} (r_{1}^{2}+ r_{2}^{2}+r_{1}r_{2})$
$=\frac{22 \times 35}{7 \times 3}(22^{2}+12^{2}+22 \times 12)$
$= \frac{110}{3}[484 +144+264]$
$= \frac{110}{3}[892]$
$= 32706.67 cm^{3}$
We know that 1 liter = 1000 cm3
$\therefore 32706.67 cm^{3} =32.7 l$
Question:19
In a right circular cone, the cross-section made by a plane parallel to the base is a
(A) circle (B) frustum of a cone
(C) sphere (D) hemisphere
Answer:
According to the question if a right circular cone is cut by a plane parallel to its base the figure formed is
Here BECD is not a circle, not a sphere not a hemisphere but it is a frustum of a cone.
Hence in a right circular cone, the cross-section made by a plane parallel to the base is a frustum of a cone.
Question:20
Volumes of two spheres are in the ratio 64:27. The ratio of their surface areas is
(A) 3 : 4 (B) 4 : 3 (C) 9 : 16 (D) 16 : 9
Let two sphere having radius $r_{1}$ and $r_{2}$
According to question
$\frac{\text {volume of first sphere}}{\text {volume of second sphere}}=\frac{64}{27}$
$\Rightarrow \frac{\frac{4}{3}\pi r_{1}^{3}}{\frac{4}{3}\pi r_{2}^{3}}=\frac{64}{27}$
$\Rightarrow \left ( \frac{r_{1}}{r_{2}} \right )^{3}=\frac{64}{27}$
$\Rightarrow \frac{r_{1}}{r_{2}} =\sqrt[3]{\frac{64}{27}}=\frac{4}{3}$
Ratio of their surface area is $=\frac{4\pi r_{1}^{2}}{4\pi r_{2}^{2}}$
$=\frac{r_{1}^{2}}{r_{2}^{2}}=\left ( \frac{r_{1}}{r_{2}} \right )^{2}$
$=\left ( \frac{4}{3} \right )^{2}=\frac{16}{9}$
Hence required ratio is 16: 9
| Class 10 Maths chapter 12 exemplar solutions Exercise: 12.2 Page number: 142-143 Total questions: 8 |
Question:1
Write ‘True’ or ‘False’ and justify your answer in the following:
Two identical solid hemispheres of equal base radius r cm are stuck together along their bases. The total surface area of the combination is $6 \pi r^2$.
Answer:
It is given that there is two hemispheres of radius r.Let A and B be two hemispheres of radius r.
Join A and B along with their bases
Now it is a full sphere of radius r
The total surface area of a sphere $=4 \pi r^{2}$
Here we found that the total surface area of the combination is $4 \pi r^{2}$, but not $6 \pi r^{2}$
Question:2
Write ‘True’ or ‘False’ and justify your answer in the following :
A solid cylinder of radius r and height h is placed over other cylinder of same height and radius. The total surface area of the shape so formed is $4\pi rh + 4\pi r^2.$
Answer:
It is given that there are two cylinders of height h and radius r.
Where one is placed on another then the shape formed is
The total surface area of the shape formed $=2\pi r (r +2h)$
$\text{ [Using the total surface area of cylinder }=2\pi r (r +h)]$
$=2\pi r (r +h)$
$=2\pi r^2 + 4 \pi r h$
So the surface area is not equal to $4\pi rh + 4\pi r^2.$
Question:3
Write ‘True’ or ‘False’ and justify your answer in the following :
A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. The total surface area of the combined solid is$\pi r\left [ \sqrt{r^{2}+h^2}+3r+2h \right ]$
Answer:
It is given that there is a cone of radius r and height h and a cylinder of height h and radius r.
Where A is placed on B
Total surface area = Surface area of cone + Total surface area of cylinder – Surface area of part I – the surface area of part II
$=\pi r (r +l)+2\pi r(r+h)-\pi r^{2}- \pi r^{2}$
$= \pi r (r +\sqrt{r^2 +h^2})+2 \pi r (r+h)-2\pi r ^2 (QI= \sqrt{r^2 +h^2})$
$= \pi r (r +\sqrt{r^2 +h^2}+2r+2h -2r)$
$= \pi r (r +\sqrt{r^2 +h^2}+r+2h )$
Total surface area is not equal to
$\pi r\left [ \sqrt{r^{2}+h^2}+3r+2h \right ]$
Question:4
Write ‘True’ or ‘False’ and justify your answer in the following :
A solid ball is exactly fitted inside the cubical box of side a. The volume of the ball is $\frac{4}{3}\pi a ^{3}$
Answer:
It is given that the ball is exactly filled inside the cubical box of side a.
Hence the diameter of the sphere = a
$\text{ Radius of sphere}$ $=\frac{a}{2}$
$\text{ Volume of sphere}$ $=\frac{4}{3} \pi r^{3}$
$=\frac{4}{3} \pi \left (\frac{a}{2} \right )^{3}$
$=\frac{4}{3} \pi \times \frac{a^3}{8}$
$\text{Volume of sphere}=\frac{\pi a ^{3}}{6}$
$\text{Hence the volume of the sphere is not equal to }\frac{4}{3}\pi a ^{3}$
Hence, the given statement is False.
Question:5
Write ‘True’ or ‘False’ and justify your answer in the following:
The volume of the frustum of a cone is$\frac{1}{3}\pi h\left [ r_{1}^2 +r_{2}^2 -r_{1} r_{2} \right ]$ where h is vertical height of the frustum and $r_{1},r_{2}$ are the radii of the ends.
According to question
In this figure ABCE is a frustum of cone ABD, h is the height of the frustum, and $r_{1},r_{2}$ are the radii of the frustum.
From the figure
$\Delta ADF:\Delta EDF$
$\Rightarrow \frac{DF}{DG}=\frac{AF}{EG}$
$\Rightarrow \frac{h+h'}{h'}=\frac{r_{1}}{r_{2}}$
$\Rightarrow \frac{h}{h'}+1=\frac{r_{1}}{r_{2}}$
$\Rightarrow \frac{h}{h'}=\frac{r_{1}}{r_{2}}-1$
$\Rightarrow \frac{h}{h'}=\frac{r_{1}-r_{2}}{r_{2}}$
$\Rightarrow h^{'} = \frac{r_{2}h}{r_{1}-r_{2}} \; \; \; \; \; \; \; \; \; \; \; \; \; ......(1)$
Volume of frustum ABCE = volume of ABD – volume of ECD
$=\frac{1}{3}\pi r^{2}\left [ h'+h \right ]=\frac{1}{3}\pi r{_{1}}^{2}h'$ $\left ( \therefore \text {Volume of cone }=\frac{1}{3}\pi r^{2}h \right )$
$=\frac{1}{3}\pi r{_{1}}^{2}h'+\frac{1}{3}\pi r{_{1}}^{2}h'-\frac{1}{3}\pi r{_{2}}^{2}h'$
$=\frac{1}{3}\pi \left [ r{_{1}}^{2}h'+ \pi r{_{1}}^{2}h'-\pi r{_{2}}^{2}h' \right ]$
$=\frac{1}{3}\pi \left [ r{_{1}}^{2}h'+ h' \left ( r_{1}^{2} -r_{2}^{2}\right ) \right ]$
$=\frac{1}{3}\pi \left [ r{_{1}}^{2}h'+ h' \left ( r_{1} -r_{2}\right )\left ( r_{1}+r_{2} \right ) \right ]$ $\left [ Q\left ( a^{2}-b^{2} \right )=(a-b)(a+b) \right ]$
$=\frac{1}{3}\pi \left [ r_{1}^{2}h+\frac{r_{2}h}{\left ( r_{1}-r_{2} \right )}\left ( r_{1}-r_{2} \right ) \left ( r_{1}+r_{2} \right ) \right ]$ [ using (1) ]
$=\frac{1}{3}\pi h\left [ r_{1}^{2}+r_{2}^{2}+r_{1}r_{2} \right ]$
Hence the volume of the frustum of the cone is not equal to $=\frac{1}{3}\pi h\left [ r_{1}^{2}+r_{2}^{2}-r_{1}r_{2} \right ]$
Hence, the given statement is false.
Question:6
Write ‘True’ or ‘False’ and justify your answer in the following:
The capacity of a cylindrical vessel with a hemispherical portion raised upward at the bottom as shown in the Figure is $\frac{\pi r^{2}}{3}[3h-2r]$
Solution
It is given that a cylindrical vessel of height h and radius r is raised upward with a hemispherical portion.
From the figure radius of the hemisphere = r cm
The volume of the figure = volume of the cylinder – the volume of the hemisphere
$=\pi r^{2}h - \frac{2}{3}\pi r^{3}$
$=\pi r^{2}\left [h-\frac{2}{3}r \right ]$
$=\pi r^{2}\left [\frac{3h -2r}{3} \right ]$
$=\frac{\pi r^{2}}{3}[3h-2r]$
$\text{Hence the capacity of the vessel is }\frac{\pi r^{2}}{3}[3h-2r]$
So the given statement is True.
Question:7
Write ‘True’ or ‘False’ and justify your answer in the following:
An open metallic bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The surface area of the metallic sheet used is equal to curved surface area of frustum of a cone + area of circular base + curved surfacearea of cylinder
Solution
According to question, here is a metallic bucket in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet.
The surface area of Figure (A) is the surface area of (a), (b), (c)
(a) = curved surface area of frustum
(b) = area of circular base
(c) = curved area of cylinder
Total surface area = curved surface area of a frustum of cone + area of circular base + curved surface are of the cylinder.
So the given statement is True.
| Class 10 Maths Chapter 12 exemplar solutions Exercise: 12.3 Page number: 146-147 Total questions: 14 |
Question:1
Answer 6 cmSolution
It is given that there are three cubes of sides
$a_{1}=3cm , a_{2}=4cm, a_{3}=5cm$
The volume of the cube formed by melting these three cubes = volume of first + volume of second + volume of the third.
Let the edge of the cube formed by melting these three cubes is $a_{4}$ .
$(a_{4})^3=(a_{1})^3+(a_{2})^3+(a_{3})^3$
$\Rightarrow (a_{4})^3=27+64+125$
$\Rightarrow (a_{4})^3=216$
$\Rightarrow (a_{4})^3=(6)^3$
$\Rightarrow a_{4}=6cm$
Hence, the edge of the cube formed is 6 cm.
Question:2
Answer 84Solution
Here the dimensions of a cuboid are
$9cm \times 11cm \times 12cm$
Volume of cuboid $=l \times b \times h$
$=9 \times 11 \times 12$
$=1188cm^3$
The diameter of the shot is 3 cm
Radius of shot $\frac{3}{2}=0.5 cm$
The volume of 1 shot
$=\frac{4}{3}\pi r^3$ $\left (\because \text{volume of sphere}=\frac{4}{3}\pi r^3 \right )$
$=\frac{4}{3}\times (3.14) \times (1.5)^3$
$=\frac{4}{3}\times 3.14 \times (1.5 )^3$
Number of shots
$=\frac{\text{volume of cuboid }}{\text {volume of sphere}}=\frac{1188}{14.13}=84$
Question:3
Answer15 cmSolution
Given :
Volume of bucket = 28.490 liters
Radii of the top $r_{1}=28cm$
Radii of the bottom $(r_2) = 21cm$
Volume of bucket = 28.490 liters
Or
Volume of bucket = 28.490 liters × 1000 $(1L=1000cm^{3})$
=28490 cm3
$\frac{1}{3}\pi h =\left [ r_{1}^2 +r_{2}^2+r_{3}^2\right ]=28490$
( volume of frustum of cone $\frac{1}{3}\pi h \left [ r_{1}^2 +r_{2}^2+r_{3}^2\right ]$ )
$\frac{1}{3} \times 3.14 \times h [(28^2)+(21)^2+28 \times 21]=28490$
$=h[784+441+588]=\frac{28940 \times 3}{3.14}$
$h[1813] = 27219.74$
$\Rightarrow h= \frac{27219.74}{1813}=15$
$\Rightarrow h = 15 cm$
Hence the height of the bucket is 15 cm.
Question:4
Answer 1:7Solution
When a cone is divided into two parts by a plane through the mid-point the image formed is
In figure $\Delta AGE:\Delta EFC$ $Q\angle E$ is common angle $\angle F=\angle G=90^{\circ}$
So the corresponding sides are in equal ratio.
$\frac{EF}{FG}=\frac{FC}{GA}$
$\Rightarrow \frac{ 6}{12} =\frac{ FC}{8}$
$\Rightarrow FC = 4 cm$
Volume of cone $EDC= \frac{1}{3}\pi r_{2}^2h$
$= \frac{1}{3}\times 3.14 \times (4)^2 \times 6=100.48cm^3$
Volume of frustum of a cone
$ABCD =\frac{1}{3}\pi h[r_{1}^2+r_{2}^2 +r_{1}r_{2}]$
$=\frac{1}{3}\times 3.14 \times 6[(8)^2+(4)^2 +8 \times 4]$
$=6.28 [64+16+32]$
$= 6.28[112] = 703.36$
Volume of cone EDC : volume of ABCD
100.48 : 703.36
1 : 7
Question:5
Answer:
It is given that volume of cube = 64 cm3
$a^3=64cm^3$ ( Because the volume of cube = a3 )
$\Rightarrow a^3=4^3$
$\Rightarrow a=4$
So the side of the two cubes are 4 cm
The cuboid formed by joining two cubes.
The surface area of the cuboid $=2(lb +bh+hl)$
$=2(8 \times 4 + 4 \times + 4 \times 8)$
$=2(8 \times 4 +4 \times 4 + 4 \times 8)$
$=2(32+16 +32)$
$=2(80)=160cm^2$
Question:6
Answer 277 cm3Solution
The figure formed when a conical cavity is cut out from a cube.
Volume of cube $=a^3$
$=(7)^3=343 cm^3$
The volume of the conical cavity
$=\frac{1}{3}\pi r^2h$
$=\frac{1}{3}\times 3.14 \times (3)^2 \times 7$ $\left ( \because r=3cm ,h=7cm \right )$
$=21\times 3.14= 66cm^3$
The volume of the remaining solid = volume of the cube – the volume of the conical cavity
$=343-66= 277cm^3$
Question:7
Answer 854 cm2Solution
According to question
Here are two cones joined together along their bases
Height of both cone = 15 cm
Base radius of both cone = 8 cm
Surface area of combination = 2(surface area of one cone)
(Q both cones are same)
$=2(\pi r l)$
$=2\pi r \sqrt{r^2+h^2}$ $\left (Q1= \sqrt{r^2+h^2} \right )$
$= 2 \times 3.14 \times 8 \times \sqrt{64+225}$
$= 2 \times 3.14 \times 8 \times 17$
$=854cm^2$
Hence, the surface area of the combination is 854 cm2
Question:8
Answer 396.18 cm3
Solution
Height of the tube = 21 cm
Base radius of the tube =3cm
Volume of tube $=\pi r ^2h$
$=\frac{22}{7}\times 3\times 3\times21=594cm^3$
Let the height of cone A is h cm
Height of cone $B=21-h cm$
Base radius of both A and B =3 cm
Volume of a cone
$A=\frac{1}{3}\pi r^2h=\frac{1}{}3\pi (3)^2h$
$=3 \pi h$
Volume of a cone
$B=\frac{1}{3}\pi r^2h=\frac{1}{}3\pi (3)^2(21-h)$
$ =3\pi (21-h)$
It is given that the ratio of the volumes is 2: 1
$\Rightarrow \frac{3\pi h}{3 \pi (21-h)}=\frac{2}{1}$
$\Rightarrow h=2(21-h)$
$\Rightarrow h=42-2h$
$\Rightarrow 3h=42$
$\Rightarrow h=14$
Height of cone A = 14 cm
Height of cone B =21-4=7 cm
Volume of cone $A=3 \pi h=3(3.14)(14)$
$=131.88cm^3$
Volume of cone $B = 3\pi (21-h)=2(3.14)(7)$
$=65.94cm^3$
The volume of the remaining portion = Volume of the tube – the volume of cone A – the volume of cone B
$594-131.88 -65.94$
= 396.18 cm3
Volume of remaining portion = 396.18 cm3
Question:9
Answer:
In this figure, there is a hemisphere of radius of 5 cmAnd a cone of radius 5 cm and of height $10-5 = 5 cm$
Volume of cone
$=\frac{1}{3}\pi r^2 h=\frac{1}{3}\times 3.14 \times (5)^2\times 5=130.83cm^3$
Volume of hemisphere
$=\frac{2}{3}\pi r^3$
$=\frac{2}{3}\times 3.14 \times (5)^3=261.66cm^2$
The volume of the complete figure = volume of cone + volume of the hemisphere
$= 130.83 +261.66 = 392.49 cm^3$
$\text{The volume of the unfilled part }=\frac{392.49}{6}=65.41cm^3$
Volume of ice cream = volume of complete figure - volume of unfilled part
$392.49- 65.41=327.08 cm^3$
Hence, the volume of ice cream is 327.08 cm3
Question:10
Answer 150Solution
Given:- Diameter of marble = 1.4 cm
Diameter of beaker = 7cm
Diameter of marble = 1.4 cm
$\text{ Radius of marble}=\frac{1.4}{2}=0.7 cm$
The volume of 1 marble
$=\frac{4}{3} \pi r^3=\frac{4}{3}\pi (0.7)^3$
$=\frac{4}{3} \times 3.14 \times 0.343=1.43cm^3$
Diameter of beaker = 7 cm
$\text{Radius of beaker}=\frac{7}{2}=3.5 cm$
Water level rises(h) = 5.6cm
Volume of water
$=\pi r^2 h=(3.14)(3.5)^2(5.6)$
$=215.40$
$\text{Number of marbles required}=\frac{\text {volume of water }}{\text {volume of 1 marble }}$
$=\frac{215.40}{1.43}=150$
Hence 150 marbles should be dropped into the beaker.
So that the water level rises by 5.6 cm.
Question:11
Answer 1501Solution
It is given that the length, breadth and height of rectangular solid is 66cm, 42cm and 21cm respectively.
Volume of solid rectangular lead piece = $l \times b \times h$
$66 \times 42 \times 21$
$=5821 cm^3$
The diameter of spherical lead shot =4.2
The radius of spherical lead shot
$=\frac{4.2}{2}=2.1 cm$
$\text{ The volume of lead shot }=\frac{4}{3}\pi r^3$
$=\frac{4}{3}\times 3.14 \times (2.1)^3=38.77 cm^3$
$\text{Number of lead shot can be obtained}=\frac{\text {volume of lead piece}}{\text{volume of lead shot}}$
$=\frac{58212}{38.77}=1501$
Hence, 1501 lead shot can be obtained from the lead piece of dimensions 66cm, 42cm and 21cm
Question:12
Answer 2542Solution
Given: Diameter of spherical lead shot = 4 cm
Edge of cube = 44 cm
Volume of cube =a3
=443 (=44 cm)
=85184cm3
Radius of spherical lead shot =2cm
$\text{Volume of lead shot}=\frac{4}{3}\pi r^3$
$=\frac{4}{3}\times 3.14 \times (2)^3=33.5$
$\text{ Number of lead shots}=\frac{\text {volume of cube}}{\text{volume of lead shot}}$
$=\frac{85184}{33.5}=2542$
Hence 2542 lead shots can be made out of a cube of lead whose edge measures 44 cm.
Question:13
Answer 12960
Solution
Length of wall $=24 m =24 \times 100 =2400 cm$ ( because 1m = 100cm )
Breadth of wall $=0.4m =0.4 \times 100 =40 cm$
Height of wall $= 6m = 6 \times 100 = 600cm$
The volume of wall = length × breadth × height
$=2400 \times 40 \times 600$
$=5760000cm^3$
$\text{ Mortar occupied}=\frac{5760000}{10} =5760000cm^3$
Remaining volume = 57600000 – 5760000 = 51840000 cm3
Length of brick = 25 cm
Breadth of brick = 16cm
Height of brick = 10cm
Volume of brick = length × breadth × height
= 25 × 16 × 10 = 4000 cm3
$\text{Number of bricks}=\left [ \frac{\text{remaining volume} }{\text {volume of brick}} \right ]=\frac{5184000}{4000}=12960$
Hence, the number of bricks is 12960.
Question:14
Answer 450Solution
Base diameter of disc = 1.5 cm
Radius of disc $=\frac{1.5}{2}=0.75cm$
Height of disc = 0.2 cm
Volume of disc $= \pi r^2 h = (3.14 )(0.75)^2(0.2)$
$= 0.353 cm^3$
Height of required cylinder = 10 cm
Diameter of required cylinder = 4.5cm
Radius of required cylinder $=\frac{4.5}{2}=2.25cm$
Volume of required cylinder $=\pi r^2 h$
$=3.14 \times (2.25)^2(10)$
$=158.96cm^3$
Number of disc $=\frac{\text{volume of required cylinder }}{\text{volume of disc}}$
$=\frac{158.96}{0.353}=450$
Hence, 450 metallic discs are required to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
| Class 10 Maths Chapter 12 exemplar solutions Exercise: 12.4 Page number: 150-152 Total questions: 20 |
Question:1
Answer h = 28.44 cmSolution
Radius of hemisphere $=8cm$
Volume=
$\frac{2}{3}\times\pi r^3$
$\frac{2}{3}\times\frac{22}{7}\times8\times8\times8$
Radius of cone = 6 cm
Let height = h
Volume = $\frac{1}{3}\times\pi r^2h = \frac{1}{3}\times\frac{22}{7}\times6\times6\times h$
If hemisphere is melted and recast into a right circular cone.
Then, the volume of hemisphere = volume of the cone
$\Rightarrow \frac{2}{3}\times\frac{22}{7}\times8\times8\times8 = \frac{1}{3}\times\frac{22}{7}\times6\times6\times h$
$\Rightarrow 2\times8\times8\times8 = \times6\times6\times h$
$\Rightarrow \frac{2\times8\times8\times8 }{6\times6}= h$
$\Rightarrow \frac{256 }{9}= h$
$\Rightarrow 28.44 = h$
Question:2
Answer h = 8.579mSolution
Length of cuboid = 11m
Breadth = 6m
Height = 5m
$Volume=1\times b\times h$
$=11\times6\times5 = 330m^3$
Radius of cylindrical tank = 3.5m
Let height = h
$\text{Volume }\pi r^2 h = \pi (3.5)^2 h$
To find the height of water level
Volume of cuboid = volume of cylindrical tank
$\Rightarrow 330= \pi (3.5)^2 h$
$\Rightarrow h = \frac{330\times7\times100}{22\times35\times35} = \frac{600}{70} = 8.579m$
Question:3
Answer 37867.5g or 37.867 kgSolution
External Length = 36 cm
Breadth = 25 cm
Height = 16.5 cm
Volume $1\times b\times h$
= 36 × 25 × 16.5
$= 14850 cm^3$
Thickness of iron = 1.5 cm
Internal length $=36 -1.5-1.5$ {subtract border from both sides}
= 33 cm
Breadth $= 25-1.5-1.5 = 22cm$
Height $16.5-1.5-1.5=13cm$
Internal volume =$1\times b\times h$
$33\times22\times13.5 = 9801cm^3$
Volume of iron = external volume – internal volume
$\Rightarrow 14850-9801=5049cm^3$
Weight of one cubic cm of iron = 7.5 g
$\text{Weight of 5049 cm3 of iron }=5049\times7.5 = 37867.5g$
Question:4
The barrel of a fountain pen, cylindrical in shape, is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen is used upon writing 3300 words on average. How many words can be written in a bottle of ink containing one-fifth of a litre?
$\\\text{Volume of the barrel}=\pi r^2h=\frac{22}{7}\times(0.25)^2\times7\\=1.375cm^3=\frac{1.375}{1000}L$
3300 words can be written with 0.001375 L of ink
So with 1L of ink 3300/0.001375 words can be written=2400000
So with 1/5th of a litter 2400000/5 words can be written=48000
Answer:
Mastermind of math class 10thQuestion:5
Answer:
$\text{The diameter of the conical vessel}= 40cm$$\text{Radius}= \frac{40cm}{2} = 20cm$
$\text{Height}=24cm$
$\text{Volume}=\frac{1}{3}\pi r^2 h=\frac{1}{3}\pi\times20\times20\times24 = 3200\pi cm^3$
Diameter of water that flows out of cylinder = 5mm
$\text{Radius}=\frac{5}{10\times2}=\frac{5}{20}$
(Because 1 cm = 10mm)
$\text{Height}=10m=1000cm$ ( Because 1m =100cm)
$\text{Volume}=\pi r^2h=\pi\times\frac{5}{20}\times\frac{5}{20}\times1000\Rightarrow \frac{125}{2}\pi cm^3$
$\text{Time required}=\frac{\text {volume of conical flask}}{\text{volume of cylindrical water}}=\frac{3200\pi}{125\pi}\times2$
$\Rightarrow \frac{640\times2}{25}\Rightarrow \frac{1280}{25}=51.2\ minutes$
Question:6
Answer 74.18 m3, 67.11 m2Solution
$\text{Height of cone}=3.5 m$
$\text{Diameter}=9 m$
$\text{Radius}=\frac{9}{2}= 4.5m$
$\text{Volume}=\frac{1}{3}\pi r^2h=\frac{1}{3}\times\frac{22}{7}\times(4.5)^{2}\times3.5=74.18m^3$
$\text{Canvas cloth required to covers the heap}=\pi r l$
Here l is slant height
$1=\sqrt{r^2+h^2}=\sqrt{(4.5)^2+(3.5)^2}\Rightarrow 4.75$
Curved surface area is $=\pi r l$
$=3.14\times4.5\times4.75 = 67.11m^2$
Hence 67.11m2 canvas cloth is required to just cover the heap.
Question:7
Answer Rs. 2250Solution
Given
$\text{Circumference of base}=1.5cm$
$2\pi r=1.5cm$
$r=\frac{1.5}{2\times22}\times7$
$r=\frac{15\times7}{10\times44}=\frac{105}{440}=0.2386cm$
$\text{Radius }=0.2386cm$
$\text{Height}=25cm$
$\text{Curved surface area of one pencil}=2\pi r h$
$=2\times\frac{22}{7}\times0.2386\times25=\frac{262.46}{7}$
$=37.49cm^2$
$1cm=\frac{1}{10}dm$
$\Rightarrow \frac{37.49}{100}dm^2=0.3749dm^2$
$=0.375dm^2$
$\text{Curved surface area of 120000 pencils}=0.375\times120000=45000dm^2$
Cost of coloring 1 dm2 in one day =0.05 Rs
Cost of coloring 45000 dm2=0.05 x 45000
= 2250 Rs.
Question:8
Answer 2 hoursSolution
Length of cuboidal pond = 50m
Breadth = 44 m
$\text{Height}=21 cm =\frac{21}{100}m$
$\text{Volume}=l \times b \times h$
$=50 \times 44 \times \frac{21}{100}$
Speed of water = 15 km per hour = 15000 m
$\text{The diameter of the cylindrical pipe }=14 cm =\frac{14}{100}m$
$\text{Radius} =\frac{7}{100}m$
$\text{Volume}=\pi r^2 h$
$=\frac{22}{7}\times \frac{7}{100}\times \frac{7}{100}\times 15000 = 213m^3$
$\text{Time required}=\frac{\text{volume of cuboid pond}}{\text{volume of cylindrical pipe}}$
$=\frac{462}{231}=2hours$
Question:9
Answer:
Answer 112mSolution
Length of cuboidal block = 4.4m
Breadth = 2.6 m
Height = 1 m
Volume $=l \times b \times h$
$= 4.4 \times 2.6 \times 1$
$= 4.4 \times 2.6 \times m^3$
Radius of cylindrical pipe r1 = 30cm = 0.3m
r2 = 30+5 = 35cm = 0.35 m
Let, Height h1
Volume $=\pi r ^2 h$
$=\frac{22}{7}\times h_{1} \left ( (0.35)^2-(0.3)^2 \right )$
The volume of cuboid = volume of the cylindrical pipe
$=4.4 \times 2.6\times \frac{22}{7}\times h_{1}\left [ \left ( \frac{35}{100} \right )^2 -\left ( \frac{30}{100} \right )^2 \right ]$
$=\frac{44}{10} \times \frac{26}{10}\times \frac{22}{7}\times h_{1}\left [\frac{(35-30) (35+30)}{(100)^2} \right ]$ $\left (a^2-b^2)=(a-b)(a+b) \right )$
$h_{1}=\frac{44}{10} \times \frac{26}{10}\times \frac{7}{22}\times \frac{100 \times 100}{5 \times 65}$
$h_{1}=112m$
Question:10
Answer:
Length of cuboidal pond = 80mBreadth = 50 m
Let, Height = h
$\text{Volume}\ =l \times b \times h$
$80 \times 50 \times h=400 h m^3$
Average water of one person =0.04m3
Average water of 500 persons = $0.04 \times 500$
According to question
The volume of cuboidal pond = Average water of 500 persons
$400 h =0.04 \times 500$
$h = 4 \times \frac{500 }{100\times 400}=\frac{5}{100}=0.05m$
Question:11
Answer 487.6 cm3Solution
Length of cuboidal box = 16 cm
Breadth = 8cm
Height = 8 cm
$\text{Volume}=16 \times 8 \times 8$
Radius of sphere = 2 cm
$\text{Volume of sphere }=\frac{4}{3}\pi r^3$
$=\frac{4}{3}\times \frac{22}{7}\times 2\times 2\times 2 =33.5238cm^3$
$\text{ The volume of 16 sphere}=16 \times 33.5238$
$=536.3808$
The volume of liquid = volume of the cuboidal box – the volume of 16 spheres
$=1024 -536.3808$
$=487.6cm^3$
Question:12
Answer 230.10 Rs.Solution
Upper radius of frustum of cone (R) = 20cm
Lower radius of frustum of cone r = 8cm
Height (h)= 16cm
Volume =$\frac{\pi h}{3}[R^2+r^2+Rr]$
$=\frac{22 \times 16}{7 \times 3}(20^2+8^2+20 \times 8)$
$=\frac{22 \times 16}{21}(400 + 64+160)$
$=\frac{22 \times 16}{21}(624)$
$=\frac{22 \times 16\times 208}{7}=10459.428 m^3$
= 10.459 liter
Cost of 1 liter milk = 22 Rs.
Cost of 10.459 liter milk =$22 \times 10.459$
= 2301.10 Rs
Question:13
Answer:
r = 36 cm, $l = 12\sqrt{13} cm$Height of cylindrical bucket (h1) = 32 cm
Radius (r1) = 18 cm
Volume = $\pi r{_{1}}^{2}h_{1}$
$=\frac{22}{7}\times 18 \times 18 \times 32$
Height of conical heap (h2) = 24 cm
Let radius = r2
Volume $=\frac{1}{3}\pi r_{2}^{2}h_{2}=\frac{1}{3}\times \frac{22}{7} \times r_{2}^{2}\times 24$
According to question
Volume of cylindrical bucket = Volume of conical heap
$\Rightarrow \frac{22}{7}\times 18 \times 18 \times 32 = \frac{1}{3}\times \frac{22}{7}\times r_{2}^{2}\times 24$
$\Rightarrow \frac{18 \times 18 \times 32 \times 3}{24}=r_{2}^{2}$
$\Rightarrow 18^{2}\times 4 = r_{2}^{2}$
$\Rightarrow r_{2}=\sqrt{18 \times 18 \times 2 \times 2}$
$\Rightarrow r_{2}= 18 \times 2 = 36\; cm$
Slant height $(l)=\sqrt{r_{2}^{2}+h_{2}^{2}}$
$\sqrt{36^{2}+24^{2}}$
$=\sqrt{1296+576}$
$=\sqrt{1872}$
$\sqrt{12 \times 12 \times 13}$
$l=12\sqrt{13}cm$
Question:14
Answer:
Diameter of cylinder = 6 cmRadius = 3 cm
Height = 12 cm
$\text{Surface are}$ $=2 \pi r h = 2\pi \times 3 \times 12 = 72 \pi cm^2$
Similarly radius of circle = 3 cm
$\text{Area}$ $=\pi r^2=\pi 3 \times 3 = 9 \pi cm^2$
Slant height of cone (l)=5cm
Radius = 3 cm
$\text{Surface area}=\pi r l =\pi \times 5 \times 3 = 15\pi cm^2$
Total surface area = area of cylinder + area of circle + area of the cone
$=72\pi + 9 \pi + 15 \pi$
$=96\pi$
$=96\times 3.14=301.7 cm^2$
Slant height (l) = 5cm
We know that,
$h^2+r^2=l^2$
$h^2+3^2=5^2$
$\\h^2= 25 -9 \\ h^2=16 \\\ h = 4$
$\text{Volume of cylinder= }\pi r^2 h \\ = \pi \times 3 \times 3 \times 12 = 108 \pi cm^3$
$\\\text{Volume of cone}=\frac{1}{3}\pi r^2 h \\ = \frac {1}{3} \pi \times 3 \times 3 \times 12 = 12 \pi cm^3$
$\text{Volume of rocket }$$=180 \pi + 12 \pi$
$=120 \pi$
$=120 \times 3.14 =377.14 cm^3$
Question:15
Answer:
Given: Volume of building
$41\frac{19}{21}=\frac{880}{21}$
Let total height above the floor = h
Hemisphere‘s diameter = h (given)
$\text{Radius} =\frac{h}{2}$
$\text{Volume}=\frac{2}{3}\pi r^3=\frac{2}{3}\pi \left ( \frac{h}{2} \right )^3$
Height of cylinder = total height – the height of hemisphere
$h-\frac{h}{2}=\frac{h}{2}$
Volume $\pi r^2 h=\pi \times \left (\frac{h}{2} \right )^2 \times \frac{h}{2} =\pi \left (\frac{h}{2} \right )^3$
According to question
The volume of building = Volume of cylinder + volume of the hemisphere
$\Rightarrow \frac{880}{21}=\left ( \frac{h}{2} \right )^3\left [ \pi + \frac{2}{3} \pi \right ]$
$\Rightarrow \frac{880}{21}=\left ( \frac{h}{2} \right )^3\left [ \frac{3\pi +2\pi }{3} \right ]$
$\Rightarrow \frac{880 \times 2^3}{21}=h^3 \left [ \frac{5\pi }{3} \right ]$
$\Rightarrow \frac{880 \times 2\times 2\times 2\times 7\times 3}{21\times 5\times 22}=h^3$
$\Rightarrow h^3 = 2 \times 2 \times 2\times 2\times 2\times 2$
$\Rightarrow h = \sqrt[3]{2 \times 2 \times 2\times 2\times 2\times 2}$
$\Rightarrow h = 2 \times 2$
$\Rightarrow h=4m$
Question:16
Answer:
The radius of the hemispherical bowl = 9 cm$Volume =\frac{2}{3}\pi r^3$ $=\frac{2}{3} \times \frac{22}{7}\times 9\times 9\times 9$
Radius of cylindrical bottle = 1.5 cm
Height = 4cm
$Volume$$=\pi r^2h$
$=\frac{22}{7}\times \frac{15}{10}\times \frac{15}{10}\times 4$
$\text{ Number of bottles needed}=\frac{\text {volume of hemispherical bowl}}{\text {volume of cylindrical bottle}}$
$=\frac{2}{3} \times \frac{22}{7}\times 9\times 9\times 9$
$=\frac{22}{7}\times \frac{15}{10}\times \frac{15}{10}\times 4$
$=\frac{2 \times 9 \times 9 \times \times 10 \times 10}{3 \times 15 \times 15 \times 4} =54$
Question:17
Answer:
Height of cone = 120cmRadius =60cm
Volume =$\frac{1}{3}\pi r^2 h$
$=\frac{1}{3}\pi( 60)^2 120$
$=452571.43cm^3$
Height of cylinder = 180
Radius = 60 cm (given that radius of the cylinder is equal to the radius of the cone)
$Volume=\pi r^2 h$
$=\pi( 60)^2 180=2036571.43cm^3$
Volume of water left in the cylinder = volume of cylinder – volume of cone
2036571.43 – 452571.43
= 1584000 cm3
Or 1.584 m3 [1m = 100cm]
2m3 (approximate)
Question:18
Answer:
Radius of cylindrical pipe = 1 cmHeight = 80 cm
Volume=$\pi r ^2 h$
$=\frac{22}{7} \times 1 \times 1 \times 80 = 251.4285 cm^3 /sec$
In half an hour volume of water is
$=251.4285 \times30 \times60 = 452571.5 cm^3$
Radius of cylindrical tank = 40 cm
Let height = h
Volume $=\pi r ^2 h$
$\frac{22}{7}\times (40)^2 h= 5828.5714 cm^3$
According to question
The volume of cylindrical pipe = volume of the cylindrical tank
$= 452571.5 = 5028.5714h$
$\frac{452571.5}{5028.5714} = h$
h =89.99
h = 90 cm (approximate)
Question:19
Answer:
The radius of the cylindrical vessel$=\frac{2}{2}=1cm$
Height = 3.5 cm
$\text{ Volume}$ $=\pi r^2 h=\frac{22}{7}\times 1 \times 1 \times \frac{35}{10}=11m^3$
Let the height of rainfall = x
Length = 22m
Breadth = 20m
Volume=$ l \times b \times h$
$= 22 \times 20 \times x$
Rainfall = volume of water = volume of the cylindrical vessel
$22 \times 20 \times x=11$
$x=\frac{11}{22 \times 20}=\frac{1}{40}=0.025 m$
x=0.025 m
Or x= 2.5cm [1 m = 100 cm]
Hence the rainfall is in 2.5 cm
Question:20
Answer:
Radius of conical depression = 0.5 cmDepth = 2.1 cm
Volume=$\frac{1}{3}\pi r^2 h$
$=\frac{1}{3}\times \frac{22}{7} \times (0.5)^2 \times 2.1$
$=0.55cm^3$
$\therefore$the volume of 4 cones $=4 \times 0.55=2.2cm^3$
Edge of cube = 3
The volume of cube =33 ( Because the volume of cube = a3 )
Length of cuboid = 10 cm
Breadth = 5 cm
Height = 4 cm
Volume $=l \times b \times h$
$=10 \times 5 \times 4=200 cm^3$
Volume of wood = volume of cuboid – volume of cube - volume of 4 cones
=200 - 2.2 -27 = 170.8 cm3
NCERT Exemplar Solutions Class 10 Maths Chapter 12 Important Topics:
NCERT exemplar Class 10 chapter 12 Maths solutions covers the following topics:
- Surface area and Volume up of frustum.
- Area and volume of multiple composite bodies made by known structures.
- NCERT exemplar Class 10 Maths solutions chapter 12 discusses the method to find out curved surface area and total surface area.
NCERT Class 10 Exemplar Solutions for Other Subjects:
NCERT Class 10 Maths Exemplar Solutions for Other Chapters:
Importance of NCERT Exemplar Class 10 Maths Solutions Chapter 12:
- These Class 10 Maths NCERT exemplar chapter 12 solutions emphasize finding out curved surface area, total surface area, and volume of various three-dimensional objects such as cones, cylinders, and spheres. These calculations and learning will be helpful in Physics and Maths of higher classes and are essential for both medical and engineering aspirants.
- The expressive nature of these solutions provides the students a perfect environment to attempt and practice Surface Areas and Volumes-based practice problems. The Class 10 Maths NCERT exemplar solutions chapter 12, Surface Areas and Volume, consists of plenty of practice problems.
NCERT exemplar Class 10 Maths solutions chapter 12 pdf download is a free-to-use feature that provides the students with the facility to study the NCERT exemplar Class 10 Maths chapter 12 in an offline environment.
Check Chapter-Wise Solutions of Book Questions
Must Read NCERT Solution Subject Wise
Here, you can find solutions to NCERT class 10 Maths and Science.
Check NCERT Notes Subject Wise
Here, you can find notes of NCERT class 10 Maths and Science.
Also, check the NCERT Books and the NCERT Syllabus here
Here, you can find the syllabus and books of the NCERT class 10 Maths and Science.
Frequently Asked Questions (FAQs)
Q: How to find out the volume of an ice cream cone?
A:
Ice cream cones can be seen as a combination of a hemisphere and a cone in simplified form. We know the volume of cone and volume of the hemisphere, so we can find out its complete volume.
Q: How to find out the volume of a sharpened pencil?
A:
We can find out the volume of sharpened pencil by assuming it as a combination of cylinder and a cone.
Q: Is the chapter Surface Areas and Volumes important for Board examinations?
A:
The chapter Surface Areas and Volumes is vital for Board examinations as it holds around 8-10% weightage of the whole paper.
Q: What are the critical topics of Surface Areas and Volumes from a board examination perspective?
A:
It is highly suggested that students practice and study every topic covered in NCERT exemplar Class 10 Maths solutions chapter 12 to score high in Surface Areas and Volumes.
Articles
Related Stories
|
Upcoming School Exams
Certifications By Top Providers
Explore Top Universities Across Globe
Questions related to CBSE Class 10th
On Question asked by student community
Have a question related to CBSE Class 10th ?
HELLO,
If you want admission to 9th grade under the CBSE board in Andhra Pradesh , visit nearby CBSE affiliated schools during the admission period that is generally from January to April or you can check the official websites of the schools in which you are interested for admission if they are accepting the admissions now .
After deciding the school and getting information about admission deadline from the school you can fill out the admission form with documents submission like your previous report card , transfer certificate and birth certificate , they make take entrance test or interview to confirm your admission
To know more visit :- https://school.careers360.com/schools/cbse-schools-in-andhra-pradesh
Hope this Helps!
Hello,
From the below website, you can get the CBSE Maths Sample paper of class 10.
https://school.careers360.com/boards/cbse/cbse-class-10-sample-papers-2025-26
Visit the below website to obtain the previous year question papers of class 10 CBSE.
https://school.careers360.com/boards/cbse/cbse-previous-year-question-papers-class-10
By solving both sample papers and previous year question papers, you can score well in your examination.
All the best.
Hello,
From the below website, you can get the sample papers of CBSE class 10 Hindi subject.
https://school.careers360.com/boards/cbse/cbse-class-10-sample-papers-2025-26
You'll also get sample papers of other subjects. Refer them to prepare well.
Hello,
If you're from Karnataka Board, then visit the below website to get the key answers of Social Science question paper of SA 1 of class 10.
https://school.careers360.com/boards/kseeb/karnataka-sslc-mid-term-exam-question-paper-2025-26
Let us know if you're from a different board.
Hello,
Since you applied over a month and a half ago and haven't received your 10th-grade certificate, the best course of action is to check the status of your application on the official website. If that doesn't yield results, you should contact your school and the relevant education board's regional office for an update.
I hope it will clear your query!!
Popular CBSE Class 10th Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
CBSE Class 10th Notifications
Never miss an CBSE Class 10th update
Get timely CBSE Class 10th updates directly to your inbox. Stay informed!