NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry

NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry: Download PDF

The NCERT Solutions for Class 10 Maths Chapter 7 have been prepared by Careers360 experts to make learning simpler and to help you score better in exams. A downloadable PDF is available — click the link below to access it.

Download PDF

NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry (Exercise)

Below, you will find the NCERT Class 10 Maths Chapter 7 Coordinate Geometry question answers explained step by step.

Q1 (i): Find the distance between the following pairs of points : (2, 3), (4, 1)

Answer:

Given points: (2, 3), (4, 1)

Distance between the points will be: $(x_{1},y_{1})$ and $(x_{2},y_{2})$

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

$⇒D= \sqrt{(4-2)^2+(1-3)^2} = \sqrt{4+4} = 2\sqrt{2}$

Q1 (ii): Find the distance between the following pairs of points : (– 5, 7), (– 1, 3)

Answer:

Given points: (– 5, 7), (– 1, 3)

Distance between the points will be: $(x_{1},y_{1})$ and $(x_{2},y_{2})$

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

$⇒D= \sqrt{(-1+5)^2+(3-7)^2} = \sqrt{16+16} = 4\sqrt{2}$

Q1 (iii): Find the distance between the following pairs of points :(a, b), (– a, – b)

Answer:

Given points: (a, b), (– a, – b)

Distance between the points will be: $(x_{1},y_{1})$ and $(x_{2},y_{2})$

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

$⇒D= \sqrt{(-a-a)^2+(-b-b)^2} = \sqrt{4(a^2+b^2)} = 2\sqrt{a^2+b^2}$

Q2: Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B discussed in Section 7.2?

Answer:

Given points: (0, 0) and (36, 15)

Distance between the points will be: $(x_{1},y_{1})$ and $(x_{2},y_{2})$

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

$⇒D= \sqrt{(36-0)^2+(15-0)^2} =\sqrt{1296+225} = \sqrt{1521} = 39$

The distance between the two towns A and B is, thus, 39 km for the given town location

$(0,0)$ and $(36,15)$.

Q3: Determine if the points (1, 5), (2, 3), and (– 2, – 11) are collinear.

Answer:

Let the points (1, 5), (2, 3), and (– 2, – 11) represent the vertices A, B, and C of the given triangle, respectively.

$A = (1,5),\ B = (2,3),\ C = (-2,-11)$

Therefore,

$AB = \sqrt{(1-2)^2+(5-3)^2} = \sqrt{5}$

$BC = \sqrt{(2-(-2))^2+(3-(-11))^2} = \sqrt{4^2+14^2} = \sqrt{16+196} = \sqrt{212}$ $CA = \sqrt{(1-(-2))^2+(5-(-11))^2} = \sqrt{3^2+16^2} = \sqrt{9+256} = \sqrt{265}$ Since these are not satisfied.

$AB+BC \neq CA$

$BA+AC \neq BC$

$BC+CA \neq BA$

As these cases are not satisfied.
Hence, the points are not collinear.

Q4: Check whether (5, – 2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.

Answer:

The distance between two points $A(x_{1},y_{1})$ and $B(x_{2},y_{2})$ is given by:

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

So, we have the following points: (5, – 2), (6, 4) and (7, – 2), assuming them to be the vertices of triangles A, B, and C, respectively.

$AB = \sqrt{(5-6)^2+(-2-4)^2} = \sqrt{1+36} = \sqrt{37}$

$BC = \sqrt{(6-7)^2+(4+2)^2} = \sqrt{1+36} = \sqrt{37}$

$CA = \sqrt{(5-7)^2+(-2+2)^2} = \sqrt{4+0} = 2$

Therefore, AB = BC

Here, the two sides are equal in length.

Therefore, ABC is an isosceles triangle.

Q5: In a classroom, 4 friends are seated at points A, B, C and D, as shown in Fig. 7.8. Champa and Chameli walk into the class, and after observing for a few minutes, Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using the distance formula, find which of them is correct.

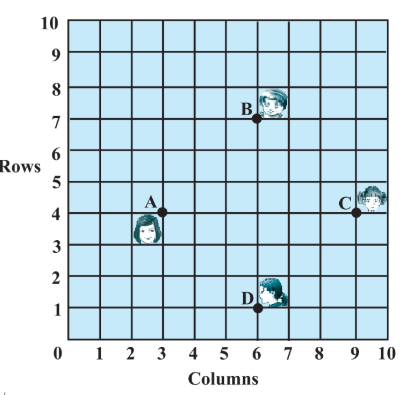
Answer:

The coordinates of the points:

$A(3,4),\ B(6,7),\ C(9,4),$ and $D(6,1)$ are the positions of 4 friends.

The distance between two points $A(x_{1},y_{1}),$ and $B(x_{2},y_{2})$ is given by:

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

Hence,

$AB = \sqrt{(3-6)^2+(4-7)^2} = \sqrt{9+9} = \sqrt{18} = 3\sqrt2$

$BC = \sqrt{(6-9)^2+(7-4)^2} = \sqrt{9+9} = \sqrt{18} = 3\sqrt2$

$CD = \sqrt{(9-6)^2+(4-1)^2} = \sqrt{9+9} = \sqrt{18} = 3\sqrt2$

$AD= \sqrt{(3-6)^2+(4-1)^2} = \sqrt{9+9} = \sqrt{18} = 3\sqrt2$

And the lengths of diagonals:

$AC = \sqrt{(3-9)^2+(4-4)^2} =\sqrt{36+0} = 6$

$BD = \sqrt{(6-6)^2+(7-1)^2} =\sqrt{36+0} = 6$

So, here it can be seen that all sides of the quadrilateral ABCD are of the same length, and the diagonals are also of the same length.

Therefore, quadrilateral ABCD is a square, and Champa is right.

Q6 (i): Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer: (– 1, – 2), (1, 0), (– 1, 2), (– 3, 0)

Answer:

Let the given points $(-1,-2),\ (1,0),\ (-1,2),$ and $(-3,0)$ represent the vertices A, B, C, and D of the given quadrilateral, respectively.

The distance formula:

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

$AB= \sqrt{(-1-1)^2+(-2-0)^2} =\sqrt{4+4} = \sqrt{8} = 2\sqrt2$

$BC= \sqrt{(1+1)^2+(0-2)^2} =\sqrt{4+4} = \sqrt{8} = 2\sqrt2$

$CD= \sqrt{(-1+3)^2+(2-0)^2} =\sqrt{4+4} = \sqrt{8} = 2\sqrt2$

$AD= \sqrt{(-1+3)^2+(-2-0)^2} =\sqrt{4+4} = \sqrt{8} = 2\sqrt2$

Finding the length of the diagonals:

$AC= \sqrt{(-1+1)^2+(-2-2)^2} =\sqrt{0+16} = 4$

$BD= \sqrt{(1+3)^2+(0-0)^2} =\sqrt{16+0} = 4$

It is clear that all sides are of the same length, and also, the diagonals have the same length.

Hence, the given quadrilateral is a square.

Q6 (ii): Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer: (–3, 5), (3, 1), (0, 3), (–1, – 4)

Answer:

Let the given points $(-3,5),\ (3,1),\ (0,3),$ and $(-1,-4)$ represent the vertices A, B, C, and D of the given quadrilateral, respectively.

The distance formula:

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

$AB= \sqrt{(-3-3)^2+(5-1)^2} =\sqrt{36+16} = \sqrt{52} = 2\sqrt{13}$

$BC= \sqrt{(3-0)^2+(1-3)^2} =\sqrt{9+4} = \sqrt{13}$

$CD= \sqrt{(0+1)^2+(3+4)^2} =\sqrt{1+49} = \sqrt{50} = 5\sqrt2$

$AD= \sqrt{(-3+1)^2+(5+4)^2} =\sqrt{4+81} = \sqrt{85}$

All the sides of the given quadrilateral have different lengths.

Therefore, it is only a general quadrilateral and not a specific one like a square, rectangle, etc.

Q6 (iii): Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer: (4, 5), (7, 6), (4, 3), (1, 2)

Answer:

Let the given points $(4,5),\ (7,6),\ (4,3),\ (1,2)$ represent the vertices A, B, C, and D of the given quadrilateral, respectively.

The distance formula:

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

$AB= \sqrt{(4-7)^2+(5-6)^2} =\sqrt{9+1} = \sqrt{10}$

$BC= \sqrt{(7-4)^2+(6-3)^2} =\sqrt{9+9} = \sqrt{18}$

$CD= \sqrt{(4-1)^2+(3-2)^2} =\sqrt{9+1} = \sqrt{10}$

$AD= \sqrt{(4-1)^2+(5-2)^2} =\sqrt{9+9} = \sqrt{18}$

And the diagonals:

$AC =\sqrt{(4-4)^2+(5-3)^2} = \sqrt{0+4} = 2$

$BD =\sqrt{(7-1)^2+(6-2)^2} = \sqrt{36+16} = \sqrt{52} = 2\sqrt{13}$

Here, we can observe that the opposite sides of this quadrilateral are of the same length.

However, the diagonals are of different lengths.

Therefore, the given points are the vertices of a parallelogram.

Q7: Find the point on the x-axis which is equidistant from (2, –5) and (–2, 9).

Answer:

Let the point which is equidistant from $A(2,-5)\ and \ B(-2,9)$ be $X(x,0)$ as it lies on X-axis.

Then, we have,

Distance AX $= \sqrt{(x-2)^2+(0+5)^2}$

and Distance BX $= \sqrt{(x+2)^2+(0+9)^2}$

According to the question, these distances are equal in length.

Hence, we have,

$\sqrt{(x-2)^2+(0+5)^2}$ $= \sqrt{(x+2)^2+(0+9)^2}$

Squaring both sides, we get,

$(x-2)^2+25 = (x+2)^2+81$
$⇒x^2-4x+4+25=x^2+4x+4+81$
$⇒4x+4x=-81+25$
$⇒8x=-56$
$\therefore x=-7$

Hence, the point is $X(-7,0)$.

Q8: Find the values of y for which the distance between the points P(2, – 3) and Q(10, y) is 10 units.

Answer:

Given the distance between the points $P(2,-3)$ and $Q(10,y)$ is 10 units.

The distance formula :

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

So, given $PQ = 10$ units

$PQ= \sqrt{(10-2)^2+(y-(-3))^2} = 10$

After squaring both sides,

$\Rightarrow (10-2)^2+(y-(-3))^2 = 100$

$\Rightarrow (y+3)^2 = 100 - 64$

$\Rightarrow y+3 = \pm 6$

$\Rightarrow y = 6 - 3$ or $y = -6-3$

Therefore, the values are $y = 3$ or $y=-9$.

Q9: If Q(0, 1) is equidistant from P(5, –3) and R(x, 6), find the values of x. Also, find the distances QR and PR.

Answer:

Given $Q(0,1)$ is equidistant from $P(5,-3)$ and $R(x,6)$ .

Then, the distances $PQ = RQ$.

Distance $PQ = \sqrt{(5-0)^2+(-3-1)^2} = \sqrt{25+16} = \sqrt{41}$

Distance $RQ = \sqrt{(x-0)^2+(6-1)^2} = \sqrt{x^2+25}$

$\Rightarrow \sqrt{x^2+25} = \sqrt{41}$

Squaring both sides, we get,
$⇒x^2+25=41$

$\Rightarrow x^2 = 16$

$\Rightarrow x = \pm 4$

The points are: $R(4,6)\ or\ R(-4,6.)$

CASE I: when R is $(4,6)$

The distances QR and PR.

$QR = \sqrt{(0-4)^2+(1-6)^2} = \sqrt{16+25} = \sqrt{41}$

$PR = \sqrt{(5-4)^2+(-3-6)^2} = \sqrt{1^2+(-9)^2} = \sqrt{1+81} = \sqrt{82}$

CASE II: when R is $(-4,6)$

The distances QR and PR.

$QR = \sqrt{(0-(-4))^2+(1-6)^2} = \sqrt{16+25} = \sqrt{41}$

$PR = \sqrt{(5-(-4))^2+(-3-6)^2} = \sqrt{9^2+(-9)^2} = \sqrt{81+81} = 9\sqrt{2}$

Q10: Find a relation between x and y such that the point (x, y) is equidistant from the points (3, 6) and (– 3, 4).

Answer:

Let the point $P(x,y )$ is equidistant from $A(3,6)$ and $B(-3,4)$ .

Then, the distances $AP =BP$

$AP = \sqrt{(x-3)^2+(y-6)^2}$ and $BP = \sqrt{(x-(-3))^2+(y-4)^2}$

$\Rightarrow \sqrt{(x-3)^2+(y-6)^2} = \sqrt{(x-(-3))^2+(y-4)^2}$

Squaring both sides, we obtain

$\Rightarrow (x-3)^2+(y-6)^2= (x+3)^2+(y-4)^2$

$\Rightarrow (2x)(-6)+(2y-10)(-2)= 0$ $\left [\because a^2-b^2 = (a+b)(a-b) \right ]$

$\Rightarrow -12x-4y+20 = 0$

$\Rightarrow 3x+y-5 = 0$

Thus, the relation is $3x+y-5 = 0$ between x and y.

Q1: Find the coordinates of the point which divides the join of (–1, 7) and (4, –3) in the ratio 2 : 3.

Answer:

Let the coordinates of point $P(x,y)$ which divides the line segment joining the points $A(-1,7)$ and $B(4,-3)$ , internally, in the ratio $m_{1}:m_{2}$ then,

Section formula: $\left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )$

Substituting the values in the formula:

Here, $m_{1}:m_{2} = 2:3$

$\Rightarrow \left (\frac{2(4)+3(-1)}{2+3} , \frac{2(-3)+3(7)}{2+3} \right )$

$\Rightarrow \left (\frac{5}{5} , \frac{15}{5} \right )$

$⇒(1,3)$

Hence, the coordinate is $P \left (1, 3 \right )$.

Q2: Find the coordinates of the points of trisection of the line segment joining (4, –1) and (–2, –3).

Answer:

Let the trisection of the line segment $A(4,-1)$ and $B(-2,-3)$ have the points $P(x_{1},y_{1})$ and $Q(x_{2},y_{2})$

Then,

Section formula: $\left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )$

By observation point, P divides AB internally in the ratio $1:2$.

Hence, $m:n = 1:2$

Substituting the values in the equation, we get;

$\Rightarrow P\left (\frac{1(-2)+2(4)}{1+2} , \frac{1(-3)+2(-1)}{1+2} \right )$

$\Rightarrow P \left (\frac{-2+8}{3} , \frac{-3-2}{3} \right )$

$\Rightarrow P \left (2 , \frac{-5}{3} \right )$

And by observation point Q, divides AB internally in the ratio $2:1$

Hence, $m:n = 2:1$

Substituting the values in the equation above, we get

$\Rightarrow Q\left (\frac{2(-2)+1(4)}{2+1} , \frac{2(-3)+1(-1)}{2+1} \right )$

$\Rightarrow Q \left (\frac{-4+4}{3} , \frac{-6-1}{3} \right )$

$\Rightarrow Q\left (0 , \frac{-7}{3} \right )$

Hence, the points of trisections are $P \left (2 , \frac{-5}{3} \right )$ and $Q\left (0 , \frac{-7}{3} \right )$

Q3: To conduct Sports Day activities in your rectangular-shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1m each. 100 flower pots have been placed at a distance of 1m from each other along AD, as shown in Fig. 7.12. Niharika runs $\frac14$th the distance AD on the 2nd line and posts a green flag. Preet runs $\frac15$th the distance AD on the eighth line and posts a red flag. What is the distance between both flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag

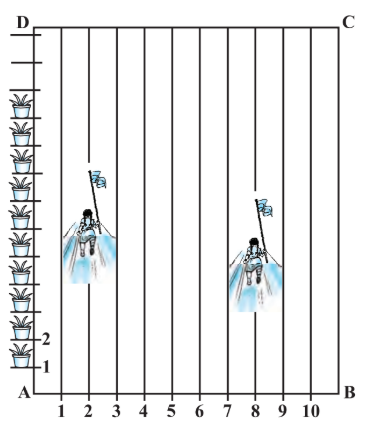
Answer:

Niharika posted the green flag at the distance P, i.e.,

$\frac{1}{4}\times100\ m = 25\ m$ from the starting point of $2^{nd}$ line.

Therefore, the coordinates of this point $P$ are $(2,25).$

Similarly, Preet posted red flag at $\frac{1}{5}$ of the distance Q i.e.,

$\frac{1}{5}\times100\ m = 20\ m$ from the starting point of $8^{th}$ line.

Therefore, the coordinates of this point Q are $(8,20)$.

The distance $PQ$ is given by,

$PQ = \sqrt{(8-2)^2+(25-20)^2} = \sqrt{36+25} = \sqrt{61} m$

and the point at which Rashmi should post her Blue Flag is the mid-point of the line joining these points. Let this point be $R(x,y)$.

Then, by the Section Formula,

$P(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )$

$⇒x = \frac{2+8}{2},\ y = \frac{25+20}{2}$

$⇒x = 5,\ y = 22.5$

Therefore, Rashmi should post her Blue Flag at 22.5 m on the 5th line.

Q4: Find the ratio in which the line segment joining the points (– 3, 10) and (6, – 8) is divided by (– 1, 6).

Answer:

Let the ratio be $k:1$

Then, by the section formula:

$P(x,y) = \left (\frac{kx_{2}+x_{1}}{k+1} , \frac{ky_{2}+y_{1}}{k+1} \right )$

Given point $P(x,y) = (-1,6)$

$-1 = \frac{6k-3}{k+1}$

$\Rightarrow -k-1 = 6k-3$

$\Rightarrow k = \frac{2}{7}$

Hence, the point $P$ divides the line AB in the ratio $2:7$.

Q5: Find the ratio in which the line segment joining A(1, – 5) and B(– 4, 5) is divided by the x-axis. Also, find the coordinates of the point of division.

Answer:

Let the point on the x-axis be $P(x,0)$, and it divides it in the ratio $k:1$.

Then, we have

Section formula:

$P(x,y) = \left (\frac{kx_{2}+x_{1}}{k+1} , \frac{ky_{2}+y_{1}}{k+1} \right )$

$⇒ \frac{ky_{2}+y_{1}}{k+1} = 0$

$⇒k =-\frac{y_{1}}{y_{2}}$

Hence, the value of k will be: $k =-\frac{-5}{5}= 1$

Therefore, the x-axis divides the line in the ratio $1:1$, and the point will be,

Putting the value of $k=1$ in the section formula.

$P(x,0) = \left ( \frac{x_{2}+x_{1}}{2}, 0 \right )$

$P(x,0) = \left ( \frac{1-4}{2}, 0 \right ) = \left ( \frac{-3}{2}, 0 \right )$

Q6: If (1, 2), (4, y), (x, 6), and (3, 5) are the vertices of a parallelogram taken in order, find x and y.

Answer:

Let the given points $A(1,2),\ B(4,y),\ C(x,6),\ D(3,5)$

Since the diagonals of a parallelogram bisect each other. Intersection point O of diagonals AC and BD also divides these diagonals.

Therefore, O is the midpoint of AC and BD.

The coordinates of the point O are when it is the midpoint of AC.

$\left ( \frac{1+x}{2}, \frac{2+6}{2} \right ) \Rightarrow \left ( \frac{x+1}{2}, 4 \right )$

The coordinates of the point O are when it is the mid-point of BD.

$\left ( \frac{4+3}{2}, \frac{5+y}{2} \right ) \Rightarrow \left ( \frac{7}{2}, \frac{5+y}{2} \right )$

Since both coordinates are of the same point O.

Therefore,

$\frac{x+1}{2} =\frac{7}{2}$ and $4 = \frac{5+y}{2}$

Or,

$x = 6\ and\ y = 3$

Q7: Find the coordinates of point A, where AB is the diameter of a circle whose centre is (2, – 3) and B is (1, 4).

Answer:

As the centre point $C(2,-3)$ will be the midpoint of the diameter AB.

Then, the coordinates of point A will be $A(x,y)$.

Given point $B(1,4)$ .

Therefore,

$(2,-3) = \left ( \frac{x+1}{2}, \frac{y+4}{2} \right )$

$\frac{x+1}{2} = 2\ and\ \frac{y+4}{2} = -3$

$\Rightarrow x = 3\ and\ y = -10$ .

Therefore, the coordinates of A are $(3,-10).$

Q8: If A and B are (- 2, - 2) and (2, - 4), respectively, find the coordinates of P such that AP = 3 AB 7 and P lies on the line segment AB.

Answer:

From the figure:

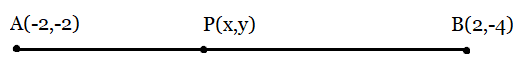
As $AP = \frac{3}{7}AB$

$\Rightarrow PB = \frac{4}{7}AB$ hence the ratio is 3:4,

Now, from the section formula, we can find the coordinates of Point P.

Section Formula:

$P(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )$

$⇒P(x,y)= \left (\frac{3(2)+4(-2)}{3+4} , \frac{3(-4)+4(-2)}{3+4} \right )$

$⇒P(x,y)= \left (\frac{6-8}{7} , \frac{-12-8}{7} \right )$

$⇒P(x,y)= \left (\frac{-2}{7} , \frac{-20}{7} \right )$

Q9: Find the coordinates of the points which divide the line segment joining A (– 2, 2) and B(2, 8) into four equal parts.

Answer:

From the figure:

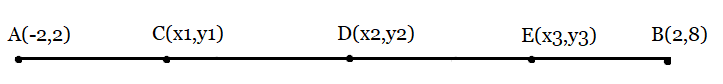
Points C, D, and E divide the line segment AB into four equal parts.

Now, from the section formula, we can find the coordinates of Points C, D, and E.

Section Formula:

$P(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )$

Here, point D divides the line segment AB into two equal parts; hence

$D(x_{2},y_{2})= \left (\frac{-2+2}{2} , \frac{2+8}{2} \right )$

$⇒D(x_{2},y_{2})= \left (0 , 5 \right )$

Now, point C divides the line segment AD into two equal parts hence

$C(x_{1},y_{1})= \left (\frac{-2+0}{2} , \frac{2+5}{2} \right )$

$⇒C(x_{2},y_{2})= \left (-1 , \frac{7}{2} \right )$

Also, point E divides the line segment DB into two equal parts, hence

$E(x_{1},y_{1})= \left (\frac{2+0}{2} , \frac{8+5}{2} \right )$

$⇒E(x_{2},y_{2})= \left (1 , \frac{13}{2} \right )$

Q10: Find the area of a rhombus if its vertices are (3, 0), (4, 5), (– 1, 4) and (– 2, – 1) taken in order.

Answer:

From the figure:

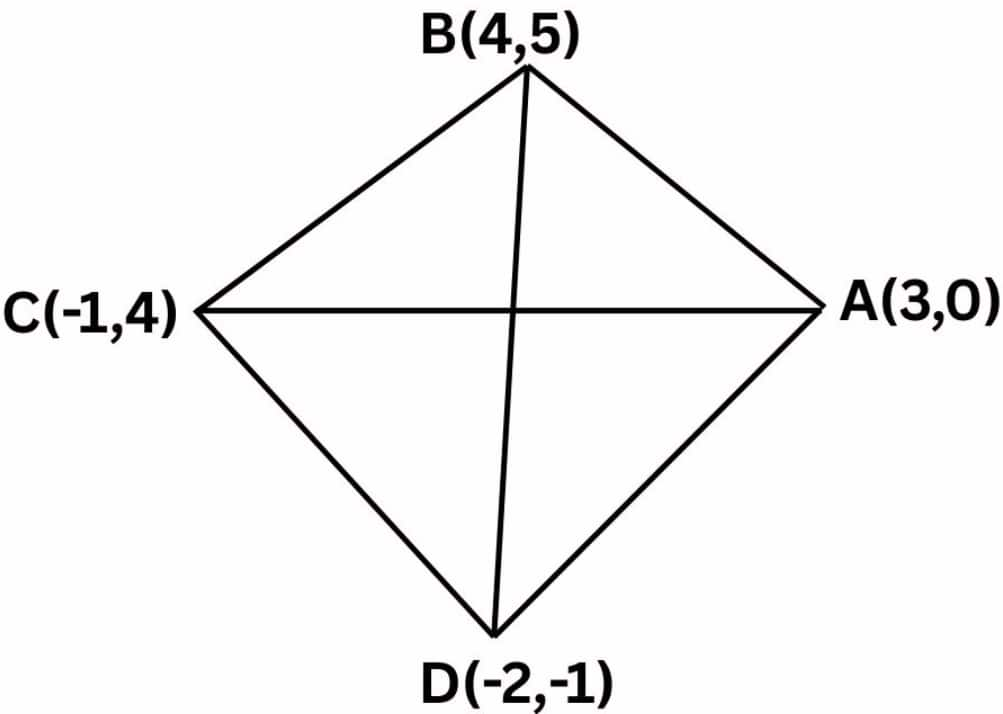
Let the vertices of the rhombus be:

$A(3,0),\ B(4,5),\ C(-1,4),\ D(-2,-1)$

Area of the rhombus ABCD is given by:

$= \frac{1}{2}\times$ Product of length of diagonals

Hence, we have to find the lengths of the diagonals AC and BD of the rhombus.

The distance formula:

$D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}$

Length of the diagonal AC:

$AC = \sqrt{(3-(-1))^2+(0-4)^2} = \sqrt{16+16} = 4\sqrt{2}$

Length of the diagonal BD:

$BD = \sqrt{(4-(-2))^2+(5-(-1))^2} = \sqrt{36+36} = 6\sqrt{2}$

Thus, the area will be,

$= \frac{1}{2}\times (AC)\times(BD)$

$= \frac{1}{2}\times (4\sqrt{2})\times(6\sqrt{2}) = 24$ square units

Coordinate Geometry Class 10 NCERT Solutions: Exercise-wise

Exercise-wise NCERT Solutions of Coordinate Geometry Class 10 Maths Chapter 7 are provided in the links below.

• Coordinate Geometry Class 10 NCERT Solutions Exercise 7.1
• Coordinate Geometry Class 10 NCERT Solutions Exercise 7.2

Class 10 Maths NCERT Chapter 7: Extra Question

Question:

Find the coordinates of the points where the graph $57x – 19y = 399$ cuts the coordinate axes.

Answer:

$57x-19y=399$
⇒ $\frac{57x}{399}-\frac{19y}{399} = 1$
⇒ $\frac{x}{7}-\frac{y}{21} = 1$ -------------(i)
Comparing it with the equation of a line:
$\frac{x}{a}+\frac{y}{b} = 1$
x-intercept = $a$ = 7
y-intercept = $b$ = –21
The line, $57x-19y=399$, cuts the x-axis at (7, 0) and the y-axis at (0, –21)
Hence, the correct answer is 'x-axis at (7, 0) and y-axis at (0, –21)'.

Coordinate Geometry Class 10 Chapter 7: Topics

Topics you will learn in NCERT Class 10 Maths Chapter 7 Coordinate Geometry include:

• Introduction
• Distance Formula
• Section Formula

Coordinate Geometry Class 10 Solutions: Important Formulae

Distance Formulae:

• For a line defined by two points A$(x_1,y_1)$ and B$(x_2,y_2)$, the distance between these points can be calculated using the formula:

• Distance AB = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Section Formula:

• When a point P divides a line AB, with A(x₁, y₁) and B(x₂, y₂) as endpoints, in a ratio of m:n, the coordinates of point P can be found using the formula:

• Point P = $\{\frac{mx_2+nx_1}{m+n},\frac{my_2+ny_1}{m+n} \}$

Midpoint Formula:

• The midpoint of a line AB, defined by A(x₁, y₁) and B(x₂, y₂), can be determined using the following formula:

• Midpoint P = $\{ \frac{x_1+x_2}2,\frac{(y_1+y_2}2\}$

NCERT Solutions for Class 10 Maths: Chapter Wise

For students' preparation, Careers360 has gathered all Class 10 Maths NCERT solutions here for quick and convenient access.

Also, read,

• NCERT Exemplar Class 10 Maths Solutions Chapter 7 Coordinate Geometry
• NCERT Notes Class 10 Maths Chapter 7 Coordinate Geometry

NCERT Exemplar solutions: Subject-wise

After solving all the exercises, if students want to practice more, then the exemplar solutions can be practised. For that, the following links can be used.

• NCERT Exemplar Solutions Class 10th Maths
• NCERT Exemplar Solutions Class 10th Science

NCERT Books and NCERT Syllabus

Here are the links to access the latest NCERT syllabus, which is very useful for students before strategising their study plan. Also, links to some reference books which are important for further studies.

• NCERT Books Class 10 Maths
• NCERT Syllabus Class 10 Maths
• NCERT Books Class 10
• NCERT Books for Class 10 Science
• NCERT Books for Class 10 English
• NCERT Syllabus Class 10