Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Exercise 7.1 Class 10 Maths Chapter 7 - Coordinate Geometry

NCERT Solutions for Exercise 7.1 Class 10 Maths Chapter 7 - Coordinate Geometry

Edited By Ramraj Saini | Updated on Nov 27, 2023 08:34 AM IST | #CBSE Class 10th

NCERT Solutions For Class 10 Maths Chapter 7 Exercise 7.1

NCERT Solutions for Exercise 7.1 Class 10 Maths Chapter 7 Coordinate Geometry are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Class 10 maths ex 7.1 introduces us to the concept of a distance formula which is used to find out distance between coordinates of two points. This exercise also gives an idea of how to apply this distance formula in real life problems.

This Story also Contains
  1. NCERT Solutions For Class 10 Maths Chapter 7 Exercise 7.1
  2. Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 7 exercise 7.1
  3. Assess NCERT Solutions for Class 10 Maths chapter 7 exercise 7.1
  4. More About NCERT Solutions for Class 10 Maths Exercise 7.1
  5. NCERT Solutions Subject Wise
  6. Subject Wise NCERT Exemplar Solutions
  7. NCERT Exemplar Class 10 Maths
NCERT Solutions for Exercise 7.1 Class 10 Maths Chapter 7 - Coordinate Geometry
NCERT Solutions for Exercise 7.1 Class 10 Maths Chapter 7 - Coordinate Geometry

NCERT solutions for exercise 7.1 Class 10 Maths chapter 7 Coordinate Geometry focus is on how to apply distance formula between two coordinates and we also see this by an analogy of right-angle triangle formation or we also know it as Pythagoras theorem. 10th class Maths exercise 7.1 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.

Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 7 exercise 7.1

Download PDF

Assess NCERT Solutions for Class 10 Maths chapter 7 exercise 7.1

Coordinate Geometry Class 10 Chapter 7 Exercise: 7.1

Q1 (i) Find the distance between the following pairs of points : (2, 3), (4, 1)

Answer:

Given points: (2, 3), (4, 1)

Distance between the points will be: (x_{1},y_{1})\ and\ (x_{2},y_{2})

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

D= \sqrt{(4-2)^2+(1-3)^2} = \sqrt{4+4} = 2\sqrt{2}

Q1 (ii) Find the distance between the following pairs of points : (– 5, 7), (– 1, 3)

Answer:

Given points: (– 5, 7), (– 1, 3)

Distance between the points will be: (x_{1},y_{1})\ and\ (x_{2},y_{2})

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

D= \sqrt{(-1+5)^2+(3-7)^2} = \sqrt{16+16} = 4\sqrt{2}

Q1 (iii) Find the distance between the following pairs of points :(a, b), (– a, – b)

Answer:

Given points: (a, b), (– a, – b)

Distance between the points will be: (x_{1},y_{1})\ and\ (x_{2},y_{2})

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

D= \sqrt{(-a-a)^2+(-b-b)^2} = \sqrt{4(a^2+b^2)} = 2\sqrt{a^2+b^2}

Q2 Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B discussed in Section 7.2?

Answer:

Given points: (0, 0) and (36, 15)

Distance between the points will be: (x_{1},y_{1})\ and\ (x_{2},y_{2})

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

D= \sqrt{(36-0)^2+(15-0)^2} =\sqrt{1296+225} = \sqrt{1521} = 39

The distance between the two towns A and B is, thus 39 km for given towns location

(0,0) and (36,15) .

Q3 Determine if the points (1, 5), (2, 3) and (– 2, – 11) are collinear.

Answer:

Let the points (1, 5), (2, 3) and (– 2, – 11) be representing the vertices A, B, and C of the given triangle respectively.

A = (1,5),\ B = (2,3),\ C = (-2,-11)

Therefore,

AB = \sqrt{(1-2)^2+(5-3)^2} = \sqrt{5}

BC = \sqrt{(2-(-2))^2+(3-(-11))^2} = \sqrt{4^2+14^2} = \sqrt{16+196} = \sqrt{212} CA = \sqrt{(1-(-2))^2+(5-(-11))^2} = \sqrt{3^2+16^2} = \sqrt{9+256} = \sqrt{265} Since these are not satisfied.

AB+BC \neq CA

BA+AC \neq BC

BC+CA \neq BA

As these cases are not satisfied.

Hence the points are not collinear.

Q4. Check whether (5, – 2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.

Answer:

The distance between two points A(x_{1},y_{1})\ and\ B(x_{2},y_{2}) is given by:

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

So, we have the following points: (5, – 2), (6, 4) and (7, – 2) assuming it to be the vertices of triangle A, B, and C respectively.

AB = \sqrt{(5-6)^2+(-2-4)^2} = \sqrt{1+36} = \sqrt{37}

BC = \sqrt{(6-7)^2+(4+2)^2} = \sqrt{1+36} = \sqrt{37}

CA = \sqrt{(5-7)^2+(-2+2)^2} = \sqrt{4+0} = 2

Therefore, AB = BC

Here two sides are equal in length.

Therefore, ABC is an isosceles triangle.

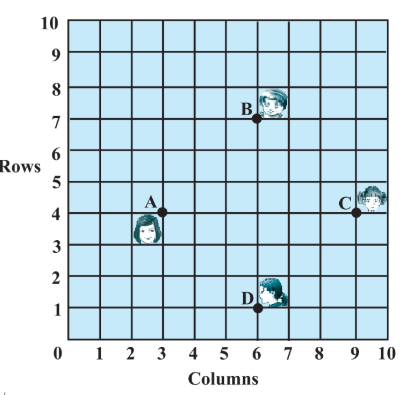
Q5 In a classroom, 4 friends are seated at the points A, B, C and D as shown in Fig. 7.8. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct.

Answer:

The coordinates of the points:

A(3,4),\ B(6,7),\ C(9,4),\ and\ D(6,1) are the positions of 4 friends.

The distance between two points A(x_{1},y_{1}), \ and\ B(x_{2},y_{2}) is given by:

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

Hence,

AB = \sqrt{(3-6)^2+(4-7)^2} = \sqrt{9+9} = \sqrt{18} = 3\sqrt2

BC = \sqrt{(6-9)^2+(7-4)^2} = \sqrt{9+9} = \sqrt{18} = 3\sqrt2

CD = \sqrt{(9-6)^2+(4-1)^2} = \sqrt{9+9} = \sqrt{18} = 3\sqrt2

AD= \sqrt{(3-6)^2+(4-1)^2} = \sqrt{9+9} = \sqrt{18} = 3\sqrt2

And the lengths of diagonals:

AC = \sqrt{(3-9)^2+(4-4)^2} =\sqrt{36+0} = 6

BD = \sqrt{(6-6)^2+(7-1)^2} =\sqrt{36+0} = 6

So, here it can be seen that all sides of quadrilateral ABCD are of the same lengths and diagonals are also having the same length.

Therefore, quadrilateral ABCD is a square and Champa is saying right.

Q6 (i) Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer: (– 1, – 2), (1, 0), (– 1, 2), (– 3, 0)

Answer:

Let the given points (-1,-2),\ (1,0),\ (-1,2),\ and\ (-3,0) be representing the vertices A, B, C, and D of the given quadrilateral respectively.

The distance formula:

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

AB= \sqrt{(-1-1)^2+(-2-0)^2} =\sqrt{4+4} = \sqrt{8} = 2\sqrt2

BC= \sqrt{(1+1)^2+(0-2)^2} =\sqrt{4+4} = \sqrt{8} = 2\sqrt2

CD= \sqrt{(-1+3)^2+(2-0)^2} =\sqrt{4+4} = \sqrt{8} = 2\sqrt2

AD= \sqrt{(-1+3)^2+(-2-0)^2} =\sqrt{4+4} = \sqrt{8} = 2\sqrt2

Finding the length of the diagonals:

AC= \sqrt{(-1+1)^2+(-2-2)^2} =\sqrt{0+16} = 4

BD= \sqrt{(1+3)^2+(0-0)^2} =\sqrt{16+0} = 4

It is clear that all sides are of the same lengths and also the diagonals have the same lengths.

Hence, the given quadrilateral is a square.

Q6 (ii) Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer: (–3, 5), (3, 1), (0, 3), (–1, – 4)

Answer:

Let the given points (-3,5),\ (3,1),\ (0,3),\ and\ (-1,-4) be representing the vertices A, B, C, and D of the given quadrilateral respectively.

The distance formula:

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

AB= \sqrt{(-3-3)^2+(5-1)^2} =\sqrt{36+16} = \sqrt{52} = 2\sqrt{13}

BC= \sqrt{(3-0)^2+(1-3)^2} =\sqrt{9+4} = \sqrt{13}

CD= \sqrt{(0+1)^2+(3+4)^2} =\sqrt{1+49} = \sqrt{50} = 5\sqrt2

AD= \sqrt{(-3+1)^2+(5+4)^2} =\sqrt{4+81} = \sqrt{85}

All the sides of the given quadrilateral have different lengths.

Therefore, it is only a general quadrilateral and not a specific one like square, rectangle, etc.

Q6 (iii) Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer: (4, 5), (7, 6), (4, 3), (1, 2)

Answer:

Let the given points (4,5),\ (7,6),\ (4,3),\ (1,2) be representing the vertices A, B, C, and D of the given quadrilateral respectively.

The distance formula:

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

AB= \sqrt{(4-7)^2+(5-6)^2} =\sqrt{9+1} = \sqrt{10}

BC= \sqrt{(7-4)^2+(6-3)^2} =\sqrt{9+9} = \sqrt{18}

CD= \sqrt{(4-1)^2+(3-2)^2} =\sqrt{9+1} = \sqrt{10}

AD= \sqrt{(4-1)^2+(5-2)^2} =\sqrt{9+9} = \sqrt{18}

And the diagonals:

AC =\sqrt{(4-4)^2+(5-3)^2} = \sqrt{0+4} = 2

BD =\sqrt{(7-1)^2+(6-2)^2} = \sqrt{36+16} = \sqrt{52} = 2\sqrt{13}

Here we can observe that the opposite sides of this quadrilateral are of the same length.

However, the diagonals are of different lengths.

Therefore, the given points are the vertices of a parallelogram.

Q7 Find the point on the x-axis which is equidistant from (2, –5) and (–2, 9).

Answer:

Let the point which is equidistant from A(2,-5)\ and \ B(-2,9) be X(x,0) as it lies on X-axis.

Then, we have

Distance AX: = \sqrt{(x-2)^2+(0+5)^2}

and Distance BX = \sqrt{(x+2)^2+(0+9)^2}

According to the question, these distances are equal length.

Hence we have,

\sqrt{(x-2)^2+(0+5)^2} = \sqrt{(x+2)^2+(0+9)^2}

Solving this to get the required coordinates.

Squaring both sides we get,

(x-2)^2+25 = (x+2)^2+81

\Rightarrow (x-2+x+2)(x-2-x-2)= 81 - 25 = 56

\Rightarrow (-8x)= 56

Or, \Rightarrow x = -7

Hence the point is X(-7,0) .

Q8 Find the values of y for which the distance between the points P(2, – 3) and Q(10, y) is 10 units.

Answer:

Given the distance between the points P(2,-3) and Q(10,y) is 10 units.

The distance formula :

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

So, given PQ = 10\ units

PQ= \sqrt{(10-2)^2+(y-(-3))^2} = 10

After squaring both sides

\Rightarrow (10-2)^2+(y-(-3))^2 = 100

\Rightarrow (y+3)^2 = 100 - 64

\Rightarrow y+3 = \pm 6

\Rightarrow y = 6 - 3\ or\ y = -6-3

Therefore, the values are y = 3\ or -9 .

Q9 If Q(0, 1) is equidistant from P(5, –3) and R(x, 6), find the values of x. Also, find the distances QR and PR.

Answer:

Given Q(0,1) is equidistant from P(5,-3) and R(x,6) .

Then, the distances PQ = RQ .

Distance PQ = \sqrt{(5-0)^2+(-3-1)^2} = \sqrt{25+16} = \sqrt{41}

Distance RQ = \sqrt{(x-0)^2+(6-1)^2} = \sqrt{x^2+25}

\Rightarrow \sqrt{x^2+25} = \sqrt{41}

Squaring both sides, we get

\Rightarrow x^2 = 16

\Rightarrow x = \pm 4

The points are: R(4,6)\ or\ R(-4,6.)

CASE I: when R is (4,6)

The distances QR and PR.

QR = \sqrt{(0-4)^2+(1-6)^2} = \sqrt{16+25} = \sqrt{41}

PR = \sqrt{(5-4)^2+(-3-6)^2} = \sqrt{1^2+(-9)^2} = \sqrt{1+81} = \sqrt{82}

CASE II: when R is (-4,6)

The distances QR and PR.

QR = \sqrt{(0-(-4))^2+(1-6)^2} = \sqrt{16+25} = \sqrt{41}

PR = \sqrt{(5-(-4))^2+(-3-6)^2} = \sqrt{9^2+(-9)^2} = \sqrt{81+81} = 9\sqrt{2}

Q10 Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (– 3, 4).

Answer:

Let the point P(x,y ) is equidistant from A(3,6) and B(-3,4) .

Then, the distances AP =BP

AP = \sqrt{(x-3)^2+(y-6)^2} and BP = \sqrt{(x-(-3))^2+(y-4)^2}

\Rightarrow \sqrt{(x-3)^2+(y-6)^2} = \sqrt{(x-(-3))^2+(y-4)^2}

Squaring both sides: we obtain

\Rightarrow (x-3)^2+(y-6)^2= (x+3)^2+(y-4)^2

\Rightarrow (2x)(-6)+(2y-10)(-2)= 0 \left [\because a^2-b^2 = (a+b)(a-b) \right ]

\Rightarrow -12x-4y+20 = 0

\Rightarrow 3x+y-5 = 0

Thus, the relation is 3x+y-5 = 0 between x and y.

More About NCERT Solutions for Class 10 Maths Exercise 7.1

The questions in exercise 7.1 Class 10 Maths, broadly consist of all the basic topics which we have learned till now about coordinate geometry such as isosceles triangle, collinear points and it also has many questions about equidistant. NCERT solutions for Class 10 Maths exercise 7.1 also consist of questions in which we are given a real-life scenario and we have to use a distance formula. Exercise 7.1 Class 10 Maths covers all types of basic questions that can be formed on the distance formula. Students can find Coordinate Geometry Class 10 Notes here which can be used to quick revision of the concepts discussed in this chapter.

Benefits of NCERT Solutions for Class 10 Maths Exercise 7.1

  • Class 10 Maths chapter 7 exercise 7.1 broadly covers a basic knowledge which we would be required to proceed in Class 10 Maths chapter 7 exercise 7.2
  • NCERT Class 10 Maths chapter 7 exercise 7.1, will be helpful in Class 11 Maths chapter 10 straight line and Class 11 Maths chapter 11 conic section.
  • Exercise 7.1 Class 10 Maths, is also a base builder concept for many topics of Joint Entrance Exam (JEE) Main.

Also, see-

NCERT Solutions Subject Wise

Subject Wise NCERT Exemplar Solutions


Frequently Asked Question (FAQs)

1. What is analogy of deriving distance formula by pythagoras theorem according to NCERT solutions for Class 10 Maths exercise 7.1?

We assume that the line between two coordinates is hypotenuse so with the help x axis and y axis we will find perpendicular and base and by applying pythagoras theorem we will find hypotenuse .

2. What is the formula of pythagoras theorem ?

H =square root of [(P)²+(B)²]

In the above formula, H is the hypotenuse, P is perpendicular and B is base

3. What do you mean by collinear points as referred in NCERT solutions for Class 10 Maths exercise 7.1?

Collinear points are set of three or more points which is on exact same line

4. According to NCERT solutions for Class 10 Maths exercise 7.1 where can we use distance formula.

The distance formula is used in NCERT solutions for Class 10 Maths exercise 7.1  to find area of triangle length of vertices of different types of triangles such as an isosceles triangle.

5. According to NCERT solutions for Class 10 Maths exercise 7.1 what is equidistant points.

Set of points all at equal distance from each other.

6. What is the total number of solved examples prior to the Class 10 Maths Exercise 7.1?

Before the Class 10 Mathematics chapter 7 activity 7.1, there are five key questions that must be answered.

7. In the NCERT answers for Class 10 Maths chapter 7 exercise, how many questions are covered?

There are 10 questions in Class 10 Maths chapter exercise 7.1. Question 1 consists of three subparts.

8. What are the types of questions covered in the NCERT solutions for Class 10 Maths chapter 7 exercise?

Question 1 and question 2 is very basic coordinates are given and we have to find the distance then we have question 3 based on collinear point question 4 on finding vertices of an isosceles triangle then we have question 5 based on real-life scenario and then we have some question of  equidistant point

Also Read

Articles

Upcoming School Exams

National Means Cum-Merit Scholarship

Application Date:01 August,2024 - 16 September,2024

International General Knowledge Olympiad

Exam Date:19 September,2024 - 19 September,2024

Unified Cyber Olympiad

Exam Date:20 September,2024 - 20 September,2024

International English Olympiad

Exam Date:26 September,2024 - 26 September,2024

International Olympiad of Mathematics

Application Date:30 September,2024 - 30 September,2024

View All School Exams

Certifications By Top Providers

Edx
 1113 courses
Coursera
 804 courses
Udemy
 394 courses
Futurelearn
 222 courses
Harvard University, Cambridge
 98 courses
IBM
 85 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
sadhu ashram ramgart road aligarh

Hello

The Sadhu Ashram in Aligarh is located in Chhalesar . The ashram is open every day of the week, except for Thursdays . On Mondays, Wednesdays, and Saturdays, it's open from 8:00 a.m. to 7:30 p.m., while on Tuesdays and Fridays, it's open from 7:30 a.m. to 7:30 p.m. and 7:30 a.m. to 6:00 a.m., respectively . Sundays have varying hours from 7:00 a.m. to 8:30 p.m. . You can find it at Chhalesar, Aligarh - 202127 .

Read Complete Answer
vaibhavi bhalsod 01 September,2024
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

Tallentex 2025 - ALLEN's Talent Encouragement Exam
Tallentex 2025 - ALLEN's Talent Encouragement Exam
Apply

Register for Tallentex '25 - One of The Biggest Talent Encouragement Exam

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

PTE Registrations 2024
PTE Registrations 2024
Apply

Register now for PTE & Unlock 10% OFF : Use promo code: 'C360SPL10'. Limited Period Offer!

JEE Main high scoring chapters and topics
JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

View All Application Forms
News and Notifications
CBSE Class 10 compartment result 2024 declared; 48.83% pass
August 05, 2024 - 03:14 PM IST
CBSE Class 10 compartment result 2024 soon; passing marks, websites to check
August 05, 2024 - 02:44 PM IST
CBSE Class 10 compartment result 2024 expected soon at cbseresults.nic.in; grading system, passing marks
August 04, 2024 - 04:20 PM IST
CBSE Class 10 compartment result 2024 soon at cbseresults.nic.in; websites to check
August 03, 2024 - 04:38 PM IST
CBSE 10th, 12th revaluation lot 2 result 2024 out at cbseresults.nic.in; passing marks
July 30, 2024 - 06:39 PM IST
CBSE: No open book exams for Classes 10, 12 this year; pilot only in a few schools
June 12, 2024 - 10:52 AM IST
CBSE Class 10 result 2024 revaluation application begins at cbse.gov.in; apply by May 24
May 21, 2024 - 02:20 PM IST

Stay up-to date with CBSE Class 10th News

Back to top