Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Exercise 7.2 Class 10 Maths Chapter 7 - Coordinate Geometry

NCERT Solutions for Exercise 7.2 Class 10 Maths Chapter 7 - Coordinate Geometry

Edited By Ramraj Saini | Updated on Nov 27, 2023 08:26 AM IST | #CBSE Class 10th

NCERT Solutions For Class 10 Maths Chapter 7 Exercise 7.2

NCERT Solutions for Exercise 7.2 Class 10 Maths Chapter 7 Coordinate Geometry are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Class 10 maths ex 7.2 deals with the concept of section formula which is used in mathematics to obtain the coordinates of the point that splits a line segment into a ratio either externally or internally. We can use the section formula to discover the coordinates of a point that divides a line segment externally or internally in some ratio. When a point P(x,y) divides the line segment into two segments, labelled as A (x1, y1) and B (x2,y2) then the method used to find the coordinates of that point is known as the section formula, which is mathematically represented as P(x, y) = [(mx2 + nx1)/(m + n), (my2 + ny1)/m + n]

This Story also Contains
  1. NCERT Solutions For Class 10 Maths Chapter 7 Exercise 7.2
  2. Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 7 exercise 7.2
  3. Assess NCERT Solutions for Class 10 Maths chapter 7 exercise 7.2
  4. More About NCERT Solutions for Class 10 Maths Exercise 7.2: Section formula
  5. Benefits of NCERT Solutions for Class 10 Maths Exercise 7.2 :
  6. NCERT Solutions Subject Wise
  7. Subject Wise NCERT Exemplar Solutions
NCERT Solutions for Exercise 7.2 Class 10 Maths Chapter 7 - Coordinate Geometry
NCERT Solutions for Exercise 7.2 Class 10 Maths Chapter 7 - Coordinate Geometry

NCERT solutions for exercise 7.2 Class 10 Maths chapter 7 Coordinate Geometry focus on section formula that divided into two sections namely the internal section formula and the external section formula. 10th class Maths exercise 7.2 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.

Tallentex 2025 - ALLEN's Talent Encouragement Exam

Register for Tallentex '25 - One of The Biggest Talent Encouragement Exam

Apply

Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 7 exercise 7.2

Download PDF

Assess NCERT Solutions for Class 10 Maths chapter 7 exercise 7.2

Coordinate Geometry Class 10 Chapter 7 Exercise: 7.2

Q1 Find the coordinates of the point which divides the join of (–1, 7) and (4, –3) in the ratio 2 : 3.

Answer:

Let the coordinates of point P(x,y) which divides the line segment joining the points A(-1,7) and B(4,-3) , internally, in the ratio m_{1}:m_{2} then,

Section formula: \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

Substituting the values in the formula:

Here, m_{1}:m_{2} = 2:3

\Rightarrow \left (\frac{2(4)+3(-1)}{2+3} , \frac{2(-3)+3(7)}{2+3} \right )

\Rightarrow \left (\frac{5}{5} , \frac{15}{5} \right )

Hence the coordinate is P \left (1 , 3 \right ) .

Q2 Find the coordinates of the points of trisection of the line segment joining (4, –1) and (–2, –3).

Answer:

Let the trisection of the line segment A(4,-1) and B(-2,-3) have the points P(x_{1},y_{1}) and Q(x_{2},y_{2})

Then,

Section formula: \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

By observation point, P divides AB internally in the ratio 1:2 .

Hence, m:n = 1:2

Substituting the values in the equation we get;

\Rightarrow P\left (\frac{1(-2)+2(4)}{1+2} , \frac{1(-3)+2(-1)}{1+2} \right )

\Rightarrow P \left (\frac{-2+8}{3} , \frac{-3-2}{3} \right )

\Rightarrow P \left (2 , \frac{-5}{3} \right )

And by observation point Q, divides AB internally in the ratio 2:1

Hence, m:n = 2:1

Substituting the values in the equation above, we get

\Rightarrow Q\left (\frac{2(-2)+1(4)}{2+1} , \frac{2(-3)+1(-1)}{2+1} \right )

\Rightarrow Q \left (\frac{-4+4}{3} , \frac{-6-1}{3} \right )

\Rightarrow Q\left (0 , \frac{-7}{3} \right )

Hence, the points of trisections are P \left (2 , \frac{-5}{3} \right ) and Q\left (0 , \frac{-7}{3} \right )

Q3 To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1m each. 100 flower pots have been placed at a distance of 1m from each other along AD, as shown in Fig. 7.12. Niharika runs 1/4 th the distance AD on the 2nd line and posts a green flag. Preet runs 1/5th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag

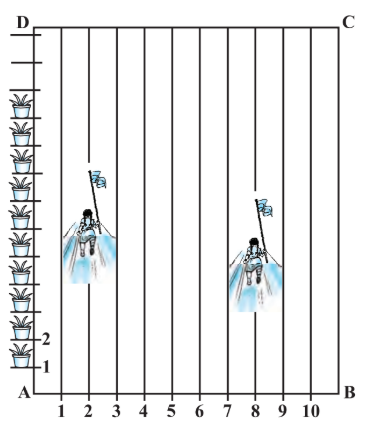
1638427152215

Answer:

Niharika posted the green flag at the distance P, i.e.,

\frac{1}{4}\times100\ m = 25\ m from the starting point of 2^{nd} line.

Therefore, the coordinates of this point P are (2,25).

Similarly, Preet posted red flag at \frac{1}{5} of the distance Q i.e.,

\frac{1}{5}\times100\ m = 20\ m from the starting point of 8^{th} line.

Therefore, the coordinates of this point Q are (8,20) .

The distance PQ is given by,

PQ = \sqrt{(8-2)^2+(25-20)^2} = \sqrt{36+25} = \sqrt{61} m

and the point at which Rashmi should post her Blue Flag is the mid-point of the line joining these points. Let this point be R(x,y) .

Then, by Section Formula,

P(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

x = \frac{2+8}{2},\ y = \frac{25+20}{2}

x = 5,\ y = 22.5

Therefore, Rashmi should post her Blue Flag at 22.5 m on the 5th line.

Q4 Find the ratio in which the line segment joining the points (– 3, 10) and (6, – 8) is divided by (– 1, 6).

Answer:

Let the ratio be : k:1

Then, By section formula:

P(x,y) = \left (\frac{kx_{2}+x_{1}}{k+1} , \frac{ky_{2}+y_{1}}{k+1} \right )

Given point P(x,y) = (-1,6)

-1 = \frac{6k-3}{k+1}

\Rightarrow -k-1 = 6k-3

\Rightarrow k = \frac{7}{2}

Hence, the point P divides the line AB in the ratio 2:7 .

Q5 Find the ratio in which the line segment joining A(1, – 5) and B(– 4, 5) is divided by the x-axis. Also find the coordinates of the point of division.

Answer:

Let the point on the x-axis be P(x,0) and it divides it in the ratio k:1 .

Then, we have

Section formula:

P(x,y) = \left (\frac{kx_{2}+x_{1}}{k+1} , \frac{ky_{2}+y_{1}}{k+1} \right )

\implies \frac{ky_{2}+y_{1}}{k+1} = 0

k =-\frac{y_{1}}{y_{2}}

Hence, the value of k will be: k =-\frac{-5}{5}= 1

Therefore, the x-axis divides the line in the ratio 1:1 and the point will be,

Putting the value of k=1 in section formula.

P(x,0) = \left ( \frac{x_{2}+x_{1}}{2}, 0 \right )

P(x,0) = \left ( \frac{1-4}{2}, 0 \right ) = \left ( \frac{-3}{2}, 0 \right )

Q6 If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.

Answer:

Let the given points A(1,2),\ B(4,y),\ C(x,6),\ D(3,5) .

Since the diagonals of a parallelogram bisect each other. Intersection point O of diagonal AC and BD also divides these diagonals.

Therefore, O is the mid-point of AC and BD.

The coordinates of the point O when it is mid-point of AC.

\left ( \frac{1+x}{2}, \frac{2+6}{2} \right ) \Rightarrow \left ( \frac{x+1}{2}, 4 \right )

The coordinates of the point O when it is mid-point of BD.

\left ( \frac{4+3}{2}, \frac{5+y}{2} \right ) \Rightarrow \left ( \frac{7}{2}, \frac{5+y}{2} \right )

Since both coordinates are of same point O.

Therefore,

\frac{x+1}{2} =\frac{7}{2} and 4 = \frac{5+y}{2}

Or,

x = 6\ and\ y = 3

Q7 Find the coordinates of point A, where AB is the diameter of a circle whose centre is (2, – 3) and B is (1, 4).

Answer:

As the centre point C(2,-3) will be the mid-point of the diameter AB.

Then, the coordinates of point A will be A(x,y) .

Given point B(1,4) .

Therefore,

(2,-3) = \left ( \frac{x+1}{2}, \frac{y+4}{2} \right )

\frac{x+1}{2} = 2\ and\ \frac{y+4}{2} = -3

\Rightarrow x = 3\ and\ y = -10 .

Therefore, the coordinates of A are (3,-10).

Q8 If A and B are (- 2, - 2) and (2, - 4), respectively, find the coordinates of P such that AP = 3 AB 7 and P lies on the line segment AB.

Answer:

From the figure:

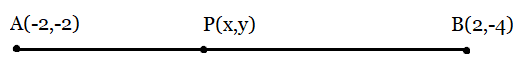
1638427203509

As AP = \frac{3}{7}AB

\Rightarrow PB = \frac{4}{7}AB hence the ratio is 3:4,

Now, from the section formula, we can find the coordinates of Point P.

Section Formula:

P(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

P(x,y)= \left (\frac{3(2)+4(-2)}{3+4} , \frac{3(-4)+4(-2)}{3+4} \right )

P(x,y)= \left (\frac{6-8}{7} , \frac{-12-8}{7} \right )

P(x,y)= \left (\frac{-2}{7} , \frac{-20}{7} \right )

Q9 Find the coordinates of the points which divide the line segment joining A (– 2, 2) and B(2, 8) into four equal parts.

Answer:

From the figure:

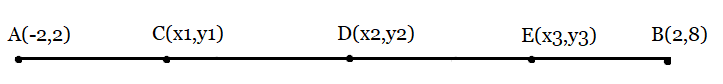
1638427222556

Points C, D, and E divide the line segment AB into four equal parts.

Now, from the section formula, we can find the coordinates of Point C, D, and E.

Section Formula:

P(x,y)= \left (\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}} , \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}} \right )

Here point D divides the line segment AB into two equal parts hence

D(x_{2},y_{2})= \left (\frac{-2+2}{2} , \frac{2+8}{2} \right )

D(x_{2},y_{2})= \left (0 , 5 \right )

Now, point C divides the line segment AD into two equal parts hence

C(x_{1},y_{1})= \left (\frac{-2+0}{2} , \frac{2+5}{2} \right )

C(x_{2},y_{2})= \left (-1 , \frac{7}{2} \right )

Also, point E divides the line segment DB into two equal parts hence

E(x_{1},y_{1})= \left (\frac{2+0}{2} , \frac{8+5}{2} \right )

E(x_{2},y_{2})= \left (1 , \frac{13}{2} \right )

Q10 Find the area of a rhombus if its vertices are (3, 0), (4, 5), (– 1, 4) and (– 2, – 1) taken in order.

Answer:

From the figure:

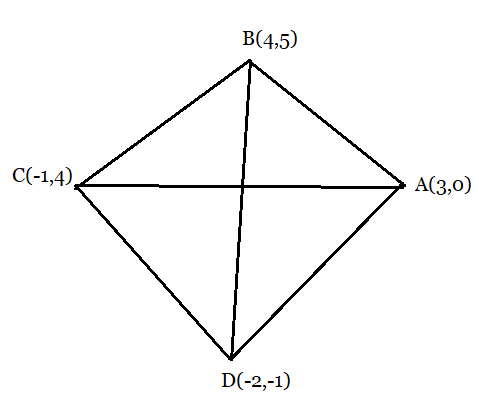
1638427243029

Let the vertices of the rhombus are:

A(3,0),\ B(4,5),\ C(-1,4),\ D(-2,-1)

Area of the rhombus ABCD is given by;

= \frac{1}{2}\times(Product\ of\ lengths\ of\ diagonals)

Hence we have to find the lengths of the diagonals AC and BD of the rhombus.

The distance formula:

D = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}

Length of the diagonal AC:

AC = \sqrt{(3-(-1))^2+(0-4)^2} = \sqrt{16+16} = 4\sqrt{2}

Length of the diagonal BD:

BD = \sqrt{(4-(-2))^2+(5-(-1))^2} = \sqrt{36+36} = 6\sqrt{2}

Thus, the area will be,

= \frac{1}{2}\times (AC)\times(BD)

= \frac{1}{2}\times (4\sqrt{2})\times(6\sqrt{2}) = 24\ square\ units.

More About NCERT Solutions for Class 10 Maths Exercise 7.2: Section formula

Exercise 7.2 Class 10 Maths consists of a question based on the section formula. Internal section formula is used when a point P(x, y) divides the line segment AB internally into two segments in the ratio m:n which is expressed as P(x, y) = [(mx2 + nx1)/(m + n),(my2 + ny1)/(m + n)]. Similarly, the external section formula is used when a point P(x, y) divides the line segment AB externally into two segments in the ratio m:n which is expressed as P(x, y) = [(mx2 - nx1)/(m - n) ,(my2 - ny1)/(m - n)]. Section formula is also used to find the midpoint of a line segment. If M is the midpoint that divides the line segment AB in the ratio 1:1, then the coordinate of M is expressed as M(x, y) = [(x2 + x1)/2, (y2 + y1)/2] . The NCERT solutions for Class 10 Maths exercise 7.2 also focused on the distance formula. A few questions related to the distance formula are given also in exercise 7.2 Class 10 Maths. Students can find Coordinate Geometry Class 10 Notes here which can be used to quick revision of the concepts discussed in this chapter.

Benefits of NCERT Solutions for Class 10 Maths Exercise 7.2 :

  • NCERT solutions for Class 10 Maths exercise 7.2 helps us to understand how to find the coordinates of a point on a line segment AB which is divided in the ratio of m:n.
  • The section formula can also be used to locate the midpoint of a line segment in exercise 7.2 Class 10 Maths.
  • Students can achieve a good mark in term exams as well as competitive tests such as the joint admission exam by solving the NCERT solution for Class 10 Maths chapter 7 exercise 7.2 exercises.

Also see-

NCERT Solutions Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Question (FAQs)

1. What are the two subsections of the section formula?

Solution : 

  • Internal section formula

  • External section formula 

2. The section formula is the formula which is used for finding ________

The section formula is the formula that is used for finding the midpoint of a line segment. 

3. What is m in the section formula?

A point P(x,y) divides the line segment AB into two segments in the ratio m:n. m is the ratio in dividing the line segment. 

4. In what case is the section formula used to determine the coordinates of the point?

When a point on the line segment divides into two segments, then the section formula is used to determine the coordinates of that point.

5. What is the section formula consistent with NCERT solutions for Class 10 Maths chapter 7 exercise 7.2 ?

When some extent P(x,y) divides the segment into two segments, with marked points as A (x1,y1) and B(x2,y2) then the formula which is employed to work out the coordinates of that time is understood because of the section formula.

6. How many questions are there within the NCERT solutions for Class 10 Maths chapter 7 exercise 7.2 ?

There are 10 questions within the NCERT solutions for Class 10 Maths chapter 7 exercise 7.2 . 

Also Read

Articles

Upcoming School Exams

National Means Cum-Merit Scholarship

Application Date:01 August,2024 - 16 September,2024

International General Knowledge Olympiad

Exam Date:19 September,2024 - 19 September,2024

Unified Cyber Olympiad

Exam Date:20 September,2024 - 20 September,2024

International English Olympiad

Exam Date:26 September,2024 - 26 September,2024

International Olympiad of Mathematics

Application Date:30 September,2024 - 30 September,2024

View All School Exams

Certifications By Top Providers

Edx
 1113 courses
Coursera
 804 courses
Udemy
 394 courses
Futurelearn
 222 courses
Harvard University, Cambridge
 98 courses
IBM
 85 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024
can we apply for diploma if we have passed 10th cbse lo

Yes, you can definitely apply for diploma courses after passing 10th CBSE. In fact, there are many diploma programs designed specifically for students who have completed their 10th grade.

Generally, passing 10th CBSE with a minimum percentage (often 50%) is the basic eligibility for diploma courses. Some institutes might have specific subject requirements depending on the diploma specialization.

There is a wide range of diploma courses available in various fields like engineering (e.g., mechanical, civil, computer science), computer applications, animation, fashion design, hospitality management, and many more.

You can pursue diplomas at various institutions like:


Read Complete Answer
Nitin Kumar 14 June,2024
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

Tallentex 2025 - ALLEN's Talent Encouragement Exam
Tallentex 2025 - ALLEN's Talent Encouragement Exam
Apply

Register for Tallentex '25 - One of The Biggest Talent Encouragement Exam

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

PTE Registrations 2024
PTE Registrations 2024
Apply

Register now for PTE & Unlock 10% OFF : Use promo code: 'C360SPL10'. Limited Period Offer!

JEE Main high scoring chapters and topics
JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

View All Application Forms
News and Notifications
CBSE Class 10 compartment result 2024 declared; 48.83% pass
August 05, 2024 - 03:14 PM IST
CBSE Class 10 compartment result 2024 soon; passing marks, websites to check
August 05, 2024 - 02:44 PM IST
CBSE Class 10 compartment result 2024 expected soon at cbseresults.nic.in; grading system, passing marks
August 04, 2024 - 04:20 PM IST
CBSE Class 10 compartment result 2024 soon at cbseresults.nic.in; websites to check
August 03, 2024 - 04:38 PM IST
CBSE 10th, 12th revaluation lot 2 result 2024 out at cbseresults.nic.in; passing marks
July 30, 2024 - 06:39 PM IST
CBSE: No open book exams for Classes 10, 12 this year; pilot only in a few schools
June 12, 2024 - 10:52 AM IST
CBSE Class 10 result 2024 revaluation application begins at cbse.gov.in; apply by May 24
May 21, 2024 - 02:20 PM IST

Stay up-to date with CBSE Class 10th News

Back to top