Light- Reflection and Refraction Class 10th Notes- Free NCERT Class 10 Science Chapter 10 Notes - Download PDF
Have you ever thought about why the car headlights are so bright at night or that the objects in the water are displaced as compared to their real location? The solution is in the NCERT notes Class 10 Science Chapter 9 Light Reflection and Refraction. This chapter describes the basics of light, such as light reflection off mirrors and refraction through transparent substances such as glass and water. It is among the most significant chapters as far as CBSE Class 10 Board exams, NTSE, NSO, NSEJS and other competitive science exams are concerned.
This Story also Contains
- NCERT Class 10 Science Chapter 9 Notes Light – Reflection and Refraction: Download PDF
- Light Reflection and Refraction Class 10 Science Notes
- How to Master Class 10 Science Chapter 9: Light Reflection and Refraction?
- Importance of Class 10 Physics Chapter 9 Notes
- Class 10 Chapter Wise Notes
- NCERT Books and Syllabus
The NCERT notes Class 10 Science Chapter 9 Light Reflection and Refraction PDF is made in line with the new CBSE syllabus and is simplified by the experts in the field of science. Such NCERT notes Class 10 Science Chapter 9 Light Reflection and Refraction encompass all the high-weightage concepts, including the types of mirrors and lenses, ray diagrams, laws of refraction and reflection, and real-life use of light. They also contain valuable formulas, shortcut techniques, and exam-oriented tips to enable students to solve numerical problems in a fast and accurate manner. Be it at the beginning of your preparation or in the process of last-minute revision, these Class 10 science light NCERT notes offer crystal-clear explanations, reinforce conceptual knowledge and stand a high likelihood of scoring good grades in exams.
Also Read
NCERT Class 10 Science Chapter 9 Notes Light – Reflection and Refraction: Download PDF
The NCERT notes for class 10 Science chapter 9 PDF is a simple and well-organised approach to all the key concepts of Light - Reflection and Refraction. This PDF can be downloaded by students to refresh mirror and lens equations, ray diagrams and real-world examples within minutes and is very useful during CBSE board exams and competitive tests.
Light Reflection and Refraction Class 10 Science Notes
Light – Reflection and Refraction Class 10 Notes provide a clear understanding of how light behaves when it bounces off a surface or bends while passing through different media. These notes cover important concepts like laws of reflection, refraction, refractive index, and applications in daily life, making them very useful for board exam preparation.
Reflection Of Light
Reflection is defined as the bouncing back of light rays into the same medium when these rays strike a surface or a boundary separating two media.
Laws of Reflection:
-
The angle of incidence is equal to the angle of reflection.
-
The incident ray, the normal to the mirror at the point of incidence and the reflected ray all lie in the same plane.
Spherical Mirrors:
Consider a hollow sphere with a highly polished internal surface and a mercury-coated exterior surface that prevents light from passing through. After that, we can cut a thin slice out of the shell to make a curved mirror known as a spherical mirror.
Concave Mirror: A concave mirror is a spherical mirror with a reflecting surface that is curved inwards, towards the centre of the sphere.
Convex Mirror: A convex mirror is a spherical mirror with a curved outward reflecting surface.
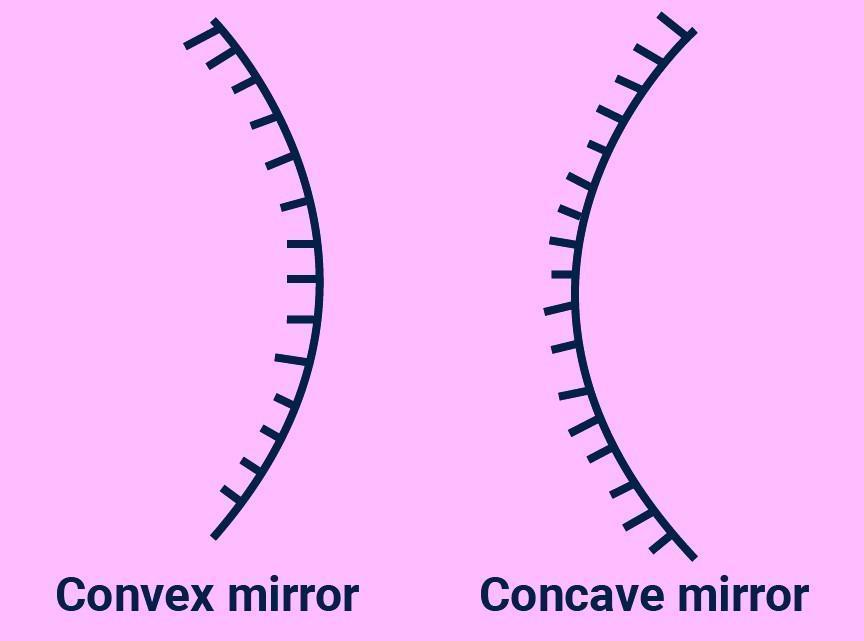
When studying spherical mirrors, there are a few essential terms to be aware of.
Principal axis: The imaginary line that passes through the optical centre and curvature centre of any lens or spherical mirror.
Centre of Curvature: The point in the mirror's centre that passes through its curve and has the same tangent and curvature as the curve.
Radius of Curvature: The linear distance between the pole and the centre of curvature is known as the radius of curvature.
Pole: It is the midpoint of the spherical mirror.
Principal focus: Focal Point is another word for the Principal Focus. After reflection or refraction on the axis of a mirror or lens occurs, it is the point at which light rays parallel to the axis converge or appear to converge.
Focus: It is any point at which light rays parallel to the principal axis converge after being reflected by the mirror.
Focal length: The distance between the pole and the principal focus is the focal length of a spherical mirror.
Aperture: An aperture in a mirror or lens is the point at which light is reflected. It also specifies the size of the mirror.
The radius of curvature of small-aperture spherical mirrors is found to be twice the focal length. This is denoted by R = 2f. This means that the principal focus of a spherical mirror is located midway between the pole and the centre of curvature.
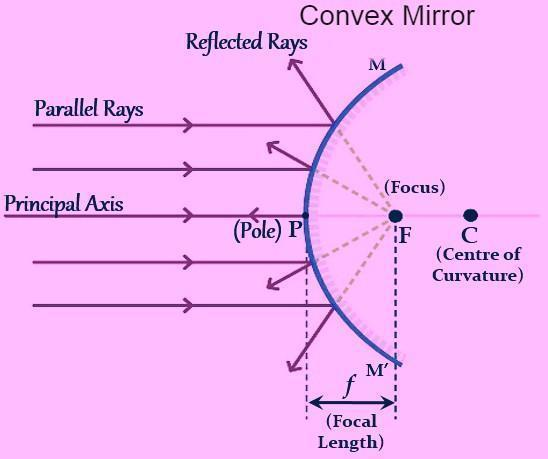
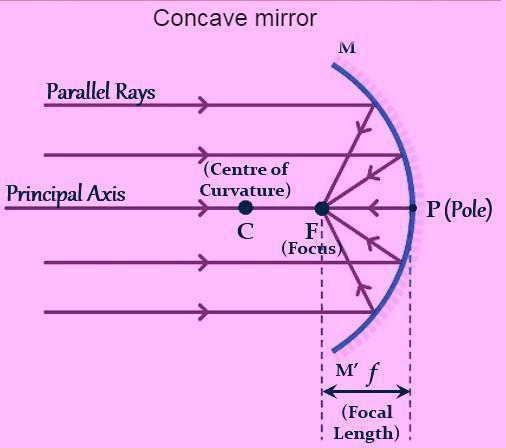
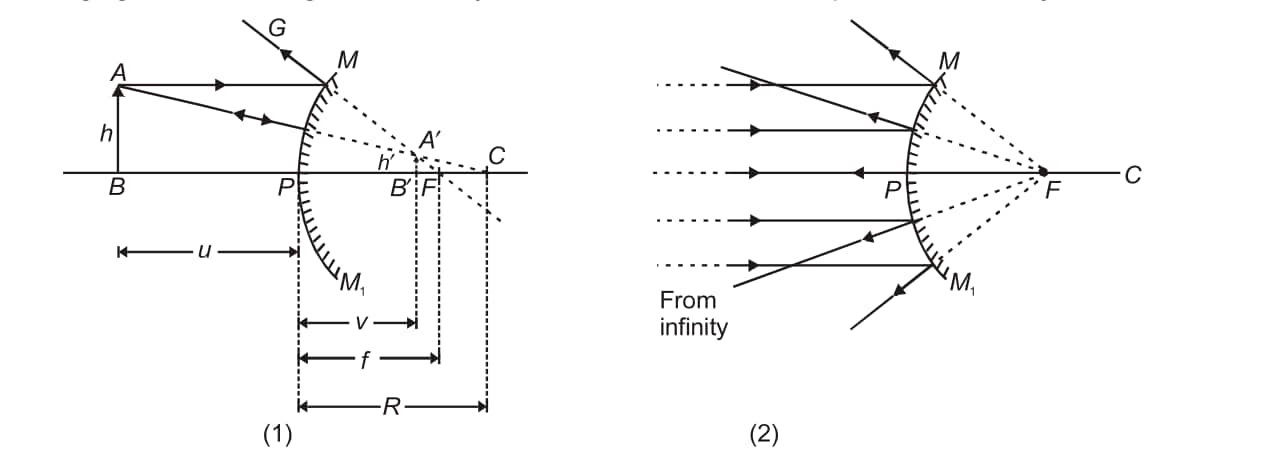
Image Formation by Spherical Mirrors:
Representation of Images Formed by Spherical Mirrors Using Ray Diagrams
-
A ray of light that converges or diverges from the focus after reflection and is parallel to the major axis of a spherical mirror.
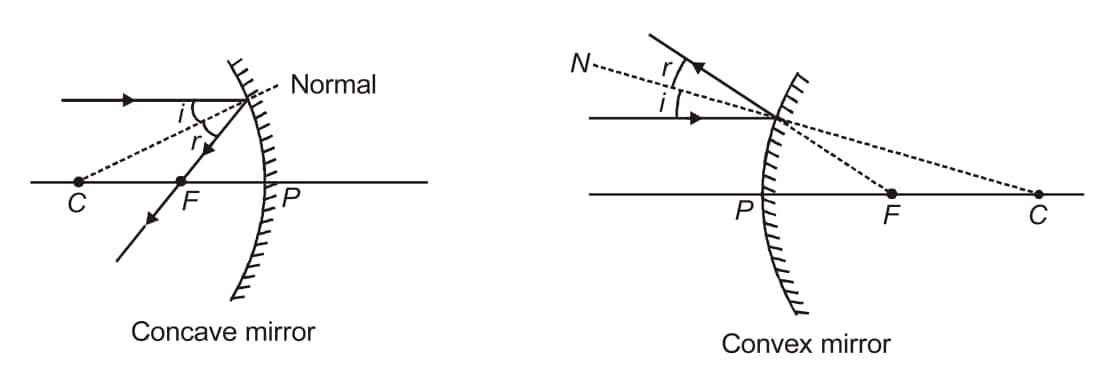
-
A light ray travelling through or appearing from the spherical mirror's centre of curvature is reflected back along the same path.
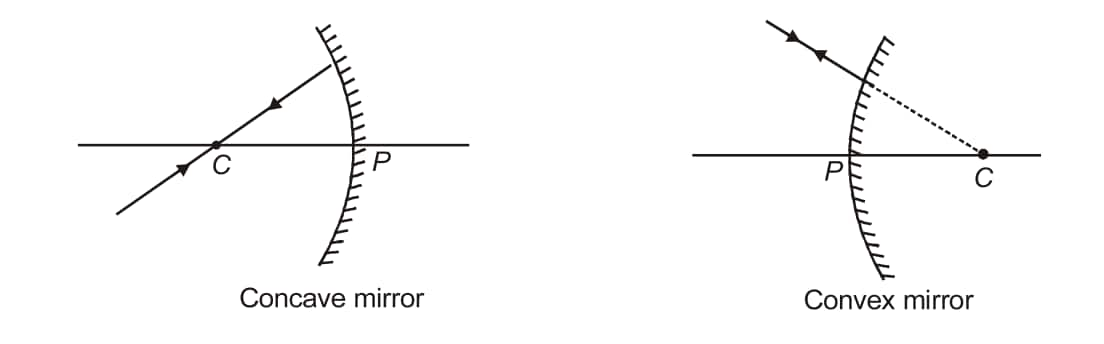
-
A light ray travelling through or coming from the focus of a spherical mirror becomes parallel to the principal axis.
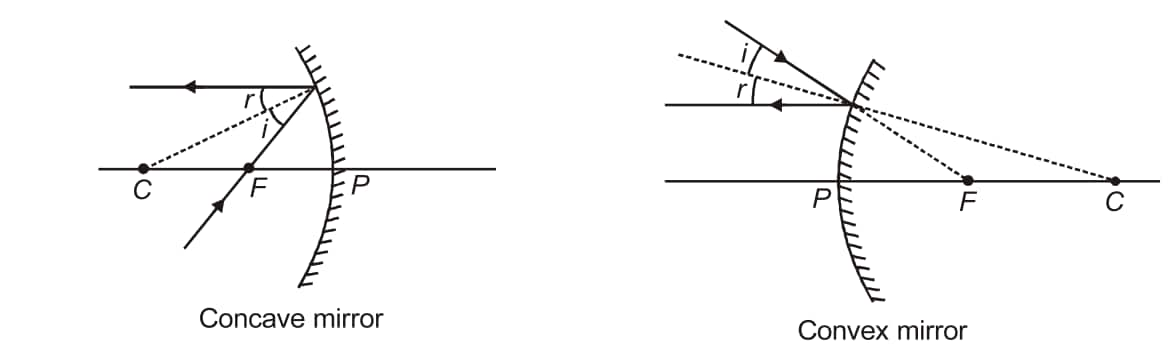
-
A ray of light incident at a spherical mirror's pole is reflected back, making the same angle at the principal axis.
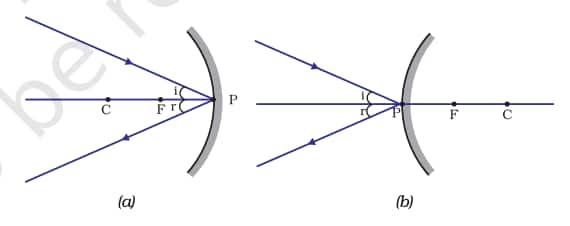
Image formation by a concave mirror:
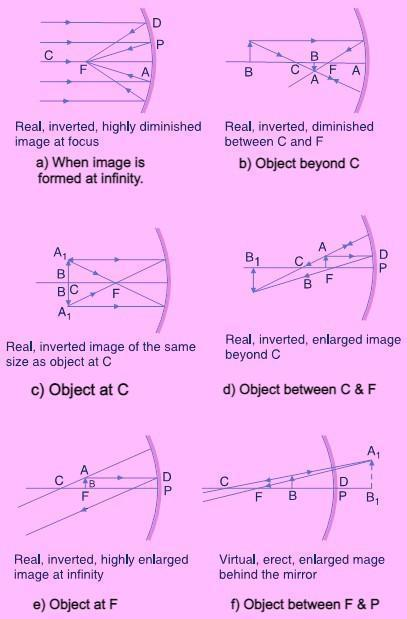
Uses of Concave Mirrors:
To obtain intense parallel beams of light, concave mirrors are often employed in torches, searchlights, and vehicle headlights.
They're frequently utilised as shaving mirrors to get a better view of one's face. Concave mirrors are used by dentists to see large images of patients' teeth.
Solar furnaces use large concave mirrors to focus sunlight and produce heat.
Image Formation by Convex Mirror

Uses of Convex Mirrors
Vehicles frequently employ convex mirrors as rear-view (wing) mirrors. These side mirrors are mounted on the vehicle's flanks and allow the driver to observe traffic behind him or her, ensuring safer driving. Convex mirrors are preferred because they produce an erect, if diminished, picture every time. Furthermore, because they are curved outwards, they have a larger field of view. As a result, convex mirrors allow the driver to see a considerably wider area than a plane mirror would
Sign Convention for Reflection by Spherical Mirrors
All distances are measured from the origin, which is the pole of the mirror.
-
Positive distances are those measured in the direction of incident rays.
-
The lengths measured in the opposite direction of the incoming rays are known as negative distances.
-
Positive distances are those measured upward and perpendicular to the principal axis.
-
Distances measured below and perpendicular to the principal axis are considered negative.
Mirror Formula and Magnification
The distance between an object and its pole in a spherical mirror is known as the object distance (u). The image distance is the distance between the picture and the pole of the mirror (v). The focal length (f) is the distance between the primary focus and the pole. The mirror formula provides a relationship between these three quantities, which is stated as
$\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$
Magnification:
Magnification ( $m$ ) of a spherical mirror is defined as the ratio of the height of the image to the height of the object. Its magnitude indicates how many times the size of the image is compared to that of the object, and its sign indicates whether it is erect or inverted. A positive sign indicates an erect image and a negative sign indicates an inverted image.
$
m=\frac{\text { height of the image }}{\text { height of the object }}=\left[\frac{h^{\prime}}{h}\right]=-\frac{v}{u}
$
Refraction of Light
The refraction of light is the bending of light beams as they move from one medium to another.
Laws of Refraction
The incident ray, the refracted ray and the normal to the interface of two transparent media at the point of incidence all lie in the same plane.
The ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant, for the light of a given colour and for the given pair of media. This law is also known as Snell’s law of refraction.
If i is the angle of incidence and r is the angle of refraction, then,
$\frac{\sin i}{\sin r}$ constant
The Refractive Index:
The refractive index expresses the magnitude of the change in light direction that occurs in a given pair of media. This can be stated mathematically as,
$\mathrm{n}_{21}= \frac{\text{Speed of light in medium 1}}{\text{Speed of light in medium 2}} =\frac{\mathrm{v}_1}{\mathrm{v}_2}$
Similarly, the refractive index of medium 1 in comparison to medium 2 is denoted as $n_{12}$.
If medium 1 is vacuum or air, the refractive index of medium 2 with respect to vacuum is taken into account. This is referred to as the medium's absolute refractive index.
Refraction by Spherical Lenses
Lens: A spherical lens is a piece of transparent glass joined by two spherical surfaces.
Spherical lenses are classified into two categories.
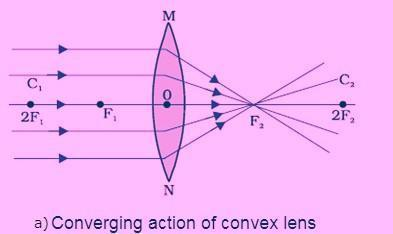
Convex lens: A convex lens bulges outward and is thicker in the centre and narrower at the corners. As depicted below, a convex lens converges the light rays. As a result, convex lenses are called converging lenses.
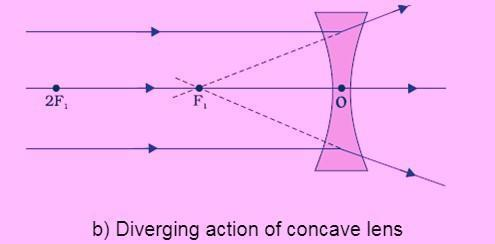
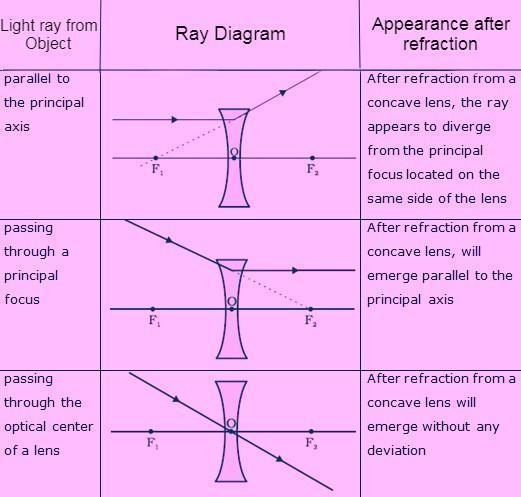
Concave lens: A concave lens bulges inward and is thinner in the centre and thicker at the borders. As seen in the Figure below, such lenses diverge light rays.
A lens, whether convex or concave, has two spherical surfaces that form a sphere. The centres of these spheres are known as the lens's centres of curvature, which are generally denoted by the letter C. Because there are two centres of curvature, we can refer to them as C1 and C2.
The principal axis of a lens is an imaginary straight line that passes across its two centres of curvature, as shown in Figure (a).
The optical centre of a lens is located at its central point. It is commonly represented by the letter O. A ray of light travels through the optical centre of a lens without deviating.
The effective diameter of a spherical lens's circular contour is referred to as its aperture.
Figure (a) shows numerous beams of light parallel to the primary axis falling on a convex lens. These rays are converging to a point on the primary axis after being refracted by the lens. This position on the major axis is referred to as the lens's principal focus.
The letter F is commonly used to denote principal focus. A lens has two principal foci.
Similarly, in Figure (b), numerous beams of light parallel to the principal axis fall on a concave lens. These rays appear to diverge from a point on the principal axis after being refracted by the lens. The principal focus of the concave lens is located on the principal axis.
The focal length of a lens is the distance between the principal focus and the optical centre, denoted by the letter f.
Image Formation by Lenses
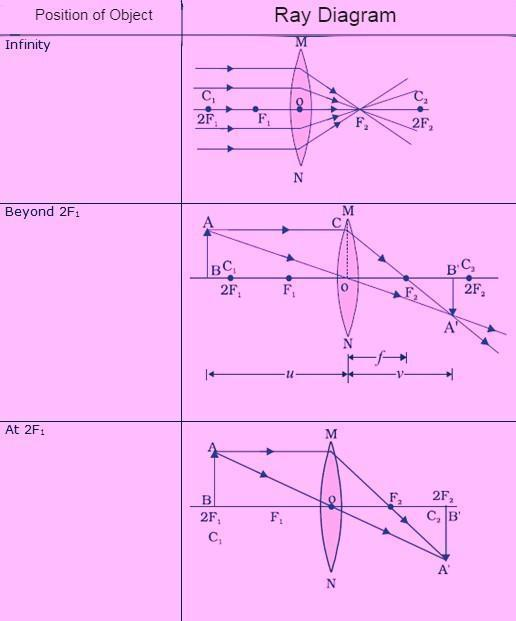
Nature, position and relative size of the image formed by a convex lens for various positions of the object
| Position of the object | Position of the image | Relative size of the image | Nature of the image |
| At infinity | At focus F2 | Highly diminished, point-sized | Real and inverted |
| Beyond 2F1 | Between F2 and 2F2 | Diminished | Real and inverted |
| At 2F1 | At 2F2 | Same size | Real and inverted |
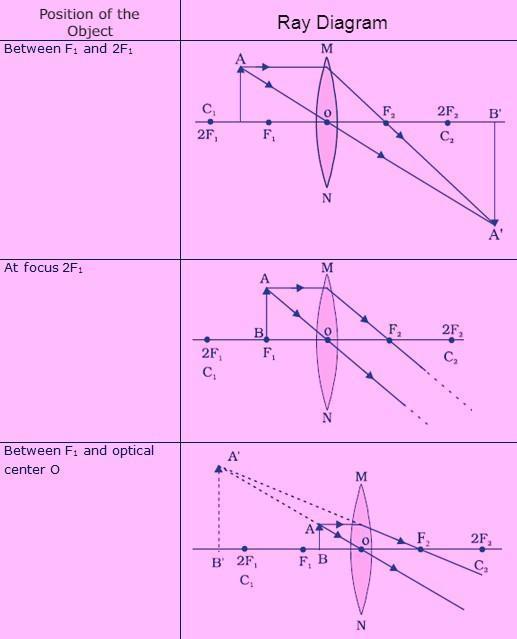
| Between F1 and 2F1 | Beyond 2F2 | Enlarged | Real and inverted |
| At focus F1 | At Infinity | Infinitely large or very large | Real and inverted |
| Between Focus F1 and Optical Centre O. | On the same side of the lens as the Object. | Enlarged | Virtual and erect |
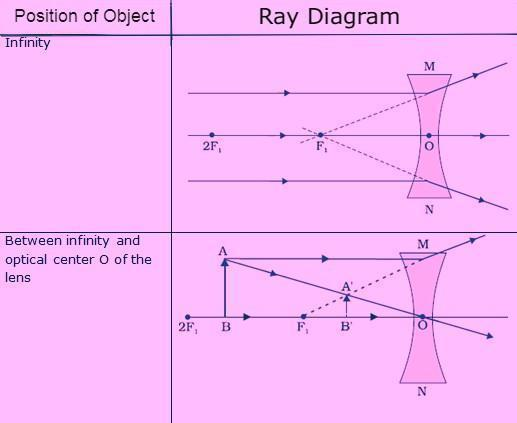
Nature, position and relative size of the image formed by a concave lens for various positions of the object
| Position of the object | Position of the image | Relative size of the image | Nature of the image |
| At infinity | At focus F1 | Highly diminished, point-sized | Virtual and erect |
| Between Infinity and the Optical centre O of the lens. | Between Focus F1 and Optical Centre O. | Diminished | Virtual and erect |
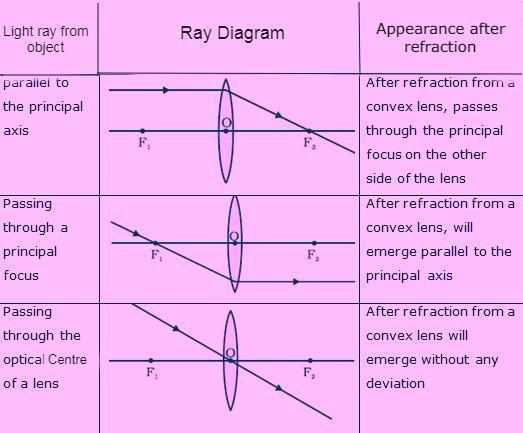
Image Formation in Lenses Using Ray Diagrams:
The ray diagram allows us to investigate the nature, position, and relative size of the picture created by lenses.
For Convex lens:
For Concave lens:
The ray diagrams for image generation in a convex lens for a few object placements are presented in the table below.
The ray diagrams for image generation in a concave lens for a few object placements are presented in the table below.
Sign Convention for Spherical Lenses
-
All distances are measured from the optical centre of the lens.
-
Positive distances are those measured in the same direction as the incident light.
-
Negative distances are those measured in the direction of incident light.
-
Positive distances are those measured upward and perpendicular to the principal axis.
-
Distances measured downhill and perpendicular to the principal axis are considered negative.
Lens Formula and Magnification
We also have a spherical lens formula. This equation expresses the relationship between object distance (u), image distance (v), and focal length (f). The lens formula is written as
$\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$
The letter M stands for magnification. If h is the height of the object and h′ is the height of the image generated by a lens, then the lens's magnification is given by,
$m=$ Height of image(h') / Height of Object (h)
$\mathrm{m}=\mathrm{h'} / \mathrm{h}$
Power of a Lens
A lens's power is defined as the reciprocal of its focal length. It is denoted by the letter P. The power P of the focal length f of a lens is given by,
$P=\frac{1}{f}$
How to Master Class 10 Science Chapter 9: Light Reflection and Refraction?
Chapter 9 Light - Reflection and Refraction describes the behaviour of light upon hitting a surface or even traversing a transparent medium. It discusses the key concepts such as mirror reflection, lens refraction, ray diagrams, and the formation of an image, which are frequently asked in exams. Having a good conceptual clarity and a good command of numericals and ray diagrams, this chapter becomes simple and high scoring among Class 10 students.
- Begin by learning the fundamental laws of refraction and reflection.
- Study all the terms of the mirrors and lenses: principal axis, pole, focus, centre of curvature, radius of curvature.
- Practice ray diagrams of concave and convex mirrors and lenses until you can draw a correct ray diagram without consulting the book.
- Learn sign conventions (New Cartesian Sign Convention) to prevent the majority of numerical errors.
- Master the mirror formula and numericals related to magnification one by one by practising step by step to gain higher speed and accuracy.
- Learn the lens formula and magnification formula, and solve numerous problems with both concave and convex lenses.
- Use real-life examples (shining torches, water refraction, mirrors in vehicles) to connect concepts and build understanding.
- Revise applications like the working of the human eye, refractive index, apparent depth, and reasons for phenomena like the bending of light in water.
- Complete all NCERT exercise questions and exemplar problems, as too many of the questions in the board exam would directly be of this pattern.
- Make a sheet of the formula sheet, with the mirror formula, lens formula, magnification and relation with refractive index, so that one can revise quickly.
- Practise HOTS questions involving multiple steps or combined optical systems for better conceptual clarity.
Importance of Class 10 Physics Chapter 9 Notes
Light Reflection and Refraction Class 10 Science Chapter 9 CBSE notes provide a clear and concise summary of all key concepts of Light – Reflection and Refraction, making revision faster and more effective. These Light Reflection and Refraction Class 10 Science notes simplify complex ideas like ray diagrams, mirror formulas, and refraction principles so students can understand and remember them easily. They are designed to support exam-focused learning and strengthen conceptual clarity. With these notes, students can prepare efficiently and score higher in board exams.
Quick Revision Tool
- Class 10 physics chapter 9 notes offer a brief overview of the reflection and refraction of light, so last-minute preparation before CBSE board exams is easier.
Covering All the Major Concepts
- The Light – Reflection and Refraction Class 10 Notes cover laws of reflection, refraction, refractive index, mirror formula, and lens formula, so that students do not miss anything important.
Exam-Oriented Preparation
- These NCERT notes for class 10 Science chapter 9 PDF serve to emphasise key formulas and diagrams that are very common in board exams and which may be answered to gain better marks.
Time-Saving Advantage
- The students do not have to update the entire NCERT textbook to be ready to take the exams: short and structured Class 10 physics chapter 9 notes will be enough to study.
Increases Competitiveness Examination Readiness
- Class 10 physics chapter 9 notes can also be used in NEET, NTSE and JEE foundation exams, where light and optics are significant aspects of the exam.
Simplified Diagrams to Practice
- Ray diagrams and concave mirror diagrams (convex lens and refraction through a prism) with well-labelled diagrams are provided as a way to learn visually and to remember easily.
Improves Conceptual Learning
- Structured notes provide an easy way to distinguish between reflection and refraction, and total internal reflection, as well as apply concepts to real life.
Anywhere and Everywhere
- Students are given the chance to download PDF notes of Chapter 9 Physics of Class 10 in order to revise them offline and prepare anywhere and anytime.
Class 10 Chapter Wise Notes
Well-organised revision notes help students prepare better for Class 10 Science exams. These Chapter-wise notes on NCERT Class 10 Science are comprehensive in terms of definitions and formulas, diagrams and key concepts of the latest CBSE syllabus. The notes will assist the students to revise within a short time and not only in board exams but also in competitive exams.
NCERT Solutions of Class 10 Subject Wise
NCERT Class 10 Exemplar Solutions for Other Subjects:
NCERT Books and Syllabus
Frequently Asked Questions (FAQs)
Because of refraction — the light bends when it moves from water to air, making the straw look bent.
It helps us understand things like how we see ourselves in mirrors, how glasses or lenses work, and why stars twinkle.
Most students construct rays without rules (such as rays parallel to the principal axis running through the focus, rays passing through the optical centre without deviation). Always use two or more standard rules of the rays in order to be able to locate the images.
Dotted lines (dashed rays) should be placed behind the lens or mirror, and represented as a virtual image.
Adopt the New Cartesian Sign Convention:
When the distances are to the right of the pole (mirror) or optical centre (lens), the distances are positive.
Distances to the left are negative.
Positive heights are upwards, and negative heights are downwards.
Due to the fact that they forget to use the sign convention correctly or to mix up the distance of the object (u) and the distance of the image (v).
In concave mirrors/lenses, v is negative in the real images.
In the case of convex lenses, real image distances are positive.
Cross-check with the type of image expected from the ray diagram.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
