NCERT Solutions for Exercise 12.2 Class 10 Maths Chapter 12

Q: How exercise 12.2 is different from 12.1 ?

E xercise 12.2 consist of many numericals based on real life examples and their concepts are little bit different from the previous exercise.

Q: What are the important points to be covered in exercise 12.2?

T he exercise deals with a question related to the area of circles. These are important topics which will be important and covered in higher classes

Q: From How many points we can draw a circle, and can we trace these points in straight line and form triangle with them?

F rom three non-collinear points we can draw a circle, talking about triangle then yes we can make depending upon coordinates of point we draw a triangle out of it.

NCERT Solutions for Exercise 12.2 Class 10 Maths Chapter 12 - Areas related to circles

Edited By Ramraj Saini | Updated on Nov 27, 2023 05:06 PM IST

NCERT Solutions For Class 10 Maths Chapter 12 Exercise 12.2

NCERT Solutions for Exercise 12.2 Class 10 Maths Chapter 12 Areas related to circles are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Class 10 Maths ex 12.2 lists a few practice numerical problems on, area of a quadrant of the circle, the area swept by the hands of the clock, etc. The Class 10 Maths chapter 12 exercise 12.2 covers the topics like the concept of finding major and minor segment/sectors subtended by the chord of the circle. Also, some properties and technical terms of circular curves are enclosed with some special conditions

Scholarship Test: Vidyamandir Intellect Quest (VIQ)

Don't Miss: JEE Main & NEET 2026 Scholarship Test (Class 10): Narayana | Aakash

This Story also Contains

NCERT Solutions For Class 10 Maths Chapter 12 Exercise 12.2
Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 12 exercise 12.2
Assess NCERT Solutions for Class 10 Maths chapter 12 exercise 12.2
More About NCERT Solutions for Class 10 Maths Chapter 12 Exercise 12.2
Benefits of NCERT Solutions for Class 10 Maths Chapter 12 Exercise 12.2
NCERT Solutions for Class 10 Subject Wise

NCERT Solutions for Exercise 12.2 Class 10 Maths Chapter 12 - Areas related to circles

Exercise 12.2 Class 10 Maths which is another exercise followed by exercise 12.1 that includes the rest of the part of areas related to circles, and is important as per the exams. Questions based on the area of sector out of some given conditions like radius and angle of the sector, and is like a base for the exam. 10th class Maths exercise 12.2 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.

Areas Related to Circles Exercise 12.1
Areas Related to Circles Exercise 12.3

Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 12 exercise 12.2

Download PDF

Assess NCERT Solutions for Class 10 Maths chapter 12 exercise 12.2

Areas Related to Circles Class 10 Chapter 12 Exercise: 12.2

Q1 Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60°.

Answer:

We know that the area of a sector having radius r and angle $\Theta$ is given by:-

$Area\ =\ \frac{\Theta}{360^{\circ}}\times \pi r^2$

Thus the area of the given sector is:-

$\\=\ \frac{60^{\circ}}{360^{\circ}}\times \pi \times 6^2\\\\=\ \frac{132}{7}\ cm^2$

Q2 Find the area of a quadrant of a circle whose circumference is 22 cm.

Answer:

We are given the circumference of the circle.

Thus,

$\\2\pi r\ =\ 22\\\\r\ =\ \frac{11}{\pi}\ cm$

Also, we know that the area of a sector is given by :

$Area\ =\ \frac{\Theta}{360^{\circ}}\times \pi r^2$

It is given that we need to find the area of a quadrant thus $\Theta\ =\ 90^{\circ}$

Hence the area becomes:-

$\\=\ \frac{90}{360^{\circ}}\times \pi \left ( \frac{11}{\pi} \right )^2\\\\=\ \frac{77}{8}\ cm^2$

Q3 The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.

Answer:

The minute hand rotates 360 ^o in one hour.

We need to find rotation in 5 min. :-

$=\ \frac{360^{\circ}}{60}\times 5\ =\ 30^{\circ}$

The area of the sector is given by :

$\\Area\ =\ \frac{\Theta}{360^{\circ}}\times \pi r^2\\\\Area=\ \frac{30}{360^{\circ}}\times \pi \times 14^2\\\\Area=\ \frac{154}{3}\ cm^2$

Hence the area swept by minute hand in 5 minutes is .

Q4 A chord of a circle of radius 10 cm subtends a right angle at the center. Find the area of the corresponding : (i) minor segment

Answer:

The angle in the minor sector is 90 ^o .

Thus the area of the sector is given by:-

$\\Area\ =\ \frac{\Theta}{360^{\circ}}\times \pi r^2\\\\Area=\ \frac{90^{\circ}}{360^{\circ}}\times \pi \times 10^2\\\\Area=\ \frac{1100}{14}\ cm^2\ =\ 78.5\ cm^2$

Now the area of a triangle is:-

$Area\ =\ \frac{1}{2}bh\ =\ \frac{1}{2}\times 10\times 10\ =\ 50\ cm^2$

Thus the area of minor segment = Area of the sector - Area of a triangle

or $=\ 78.5\ -\ 50\ =\ 28.5\ cm^2$

Q4 A chord of a circle of radius 10 cm subtends a right angle at the center. Find the area of the corresponding : (ii) major sector. (Use π = 3.14)

Answer:

The area of the major sector can be found directly by using the formula :

$Area\ =\ \frac{\Theta}{360^{\circ}}\times \pi r^2$

In the case of this, the angle is 360 ^o - 90 ^o = 270 ^o .

Thus the area is : -

$\\=\ \frac{270^{\circ}}{360^{\circ}}\times \pi \times 10\times 10\\\\=\ \frac{3300}{14}\ =\ 235.7\ cm^2$

Q5 In a circle of radius 21 cm, an arc subtends an angle of 60° at the center. Find: (i) the length of the arc

Answer:

The length of the arc is given by:-

$Length\ of\ arc\ =\ \frac{\Theta}{360^{\circ}} \times 2\pi r$

$\\=\ \frac{60^{\circ}}{360^{\circ}} \times 2\times \pi \times 21\\\\=\ 22\ cm$

Hence the length of the arc is 22 cm.

Q5 In a circle of radius 21 cm, an arc subtends an angle of 60° at the center. Find: (ii) area of the sector formed by the arc

Answer:

We know that the area of the sector is given by:-

$Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2$

$\\=\ \frac{60}{360^{\circ}}\ \times \pi \times 21^2\\\\=\ 231\ cm^2$

Thus the area of the sector is 231 cm ² .

Q5 In a circle of radius 21 cm, an arc subtends an angle of 60° at the center. Find: (iii) area of the segment formed by the corresponding chord

Answer:

For the area of the segment, we need to subtract the area of the triangle attached with the area of arc.

Thus consider the triangle:-

It is given that the angle of arc is 60 ^o , or we can say that all angles are 60 ^o (since two sides are equal). Hence it is an equilateral triangle.

Area of triangle is:-

$\\=\ \frac{\sqrt{3}}{4}\times a^2\\\\\\=\ \frac{\sqrt{3}}{4}\times 21^2\\\\=\ \frac{441\sqrt{3}}{4}\ cm^2$

Hence the area of segment is:-

$=\ \left (231\ -\ \frac{441\sqrt{3}}{4} \right )\ cm^2$

Q6 A chord of a circle of radius 15 cm subtends an angle of 60° at the center. Find the areas of the corresponding minor and major segments of the circle.
(Use $\pi = 3.14$ and $\sqrt 3 = 1.73$ )

Answer:

The area of the sector is :

$\\=\ \frac{\Theta }{360^{\circ}}\times \pi r^2\\\\=\ \frac{60^{\circ} }{360^{\circ}}\times \pi \times 15^2\\\\=\ 117.85\ cm^2$

Now consider the triangle, the angle of the sector is 60 ⁰ .

This implies it is an equilateral triangle. (As two sides are equal so will have the same angle. This possible only when all angles are equal i.e., 60 ^o .)

Thus, the area of the triangle is:-

$=\ \frac{\sqrt{3}}{4}\times 15^2$

or $=\ 56.25 \sqrt{3}\ =\ 97.31\ cm^2$

Hence area of the minor segment : $=\117.85\ -\ 97.31\ =\ 20.53\ cm^2$

And the area of the major segment is :

$=\ \pi r^2\ -\ 20.53$

or $=\ \pi\times 15^2\ -\ 20.53$

or $=\ 707.14\ -\ 20.53$

or $=\ 686.6\ cm^2$

Q7 A chord of a circle of radius 12 cm subtends an angle of 120° at the center. Find the area of the corresponding segment of the circle.
(Use $\pi = 3.14$ and $\sqrt3 = 1.73$ )

Answer:

For the area of the segment, we need the area of sector and area of the associated triangle.

So, the area of the sector is :

$=\ \frac{120^{\circ}}{360^{\circ}}\times \pi \times 12^2$

or $=\ 150.72\ cm^2$

Now, consider the triangle:-

Draw a perpendicular from the center of the circle on the base of the triangle (let it be h).

Using geometry we can write,

$\frac{h}{r}\ =\ \cos 60^{\circ}$

or $h\ =\ 6\ cm$

Similarly, $\frac{\frac{b}{2}}{r}\ =\ \sin 60^{\circ}$

or $b\ =\ 12\sqrt{3}\ cm$

Thus the area of the triangle is :

$=\ \frac{1}{2}\times 12\sqrt{3}\times 6$

or $=\ 62.28\ cm^2$

Hence the area of segment is: $=\ 150.72\ -\ 62.28\ =\ 88.44\ cm^2$ .

Q8 A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see Fig.). Find (i) the area of that part of the field in which the horse can graze.

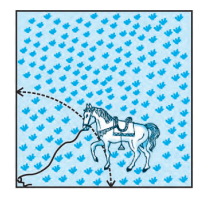
1636091304687

Answer:

The part grazed by the horse is given by = Area of sector

$Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2$

$=\ \frac{90^{\circ}}{360^{\circ}}\ \times \pi \times 5^2$

$=\ 19.62\ m^2$

Q8 A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see Fig.). Find (ii) the increase in the grazing area if the rope were 10 m long instead of 5 m. (Use $\pi = 3.14$ )

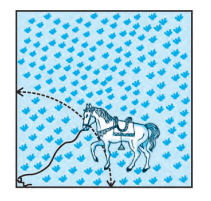
1636091352998

Answer:

When the length of the rope is 10 m, the area grazed will be:-

$Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2$

$=\ \frac{90^{\circ}}{360^{\circ}}\ \times \pi \times 10^2$

$=\ 25 \pi\ m^2$

Hence the change in the grazing area is given by :

$=\ 25 \pi\ -\ \frac{25 \pi}{4}\ =\ 58.85\ m^2$

Q9 A brooch is made with silver wire in the form of a circle with a diameter of 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in Fig. Find: (i) the total length of the silver wire required.

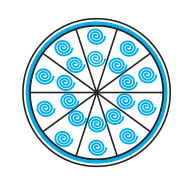
1636091383511

Answer:

The total wire required will be for 5 diameters and the circumference of the brooch.

The circumference of the brooch:-

$\\=\ 2\pi r\\\\=\ 2\times \pi \times \frac{35}{2}\\\\=\ 110\ mm$

Hence the total wire required will be:- _.

Q9 A brooch is made with silver wire in the form of a circle with a diameter of 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in Fig. 12.12. Find : (ii) the area of each sector of the brooch.

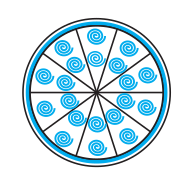
1636091389686

Answer:

The total number of lines present in the brooch is 10 (line starting from the centre).

Thus the angle of each sector is 36 ^o .

The area of the sector is given by:-

$\\Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2\\\\Area=\ \frac{36^{\circ}}{360^{\circ}}\ \times \pi \times \left ( \frac{35}{2} \right )^2\\\\Area=\ \frac{385}{4}\ mm^2$

Q10 An umbrella has 8 ribs that are equally spaced (see Fig. ). Assuming umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.

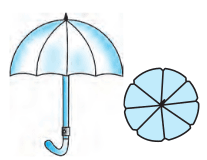
Answer:

It is given that the umbrella has 8 ribs so the angle of each sector is 45 ^o .

Thus the area of the sector is given by:-

$\\Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2\\\\Area=\ \frac{45^{\circ}}{360^{\circ}}\ \times \pi \times 45^2\\\\Area=\ \frac{22275}{28}\ cm^2$

Hence the area between two consecutive ribs is .

Q11 A car has two wipers that do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades.

Answer:

The area cleaned by one wiper is:-

$Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2$

or $=\ \frac{115^{\circ}}{360^{\circ}}\ \times \pi \times 25^2$

or $=\ \frac{158125}{252}\ cm^2$

Hence the required area (area cleaned by both blades) is given by:-

$=\ 2\times \frac{158125}{252}\ =\ \frac{158125}{126}\ cm^2$

Q12 To warn ships for underwater rocks, a lighthouse spreads a red-colored light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships are warned. (Use π = 3.14)

Answer:

The area of the sector is given by:-

$Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2$

In this case, the angle is 80 ^o .

Thus the area is:-

$=\ \frac{80^{\circ}}{360^{\circ}}\ \times \pi \times 16.5^2$

or $=\ 189.97\ Km^2$

Q13 A round table cover has six equal designs as shown in Fig. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs. 0.35 per cm ² . (Use $\sqrt3 = 1.7$ )

Answer:

The angle of each of the six sectors is 60 ^o at the center. $\left ( \because \frac{360^{\circ}}{6}\ =\ 60^{\circ} \right )$

Area of the sector is given by:-

$Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2$

or $=\ \frac{60^{\circ}}{360^{\circ}}\ \times \pi \times 78^2$

or $=\ 410.66\ cm^2$

And the area of the equilateral triangle associated with segment:-

$=\ \frac{\sqrt{3}}{4}\times a^2$

or $=\ \frac{\sqrt{3}}{4}\times 28^2\ =\ 333.2\ cm^2$

Hence the area of segment is : $=\ 410.66\ -\ 333.2\ =\ 77.46\ cm^2$

Thus the total area of design is : $=\6\times 77.46\ =\ 464.76\ cm^2$

So, the total cost for the design is:- $=\ 0.35\times 464.76\ =\ Rs. 162.66$

Q14 Tick the correct answer in the following :

Area of a sector of angle p (in degrees) of a circle with radius R is

(A) $\frac{p}{180}\times 2\pi R$

(B) $\frac{p}{180}\times \pi R^2$

(D) $\frac{p}{720}\times 2\pi R^2$

Answer:

We know that the area of the sector is given by:-

$Area\ =\ \frac{\Theta}{360^{\circ}}\ \times \pi r^2$

$=\ \frac{p}{360^{\circ}}\ \times \pi r^2$

Hence option (d) is correct.

Benefits of NCERT Solutions for Class 10 Maths Chapter 12 Exercise 12.2

Initial benefits of exercise 12.2 Class 10 Maths and the NCERT solutions for Class 10 Maths chapter 12 exercise 12.2 is that as it covers a variety of questions from the basic to a higher level which gives a better understanding of the play
Taking about higher level in exercise 12.2 Class 10 Maths understanding the concepts makes students work on related topics which is helpful to solve better examples under given conditions as mentioned in Class 10 Maths chapter 12 exercise 12.2.
For Class 10 final exams students might find some MCQs, short numerical or long numerical questions from all types are covered in the Class 10 Maths chapter 12 exercise 12.2

Also, see-

NCERT Solutions for Class 10 Subject Wise

Frequently Asked Questions (FAQs)

1. How exercise 12.2 is different from 12.1 ?

Exercise 12.2 consist of many numericals based on real life examples and their concepts are little bit different from the previous exercise.

2. What are the important points to be covered in exercise 12.2?

The exercise deals with a question related to the area of circles. These are important topics which will be important and covered in higher classes

3. What is the formula of the area of a segment of the circle?

Area of a segment of circle = area of the corresponding sector – the area of the corresponding triangle

4. From How many points we can draw a circle, and can we trace these points in straight line and form triangle with them?

From three non-collinear points we can draw a circle, talking about triangle then yes we can make depending upon coordinates of point we draw a triangle out of it.

5. Total how many exercises are there in chapter 12 areas related to circle?

There is a total of 3 exercises there in chapter 12 namely exercise 12.2 exercise 12.2 and exercise 12.3 which have a variety of questions to give a brief analysis of the topic as well as subject.

6. What is the area of the right angled triangle ABC, the right angle at point B ?

Ans: The area of the right-angle triangle is equal to 0.5*base*(height)

Also Read

The Human Eye and The Colorful world Class 10th Notes- Free NCERT Class 10 Science Chapter 11 Notes - Download PDF

NCERT Class 10 Science Chapter 14 Notes Sources Of Energy - Download PDF

Magnetic Effects of Electric Current Class 10th Notes - Free NCERT Class 10 Science Chapter 13 Notes - Download PDF

Electricity Class 10th Notes - Free NCERT Class 10 Science Chapter 12 Notes - Download PDF

Light- Reflection and Refraction Class 10th Notes- Free NCERT Class 10 Science Chapter 10 Notes - Download PDF

Free NCERT Class 10 Maths Chapter 2 Notes - Download PDF

NCERT Syllabus for Class 10 Maths 2024-25 - Download Free PDF

NCERT Solutions for Exercise 12.3 Class 10 Maths Chapter 12 - Areas related to circles

NCERT Solutions for Exercise 12.2 Class 10 Maths Chapter 12 - Areas related to circles

NCERT Solutions for Exercise 12.1 Class 10 Maths Chapter 12 - Areas related to circles

NCERT Solutions for Class 10 Science Chapter 6 Life Processes

NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations

NCERT Exemplar Class 10 Maths Solutions - Chapter Wise Problems with Solutions

NCERT Exemplar Class 10 Science Solutions Chapter 1 Chemical Reactions and Equations

NCERT Exemplar Class 10 Science Solutions - Chapter Wise Problems with Solutions

Articles

Maharashtra State Board 10th Geography Books - Download PDF Free Online

Nov 21, 2024

NMMS Karnataka Result 2024-25: Download DSERT Karnataka Merit List Here

Nov 21, 2024

NMMS Karnataka 2024-25: Exam Date (8 Dec), Admit Card, Answer Key, Cut off, Result

Nov 21, 2024

Maharashtra Board Grading System 2025: SSC & HSC Passing Marks & Important Updates

Nov 21, 2024

Maharashtra Board Seat Number 2025 for HSC & SSC Exams

Nov 21, 2024

10th Time Table 2025 - Check CBSE (OUT) UP, Bihar 10th Exam Dates Here

Nov 21, 2024

Maharashtra SSC Marksheet 2025 Verification: Download MH Board Class 10 Marksheet Here

Nov 21, 2024

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:04 October,2024 - 29 November,2024

Application Process

Exam Pattern

Admit Card

National Institute of Open Schooling 10th examination

Admit Card Date:04 October,2024 - 29 November,2024

Application Process

Exam Pattern

Mock Test

Mizoram Board of School Education 12th Examination

Application Date:07 October,2024 - 22 November,2024

Exam Pattern

Result

Mock Test

Mizoram Board 10th Examination

Application Date:07 October,2024 - 22 November,2024

Exam Pattern

Admit Card

Result

Punjab Board of Secondary Education 10th Examination

Application Correction Date:08 October,2024 - 27 November,2024

Exam Pattern

Result

Admit Card

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Exercise 12.2 Class 10 Maths Chapter 12 - Areas related to circles

NCERT Solutions For Class 10 Maths Chapter 12 Exercise 12.2

Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 12 exercise 12.2

Assess NCERT Solutions for Class 10 Maths chapter 12 exercise 12.2

More About NCERT Solutions for Class 10 Maths Chapter 12 Exercise 12.2

Benefits of NCERT Solutions for Class 10 Maths Chapter 12 Exercise 12.2

NCERT Solutions for Class 10 Subject Wise

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

National Institute of Open Schooling 10th examination

Mizoram Board of School Education 12th Examination

Mizoram Board 10th Examination

Punjab Board of Secondary Education 10th Examination

Popular Questions

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

VMC VIQ Scholarship Test

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

Schools By Medium

By Ownership

By City

By State

NVS

JNVST

Download Careers360 App

All this at the convenience of your phone

Scan and download the app