Some Applications of Trigonometry Class 10th Notes - Free NCERT Class 10 Maths Chapter 9 Notes - Download PDF

Class 10 Some Applications of Trigonometry Notes PDF – Download Free Study Material

Students who wish to access the Some Applications of Trigonometry Class 10 Maths notes can click on the link below to download the entire notes in PDF.

Download PDF

Some Applications of Trigonometry Class 10 Notes

Careers360 experts have curated these Some Applications of Trigonometry Class 10 Notes to help students revise quickly and confidently.

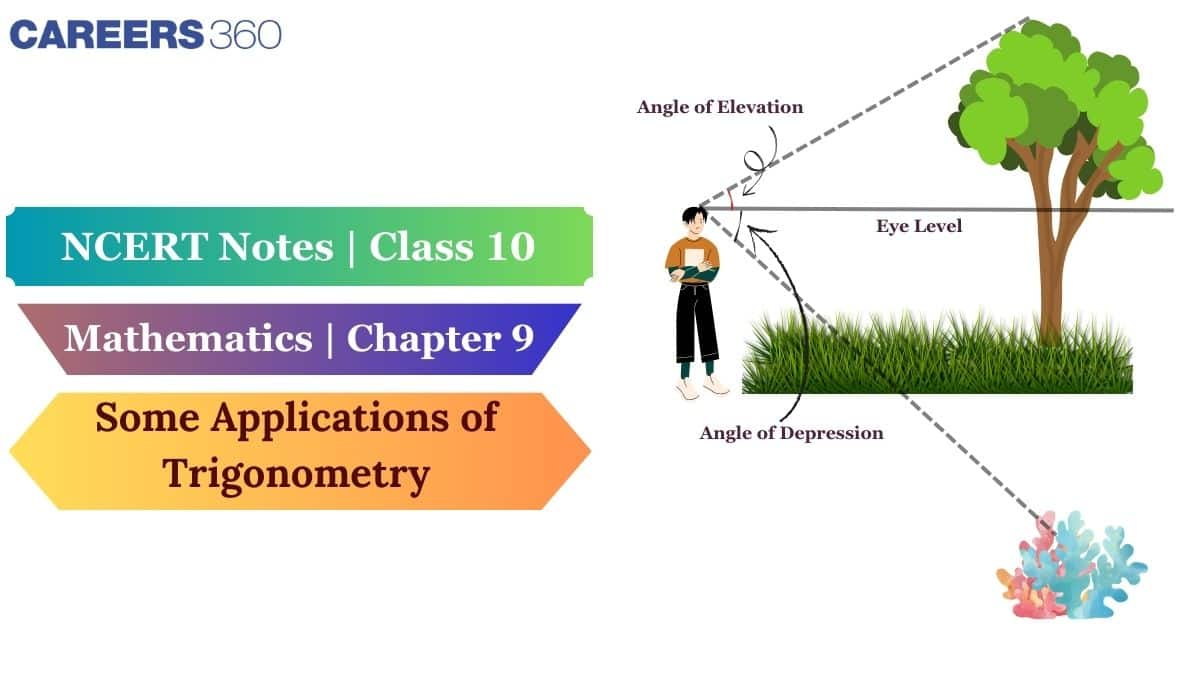
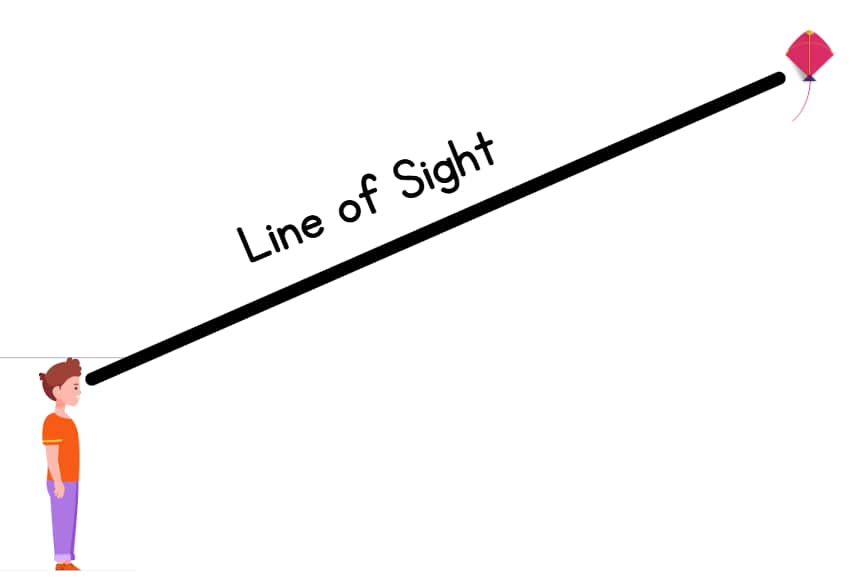
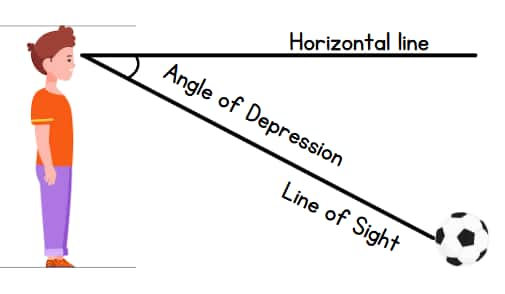
Line of Sight

Observers create an imaginary straight line that extends from their eyes toward the viewed object. The study of trigonometry requires this tool because it enables users to identify angles at specific observational heights.

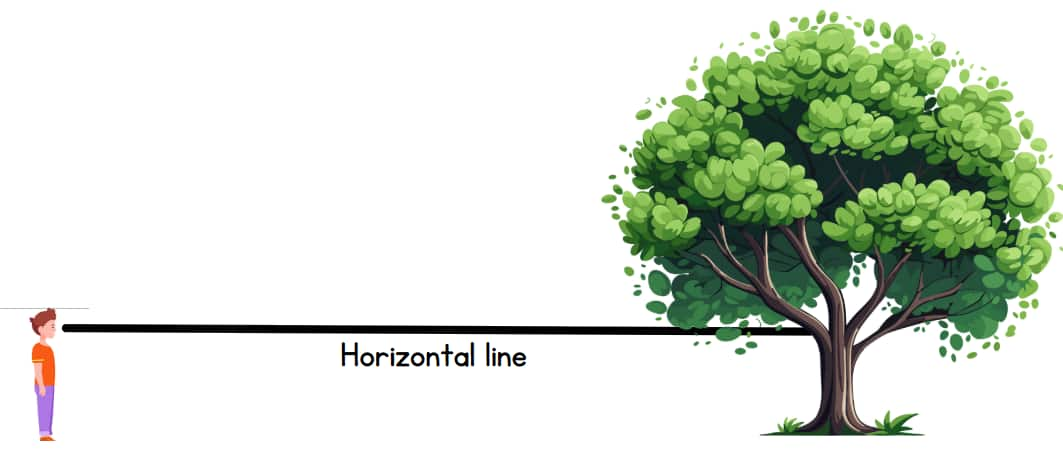
Horizontal line

The horizontal line represents an invisible straight path which runs parallel to the ground, starting from the viewer's eye level. A horizontal line establishes a reference for trigonometry to measure the angles of elevation and depression.

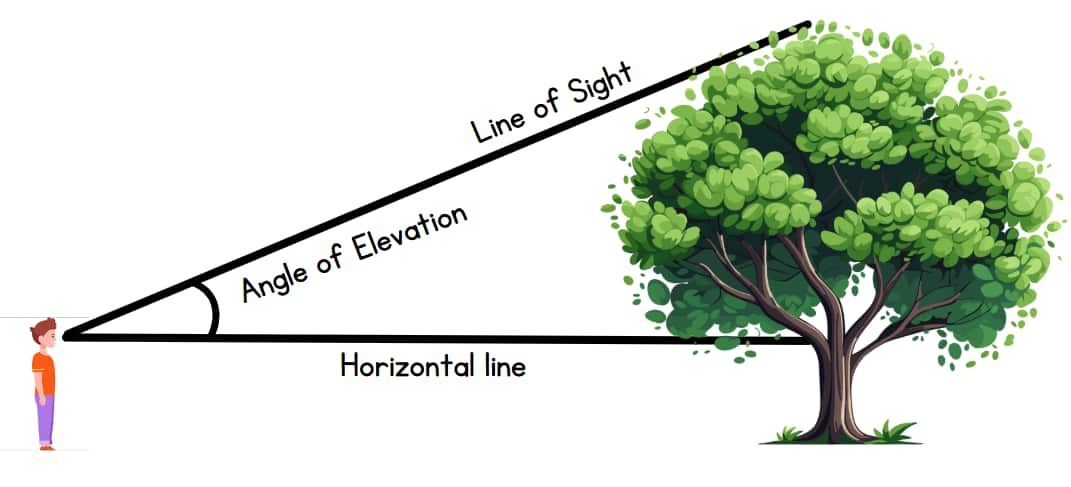
Angle of Elevation

An observer who looks up toward an object will experience this phenomenon. To determine the measurement, the angle formed between the sightline and the eye-level horizontal line.

For Example, if a person looks at the top of a tree, the angle formed between their line of sight and the horizontal line is the angle of elevation.

Angle of Depression

An observer who looks down toward an object will experience this phenomenon. To determine the measurement, the angle formed between the sightline and the eye-level horizontal line.

For Example, if you are standing on a cliff and looking at a boat in the sea, the angle between your line of sight and the horizontal line at your eye level is the angle of depression.

Height and Distance Problems Using Trigonometry

The application of trigonometric ratios enables the solution of problems regarding the measurement of height and distance. The following key sequence directs a solution to these problems:

1. Spot the right-angled triangle present in the provided problem.
2. Identify known along with unknown values of height, distance and angle in this problem.
3. Select the appropriate trigonometric ratio according to the available information.
4. Solve for the unknown value.

Case 1: When the Angle of Elevation is known:

• The observer looks up towards an object.
• The height of the object and the horizontal distance form a right-angled triangle.
• Use the Trigonometric ratios accordingly.

For example, A tower is 30 meters high. The angle of elevation of the top of the tower from a point on the ground is 60°. Find the distance of the point from the base of the tower.

Solution: Given:

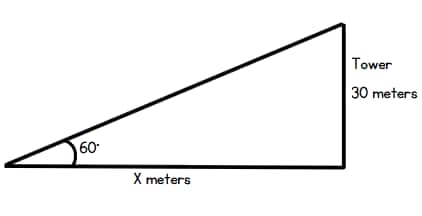
• Height of tower (Perpendicular) = 30 m
• Angle of elevation = 60°
• Distance of the point from the base (Base) = x

Using the formula:

tan θ = $\frac{\text{Perpendicular}}{\text{Base}}$

⇒ tan 60° = $\frac{30}{x}$

⇒ $\sqrt 3$ = $\frac{30}{x}$

⇒ x = $\frac{30}{\sqrt3}$

⇒ x = 10√3 m ≈ 17.32 m

Case 2: When the Angle of Depression is known:

• The observer looks down towards an object.
• The height of the object and the horizontal distance form a right-angled triangle.
• Use the Trigonometric ratios accordingly.

For example, A lighthouse stands on a cliff 50 meters above sea level. A boat is spotted at sea, and the angle of depression from the top of the lighthouse to the boat is 30°. Find the distance of the boat from the base of the cliff.

Solution: Given:

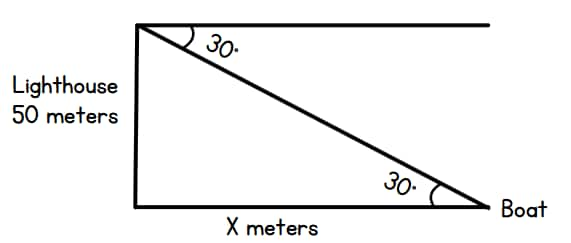
• Height of lighthouse (Perpendicular) = 50 m
• Angle of depression = 30°
• Distance of boat from the base of the cliff (Base) = x

Using the formula:

tan θ = $\frac{\text{Perpendicular}}{\text{Base}}$

⇒ tan 30° = $\frac{50}{x}$

⇒ $ \frac{1}{\sqrt3} = \frac{50}{x}$

⇒ x = 50√3 ≈ 86.6 meters

Some Applications of Trigonometry: Previous Year Question and Answer

Listed below are important previous year question answers for NCERT Class 10 Maths Chapter 9 Some Applications of Trigonometry compiled from different board exams.

Question 1:
A tree of height $h$ metres is broken by a storm in such a way that its top touches the ground at a distance of $x$ metres from its root. Find the height at which the tree is broken. (Here $h>x$)

Solution:

Given:
AB = Height of tree = $h$ metre
Let the height at which the tree is broken, AC = $y$ metres
BC = CD = Broken part of tree = $(h – y)$ metre
∴ In ∆ ACD,
AC² + AD² = CD²
⇒ $y^2 + x^2 = (h – y)^2$
⇒ $y^2 + x^2 = h^2 + y^2 – 2hy$
⇒ $x^2 = h^2 – 2hy$
⇒ $2hy = h^2 – x^2$
$\therefore y =\frac{h^2-x^2}{2h}$ metre
Hence, the correct answer is $\frac{h^2-x^2}{2h}$ metres.

Question 2:
Subhas, a 3.15 m tall tree, and an 11.25 m tall building are positioned such that their feet on the ground are collinear and the tree is located between Subhas and the building. The tree is located at a distance of 7.5 m from Subhas and a distance of 45 m from the building. Further, the eyes of Subhas, the top of the tree, and the top of the building fall in one line. Find the height (in m ) from the ground at which Subhas's eyes are situated.

Solution:

Let XA be Subhas, YB be the tree, and ZC be the building.
YB = 3.15 m
ZC = 11.25 m
AB = 7.5 m
BC = 45 m
XO = AB = 7.5 m
OP = BC = 45 m
⇒ XP = XO + OP = 7.5 + 45 = 52.5 m
Let the height from the ground at which Subhas's eyes are situated be $h$.
OY = BY – OB = 3.15 – $h$
PZ = ZC – PC = 11.25 – $h$
Let the angle of elevation be $\theta$.
In $\triangle$XPZ, $\tan \theta = \frac{\text{PZ}}{\text{PX}} = \frac{11.25-h}{52.5}$ -----------(i)
In $\triangle$XOY, $\tan \theta = \frac{\text{OY}}{\text{OX}} = \frac{3.15-h}{7.5}$ ------------(ii)
$⇒ \frac{11.25-h}{52.5} = \frac{3.15-h}{7.5}$
$⇒ \frac{11.25-h}{7} = \frac{3.15-h}{1}$
$⇒11.25-h = 7(3.15-h)$
$⇒11.25-h = 22.05-7h$
$⇒6h = 10.8$
$\therefore h = \frac{10.8}{6} = 1.8$ m
Hence, the correct answer is 1.8.

Question 3:
The angle of elevation of the top of a building at a distance of 70 m from its foot on a horizontal plane is found to be 60°. Find the height of the building.

Solution:

Height = AC
We know, $\tan \theta=\frac{\text{Perpendicular}}{\text{Base}}$
⇒ $\tan60° =\frac{AC}{70}$
⇒ $\sqrt3=\frac{AC}{70}$
⇒ $AC=70\sqrt3\text{ m}$
Hence, the correct answer is $70\sqrt3\text{ m}$.

NCERT Class 10 Maths Notes – Chapter-Wise Links

We at Careers360 compiled all the NCERT class 10 Maths notes in one place for easy student reference. The following links will allow you to access them.

NCERT Exemplar Solutions for Class 10

Students must check the NCERT Exemplar solutions for class 10 of Mathematics and Science Subjects.

• NCERT Exemplar Class 10 Maths solutions
• NCERT Exemplar Class 10 Science Solutions

NCERT Solutions for Class 10

Students must check the NCERT solutions for class 10 of Mathematics and Science Subjects.

• NCERT Solutions for Class 10 Maths
• NCERT Solutions for Class 10 Science

NCERT Books and NCERT Syllabus

Before the start of a new academic year, students should refer to the latest syllabus to determine the chapters they’ll be studying. Below are the updated syllabus links, along with some recommended reference books.

• NCERT Books Class 10 Maths
• NCERT Books for Class 10 Science
• NCERT Syllabus Class 10 Maths
• NCERT Books Class 10
• NCERT Books for Class 10 English
• NCERT Syllabus Class 10