Free NCERT Class 10 Maths Chapter 2 Notes - Download PDF

A polynomial is an algebraic expression that contains a variable and a degree. In polynomial theory, a variable is also called an indeterminate, and the degree is known as the highest power of the variable. Polynomial expressions are made by arithmetic operations like addition, subtraction, and multiplication. These arithmetic operations are used to define the relationship between variables. Polynomials are used in many areas, like science, economics, mathematics, engineering, etc. In these areas, polynomials are considered as the fundamental tool for analysis and solving problems.

New: Get up to 90% Scholarship on NEET/JEE Coaching from top Coaching Institutes

Don't Miss: JEE Main & NEET 2026 Scholarship Test (Class 10): Narayana | Aakash

This Story also Contains

1. NCERT Class 10 Maths Chapter 2 Polynomials: Notes
2. Types of Polynomials:
3. Graphical Representation
4. Relationship Between Zeros and Coefficients of a Polynomial:
5. Divisor Algorithm:
6. Class 10 Chapter-Wise Notes
7. NCERT Exemplar Solutions for Class 10
8. NCERT Solutions for Class 10
9. NCERT Books and Syllabus

These notes contain all the topics, subtopics, short tricks, formulae, and all the required important key points. These notes cover the basic definition of polynomials, algebraic expressions, degree of polynomials and types of polynomials and their graphical representation. CBSE Class 10 chapter Polynomials also includes the geometrical representation of the zeroes of polynomials. The NCERT class 10th maths notes help the students to understand the concepts of each chapter with the help of definitions, formulas, and examples, and these NCERT notes are designed according to the latest syllabus of NCERT.

NCERT Class 10 Maths Chapter 2 Polynomials: Notes

Polynomials: It is an algebraic expression that can have an exponent as a real number or a whole number. A polynomial represented by p(x), where p is a polynomial in x, and the exponent of x is called the highest degree of x.

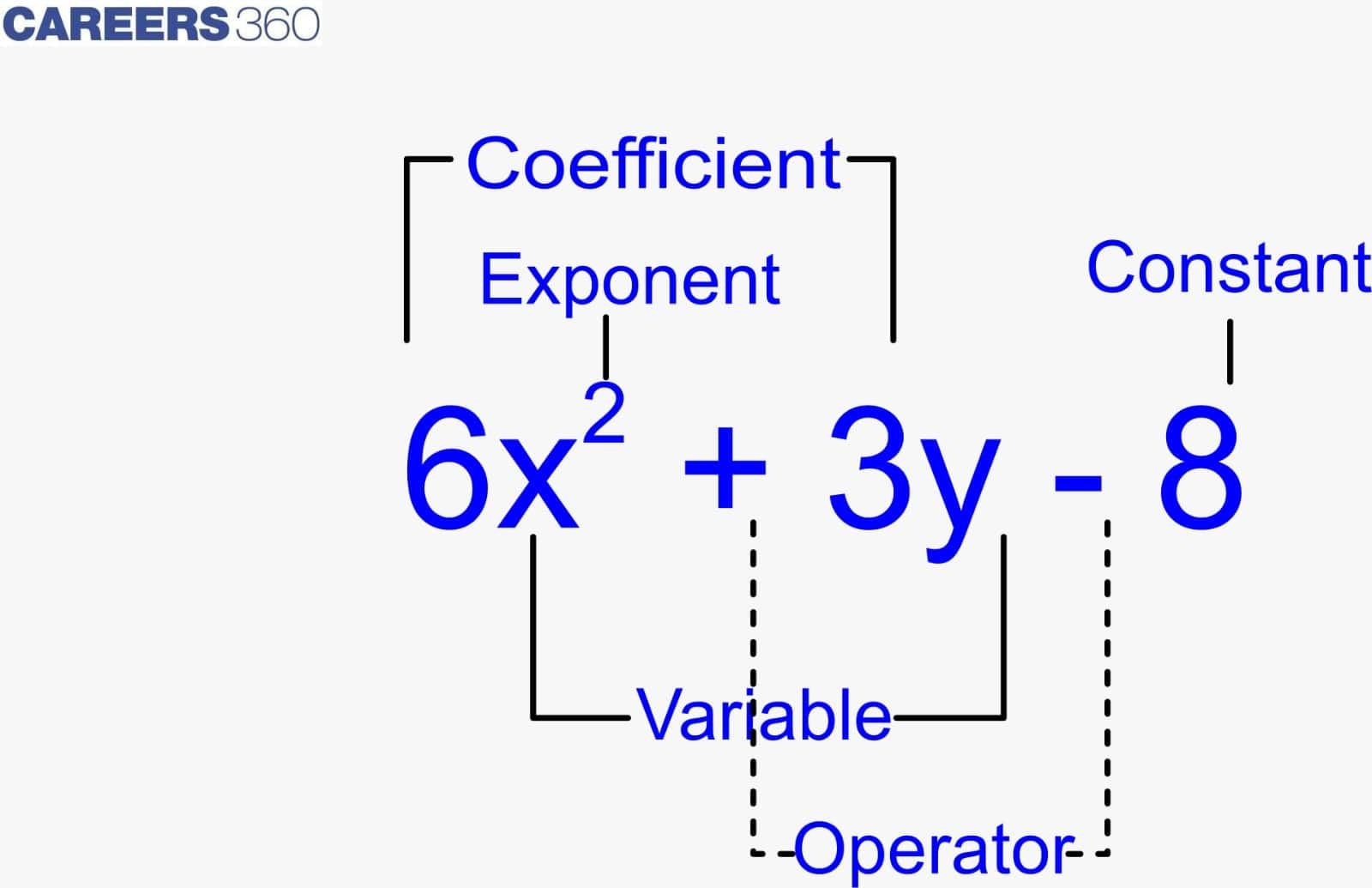
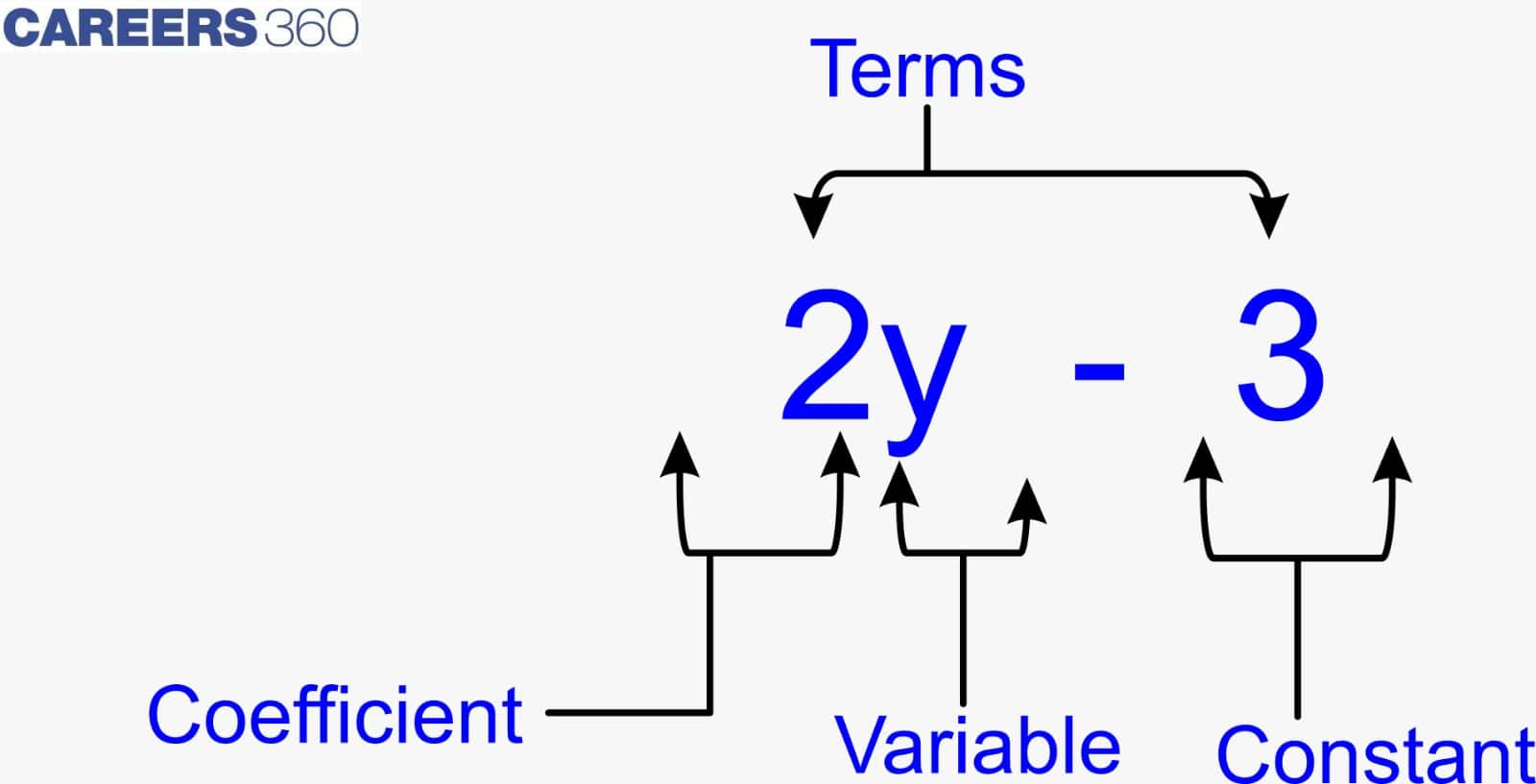
Algebraic Expressions: An algebraic expression is an equation with variables and constants that is made up of arithmetic operators.

Types of Polynomials:

Polynomials can be divided into two categories based on the following characteristics:
1. Number of terms
2. Degree of polynomials

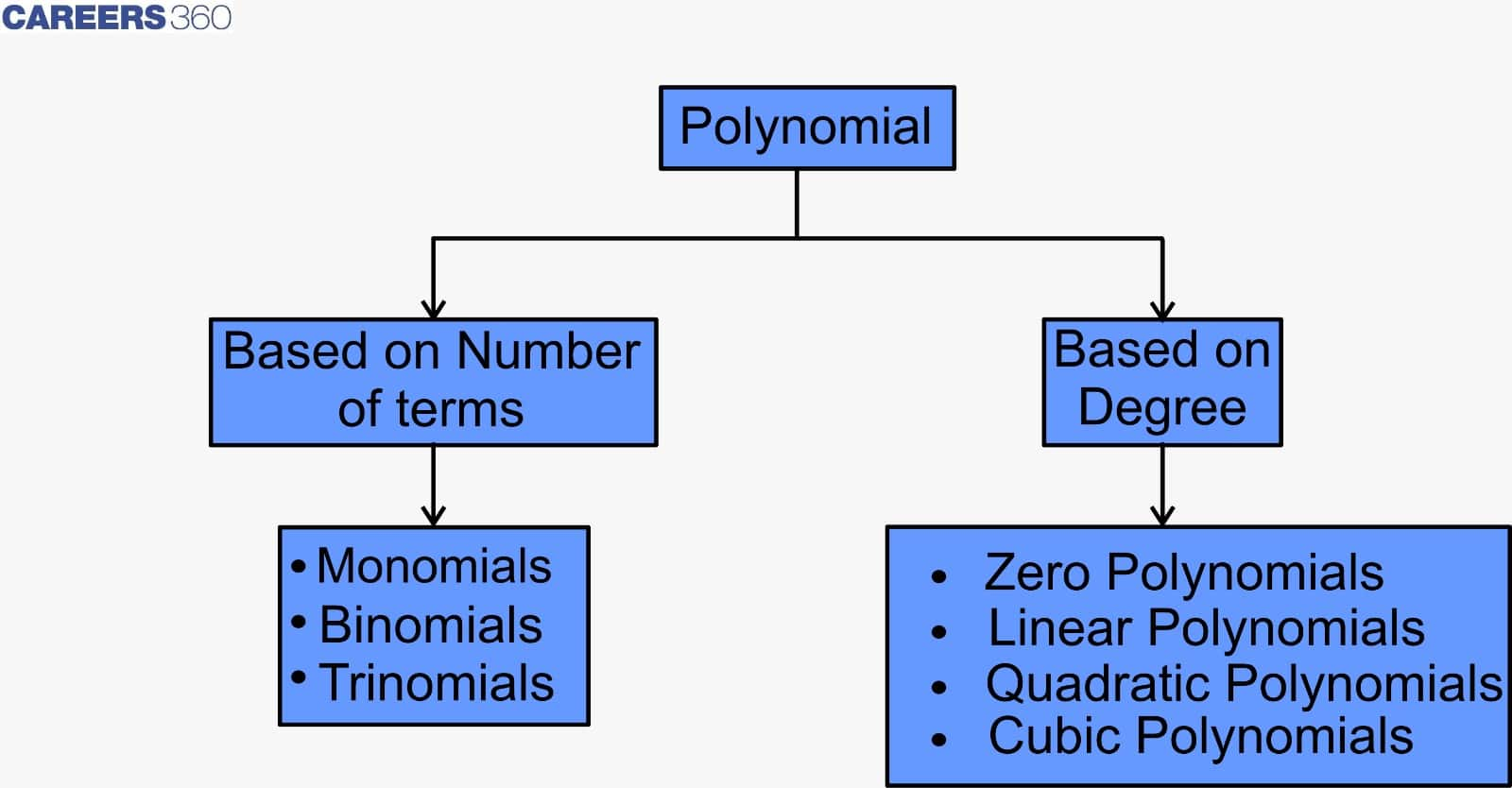
Based on the number of Terms:

A polynomial expression can have one or more terms, and according to the number of terms, polynomials are as follows:
1. Monomials: A polynomial that has only one term is called a monomial.
Example: 3x, 5pq, 6p²

2. Binomials: A polynomial that has two unlike terms is called a binomial.
Example: 3x + 2, 4x² + 6

3. Trinomials: A polynomial that has three unlike terms is called a trinomial.
Example: 6x² + 3x - 2

Based on Degree of Polynomials:

1. Zero Polynomials: A polynomial that has 0 as a degree is called a zero or constant polynomial.
Example: 2x⁰, 5y⁰

2. Linear Polynomial: A polynomial that has 1 as a degree is called a linear polynomial.
Example: 3x + 1, 4y + 5

3. Quadratic Polynomial: A polynomial that has 2 as a degree is called a quadratic polynomial.
Example: 5x² + 3x + 1

4. Cubic Polynomial: A polynomial that has 3 as a degree is called a cubic polynomial.
Example: 7x³ + 5x - 2

Zeros of a Polynomial:

The value of the polynomials that make the polynomials equal to zero.
Example: For the polynomial p(x) = x² - 9, the zeros are x=3 and x=−3, because p(3) = 3² - 9 = 0 and p(−3)=(−32)−9=0.

Graphical Representation

The representation of different types of polynomials is as follows.

Geometrical Meaning of the Zeros of a Polynomial:

When the x-coordinate of the point of intersection is at the x-axis of the graph, then this is called geometrically the zeroes of a polynomial.

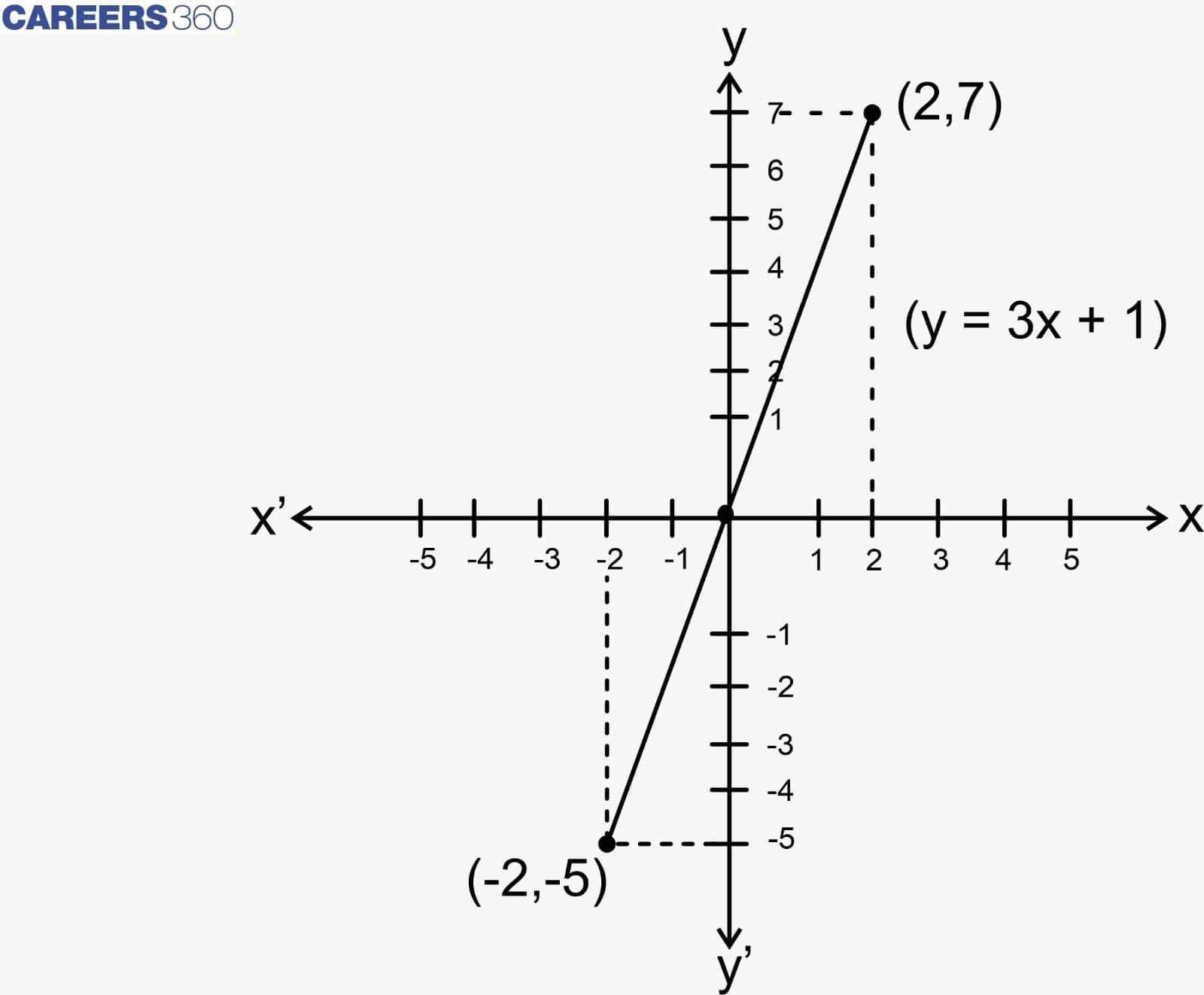
Geometrical Meaning of Zeros of Linear Polynomial:

The general form of the linear polynomial is y = ax + b, where a must not be equal to 0. For example, the equation is y = 3x + 1 for x = 2, and -2, the line of the graph passing through the points (2, 7) and (-2, -5)

The graph is shown below:

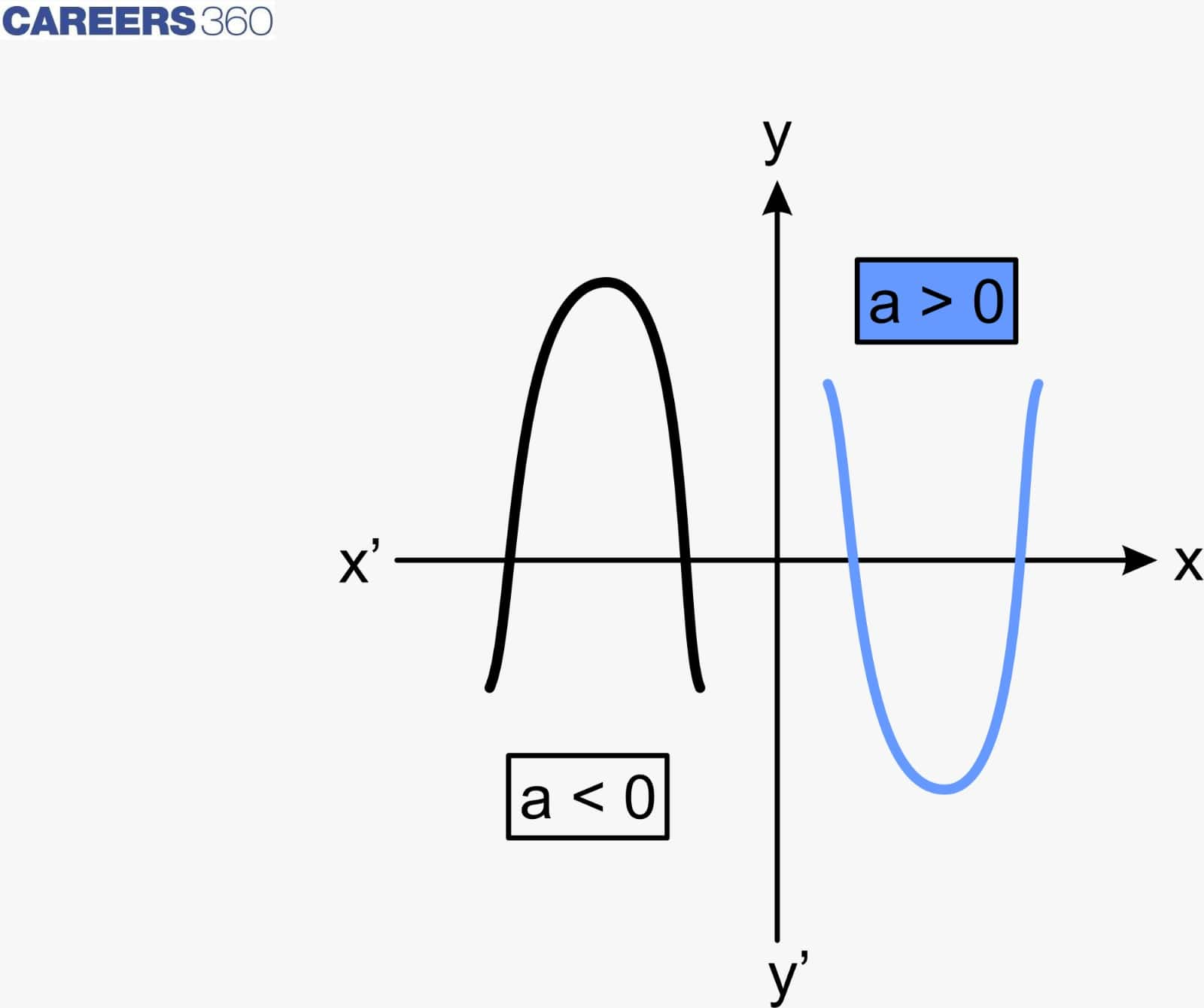
Geometrical Meaning of Zeros of a Quadratic Polynomial:

The general form of the quadratic polynomials is ax² + bx + c, where a is not equal to zero. The graph for a quadratic equation looks like a symbol U or a parabola, and the direction of U or the parabola may be upward or downward depending on the value of a. It can cut the points at zero, one, or two points.
The geometrical representation of quadratic polynomials when a > 0 and a < 0 is as follows:

According to the shape of the graph, there are three possible cases:
Case 1: When the graph cuts the x-axis at two distinct points, P and P'. Here, P and P' are the zeros of the quadratic equation ax² + bx + c.

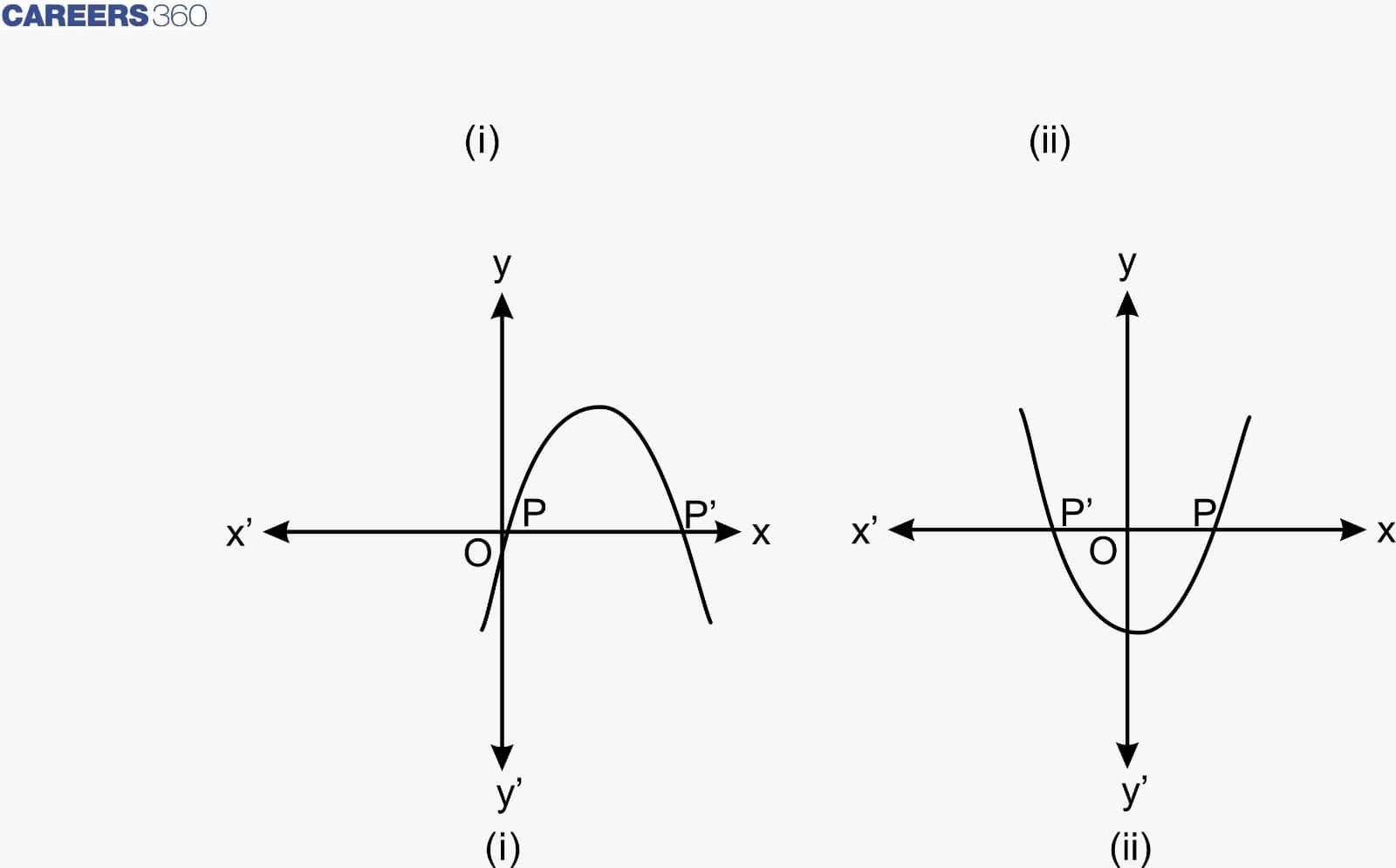
Case 2: When the graph cuts the x-axis at exactly one point, i.e., at two coincident
points. Therefore, the two points P and P' of Figure 1 of case 1 coincide here to become one point P. So, the x-coordinate of P is the only zero for the quadratic polynomial ax² + bx + c.

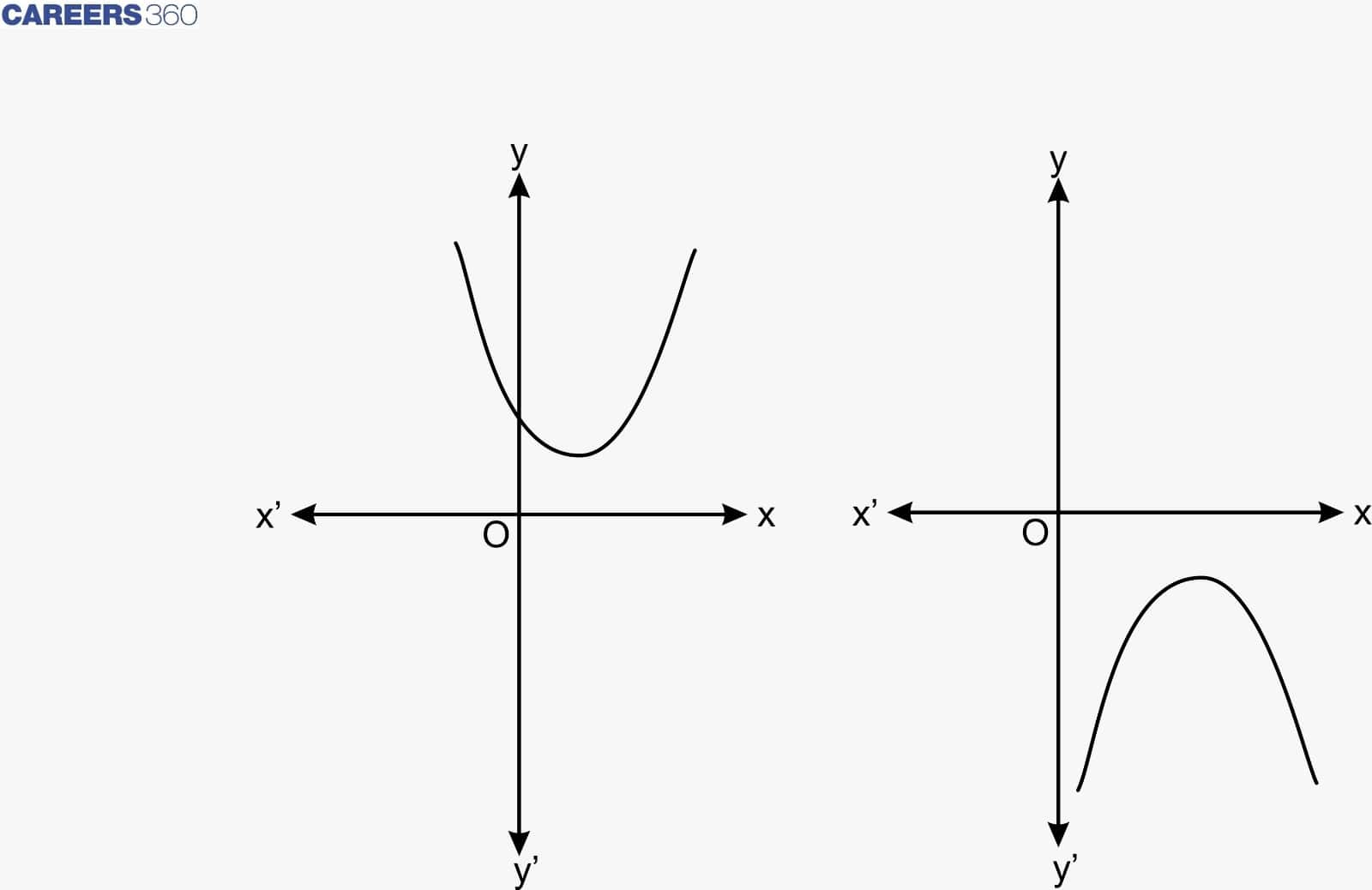
Case 3: When the graph is either completely above the x-axis or completely below
the x-axis, then it does not cut the x-axis at any point. So, the quadratic polynomial ax²
+ bx + c has no zero in this case.

Relationship Between Zeros and Coefficients of a Polynomial:

For quadratic Polynomials: Let α and β be the roots of the quadratic equation ax²
+ bx + c, then,
Sum of the zeroes (α + β) = −ba or -Coefficient of xCoefficient of x^2

Product of the zeroes (αβ) = ca or Constant termCoeffiecient of x^2

Example: x² + 7x + 10
Sum of the zeroes (α + β) = −71

Product of the zeroes (αβ) = 101

For Cubic Polynomials: Let α, β and γ be the roots of a cubic polynomial ax³ + bx² + cx + d; then
α + β + γ = −ba
αβ + βγ + γα = ca
αβγ = −da

Divisor Algorithm:

If P(x), D(x), Q(x) and R(x) are the three polynomials where,
P(x) = Polynomial
D(x) = Divisor polynomial
Q(x) = Quotient polynomial
R(x) = Remainder polynomial
Therefore, the formula for the division algorithm is as follows:
P(x) = D(x) × Q(x) + R(x)

Where D(x) ≠ 0, and R(x) = 0 or the degree of R(x) < the degree of D(x).
Example: Divide the cubic polynomial 4x³ + 3x² + 3x + 2 by the quadratic polynomial x² + 2x + 1
The division is shown in the figure:

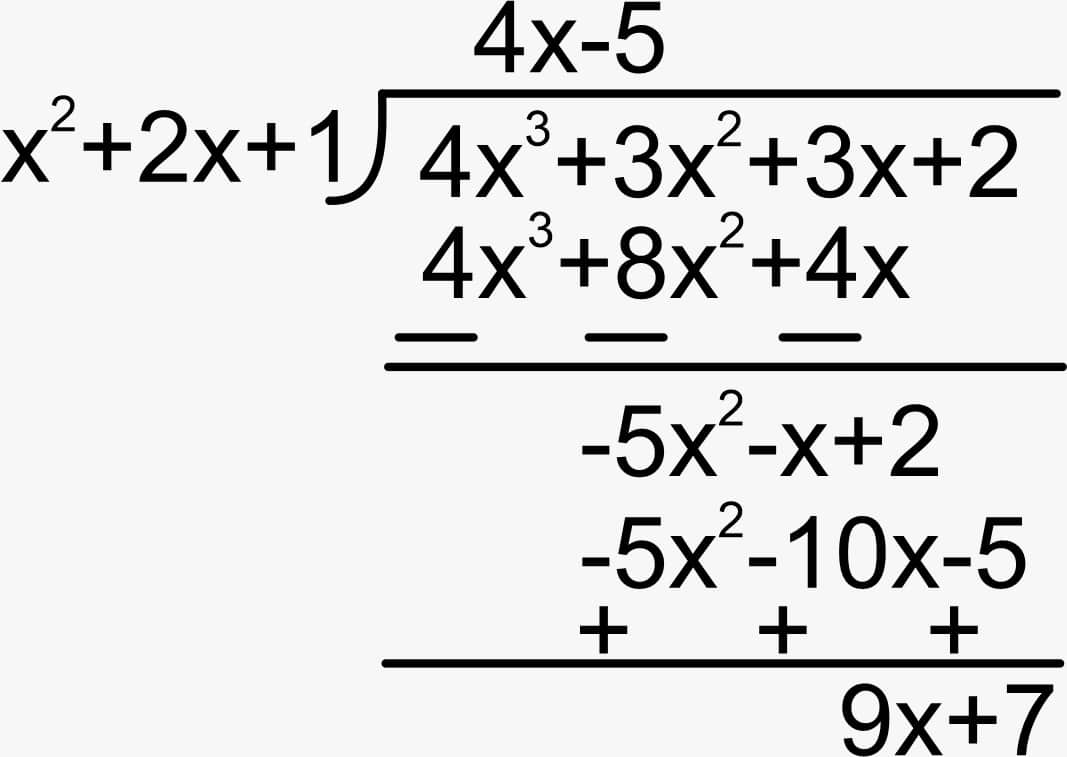
Proof Using Divisor Algorithm:
P(x) = D(x) × Q(x) + R(x)
P(x) = 4x³ + 3x² + 3x + 2
D(x) = x² + 2x + 1
Q(x) = 4x - 5
R(x) = 9x + 7
Now, putting the values in the formula, we get:
4x³ + 3x² + 3x + 2 = (x² + 2x + 1) × (4x - 5) + 9x + 7
4x³ + 3x² + 3x + 2 = 4x³ + 8x² + 4x - 5x² - 10x - 5 + 9x + 7
4x³ + 3x² + 3x + 2 = 4x³ + 3x² + 3x + 2
L.H.S. = R.H.S.

Class 10 Chapter-Wise Notes

Students must download the notes below for each chapter to ace the topics.

NCERT Exemplar Solutions for Class 10

Students must check the NCERT Exemplar solutions for class 10 of Mathematics and Science Subjects.

• NCERT Exemplar Class 10 Maths solutions
• NCERT Exemplar Class 10 Science solutions

NCERT Solutions for Class 10

Students must check the NCERT solutions for class 10 of Mathematics and Science Subjects.

• NCERT Solutions for Class 10 Maths
• NCERT Solutions for Class 10 Science

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

• NCERT Books for Class 10
• NCERT Syllabus for Class 10