Coordinate Geometry Class 10th Notes - Free NCERT Class 10 Maths Chapter 7 Notes - Download PDF

Class 10 Coordinate Geometry Notes PDF – Download Free Study Material

Students who wish to access these NCERT Class 10 Maths Chapter 7 Notes can click on the link below to download the entire notes in PDF.

Download PDF

Coordinate Geometry Class 10 Notes

Careers360 has prepared these NCERT Class 10 Maths Chapter 7 Notes to make your revision smoother and faster.

Coordinate Geometry: Coordinate geometry is a branch of geometry that is used to determine the position of points using coordinates.

Coordinates: Coordinates are the set of values that are used to define the exact position of a point in the coordinate plane.

Coordinate Plane: It is a 2-dimensional plane that has two perpendicular axes called the x-axis and y-axis that intersect at a point. The point where both axes intersect is called the origin.

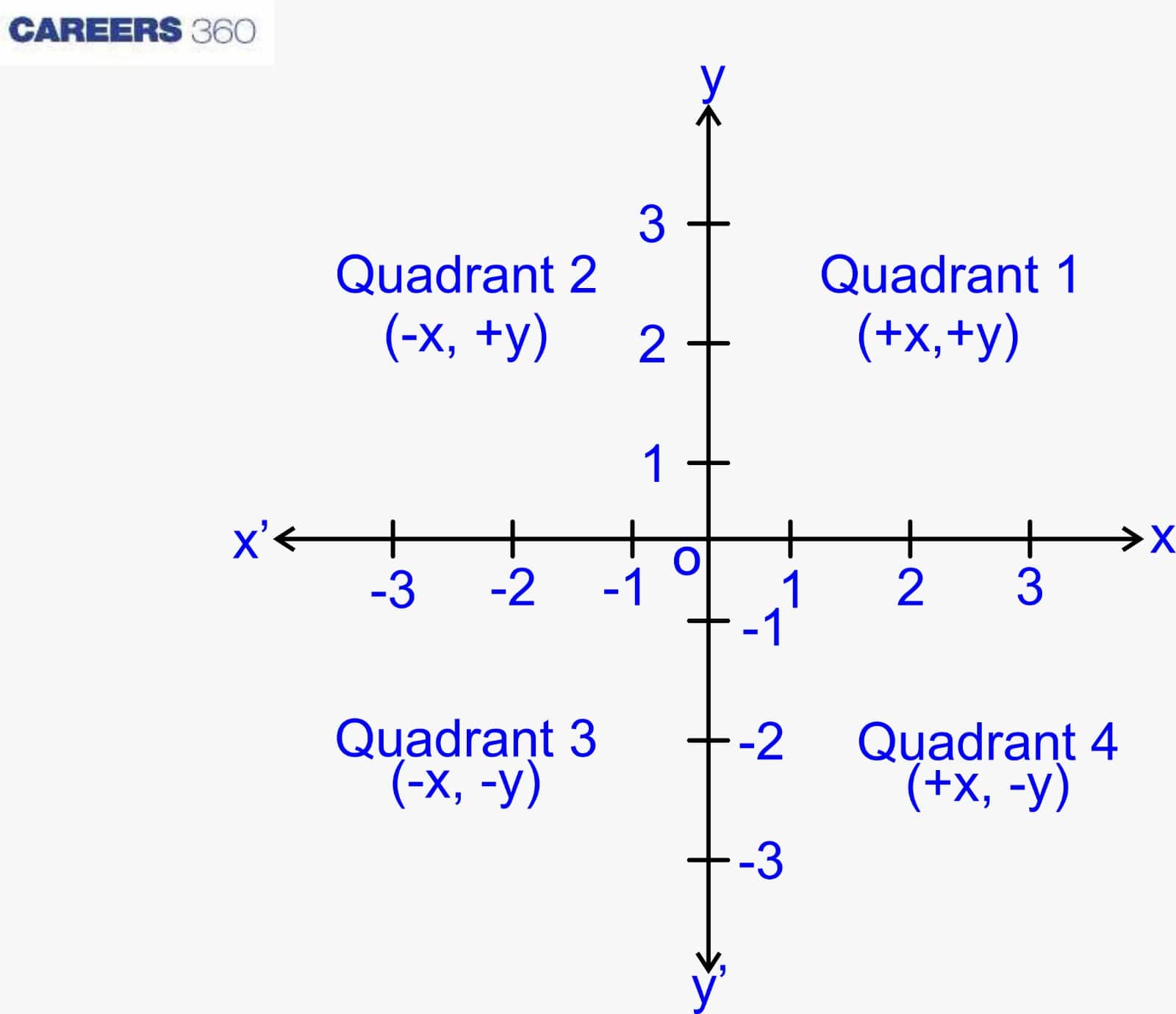
The 2-dimensional coordinate plane has four quadrants that are shown below:
1. Quadrant 1: (+x, +y)
2. Quadrant 2: (-x, +y)
3. Quadrant 3: (-x, -y)
4. Quadrant 4: (+x, -y)

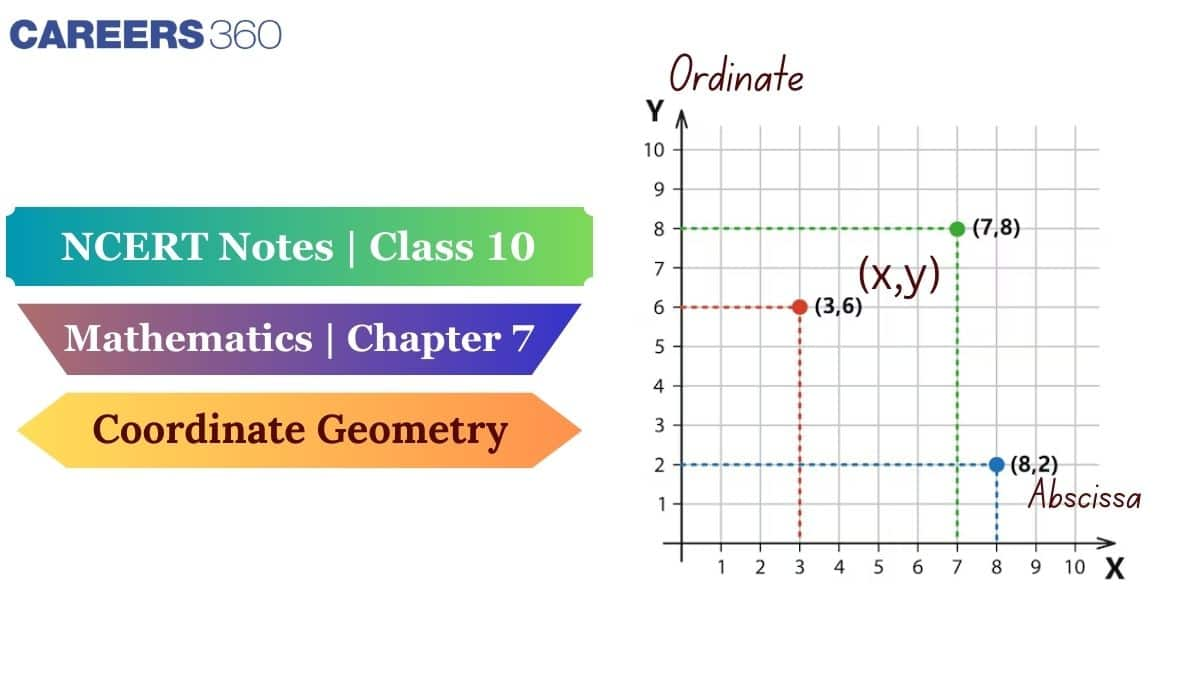
Coordinates or Points On the Cartesian or Coordinate Plane

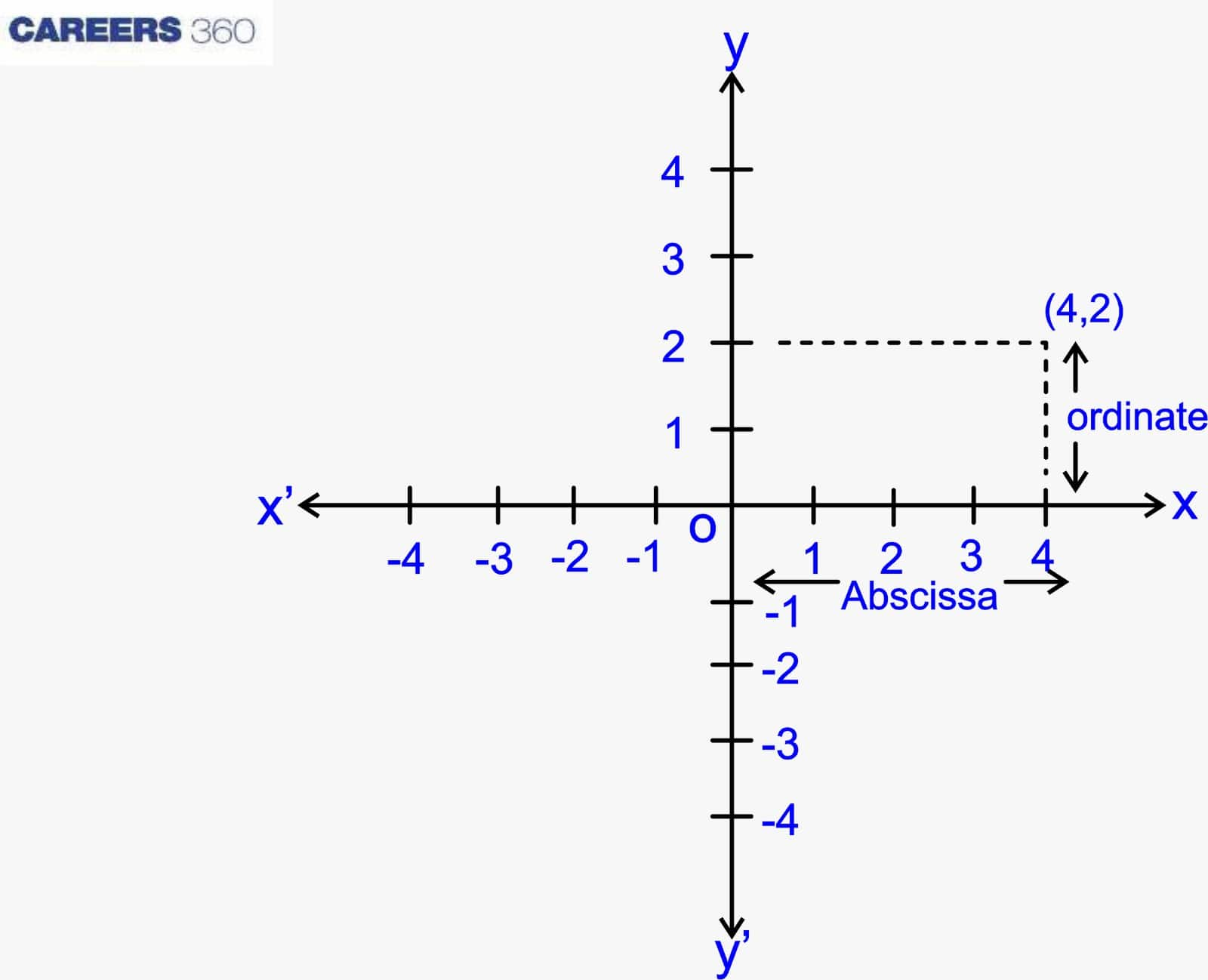
A pair of numbers is generally given in the terms of (x, y), and these numbers are called coordinates, and these coordinates define the position in the coordinate plane. In this plane, the distance from the point on the y-axis is called the abscissa or x-coordinate, and the distance of a point from the x-axis is called the y-coordinate or ordinate.

Example: Consider the coordinate (4, 2) as shown in Figure 4 is the abscissa, and 2 is the ordinate. 4 represents the distance from the y-axis, and 2 represents the distance of a point from the x-axis.

Distance Formula

The distance between the given points is calculated differently based on the coordinates and the position of the points.

The Distance Between Two Points on the Same Axis Coordinates

If the two points are on the same axis, x-axis or y-axis, then the difference will be determined by subtracting the value of the x-axis from the x-axis and the y-axis from the y-axis.

Example: Consider the figure shown below:

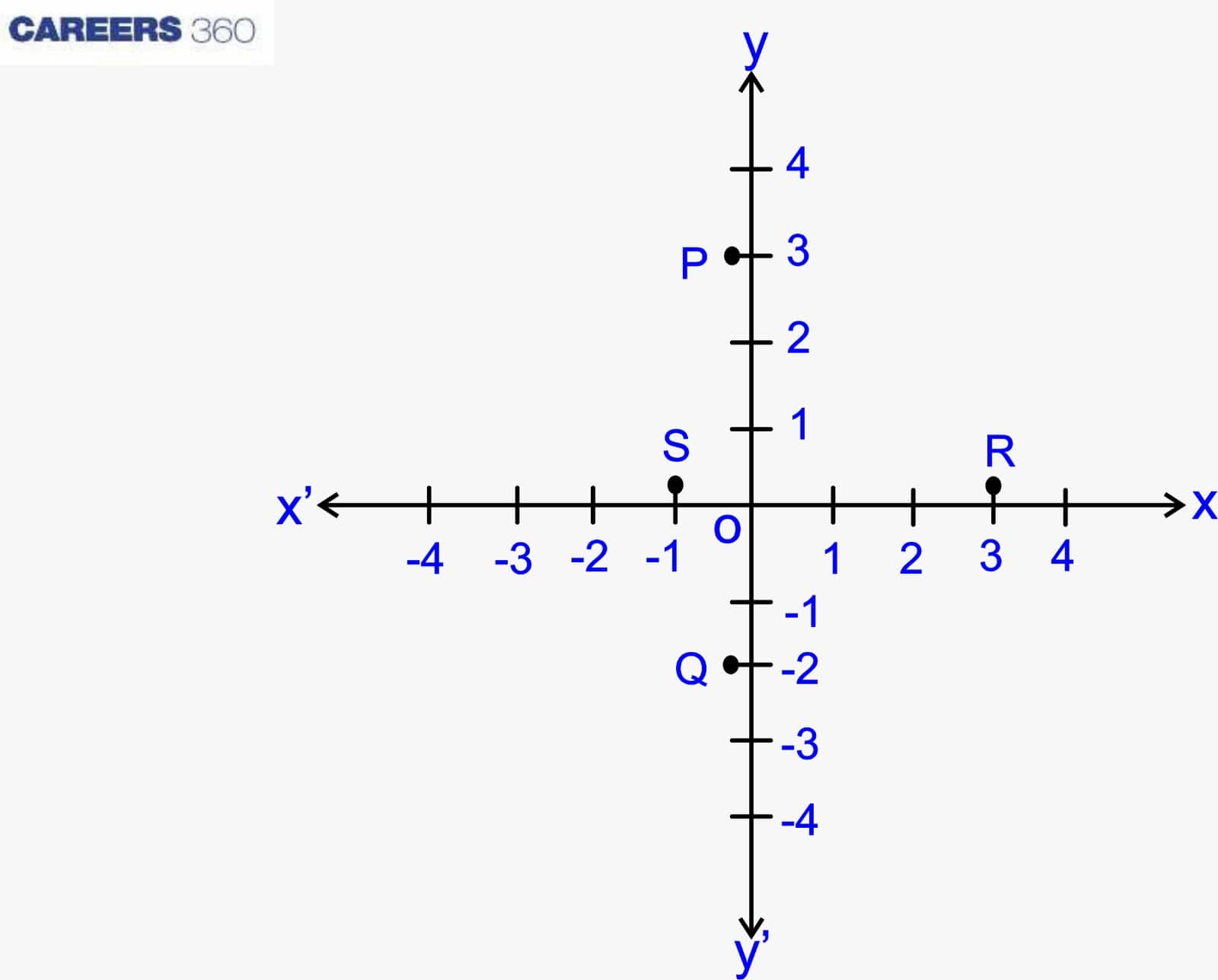
Distance between PQ = 3 - (-2) = 5
Distance between RS = 3 - (-1) = 4

Calculating Distance Between Two Points Using Pythagoras' Theorem

The distance between two points can be calculated using the Pythagorean theorem by extending the lines and creating a right-angle triangle.

Example: Consider points A(0, 3), B(4, 3), C(-4, -4), and D(-4, 0), determine the distance between C and D.
Given:
A(0, 3), B(4, 3), C(-4, -4), and D(-4, 0)
Extend the BA up to E and join C, D and E to make a right-angle triangle as shown below.

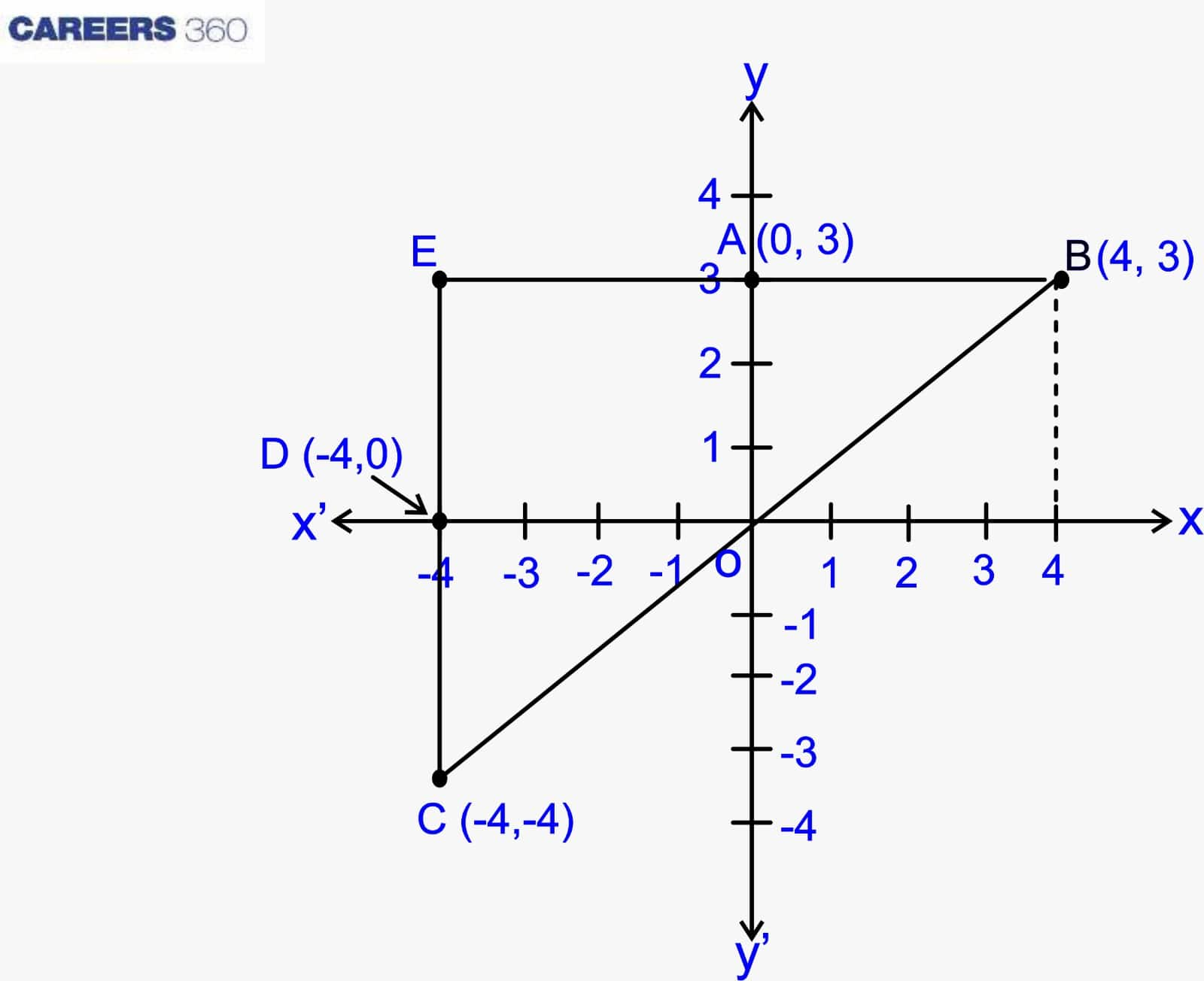
The distance between CD by using Pythagoras' Theorem is:
CD² = BE² + EC²
⇒ CD² = (4 - (-4))² + (0 - (-4))²
⇒ CD² = 8² + 4²
⇒ CD² = 64 + 16
⇒ CD = $\sqrt{80}$ units

Distance Formula

If two points (x₁, y₁) and (x₂, y₂) then the distance can be calculated as:
$d= \sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}$

Section Formula

If a point P divides the line segment in the ratio of m : n, then the point P can be determined by the section formula. Suppose point P(x, y) divides the line segment A(x₁, y₁) and B(x₂, y₂) in m : n ratio, then to determine the P(x, y) the section formula is as follows:

$P(x, y)$ = $ (\frac{mx_2 + nx_1}{m + n}$, $ \frac{my_2 + ny_1}{m + n})$

Example: Find the coordinates of the point which divides the line segment joining the points (3, 1) and (7, 4) in the ratio 2 : 1 internally.

Given:
m : n = 2 : 1

x = $ (\frac{2(7) + 1(1)}{2 + 1})$, y = $ (\frac{2(4) + 1(-2)}{2 + 1})$

⇒ x = $ (\frac{14 + 1}{3})$, y = $ (\frac{8 - 2}{3})$

⇒ x = 5, y = 2

Finding The Ratio Given Points

If P(x, y) is the point that divides the line segments A(x1, y1) and B(x2, y2) internally, then the ratio of the line can be determined as follows:
Assume that the ratio is k : 1
Substitute the ratio in the section formula for any of the coordinates to get the value of k.

x = $ (\frac{kx_2+ x_1}{k + 1})$
or y = $ (\frac{ky_2+ y_1}{k + 1})$

Example: Find the ratio when point (– 3, 5) divides the line segment joining the points A(– 5, 9) and B(2, – 7)?
Given:
A(– 5, 9) and B(2, – 7)

P (– 3, 5)

$\frac mn$ : 1 = k : 1

P(– 3, 5) divide the line into k : 1 segment,

x = $ (\frac{kx_2+ x_1}{k + 1})$, y = $ (\frac{ky_2+ y_1}{k + 1})$

After substituting the values we get,

⇒ -3 = $ (\frac{2k+ (-5)}{k + 1})$

⇒ -3 = $ (\frac{2k - 5}{k + 1})$

⇒ -3k - 3 = 2k - 5

⇒ 5k = 2

⇒ k = $ (\frac{2}{5})$

Therefore, the required ratio is 2 : 5.

Midpoint

Midpoint is a point in a line that divides the line into two equal parts or in 1 : 1 ratio. If P is the point that divides the line A(x₁, y₁) and B(x₂, y₂).
Therefore,

$P(x, y)$ = $ (\frac{x_1 + x_2}{2}$, $ \frac{y_1 + y_2}{2})$

Example: What is the midpoint of line segment AB whose coordinates are A(-4, 4) and B(2, 6), respectively?

Given:
A(-4, 4) and B(2, 6)

$P(x, y)$ = $ (\frac{-4 + 2}{2}$, $ \frac{4 + 6}{2})$

$⇒P(x, y)$ = $ (\frac{2}{2}$, $ \frac{10}{2})$

$⇒P(x, y)$ = $(1, 5)$

Therefore, the midpoint is (1, 5).

Centroid of a Triangle

If P(x₁, y₁), Q(x₂, y₂), and R(x₃, y₃) are the vertices of a ΔPQR, then the coordinates of its centroid(A) are defined by,

$A(x, y)$ = $ (\frac{x_1 + x_2 + x_3}{3}$, $ \frac{y_1 + y_2 + y_3}{3})$

Example: Find the coordinates of the centroid of a triangle whose vertices are given as (-2, -4), (5, 1) and (9, -3)

Given:
(-2, -4), (5, 2) and (9, -3)

$A(x, y)$ = $ (\frac{x_1 + x_2 + x_3}{3}$, $ \frac{y_1 + y_2 + y_3}{3})$

After substituting the values we get,

$A(x, y)$ = $ (\frac{-2 + 5 + 9}{3}$, $ \frac{-4 + 1 + (-3)}{3})$

$⇒A(x, y)$ = $ (\frac{12}{3}$, $ \frac{-6)}{3})$

$⇒A(x, y)$ = $(4, -2)$

Therefore, the centroid of the triangle is (4, -2)

Area of a Triangle Using Coordinate Geometry

If P(x₁, y₁), Q(x₂, y₂), and R(x₃, y₃) are the vertices of a ΔPQR, then the area of ΔPQR can be defined as,

$Area$ = $ \frac{1}{2}$ $[x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)]$

Example: Find the area of the triangle ABC whose vertices are A(2, 3), B(5, 3) and C(4, 6).
Given:
A(2, 3), B(5, 3) and C(4, 6)

$Area$ = $ \frac{1}{2}$ $[x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)]$

After substituting the values, we get:

$Area$ = $ \frac{1}{2}$ $[2(3 - 6) + 5(6 - 3) + 4(3 - 3)]$

$⇒Area$ = $ \frac{1}{2}$ $[2(-3) + 5(3) + 4(0)]$

$⇒Area$ = $ \frac{1}{2}$ $[-6 + 15 + 0]$

$⇒Area$ = $ \frac{1}{2}\times[9]$

$⇒Area$ = $ \frac{9}{2}$

Therefore, the area of the triangle is $ \frac{9}{2}$ square units.

Coordinate Geometry Class 10 Notes: Previous Year Question and Answer

Given below are selected previous year question answers for NCERT Class 10 Maths Chapter 7 Coordinate Geometry, collected from various examinations.

Question 1:
Find the coordinates of the points where the graph $57x – 19y = 399$ cuts the coordinate axes.

Solution:
$57x-19y=399$
⇒ $\frac{57x}{399}-\frac{19y}{399} = 1$
⇒ $\frac{x}{7}-\frac{y}{21} = 1$ -------------(i)
Comparing it with the equation of a line:
$\frac{x}{a}+\frac{y}{b} = 1$
x-intercept = $a$ = 7
y-intercept = $b$ = –21
The line, $57x-19y=399$, cuts the x-axis at (7, 0) and the y-axis at (0, –21)
Hence, the correct answer is 'x-axis at (7, 0) and y-axis at (0, –21)'.

Question 2:
The graph of the equation $x=a(a \neq 0)$ is a_____.

Solution:
Given: $x=a(a \neq 0)$
A diagram that shows the change of one variable to one or more other variables, such as a collection of one or more points, lines, line segments, curves, or regions.
The value of $x$ = The value of $a$ = 1, 2, 3, and so on to infinity.
The value of $y$ = constant (assume $y=4$)
As a result, the graph these points create will be a straight line parallel to the y-axis.
Hence, the correct answer is a line parallel to the y-axis.

Question 3:
The area of triangle formed by the straight line $3x + 2y = 6$ and the co-ordinate axes is:

Solution:
The area of a triangle formed by a line and the coordinate axes $=\frac{1}{2} \times \text{base} \times \text{height}$
The line $3x + 2y = 6$
At $y = 0⇒x = \frac{6}{3} = 2$
At $x = 0⇒y = \frac{6}{2} = 3$
So, the base and the height of the triangle are $2$ units and $3$ units, respectively.
$\text{Area of the triangle formed} = \frac{1}{2} \times 2 \times 3 = 3$
Hence, the correct answer is 3 square units.

NCERT Class 10 Maths Notes – Chapter-Wise Links

Access all NCERT Class 10 Maths notes from one place using the links below.

NCERT Exemplar Solutions for Class 10

Students must check the NCERT Exemplar solutions for class 10 of Mathematics and Science Subjects.

• NCERT Exemplar Class 10 Maths solutions

• NCERT Exemplar Class 10 Science Solutions

NCERT Solutions for Class 10

Students must check the NCERT solutions for class 10 of Mathematics and Science Subjects.

• NCERT Solutions for Class 10 Maths

• NCERT Solutions for Class 10 Science

NCERT Books and Syllabus

As students step into a new class, they must first explore the latest syllabus to identify the chapters included. Below are the links to the most recent syllabus and essential reference books

• NCERT Books Class 10 Maths
• NCERT Books for Class 10 Science
• NCERT Syllabus Class 10 Maths
• NCERT Books Class 10
• NCERT Books for Class 10 English
• NCERT Syllabus Class 10