NCERT Solutions for Exercise 12.1 Class 10 Maths Chapter 12

NCERT Solutions for Exercise 12.1 Class 10 Maths Chapter 12 - Areas related to circles

Edited By Ramraj Saini | Updated on Nov 27, 2023 04:59 PM IST

NCERT Solutions For Class 10 Maths Chapter 12 Exercise 12.1

NCERT Solutions for Exercise 12.1 Class 10 Maths Chapter 12 Areas related to circles are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Class 10 Maths ex 12.1 includes the Introductory part of areas related to circles and the questions related to finding distance between the two circles out of some given conditions which are congruent or not, etc. The Numerical problems present in this introductory exercise is very important to cover in order to get better understanding of concepts. The Class 10 Maths chapter 12 exercise 12.1 lists a few practice problems on, circumference and area of Circle. The class 10th maths chapter 12 exercise 12.1 covers the topics like the concept of finding angles subtended by hour and minute hand in one or n revolutions . Also some properties and technical terms of circles enclosed with some special conditions

Don't Miss: JEE Main & NEET 2026 Scholarship Test (Class 10): Narayana | Aakash

This Story also Contains

NCERT Solutions For Class 10 Maths Chapter 12 Exercise 12.1
Download Free PDF of NCERT Solutions for Class 10 Maths Chapter 12 Exercise 12.1
Assess NCERT Solutions for Class 10 Maths chapter 12 exercise 12.1
More About NCERT Solutions for Class 10 Maths Chapter 12 Exercise 12.1
Benefits of NCERT Solutions for Class 10 Maths Chapter 12 Exercise 12.1
NCERT Solutions for Class 10 Subject Wise

NCERT Solutions for Exercise 12.1 Class 10 Maths Chapter 12 - Areas related to circles

10th class Maths exercise 12.1 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.

Download Free PDF of NCERT Solutions for Class 10 Maths Chapter 12 Exercise 12.1

Download PDF

Assess NCERT Solutions for Class 10 Maths chapter 12 exercise 12.1

Areas Related to Circles Class 10 Chapter 12 Exercise: 12.1

Q1 The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has a circumference equal to the sum of the circumferences of the two circles.

Answer:

Circumference of 1st circle is given :

$\\=\ 2\pi r_1\\\\=\ 2\pi \times 19\ =\ 38 \pi\ cm$

And the circumference of the 2nd circle is : $=\ 2\pi \times 9\ =\ 18 \pi\ cm$

Thus the circumference of the new circle is $=\ 18\pi\ +\ 38\pi\ =\ 56\pi\ cm$

or $2\pi r =\ 56\pi$

or $r\ =\ 28\ cm$

Hence the radius of the new circle is 28 cm.

Q2 The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having an area equal to the sum of the areas of the two circles.

Answer:

We know that the area of the circle is : $=\ \pi r^2$

Thus area of a 1st circle : $=\ \pi r^2_1$

or $=\ \pi \times 8^2\ =\ 64 \pi\ cm^2$

And the area of a 2nd circle is : $=\ \pi r^2_2$

or $=\ \pi \times 6^2\ =\ 36\pi\ cm^2$

According to the question area of the new circle is $=\ 64\pi\ +\ 36\pi\ =\ 100\pi\ cm^2$

or $\pi r^2\ =\ 100 \pi$

or $r\ =\ 10\ cm$

Hence the area of the new circle is 10 cm.

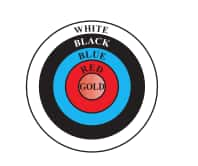
Q3 Fig. depicts an archery target marked with its five scoring regions from the center outwards as Gold, Red, Blue, Black, and White. The diameter of the region representing the Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.

Answer:

The radius of each scoring region can be found by adding 10.5 in respective colors.

The area of the golden region is : $=\ \pi r^2\ =\ \pi \times 10.5^2\ =\ 346.5\ cm^2$

Similarly area of the red region is = Area of a red score - Area of the golden region

$\\=\ \pi \times 21^2\ -\ \pi \times 10.5^2\\\\=\ 1039.5\ cm^2$

Then the area of the blue region is :

$\\=\ \pi \times (31.5)^2\ -\ \pi \times 21^2\\\\=\ 1732.5\ cm^2$

And the area of the black region is :

$\\=\ \pi \times 42^2\ -\ \pi \times (31.5)^2\\\\=\ 2425.5\ cm^2$

Area of the white region is :

$\\=\ \pi \times 52.5^2\ -\ \pi\times 42^2\\\\=\ 3118.5\ cm^2$

Q4 The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is traveling at a speed of 66 km per hour?

Answer:

Let the number of revolution of the wheel be n.

The circumference of the wheel is given by:-

$\\=\ 2\pi r\\\\=\ 2\pi \times 40\ =\ 80\pi\ cm$

Now, the speed of the car is given by:-

$\\=\ 66\ Km/hr\ \\\\=\ 66\times \frac{100000}{60}\ cm/min\ \\\\=\ 110000\ cm/min.$

Thus distance traveled in 10 minutes is: $=\ 1100000\ cm$

According to the question, we get;

$n\times 80\pi\ =\ 1100000$

or $n\ =\ 4375$

Hence the number of revolutions made by the wheel is 4372.

Q5 Tick the correct answer in the following and justify your choice : If the perimeter and the area of a circle are numerically equal, then the radius of the circle is

(A) 2 units
(B) $\pi$ units
(C) 4 units
(D) 7 units

Answer:

Let the radius of the circle be r.

Then according to question, we can write:-

Perimeter = Area

$\\2\pi r\ =\ \pi r^2\\\\r\ =\ 2\ units$

Hence option (A) is correct.

Benefits of NCERT Solutions for Class 10 Maths Chapter 12 Exercise 12.1

The very first benefits are already been mentioned in exercise 12.1 Class 10 Maths and the NCERT solutions for Class 10 Maths chapter 12 exercise 12.1 questions like equilateral triangle rolled around a circle and vertices are over it are discussed in this exercise.
Second most benefits is like in exercise 12.1 Class 10 Maths there are variety of concepts to understand in problem solving related to real life examples like wheel assembly of car and number of revolutions it is making under given conditions as discussed in Class 10 Maths chapter 12 exercise 12.1
For Class 10 final exams students may get MCQs, short numericals or long numericals questions from the type covered in the Class 10 Maths chapter 12 exercise 12.1

Also see-

NCERT Solutions for Class 10 Subject Wise

Frequently Asked Questions (FAQs)

1. Define Areas related to circles?

Ans The sectors between two radii and a neighbouring arc. A sector's area and a circle's segment: The sector of the circle is the portion of the circular region of the two radii and the associated arc is majorly called as area of circle.

2. What is the expression of area of segment of circle?

Ans: area of segment of circle = area of corresponding sector – area of corresponding triangle

3. How many total exercise are there in chapter 12 ?

Ans: There are total of 3 exercises there in chapter 12 namely exercise 12.1 exercise 12.2 and exercise 12.3 which have variety of questions to give a brief analysis of topic as well as subject.

4. How many parallel tangents does circle have?

Ans: A circle can have at most two parallel tangents.

5. What is the perimeter and area of unit circle ?

Ans: The radius of unit circle is 1 units

Hence Area = π

Perimeter = 2π

6. Which is the longest chord of circle and its length in terms of radius of circle?

Ans; The longest chord in circle is line segment of diameter and its length = 2*radius of circle

7. What is Areas of Combinations of Plane figures in chapter?

Ans: The majority of this part entails calculating the area of various shapes and patterns utilising a variety of planar figures and polygons. During the exam, the student should concentrate on mastering the formulas for determining the area of fundamental polygons.

Also Read

NCERT Class 10 Maths Notes - Download Chapter Wise PDFs

The Human Eye and The Colorful world Class 10th Notes- Free NCERT Class 10 Science Chapter 11 Notes - Download PDF

NCERT Class 10 Science Chapter 14 Notes Sources Of Energy - Download PDF

Magnetic Effects of Electric Current Class 10th Notes - Free NCERT Class 10 Science Chapter 13 Notes - Download PDF

Electricity Class 10th Notes - Free NCERT Class 10 Science Chapter 12 Notes - Download PDF

Light- Reflection and Refraction Class 10th Notes- Free NCERT Class 10 Science Chapter 10 Notes - Download PDF

NCERT Syllabus for Class 10 Maths 2024-25 - Download Free PDF

NCERT Solutions for Exercise 12.3 Class 10 Maths Chapter 12 - Areas related to circles

NCERT Solutions for Exercise 12.2 Class 10 Maths Chapter 12 - Areas related to circles

NCERT Solutions for Exercise 12.1 Class 10 Maths Chapter 12 - Areas related to circles

NCERT Solutions for Class 10 Science Chapter 6 Life Processes

NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations

NCERT Exemplar Class 10 Maths Solutions - Chapter Wise Problems with Solutions

NCERT Exemplar Class 10 Science Solutions Chapter 1 Chemical Reactions and Equations

NCERT Exemplar Class 10 Science Solutions - Chapter Wise Problems with Solutions

Articles

BSE Telangana Hall Ticket 2025 for Regular, Private, OSSC & Vocational

Sep 10, 2024

TS SSC Result 2025, Check Telangana Class 10th Result Online @bse.telangana.gov.in

Oct 03, 2024

BSE Telangana 2025 - Telangana SSC Board Full Form, Official Website, Exam Dates, Syllabus, Result

Dec 19, 2024

TS SSC Exam Date 2025 (Out), Download Telangana 10th Exam Time Table PDF

Dec 19, 2024

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Eligibility Criteria

Application Process

Exam Pattern

Gujarat Board Higher Secondary School Certificate

Late Fee Application Date:13 December,2024 - 22 December,2024

Exam Pattern

Result

Admit Card

Madhya Pradesh State Open School 10th Examination

Admit Card Date:13 December,2024 - 31 December,2024

Admit Card

Result

View All School Exams

Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms^-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×10⁷J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 ms⁻² :

Option 1)

2.45×10⁻³ kg

Option 2)

6.45×10⁻³ kg

Option 3)

9.89×10⁻³ kg

Option 4)

12.89×10⁻³ kg

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

A particle is projected at 60⁰ to the horizontal with a kinetic energy $K$ . The kinetic energy at the highest point

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

In the reaction,

$2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

How many moles of magnesium phosphate, $Mg_{3}(PO_{4})_{2}$ will contain 0.25 mole of oxygen atoms?

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

With increase of temperature, which of these changes?

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol^-1) is

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t²) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m² , the number of rotations made by the pulley before its direction of motion if reversed, is