Circles Class 10th Notes - Free NCERT Class 10 Maths Chapter 10 Notes - Download PDF

Circles Class 10 Notes: Free PDF Download

Use the link below to download the Circles Class 10 Notes PDF for free. After that, you can view the PDF anytime you desire without internet access. It is very useful for revision and last-minute studies.

Download PDF

NCERT Class 10 Maths Chapter 10 Notes: Circles

A circle is a 2-dimensional closed geometrical shape that contains a set of points, and all points are at a fixed or constant distance from a point called the centre. All the points of the surface of the circle are at an equidistance.

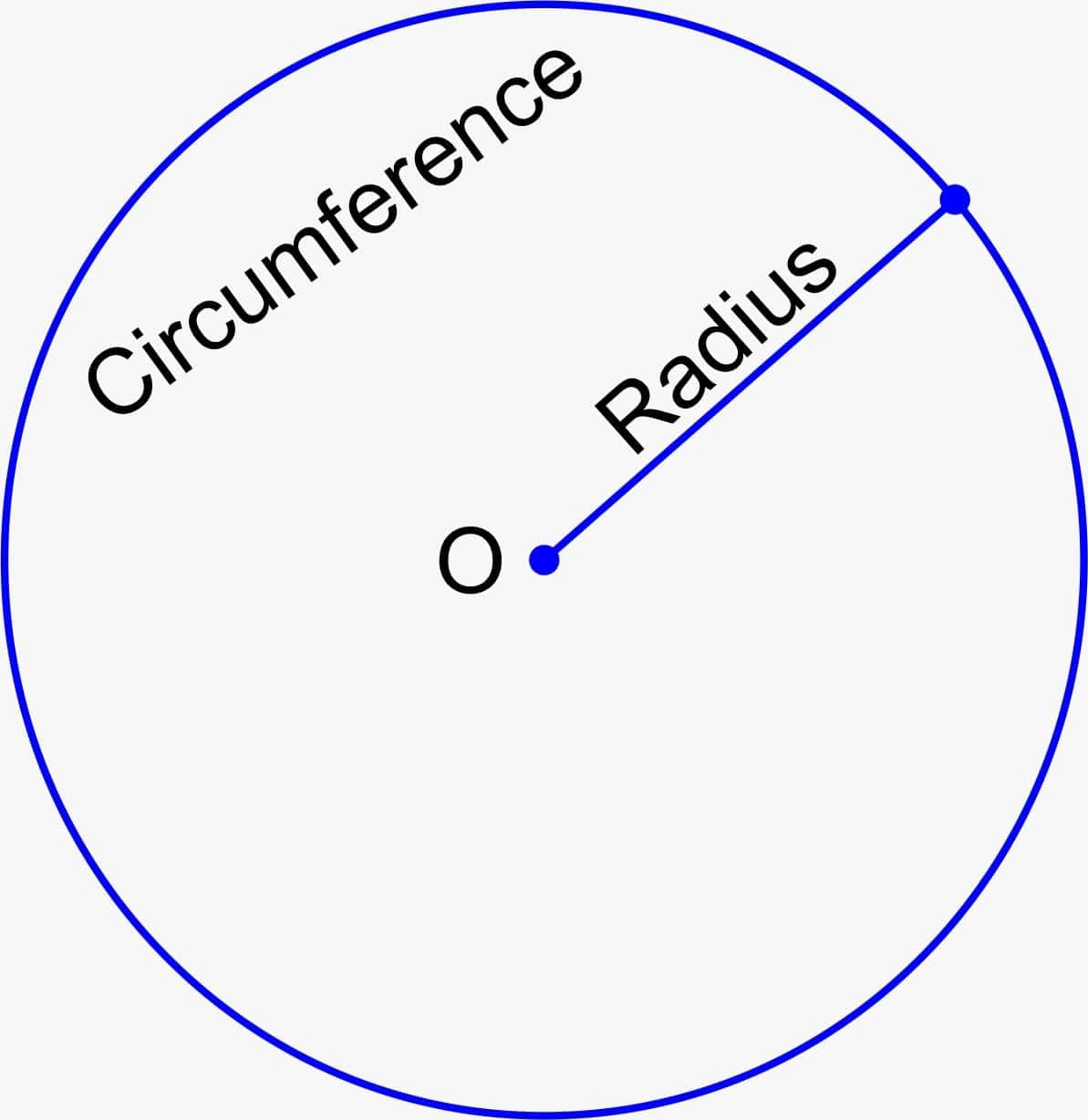
Radius: The distance from the centre of the circle to any point on the surface of the circle is called the radius of the circle. It is denoted by r.

Diameter: Any straight line segment that passes through the centre of the circle and whose endpoints lie on the surface of the circle is called a diameter. It is denoted by d.

Circle and Line in a Plane:

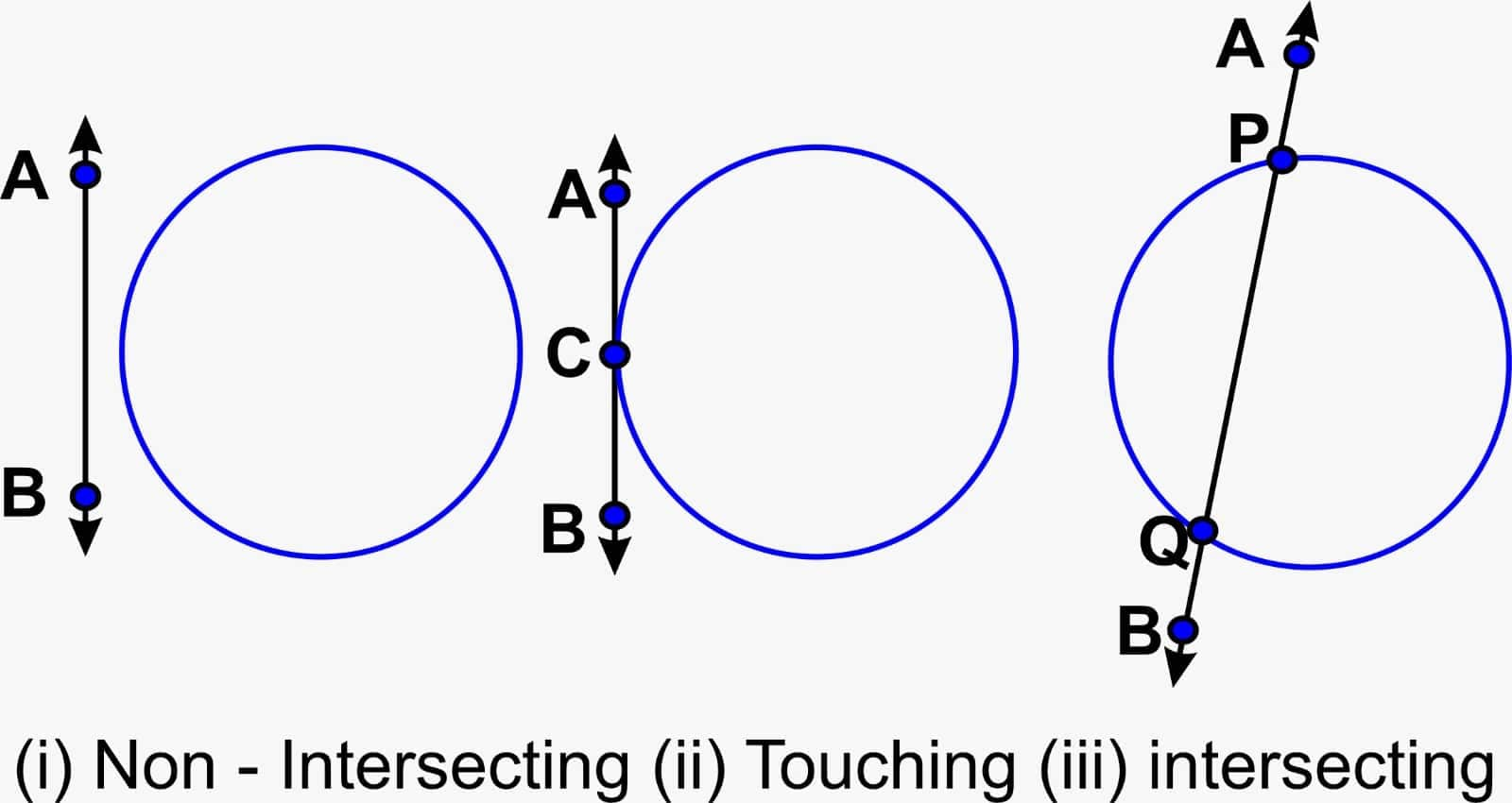
There are three possible places for a line segment and the circle:
1. Non-intersecting: In this case, there is no common point between the line segment and the circle. As shown in Figure I.

2. Touching: In this case, the line segment touches the surface of the circle at only one point, as shown in Figure II.

3. Intersecting: In this case, the line segment intersects the surface of the circle at two points, as shown in Figure III.

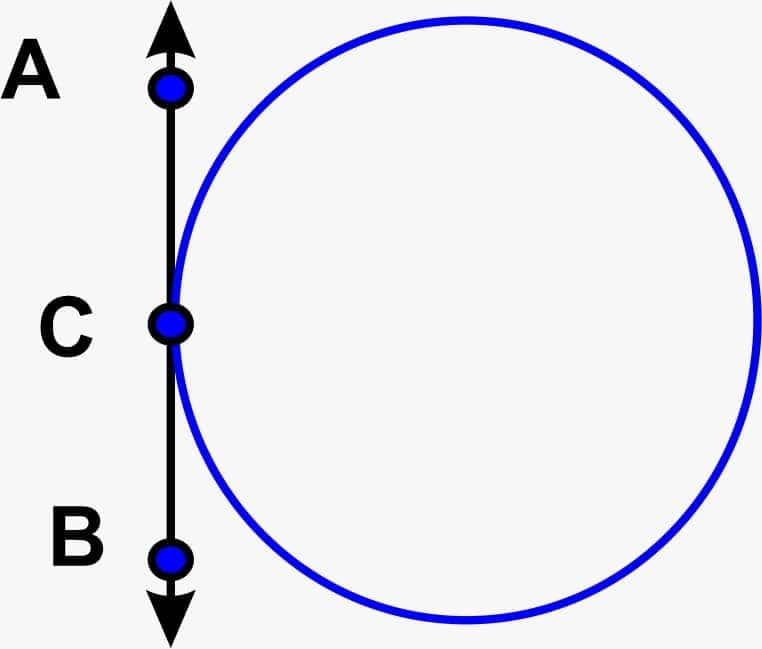
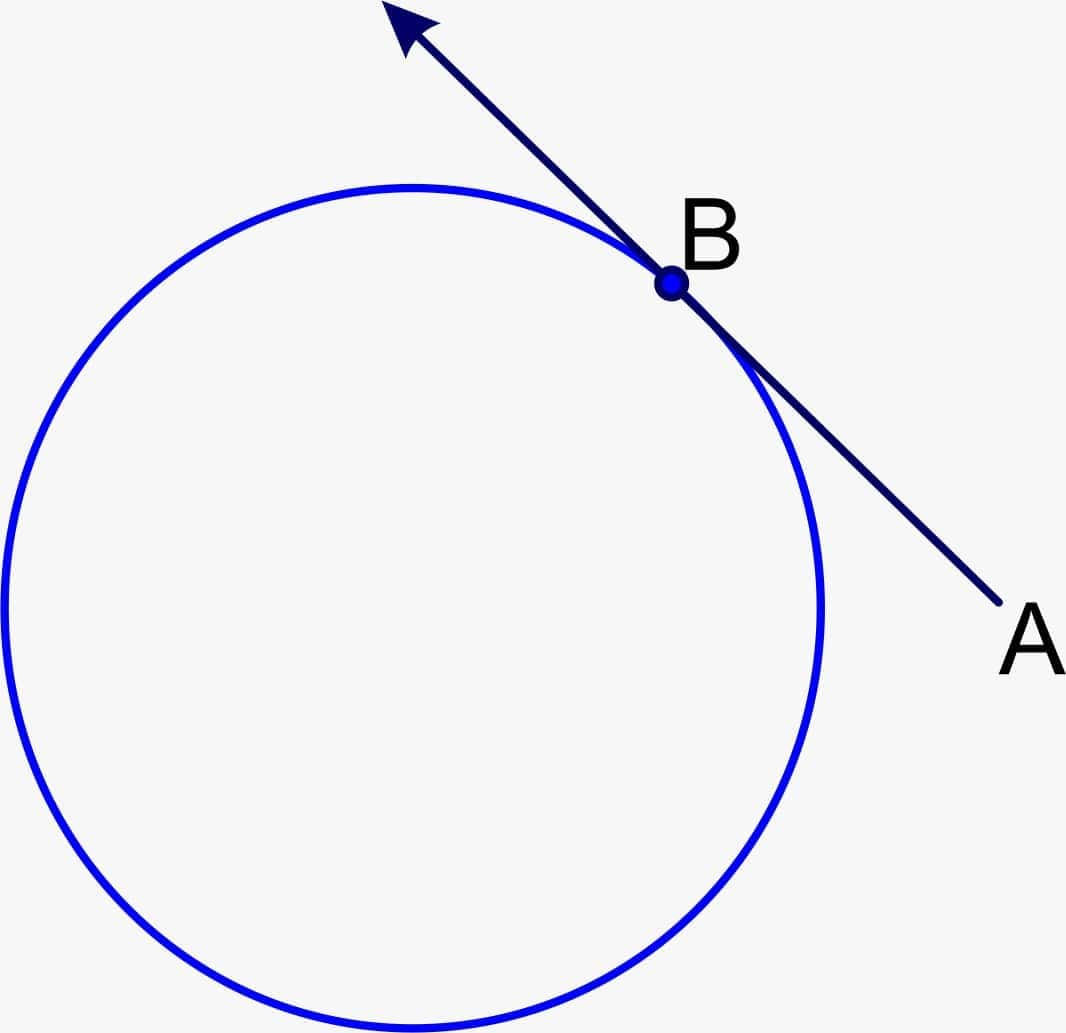
Tangent

When any straight line touches the surface of the circle at exactly one point, it is called a tangent to the circle. As shown in the figure, AB is a tangent that touches the surface of the circle at only one point, C.

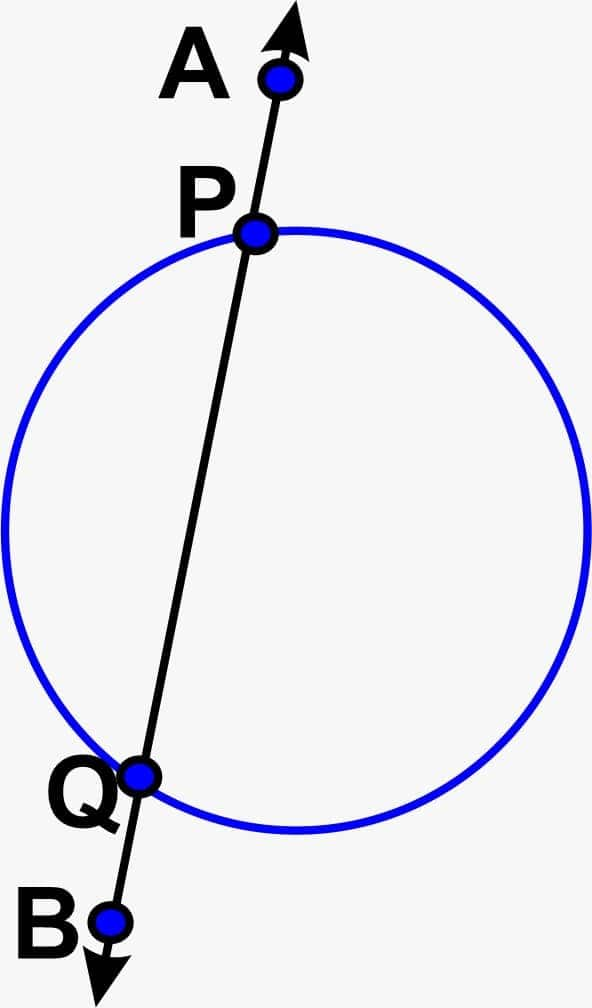
Secant

When a straight line intersects the surface of the circle or has two common points with the surface of the circle, then it is called a secant of the circle. As shown in the figure, AB is a secant that intersects the surface of the circle at points P and Q.

A Special Case of Secant

A special case of the secant is called the tangent of the circle when the two endpoints of its corresponding chord coincide. As shown in the figure, CC' is the special case of the secant.

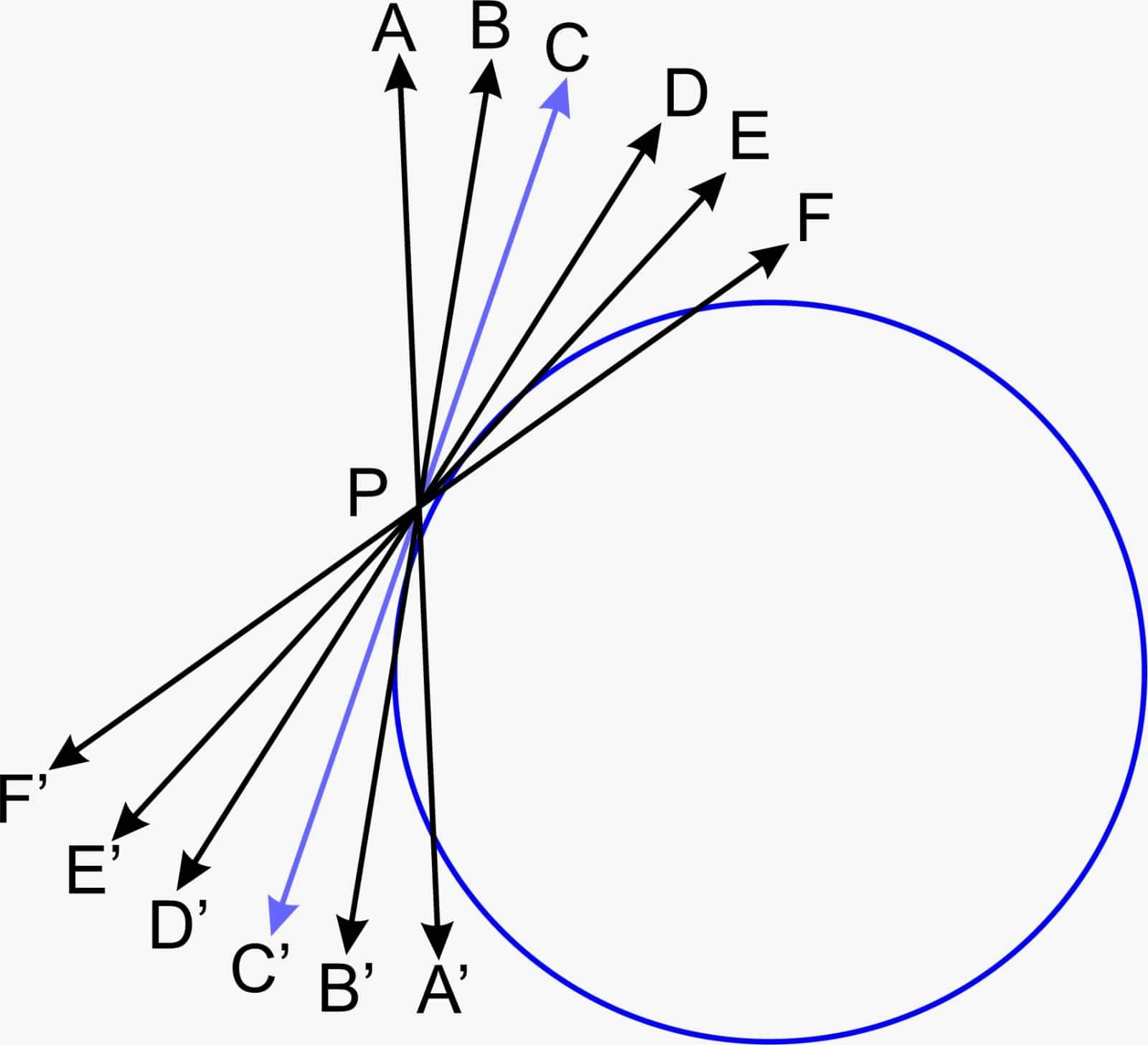
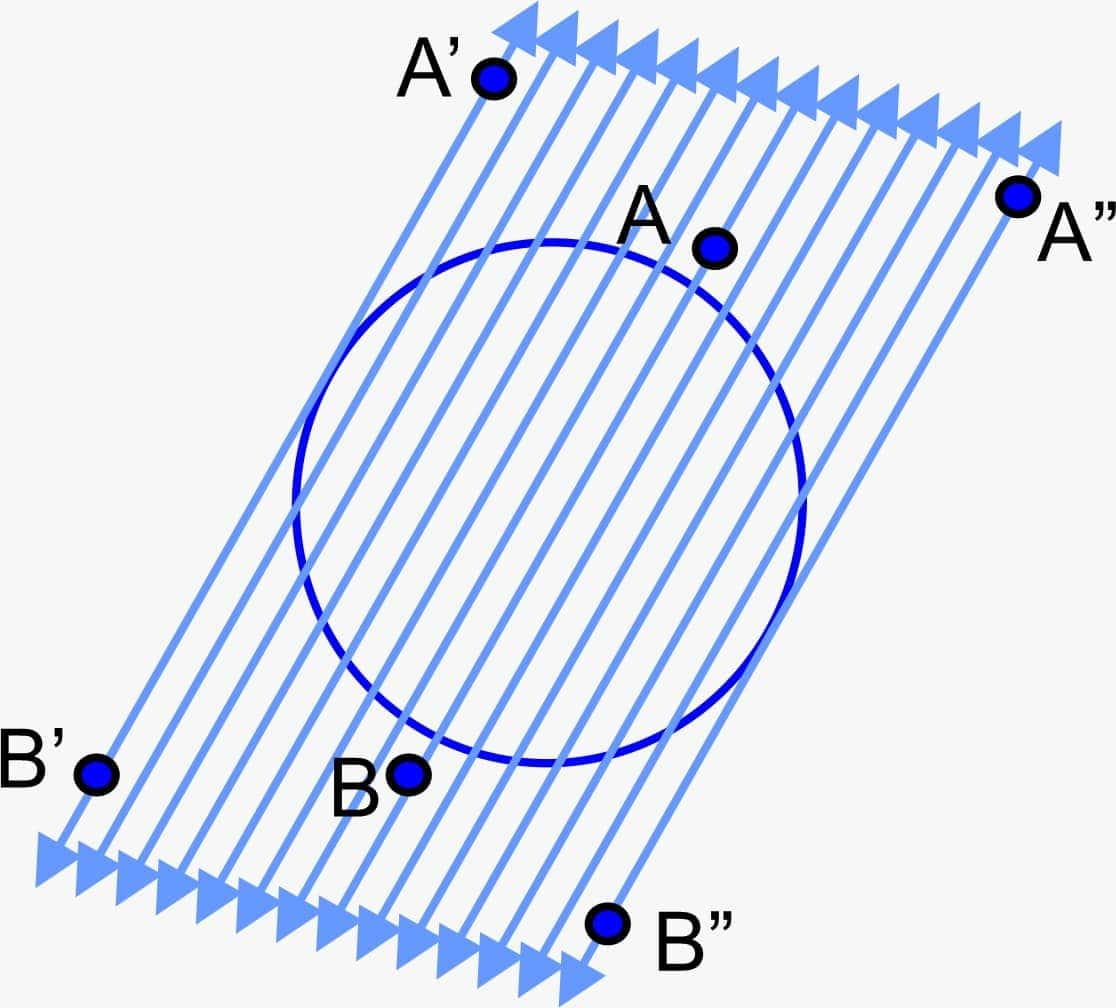
Two Parallel Tangents at Most for a Given Secant

If we try to draw some parallel tangents to the surface of the circle for every given secant, then there will be two tangents that touch the circle at two diametrically opposite points and are parallel to it. As shown in the figure, AB is a secant of the circle and A'B' and A''B'' are parallel tangents.

Theorems: Tangent Perpendicular to the Radius at the Point of Contact

Theorem: The tangent to the circle at any point is the perpendicular to the circle's radius through the point of contact.

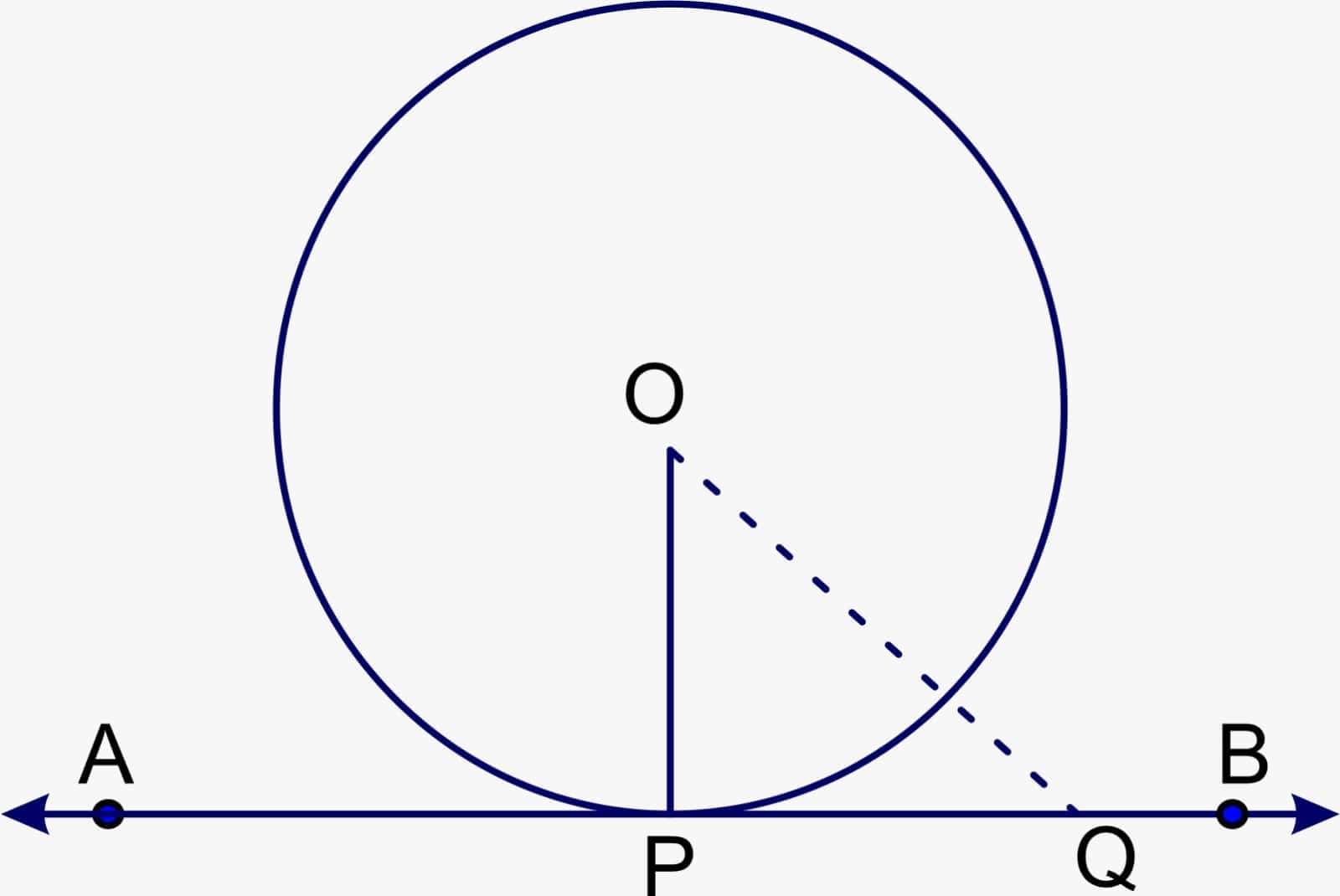
Here, OP is perpendicular to AB.

Assume a circle with centre “O” and AB being the tangent to the circle at point “P”. Now, according to the theorem, we have to prove that OP is perpendicular to the tangent AB.
Make a point Q outside the circle but on the tangent line AB, at the other place of P and join O and Q as shown in the figure. Otherwise, if Q lies inside the circle, then AB will become a secant of the circle.
As shown in the figure, Q lies outside the figure.
Therefore, OQ > OP
This is for every point that lies outside the circle, except point P, which lies on the line AB. It implies that OP is the shortest of all the points from point O to the tangent line AB.
Therefore, OP is perpendicular to AB.

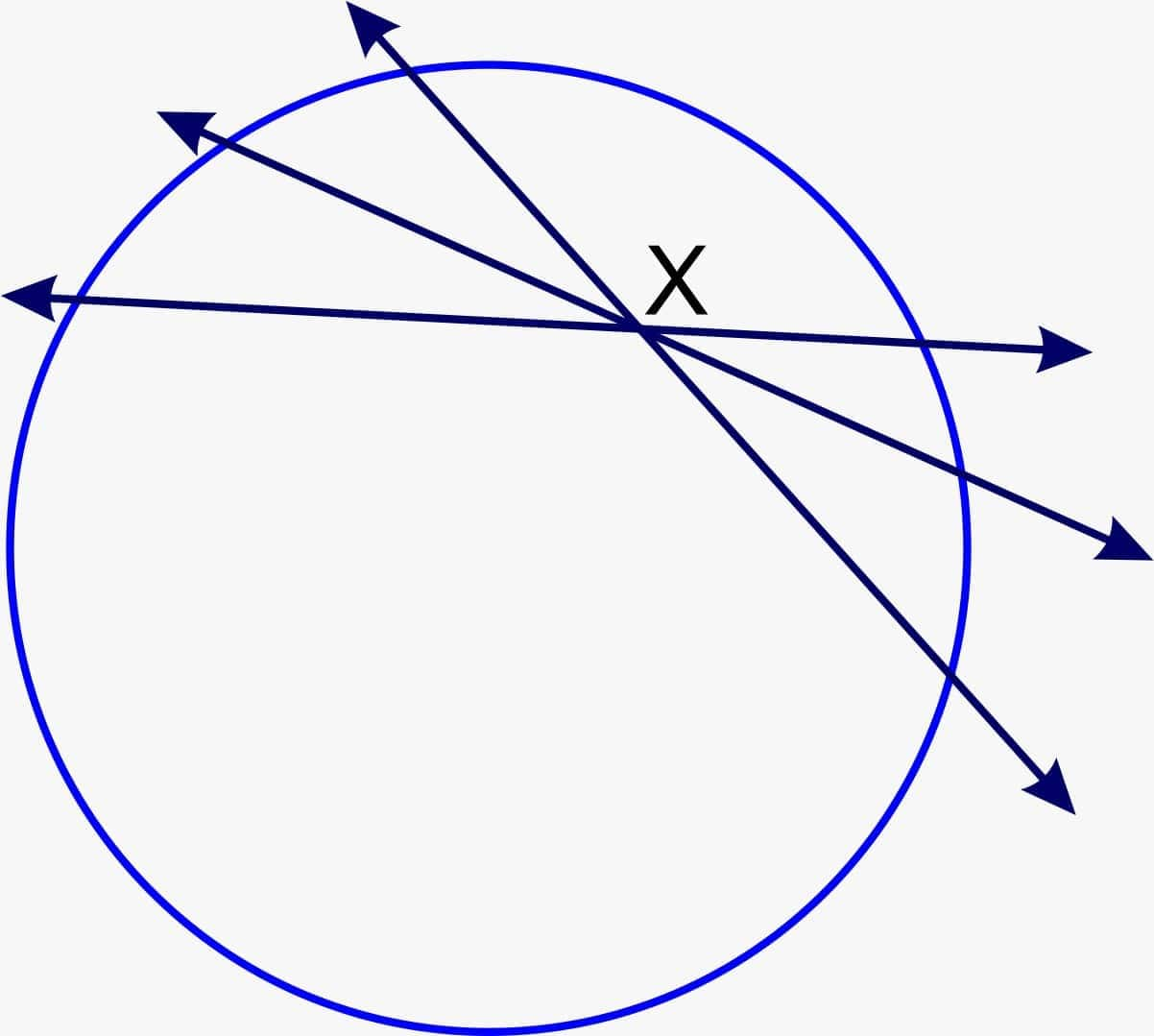
The Number of Tangents from a Given Point:

There are three possible cases to draw tangents from a given point on the circle:
1. If a point lies inside or interior region of the circle, then any line that passes through the point will be a secant. It implies that no tangent that passes through the point in the interior region of the circle is possible.

2. When there is a point lying on the surface of the circle, then only one possible tangent can be drawn that passes through that point.

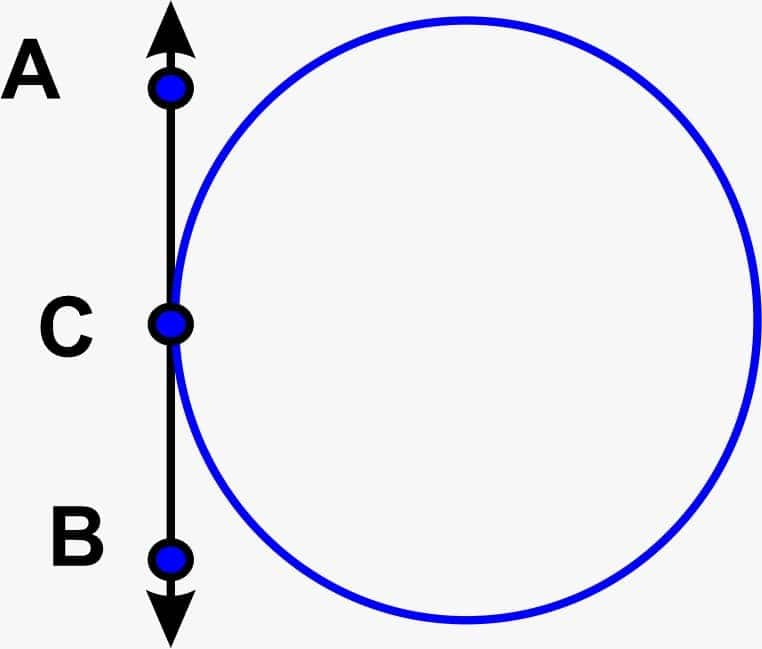
3. If a point lies outside the circle, then there are exactly two tangents that can be drawn that pass through that point, as shown in the figure.

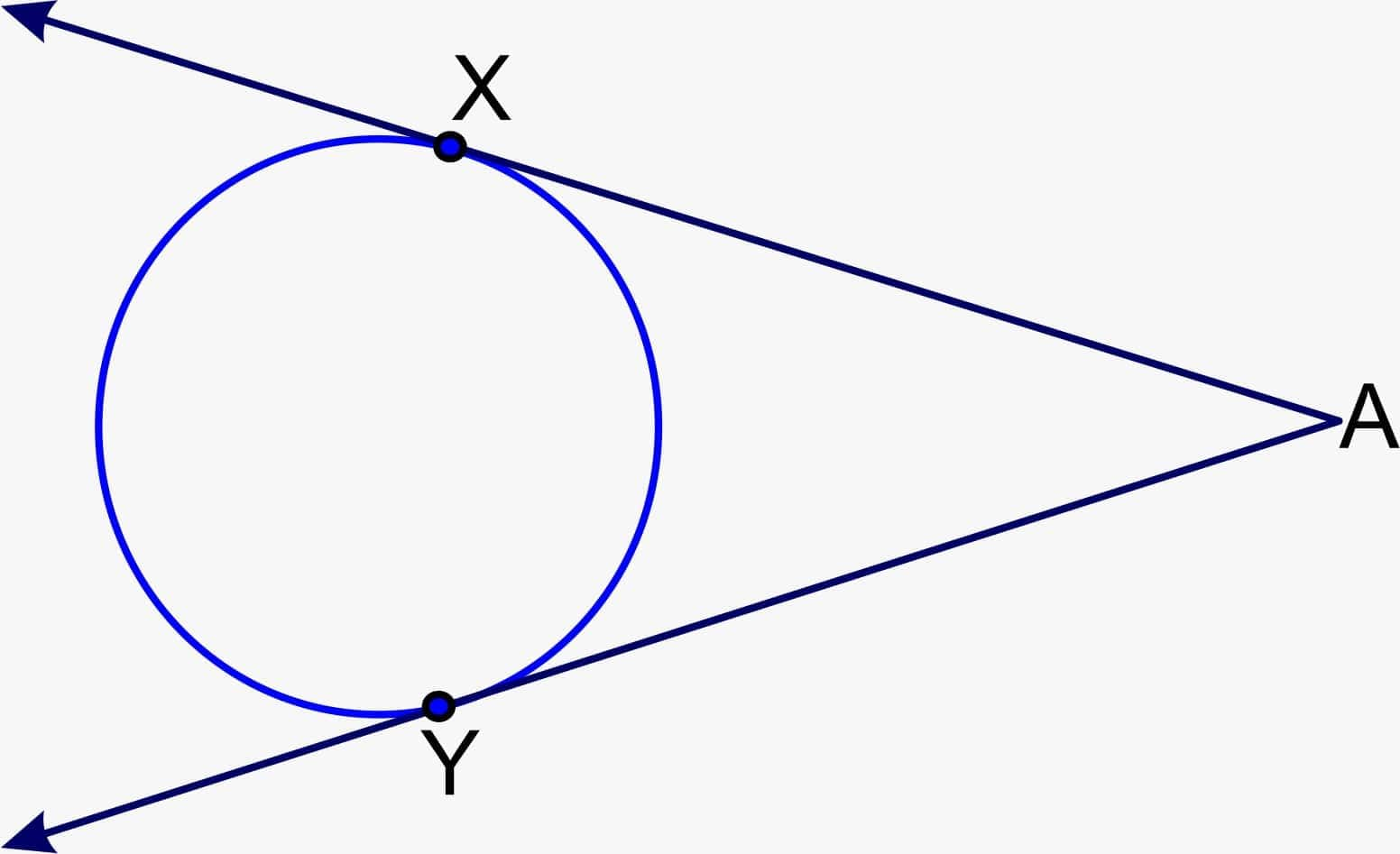
Length of a Tangent:

If an external point is given, A is given, and a point B is given at the surface of the circle, then the line segment AB is called the length of the tangent from point A to the circle.

The length of the tangent using the Pythagorean theorem:
l² = d² - r²
Where,
I = The length of the circle
d = The external point from the centre of the circle
r = radius

Lengths of Tangents Drawn from an External Point:

Theorem: The lengths of tangents drawn from an external point to a circle are equal.

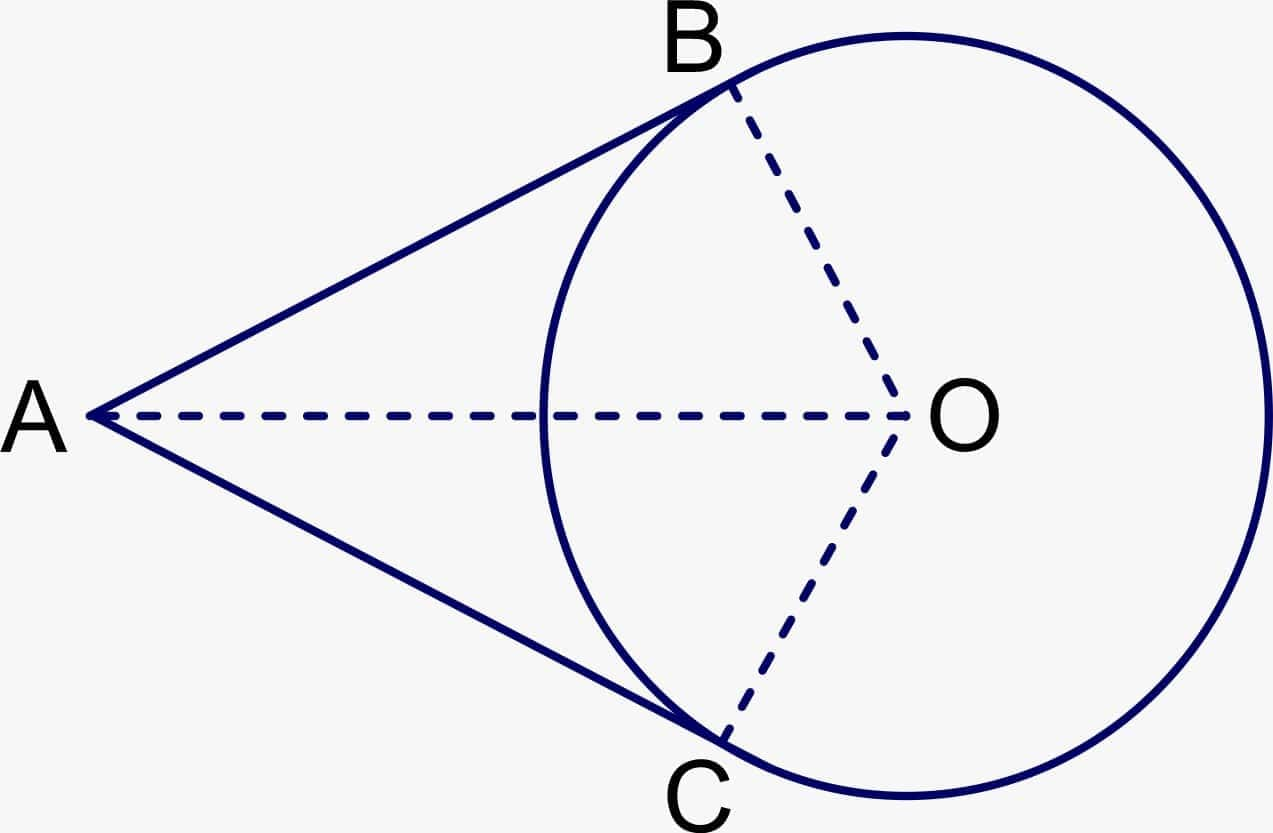
In the figure, a circle is given with center O, and a point A is an exterior point of the circle with two tangents AB, AC on the circle from A.
According to the theorem, we need to prove AB = AC
So, we need to join OA, OB and OC.
We know that the angles between the radii and tangents form a right-angled triangle.
Therefore,
∠OBA and ∠ OCA are right angles
In right triangles OBA and OCA,
OB = OC (Radii of the same circle)
OA = OA (Common in both triangles)
Therefore, ∆ OBA ≅ ∆ OCA (RHS)
This gives PQ = PR

Important Properties Of a Circle:

1. If two concentric circles are given, then the chord of the larger circle that touches the smaller circle is bisected at that contact point.
2. At the end of the diameter, when tangents are drawn, these tangents are parallel to each other.
3. The shape that is drawn circumscribing a circle is a rhombus.

Circles: Previous Year Question and Answer

Given below are some previous year question answers of various examinations from the NCERT class 10 chapter 10, Circles:

Question 1: PA and PB are tangents drawn to a circle with centre 0. If $\angle \mathrm{AOB}=120^{\circ}$ and $\mathrm{OA}=10 \mathrm{~cm}$, then find the length of chord AB.

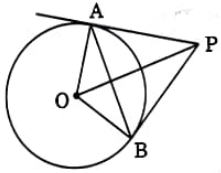
Solution:
$\triangle A O B$ is isosceles:
$O A=O B=10 \mathrm{~cm}$ [Radius]
$\angle A O B=120^{\circ}$
Draw an altitude from $O$ to $ AB$, say it meets $ AB$ at point $M$.
So $\mathrm{OM} \perp \mathrm{AB}$ and bisects AB (because triangle AOB is isosceles and OM is the angle bisector and median).

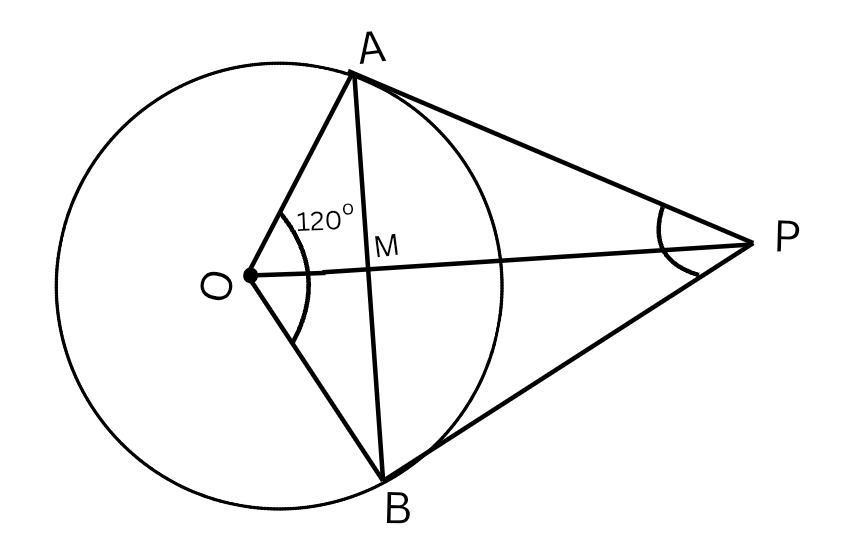
So: $A M=M B=\frac{1}{2} A B$ and $\triangle O M A$ is a right triangle.
In triangle $\triangle O M A$ :
$\angle A O M=\frac{120^{\circ}}{2}=60^{\circ}$
Hypotenuse $O A=10 \mathrm{~cm}$
Now, using basic trigonometry, we get,
$\cos \left(60^{\circ}\right)=\frac{\text {Adjacent }}{\text {Hypotenuse }}=\frac{O M}{10}$
$ \Rightarrow \frac{1}{2}=\frac{O M}{10} $
$\Rightarrow O M=5 \mathrm{~cm}
$Now using Pythagoras theorem in $\triangle$OMA, we get,$
O A^2=O M^2+A M^2$
$ \Rightarrow 10^2=5^2+A M^2$
$ \Rightarrow 100=25+A M^2$
$ \Rightarrow A M^2=75$
$ \Rightarrow A M=\sqrt{75}=5 \sqrt{3}$
So: $A B=2 \times A M=2 \times 5 \sqrt{3}=10 \sqrt{3} \mathrm{~cm}$
Hence, the answer is ($10 \sqrt{3} \mathrm{~cm}$).

Question 2: In two concentric circles centred at $O$, a chord AB of the larger circle touches the smaller circle at $C$. If $O A=3.5 \mathrm{~cm}, O C=2.1 \mathrm{~cm}$, then AB is equal to:

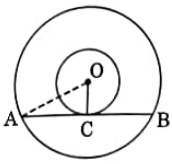
Solution:

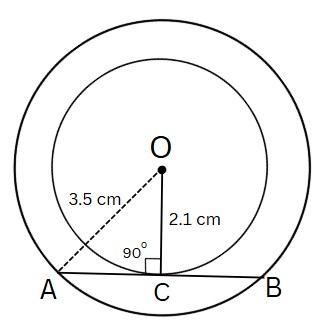
Point $C$ is the midpoint of chord $AB$, because a line from the centre to the point of tangency is perpendicular to the chord (property of tangents).

$OC \perp AB$ (radius to tangent).

$\triangle OCA$ is right-angled at $C$.

$OA^2 = OC^2 + AC^2$ (By Pythagoras' theorem)

$ \Rightarrow (3.5)^2 = (2.1)^2 + AC^2$

$ \Rightarrow 12.25 = 4.41 + AC^2$

$ \Rightarrow AC^2 = 7.84$

$\Rightarrow AC = \sqrt{7.84} = 2.8$ cm

$OC$ bisects $AB$,

$AB = 2 \times AC = 2 \times 2.8 = 5.6$ cm

Hence, the correct answer is $5.6$ cm.

Question 3: $OAB$ is a sector of a circle with centre $O$ and radius $7$ cm. If length of arc $\overparen{\mathrm{AB}}=\frac{22}{3} \mathrm{~cm}$, then $\angle \mathrm{AOB}$ is equal to

Solution:

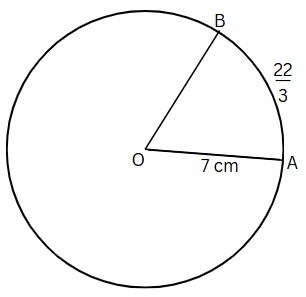
Given:

radius $r = 7\ \text{cm}$,

length of arc $AB = \frac{22}{3}\ \text{cm}\ldots(1)$

We know that,

The length of arc $l = \frac{\theta}{360} \times 2\pi r\ldots(2)$

On equating equation (1) and (2), we get

$\Rightarrow \frac{22}{3} = \frac{\theta}{360} \times 2 \times \frac{22}{7} \times 7$

$ \Rightarrow \frac{22}{3}= \frac{\theta}{360} \times 44$

$\Rightarrow \frac{22}{3} = \frac{44 \times \theta}{360}$

$\Rightarrow \frac{22}{3} = \frac{11 \times \theta}{90}$

$ \Rightarrow 22 \times 90 = 3 \times 11 \times \theta$

$ \Rightarrow1980 = 33 \times \theta$

$\Rightarrow \theta = \frac{1980}{33} = 60^\circ$

Hence, the correct answer is $60^\circ$.

Class 10 Chapter Wise Notes

All the links to chapter-wise notes for NCERT class 10 maths are given below:

NCERT Exemplar Solutions for Class 10

Students must check the NCERT Exemplar solutions for class 10 of Mathematics and Science Subjects.

• NCERT Exemplar Class 10 Maths solutions
• NCERT Exemplar Class 10 Science solutions

NCERT Solutions for Class 10

Students must check the NCERT solutions for class 10 of Mathematics and Science Subjects.

• NCERT Solutions for Class 10 Maths
• NCERT Solutions for Class 10 Science

NCERT Books and Syllabus

To learn about the NCERT books and syllabus, read the following articles and get a direct link to download them.

• NCERT Books for Class 10
• NCERT Syllabus for Class 10