NCERT Solutions for Class 10 Maths Chapter 14 Probability

Q1. Complete the following statements:
Q1 (i).Probability of an event E + Probability of the event ‘not E’ = ________

Answer:

Probability of an event E + Probability of the event ‘not E’ = 1

$\\ E \cup E' = S$
So, $P(E \cup E') = P(S) = 1$

Q1 (ii). The probability of an event that cannot happen is ______ . Such an event is called ______.

Answer:

The probability of an event that cannot happen is 0. Such an event is called an impossible event.

When there is no favorable outcome, i.e., the number of outcomes is zero.

Q1 (iii). The probability of an event that is certain to happen is_____. Such an event is called _______.

Answer:

The probability of an event that is certain to happen is 1. Such an event is called a sure/certain event

When the number of favorable outcomes is the same as the number of all possible outcomes, it is a sure event.

Q1 (iv). The sum of the probabilities of all the elementary events of an experiment is _______.

Answer:

The sum of the probabilities of all the elementary events of an experiment is 1.

Q1 (v). The probability of an event is greater than or equal to and less than or equal to ________ .

Answer:

The probability of an event is greater than or equal to 0 and less than or equal to 1.

Q2. Which of the following experiments have equally likely outcomes? Explain.
Q2 (i). A driver attempts to start a car. The car starts or does not start.

Answer:

It is not an equally likely event since it depends on various factors like there is no fuel, engine malfunctioning etc, that are not alike for both outcomes.

Q2 (ii). A player attempts to shoot a basketball. She/he shoots or misses the shot.

Answer:

It is not an equally likely event because it depends on the ability and amount of practice of the player. If he is a professional player, he will more likely have a successful shot. Whereas an amateur player will more likely miss the shot.

Q2 (iii). A trial is made to answer a true-false question. The answer is right or wrong.

Answer:

It is an equally likely event. The only options are true or false, and only one of them is correct.

Q2 (iv). A baby is born. It is a boy or a girl.

Answer:

It is an equally likely event. The only possibilities of gender are boy and girl. Hence, if not boy, then girl and vice versa.

Q3. Why is tossing a coin considered to be a fair way of deciding which team should get the ball at the beginning of a football game?

Answer:

The tossing of the coin is considered to be a fair way of deciding because the only possible outcomes are heads and tails. Hence, they are equally likely events.

Q4. Which of the following cannot be the probability of an event?

(A) $\frac23$

(B) –1.5

(C) 15%

(D) 0.7

Answer:

We know that the probability of an event is either greater than or equal to 0 and always less than or equal to 1. Hence, the probability of an event can never be negative.

Therefore, (B) $-1.5$ cannot be the probability of an event.

Also, (A) : $\frac{2}{3} = 0.67$

(C): $15\% = \frac{15}{100} = 0.15$

(D): 0.7

Hence, (A), (C), and (D) all lie between 0 and 1.

Q5. If P(E) = 0.05, what is the probability of ‘not E’?

Answer:

Given, $P(E) = 0.05$

We know,

$P(not\ E) = 1 - P(E)$

$\therefore P(not\ E) = 1 - 0.05 = 0.95$

Hence, the probability of 'not E' is 0.95

Q6 . A bag contains lemon-flavored candies only. Malini takes out one candy without looking into the bag. What is the probability that she takes out
(i) an orange-flavored candy?
(ii) a lemon-flavored candy?

Answer:

(i) According to the question, the bag contains only lemon-flavored candies. It does not contain any orange-flavored candy. Hence, every time, only lemon-flavored candy will come out. Therefore, P(an orange-flavored candy) = 0. i.e., the event of taking out an orange-flavored candy is impossible.
(ii) According to the question, the bag contains only lemon-flavored candies. So the event that Malini takes out a lemon-flavored candy is sure. Therefore, P(a lemon-flavored candy) = 1.

Q7. It is given that in a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday?

Answer:

Given,

The probability of two students not having the same birthday $P (\overline E) = 0.992$

$\therefore$ Probability of two students having the same birthday = $P (E) = 1 - P (\overline E)$

$= 1 - 0.992 = 0.008$

Hence, the probability that the 2 students have the same birthday is 0.008.

Q8. A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is (i) red?
(ii) not red?

Answer:

Total number of balls in the bag = 8
No. of red balls = 3
No. of black balls = 5

(i) Let E be the event of getting a red ball

n(E) = No. of red balls = 3
n(S) = No. of total balls = 8

$\therefore$ Probability of the ball drawn to be red =
$P = \frac{n(E)}{n(S)}$
$= \frac{3}{8}$

(ii) We know,
$P(not\ E) = P (\overline E) = 1 - P (E)$
where $E\ and\ \overline E$ are complementary events.

$\therefore$ Probability of not getting the red ball
$= 1$ - Probability of getting a red ball
$\\ = 1 - \frac{3}{8} \\ = \frac{5}{8}$

Q9. A box contains 5 red marbles, 8 white marbles, and 4 green marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be (i) red?
(ii) white?
(iii) not green?

Answer:

Given,

Total number of balls in the bag = 5 + 8 + 4 = 17

(i) Let R be the event that the ball taken out is red

The number of possible outcomes = 17

The number of outcomes favorable to the event R = 5

$\therefore$ $P(R) = \frac{\text{favourable outcomes}}{\text{total outcomes}}=\frac{5}{17}$

(ii) Let W be the event that the ball taken out is white

The number of possible outcomes = 17

The number of outcomes favorable to the event W = 8

$\therefore$ $P(W) = \frac{\text{favourable outcomes}}{\text{total outcomes}}=\frac{8}{17}$

(iii) Let G be the event that the ball taken out is green

The number of possible outcomes = 17

The number of outcomes favorable to the event G = 4

$\therefore$ $P(G) = \frac{\text{favourable outcomes}}{\text{total outcomes}}=\frac{4}{17}$

$\\ \therefore P(not\ G) =P(\overline G) =1-P(G) \\ = 1-\frac{4}{17} \\ = \frac{13}{17}$

The required probability of not getting a green ball is $\frac{13}{17}$.

Q10. A piggy bank contains a hundred 50p coins, fifty Rs 1 coins, twenty Rs 2 coins, and ten Rs 5 coins. If it is equally likely that one of the coins will fall out when the bank is turned upside down,
(i) What is the probability that the coin will be a 50 p coin?
(ii) Will not be a Rs 5 coin?

Answer:

Total number of coins in the piggy bank $= 100+50+20+10 = 180$

(i) Let E be the event of getting a 50p coin.

Number of possible outcomes = 180

Number of outcomes favorable to event E = 100

$\therefore P(E) = \frac{\text{favourable outcomes}}{\text{total outcomes}} = \frac{100}{180}$

$= \frac{5}{9}$

Therefore, the probability of getting a 50p coin is $\frac{5}{9}$

(ii) Let F be the event of getting a Rs. 5 coin.

Number of possible outcomes = 180

Number of outcomes favorable to event F = 10

$\therefore P(F) = \frac{\text{favourable outcomes}}{\text{total outcomes}} = \frac{10}{180}$

$= \frac{1}{18}$

$\therefore$ P(not getting a Rs. 5 coin) $=1 - P(F) = 1 - \frac{1}{18} = \frac{17}{18}$

Therefore, the probability of not getting a Rs. 5 coin is $\frac{17}{18}$.

Q11. Gopi buys a fish from a shop for his aquarium. The shopkeeper takes out one fish at random from a tank containing 5 male fish and 8 female fish (see Fig. 14.4). What is the probability that the fish taken out is a male fish?

Answer:

Total number of fishes in the tank = 5 (male) + 8 (female) = 13

Let E be the event that the fish taken out is a male fish.

Number of possible outcomes = 13

Number of outcomes favorable to E = 5

$\therefore P(E) = \frac{\text{favourable outcomes}}{\text{total outcomes}} = \frac{5}{13}$

Therefore, the probability that the fish taken out is a male fish is $\frac{5}{13}.$

Q12. A game of chance consists of spinning an arrow that comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see Fig. ), and these are equally likely outcomes. What is the probability that it will point at
(i) 8?
(ii) an odd number?
(i) a number greater than 2?
(i) a number less than 9?

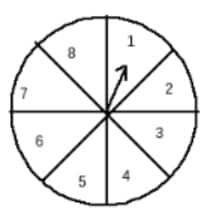
Answer:

Total possible outcomes = {1,2,3,4,5,6,7,8}

Number of possible outcomes = 8

(i) Let E be the event of getting 8.

$\therefore P(E) = \frac{\text{favourable outcomes}}{\text{total outcomes}} = \frac{1}{8}$

Therefore, the probability that it will point at 8 is $\frac{1}{8}.$

(ii) Let E be the event of pointing at an odd number.

Total number of odd numbers = n({1,3,5,7}) = 4

$\therefore P(E) = \frac{\text{favourable outcomes}}{\text{total outcomes}} = \frac{4}{8}$

$= \frac{1}{2}$
Therefore, the probability of getting an odd number is $\frac{1}{2}.$

(iii) Let E be the event of pointing at a number greater than 2

Number of favorable outcomes= n({3,4,5,6,7,8}) = 6

$\therefore P(E) = \frac{\text{favourable outcomes}}{\text{total outcomes}} = \frac{6}{8}=\frac34$
Therefore, the probability of pointing at a number greater than 2 is $\frac{3}{4}.$

(iv) Let E be the event of pointing at a number less than 9

Since all the numbers on the wheel are less than 9, this is a sure event.

Number of favorable outcomes = 8

$\therefore P(E) = \frac{\text{favourable outcomes}}{\text{total outcomes}} = \frac{8}{8} = 1$
Therefore, the probability of pointing at a number less than 9 is $1.

Q13. A die is thrown once. Find the probability of

(I) getting a prime number.

(ii) a number lying between 2 and 6.

(iii) getting an odd number.

Answer:

Possible outcomes when a die is thrown = {1,2,3,4,5,6}

Number of possible outcomes once = 6

(i) Let E be the event of getting a prime number.

Prime numbers on the die are = {2,3,5}

Number of favorable outcomes = 3

$\therefore P(E) = \frac{favourable\ outcomes}{total\ outcomes} = \frac{3}{6}$

$= \frac{1}{2}$

Therefore, the probability of getting a prime number is ${100} \frac{1}{2}$

(ii) Let F be the event of getting a number lying between 2 and 6

Numbers lying between 2 and 6 on the die are = {3,4,5}

Number of favorable outcomes = 3

$\therefore P(F) = \frac{favourable\ outcomes}{total\ outcomes} = \frac{3}{6}$

$= \frac{1}{2}$

Therefore, the probability of getting a number lying between 2 and 6 is $\frac{1}{2}$

(iii) Let O be the event of getting an odd number.

Odd numbers on the die are = {1,3,5}

Number of favorable outcomes = 3

$\therefore P(O) = \frac{favourable\ outcomes}{total\ outcomes} = \frac{3}{6}$

$= \frac{1}{2}$

Therefore, the probability of getting an odd number is $\frac{1}{2}$.

Q14. One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting

(I) a king of red color.

(ii) a face card.

(iii) a red-face card

(iv) the Jack of hearts

(v) a spade

(vi) the queen of diamonds

Answer:

The total number of cards in a well-shuffled deck = 52

Hence, the total possible outcomes = 52

(i) Let E be the event of getting a king of red color.

There are only red color kings: Hearts and diamonds

Hence, the number of favorable outcomes = 2

$\therefore P(E) = \frac{favourable\ outcomes}{total\ outcomes} = \frac{2}{52}$

$= \frac{1}{26}$

Therefore, the probability of getting a king of red color is $\frac{1}{26}.$

(ii) Let E be the event of getting a face card.

Face cards: (J, Q, K) of each four suits

Hence, the number of favorable outcomes = 12

$\therefore P(E) = \frac{favourable\ outcomes}{total\ outcomes} = \frac{12}{52}$

$= \frac{3}{13}$

Therefore, the probability of getting a face card is $\frac{3}{13}.$

(iii) Let E be the event of getting a red face card.

Face cards: (J, Q, K) of hearts and diamonds

Hence, the number of favorable outcomes = $3\times2 = 6$

$\therefore P(E) = \frac{favourable\ outcomes}{total\ outcomes} = \frac{6}{52}$

$= \frac{3}{26}$

Therefore, the probability of getting a red face card is $\frac{3}{26}.$

(iv) Let E be the event of getting the jack of hearts

Hence, the number of favorable outcomes = 1

$\therefore P(E) = \frac{favourable\ outcomes}{total\ outcomes} = \frac{1}{52}$

Therefore, the probability of getting the jack of hearts is $\frac{1}{52}.$

(v) Let E be the event of getting a spade.

There are 13 cards in each suit.

Hence, the number of favourable outcomes = 13

$\therefore P(E) = \frac{favourable\ outcomes}{total\ outcomes} = \frac{13}{52}$

$= \frac{1}{4}$

Therefore, the probability of getting a spade is $\frac{1}{4}.$

(vi) Let E be the event of getting the queen of diamonds

Hence, the number of favorable outcomes = 1

$\therefore P(E) = \frac{favourable\ outcomes}{total\ outcomes} = \frac{1}{52}$

Therefore, the probability of getting the queen of diamonds is $\frac{1}{52}.$

15. Five cards—the ten, jack, queen, king, and ace of diamonds, are well-shuffled with their face downwards. One card is then picked up at random. What is the probability that

(i) the card is the queen?

(ii) the second card picked up is (a) an ace? (b) a queen?

Answer:

Total number of cards = 5

Hence, the total possible outcomes = 5

(i) There is only one queen.

Hence, favorable outcome = 1

$\therefore P(getting\ a\ queen) = \frac{1}{5}$

(ii-a) There is only one ace.

Hence, favorable outcome = 1

$\therefore$ P(getting an ace)$= \frac{1}{4}$

Therefore, the probability of getting an ace is 0.25.

(ii-b) Since there is no queen left.

Hence, favorable outcome = 0

$\therefore$ P(getting a queen)$= \frac{0}{4} = 0$

Therefore, the probability of getting a queen is 0. Thus, it is an impossible event.

Q16. 12 defective pens are accidentally mixed with 132 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen is taken out is a good one.

Answer:

Total number of pens = 132 (good) + 12 (defective)

Hence, the total possible outcomes = 144

Number of good pens = number of favorable outcomes = 132

$\therefore$ P(getting a good pen) $= \frac{favourable\ outcome}{total\ outcome} = \frac{132}{144} = \frac{11}{12}$

17. (i) A lot of 20 bulbs contains 4 defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?

(ii) Suppose the bulb drawn in (i) is not defective and is not replaced. Now, one bulb is drawn at random from the rest. What is the probability that this bulb is not defective?

Answer:

(i) Total number of bulbs = 20

Hence, the total possible outcomes = 20

Number of defective bulbs = 4

Hence, the number of favorable outcomes = 4

$\therefore$ P(getting a defective bulb)$= \frac{favourable\ outcomes}{total\ outcomes} = \frac{4}{20}$

$= \frac{1}{5}$

(ii) Suppose the bulb drawn in (i) is not defective and is not replaced.

Number of remaining bulbs $=20-1=19$
Number of remaining non-defective bulbs $=16-1=15$
The probability that this bulb is not defective $=\frac{15}{19}$.

Q18. A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box. find the probability that it bears

(i) a two-digit number.

(ii) a perfect square number.

(iii) a number divisible by 5.

Answer:

(i) Total number of discs = 90

Number of discs having a two-digit number between 1 and 90 = 81

$\therefore$ P(getting a two-digit number) $= \frac{\text{favourable outcomes}}{\text{total outcomes}} = \frac{81}{90}=\frac{9}{10}$

(ii) Total number of discs = 90

Perfect square numbers from 1 to 90 are {1, 4, 9, 16, 25, 36, 49, 64, 81}

Therefore, the total number of discs having perfect squares = 9.
$\therefore$ P(getting a perfect square number) $= \frac{\text{favourable outcomes}}{\text{total outcomes}} = \frac{9}{90}=\frac{1}{10}$

(iii) Total number of discs = 90

Numbers between 1 and 90 that are divisible by 5 are $(5,10,15,20,25,30,35,40,45,50,55,60,65,70,75,80,85,90)$

Therefore, the total number of discs having numbers that are divisible by 5 = 18.

$\therefore$ P(getting a number divisible by 5) $= \frac{\text{favourable outcomes}}{\text{total outcomes}} = \frac{18}{90}=\frac{1}{5}$

Q19. (i) A child has a die whose six faces show the letters as given below:

The die is thrown once. What is the probability of getting

(i) A?

(ii) D?

Answer:

The six faces of the die contain: {A, B, C, D, E, A}

Total number of letters = 6

(i) Since there are two A's,

Number of favorable outcomes = 2
$\therefore$ P(getting A) $= \frac{\text{favourable outcomes}}{\text{total outcomes}} = \frac{2}{6}$

$= \frac{1}{3}$

Therefore, the probability of getting A is $\frac{1}{3}.$

(ii) Since there is only one D,

Number of favorable outcomes = 1

$\therefore$ P(getting D) $= \frac{\text{favourable outcomes}}{\text{total outcomes}} = \frac{1}{6}$

Therefore, the probability of getting D is $\frac{1}{6}.$

Q20. Suppose you drop a die at random on the rectangular region shown in Fig. (15.6). What is the probability that it will land inside the circle with a diameter of 1m?

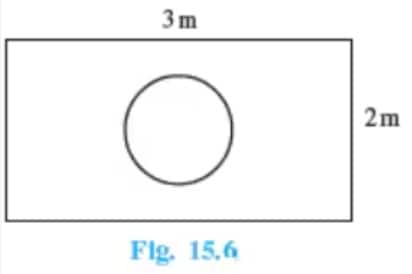
Answer:

Here, the Total outcome is the area of the rectangle, and the favorable outcome is the area of the circle.

Area of the rectangle = $l\times b = 3\times2 = 6\ m^2$

Area of the circle = $\pi r^2 = \pi \left(\frac{1}{2}\right)^2 = \frac{\pi}{4}\ m^2$

$\therefore P(die\ will\ land\ inside\ the\ hole) = \frac{Area\ of\ circle}{Total\ area}$

$= \frac{\frac{\pi}{4}}{6} = \frac{\pi}{24}$

Q21. A lot consists of 144 ball pens, of which 20 are defective and the others are good. Nuri will buy a pen if it is good but will not buy it if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that

(i) She will buy it?

(ii) She will not buy it?

Answer:

Total number of pens = 144

Total number of defective pens = 20

$\therefore$ Number of good pens = 144 - 20 = 124

She will buy it if the pen is good.

(i) Therefore, the probability that she buys = probability that the pen is good =

$P(getting\ a\ good\ pen) = \frac{number\ of\ good\ pens}{total\ pens}= \frac{124}{144}$

$= \frac{31}{36}$

(ii) The probability that she will not buy = probability that the pen is defective

$P(getting\ a\ defective\ pen) = \frac{no.\ of\ defective\ pens}{total\ pens}= \frac{20}{144}$

$= \frac{5}{36}$

Q22. Refer to Example 13. (i) Complete the following table:

Answer:

Number of possible outcomes to get the sum as 2 = (1,1) = 2

Number of possible outcomes to get the sum as 3 = (2,1), (1, 2) = 2

Number of possible outcomes to get the sum as 4 = (2, 2), (1, 3), (3,1) = 3

Number of possible outcomes to get the sum as 5 = (3, 2), (2, 3), (4,1), (1, 4) = 4

Number of possible outcomes to get the sum as 6 = (5,1), (1, 5), (3, 3), (4, 2), (2, 4) = 5

Number of possible outcomes to get the sum as 7 = (4, 3), (3, 4), (6,1), (1, 6), (5, 2), (2, 5) = 6

Number of possible outcomes to get the sum as 8 = (4, 4), (6, 2), (2, 6), (5, 3), (3, 5) = 5

Number of possible outcomes to get the sum as 9 = (5, 4), (4, 5), (6, 3), (3, 6) = 4

Number of possible outcomes to get the sum as 10 = (5, 5), (6, 4), (4, 6) = 3

Number of possible outcomes to get the sum as 11 = (6, 5), (5, 6) = 11

Number of possible outcomes to get the sum as 12 = (6, 6) = 1

The table becomes:

22. (ii) A student argues that ‘there are 11 possible outcomes: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12. Therefore, each of them has a probability of 1/11. Do you agree with this argument? Justify your answer.

Answer:

A student argues that "there are 11 possible outcomes: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12. Therefore, each of them has a probability of 1/11. We do not agree with this argument because there are a different number of possible outcomes for each sum. We can see that each sum has a different probability.

Q23. A game consists of tossing a one-rupee coin 3 times and noting its outcome each time. Hanif wins if all the tosses give the same result i.e., three heads or three tails, and loses otherwise. Calculate the probability that Hanif will lose the game.

Answer:

The possible outcomes when a coin is tossed 3 times (Same as 3 coins tossed at once)

{HHH, HHT, HTH, HTT, THH, TTH, THT, TTT}

Number of total possible outcomes = 8

For Hanif to win, there are only two favorable outcomes: {HHH, TTT}

Number of favorable outcomes = 2

$\therefore$ P(Hanif will win) $= \frac{favourable\ outcomes}{total\ outcomes} = \frac{2}{8}$

$= \frac{1}{4}$

$\therefore$ P(Hanif will lose) $= 1-\frac{1}{4}$

$=\frac{3}{4}$

Therefore, the probability that Hanif will lose is $\frac{3}{4}.$

Q24 (i) A die is thrown twice. What is the probability that 5 will not come up either time?

Answer:

When a die is thrown twice, the possible outcomes =

$\{(x,y): x,y\in\{1,2,3,4,5,6\}\}$

Total number of possible outcomes = $6\times6 = 36$

The outcomes when 5 comes up at least once =

{(5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (1,5), (2,5), (3,5), (4,5), (6,5)}

Number of such favorable outcomes = 11

$\therefore P(5\ will\ come\ up\ atleast\ once) = \frac{11}{36}$

$\therefore P(5\ will\ not\ come\ up\ either\ time) = 1-\frac{11}{36} =\frac{25}{36}$

Therefore, the probability that 5 will not come either time is $\frac{25}{36}.$

24 (ii) A die is thrown twice. What is the probability that 5 will come up at least once?

Answer:

When a die is thrown twice, the possible outcomes =

$\{(x,y): x,y\in\{1,2,3,4,5,6\}\}$

Total number of possible outcomes = $6\times6 = 36$

The outcomes when 5 comes up at least once =

{(5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (1,5), (2,5), (3,5), (4,5), (6,5)}

Number of such favorable outcomes = 11

$\therefore P(5\ comes\ up\ at\ least\ once)= \frac{11}{36}$

Therefore, the probability that 5 comes at least once is $\frac{11}{36}.$

Q25. (i) Which of the following arguments are correct, and which are not correct? Give reasons for your answer. (i) If two coins are tossed simultaneously, there are three possible outcomes—two heads, two tails, or one of each. Therefore, for each of these outcomes, the probability is 1/3

Answer:

The possible outcomes when two coins are tossed = {HH, HT, TH, TT}

Total number of possible outcomes = 4

$\therefore P(getting\ two\ heads) = \frac{favourable\ outcomes}{total\ outcomes} = \frac{1}{4}$

Hence, the given statement is not correct. This is because one of each can occur in two different ways. Hence, the mentioned events are not equally likely.

Q25 (ii). Which of the following arguments are correct and which are not correct? Give reasons for your answer. (ii) If a die is thrown, there are two possible outcomes—an odd number or an even number. Therefore, the probability of getting an odd number is $\frac12$.

Answer:

The possible outcomes when a die is thrown= {1,2,3,4,5,6}

Total number of possible outcomes = 6

Number of odd numbers, {1,3,5} = 3

And the number of even numbers {2,4,6} = 3

Hence, both these events are equally likely

$\therefore P(getting\ an\ odd) = \frac{favourable\ outcomes}{total\ outcomes} = \frac{3}{6} = \frac{1}{2}$

Similarly, $ P(getting\ an\ odd) = \frac{favourable\ outcomes}{total\ outcomes} = \frac{3}{6} = \frac{1}{2}$.

So, this argument is correct.