Answer:
Probability of an event E + Probability of the event ‘not E’ = 1. Because event E and event 'Not E' are both complementary.
Q1 (ii) The probability of an event that cannot happen is ______. Such an event is called ______.
Answer:
The probability of an event that cannot happen is 0. Such an event is called an impossible event.
Q1 (iii) The probability of an event that is certain to happen is_____ . Such an event is called _______.
Answer:
The probability of an event that is certain to happen is 1. Such an event is called a sure/certain event.
Q1 (iv) The sum of the probabilities of all the elementary events of an experiment is _______.
Answer:
The sum of the probabilities of all the elementary events of an experiment is 1.
Q1 (v) The probability of an event is greater than or equal to and less than or equal to ________ .
Answer:
The probability of an event is greater than or equal to 0 and less than or equal to 1.
Answer:
This statement does not have equally likely consequences, because the car may or may not start based on a variety of conditions, including fuel.
Answer:
It is not an equally likely event because it is determined by the player's talent and level of practice. If he is a professional player, he is more likely to make a good shot. Whereas an amateur player is more likely to miss the shot.
Answer:
It is an equally likely event. The only options are true or false, and only one of them is correct.
Answer:
It is an equally likely event. The only possibilities of gender are boy and girl. Hence, if not a boy, then a girl and vice versa.
Answer:
The answer becomes unbiased by using a coin toss due to its two possible results being heads or tails. The event that results in head or tail has equal odds since these two outcomes are equally likely outcomes, which makes tossing an unpredictable process deemed entirely unbiased.
Q4 Which of the following cannot be the probability of an event?
(A) 2/3
(B) –1.5
(C) 15%
(D) 0.7
Answer:
The probability of an event always lies between 0 and 1, and can be 0 or 1. Hence, the probability of an event can never be negative.
Therefore, (B) −1.5 cannot be the probability of an event. Also, Options (A), (C), and (D) all lie between 0 and 1; therefore, they can be the probability of an event.
Q5 If P(E) = 0.05, what is the probability of ‘not E’?
Answer:
We know,
$P(not\ E) + P(E)$ = 1
Given, P(E)=0.05
Therefore P(not E)=1−0.05=0.95
Thus, the probability of 'not E' is 0.95
Answer:
According to the question, the bag solely contains lemon-flavoured candy. It does not include any orange-flavoured candy. As a result, every time, just lemon-flavoured candy will appear. Thus, P(an orange−flavoured candy)=0.
Answer:
As per the question, the bag contains only lemon-flavoured candies. So the event that is happening in this case is a sure event. Therefore, P(a lemon flavoured candy)=1
Answer:
Probability of two students not having the same birthday P(E―)=0.992
Therefore, Probability of two students having the same birthday = P(E)=1−P(E―)
=1−0.992=0.008
Thus, the probability that the 2 students have the same birthday is 0.008
Answer:
Given, the total number of balls in the bag = 8
Number of red balls = 3
Number of black balls = 5.
Let E be the event of getting a red ball
Therefore, Favourable outcomes = Number of red balls = 3
And, Total outcomes = Number of total balls = 8
Therefore,
Probability of the ball being drawn is red = P=favourable outcomes)Total outcomes = =38
Answer:
Total number of balls in the bag = 8
Number of red balls = 3
Number of black balls = 5
We know,
P(not E)=P(E―)=1−P(E)
where E and E― are complementary events.
Therefore,
Probability of not getting the red ball =1−Probability of getting a red ball = =1−38=58
Answer:
Total number of balls in the bag = 5 + 8 + 4 = 17
Let R be the event that the ball taken out is red
Thus, the total number of possible outcomes = 17
And, the total number of favourable outcomes = 5
Therefore P(R)=favourable outcomestotal outcomes=517
Answer:
Total number of balls in the bag = 5 + 8 + 4 = 17
Let W be the event that the ball taken out is white
Thus, the total number of possible outcomes = 17
And, the total number of favourable outcomes = 8
Therefore P(W)=favourable outcomestotal outcomes=817
Answer:
Total number of balls in the bag = 5 + 8 + 4 = 17
Let G be the event that the ball taken out is green
Thus, the total number of possible outcomes = 17
And, the total number of favourable outcomes = 4
Therefore P(G)=favourable outcomestotal outcomes=417
∴P(not G)=P(G―)=1−P(G)=1−417=1317
Thus, the required probability of not getting a green ball is 1317
Answer:
Total number of coins in the piggy bank = 100 + 50 + 20 + 10 = 180
Let E be the event of getting a 50p coin.
Thus, the total number of possible outcomes = 180
And, the total number of favourable outcomes = 100
Therefore P(E) = \frac{favourable\ outcomes}{total\ outcomes} = \frac{100}{180}$ = =59
Thus, the probability of getting a 50p coin is 59
Answer:
Total number of coins in the piggy bank = 100 + 50 + 20 + 10 = 180
Let F be the event of getting an Rs. 5 coin.
Thus, the total number of possible outcomes = 180
And, the total number of favourable outcomes = 10
Therefore P(F)=favourable outcomestotal outcomes=10180
=118
Therefore P(not getting a Rs. 5 coin)=P(F―)
=1−P(F)=1−118=1718
Thus, the probability of not getting an Rs. 5 coin is 1718

Answer:
Total number of fishes in the tank = 5 (male) + 8 (female) = 13
Let E be the event that the fish taken out is a male fish.
Thus, the total number of possible outcomes = 13
And, the total number of favourable outcomes = 5
Therefore P(E)=favourable outcomestotal outcomes=513
Thus, the probability that the fish are taken out is a male fish is 513
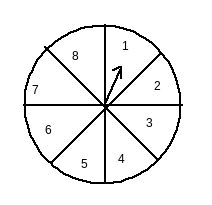
Answer:
Total possible outcomes = {1, 2, 3, 4, 5, 6, 7, 8}
Therefore, the number of possible outcomes = 8
Let E be the event of getting 8, and we can see the favourable outcome would be 1 (as 8 can appear only once)
Therefore P(E)=favourable outcomestotal outcomes=18
Thus, the probability that it will point at 8 is 18
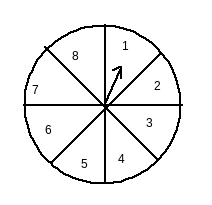
Answer:
Total posible outcomes = {1,2,3,4,5,6,7,8}
Therefore, the number of possible outcomes = 8
Let E be the event of pointing at an odd number.
And, the total number of odd numbers (favourable outcomes) = n({1,3,5,7}) = 4
Therefore P(E)=favourable outcomestotal outcomes=48 or =12
Therefore, the probability of getting an odd number is 12
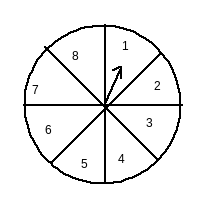
Answer:
Total posible outcomes = {1,2,3,4,5,6,7,8}
Therefore, the number of possible outcomes = 8
Let E be the event of pointing at a number greater than 2
Thus, number of favouable outcomes= n({3,4,5,6,7}) = 5
Therefore P(E)=favourable outcomestotal outcomes=58
Hence, the probability of pointing at a number greater than 2 is 58
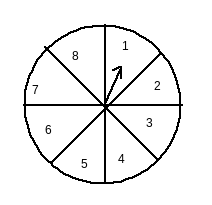
Answer:
Total possible outcomes = {1,2,3,4,5,6,7,8}
Therefore, the number of possible outcomes = 8
Let E be the event of pointing at a number less than 9
Since all the numbers on the wheel are less than 9, this is a sure event.
Thus, the number of favourable outcomes = 8
Therefore P(E)=favourable outcomestotal outcomes=88=1
Hence, the probability of pointing at a number less than 9 is 1 .
Q13 (i) A die is thrown once. Find the probability of getting a prime number
Answer:
Possible outcomes when a die is thrown = {1,2,3,4,5,6}
Therefore, the number of possible outcomes = 6
Let E be the event of getting a prime number.
Prime numbers on the die are = {2,3,5}
Thus, the number of favourable outcomes = 3
Therefore P(E)=favourable outcomestotal outcomes=36 or =12
Hence, the probability of getting a prime number is 12
Q13 (ii) A die is thrown once. Find the probability of getting a number lying between 2 and 6
Answer:
Possible outcomes when a die is thrown once = {1,2,3,4,5,6}
Therefore, the number of possible outcomes = 6
Let F be the event of getting a number lying between 2 and 6
Numbers lying between 2 and 6 on the die are = {3,4,5}
Therefore, number of favourable outcomes = 3
Therefore P(F)=favourable outcomestotal outcomes=36 or =12
Hence, the probability of getting a number lying between 2 and 6 is 12
Q13 (iii) A die is thrown once. Find the probability of getting an odd number.
Answer:
Possible outcomes when a die is thrown = {1,2,3,4,5,6}
Therefore, the number of possible outcomes = 6
Let O be the event of getting an odd number.
Odd numbers on the die are = {1,3,5}
Thus, the number of favourable outcomes = 3
Therefore P(O)=favourable outcomestotal outcomes=36 or =12
Hence, the probability of getting an odd number is 12 .
Answer:
Total number of cards in a well-shuffled deck = 52
Hence, the total possible outcomes = 52
Let E be the event of getting a king of red colour.
There are only red colour kings: Hearts and diamonds
Hence, the number of favourable outcomes = 2
Therefore P(E)=favourable outcomestotal outcomes=252 or =126
Thus, the probability of getting a king of red colour is 126
Q14 (ii) One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting a face card
Answer:
Total number of cards in a well-shuffled deck = 52
Hence, the total possible outcomes = 52
Let E be the event of getting a face card.
Face cards: (J, Q, K) of each four suits.
Hence, the number of favourable outcomes = 3 × 4 = 12
Therefore P(E)=favourable outcomestotal outcomes=1252 or =313
Thus, the probability of getting a face card is 313
Answer:
Total number of cards in a well-shuffled deck = 52
Hence, the total possible outcomes = 52
Let E be the event of getting a red face card.
Face cards: (J, Q, K) of hearts and diamonds
Hence, the number of favourable outcomes = 3 × 2 = 6
Therefore P(E)=favourable outcomestotal outcomes=652 or =326
Therefore, the probability of getting a red face card is 326
Answer:
Total number of cards in a well-shuffled deck = 52
Hence, the total possible outcomes = 52
Let E be the event of getting the jack of hearts, and the number of times it is possible is 1.
Hence, the number of favourable outcomes = 1
Therefore P(E)=favourable outcomestotal outcomes=152
Thus, the probability of getting the jack of hearts is 152
14 (v) One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting a spade
Answer:
Total number of cards in a well-shuffled deck = 52
Hence, the total possible outcomes = 52
Let E be the event of getting a spade.
There are 13 cards in each suit. {2, 3, 4, 5, 6, 7, 8, 9,10, J, Q, K, A}
Hence, the number of favourable outcomes = 13
Therefore P(E)=favourable outcomestotal outcomes=1352 or =14
Therefore, the probability of getting a spade is 14
Answer:
Total number of cards in a well-shuffled deck = 52
Hence, the total possible outcomes = 52
Let E be the event of getting the queen of diamonds
Hence, the number of favourable outcomes = 1
Therefore P(E)=favourable outcomestotal outcomes=152
Therefore, the probability of getting the queen of diamonds is 152
Answer:
Total number of cards = 5
Hence, the total possible outcomes = 5
There is only one queen.
Hence, favourable outcome = 1
Therefore P(getting a queen)=15
Answer:
When the queen is kept aside, there are only 4 cards left
Hence, the total possible outcomes = 4
There is only one ace.
Hence, favourable outcome = 1
Therefore P(getting an ace)=14
Thus, the probability of getting an ace is 0.25
Answer:
When the queen is kept aside, there are only 4 cards left
Hence, the total possible outcomes = 4
Since there is no queen left.
Hence, favourable outcome = 0
Therefore P(getting a queen)=04=0
Thus, the probability of getting a queen is 0. Thus, it is an impossible event.
Answer:
Total number of pens = 132(good) + 12(defective)
Hence, the total possible outcomes = 144
The total number of good pens = number of favourable outcomes = 132
Therefore P(getting a good pen)=favourable outcometotal outcome=132144=1112
Answer:
Total number of bulbs = 20
Hence, the total possible outcomes = 20
Number of defective bulbs = 4
Hence, the number of favourable outcomes = 4
Therefore P(getting a defective bulb)=favourable outcomestotal outcomes=420 =15
Answer:
Total number of bulbs = 20
Hence, the total possible outcomes = 20
Number of defective bulbs = 4
Hence, the number of favourable outcomes = 4
Therefore P(getting a defective bulb)=favourable outcomestotal outcomes=420 or =15
Thus, P(getting a non defective bulb)=1−15=45
Answer:
Total number of discs = 90
Number of discs having a two-digit number between 1 and 90 (favourable outcomes) = 81
Therefore P(getting a two−digit number)=favourable outcomestotal outcomes=8190 or =910
Answer:
Total number of discs = 90
Perfect square numbers between 1 and 90 are {1, 4, 9, 16, 25, 36, 49, 64, 81}
Therefore, the total number of discs having perfect squares = 9.
Therefore P(getting a perfect square)=favourable outcomestotal outcomes=990 =110
Answer:
Total number of discs = 90
Numbers between 1 and 90 that are divisible by 5 are {5,10,15,20,25,30,35,40,45,50,55,60,65,70,75,80,85,90}
Therefore, the total number of discs having numbers that are divisible by 5 = 18.
∴P(getting a number divisible by 5)=favourable outcomestotal outcomes=1890
=15
Q19 (i) A child has a die whose six faces show the letters as given below:

The die is thrown once. What is the probability of getting (i) A?
Answer:
The six faces of the die contain: {A, B, C, D, E, A}
Thus, the total number of letters = 6
Since there are two A's,
Therefore, the number of favourable outcomes = 2
Therefore P(getting A)=favourable outcomestotal outcomes=26 =13
Hence, the probability of getting A is 13
Q19 (ii) A child has a die whose six faces show the letters as given below:

The die is thrown once. What is the probability of getting (ii) D?
Answer:
The six faces of the die contain: {A, B, C, D, E, A}
Therefore, the total number of letters = 6
Since there is only one D,
Thus, the number of favourable outcomes = 1
Therefore P(getting A)=favourable outcomestotal outcomes=16
Hence, the probability of getting D is 16
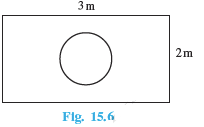
Answer:
Here, the Total outcome in the area of the rectangle and the favourable outcome is the area of the circle.
Area of the rectangle = l×b=3×2=6 m2
Area of the circle = πr2=π(12)2=π4 m2
Therefore P(die will land inside the hole)=Area of circleTotal area
=π46=π24
Answer:
Total number of pens = 144
Total number of defective pens = 20
Therefore, the number of good pens = 144 - 20 = 124
She will buy it if the pen is good.
Therefore, the probability that she buys = the probability that the pen is good =
P(getting a good pen)=number of good penstotal pens=124144 =3136
Answer:
Total number of pens = 144
Total number of defective pens = 20
She will buy it if the pen is good.
Therefore, the probability that she will not buy = the probability that the pen is defective =
P(getting a defective pen)=no. of defective penstotal pens=20144 =536
Q22 (i) Refer to Example 13. (i) Complete the following table:
Event: 'sum on 2 dice' | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
1/36 | 5/36 | 1/36 |
Answer:
The table becomes:
The sum of two dice | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Probability | 1/36 | 1/18 | 1/12 | 1/9 | 5/36 | 1/6 | 5/36 | 1/9 | 1/12 | 1/18 | 1/36 |
Answer:
A student argues that there are 11 possible outcomes: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. Hence, each of them has a probability of 1/11. We do not agree with this argument because there are a different number of possible outcomes for each sum. We can see that each sum has a different probability.
Answer:
The possible outcomes when a coin is tossed 3 times: {HHH, HHT, HTH, HTT, THH, TTH, THT, TTT}
Therefore, the number of total possible outcomes = 8
For Hanif to win, all the tosses should give the same result, so there are only two favourable outcomes: {HHH, TTT}
Therefore, the number of favourable outcomes = 2
Thus, P(Hanif will win)=favourable outcomestotal outcomes=28 =14
And, P(Hanif will lose)=1−14 =34
Hence, the probability that Hanif will lose is 34
Q24 (i) A die is thrown twice. What is the probability that 5 will not come up either time?
Answer:
When a die is thrown twice, the possible outcomes = {(x,y):x,y∈{1,2,3,4,5,6}}
Total number of possible outcomes = 6 × 6 = 36
The outcomes when 5 comes up are either on them =
{(5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (1,5), (2,5), (3,5), (4,5), (6,5)}
Therefore, the number of such favourable outcomes = 11
Thus, P(5 will come up either time)=1136
Therefore P(5 will not come up either time)=1−1136=2536
Hence, the probability that 5 will not come either time is 2536
24 (ii) A die is thrown twice. What is the probability that 5 will come up at least once?
Answer:
When a die is thrown twice, the possible outcomes = {(x,y):x,y∈{1,2,3,4,5,6}}
Total number of possible outcomes = 6 $times$ 6 = 36
The outcomes when 5 comes up at least once =
{(5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (1,5), (2,5), (3,5), (4,5), (6,5)}
Number of such favourable outcomes = 11
Therefore P(5 comes up at least once)=1136
Hence, the probability that 5 comes at least once is 1136
Answer:
The possible outcomes when two coins are tossed = {HH, HT, TH, TT}
Therefore, the total number of possible outcomes = 4
Thus P(getting two heads)=favourable outcomestotal outcomes=14
Hence, the given statement is not correct. This is because one of each can occur in two different ways. Hence, the mentioned events are not equally likely.
Answer:
The possible outcomes when a die is thrown are {1,2,3,4,5,6}
Total number of possible outcomes = 6
Number of odd numbers, {1,3,5} = 3
And, the number of even numbers {2,4,6} = 3
Hence, both these events are equally likely
∴P(getting an odd)=favourable outcomestotal outcomes=36=12
