NCERT Solutions For Class 10 Maths Chapter 1 Real Numbers

Real numbers are like real-life friends—they include everyone: naturals, integers, rationals, and irrationals. NCERT solutions for class 10, chapter 1 Real numbers include all rational and irrational numbers that can be represented on the number line. This chapter lays a strong foundation with important topics such as Euclid's Division Lemma, Fundamental Theorem of Arithmetic, HCF, and LCM using factorisation and properties of rational and irrational numbers. Real numbers apply everywhere in our daily lives, from finance to engineering, music to science, weather forecasting to sports, and navigation to time management. These NCERT solutions for class 10 will provide a systematic method to prepare and do well for your board exams, with a comprehensive solution to each exercise question from the NCERT textbook.

Real numbers are the connection between what we know and what we don't know: whole numbers, fractions, and irrationals flow together seamlessly into one whole universe of value. Our academic team here at Careers360 is comprised of experienced experts with years of teaching experience who developed these NCERT Solutions for Class 10 Maths content based on the modified CBSE curriculum. Explore this link for NCERT syllabus outlines, notes, and PDF downloads: NCERT.

NCERT Solution for Class 10 Maths Chapter 1 Solutions: Download PDF

Students who wish to access the NCERT solutions for class 10, chapter 1 can click on the link below to download the entire solution in PDF.

Download Solution PDF

NCERT Solutions for Class 10 Maths Chapter 1: Exercise Questions

Below are the NCERT solutions for Chapter 1, Class 10 maths exercise questions.

Q1 (1): Express each number as a product of its prime factors: 140

Answer:

The number can be a product of its prime factors as follows

$\begin{array}{rl}& 140=2\times 2\times 5\times 7\\ & \Rightarrow 140=2^2\times 5\times 7\end{array}$

Q1 (2): Express each number as a product of its prime factors: 156

Answer:

The given number can be expressed as follows

$\begin{array}{rl}& 156=2\times 2\times 3\times 13\\ & \Rightarrow 156=2^2\times 3\times 13\end{array}$

Q1 (3): Express each number as a product of its prime factors: 3825

Answer:

The number is expressed as the product of the prime factors as follows

$\begin{array}{rl}& 3825=3\times 3\times 5\times 5\times 17\\ & \Rightarrow 3825=3^2\times 5^2\times 17\end{array}$

Q1 (4): Express each number as a product of its prime factors: 5005

Answer:

The given number can be expressed as the product of its prime factors as follows.

$5005=5\times 7\times 11\times 13$

Q1 (5): Express each number as a product of its prime factors: 7429

Answer:

The given number can be expressed as the product of their prime factors as follows

$7429=17\times 19\times 23$

Q2 (1): Find the LCM and HCF of the following pairs of integers and verify that LCM X HCF = product of the two numbers: 26 and 91

Answer:

26 = 2 × 13

91 = 7 × 13

HCF of (26,91) = 13

LCM of (26,91) = 2 × 7 × 13 = 182

HCF × LCM = 13 × 182 = 2366

Also, 26 × 91 = 2366

$\therefore$ 26 × 91 = HCF × LCM

Hence, it is verified.

Q2 (2): Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers. 510 and 92

Answer:

The number can be expressed as the product of prime factors as

510 = 2 × 3 × 5 × 17

92 = 2² × 23

HCF of (510,92) = 2

LCM of (510,92) = 2² × 3 × 5 × 17 × 23 = 23460

HCF × LCM = 2 × 23460 = 46920

Also, 510 × 92 = 46920

$\therefore$ 510 × 92 = HCF × LCM

Hence, it is verified.

Q2 (3): Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers. 336 and 54

Answer:

336 is expressed as the product of its prime factor as

336 = 2⁴ x 3 x 7

54 is expressed as the product of its prime factor as

54 = 2 × 3³

HCF(336,54) = 2 x 3 = 6

LCM(336,54) = 2 ⁴ x 3 ³ x 7 = 3024

HCF x LCM = 6 x 3024 = 18144

336 x 54 = 18144

$\therefore$ 336 x 54 = HCF x LCM

Hence, it is verified.

Q3 (1): Find the LCM and HCF of the following integers by applying the prime factorization method. 12, 15, and 21

Answer:

The numbers can be written as the product of their prime factors as follows

12 = 2² x 3

15 = 3 x 5

21 = 3 x 7

So, HCF = 3

LCM = 2² x 3 x 5 x 7 = 420

Q3 (2): Find the LCM and HCF of the following integers by applying the prime factorization method. 17, 23 and 29

Answer:

The given numbers are written as the product of their prime factors as follows

17 = 1 x 17

23 = 1 x 23

29 = 1 x 29

HCF = 1

LCM = 17 x 23 x 29 = 11339

Q3 (3): Find the LCM and HCF of the following integers by applying the prime factorization method. 8, 9, and 25

Answer:

The given numbers are written as the product of their prime factors as follows

8 = 2³

9 = 3²

25 = 5²

HCF = 1

LCM = 2³ x 3² x 5² = 1800

Q4: Given that HCF (306, 657) = 9, find LCM (306, 657).

Answer:

As we know, the product of the HCF and LCM of two numbers is equal to the product of the two numbers we have

HCF (306, 657) x LCM (306, 657) = 306 x 657

$\begin{array}{rl}& \Rightarrow \mathrm{LCM}(306,657)=\frac{306\times 657}{HCF(306,657)}\\ & \Rightarrow \mathrm{LCM}(306,657)=\frac{306\times 657}{9}\\ & \Rightarrow \mathrm{LCM}(306,657)=22338\end{array}$

Q5: Check whether $6^n$ can end with the digit 0 for any natural number n.

Answer:

By prime factorizing, we have,

6ⁿ = 2ⁿ x 3ⁿ

A number will end with 0 if it has at least 1 as the power of both 2 and 5 in its prime factorization. Since the power of 5 is 0 in the prime factorization of 6ⁿ, we can conclude that for no value of n, 6ⁿ will end with the digit 0.

Q6: Explain why 7x 11 x 13 + 13 and 7 x 6 x 5 x 4 x 3 x2 x 1 + 5 are composite numbers.

Answer:

7 x 11 x 13 + 13

= (7 x 11 + 1) x 13

= 78 x 13

= 2 x 3 x 13²

7 x 6 x 5 x 4 x 3 x 2 x 1 + 5

= (7 x 6 x 4 x 3 x 2 x 1 + 1) x 5

= 5 x 1008

After solving, we observed that both numbers are even numbers, and the number rule says that we can take at least two common out of two numbers.
So, these numbers are composite.

Q7: There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time and go in the same direction. After how many minutes will they meet again at the starting point?

Answer:

The time after which they meet again at the starting point will be equal to the LCM of the times they individually take to complete one round.

Time taken by Sonia = 18 = 2 x 3²

Time taken by Ravi = 12 = 2² x 3

LCM of (18,12) = 2² x 3² = 36

Therefore, they would again meet at the starting point after 36 minutes.

Q1: Prove that $\sqrt{5}$ is irrational.

Answer:

Let us assume $\sqrt{5}$ is rational.
It means $\sqrt{5}$ can be written in the form $\frac{p}{q}$ where p and q are co-primes and $q\ne 0$

$\sqrt{5}=\frac{p}{q}$
Squaring both sides, we obtain,

$\begin{array}{rl}& (\sqrt{5}{)}^2={\left(\frac{p}{q}\right)}^2\\ & \Rightarrow 5=\frac{p^2}{q^2}\\ & \Rightarrow p^2=5q^2\end{array}$
From the above equation, we can see that ${\mathrm{p}}^2$ is divisible by 5, Therefore, p will also be divisible by 5 as 5 is a prime number. --------(i)

Therefore, p can be written as 5r.

p = 5r

⇒ p² = (5r)²

⇒ 5q² = 25r²

⇒ q² = 5r²

From the above equation, we can see that q² is divisible by 5.
Therefore, q will also be divisible by 5, as 5 is a prime number. ----(ii).

From (i) and (ii), we can see that both p and q are divisible by 5. This implies that p and q are not co-primes. This contradiction arises because our initial assumption that $\sqrt{5}$ is rational was wrong.
Hence, it is proved that $\sqrt{5}$ is irrational.

Q2: Prove that $3+2\sqrt{5}$ is irrational.

Answer:

Let us assume $3+2\sqrt{5}$ is rational.
This means $3+2\sqrt{5}$ can be written in the form $\frac{p}{q}$ where p and $q$ are co-prime integers.

$\begin{array}{rl}& 3+2\sqrt{5}=\frac{p}{q}\\ & \Rightarrow 2\sqrt{5}=\frac{p}{q}-3\\ & \Rightarrow \sqrt{5}=\frac{p-3q}{2q}\end{array}$

$\sqrt{5}=\frac{p-3q}{2q}$ is rational as it is expressed in form of $\frac{p}{q}$.

This contradicts the fact that $\sqrt{5}$ is irrational. This contradiction arises because our initial assumption that $3+2\sqrt{5}$ is rational was wrong. Therefore, $3+2\sqrt{5}$ is irrational.

Q3 (1): Prove that the following are irrationals :

(i) $\frac{1}{\sqrt{2}}$

Answer:

Let us assume $\frac{1}{\sqrt{2}}$ is rational.
This means $\frac{1}{\sqrt{2}}$ can be written in the form $\frac{p}{q}$ where p and q are co-prime integers.

$\begin{array}{rl}& \frac{1}{\sqrt{2}}=\frac{p}{q}\\ & \Rightarrow \sqrt{2}=\frac{q}{p}\end{array}$

Since p and q are co-prime integers, $\frac{q}{p}$ will be rational, and this contradicts the fact that $\sqrt{2}$ is irrational. This contradiction arises because our initial assumption that $\frac{1}{\sqrt{2}}$ is rational was wrong.
Therefore, $\frac{1}{\sqrt{2}}$ is irrational.

Q3 (2): Prove that the following are irrationals :

(ii) $7\sqrt{5}$

Answer:

Let us assume $7\sqrt{5}$ is rational.
This means $7\sqrt{5}$ can be written in the form $\frac{p}{q}$ where p and q are co-prime integers.

$\begin{array}{rl}& 7\sqrt{5}=\frac{p}{q}\\ & \Rightarrow \sqrt{5}=\frac{p}{7q}\end{array}$
As p and q are integers, $\frac{p}{7q}$ would be rational; this contradicts the fact that $\sqrt{5}$ is irrational. This contradiction arises because our initial assumption that $7\sqrt{5}$ is rational was wrong.
Therefore, $7\sqrt{5}$ is irrational.

Q3 (3): Prove that the following are irrationals: $6+\sqrt{2}$

Answer:

Let us assume $6+\sqrt{2}$ is rational.

This means $6+\sqrt{2}$ can be written in the form $\frac{p}{q}$ where p and $q$ are co-prime integers.

$\begin{array}{rl}& 6+\sqrt{2}=\frac{p}{q}\\ & \Rightarrow \sqrt{2}=\frac{p}{q}-6\\ & \Rightarrow \sqrt{2}=\frac{p-6q}{q}\end{array}$
As p and q are integers, $\frac{p-6q}{q}$ would be rational.
This contradicts the fact that $\sqrt{2}$ is irrational. This contradiction arises because our initial assumption that $6+\sqrt{2}$ is rational was wrong.
Therefore, $6+\sqrt{2}$ is irrational.

• Class 10 Maths Chapter 1 Real Numbers Exercise 1.1
• Class 10 Maths Chapter 1 Real Numbers Exercise 1.2
• Class 10 Maths Chapter 1 Real Numbers Exercise 1.3
• Class 10 Maths Chapter 1 Real Numbers Exercise 1.4

Real Numbers Class 10 Chapter 1: Topics

The topics discussed in the NCERT Solutions for class 10, chapter 1, Real Numbers are:

• Introduction
• The Fundamental Theorem of Arithmetic
• Revisiting Irrational Numbers

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers - Notes

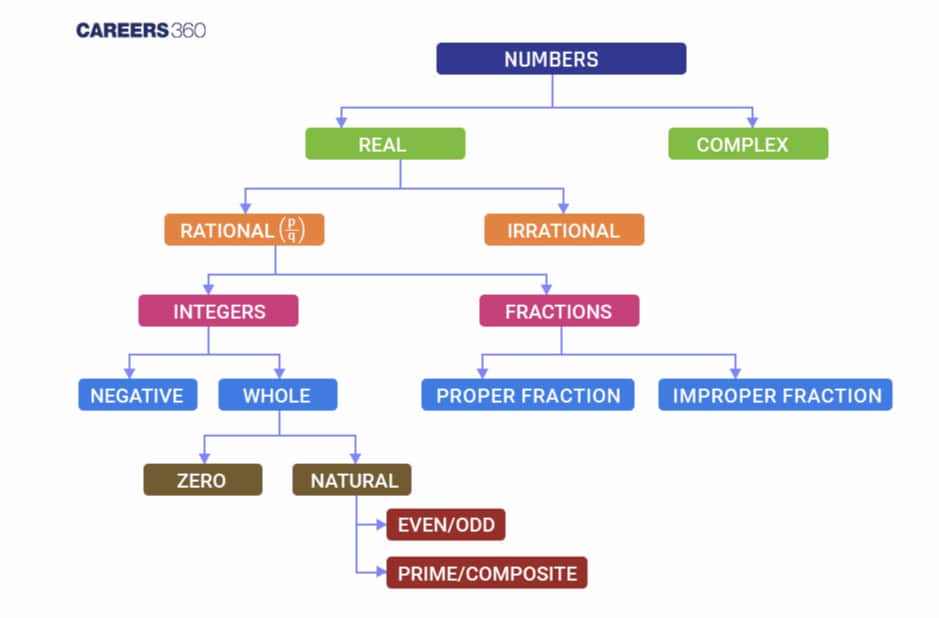
Types of Numbers

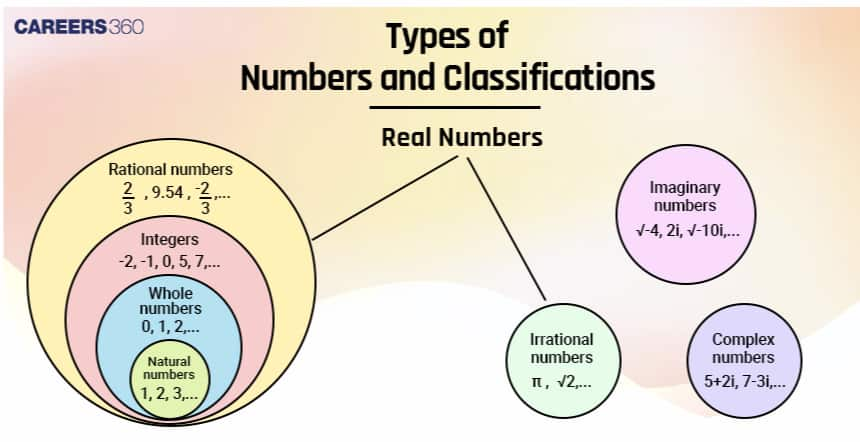
Numbers are of two main types. Namely, Real numbers and Imaginary numbers.

Real Numbers: Real numbers are numbers which can be represented in a number line. Real numbers are represented by $\mathrm{R}$. Real numbers include other numbers like,

• Natural Numbers: Natural numbers are positive numbers starting from 1 to $\mathrm{\infty }$(infinity)
  N = {1, 2, 3, 4, 5, ...}
• Whole Numbers: Whole numbers are natural numbers along with 0
  W = {0, 1, 2, 3, 4, 5, ...}
• Integers: Integers include both positive and negative numbers, along with zero.
  Z = {..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ...}
• Prime Numbers: Numbers that can not be divided by any number other than 1 and the number itself are known as prime numbers. Example: 2,3,5,7,9,....
• Composite Numbers: Numbers that can be divided by at least one of the numbers other than 1 and itself are known as composite numbers. Example: 4,6,8,9,10,12,...
• Rational Numbers: Rational numbers are numbers that can be expressed in the form of $\frac{p}{q}$ where $q\ne 0$.
  Eg: $\frac{2}{3},-\frac{7}{8},0.333\dots ,\frac{22}{7},\dots$
• Irrational numbers: Irrational numbers are numbers that can not be expressed in the form of $\frac{p}{q}$ where $q\ne 0$.
  Eg: $\pi ,\sqrt{5},\sqrt{17},\dots$

Imaginary Numbers:

Imaginary numbers are numbers that are expressed in terms of the square root of a negative number.

Example: $\sqrt{-2},5i,\dots$

Euclid's Division Algorithm (Lemma):

Any positive integer $a$ can be divided by another positive integer $b$ in such a way that it leaves a remainder $r$ that is smaller than $b$.

Lemma: Given positive integers $a$ and $b$, there exist unique integers $q$ and $r$ satisfying $a=bq+r,0\le r<b$. Here, " $a$ " is a dividend, " $b$ " is a divisor, " $q$ " is the quotient, and $r$ is the remainder.

In simple terms, Dividend $=($ divisor $\times$ quotient $)+$ remainder

Example: If we divide 35 by 3, then we get, quotient = 11 and remainder = 2. Here, dividend = 35 and divisor = 3.

By Euclid's Division Lemma, this can be represented as 35 = (3 $\times$ 11) + 2

Fundamental Theorem of Arithmetic

Fundamental theorem of arithmetic states that composite numbers can be expressed as the product of prime numbers.

Statement: Every composite number can be expressed (factorised) as a product of primes, and this factorisation is unique, apart from the order in which the prime factors occur.

For example:
$15=3\times 5$
$21=3\times 7$
$10=2\times 5$

This fundamental theorem of arithmetic is mainly used to find the HCF and LCM of numbers.

HCF and LCM by Prime Factorisation:

Highest Common Factor (HCF): The greatest number that divides two or more numbers exactly.

Least Common Multiple (LCM): The smallest number that is a multiple of two or more numbers.

Example:

HCF of 12 and 18: The factors of 12 are 1,2,3,4,6,12. The factors of 18 are 1,2,3,6,9,18. The common factors of 12 and 18 are 1,2,3,6. The greatest common factor is 6. So, the HCF of 12 and 18 is 6.

LCM of 12 and 18: The multiples of 12 are 12, 24, 36, 48,.... and the multiples of 18 are 18, 36, 54,.... The least multiple is 36. So, the LCM of 12 and 18 are 36.

NCERT Solutions for Class 10 Maths: Chapter Wise

Also, read

• NCERT Exemplar Class 10 Maths Solutions Chapter 1 Real Numbers

• NCERT Notes Class 10 Maths Chapter 1 Real Numbers

NCERT solutions of class 10: Subject-wise

Students can check the following links for more in-depth learning.

• NCERT Solutions for Class 10 Maths
• NCERT Solutions for Class 10 Science

NCERT Exemplar Solutions Subject-wise

After completing the NCERT textbooks, students should practice exemplar exercises for a better understanding of the chapters and clarity. The following links will help students find exemplar exercises.

• NCERT Exemplar Class 10th Maths
• NCERT Exemplar Class 10th Science

NCERT Books and NCERT Syllabus

Students can use the following links to check the latest NCERT syllabus and read some reference books.

• NCERT Books Class 10 Maths
• NCERT Syllabus Class 10 Maths
• NCERT Books Class 10
• NCERT Syllabus Class 10