Class 10 Maths NCERT Chapter 9: Extra Question
Question:
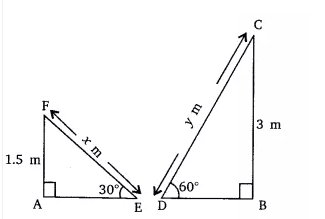
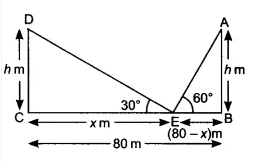
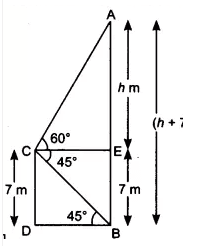
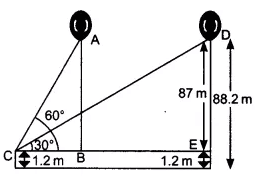
From the top of an upright pole 17.75 m high, the angle of elevation of the top of an upright tower was 60°. If the tower was 57.75 m tall, how far away (in m) from the foot of the pole was the foot of the tower?
Answer:

We have to find the value of $x$.
In $\triangle ABC,$
$\tan60° = \frac{AC}{BC}$
We know, $CE=BD$
⇒ $AC=AE-CE$
⇒ $AC=57.75-17.75$
⇒ $AC=40$
In $\triangle ABC,$
$\tan60° = \frac{40}{x}$
⇒ $\sqrt3=\frac{40}{x}$
⇒ $x=\frac{40}{\sqrt3}$
⇒ $x=\frac{40\sqrt3}{3}$ m
Hence, the correct answer is $\frac{40\sqrt3}{3}$.
Some Applications of Trigonometry Class 10 Solutions: Important Formulae
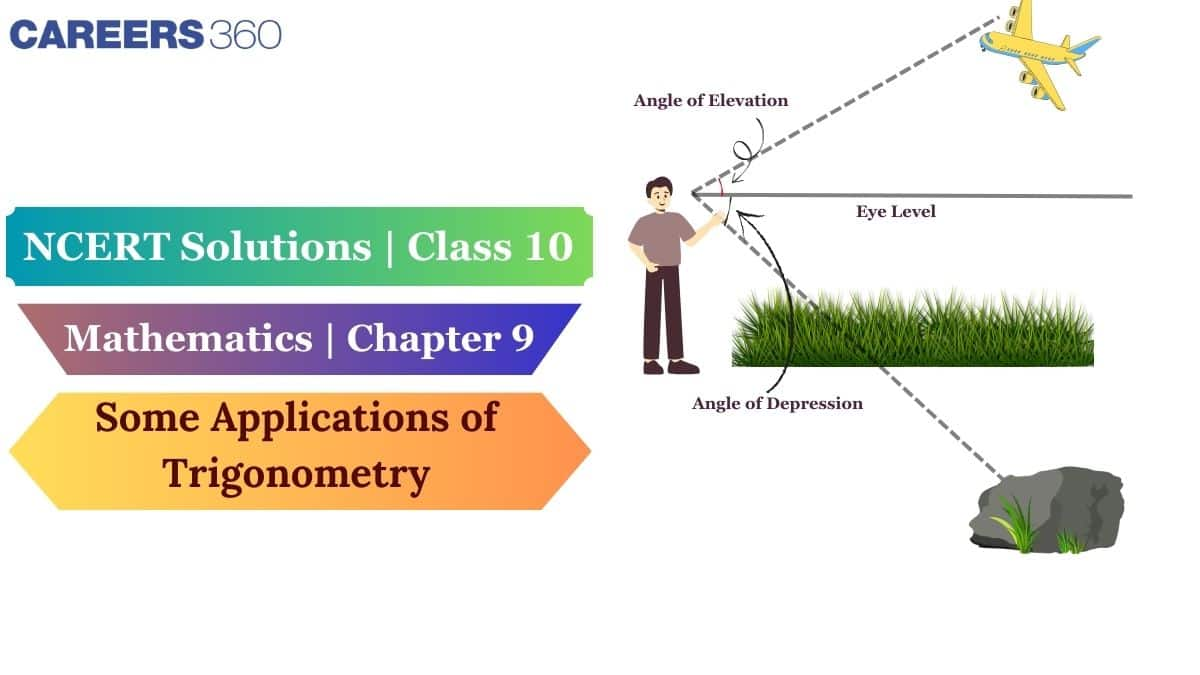
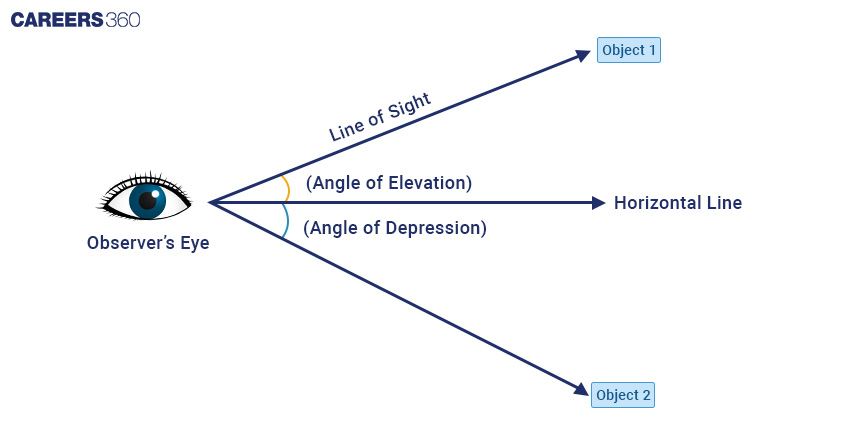
Line of Sight - The Line of Sight is the line formed by our vision as it passes through an item when we look at it.

Horizontal Line - The distance between the observer and the object is measured by a horizontal line.
The angle of Elevation:
-
The angle formed by the line of sight to the top of the item and the horizontal line is called an angle of elevation.
-
It is above the horizontal line, i.e., when we gaze up at the item, we make an angle of elevation.
The angle of Depression:
-
When the spectator must look down to perceive the item, an angle of depression is formed.
-
When the horizontal line is above the angle, the angle of depression is formed between it and the line of sight.
Case 1:
In this case, we can observe the following:
-
Height of a tower, hill, or building
-
Distance of an object from the foot of the tower, hill, or building and sometimes the shadow of it
-
The angle of elevation or the angle of depression
Any two of the above three parameters will be provided in the question. This type of problem can be solved using the formulas given below.
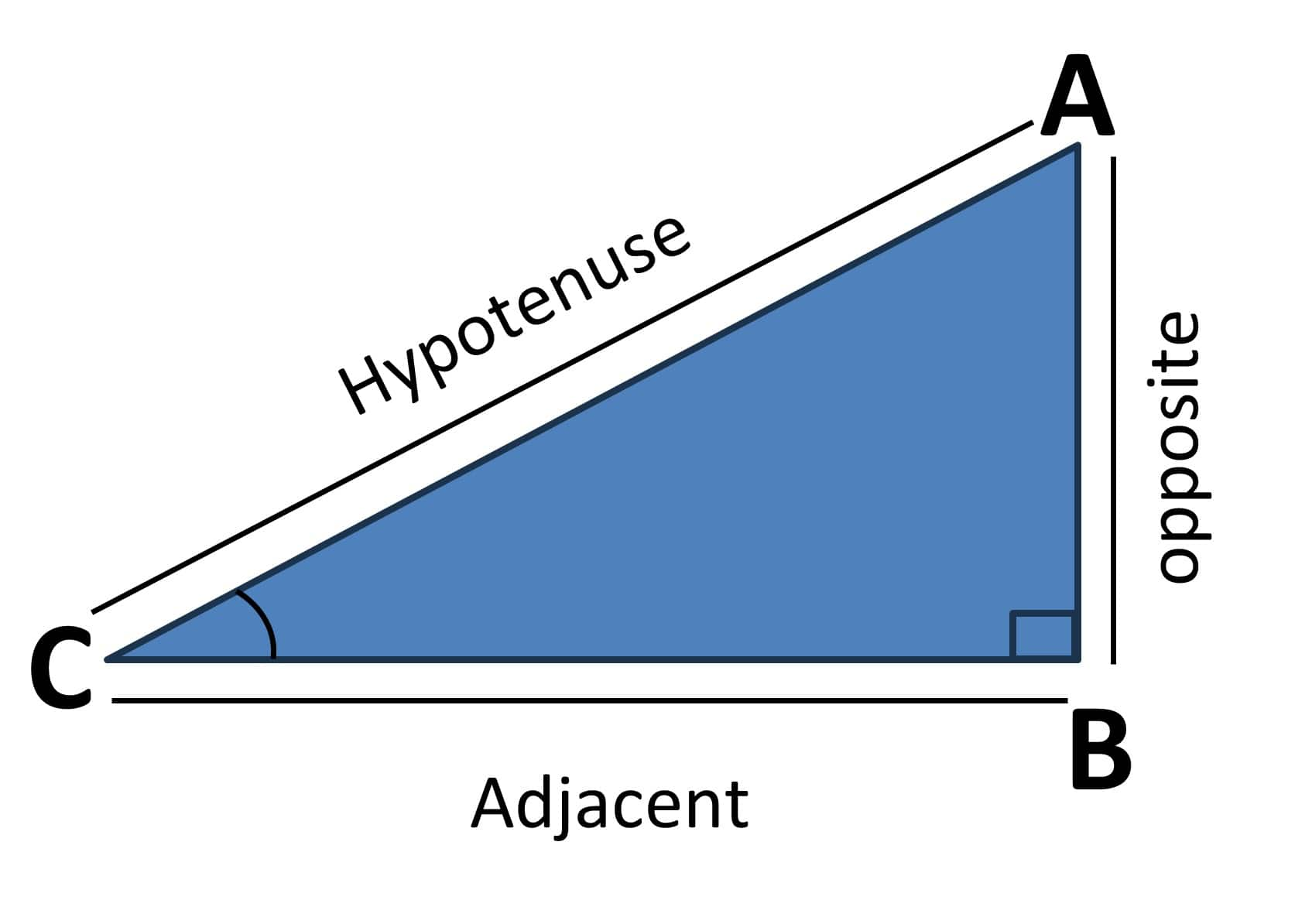
In the right triangle $ABC$,
$\begin{aligned} & \sin \theta=\frac{\text { Opposite } }{ \text { Hypotenuse }}=\frac{\mathrm{AB} }{ \mathrm{AC}} \\ & \cos \theta=\frac{\text { Adjacent } }{ \text { Hypotenuse }}=\frac{\mathrm{BC} }{ \mathrm{AC}} \\ & \tan \theta=\frac{\text { Opposite } }{ \text { Adjacent }}=\frac{\mathrm{AB} }{\mathrm{BC}}\end{aligned}$
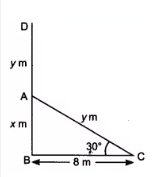
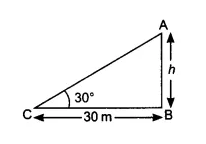
Case 2:
In this case, we can deal with different illustrations. One of the commonly solved problems is about the movement of an observer. If the observer moves toward objects like a tower, building, hill, etc., then the angle of elevation increases. The angle of elevation decreases when the observer moves away from the object. Here, the distance moved by the observer can be found using the formula given below:
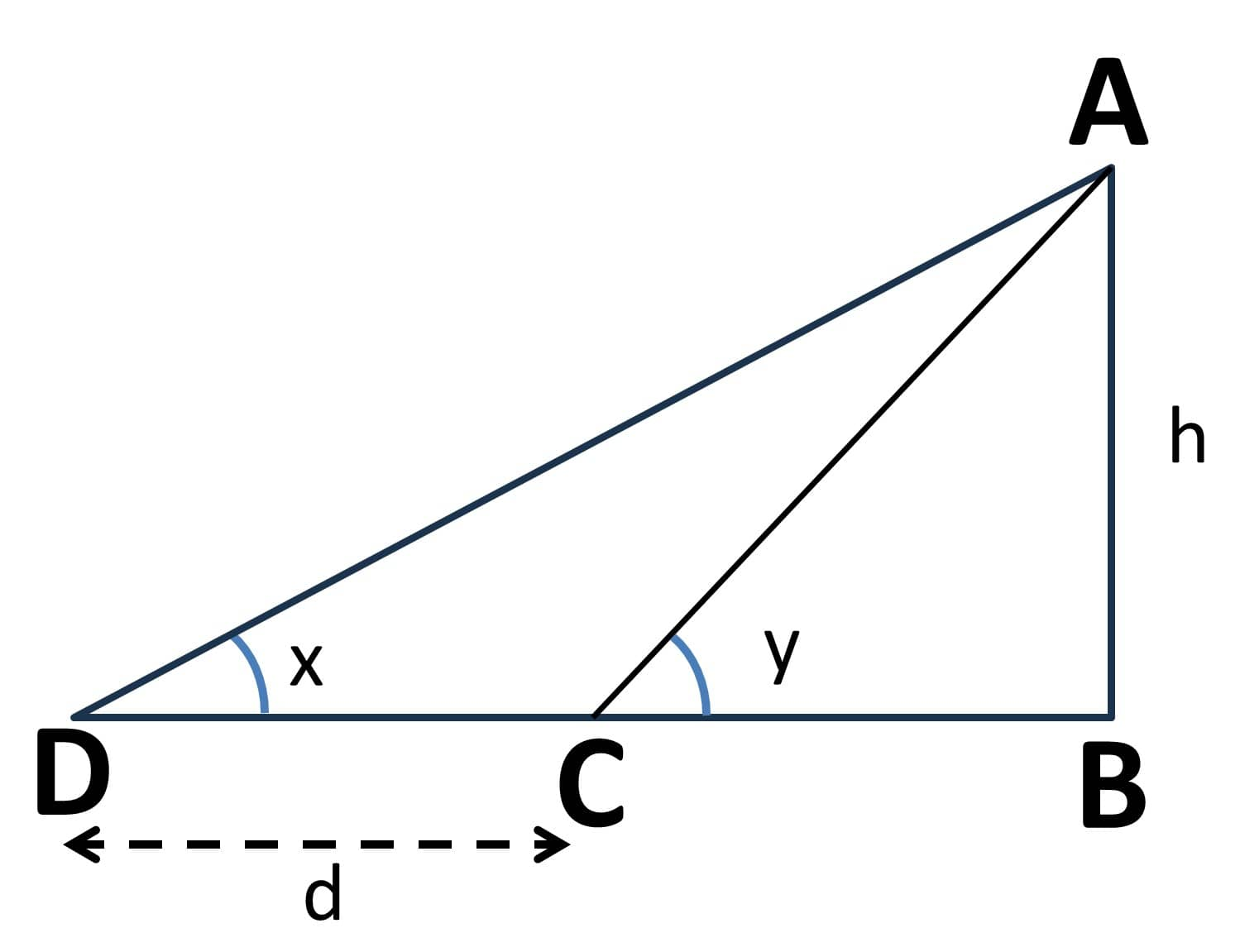
In the right triangle given below, $d$ is the distance between $C$ and $D$.
$d = h(\cot x - \cot y)$
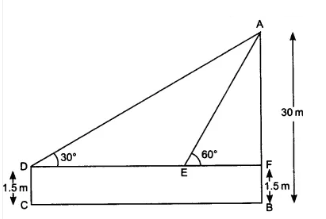
Case 3:
There is another case where two different situations happen at the same time. In this case, we get similar triangles with the same angle of elevation or angle of depression. These types of problems can be solved with the help of formulas related to similar triangles.
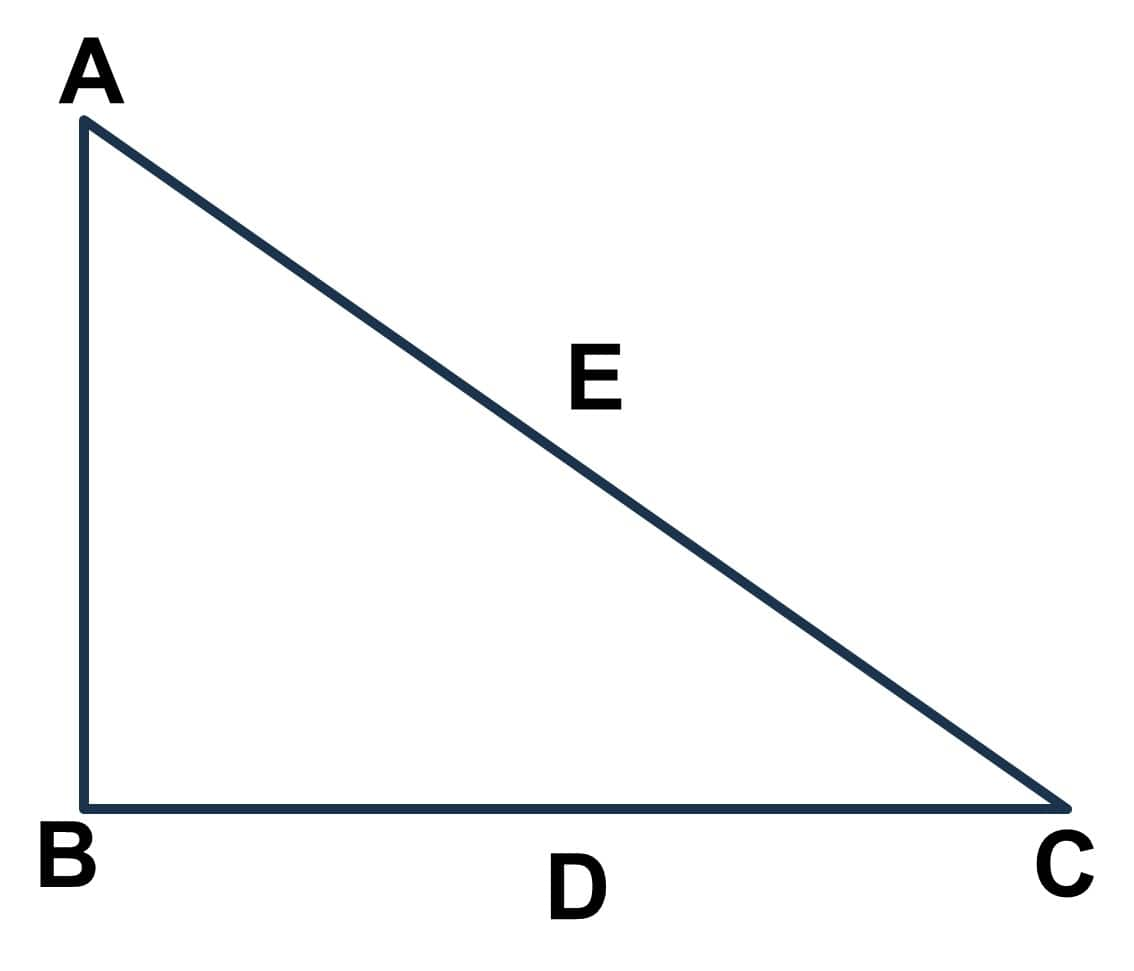
In the right triangle $ABC, DE || AB,$
Here, triangles $ABC$ and $EDC$ are similar.
Using Thales' or BPT theorem, we can write the ratio of sides as:
$\frac{AB}{ED} = \frac{BC}{DC}$
Why are Class 10 Maths Chapter 9 Some Applications of Trigonometry question answers important?
Trigonometry is not just theory, as it helps us solve real-life problems too. This chapter shows us how to use trigonometric ratios to find the heights and distances of different objects. These Class 10 Maths Chapter 9 Some Applications of Trigonometry question answers help students understand how maths connects with the real world. Here are some more points on why these question answers are important:
- These solutions help you learn how to find unknown heights and distances using angles of elevation and depression.
- These question answers make it easier to apply trigonometric concepts to real-life situations.
- These Class 10 Maths Chapter 9 Some Applications of Trigonometry question answers prepare us for higher classes where trigonometry is used in physics and engineering.