NCERT Solutions For Class 10 Maths Chapter 5 Arithmetic Progressions

Q: What are the important topics of NCERT class 10 maths chapter 5 arithmetic progressions?

Checking whether the series is an arithmetic progression or not, nth term or last term of arithmetic progression, sum of an arithmetic progression, use of linear equation concept in an arithmetic progression and application of nth term and sum of a.p. formulae are the important topics in this chapter.

Q: What kind of questions are there in NCERT solutions for class 10 chapter 5 maths?

The NCERT Solutions for Class 10 Maths Chapter 5 includes a range of question types such as multiple choice, long and short answer, fill in the blank, and real-world examples. These questions aim to enhance students' problem-solving and time management abilities, thus preparing them for success in their CBSE exams.

Q: How many exercises are there in maths chapter 5 class 10?

The number of exercises in Maths Chapter 5 for Class 10 are four. These are very important because these include all types of questions on which repeatedly questions are being asked in board exams. Students can practice and find solutions at careers360 official website

Q: Do I need to practice all questions given in NCERT class 10 maths chapter 5 solutions?

It is generally a good idea to practice all of the questions provided in the NCERT solutions for class 10 maths arithmetic progression, as they are designed to cover the key concepts and skills that are important for understanding the chapter and doing well in your exams. By practicing all the questions and arithmetic progression solutions, you will be able to identify your strengths and weaknesses and work on them accordingly. Also, chapter 5 questions and ap solutions class 10 help you build your problem-solving skills, time management skills and confidence, which will be beneficial for you in your exams. Students can also use arithmetic progression class 10 pdf as to study offline.

Q: Why should I practice NCERT maths class 10 chapter 5 solutions?

There are several reasons why you should practice the class 10 maths NCERT solution arithmetic progression. Practising the NCERT Solutions for Class 10 Maths Chapter 5 is a valuable step in your studies as it will help you to understand the concepts, improve your problem-solving skills, and prepare for your exams. Students can use NCERT solutions for class 10 maths arithmetic progression pdf to study comfortable this chapter.

Q: What is the arithmetic progression in class 10 chapter 5 maths?

Arithmetic Progression (AP) is a sequence of numbers in which the difference between any two consecutive terms is always the same. In other words, it is a sequence of numbers in which the difference between two consecutive terms is a constant. Arithmetic progression class 10 NCERT solutions pdf covers various concepts related to arithmetic progressions such as finding the common difference, the nth term, the sum of an arithmetic series, and solving word problems using arithmetic progressions.

NCERT Solutions For Class 10 Maths Chapter 5 Arithmetic Progressions

Edited By Apoorva Singh | Updated on Sep 05, 2023 08:12 PM IST | #CBSE Class 10th

NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions

NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions provided here. These solutions are created by expert team at Careers360 keeping in mind the latest syllabus and pattern of CBSE 2023-24. Arithmetic Progression class 10 solutions are designed covering all the topics and concepts comprehensively with step by step solutions of all exercise. After practicing these NCERT solutions for Class 10 students get command and in-depth understanding of the concepts which ultimately lead to score well in the exams.

Scholarship Test: Vidyamandir Intellect Quest (VIQ)

Don't Miss: JEE Main & NEET 2026 Scholarship Test (Class 10): Narayana | Aakash

This Story also Contains

NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions PDF Free Download
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions - Important Formulae
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions (Intext Questions and Exercise)
Arithmetic Progression Class 10 Maths chapter 5 - Topics
Features of NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions
NCERT Books and NCERT Syllabus
NCERT Solutions of Class 10 - Subject Wise
NCERT Exemplar solutions - Subject Wise

NCERT Solutions For Class 10 Maths Chapter 5 Arithmetic Progressions

This Class 10 Maths Chapter 5 covers the type of questions in which succeeding terms are obtained by adding the same number to the preceding terms. NCERT solutions are not only important for Board exams but also foundation for higher class therefore, students can take help from these solutions if they are facing any problems. here in this page students can find detailed arithmetic progression class 10 notes NCERT solutions also they can download class 10 maths chapter 5 pdf.

Also See,

VMC VIQ Scholarship Test

Apply

Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 30th NOV'24! Trusted by 3,500+ universities globally

Apply

NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions PDF Free Download

Download PDF

NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions - Important Formulae

Arithmetic Progressions (AP) involve sequence terms denoted as a₁, a₂, a₃, ..., a_n representing a series of integers.
An AP maintains a constant difference between consecutive terms, known as the common difference.
For terms a₁, a₂, a₃, a₄, a₅, and a₆ in an AP, the common difference can be expressed as D = a₂ – a₁ = a₃ – a₂ = a₄ – a₃ = ...
The nth term of an AP is given by the formula: a_n = a + (n – 1) d.

Where

a = First term of the sequence.

n = Term's position in the sequence.

d = Common difference.

The sum of the first 'n’ terms in an AP is calculated using the formula:
S_n = (n/2) [2a + (n – 1)d]

Where

S_n denotes the sum of the terms.
'n' is the number of terms being summed.
'a' is the first term.
'd' stands for the common difference.

Free download NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions PDF for CBSE Exam.

NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions (Intext Questions and Exercise)

NCERT Solutions for 5 chapter maths class 10 Arithmetic Progressions Excercise: 5.1

Q1 (i) In which of the following situations, does the list of numbers involved make an arithmetic progression, and why? (i) The taxi fare after each km when the fare is $\small Rs\hspace{1mm}15$ for the first km and $\small Rs\hspace{1mm}8$ for each additional $\small km$ .

Answer:

It is given that
Fare for $1^{st} \ km$ = Rs. 15
And after that $\small Rs\hspace{1mm}8$ for each additional $\small km$
Now,
Fare for $2^{nd} \ km$ = Fare of first km + Additional fare for 1 km
= Rs. 15 + 8 = Rs 23

Fare for $3^{rd} \ km$ = Fare of first km + Fare of additional second km + Fare of additional third km
= Rs. 23 + 8= Rs 31

Fare of n km = $15 + 8 \times (n - 1)$
( We multiplied by n - 1 because the first km was fixed and for rest, we are adding additional fare.

In this, each subsequent term is obtained by adding a fixed number (8) to the previous term.)

Now, we can clearly see that this is an A.P. with the first term (a) = 15 and common difference (d) = 8

Q1 (ii) In which of the following situations, does the list of numbers involved make an arithmetic progression, and why? (ii) The amount of air present in a cylinder when a vacuum pump removes $\small \frac{1}{4}$ of the air remaining in the cylinder at a time.

Answer:

It is given that
vacum pump removes $\small \frac{1}{4}$ of the air remaining in the cylinder at a time
Let us take initial quantity of air = 1

Now, the quantity of air removed in first step = 1/4

Remaining quantity after 1 ^st step

$= 1-\frac{1}{4}= \frac{3}{4}$

Similarly, Quantity removed after 2 ^nd step = Quantity removed in first step $\times$ Remaining quantity after 1 ^st step

$=\frac{3}{4}\times \frac{1}{4}= \frac{3}{16}$
Now,

Remaining quantity after 2 ^nd step would be = Remaining quantity after 1 ^st step - Quantity removed after 2 ^nd step

$=\frac{3}{4}- \frac{3}{16}= \frac{12-3}{16}= \frac{9}{16}$
Now, we can clearly see that

After the second step the difference between second and first and first and initial step is not the same, hence

the common difference (d) is not the same after every step

Therefore, it is not an AP

Q1 (iii) In which of the following situations, does the list of numbers involved make an arithmetic progression, and why? (iii) The cost of digging a well after every meter of digging, when it costs $\small Rs\hspace{1mm}150$ for the first metre and rises by $\small Rs\hspace{1mm}50$ for each subsequent meter.

Answer:

It is given that
Cost of digging of 1st meter = Rs 150
and
rises by $\small Rs\hspace{1mm}50$ for each subsequent meter
Therefore,

Cost of digging of first 2 meters = cost of digging of first meter + cost of digging additional meter

Cost of digging of first 2 meters = 150 + 50

= Rs 200

Similarly,
Cost of digging of first 3 meters = cost of digging of first 2 meters + cost of digging of additional meter

Cost of digging of first 3 meters = 200 + 50

= Rs 250

We can clearly see that 150, 200,250, ... is in AP with each subsequent term is obtained by adding a fixed number (50) to the previous term.

Therefore, it is an AP with first term (a) = 150 and common difference (d) = 50

Q1 (iv) In which of the following situations, does the list of numbers involved make an arithmetic progression, and why? (iv) The amount of money in the account every year, when $\small Rs\hspace{1mm}10000$ is deposited at compound interest at $\small 8\hspace{1mm}\%$ per annum .

Answer:

Amount in the beginning = Rs. 10000

Interest at the end of 1st year at the rate of $\small 8\hspace{1mm}\%$
is $\small 8\hspace{1mm}\%$ of 10000 = $\frac{8\times 10000}{100}= 800$

Therefore, amount at the end of 1st year will be

= 10000 + 800

= 10800

Now,

Interest at the end of 2nd year at rate of $\small 8\hspace{1mm}\%$
is $\small 8\hspace{1mm}\%$ of 10800 = $\frac{8\times 10800}{100}= 864$

Therefore,, amount at the end of 2 ^nd year

= 10800 + 864 = 11664

Since each subsequent term is not obtained by adding a unique number to the previous term; hence, it is not an AP

Q2 (i) Write first four terms of the AP, when the first term a and the common difference d are given as follows $\small a=10,d=10$

Answer:

It is given that
$\small a=10,d=10$
Now,
$a_1= a =10$
$a_2= a_1 + d= 10 + 10 = 20$
$a_3= a_2 + d= 20 + 10 = 30$
$a_4= a_3 + d= 30 + 10 = 40$
Therefore, the first four terms of the given series are 10,20,30,40

Q2 (ii) Write first four terms of the AP when the first term a and the common difference d are given as follows: $\small a=-2,d=0$
Answer:

It is given that
$\small a=-2,d=0$
Now,
$a_1= a = -2$
$a_2= a_1 + d= -2 + 0 = -2$
$a_3= a_2 + d= -2 + 0 = -2$
$a_4= a_3 + d= -2 + 0 = -2$
Therefore, the first four terms of the given series are -2,-2,-2,-2

Q2 (iii) Write first four terms of the AP when the first term a and the common difference d are given as follows $\small a=4,d=-3$

Answer:

It is given that
$\small a=4,d=-3$
Now,
$a_1= a =4$
$a_2= a_1 + d= 4 - 3 = 1$
$a_3= a_2 + d= 1 - 3 = -2$
$a_4= a_3 + d= -2- 3 = -5$
Therefore, the first four terms of the given series are 4,1,-2,-5

Q2 (iv) Write first four terms of the AP when the first term a and the common difference d are given as follows $\small a=-1,d=\frac{1}{2}$

Answer:

It is given that
$\small a=-1,d=\frac{1}{2}$
Now,
$a_1= a =-1$
$a_2= a_1 + d= -1 + \frac{1}{2} = -\frac{1}{2}$
$a_3= a_2 + d= -\frac{1}{2} + \frac{1}{2} = 0$
$a_4= a_3 + d= 0+\frac{1}{2}= \frac{1}{2}$
Therefore, the first four terms of the given series are $-1,-\frac{1}{2},0, \frac{1}{2}$

Q2 (v) Write first four terms of the AP when the first term a and the common difference d are given as follows $\small a=-1.25,d=-0.25$

Answer:

It is given that
$\small a=-1.25,d=-0.25$
Now,
$a_1= a =-1.25$
$a_2= a_1 + d= -1.25 -0.25= -1.50$
$a_3= a_2 + d= -1.50-0.25=-1.75$
$a_4= a_3 + d= -1.75-0.25=-2$
Therefore, the first four terms of the given series are -1.25,-1.50,-1.75,-2

Q3 (i) For the following APs, write the first term and the common difference: $\small 3,1,-1,-3,...$

Answer:

Given AP series is

$\small 3,1,-1,-3,...$

Now, first term of this AP series is 3

Therefore,

First-term of AP series (a) = 3

Now,

$a_1=3 \ \ and \ \ a_2 = 1$

And common difference (d) = $a_2-a_1 = 1-3 = -2$

Therefore, first term and common difference is 3 and -2 respectively

Q3 (ii) For the following APs, write the first term and the common difference: $\small -5,-1,3,7,...$

Answer:

Given AP series is

$\small -5,-1,3,7,...$

Now, the first term of this AP series is -5

Therefore,

First-term of AP series (a) = -5

Now,

$a_1=-5 \ \ and \ \ a_2 = -1$

And common difference (d) = $a_2-a_1 = -1-(-5) = 4$

Therefore, the first term and the common difference is -5 and 4 respectively

Q3 (iii) For the following APs, write the first term and the common difference: $\small \frac{1}{3},\frac{5}{3},\frac{9}{3},\frac{13}{3},...$

Answer:

Given AP series is

$\small \frac{1}{3},\frac{5}{3},\frac{9}{3},\frac{13}{3},...$
Now, the first term of this AP series is $\frac{1}{3}$

Therefore,

The first term of AP series (a) = $\frac{1}{3}$

Now,

$a_1=\frac{1}{3} \ \ and \ \ a_2 = \frac{5}{3}$

And common difference (d) = $a_2-a_1 = \frac{5}{3}-\frac{1}{3} = \frac{5-1}{3} =\frac{4}{3}$

Therefore, the first term and the common difference is $\frac{1}{3}$ and $\frac{4}{3}$ respectively

Q3 (iv) For the following APs, write the first term and the common difference: $\small 0.6,1.7,2.8,3.9,...$

Answer:

Given AP series is

$\small 0.6,1.7,2.8,3.9,...$

Now, the first term of this AP series is 0.6

Therefore,

First-term of AP series (a) = 0.6

Now,

$a_1=0.6 \ \ and \ \ a_2 = 1.7$

And common difference (d) = $a_2-a_1 = 1.7-0.6 = 1.1$

Therefore, the first term and the common difference is 0.6 and 1.1 respectively.

Q4 (i) Which of the following are APs? If they form an AP, find the common difference d and write three more terms. $\small 2,4,8,12,...$

Answer:

Given series is
$\small 2,4,8,12,...$
Now,
the first term to this series is = 2
Now,
$a_1 = 2 \ \ and \ \ a_2 = 4 \ \ and \ \ a_3 = 8$
$a_2-a_1 = 4-2 = 2$
$a_3-a_2 = 8-4 = 4$
We can clearly see that the difference between terms are not equal
Hence, given series is not an AP

Q4 (ii) Which of the following are APs ? If they form an AP, find the common difference d and write three more terms. $\small 2,\frac{5}{2},3,\frac{7}{2},...$

Answer:

Given series is
$\small 2,\frac{5}{2},3,\frac{7}{2},...$
Now,
first term to this series is = 2
Now,
$a_1 = 2 \ \ and \ \ a_2 = \frac{5}{2} \ \ and \ \ a_3 = 3 \ \ and \ \ a_4 = \frac{7}{2}$
$a_2-a_1 = \frac{5}{2}-2 = \frac{5-4}{2}=\frac{1}{2}$
$a_3-a_2 = 3-\frac{5}{2} = \frac{6-5}{2} = \frac{1}{2}$
$a_4-a_3=\frac{7}{2}-3=\frac{7-6}{2} =\frac{1}{2}$
We can clearly see that the difference between terms are equal and equal to $\frac{1}{2}$
Hence, given series is in AP
Now, the next three terms are
$a_5=a_4+d = \frac{7}{2}+\frac{1}{2} = \frac{8}{2}=4$
$a_6=a_5+d = 4+\frac{1}{2} = \frac{8+1}{2}=\frac{9}{2}$
$a_7=a_6+d =\frac{9}{2} +\frac{1}{2} = \frac{10}{2}=5$

Therefore, next three terms of given series are $4,\frac{9}{2} ,5$

Q4 (iii) Which of the following are APs ? If they form an AP, find the common difference d and write three more terms. $\small -1.2,-3.2,-5.2,-7.2,...$

Answer:

Given series is
$\small -1.2,-3.2,-5.2,-7.2,...$
Now,
the first term to this series is = -1.2
Now,
$a_1 = -1.2 \ \ and \ \ a_2 = -3.2 \ \ and \ \ a_3 = -5.2 \ \ and \ \ a_4 = -7.2$
$a_2-a_1 = -3.2-(-1.2) =-3.2+1.2=-2$
$a_3-a_2 = -5.2-(-3.2) =-5.2+3.2 = -2$
$a_4-a_3=-7.2-(-5.2)=-7.2+5.2=-2$
We can clearly see that the difference between terms are equal and equal to -2
Hence, given series is in AP
Now, the next three terms are
a_5=a_4+d = -7.2-2 =-9.2 $a_6=a_5+d = -9.2-2 =-11.2$
$a_7=a_6+d = -11.2-2 =-13.2$
Therefore, next three terms of given series are -9.2,-11.2,-13.2

Q4 (iv) Which of the following are APs? If they form an AP, find the common difference d and write three more terms. $\small -10,-6,-2,2,...$

Answer:

Given series is
$\small -10,-6,-2,2,...$
Now,
the first term to this series is = -10
Now,
$a_1 = -10 \ \ and \ \ a_2 = -6 \ \ and \ \ a_3 = -2 \ \ and \ \ a_4 = 2$
$a_2-a_1 = -6-(-10) =-6+10=4$
$a_3-a_2 = -2-(-6) =-2+6 = 4$
$a_4-a_3=2-(-2)=2+2=4$
We can clearly see that the difference between terms are equal and equal to 4
Hence, given series is in AP
Now, the next three terms are
$a_5=a_4+d = 2+4 =6$
$a_6=a_5+d = 6+4=10$
$a_7=a_6+d = 10+4=14$
Therefore, next three terms of given series are 6,10,14

Q4 (v) Which of the following are APs? If they form an AP, find the common difference d and write three more terms. $\small 3,3+\sqrt{2},3+2\sqrt{2},3+3\sqrt{2},...$

Answer:

Given series is
$\small 3,3+\sqrt{2},3+2\sqrt{2},3+3\sqrt{2},...$
Now,
the first term to this series is = 3
Now,
$a_1 = 3 \ \ and \ \ a_2 = 3+\sqrt2 \ \ and \ \ a_3 = 3+2\sqrt2 \ \ and \ \ a_4 = 3+3\sqrt2$
$a_2-a_1 = 3+\sqrt2-3= \sqrt2$
$a_3-a_2 = 3+2\sqrt2-3-\sqrt2 = \sqrt2$
$a_4-a_3 = 3+3\sqrt2-3-2\sqrt2 = \sqrt2$
We can clearly see that the difference between terms are equal and equal to $\sqrt2$
Hence, given series is in AP
Now, the next three terms are
$a_5=a_4+d = 3+3\sqrt2+\sqrt2=3+4\sqrt2$
$a_6=a_5+d = 3+4\sqrt2+\sqrt2=3+5\sqrt2$
$a_7=a_6+d = 3+5\sqrt2+\sqrt2=3+6\sqrt2$
Therefore, next three terms of given series are $3+4\sqrt2, 3+5\sqrt2,3+6\sqrt2$

Q4 (vi) Which of the following are APs? If they form an AP, find the common difference d and write three more terms. $\small 0.2,0.22,0.222,0.2222,...$

Answer:

Given series is
$\small 0.2,0.22,0.222,0.2222,...$
Now,
the first term to this series is = 0.2
Now,
$a_1 = 0.2 \ \ and \ \ a_2 = 0.22 \ \ and \ \ a_3 = 0.222 \ \ and \ \ a_4 = 0.2222$
$a_2-a_1 = 0.22-0.2=0.02$
$a_3-a_2 = 0.222-0.22=0.002$

We can clearly see that the difference between terms are not equal
Hence, given series is not an AP

Q4 (vii) Which of the following are APs? If they form an AP, find the common difference d and write three more terms. $\small 0,-4,-8,-12,...$

Answer:

Given series is
$\small 0,-4,-8,-12,...$
Now,
first term to this series is = 0
Now,
$a_1 = 0 \ \ and \ \ a_2 = -4 \ \ and \ \ a_3 = -8 \ \ and \ \ a_4 = -12$
$a_2-a_1 = -4-0 =-4$
$a_3-a_2 = -8-(-4) =-8+4 = -4$
$a_4-a_3=-12-(-8)=-12+8=-4$
We can clearly see that the difference between terms are equal and equal to -4
Hence, given series is in AP
Now, the next three terms are
$a_5=a_4+d = -12-4 =-16$
$a_6=a_5+d = -16-4=-20$
$a_7=a_6+d = -20-4=-24$
Therefore, the next three terms of given series are -16,-20,-24

Q4 (viii) Which of the following are APs? If they form an AP, find the common difference d and write three more terms. $\small -\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},...$

Answer:

Given series is
$\small -\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},...$
Now,
the first term to this series is = $-\frac{1}{2}$
Now,
$a_1 = -\frac{1}{2} \ \ and \ \ a_2 = -\frac{1}{2} \ \ and \ \ a_3 = -\frac{1}{2} \ \ and \ \ a_4 = -\frac{1}{2}$
$a_2-a_1 = -\frac{1}{2}-\left ( -\frac{1}{2} \right ) = -\frac{1}{2}+\frac{1}{2}=0$
$a_3-a_2 = -\frac{1}{2}-\left ( -\frac{1}{2} \right ) = -\frac{1}{2}+\frac{1}{2}=0$
$a_4-a_3 = -\frac{1}{2}-\left ( -\frac{1}{2} \right ) = -\frac{1}{2}+\frac{1}{2}=0$
We can clearly see that the difference between terms are equal and equal to 0
Hence, given series is in AP
Now, the next three terms are
$a_5=a_4+d = -\frac{1}{2}+0=-\frac{1}{2}$
$a_6=a_5+d = -\frac{1}{2}+0=-\frac{1}{2}$
$a_7=a_6+d = -\frac{1}{2}+0=-\frac{1}{2}$
Therefore, the next three terms of given series are $-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}$

Q4 (ix) Which of the following are APs? If they form an AP, find the common difference d and write three more terms. $\small 1,3,9,27,...$

Answer:

Given series is
$\small 1,3,9,27,...$
Now,
the first term to this series is = 1
Now,
$a_1 = 1 \ \ and \ \ a_2 = 3 \ \ and \ \ a_3 = 9 \ \ and \ \ a_4 = 27$
$a_2-a_1 = 3-1=2$
$a_3-a_2 =9-3=6$

We can clearly see that the difference between terms are not equal
Hence, given series is not an AP

Q4 (x) Which of the following are APs ? If they form an AP, find the common difference d and write three more terms. $\small a,2a,3a,4a,...$

Answer:

Given series is
$\small a,2a,3a,4a,...$
Now,
the first term to this series is = a
Now,
$a_1 = a \ \ and \ \ a_2 = 2a \ \ and \ \ a_3 = 3a \ \ and \ \ a_4 = 4a$
$a_2-a_1 = 2a-a =a$
$a_3-a_2 = 3a-2a =a$
$a_4-a_3=4a-3a=a$
We can clearly see that the difference between terms are equal and equal to a
Hence, given series is in AP
Now, the next three terms are
$a_5=a_4+d =4a+a=5a$
$a_6=a_5+d =5a+a=6a$
$a_7=a_6+d =6a+a=7a$
Therefore, next three terms of given series are 5a,6a,7a

Q4 (xi) Which of the following are APs ? If they form an AP, find the common difference d and write three more terms. $\small a,a^2,a^3,a^4,...$
Answer:

Given series is
$\small a,a^2,a^3,a^4,...$
Now,
the first term to this series is = a
Now,
$a_1 = a \ \ and \ \ a_2 = a^2 \ \ and \ \ a_3 = a^3 \ \ and \ \ a_4 = a^4$
$a_2-a_1 = a^2-a =a(a-1)$
$a_3-a_2 = a^3-a^2 =a^2(a-1)$

We can clearly see that the difference between terms are not equal
Hence, given series is not in AP

Q4 (xii) Which of the following are APs ? If they form an AP, find the common difference d and write three more terms. $\small \sqrt{2},\sqrt{8},\sqrt{18},\sqrt{32},...$

Answer:

Given series is
$\small \sqrt{2},\sqrt{8},\sqrt{18},\sqrt{32},...$
We can rewrite it as
$\sqrt2,2\sqrt2,3\sqrt2,4\sqrt2,....$
Now,
first term to this series is = a
Now,
$a_1 = \sqrt2 \ \ and \ \ a_2 = 2\sqrt2 \ \ and \ \ a_3 = 3\sqrt2 \ \ and \ \ a_4 = 4\sqrt2$
$a_2-a_1 = 2\sqrt2-\sqrt2 =\sqrt2$
$a_3-a_2 = 3\sqrt2-2\sqrt2 =\sqrt2$
$a_4-a_3=4\sqrt2-3\sqrt2=\sqrt2$
We can clearly see that difference between terms are equal and equal to $\sqrt2$
Hence, given series is in AP
Now, the next three terms are
$a_5=a_4+d =4\sqrt2+\sqrt2=5\sqrt2$
$a_6=a_5+d =5\sqrt2+\sqrt2=6\sqrt2$
$a_7=a_6+d =6\sqrt2+\sqrt2=7\sqrt2$
Therefore, next three terms of given series are $5\sqrt2,6\sqrt2,7\sqrt2$

That is the next three terms are $\sqrt{50},\ \sqrt{72},\ \sqrt{98}$

Q4 (xiii) Which of the following are APs? If they form an AP, find the common difference d and write three more terms. $\small \sqrt{3},\sqrt{6},\sqrt{9},\sqrt{12},...$

Answer:

Given series is
$\small \sqrt{3},\sqrt{6},\sqrt{9},\sqrt{12},...$
Now,
the first term to this series is = $\sqrt3$
Now,
$a_1 = \sqrt3 \ \ and \ \ a_2 = \sqrt6 \ \ and \ \ a_3 = \sqrt9 \ \ and \ \ a_4 = \sqrt{12}$
$a_2-a_1 = \sqrt6-\sqrt3 =\sqrt3(\sqrt2-1)$
$a_3-a_2 = 3-\sqrt3 =\sqrt3(\sqrt3-1)$
We can clearly see that the difference between terms are not equal
Hence, given series is not in AP

Q4 (xiv) Which of the following are APs ? If they form an AP, find the common difference d and write three more terms. $\small 1^2,3^2,5^2,7^2,...$

Answer:

Given series is
$\small 1^2,3^2,5^2,7^2,...$
we can rewrite it as
$1,9,25,49,....$
Now,
the first term to this series is = 1
Now,
$a_1 =1 \ \ and \ \ a_2 = 9 \ \ and \ \ a_3 =25 \ \ and \ \ a_4 = 49$
$a_2-a_1 = 9-1 = 8$
$a_3-a_2 = 25-9=16$
We can clearly see that the difference between terms are not equal
Hence, given series is not in AP

Q4 (xv) Which of the following are APs ? If they form an AP, find the common difference d and write three more terms. $\small 1^2,5^2,7^2,73,...$

Answer:

Given series is
$\small 1^2,5^2,7^2,73,...$
we can rewrite it as
$1,25,49,73....$
Now,
the first term to this series is = 1
Now,
$a_1 =1 \ \ and \ \ a_2 = 25 \ \ and \ \ a_3 =49 \ \ and \ \ a_4 = 73$
$a_2-a_1 = 25-1 = 24$
$a_3-a_2 = 49-25=24$
$a_4-a_3 = 73-49=24$
We can clearly see that the difference between terms are equal and equal to 24
Hence, given series is in AP
Now, the next three terms are
$a_5=a_4+d = 73+24=97$
$a_6=a_5+d = 97+24=121$
$a_7=a_6+d = 121+24=145$
Therefore, the next three terms of given series are 97,121,145

NCERT Solutions Class 10 Chapter 5 Arithmetic Progressions Excercise: 5.2

Q1 Fill in the blanks in the following table, given that a is the first term, d the common difference and $\small a_n$ the $\small n$ th term of the AP:

$\small a_n$

(i)

(ii)

(iii)

(iv)

(v)

$\small -18$

$\small ...$

$\small -18.9$

$\small 3.5$

$\small ...$

$\small -3$

$\small 2.5$

$\small ...$

105

$\small ...$

$\small -5$

$\small 3.6$

$\small ...$

Answer:

(i)
It is given that
$a=7, d = 3 , n = 8$
Now, we know that
$a_n = a+(n-1)d$
$a_8 = 7+(8-1)3= 7+7\times 3 = 7+21 = 28$
Therefore,
$a_8 = 28$

(ii) It is given that
$a=-18, n = 10, a_{10} = 0$
Now, we know that
$a_n = a+(n-1)d$
$a_{10} = -18+(10-1)d$
$0 +18=9d$
$d = \frac{18}{9}=2$
(iii) It is given that
$d=-3, n = 18, a_{18} = -5$
Now, we know that
$a_n = a+(n-1)d$
$a_{18} = a+(18-1)(-3)$
$-5=a+17\times (-3)$
$a = 51-5 = 46$
Therefore,
$a = 46$

(iv) It is given that
$a=-18.9, d = 2.5, a_{n} = 3.6$
Now, we know that
$a_n = a+(n-1)d$
$a_{n} = -18.9+(n-1)2.5$
$3.6+18.9= 2.5n-2.5$
$n = \frac{22.5+2.5}{2.5}= \frac{25}{2.5}= 10$
Therefore,
$n = 10$

(v) It is given that
$a=3.5, d = 0, n = 105$
Now, we know that
$a_n = a+(n-1)d$
$a_{105} = 3.5+(105-1)0$
$a_{105} = 3.5$
Therefore,
$a_{105} = 3.5$

Q2 (i) Choose the correct choice in the following and justify: $\small 30$ th term of the AP: $\small 10,7,4,...,$ is

(A) $\small 97$ (B) $\small 77$ (C) $\small -77$ (D) $\small -87$

Answer:

Given series is
$\small 10,7,4,...,$
Here, $a = 10$
and
$d = 7 - 10 = -3$
Now, we know that
$a_n = a+(n-1)d$
It is given that $n = 30$
Therefore,
$a_{30} = 10+(30-1)(-3)$
$a_{30} = 10+(29)(-3)$
$a_{30} = 10-87 = -77$
Therefore, $\small 30$ th term of the AP: $\small 10,7,4,...,$ is -77
Hence, Correct answer is (C)

Q2 (ii) Choose the correct choice in the following and justify : 11th term of the AP: $\small -3,-\frac{1}{2},2,...,$ is

(A) $\small 28$ (B) $\small 22$ (C) $\small -38$ (D) $\small -48\frac{1}{2}$

Answer:

Given series is
$\small -3,-\frac{1}{2},2,...,$
Here, $a = -3$
and
$d =-\frac{1}{2} -(-3)= -\frac{1}{2} + 3 = \frac{-1+6}{2}= \frac{5}{2}$
Now, we know that
$a_n = a+(n-1)d$
It is given that $n = 11$
Therefore,
$a_{11} = -3+(11-1)\left ( \frac{5}{2} \right )$
$a_{11} = -3+(10)\left ( \frac{5}{2} \right )$
$a_{11} = -3+5\times 5 = -3+25 = 22$
Therefore, 11th term of the AP: $\small -3,-\frac{1}{2},2,...,$ is 22
Hence, the Correct answer is (B)

Q3 (i) In the following APs, find the missing terms in the boxes : $\small 2,\hspace {1mm}\fbox{ },\hspace {1mm} 26$

Answer:

Given AP series is
$\small 2,\hspace {1mm}\fbox{ },\hspace {1mm} 26$
Here, $a = 2 , n = 3 \ and \ a_3 = 26$
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow a_3 =2+(3-1)d$
$\Rightarrow 26 -2=(2)d$
$\Rightarrow d = \frac{24}{2}= 12$
Now,
$a_2= a_1+d$
$a_2= 2+12 = 14$
Therefore, the missing term is 14

Q3 (ii) In the following APs, find the missing terms in the boxes: $\small \fbox { },\hspace {1mm}13,\hspace{1mm}\fbox { }, \hspace {1mm} 3$

Answer:

Given AP series is
$\small \fbox { },\hspace {1mm}13,\hspace{1mm}\fbox { }, \hspace {1mm} 3$
Here, $a_2 = 13 , n = 4 \ and \ a_4 = 3$
Now,
$a_2= a_1+d$
$a_1= a = 13 - d$
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow a_4 =13-d+(4-1)d$
$\Rightarrow 3-13=-d+3d$
$\Rightarrow d = -\frac{10}{2}= -5$
Now,
$a_2= a_1+d$
$a_1= a = 13 - d= 13-(-5 ) = 18$
And
$a_3=a_2+d$
$a_3=13-5 = 8$
Therefore, missing terms are 18 and 8
AP series is 18,13,8,3

Q3 (iii) In the following APs, find the missing terms in the boxes : $\small 5,\: \fbox { },\: \fbox { },\: 9\frac{1}{2}$

Answer:

Given AP series is
$\small 5,\: \fbox { },\: \fbox { },\: 9\frac{1}{2}$
Here, $a = 5 , n = 4 \ and \ a_4 = 9\frac{1}{2}= \frac{19}{2}$
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow a_4 =5+(4-1)d$
$\Rightarrow \frac{19}{2} -5=3d$
$\Rightarrow d = \frac{19-10}{2\times 3} = \frac{9}{6} = \frac{3}{2}$
Now,
$a_2= a_1+d$
$a_2 = 5+\frac{3}{2} = \frac{13}{2}$
And
$a_3=a_2+d$
$a_3=\frac{13}{2}+\frac{3}{2} = \frac{16}{2} = 8$
Therefore, missing terms are $\frac{13}{2}$ and 8
AP series is $5,\frac{13}{2}, 8 , \frac{19}{2}$

Q3 (iv) In the following APs, find the missing terms in the boxes : $\small -4,\: \fbox { },\: \fbox { },\: \fbox { },\: \fbox { },\: 6$

Answer:

Given AP series is
$\small -4,\: \fbox { },\: \fbox { },\: \fbox { },\: \fbox { },\: 6$
Here, $a = -4 , n = 6 \ and \ a_6 = 6$
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow a_6 =-4+(6-1)d$
$\Rightarrow 6+4 = 5d$
$\Rightarrow d = \frac{10}{5} = 2$
Now,
$a_2= a_1+d$
$a_2 = -4+2 = -2$
And
$a_3=a_2+d$
$a_3=-2+2 = 0$
And
$a_4 = a_3+d$
$a_4 = 0+2 = 2$
And
$a_5 = a_4 + d$
$a_5 = 2+2 = 4$
Therefore, missing terms are -2,0,2,4
AP series is -4,-2,0,2,4,6

Q3 (v) In the following APs, find the missing terms in the boxes : $\small \fbox { },\: 38,\; \fbox { },\: \fbox { },\: \fbox { },\; -22$

Answer:

Given AP series is
$\small \fbox { },\: 38,\; \fbox { },\: \fbox { },\: \fbox { },\; -22$
Here, $a_2 = 38 , n = 6 \ and \ a_6 = -22$
Now,
$a_2=a_1+d$
$a_1=a =38-d \ \ \ \ \ \ \ \ \ -(i)$
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow a_6 =38-d+(6-1)d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))$
$\Rightarrow -22-38-=-d+5d$
$\Rightarrow d = -\frac{60}{4} = - 15$
Now,
$a_2= a_1+d$
$a_1 = 38-(-15) = 38+15 = 53$
And
$a_3=a_2+d$
$a_3=38-15 = 23$
And
$a_4 = a_3+d$
$a_4 = 23-15 = 8$
And
$a_5 = a_4 + d$
$a_5 =8-15 = -7$
Therefore, missing terms are 53,23,8,-7
AP series is 53,38,23,8,-7,-22

Q4 Which term of the AP : $\small 3,8,13,18,...,$ is $\small 78$ ?
Answer:

Given AP is
$\small 3,8,13,18,...,$
Let suppose that nth term of AP is 78
Here, $a = 3$
And
$d = a_2-a_1 = 8 - 3 = 5$
Now, we know that that
$a_n = a + (n-1)d$
$\Rightarrow 78 = 3 + (n-1)5$
$\Rightarrow 78 -3 = 5n-5$
$\Rightarrow n = \frac{75 +5}{5}= \frac{80}{5} = 16$
Therefore, value of 16th term of given AP is 78

Q5 (i) Find the number of terms in each of the following APs : $\small 7,13,19,...,205$

Answer:

Given AP series is
$\small 7,13,19,...,205$
Let's suppose there are n terms in given AP
Then,
$a = 7 , a_n = 205$
And
$d= a_2-a_1 = 13-7 = 6$
Now, we know that
$a_n =a + (n-1)d$
$\Rightarrow 205=7 + (n-1)6$
$\Rightarrow 205-7 = 6n-6$
$\Rightarrow n = \frac{198+6}{6} = \frac{204}{6} = 34$
Therefore, there are 34 terms in given AP

Q5 (ii) Find the number of terms in each of the following APs : $\small 18,15\frac{1}{2},13,...,-47$

Answer:

Given AP series is
$\small 18,15\frac{1}{2},13,...,-47$
suppose there are n terms in given AP
Then,
$a = 18 , a_n = -47$
And
$d= a_2-a_1 = \frac{31}{2}-18 = \frac{31-36}{2} = -\frac{5}{2}$
Now, we know that
$a_n =a + (n-1)d$
$\Rightarrow -47=18 + (n-1)\left ( -\frac{5}{2} \right )$
$\Rightarrow -47-18= -\frac{5n}{2}+\frac{5}{2}$
$\Rightarrow -\frac{5n}{2}= -65-\frac{5}{2}$
$\Rightarrow -\frac{5n}{2}= -\frac{135}{2}$
$\Rightarrow n = 27$
Therefore, there are 27 terms in given AP

Q6 Check whether $\small -150$ is a term of the AP : $\small 11,8,5,2...$

Answer:

Given AP series is
$\small 11,8,5,2...$
Here, $a = 11$
And
$d = a_2-a_1 = 8-11 = -3$
Now,
suppose -150 is nth term of the given AP
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow -150 = 11+(n-1)(-3)$
$\Rightarrow -150- 11=-3n+3$
$\Rightarrow =n = \frac{161+3}{3}= \frac{164}{3} = 54.66$
Value of n is not an integer
Therefore, -150 is not a term of AP $\small 11,8,5,2...$

Q7 Find the $\small 31$ st term of an AP whose $\small 11$ th term is $\small 38$ and the $\small 16$ th term is $\small 73$ .

Answer:

It is given that
$\small 11$ th term of an AP is $\small 38$ and the $\small 16$ th term is $\small 73$
Now,
$a_{11} =38= a+ 10d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$
And
$a_{16} =73= a+ 15d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(ii)$
On solving equation (i) and (ii) we will get
$a= -32 \ \ \ and \ \ \ d = 7$
Now,
$a_{31} = a+30d = -32 + 30\times 7 = -32+210 = 178$
Therefore, 31st terms of given AP is 178

Q8 An AP consists of $\small 50$ terms of which $\small 3$ rd term is $\small 12$ and the last term is $\small 106$ . Find the $\small 29$ th term.
Answer:

It is given that
AP consists of $\small 50$ terms of which $\small 3$ rd term is $\small 12$ and the last term is $\small 106$
Now,
$a_3 = 12=a+2d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$
And
$a_{50} = 106=a+49d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(ii)$
On solving equation (i) and (ii) we will get
$a= 8 \ \ \ and \ \ \ d = 2$
Now,
$a_{29} = a+28d=8+28\times 2 = 8 +56 = 64$
Therefore, 29th term of given AP is 64

Q9 If the $\small 3$ rd and the $\small 9$ th terms of an AP are $\small 4$ and $\small -8$ respectively, which term of this AP is zero?
Answer:

It is given that
$\small 3$ rd and the $\small 9$ th terms of an AP are $\small 4$ and $\small -8$ respectively
Now,
$a_3 = 4=a+2d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$
And
$a_{9} = -8=a+8d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(ii)$
On solving equation (i) and (ii) we will get
$a= 8 \ \ \ and \ \ \ d = -2$
Now,
Let nth term of given AP is 0
Then,
$a_{n} = a+(n-1)d$
$0 = 8+(n-1)(-2)$
$2n = 8+2= 10$
$n = \frac{10}{2} = 5$
Therefore, 5th term of given AP is 0

Q10 The $\small 17$ th term of an AP exceeds its $\small 10$ th term by $\small 7$ . Find the common difference.
Answer:

It is given that
$\small 17$ th term of an AP exceeds its $\small 10$ th term by $\small 7$
i.e.
$a_{17}= a_{10}+7$
$\Rightarrow a+16d = a+9d+7$
$\Rightarrow a+16d - a-9d=7$
$\Rightarrow 7d=7$
$\Rightarrow d = 1$
Therefore, the common difference of AP is 1

Q11 Which term of the AP : $\small 3,15,27,39,...$ will be $\small 132$ more than its $\small 54$ th term?
Answer:

Given AP is
$\small 3,15,27,39,...$
Here, $a= 3$
And
$d= a_2-a_1 = 15 - 3 = 12$
Now, let's suppose nth term of given AP is $\small 132$ more than its $\small 54$ th term
Then,
$a_n= a_{54}+132$
$\Rightarrow a+(n-1)d = a+53d+132$
$\Rightarrow 3+(n-1)12 = 3+53\times 12+132$
$\Rightarrow 12n = 3+636+132+12$
$\Rightarrow 12n = 636+132+12$
$\Rightarrow n = \frac{780}{12}= 65$
Therefore, 65th term of given AP is $\small 132$ more than its $\small 54$ th term

Q12 Two APs have the same common difference. The difference between their $\small 100$ th terms is $\small 100$ , what is the difference between their $\small 1000$ th terms?
Answer:

It is given that
Two APs have the same common difference and difference between their $\small 100$ th terms is $\small 100$
i.e.
$a_{100}-a'_{100}= 100$
Let common difference of both the AP's is d
$\Rightarrow a+99d-a'-99d=100$
$\Rightarrow a-a'=100 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ - (i)$
Now, difference between 1000th term is
$a_{1000}-a'_{1000}$
$\Rightarrow a+999d -a'-999d$
$\Rightarrow a-a'$
$\Rightarrow 100 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i) )$
Therefore, difference between 1000th term is 100

Q 13 How many three-digit numbers are divisible by $\small 7$ ?
Answer:

We know that the first three digit number divisible by 7 is 105 and last three-digit number divisible by 7 is 994
Therefore,
$a = 105 , d = 7 \ and \ a_n = 994$
Let there are n three digit numbers divisible by 7
Now, we know that
$a_n = a+ (n-1)d$
$\Rightarrow 994 = 105 + (n-1)7$
$\Rightarrow 7n = 896$
$\Rightarrow n = \frac{896}{7} = 128$
Therefore, there are 128 three-digit numbers divisible by 7

Q14 How many multiples of $\small 4$ lie between $\small 10$ and $\small 250$ ?
Answer:

We know that the first number divisible by 4 between 10 to 250 is 12 and last number divisible by 4 is 248
Therefore,
$a = 12 , d = 4 \ and \ a_n = 248$
Let there are n numbers divisible by 4
Now, we know that
$a_n = a+ (n-1)d$
$\Rightarrow 248 = 12 + (n-1)4$
$\Rightarrow 4n = 240$
$\Rightarrow n = \frac{240}{4} = 60$
Therefore, there are 60 numbers between 10 to 250 that are divisible by 4

Q15 For what value of $\small n$ , are the $\small n$ th terms of two APs: $\small 63,65,67,...$ and $\small 3,10,17,...$ equal?

Answer:

Given two AP's are
$\small 63,65,67,...$ and $\small 3,10,17,...$
Let first term and the common difference of two AP's are a , a' and d , d'
$a = 63 \ , d = a_2-a_1 = 65-63 = 2$
And
$a' = 3 \ , d' = a'_2-a'_1 = 10-3 = 7$
Now,
Let nth term of both the AP's are equal
$a_n = a'_n$
$\Rightarrow a+(n-1)d=a'+(n-1)d'$
$\Rightarrow 63+(n-1)2=3+(n-1)7$
$\Rightarrow 5n=65$
$\Rightarrow n=\frac{65}{5} = 13$
Therefore, the 13th term of both the AP's are equal

Q16 Determine the AP whose third term is $\small 16$ and the $\small 7$ th term exceeds the $\small 5$ th term by $\small 12$ .
Answer:

It is given that
3rd term of AP is $\small 16$ and the $\small 7$ th term exceeds the $\small 5$ th term by $\small 12$
i.e.
$a_3=a+2d = 16 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$
And
$a_7=a_5+12$
$a+6d=a+4d+12$
$2d = 12$
$d = 6$
Put the value of d in equation (i) we will get
$a = 4$
Now, AP with first term = 4 and common difference = 6 is
4,10,16,22,.....

Q17 Find the $\small 20$ th term from the last term of the AP : $\small 3,8,13,...,253$ .

Answer:

Given AP is
$\small 3,8,13,...,253$
Here, $a = 3 \ and \ a_n = 253$
And
$d = a_2-a_1=8-3 = 5$
Let suppose there are n terms in the AP
Now, we know that
$a_n = a+(n-1)d$
$253= 3+(n-1)5$
$5n = 255$
$n = 51$
So, there are 51 terms in the given AP and 20th term from the last will be 32th term from the starting
Therefore,
$a_{32} = a+31d$
$a_{32} = 3+31\times 5 = 3+155 = 158$
Therefore, 20th term from the of given AP is 158

Q18 The sum of the $\small 4$ th and $\small 8$ th terms of an AP is $\small 24$ and the sum of the $\small 6$ th and $\small 10$ th terms is $\small 44$ Find the first three terms of the AP.
Answer:

It is given that
sum of the $\small 4$ th and $\small 8$ th terms of an AP is $\small 24$ and the sum of the $\small 6$ th and $\small 10$ th terms is $\small 44$
i.e.
$a_4+a_8=24$
$\Rightarrow a+3d+a+7d=24$
$\Rightarrow 2a+10d=24$
$\Rightarrow a+5d=12 \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$
And
$a_6+a_{10}=44$
$\Rightarrow a+5d+a+9d=44$
$\Rightarrow 2a+14d=44$
$\Rightarrow a+7d=22 \ \ \ \ \ \ \ \ \ \ \ \ \ -(ii)$
On solving equation (i) and (ii) we will get
$a= -13 \ and \ d= 5$
Therefore,first three of AP with a = -13 and d = 5 is
-13,-8,-3

Q19 Subba Rao started work in 1995 at an annual salary of Rs 5000 and received an increment of Rs 200 each year. In which year did his income reach Rs 7000?

Answer:

It is given that
Subba Rao started work at an annual salary of Rs 5000 and received an increment of Rs 200 each year
Therefore, $a = 5000 \ and \ d =200$
Let's suppose after n years his salary will be Rs 7000
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow 7000=5000+(n-1)200$
$\Rightarrow 2000=200n-200$
$\Rightarrow 200n=2200$
$\Rightarrow n = 11$
Therefore, after 11 years his salary will be Rs 7000
after 11 years, starting from 1995, his salary will reach to 7000, so we have to add 10 in 1995, because these numbers are in years
Thus , 1995+10 = 2005

Q20 Ramkali saved Rs 5 in the first week of a year and then increased her weekly savings by Rs $\small 1.75$ . If in the $\small n$ th week, her weekly savings become Rs $\small 20.75$ , find $\small n$

Answer:

It is given that
Ramkali saved Rs 5 in the first week of a year and then increased her weekly savings by Rs $\small 1.75$
Therefore, $a = 5 \ and \ d = 1.75$
after $\small n$ th week, her weekly savings become Rs $\small 20.75$
Now, we know that
$a_n = a +(n-1)d$
$\Rightarrow 20.75= 5+(n-1)1.75$
$\Rightarrow 15.75= 1.75n-1.75$
$\Rightarrow 1.75n=17.5$
$\Rightarrow n=10$
Therefore, after 10 weeks her saving will become Rs 20.75

NCERT Arithmetic Progression Class 10 Solutions Excercise: 5.3

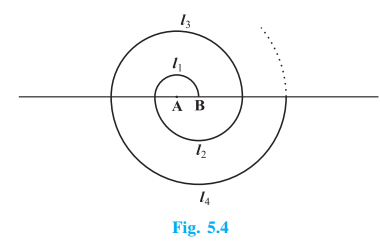
Q1 (i) Find the sum of the following APs: $\small 2,7,12,...,$ to $\small 10$ terms.

Answer:

Given AP is
$\small 2,7,12,...,$ to $\small 10$ terms
Here, $a = 2 \ and \ n = 10$
And
$d = a_2-a_1=7-2=5$
Now, we know that
$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S = \frac{10}{2}\left \{ 2\times 2 +(10-1)5\right \}$
$\Rightarrow S = 5\left \{ 4 +45\right \}$
$\Rightarrow S = 5\left \{ 49\right \}$
$\Rightarrow S =245$
Therefore, the sum of AP $\small 2,7,12,...,$ to $\small 10$ terms is 245

Q1 (ii) Find the sum of the following APs: $\small -37,-33,-29,...,$ to $\small 12$ terms.

Answer:

Given AP is
$\small -37,-33,-29,...,$ to $\small 12$ terms.
Here, $a = -37 \ and \ n = 12$
And
$d = a_2-a_1=-33-(-37)=4$
Now, we know that
$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S = \frac{12}{2}\left \{ 2\times (-37) +(12-1)4\right \}$
$\Rightarrow S = 6\left \{ -74 +44\right \}$
$\Rightarrow S = 5\left \{ -30\right \}$
$\Rightarrow S =-180$
Therefore, the sum of AP $\small -37,-33,-29,...,$ to $\small 12$ terms. is -180

Q1 (iii) Find the sum of the following APs: $\small 0.6,1.7,2.8,...,$ to $\small 100$ terms.

Answer:

Given AP is
$\small 0.6,1.7,2.8,...,$ to $\small 100$ terms..
Here, $a = 0.6 \ and \ n = 100$
And
$d = a_2-a_1=1.7-0.6=1.1$
Now, we know that
$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S = \frac{100}{2}\left \{ 2\times (0.6) +(100-1)(1.1)\right \}$
$\Rightarrow S = 50\left \{ 1.2 +108.9\right \}$
$\Rightarrow S = 50\left \{ 110.1\right \}$
$\Rightarrow S =5505$
Therefore, the sum of AP $\small 0.6,1.7,2.8,...,$ to $\small 100$ terms. is 5505

Q1 (iv) Find the sum of the following APs: $\small \frac{1}{15},\frac{1}{12},\frac{1}{10},...,$ to $\small 11$ terms.

Answer:

Given AP is
$\small \frac{1}{15},\frac{1}{12},\frac{1}{10},...,$ to $\small 11$ terms.
Here, $a = \frac{1}{15} \ and \ n = 11$
And
$d = a_2-a_1=\frac{1}{12}-\frac{1}{15}= \frac{5-4}{60}= \frac{1}{60}$
Now, we know that
$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S = \frac{11}{2}\left \{ 2\times \frac{1}{15} +(11-1)(\frac{1}{60})\right \}$
$\Rightarrow S = \frac{11}{2}\left \{ \frac{2}{15} +\frac{1}{6}\right \}$
$\Rightarrow S = \frac{11}{2}\left \{ \frac{9}{30}\right \}$
$\Rightarrow S =\frac{99}{60}= \frac{33}{20}$
Therefore, the sum of AP $\small \frac{1}{15},\frac{1}{12},\frac{1}{10},...,$ to $\small 11$ terms. is $\frac{33}{20}$

Q2 (i) Find the sums given below : $\small 7+10\frac{1}{2}+14+...+84$

Answer:

Given AP is
$\small 7+10\frac{1}{2}+14+...+84$
We first need to find the number of terms
Here, $a = 7 \ and \ a_n = 84$
And
$d = a_2-a_1=\frac{21}{2}-7= \frac{21-14}{2}= \frac{7}{2}$
Let suppose there are n terms in the AP
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow 84 = 7 + (n-1)\frac{7}{2}$
$\Rightarrow \frac{7n}{2}= 77+\frac{7}{2}$
$\Rightarrow n = 23$
Now, we know that
$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S = \frac{23}{2}\left \{ 2\times7 +(23-1)(\frac{7}{2})\right \}$
$\Rightarrow S = \frac{23}{2}\left \{ 14 +77\right \}$
$\Rightarrow S = \frac{23}{2}\left \{ 91\right \}$
$\Rightarrow S =\frac{2093}{2}=1046\frac{1}{2}$
Therefore, the sum of AP $\small 7+10\frac{1}{2}+14+...+84$ is $1046\frac{1}{2}$

Q2 (ii) Find the sums given below : $\small 34+32+30+...+10$

Answer:

Given AP is
$\small 34+32+30+...+10$
We first need to find the number of terms
Here, $a = 34 \ and \ a_n = 10$
And
$d = a_2-a_1=32-34=-2$
Let suppose there are n terms in the AP
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow 10 = 34 + (n-1)(-2)$
$\Rightarrow -26 = -2n$
$\Rightarrow n = 13$
Now, we know that
$S = \frac{n}{2}\left \{ a+a_n \right \}$

$\Rightarrow S = \frac{13}{2}\left \{ 44\right \}$
$\Rightarrow S =13\times 22 = 286$
Therefore, the sum of AP $\small 34+32+30+...+10$ is 286

Q2 (iii) Find the sums given below : $\small -5+(-8)+(-11)+...+(-230)$

Answer:

Given AP is
$\small -5+(-8)+(-11)+...+(-230)$
We first need to find the number of terms
Here, $a = -5 \ and \ a_n = -230$
And
$d = a_2-a_1=-8-(-5)= -3$
Let suppose there are n terms in the AP
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow -230 = -5 + (n-1)(-3)$
$\Rightarrow -228 = -3n$
$\Rightarrow n = 76$
Now, we know that
$S = \frac{n}{2}\left \{ a+a_n \right \}$
$\Rightarrow S = \frac{76}{2}\left \{ (-5-230 )\right \}$

$\Rightarrow S = 38\left \{ -235\right \}$
$\Rightarrow S = -8930$
Therefore, the sum of AP $\small -5+(-8)+(-11)+...+(-230)$ is -8930

Q3 (i) In an AP: given $\small a=5$ , $\small d=3$ , $\small a_n=50$ , find $\small n$ and $\small S_n$ .

Answer:

It is given that
$a = 5, d = 3 \ and \ a_n = 50$
Let suppose there are n terms in the AP
Now, we know that
$a_n = a+(n-1)d$
$\Rightarrow 50 = 5 + (n-1)3$
$\Rightarrow 48 = 3n$
$\Rightarrow n = 16$
Now, we know that
$S = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S = \frac{16}{2}\left \{ 2\times(5) +(16-1)(3)\right \}$
$\Rightarrow S = 8\left \{ 10+45\right \}$
$\Rightarrow S = 8\left \{ 55\right \}$
$\Rightarrow S =440$
Therefore, the sum of the given AP is 440

Q3 (ii) In an AP: given $\small a=7$ , $\small a_1_3=35$ , find $\small d$ and $\small S_1_3$ .

Answer:

It is given that
$a = 7 \ and \ a_{13} = 35$
$a_{13}= a+12d = 35$
$= 12d = 35-7 = 28$
$d = \frac{28}{12}= \frac{7}{3}$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{13} = \frac{13}{2}\left \{ 2\times(7) +(13-1)(\frac{7}{3})\right \}$
$\Rightarrow S_{13} = \frac{13}{2}\left \{14 +28\right \}$
$\Rightarrow S_{13} = \frac{13}{2}\left \{42\right \}$
$\Rightarrow S_{13} = 13 \times 21 = 273$
Therefore, the sum of given AP is 273

Q3 (iii) In an AP: given $\small a_1_2=37,d=3,$ find $\small a$ and $\small S_1_2$ .

Answer:

It is given that
$d = 3 \ and \ a_{12} = 37$
$a_{12}= a+11d = 37$
$= a= 37-11\times 3 = 37-33=4$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{12} = \frac{12}{2}\left \{ 2\times(4) +(12-1)3\right \}$
$\Rightarrow S_{12} = 6\left \{ 8+33\right \}$
$\Rightarrow S_{12} = 6\left \{41\right \}$
$\Rightarrow S_{12} =246$
Therefore, the sum of given AP is 246

Q3 (iv) In an AP: given $\small a_3=15, S_1_0=125,$ find $\small d$ and $\small S_1_0$
Answer:

It is given that
$\small a_3=15, S_1_0=125$
$a_{3}= a+2d = 15 \ \ \ \ \ \ \ \ -(i)$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{10} = \frac{10}{2}\left \{ 2\times(a) +(10-1)d\right \}$
$\Rightarrow 125 = 5\left \{ 2a+9d\right \}$
$\Rightarrow 2a+9d = 25 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(ii)$
On solving equation (i) and (ii) we will get
$a= 17 \ and \ d = -1$
Now,
$a_{10} = a+ 9d = 17 + 9(-1)= 17-9 = 8$
Therefore, the value of d and 10th terms is -1 and 8 respectively

Q3 (v) In an AP: given $\small d=5, S_9=75$ , find $\small a$ and $\small a_9$ .

Answer:

It is given that
$\small d=5, S_9=75$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{9} = \frac{9}{2}\left \{ 2\times(a) +(9-1)5\right \}$
$\Rightarrow 75= \frac{9}{2}\left \{ 2a +40\right \}$
$\Rightarrow 150= 18a+360$
$\Rightarrow a = -\frac{210}{18}=-\frac{35}{3}$
Now,
$a_{9} = a+ 8d = -\frac{35}{3} + 8(5)= -\frac{35}{3}+40 = \frac{-35+120}{3}= \frac{85}{3}$

Q3 (vi) In an AP: given $\small a=2,d=8,S_n=90,$ find $\small n$ and $\small a_n$ .

Answer:

It is given that
$\small a=2,d=8,S_n=90,$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow 90 = \frac{n}{2}\left \{ 2\times(2) +(n-1)8\right \}$
$\Rightarrow 180 = n\left \{ 4+8n-8\right \}$
$\Rightarrow 8n^2-4n-180=0$
$\Rightarrow 4(2n^2-n-45)=0$
$\Rightarrow 2n^2-n-45=0$
$\Rightarrow 2n^2-10n+9n-45=0$
$\Rightarrow (n-5)(2n+9)=0$
$\Rightarrow n = 5 \ \ and \ \ n = - \frac{9}{2}$
n can not be negative so the only the value of n is 5
Now,
$a_{5} = a+ 4d = 2+4\times 8 = 2+32 = 34$
Therefore, value of n and nth term is 5 and 34 respectively

Q3 (vii) In an AP: given $\small a=8,a_n=62,S_n=210,$ find $\small n$ and $\small d$ .

Answer:

It is given that
$\small a=8,a_n=62,S_n=210,$
Now, we know that
$a_n = a+(n-1)d$
$62 = 8+(n-1)d$
$(n-1)d= 54 \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$

Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow 210 = \frac{n}{2}\left \{ 2\times(8) +(n-1)d\right \}$
$\Rightarrow 420 = n\left \{ 16+54 \right \} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))$
$\Rightarrow 420 = n\left \{ 70 \right \}$
$\Rightarrow n = 6$
Now, put this value in (i) we will get
$d = \frac{54}{5}$
Therefore, value of n and d are $6 \ and \ \frac{54}{5}$ respectively

Q3 (viii) In an AP: given $\small a_n=4,d=2,S_n=-14,$ find $\small n$ and $\small a$ .

Answer:

It is given that
$\small a_n=4,d=2,S_n=-14,$
Now, we know that
$a_n = a+(n-1)d$
$4 = a+(n-1)2$
$a+2n = 6\Rightarrow a = 6-2n \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$

Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow -14 = \frac{n}{2}\left \{ 2\times(a) +(n-1)2\right \}$
$\Rightarrow -28 = n\left \{ 2(6-2n)+2n-2 \right \} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))$
$\Rightarrow -28 = n\left \{ 10-2n \right \}$
$\Rightarrow 2n^2-10n-28=0$
$\Rightarrow 2(n^2-5n-14)=0$
$\Rightarrow n^2-7n+2n-14=0$
$\Rightarrow(n+2)(n-7)=0$
$\Rightarrow n = -2 \ \ and \ \ n = 7$
Value of n cannot be negative so the only the value of n is 7
Now, put this value in (i) we will get
a = -8
Therefore, the value of n and a are 7 and -8 respectively

Q3 (ix) In an AP: given $\small a=3,n=8,S=192,$ find $\small d$ .

Answer:

It is given that
$\small a=3,n=8,S=192,$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow 192 = \frac{8}{2}\left \{ 2\times(3) +(8-1)d\right \}$
$\Rightarrow 192=4\left \{6 +7d\right \}$
$\Rightarrow 7d = 48-6$
$\Rightarrow d = \frac{42}{7} = 6$
Therefore, the value of d is 6

Q3 (x) In an AP: given $\small l=28,S=144 \ and \ n = 9$ and there are total $\small 9$ terms. Find $\small a$ .

Answer:

It is given that
$\small l=28,S=144 \ and \ n = 9$
Now, we know that
$l = a_n = a+(n-1)d$
$28 = a_n = a+(n-1)d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow 144 = \frac{9}{2}\left \{ a + a +(n-1)d\right \}$
$\Rightarrow 288 =9\left \{ a+ 28\right \} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -(using \ (i))$
$\Rightarrow a+28= 32$
$\Rightarrow a=4$
Therefore, the value of a is 4

Q4 How many terms of the AP: $\small 9,17,25,...$ must be taken to give a sum of $\small 636$ ?

Answer:

Given AP is
$\small 9,17,25,...$
Here, $a =9 \ and \ d = 8$
And $S_n = 636$
Now , we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow 636 = \frac{n}{2}\left \{ 18+(n-1)8 \right \}$
$\Rightarrow 1272 = n\left \{ 10+8n \right \}$
$\Rightarrow 8n^2+10n-1272=0$
$\Rightarrow 2(4n^2+5n-636)=0$
$\Rightarrow 4n^2+53n-48n-636=0$
$\Rightarrow (n-12)(4n+53)=0$
$\Rightarrow n = 12 \ \ and \ \ n = - \frac{53}{4}$
Value of n can not be negative so the only the value of n is 12
Therefore, the sum of 12 terms of AP $\small 9,17,25,...$ must be taken to give a sum of $\small 636$ .

Q5 The first term of an AP is $\small 5$ , the last term is $\small 45$ and the sum is $\small 400$ . Find the number of terms and the common difference.

Answer:

It is given that
$\small a=5,a_n=45,S_n=400,$
Now, we know that
$a_n = a+(n-1)d$
$45 = 5+(n-1)d$
$(n-1)d= 40 \ \ \ \ \ \ \ \ \ \ \ \ \ -(i)$

Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow 400 = \frac{n}{2}\left \{ 2\times(5) +(n-1)d\right \}$
$\Rightarrow 800 = n\left \{ 10+40 \right \} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (using \ (i))$
$\Rightarrow 800 = n\left \{ 50 \right \}$
$\Rightarrow n = 16$
Now, put this value in (i) we will get
$d = \frac{40}{15}= \frac{8}{3}$
Therefore, value of n and d are $16 \ and \ \frac{8}{3}$ respectively

Q6 The first and the last terms of an AP are $\small 17$ and $\small 350$ respectively. If the common difference is $\small 9$ , how many terms are there and what is their sum?

Answer:

It is given that
$\small a=17,l=350,d=9,$
Now, we know that
$a_n = a+(n-1)d$
$350 = 17+(n-1)9$
$(n-1)9 = 333$
$(n-1)=37$
$n = 38$

Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{38}= \frac{38}{2}\left \{ 2\times(17) +(38-1)9\right \}$
$\Rightarrow S_{38}= 19\left \{ 34 +333\right \}$
$\Rightarrow S_{38}= 19\left \{367\right \}$
$\Rightarrow S_{38}= 6973$
Therefore, there are 38 terms and their sun is 6973

Q7 Find the sum of first $\small 22$ terms of an AP in which $\small d=7$ and $\small 22$ nd term is $\small 149$ .

Answer:

It is given that
$\small a_{22}=149,d=7,n = 22$
Now, we know that
$a_{22} = a+21d$
$149 = a+21\times 7$
$a = 149 - 147 = 2$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{22}= \frac{22}{2}\left \{ 2\times(2) +(22-1)7\right \}$
$\Rightarrow S_{22}= 11\left \{ 4 +147\right \}$
$\Rightarrow S_{22}= 11\left \{ 151\right \}$
$\Rightarrow S_{22}= 1661$
Therefore, there are 22 terms and their sum is 1661

Q8 Find the sum of first $\small 51$ terms of an AP whose second and third terms are $\small 14$ and $\small 18$ respectively.

Answer:

It is given that
$\small a_{2}=14,a_3=18,n = 51$
And $d= a_3-a_2= 18-14=4$
Now,
$a_2 = a+d$
$a= 14-4 = 10$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{51}= \frac{51}{2}\left \{ 2\times(10) +(51-1)4\right \}$
$\Rightarrow S_{51}= \frac{51}{2}\left \{ 20 +200\right \}$
$\Rightarrow S_{51}= \frac{51}{2}\left \{ 220\right \}$
$\Rightarrow S_{51}= 51 \times 110$
$\Rightarrow S_{51}=5304$
Therefore, there are 51 terms and their sum is 5610

Q9 If the sum of first $\small 7$ terms of an AP is $\small 49$ and that of $\small 17$ terms is $\small 289$ , find the sum of first $\small n$ terms.

Answer:

It is given that
$S_7 = 49 \ and \ S_{17}= 289$
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{7}= \frac{7}{2}\left \{ 2\times(a) +(7-1)d\right \}$
$\Rightarrow 98= 7\left \{ 2a +6d\right \}$
$\Rightarrow a +3d = 7 \ \ \ \ \ \ \ -(i)$
Similarly,
$\Rightarrow S_{17}= \frac{17}{2}\left \{ 2\times(a) +(17-1)d\right \}$
$\Rightarrow 578= 17\left \{ 2a +16d\right \}$
$\Rightarrow a +8d = 17 \ \ \ \ \ \ \ -(ii)$
On solving equation (i) and (ii) we will get
a = 1 and d = 2
Now, the sum of first n terms is
$S_n = \frac{n}{2}\left \{ 2\times 1 +(n-1)2 \right \}$
$S_n = \frac{n}{2}\left \{ 2 +2n-2 \right \}$
$S_n = n^2$
Therefore, the sum of n terms is $n^2$

Q10 (i) Show that $\small a_1,a_2,...,a_n,...$ form an AP where an is defined as below : $\small a_n=3+4n$ Also find the sum of the first $\small 15$ terms.

Answer:

It is given that
$\small a_n=3+4n$
We will check values of $a_n$ for different values of n
$a_1 = 3+4(1) =3+4= 7$
$a_2 = 3+4(2) =3+8= 11$
$a_3 = 3+4(3) =3+12= 15$
and so on.
From the above, we can clearly see that this is an AP with the first term(a) equals to 7 and common difference (d) equals to 4
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ 2\times(7) +(15-1)4\right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ 14 +56\right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ 70\right \}$
$\Rightarrow S_{15}= 15 \times 35$
$\Rightarrow S_{15}= 525$
Therefore, the sum of 15 terms is 525

Q10 (ii) Show that $\small a_1,a _2,...,a_n,...$ form an AP where an is defined as below : $\small a_n=9-5n$ . Also find the sum of the first $\small 15$ terms in each case.

Answer:

It is given that
$\small a_n=9-5n$
We will check values of $a_n$ for different values of n
$a_1 = 9-5(1) =9-5= 4$
$a_2 = 9-5(2) =9-10= -1$
$a_3 = 9-5(3) =9-15= -6$
and so on.
From the above, we can clearly see that this is an AP with the first term(a) equals to 4 and common difference (d) equals to -5
Now, we know that
$S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ 2\times(4) +(15-1)(-5)\right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ 8 -70\right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ -62\right \}$
$\Rightarrow S_{15}= 15 \times (-31)$
$\Rightarrow S_{15}= -465$
Therefore, the sum of 15 terms is -465

Q11 If the sum of the first $\small n$ terms of an AP is $\small 4n-n^2$ , what is the first term (that is $\small S_1$ )? What is the sum of first two terms? What is the second term? Similarly, find the $\small 3$ rd, the $\small 10$ th and the $\small n$ th terms

Answer:

It is given that
the sum of the first $\small n$ terms of an AP is $\small 4n-n^2$
Now,
$\Rightarrow S_n = 4n-n^2$
Now, first term is
$\Rightarrow S_1 = 4(1)-1^2=4-1=3$
Therefore, first term is 3
Similarly,
$\Rightarrow S_2 = 4(2)-2^2=8-4=4$
Therefore, sum of first two terms is 4
Now, we know that
$\Rightarrow S_n = \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_2 = \frac{2}{2}\left \{ 2\times 3+(2-1)d \right \}$
$\Rightarrow 4 = \left \{6+d \right \}$
$\Rightarrow d = -2$
Now,
$a_2= a+d = 3+(-2 )= 1$
Similarly,
$a_3= a+2d = 3+2(-2 )= 3-4=-1$
$a_{10}= a+9d = 3+9(-2 )= 3-18=-15$
$a_{n}= a+(n-1)d = 3+(n-1)(-2 )= 5-2n$

Q12 Find the sum of the first $\small 40$ positive integers divisible by $\small 6$ .

Answer:

Positive integers divisible by 6 are
6,12,18,...
This is an AP with
$here, \ a = 6 \ and \ d = 6$
Now, we know that
$S_n= \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{40}= \frac{40}{2}\left \{ 2\times 6+(40-1)6 \right \}$
$\Rightarrow S_{40}= 20\left \{12+234 \right \}$
$\Rightarrow S_{40}= 20\left \{246 \right \}$
$\Rightarrow S_{40}= 4920$
Therefore, sum of the first $\small 40$ positive integers divisible by $\small 6$ is 4920

Q13 Find the sum of the first $\small 15$ multiples of $\small 8$ .

Answer:

First 15 multiples of 8 are
8,16,24,...
This is an AP with
$here, \ a = 8 \ and \ d = 8$
Now, we know that
$S_n= \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ 2\times 8+(15-1)8 \right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ 16+112 \right \}$
$\Rightarrow S_{15}= \frac{15}{2}\left \{ 128 \right \}$
$\Rightarrow S_{15}= 15 \times 64 = 960$
Therefore, sum of the first 15 multiple of 8 is 960

Q14 Find the sum of the odd numbers between $\small 0$ and $\small 50$ .

Answer:

The odd number between 0 and 50 are
1,3,5,...49
This is an AP with
$here, \ a = 1 \ and \ d = 2$
There are total 25 odd number between 0 and 50
Now, we know that
$S_n= \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
$\Rightarrow S_{25}= \frac{25}{2}\left \{ 2\times 1+(25-1)2 \right \}$
$\Rightarrow S_{25}= \frac{25}{2}\left \{ 2+48 \right \}$
$\Rightarrow S_{25}= \frac{25}{2}\times 50$
$\Rightarrow S_{25}= 25 \times 25 = 625$
Therefore, sum of the odd numbers between $\small 0$ and $\small 50$ 625

Q15 A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows: Rs $\small 200$ for the first day, Rs $\small 250$ for the second day, Rs $\small 300$ for the third day, etc., the penalty for each succeeding day being Rs $\small 50$ more than for the preceding day. How much money the contractor has to pay a penalty, if he has delayed the work by $\small 30$ days?

Answer:

It is given that
Penalty for delay of completion beyond a certain date is Rs $\small 200$ for the first day, Rs $\small 250$ for the second day, Rs $\small 300$ for the third day and penalty for each succeeding day being Rs $\small 50$ more than for the preceding day
We can clearly see that
200,250,300,..... is an AP with
$a = 200 \ and \ d = 50$
Now, the penalty for 30 days is given by the expression
$S_{30}= \frac{30}{2}\left \{ 2\times 200+(30-1)50 \right \}$
$S_{30}= 15\left ( 400+1450 \right )$
$S_{30}= 15 \times 1850$
$S_{30}= 27750$
Therefore, the penalty for 30 days is 27750

Q16 A sum of Rs $\small 700$ is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is Rs $\small 20$ less than its preceding prize, find the value of each of the prizes.

Answer:

It is given that
Each price is decreased by 20 rupees,
Therefore, d = -20 and there are total 7 prizes so n = 7 and sum of prize money is Rs 700 so $S_7 = 700$
Let a be the prize money given to the 1st student
Then,
$S_7 = \frac{7}{2}\left \{ 2a+(7-1)(-20) \right \}$
$700 = \frac{7}{2}\left \{ 2a-120 \right \}$
$2a - 120 = 200$
$a = \frac{320}{2}= 160$
Therefore, the prize given to the first student is Rs 160
Now,
Let $a_2,a_2,...,a_7$ is the prize money given to the next 6 students
then,
$a_2 = a+d = 160+(-20)=160-20=140$
$a_3 = a+2d = 160+2(-20)=160-40=120$
$a_4 = a+3d = 160+3(-20)=160-60=100$
$a_5 = a+4d = 160+4(-20)=160-80=80$
$a_6 = a+5d = 160+5(-20)=160-100=60$
$a_7 = a+6d = 160+6(-20)=160-120=40$
Therefore, prize money given to 1 to 7 student is 160,140,120,100,80,60.40

Q17 In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be the same as the class, in which they are studying, e.g., a section of Class I???? will plant $\small 1$ tree, a section of Class II will plant $\small 2$ trees and so on till Class XII. There are three sections in each class. How many trees will be planted by the students?

Answer:

First there are 12 classes and each class has 3 sections
Since each section of class 1 will plant 1 tree, so 3 trees will be planted by 3 sections of class 1. Thus every class will plant 3 times the number of their class
Similarly,

No. of trees planted by 3 sections of class 1 = 3

No. of trees planted by 3 sections of class 2 = 6

No. of trees planted by 3 sections of class 3 = 9

No. of trees planted by 3 sections of class 4 = 12
Its clearly an AP with first term (a) = 3 and common difference (d) = 3 and total number of classes (n) = 12

Now, number of trees planted by 12 classes is given by
$S_{12}= \frac{12}{2}\left \{ 2\times 3+(12-1)\times 3 \right \}$
$S_{12}= 6\left ( 6+33 \right )$
$S_{12}= 6 \times 39 = 234$
Therefore, number of trees planted by 12 classes is 234

Q18 A spiral is made up of successive semicircles, with centres alternately at $\small A$ and $\small B$ ??????, starting with centre at $\small A$ , of radii $\small 0.5\hspace {1mm}cm,1.0\hspace {1mm}cm,1.5\hspace {1mm}cm,2.0\hspace {1mm}cm,...$ as shown in Fig. $\small 5.4$ . What is the total length of such a spiral made up of thirteen consecutive semicircles? (Take $\pi =\frac{22}{7}$ )

1635921529757

[ Hint : Length of successive semicircles is $\small l_1,l_2,l_3,l_4,...$ with centres at $\small A,B,A,B,...,$ respectively.]

Answer:

From the above-given figure

Circumference of 1st semicircle $l_1 = \pi r_1 = 0.5\pi$

Similarly,

Circumference of 2nd semicircle $l_2 = \pi r_2 = \pi$

Circumference of 3rd semicircle $l_3 = \pi r_3 = 1.5\pi$

It is clear that this is an AP with $a = 0.5\pi \ and \ d = 0.5\pi$

Now, sum of length of 13 such semicircles is given by

$S_{13} = \frac{13}{2}\left \{ 2\times 0.5\pi + (13-1)0.5\pi\right \}$
$S_{13} = \frac{13}{2}\left ( \pi+6\pi \right )$
$S_{13} = \frac{13}{2}\times 7\pi$
$S_{13} = \frac{91\pi}{2} = \frac{91}{2}\times \frac{22}{7}=143$
Therefore, sum of length of 13 such semicircles is 143 cm

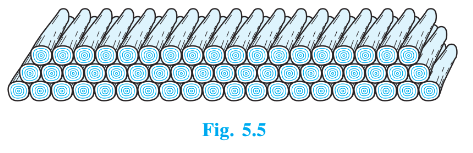
Q19 $\small 200$ logs are stacked in the following manner: $\small 20$ logs in the bottom row, $\small 19$ in the next row, $\small 18$ in the row next to it and so on (see Fig. $\small 5.5$ ). In how many rows are the $\small 200$ logs placed and how many logs are in the top row?

1635921556744

Answer:

As the rows are going up, the no of logs are decreasing,
We can clearly see that 20, 19, 18, ..., is an AP.
and here $a = 20 \ and \ d = -1$
Let suppose 200 logs are arranged in 'n' rows,
Then,
$S_n = \frac{n}{2}\left \{ 2\times 20 +(n-1)(-1) \right \}$
$200 = \frac{n}{2}\left \{ 41-n \right \}$
$\Rightarrow n^2-41n +400 = 0$
$\Rightarrow n^2-16n-25n +400 = 0$
$\Rightarrow (n-16)(n-25) = 0$
$\Rightarrow n = 16 \ \ and \ \ n = 25$
Now,
case (i) n = 25
$a_{25} =a+24d = 20+24\times (-1)= 20-24=-4$
But number of rows can not be in negative numbers
Therefore, we will reject the value n = 25

case (ii) n = 16
$a_{16} =a+15d = 20+15\times (-1)= 20-15=5$
Therefore, the number of rows in which 200 logs are arranged is equal to 5

Q20 In a potato race, a bucket is placed at the starting point, which is $\small 5$ m from the first potato, and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line (see Fig. $\small 5.6$ ).

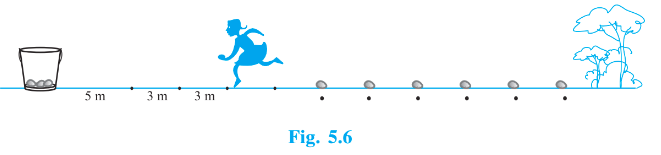
A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run?

[ Hint : To pick up the first potato and the second potato, the total distance (in metres) run by a competitor is $\small 2\times5+2\times (5+3)$ ]

Answer:

Distance travelled by the competitor in picking and dropping 1st potato $= 2 \times 5 = 10 \ m$

Distance travelled by the competitor in picking and dropping 2nd potato $= 2 \times (5+3) =2\times 8 = 16 \ m$

Distance travelled by the competitor in picking and dropping 3rd potato $= 2 \times (5+3+3) =2\times 11 = 22 \ m$

and so on
we can clearly see that it is an AP with first term (a) = 10 and common difference (d) = 6
There are 10 potatoes in the line
Therefore, total distance travelled by the competitor in picking and dropping potatoes is
$S_{10}= \frac{10}{2}\left \{ 2\times 10+(10-1)6 \right \}$
$S_{10}= 5\left ( 20+54 \right )$
$S_{10}= 5\times 74 = 370$

Therefore, the total distance travelled by the competitor in picking and dropping potatoes is 370 m

NCERT solutions for class 10 maths chapter 5 Arithmetic Progressions Excercise: 5.4

Q1 Which term of the AP: is its first negative term? [ Hint : Find $n$ for $a_n<0$ ]

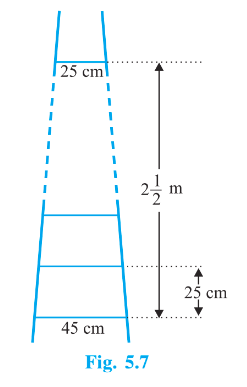
Answer:

Given AP is
$\small 121,117,113,...,$
Here $a = 121 \ and \ d = -4$
Let suppose nth term of the AP is first negative term
Then,
$a_n = a+ (n-1)d$
If nth term is negative then $a_n < 0$
$\Rightarrow 121+(n-1)(-4) < 0$
$\Rightarrow 125<4n$
$\Rightarrow n > \frac{125}{4}=31.25$
Therefore, first negative term must be 32nd term

Q2 The sum of the third and the seventh terms of an AP is $\small 6$ and their product is $\small 8$ . Find the sum of first sixteen terms of the AP.

Answer:

It is given that sum of third and seventh terms of an AP are and their product is $\small 8$
$a_3= a+ 2d$
$a_7= a+ 6d$
Now,
$a_3+a_7= a+ 2d+a+6d= 6$
$\Rightarrow 2a+8d = 6$
$\Rightarrow a+4d = 3 \Rightarrow a = 3-4d \ \ \ \ \ \ \ \ \ \ \ \ -(i)$
And
$a_3.a_7 = (a+2d).(a+6d)=a^2+8ad +12d^2 = 8 \ \ \ \ \ \ \ -(ii)$
put value from equation (i) in (ii) we will get
$\Rightarrow (3-4d)^2+8(3-4d)d+12d^2= 8$
$\Rightarrow 9+16d^2-24d+24d-32d^2+12d^2=8$
$\Rightarrow 4d^2 = 1$
$\Rightarrow d = \pm \frac{1}{2}$
Now,
case (i) $d = \frac{1}{2}$

$a= 3 - 4 \times \frac{1}{2} = 1$
Then,
$S_{16}=\frac{16}{2}\left \{ 2\times 1+(16-1)\frac{1}{2} \right \}$

$S_{16}=76$

case (ii) $d = -\frac{1}{2}$
$a= 3 - 4 \times \left ( -\frac{1}{2} \right ) = 5$
Then,
$S_{16}=\frac{16}{2}\left \{ 2\times 1+(16-1)\left ( -\frac{1}{2} \right ) \right \}$

$S_{16}=20$

Q3 A ladder has rungs $\small 25$ cm apart. (see Fig. $\small 5.7$ ). The rungs decrease uniformly in length from $\small 45$ cm at the bottom to $\small 25$ cm at the top. If the top and the bottom rungs are $\small 2\frac{1}{2}$ m apart, what is the length of the wood required for the rungs? [ Hint: Number of rungs $=\frac{250}{25}+1]$

1635921645173

Answer:

It is given that
The total distance between the top and bottom rung $= 2\frac{1}{2}\ m = 250cm$
Distance between any two rungs = 25 cm
Total number of rungs = $\frac{250}{25}+1= 11$
And it is also given that bottom-most rungs is of 45 cm length and topmost is of 25 cm length.As it is given that the length of rungs decrease uniformly, it will form an AP with $a = 25 , a_{11} = 45 \ and \ n = 11$
Now, we know that
$a_{11}= a+ 10d$

$\Rightarrow 45=25+10d$
$\Rightarrow d = 2$
Now, total length of the wood required for the rungs is equal to
$S_{11} = \frac{11}{2}\left \{ 2\times 25+(11-1)2 \right \}$
$S_{11} = \frac{11}{2}\left \{ 50+20 \right \}$
$S_{11} = \frac{11}{2}\times 70$
$S_{11} =385 \ cm$
Therefore, the total length of the wood required for the rungs is equal to 385 cm

Q4 The houses of a row are numbered consecutively from $\small 1$ to $\small 49$ . Show that there is a value of $\small x$ such that the sum of the numbers of the houses preceding the house numbered $\small x$ is equal to the sum of the numbers of the houses following it. Find this value of $\small x$ . [ Hint : $\small S_{x-1}=S_4_9-S_x$ ]

Answer:

It is given that the sum of the numbers of the houses preceding the house numbered $\small x$ is equal to the sum of the numbers of the houses following it
And 1,2,3,.....,49 form an AP with a = 1 and d = 1
Now, we know that
$S_n= \frac{n}{2}\left \{ 2a+(n-1)d \right \}$
Suppose their exist an n term such that ( n < 49)
Now, according to given conditions
Sum of first n - 1 terms of AP = Sum of terms following the nth term
Sum of first n - 1 term of AP = Sum of whole AP - Sum of first m terms of AP
i.e.
$S_{n-1}=S_{49}-S_n$

$\frac{n-1}{2}\left \{ 2a+((n-1)-1)d \right \}=\frac{49}{2}\left \{ 2a+(49-1)d \right \}-\frac{n}{2}\left \{ 2a+(n-1)d \right \}$

$\frac{n-1}{2}\left \{ 2+(n-2) \right \}=\frac{49}{2}\left \{ 2+48 \right \}-\frac{n}{2}\left \{ 2+(n-1) \right \}$

$\frac{n-1}{2}\left \{ n\right \}=\frac{49}{2}\left \{ 50 \right \}-\frac{n}{2}\left \{ n+1 \right \}$

$\frac{n^2}{2}-\frac{n}{2}=1225-\frac{n^2}{2}-\frac{n}{2}$

$n^2 = 1225$
$n = \pm 35$

Given House number are not negative so we reject n = -35

Therefore, the sum of no of houses preceding the house no 35 is equal to the sum of no of houses following the house no 35

Q5 A small terrace at a football ground comprises of $\small 15$ steps each of which is $\small 50$ m long and built of solid concrete. Each step has a rise of $\small \frac{1}{4}\: m$ and a tread of $\small \frac{1}{2}\: m$ . (see Fig. $\small 5.8$ ). Calculate the total volume of concrete required to build the terrace.
[ Hint: Volume of concrete required to build the first step $\small =\frac{1}{4}\times \frac{1}{2}\times 50\: m^3$ ]

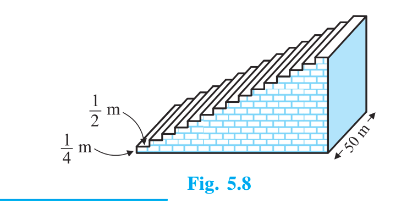
1635921665136

Answer:

It is given that
football ground comprises of $\small 15$ steps each of which is $\small 50$ m long and Each step has a rise of $\small \frac{1}{4}\: m$ and a tread of $\small \frac{1}{2}\: m$
Now,
The volume required to make the first step = $\frac{1}{4}\times \frac{1}{2}\times 50 = 6.25 \ m^3$

Similarly,

The volume required to make 2nd step = $\left ( \frac{1}{4}+\frac{1}{4}\right )\times \frac{1}{2}\times 50=\frac{1}{2}\times \frac{1}{2}\times 50 = 12.5 \ m^3$
And
The volume required to make 3rd step = $\left ( \frac{1}{4}+\frac{1}{4}+\frac{1}{4}\right )\times \frac{1}{2}\times 50=\frac{3}{4}\times \frac{1}{2}\times 50 = 18.75 \ m^3$

And so on
We can clearly see that this is an AP with $a= 6.25 \ and \ d = 6.25$
Now, the total volume of concrete required to build the terrace of 15 such step is
$S_{15} =\frac{15}{2}\left \{ 2 \times 6.25 +(15-1)6.25 \right \}$
$S_{15} =\frac{15}{2}\left \{ 12.5 +87.5\right \}$
$S_{15} =\frac{15}{2}\times 100$
$S_{15} =15\times 50 = 750$
Therefore, the total volume of concrete required to build the terrace of 15 such steps is $750 \ m^3$

Arithmetic Progression Class 10 Maths chapter 5 - Topics

Checking whether the series is an arithmetic progression or not.
To find the nth term or last term or an arithmetic progression.
Questions based on the sum of an arithmetic progression
Use of linear equation concept in an arithmetic progression
Application of nth term and sum formula

NCERT Class 10 Arithmetic Progression Exercise-Wise Solutions

Features of NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions

The NCERT solutions cover all the questions given in the exercise and in between the chapters. This makes it really helpful in homework as well as in the board exam preparations.
The Arithmetic Progression Class 10 Maths Chapter 5 NCERT solutions offer a step by step description of the solutions.
These NCERT solutions for Class 10 Maths ch 5 Arithmetic Progressions is given in a simple language and are easy to understand.
For NCERT Solutions for Class 10 Maths Chapter 5 PDF download, you can save the webpage of this article.

NCERT Books and NCERT Syllabus

NCERT Solutions for Class 10 Maths - Chapters Wise

Chapter No.	Chapter Name
Chapter 1	Real Numbers
Chapter 2	Polynomials
Chapter 3	Pair of Linear Equations in Two Variables
Chapter 4	Quadratic Equations
Chapter 5	Arithmetic Progressions
Chapter 6	Triangles
Chapter 7	Coordinate Geometry
Chapter 8	Introduction to Trigonometry
Chapter 9	Applications of Trigonometry
Chapter 10	Circles
Chapter 11	Constructions
Chapter 12	Areas Related to Circles
Chapter 13	Surface Areas and Volumes
Chapter 14	Statistics
Chapter 15	Probability

NCERT Solutions of Class 10 - Subject Wise

NCERT Exemplar solutions - Subject Wise

How to use NCERT solutions for class 10 maths chapter 5 Arithmetic Progressions?

Before practising the NCERT chapter 5 Maths Class 10 solutions, go through the conceptual theory given in the NCERT textbook.
After going through the conceptual part, jump on to practice exercises available.
While solving the exercises if you are facing problems in any specific question, then take the help of NCERT solutions for Class 10 Maths chapter 5 Arithmetic Progressions.
Once you have done the practice exercises you can move to previous year questions.

Frequently Asked Questions (FAQs)

1. What are the important topics of NCERT class 10 maths chapter 5 arithmetic progressions?

Checking whether the series is an arithmetic progression or not, nth term or last term of arithmetic progression, sum of an arithmetic progression, use of linear equation concept in an arithmetic progression and application of nth term and sum of a.p. formulae are the important topics in this chapter.

2. What kind of questions are there in NCERT solutions for class 10 chapter 5 maths?

The NCERT Solutions for Class 10 Maths Chapter 5 includes a range of question types such as multiple choice, long and short answer, fill in the blank, and real-world examples. These questions aim to enhance students' problem-solving and time management abilities, thus preparing them for success in their CBSE exams.

3. How many exercises are there in maths chapter 5 class 10?

The number of exercises in Maths Chapter 5 for Class 10 are four. These are very important because these include all types of questions on which repeatedly questions are being asked in board exams. Students can practice and find solutions at careers360 official website

4. Do I need to practice all questions given in NCERT class 10 maths chapter 5 solutions?

It is generally a good idea to practice all of the questions provided in the NCERT solutions for class 10 maths arithmetic progression, as they are designed to cover the key concepts and skills that are important for understanding the chapter and doing well in your exams. By practicing all the questions and arithmetic progression solutions, you will be able to identify your strengths and weaknesses and work on them accordingly. Also, chapter 5 questions and ap solutions class 10 help you build your problem-solving skills, time management skills and confidence, which will be beneficial for you in your exams. Students can also use arithmetic progression class 10 pdf as to study offline.

5. Why should I practice NCERT maths class 10 chapter 5 solutions?

There are several reasons why you should practice the class 10 maths NCERT solution arithmetic progression. Practising the NCERT Solutions for Class 10 Maths Chapter 5 is a valuable step in your studies as it will help you to understand the concepts, improve your problem-solving skills, and prepare for your exams. Students can use NCERT solutions for class 10 maths arithmetic progression pdf to study comfortable this chapter.

6. What is the arithmetic progression in class 10 chapter 5 maths?

Arithmetic Progression (AP) is a sequence of numbers in which the difference between any two consecutive terms is always the same. In other words, it is a sequence of numbers in which the difference between two consecutive terms is a constant. Arithmetic progression class 10 NCERT solutions pdf covers various concepts related to arithmetic progressions such as finding the common difference, the nth term, the sum of an arithmetic series, and solving word problems using arithmetic progressions.

Also Read

The Human Eye and The Colorful world Class 10th Notes- Free NCERT Class 10 Science Chapter 11 Notes - Download PDF

NCERT Class 10 Science Chapter 14 Notes Sources Of Energy - Download PDF

Magnetic Effects of Electric Current Class 10th Notes - Free NCERT Class 10 Science Chapter 13 Notes - Download PDF

Electricity Class 10th Notes - Free NCERT Class 10 Science Chapter 12 Notes - Download PDF

Light- Reflection and Refraction Class 10th Notes- Free NCERT Class 10 Science Chapter 10 Notes - Download PDF

Free NCERT Class 10 Maths Chapter 2 Notes - Download PDF

NCERT Syllabus for Class 10 Maths 2024-25 - Download Free PDF

NCERT Solutions for Exercise 12.3 Class 10 Maths Chapter 12 - Areas related to circles

NCERT Solutions for Exercise 12.2 Class 10 Maths Chapter 12 - Areas related to circles

NCERT Solutions for Exercise 12.1 Class 10 Maths Chapter 12 - Areas related to circles

NCERT Solutions for Class 10 Science Chapter 6 Life Processes

NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations

NCERT Exemplar Class 10 Maths Solutions - Chapter Wise Problems with Solutions

NCERT Exemplar Class 10 Science Solutions Chapter 1 Chemical Reactions and Equations

NCERT Exemplar Class 10 Science Solutions - Chapter Wise Problems with Solutions

Articles

Maharashtra State Board 10th Geography Books - Download PDF Free Online

Nov 21, 2024

NMMS Karnataka Result 2024-25: Download DSERT Karnataka Merit List Here

Nov 21, 2024

NMMS Karnataka 2024-25: Exam Date (8 Dec), Admit Card, Answer Key, Cut off, Result

Nov 21, 2024

Maharashtra Board Grading System 2025: SSC & HSC Passing Marks & Important Updates

Nov 21, 2024

10th Time Table 2025 - Check CBSE (OUT) UP, Bihar 10th Exam Dates Here

Nov 21, 2024

CBSE Class 10 Exam Analysis 2025 All Subject: English, Science, Maths Paper Analysis Here

Nov 21, 2024

CBSE Class 10 Marking Scheme 2025: Check CBSE 10th Subject-Wise Marking Scheme Here Keywords: marking scheme

Nov 21, 2024

CBSE Class 10 Percentage Calculation 2025, How to Calculate Percentage of Marks

Nov 21, 2024

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:04 October,2024 - 29 November,2024

Application Process

Exam Pattern

Admit Card

National Institute of Open Schooling 10th examination

Admit Card Date:04 October,2024 - 29 November,2024

Application Process

Exam Pattern

Mock Test

Mizoram Board of School Education 12th Examination

Application Date:07 October,2024 - 22 November,2024

Exam Pattern

Result

Mock Test

Mizoram Board 10th Examination

Application Date:07 October,2024 - 22 November,2024

Exam Pattern

Admit Card

Result

Punjab Board of Secondary Education 10th Examination

Application Correction Date:08 October,2024 - 27 November,2024

Exam Pattern

Result

Admit Card

View All School Exams

Certifications By Top Providers

Full-Stack Web Development

Via Masai School

Digital Banking Business Model

Via State Bank of India

Business Analytics Foundations

Via PW Skills

Master Data Management for Beginners

Via TCS iON Digital Learning Hub

Data Analytics Basics for Everyone

Via IBM

Banking 101 A Guide for Beginners in the Banking Sector

Via EduBridge

1113 courses

812 courses

394 courses

295 courses

Harvard University, Cambridge

98 courses

IBM

83 courses

IT & Software

Teaching and Academics

Programming and Development

Health, Fitness and Medicine

Business and Management

Engineering and Architecture

General Management

Financial Management

Environmental Studies

History

Artificial Intelligence

Psychology

Explore Top Universities Across Globe

University of Essex, Colchester

Wivenhoe Park Colchester CO4 3SQ

University College London, London

Gower Street, London, WC1E 6BT

The University of Edinburgh, Edinburgh

Old College, South Bridge, Edinburgh, Post Code EH8 9YL

University of Bristol, Bristol

Beacon House, Queens Road, Bristol, BS8 1QU

University of Delaware, Newark

Newark, DE 19716

University of Nottingham, Nottingham

University Park, Nottingham NG7 2RD

PR in UK After Study for International and Indian Students 2025

9 min ⋆ Nov 14, 2024 13:11 PM IST

Duolingo English Test Accepting Universities and Countries in 2025-26

12 min ⋆ Nov 14, 2024 13:11 PM IST

Top MBA Colleges in Dubai 2025 (with Tuition fees): List of Best Colleges

11 min ⋆ Nov 14, 2024 13:11 PM IST

Cheapest Universities in Germany for International Students 2025-26

15 min ⋆ Nov 14, 2024 13:11 PM IST

Cheapest Universities in Melbourne 2025: Discover Affordable Education

7 min ⋆ Nov 14, 2024 13:11 PM IST

Top Courses to Study in USA for Indian and International Students 2025

11 min ⋆ Nov 14, 2024 13:11 PM IST

Related E-books & Sample Papers

CBSE Class 10 Social Science Sample Paper with Solution 2024-25 PDF

395+ Downloads

CBSE Class 10 Mathematics (Standard) Sample Paper with Solution 2024-25 PDF

257+ Downloads

CBSE Class 10 Mathematics (Basic) Sample Paper with Solution 2024-25 PDF

114+ Downloads

CBSE Class 10 Hindi B Sample Paper with Solution 2024-25 PDF

39+ Downloads

CBSE Class 10 Hindi A Sample Paper with Solution 2024-25 PDF

27+ Downloads

CBSE Class 10 English (Language & Literature) Sample Paper with Solution 2024-25 PDF

45+ Downloads

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?

sadhu ashram ramgart road aligarh

If you're looking for directions or steps to reach Sadhu Ashram on Ramgart Road in Aligarh, here’s how you can get there:

Steps to Reach Sadhu Ashram, Ramgart Road, Aligarh:

Starting Point:
- Determine your starting point in Aligarh or the nearby area.
Use Google Maps:
- Open Google Maps on your phone or computer.
- Enter "Sadhu Ashram, Ramgart Road, Aligarh" as your destination.
- Follow the navigation instructions provided by Google Maps.
By Local Transport:
- Auto-rickshaw/Taxi: Hire an auto-rickshaw or taxi and inform the driver about your destination. Most local drivers should be familiar with Sadhu Ashram.
- Bus: Check if there are any local buses that operate on Ramgart Road. Ask the bus conductor if the bus stops near Sadhu Ashram.
Landmarks to Look For:
- As you approach Ramgart Road, look for local landmarks that might help you confirm you’re on the right path, such as known shops, temples, or schools nearby.
Ask for Directions:
- If you're unsure, ask locals for directions to Sadhu Ashram on Ramgart Road. It's a known location in the area.
Final Destination:
- Once you reach Ramgart Road, Sadhu Ashram should be easy to spot. Look for any signage or ask nearby people to guide you to the exact location.

If you need detailed directions from a specific location or more information about Sadhu Ashram, feel free to ask

Read Complete Answer

sai raja 01 September,2024

show the previous year exams ?

Hello Aspirant, Hope your doing great, your question was incomplete and regarding what exam your asking.

Read Complete Answer

SWETCHCHA MISKA 10 July,2024

as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer

Manasvini Gupta 23 July,2024

i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer

Ashvadha 03 July,2024

i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer

sadafreen356 03 July,2024

View All

Stay up-to date with CBSE Class 10th News

Download Careers360 App

All this at the convenience of your phone

Regular Exam Updates
Best College Recommendations
College & Rank predictors
Detailed Books and Sample Papers
Question and Answers

Scan and download the app

Central Board of Secondary Education Class 10th Examination

Applications Open

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9