NCERT Solutions for Class 10 Maths Chapter 12 Surface Areas and Volumes

NCERT Solutions for Class 10 Maths Chapter 12 Surface Areas and Volumes: Download PDF

The NCERT Solutions for Class 10 Maths Chapter 12 have been prepared by Careers360 experts to make learning simpler and to help you score better in exams. A downloadable PDF is available — click the link below to access it.

Download PDF

NCERT Solutions for Class 10 Maths Chapter 12 Surface Areas and Volumes (Exercise)

NCERT Class 10 Maths Chapter 12 Surface Areas and Volumes question answers with detailed explanations are provided below.

Q1. 2 cubes each of volume 64 cm³ are joined end to end. Find the surface area of the resulting cuboid.

Answer:

We are given that the volume of the cube $=\ 64\ cm^3$

Also, the volume of a cube is given by $=\ a^3$ ( here $a$ is the edge of the cube)

Thus : $a^3\ =\ 64$

$a\ =\ 4\ cm$

Now, according to the question, we have combined the two cubes.
The edge lengths of the formed cuboid are 4 cm, 4 cm, and 8 cm.

The surface area of a cuboid is : $=\ 2\left ( lb\ +\ bh\ +\ hl \right )$
$=\ 2\left ( 8\times 4\ +4\times 4\ +\ 4\times 8 \right )$
$=\ 2\left ( 80 \right )$
$=\ 160\ cm^2$

Thus, the area of the formed cuboid is 160 cm².

Q2. A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm, and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.

Answer:

Since the vessel consists of a hemisphere and a cylinder, its area is given by :

Area of vessel = Inner area of the cylinder(curved) + Inner area of the hemisphere

The inner surface area of the hemisphere $=\ 2\pi r^2$
$=\ 2\times \left ( \frac{22}{7} \right ) \times 7^2$
$=\ 308\ cm^2$

The surface area of the cylinder $=\ 2\pi rh$
$=\ 2\times \frac{22}{7}\times 7\times 6$
$=\ 264\ cm^2$

Thus, the inner surface area of the vessel is $= 308 + 264 = 572 \:cm^2.$

Q3. A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of the same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.

Answer:

The required surface area of the toy is given by :

Area of the toy = Surface area of the hemisphere + Surface area of the cone

Firstly, consider the hemisphere :

The surface area of a hemisphere $=\ 2 \pi r^2$
$=\ 2 \times \frac{22}{7}\times \left ( 3.5 \right )^2$
$=\ 77\ cm^2$

Now for cone, we have :

The surface area of a cone $=\ \pi rl$

Thus, we need to calculate the slant of the cone.

We know that :

$l^2\ =\ h^2\ +\ r^2$
$=\ 12^2\ +\ 3.5^2$
$=\ \frac{625}{4}$
$l\ =\ \frac{25}{2}\ =\ 12.5\ cm$

Thus, the surface area of a cone $=\ \pi rl$
$=\ \frac{22}{7}\times 3.5\times 12.5$
$=\ 137.5\ cm^2$

Hence, the total surface area of the toy $=\ 77\ +\ 137.5\ =\ 214.5\ cm^2.$

Q4. A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.

Answer:

It is given that the hemisphere is mounted on the cuboid; thus, the hemisphere can take on complete as its diameter (which is maximum).

Thus, the greatest diameter of the hemisphere is 7 cm.

Now, the total surface area of the solid = Surface area of the cube + Surface area of the hemisphere - Area of the base of a hemisphere (as this is counted on one side of the cube)

The surface area of the cube $=\ 6a^3$
$=\ 6\times 7^3\ =\ 294\ cm^2$

Now, the area of a hemisphere $=\ 2\pi r^2$
$=\ 2\times \frac{22}{7}\times \left ( \frac{7}{2} \right )^2\ =\ 77\ cm^2$

The area of the base of a hemisphere $=\ \pi r^2\ =\ \frac{22}{7}\times \left ( \frac{7}{2} \right )^2\ =\ 38.5\ cm^2$

Hence, the surface area of the solid is $= 294 + 77 - 38.5 = 332.5 \:cm^2$.

Q5. A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.

Answer:

It is given that the diameter of the hemisphere is equal to the edge length of the cube.

The total surface area of the solid is given by :

The surface area of a solid = Surface area of the cube + Surface area of the hemisphere - Area of the base of the hemisphere

The surface area of the cube $=\ 6l^2$

The surface area of the hemisphere:

$=\ 2\pi r^2\ =\ 2\pi \left ( \frac{l}{2} \right )^2$

Area of the base of the hemisphere:

$=\ \pi r^2\ =\ \pi \left ( \frac{l}{2} \right )^2$

Thus, the area of the solid is:

$=\ 6l^2\ +\ \pi \left ( \frac{l}{2} \right )^2\ unit^2.$

Q6. A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see Fig.). The length of the entire capsule is 14 mm, and the diameter of the capsule is 5 mm. Find its surface area.

Answer:

It is clear from the figure that the capsule has a hemisphere and cylinder structure.

The surface area of the capsule = 2 (Area of the hemisphere) + Area of the cylindrical part

Area of hemisphere $=\ 2\pi r^2$
$=\ 2\pi\times \left ( \frac{5}{2} \right )^2$
$=\ \frac{25}{2} \pi\ mm^2$

The area of the cylinder $=\ 2\pi rh$
$=\ 2\pi \times \frac{5}{2}\times 9$
$=\ 45 \pi\ mm^2$

Thus, the area of the solid $=\ 2\left ( \frac{25}{2} \right )\pi\ +\ 45 \pi$
$=\ 25\pi\ +\ 45 \pi$
$=\ 70 \pi$
$=\ 220\ mm^2.$

Q7. A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m, respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs 500 per m ². (Note that the base of the tent will not be covered with canvas.)

Answer:

The canvas will cover the cylindrical part as well as the conical part.

So, the area of the canvas = Area of the cylindrical part (curved) + Area of the conical part

Now, the area of the cylindrical part $=\ 2\pi rh$

$=\ 2\pi \times 2\times 2.1$

$=\ 8.4 \pi\ m^2$

The area of the cone is $=\ \pi rl$

$=\ \pi \times 2\times 2.8$

$=\ 5.6\pi\ m^2$

Thus, the area of the canvas $=\ 8.4\pi\ +\ 5.6\pi$

$=\ 14\pi\ =\ 44\ m^2$

Further, it is given that the rate of canvas per m² is Rs. 500.

Thus, the required money is $=500 \times 44=$ Rs. 22,000.

Q8. From a solid cylinder whose height is 2.4 cm and diameter is 1.4 cm, a conical cavity of the same height and diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm².

Answer:

Firstly, we need to calculate the slant height of the cone :

$l^2\ =\ r^2\ +\ h^2$

$=\ (0.7)^2\ +\ (2.4)^2$

or $l^2\ =\ 6.25$

or $l\ =\ 2.5\ cm$

Now, the total surface area of a solid can be calculated as :

The surface area of the solid = Surface area of the cylinder + Surface area of the cone + Area of the base of the cylinder

The surface area of the cylinder is $=\ 2 \pi rh$

$=\ 2 \pi \times 0.7\times 2.4$

$=\ 10.56\ cm^2$

Now, the surface area of a cone $=\ \pi rl$

$=\ \pi \times 0.7\times 2.5$

$=\ 5.50\ cm^2$

And the area of the base of the cylinder is $=\ \pi r^2$

$=\ \pi \times 0.7\times 0.7$

$=\ 1.54\ cm^2$

Thus, the required area of the solid = 10. 56 + 5.50 + 1.54 = 17.60 cm².

Thus, the total surface area of the remaining solid to the nearest cm² is 18 cm².

Q9. A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. 12.11. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the cylinder.

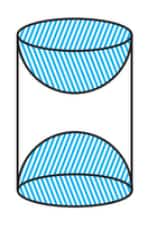
Answer:

The required surface area is given by :

The surface area of the article = Surface area of the cylindrical part + 2 (Surface area of the hemisphere)

Now, the area of the cylinder $=\ 2\pi rh$

$=\ 2\pi \times 3.5\times 10$

$=\ 70\pi \ cm^2$

The surface area of the hemisphere $=\ 2\pi r^2$

$=\ 2\pi \times 3.5\times 3.5$

$=\ 24.5\pi\ cm^2$

Thus the required area $=70 \pi +2\times 24.5 \pi = 374 cm^2.$

Q1. A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of $\pi$.

Answer:

The volume of the solid is given by :

The volume of the solid = Volume of the cone + Volume of a hemisphere

The volume of the cone $=\ \frac{1}{3} \pi r^2h$

$=\ \frac{1}{3} \pi \times 1^2\times 1$

$=\ \frac{\pi}{3}\ cm^3$

The volume of the hemisphere $=\ \frac{2}{3}\pi r^3$

$=\ \frac{2}{3}\pi \times 1^3$

$=\ \frac{2\pi}{3}\ cm^3$

Hence, the volume of so lithe d is :

$=\ \frac{\pi}{3}\ +\ \frac{2\pi}{3}\ =\ \pi\ cm^3.$

Q2. Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminum sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)

Answer:

The volume of air present = Volume of cylinder + 2 (Volume of a cone)

Now, the volume of a cylinder: $=\ \pi r^2h$

$=\ \pi \left ( \frac{3}{2} \right )^2\times 8$

$=\ 18\pi \ cm^3$

The volume of a cone is $=\ \frac{1}{3} \pi r^2h$

$=\ \frac{1}{3} \pi \times \left ( \frac{3}{2} \right )^2\times 2$

$=\ \frac{3}{2} \pi \ cm^3$

Thus, the volume of air is $=\ 18 \pi\ +\ 2\times \frac{3}{2} \pi \ =\ 21\pi$

$=\ 66\ cm^3$

Q3. A gulab jamun contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with a length of 5 cm and a diameter of 2.8 cm (see Fig).

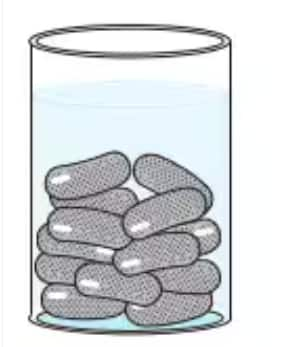
Answer:

It is clear from the figure that Gulab Jamun has one cylindrical part and two hemispherical parts.

Thus, the volume of the gulab jamun is = Volume of cylindrical part + 2 (Volume of the hemisphere )

Now, the volume of the cylinder is $=\ \pi r^2h$

$=\ \pi\times 1.4^2\times 2.2$

$=\ 13.55\ cm^3$

The volume of a hemisphere is :

$\\=\ \frac{2}{3}\pi r^3\\\\=\ \frac{2}{3}\times \pi \times (1.4)^3\\\\=\ 5.75\ cm^3$

Thus, the volume of 1 gulab jamun is $= 13.55 + 2 (5.75) = 25.05 cm^3.$

Hence, the volume of 45 gulab jamun $=\ 45(25.05)\ cm^3\ =\ 1127.25\ cm^3$

Further, it is given that one gulab jamun contains sugar syrup up to 30%.

So, the total volume of sugar present $=\ \frac{30}{100}\times 1127.25\ =\ 338\ cm^3.$

Q4. A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm, and the depth is 1.4 cm. Find the volume of wood in the entire stand (see Fig. 12.16).

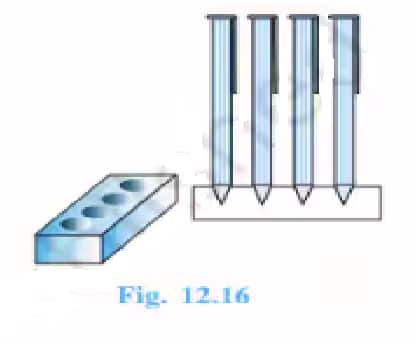
Answer:

The volume of wood is given by = volume of the cuboid - the volume of four cones.

Firstly, the volume of the cuboid $=\ lbh$

$=\ 15\times 10\times 3.5$

$=\ 525\ cm^3$

And the volume of the cone $=\frac13 \pi r^2h=\frac13 \pi \times 0.5^2 \times 1.4= 0.3665 \ cm^3$

Thus, the volume of wood is $= 525 - 4 (0.3665) = 523.53 \:cm^3.$

Q5. A vessel is in the form of an inverted cone. Its height is 8 cm, and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm, are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.

Answer:

According to the question :

Water spilt from the container = Volume of lead balls.

Let us assume the number of lead balls to be n.

Thus, the equation becomes :

$\frac{1}{4}\times Volume_{cone}\ =\ n\times \frac{4}{3} \pi r^3$

or $\frac{1}{4}\times \frac{1}{3}\pi\times5^2\times 8\ =\ n\times \frac{4}{3} \pi\times 0.5^3$

or $n\ =\ \frac{25\times 8}{16\times \left ( \frac{1}{2} \right )^3}$

or $n\ =\ 100$

Hence, the number of lead shots dropped is 100.

Q6. A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm³ of iron has approximately 8g mass. (Use $\pi = 3.14$ )

Answer:

The pole can be divided into one large cylinder and one small cylinder.

Thus, the volume of the pole = volume of a large cylinder + volume of a small cylinder

$=\ \pi r_l^2h_l\ +\ \pi r_s^2h_s$

$=\ \pi \times 12^2\times 220\ +\ \pi \times 8^2\times 60$

$=\ \pi \times \left ( 144\times 220\ +\ 64\times 60 \right )$

$=\ 3.14\times 35520$

$=\ 111532.5\ cm^3$

Now, according to the question, the mass of the pole is :

$=\ 8\times 111532.5$

$=\ 892262.4\ g\ =\ 892.262\ Kg.$

Q7. A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.

Answer:

It is clear from the question that the required volume is :

The volume of water (left) =Volume of a cylinder - Volume of a solid

Now the volume of the cylinder is $=\ \pi r^2h$

or $=\ \pi\times (60)^2\times 180\ cm^3$

The volume of the solid is :

$\\=\ \frac{1}{3} \pi r^2h\ +\ \frac{2}{3}\pi r^3\\\\=\ \frac{1}{3} \times \pi \times (60)^2\times 120\ +\ \frac{2}{3}\times \pi \times (60)^3\\\\=\ \pi (60)^2\times 80\ cm^3$

Thus, the volume of water left :

$\\=\ \pi (60)^2\times 180\ -\ \pi (60)^2\times 80\\\\=\ \pi (60)^2\times 100\\\\=\ 1131428.57\ cm^3\\\\=\ 1.131\ m^3.$

Q8. A spherical glass vessel has a cylindrical neck 8 cm long, and 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm 3. Check whether she is correct, taking the above as the inside measurements, and $\pi = 3.14$

Answer:

The volume of the vessel is given by :

The volume of the vessel = Volume of the sphere + Volume of the cylindrical part

Now, the volume of the sphere is :

$\\=\ \frac{4}{3}\pi r^3\\\\=\ \frac{4}{3}\pi \left ( \frac{8.5}{2} \right )^3\\\\=\ 321.55\ cm^3$

The volume of the cylinder is:-

$\\=\ \pi r^2h\\\\=\ \pi \times (1)^2\times 8\\\\=\ 25.13\ cm^3$

Thus, the volume of the vessel is $= 321.55 + 25.13 = 346.68\: cm^3.$

Surface Areas and Volumes Class 10 NCERT Solutions: Exercise-wise

Exercise-wise NCERT Solutions of Surface Areas and Volumes Class 10 Maths Chapter 12 are provided in the links below.

• Class 10 Maths NCERT Chapter 12 Exercise 12.1
• Class 10 Maths NCERT Chapter 12 Exercise 12.2

Class 10 Maths NCERT Chapter 12: Extra Question

Question:

A cylinder of height 8 cm and radius 6 cm is melted and converted into three cones of the same radius and height as the cylinder. Determine the total curved surface area of cones.

Answer:

The radius ($r$) of each cone = radius of the cylinder = 6 cm
The height ($h$) of each cone = height of the cylinder = 8 cm
The curved surface area of a cone, where $l$ is the slant height of the cone $= \pi r l$
Now, $l = \sqrt{r^2 + h^2}= \sqrt{(6)^2 + (8)^2} = 10 \text{ cm}$
The curved surface area of a cone, where $l$ is the slant height of the cone $= \pi r l$
So, the curved surface area of each cone,
$= \pi (6) (10) = 60\pi \text{ cm}^2$
Since there are 3 cones, the total curved surface area,
$= 3 \times 60\pi = 180\pi \text{ cm}^2$
Hence, the correct answer is $180\pi \text{ cm}^2$.

Surface Areas And Volumes Class 10 Solutions: Important Formulae

Total Surface Area (TSA)

Total Surface Area, denoted as TSA, signifies the entire expanse covered by an object's surface. This encompasses the collective area of all its external facets. Here are some prominent geometrical figures and their corresponding TSA formulas.

• Cuboid: TSA = 2[(l x b) + (b x h) + (h x l)], { where, l = length, b = breadth, h = height }.

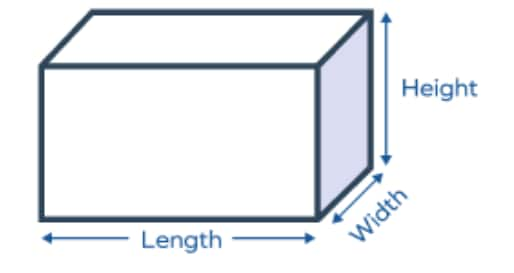
• Cube: TSA = 6a² , { where, a = length of the sides of a square }

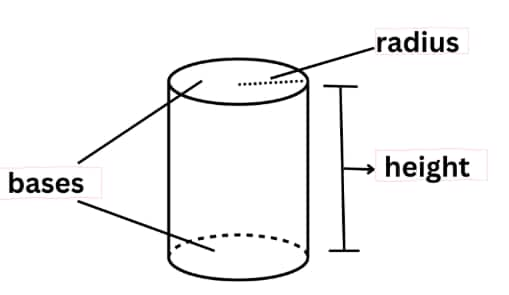
• Right Circular Cylinder: TSA = 2πr(h + r), { where, h = height of the cylinder, r = radius of the circular part }

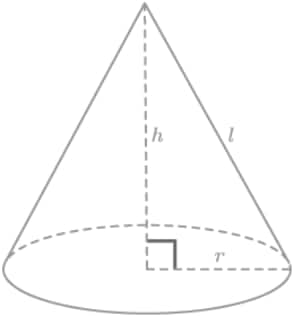
• Right Circular Cone: TSA = πr(l + r), { where, l = Slant height of the cone, r = radius of the circular part }

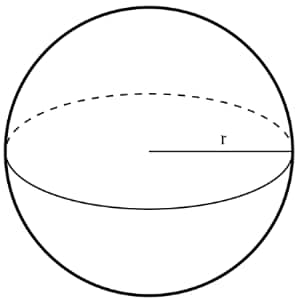
• Sphere: TSA = 4πr² , { where, r = radius of the sphere }

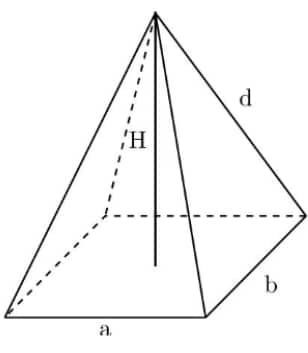
• Right Pyramid: TSA = LSA (Lateral Surface Area) + Area of the base

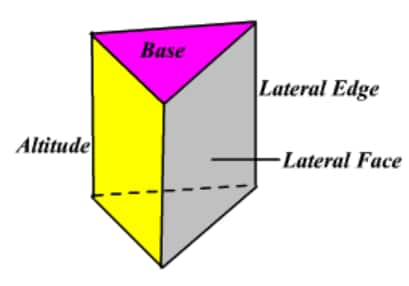
• Prism: TSA = LSA (Lateral Surface Area) × 2B (Area of the base)

• Hemisphere: TSA = 3 × π × r² , { where, r = radius of the circular part }

Lateral/Curved Surface Area (LSA/CSA)

The concept of Curved Surface Area (CSA) or Lateral Surface Area (LSA) comes into focus, particularly in forms such as cylinders, cones, and pyramids. CSA represents the area of the curved component or sides, excluding the top and bottom facets. LSA, on the other hand, pertains to the lateral area of various shapes. The following are some key examples of these surface area measures:

• Cuboid: CSA = 2h(l + b), { where, l = length, b = breadth, h = height }.
• Cube: CSA = 4a² , { where, a = length of the sides of a square }
• Right Circular Cylinder: CSA = 2πrh, { where, h = height of the cylinder, r = radius of the circular part }
• Right Circular Cone: CSA = πrl, { where, l = Slant height of the cone, r = radius of the circular part }
• Right Pyramid: LSA = $\frac12$× p × d, { where, p = base perimeter, d = slant height}
• Prism: LSA = p × h, { where, p = base perimeter, h = height}
• Hemisphere: LSA = 2 × π × r², { where, r = radius of the circular part }

Volume

Volume emerges as a fundamental attribute, denoting the spatial extent occupied by an object or substance, quantified in cubic units. The following volume formulas unravel the essence of these geometric measurements:

• Cuboid: Volume = lbh, { where, l = length, b = breadth, h = height }
• Cube: Volume = a³, { where, a = length of the sides of a square }
• Right Circular Cylinder: Volume = πr²h, { where, h = height of the cylinder, r = radius of the circular part}
• Right Circular Cone: Volume = $\frac13$πr²h, { where, h = height of the cylinder, r = radius of the circular part }
• Sphere: Volume = $\frac43$πr³, { where, r = radius of the sphere }
• Right Pyramid: Volume = $\frac13$ × Area of the base × h, { where, h = height }
• Prism: Volume = B (Area of the base) × h, { where, h = height }
• Hemisphere: Volume = $\frac23$× (πr³), { where, r = radius of the sphere

Surface Areas and Volumes Class 10 Chapter 12: Topics

Topics you will learn in NCERT Class 10 Maths Chapter 12 Surface Areas and Volumes include:

• 12.1 Introduction
• 12.2 Surface Area of a Combination of Solids
• 12.3 Volume of a Combination of Solids

NCERT Solutions for Class 10 Maths: Chapter Wise

Access all NCERT Class 10 Maths solutions from one place using the links below.

Also, read,

• NCERT Exemplar Class 10 Maths Solutions Surface Areas and Volumes
• NCERT Notes Class 10 Maths Surface Areas and Volumes

NCERT Exemplar Solutions - Subject Wise

Given below are the subject-wise exemplar solutions of class 10 NCERT:

• NCERT Exemplar Solutions Class 10th Maths
• NCERT Exemplar Solutions Class 10th Science

NCERT Books and NCERT Syllabus

Here are some useful links for NCERT books and the NCERT syllabus for class 10:

• NCERT Books Class 10 Maths
• NCERT Books Class 10
• NCERT Books for Class 10 Science
• NCERT Syllabus Class 10
• NCERT Books for Class 10 English
• NCERT Syllabus Class 10 Maths