• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Exercise 13.1 Class 10 Maths Chapter 13 - Surface Area and Volumes

NCERT Solutions for Exercise 13.1 Class 10 Maths Chapter 13 - Surface Area and Volumes

Edited By Ramraj Saini | Updated on Nov 27, 2023 05:35 PM IST | #CBSE Class 10th
Upcoming Event
CBSE Class 10th  Exam Date : 01 Jan' 2025 - 14 Feb' 2025

NCERT Solutions For Class 10 Maths Chapter 13 Exercise 13.1

NCERT Solutions for Exercise 13.1 Class 10 Maths Chapter 13 Surface Area and Volumes are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Class 10 Maths ex 13.1 presents us with the surface area of combination of Solids. Some solids, such as the cuboid, cone, cylinder, and sphere, are recognisable to you from Class IX. You've also learned how to calculate their volumes and surface areas. In our daily lives, we come across a variety of solids that are made up of two or more of the fundamental solids.

This Story also Contains
  1. NCERT Solutions For Class 10 Maths Chapter 13 Exercise 13.1
  2. Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 13 exercise 13.1
  3. Assess NCERT Solutions for Class 10 Maths chapter 13 exercise 13.1
  4. Some More Information About NCERT Solutions for Class 10 Maths Exercise 13.1
  5. Benefits of NCERT Solutions for Class 10 Maths Exercise 13.1
  6. Key Features For Class 10 Maths Chapter 13 Exercise 13.1
  7. NCERT Solutions Subject Wise
NCERT Solutions for Exercise 13.1 Class 10 Maths Chapter 13 - Surface Area and Volumes
NCERT Solutions for Exercise 13.1 Class 10 Maths Chapter 13 - Surface Area and Volumes

In exercise 13.1 Class 10 Maths we have to find the surface area of the combined solids .Some of these solids are cylinders with both sides hemisphere , cone with hemisphere on top. Surface area can be categorized into two types of surface areas, the curved surface area and total surface area. 10th class Maths exercise 13.1 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.

Pearson | PTE

Trusted by 3,500+ universities and colleges globally | Accepted for migration visa applications to AUS, CAN, New Zealand , and the UK

Apply

Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 13 exercise 13.1

Download PDF

Assess NCERT Solutions for Class 10 Maths chapter 13 exercise 13.1

Surface Areas and Volumes Class 10 Maths Chapter 13 Exercise: 13.1

Q1 2 cubes each of volume 64 cm 3 are joined end to end. Find the surface area of the resulting cuboid.

Answer:

We are given that volume of the cube =\ 64\ cm^3

Also, the volume of a cube is given by =\ a^3 ( here a is the edge of the cube)

Thus : a^3\ =\ 64

a\ =\ 4\ cm

Now according to the question we have combined the two cubes that edge lengths of the formed cuboid are 4 cm, 4 cm, and 8 cm.

The surface area of a cuboid is : =\ 2\left ( lb\ +\ bh\ +\ hl \right )

or =\ 2\left ( 8\times 4\ +4\times 4\ +\ 4\times 8 \right )

or =\ 2\left ( 80 \right )

or =\ 160\ cm^2

Thus the area of the formed cuboid is 160 cm 2 .

Q2 A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.

Answer:

Since the vessel consists of hemisphere and cylinder, thus its area is given by :

Area of vessel = Inner area of the cylinder(curved) + Inner area of hemisphere

The inner surface area of the hemisphere is :

=\ 2\pi r^2

or =\ 2\times \left ( \frac{22}{7} \right ) \times 7^2

or =\ 308\ cm^2

And the surface area of the cylinder is :

=\ 2\pi rh

or =\ 2\times \frac{22}{7}\times 7\times 6

or =\ 264\ cm^2

Thus the inner surface area of the vessel is = 308 + 264 = 572 \:cm^2.

Q3 A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of the same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.

Answer:

The required surface area of the toy is given by :

Area of toy = Surface area of hemisphere + Surface area of the cone

Firstly consider the hemisphere :

The surface area of a hemisphere is =\ 2 \pi r^2

or =\ 2 \times \frac{22}{7}\times \left ( 3.5 \right )^2

or =\ 77\ cm^2

Now for cone we have :

The surface area of a cone =\ \pi rl

Thus we need to calculate the slant of the cone.

We know that :

l^2\ =\ h^2\ +\ r^2

or =\ 12^2\ +\ 3.5^2

or =\ \frac{625}{4}

or l\ =\ \frac{25}{2}\ =\ 12.5\ cm

Thus surface area of a cone =\ \pi rl

or =\ \frac{22}{7}\times 3.5\times 12.5

or =\ 137.5\ cm^2

Hence the total surface area of toy = =\ 77\ +\ 137.5\ =\ 214.5\ cm^2

Q4 A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.

Answer:

It is given that the hemisphere is mounted on the cuboid, thus the hemisphere can take on complete as its diameter (which is maximum).

Thus the greatest diameter of the hemisphere is 7 cm.

Now, the total surface area of solid = Surface area of cube + Surface area of the hemisphere - Area of the base of a hemisphere (as this is counted on one side of the cube)

The surface area of the cube is :

=\ 6a^3

=\ 6\times 7^3\ =\ 294\ cm^2

Now the area of a hemisphere is

=\ 2\pi r^2

=\ 2\times \frac{22}{7}\times \left ( \frac{7}{2} \right )^2\ =\ 77\ cm^2

And the area of the base of a hemisphere is

=\ \pi r^2\ =\ \frac{22}{7}\times \left ( \frac{7}{2} \right )^2\ =\ 38.5\ cm^2

Hence the surface area of solid is = 294 + 77 - 38.5 = 332.5 \:cm^2 .

Q5 A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.

Answer:

It is given that the diameter of the hemisphere is equal to the edge length of the cube.

The total surface area of solid is given by :

The surface area of solid = Surface area of cube + Surface area of the hemisphere - Area of the base of the hemisphere

The surface area of the cube =\ 6l^2

And surface area of the hemisphere:

=\ 2\pi r^2\ =\ 2\pi \left ( \frac{l}{2} \right )^2

Area of base of the hemisphere:

=\ \pi r^2\ =\ \pi \left ( \frac{l}{2} \right )^2

Thus the area of solid is:

=\ 6l^2\ +\ \pi \left ( \frac{l}{2} \right )^2\ unit^2

Q6 A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see Fig.). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.

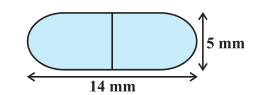
1636091994484

Answer:

It is clear from the figure that the capsule has hemisphere and cylinder structure.

The surface area of capsule = 2 (Area of the hemisphere) + Area of the cylindrical part

Area of hemisphere =\ 2\pi r^2

or =\ 2\pi\times \left ( \frac{5}{2} \right )^2

or =\ \frac{25}{2} \pi\ mm^2

And the area of the cylinder =\ 2\pi rh

or =\ 2\pi \times \frac{5}{2}\times 9

or =\ 45 \pi\ mm^2

Thus the area of the solid is :

=\ 2\left ( \frac{25}{2} \right )\pi\ +\ 45 \pi

=\ 25\pi\ +\ 45 \pi

=\ 70 \pi

=\ 220\ mm^2

Q7 A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs 500 per m 2 . (Note that the base of the tent will not be covered with canvas.)

Answer:

The canvas will cover the cylindrical part as well as the conical part.

So, the area of canvas = Area of cylindrical part (curved) + Area of the conical part

Now, the area of the cylindrical part is =\ 2\pi rh

or =\ 2\pi \times 2\times 2.1

or =\ 8.4 \pi\ m^2

And the area of the cone is =\ \pi rl

or =\ \pi \times 2\times 2.8

or =\ 5.6\pi\ m^2

Thus, the area of the canvas =\ 8.4\pi\ +\ 5.6\pi

or =\ 14\pi\ =\ 44\ m^2

Further, it is given that the rate of canvas per m 2 is = Rs. 500.

Thus the required money is =\ 500\times 44\ =\ Rs.\ 22,000

Q8 From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm 2 .

Answer:

Firstly we need to calculate the slant height of the cone :

l^2\ =\ r^2\ +\ h^2

or =\ (0.7)^2\ +\ (2.4)^2

or l^2\ =\ 6.25

or l\ =\ 2.5\ cm

Now, the total surface area of solid can be calculated as :

The surface area of solid = Surface area of cylinder + Surface area of cone + Area of base of the cylinder

The surface area of the cylinder is =\ 2 \pi rh

or =\ 2 \pi \times 0.7\times 2.4

or =\ 10.56\ cm^2

Now, the surface area of a cone =\ \pi rl

or =\ \pi \times 0.7\times 2.5

or =\ 5.50\ cm^2

And the area of the base of the cylinder is =\ \pi r^2

or =\ \pi \times 0.7\times 0.7

or =\ 1.54\ cm^2

Thus required area of solid = 10. 56 + 5.50 + 1.54 = 17.60 cm 2 .

Thus total surface area of remaining solid to nearest cm 2 is 18 cm 2 .

Q9 A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. 13.11. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.

1636092429678

Answer:

The required surface area is given by :

The surface area of article = Surface area of cylindrical part + 2 (Surface area of the hemisphere)

Now, the area of the cylinder =\ 2\pi rh

or =\ 2\pi \times 3.5\times 10

or =\ 70\pi \ cm^2

And the surface area of the hemisphere : =\ 2\pi r^2

or =\ 2\pi \times 3.5\times 3.5

or =\ 24.5\pi\ cm^2

Thus the required area =\ 70\pi\ +\ 2(24.5\pi)\ =\ 374\ cm^2



Some More Information About NCERT Solutions for Class 10 Maths Exercise 13.1

In NCERT syllabus for Class 10 Maths chapter 13 exercise 13.1 we have covered that the surface of a solid object ismeasurement of the overall area that the object's surface takes up and the curved surface of an object is that includes the area of all the curved surfaces and not the flat surfaces exampl-cone without the base.

Also Read| Surface Areas and Volumes Class 10 Notes

Benefits of NCERT Solutions for Class 10 Maths Exercise 13.1

  • Class 10 Maths chapter 13 exercise 13.1 will be helpful in further exercise of the chapter 10 surface area and volume
  • Class 10 Maths chapter 13 exercise 13.1 covers the knowledge which we can use in our real life
  • Surface area and volume are an important part of mechanical , mechtronic , tool , physics engineering
  • We can also use Class 10 Maths chapter 13 exercise 13.1 as base for the cellular changes in the volume of cell

Key Features For Class 10 Maths Chapter 13 Exercise 13.1

  • Step-by-Step Solutions: Clear and detailed explanations for each problem in Ex 13.1 class 10, ensuring students understand the methodology.
  • Conceptual Understanding: Explanation of area and volume concepts involved in the exercises, aiding students in grasping the underlying principles are discussed in class 10 maths ex 13.1.
  • Variety of Problems: In class 10 ex 13.1, diverse types of problems, offering a broad spectrum of challenges to reinforce understanding.
  • Visual Aids, Diagrams, and Examples: Use of visual representations, diagrams, and real-life examples to simplify complex concepts and aid visual learners.
  • Application-Based Problems: In 10th class maths exercise 13.1 answers, application-oriented problems that relate statistics to real-world scenarios, fostering practical understanding and problem-solving skills.

Also See:

NCERT Solutions Subject Wise

Frequently Asked Questions (FAQs)

1. What is the curved surface area of the hemisphere ?

Curved surface area of hemisphere used is =2πr²

2. What is the curved surface area of the cylinder u?

Curved surface area of hemisphere used in  2πrl

3. What is the most commonly used value of pi used in Exercise 13.1 Class 10 Maths ?

Most commonly used value of pi used in exercise 13.1 Class 10 Maths is 22/7

4. How can we use surface area in real life? Give some examples ?

We can use surface area in many places in our daily life, for example identifying the amount of paint require to paint object , determining the cost of things like clothes , covers and canvas tents 

5. What is the total number of example that have been solved before theExercise 13.1 Class 10 Maths.

The total number of example  that have been solved before the class 10 Maths chapter 13 exercise 13.1 is four 

6. What is the total number of questions in the NCERT solutions for Class 10 Maths chapter 13 exercise?

The total number of questions in the NCERT solutions for Class 10 Maths chapter 13 exercise is nine.

7. What kind of questions are asked in 10 Maths chapter 13 exercise 13.1?

There are many basic question in which we have to find the total surface of combination of solid or real life objects such as tents , capsules toys etc but some are direct that only ask about the solid  

Also Read

Articles

Upcoming School Exams

Madhya Pradesh State Open School 12th Examination

Admit Card Date:13 December,2024 - 06 January,2025

National Institute of Open Schooling 10th examination

Late Fee Application Date:21 December,2024 - 31 December,2024

National Institute of Open Schooling 12th Examination

Late Fee Application Date:21 December,2024 - 31 December,2024

All India Sainik Schools Entrance Examination

Application Date:24 December,2024 - 13 January,2025

Telangana Intermediate 1st Year Examination

Late Fee Application Date:25 December,2024 - 02 January,2025

View All School Exams

Certifications By Top Providers

My SQL Basics
 Via Great Learning
Full-Stack Web Development
 Via Masai School
Digital Banking Business Model
 Via State Bank of India
Business Analytics Foundations
 Via PW Skills
Full-Stack Android Development
 Via Masai School
Introduction to Psychology
 Via San Jose State University, San Jose
Edx
 1115 courses
Coursera
 816 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
University of Michigan, Ann Arbor
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
sadhu ashram ramgart road aligarh

If you're looking for directions or steps to reach Sadhu Ashram on Ramgart Road in Aligarh, here’s how you can get there:

Steps to Reach Sadhu Ashram, Ramgart Road, Aligarh:

  1. Starting Point:

    • Determine your starting point in Aligarh or the nearby area.

  2. Use Google Maps:

    • Open Google Maps on your phone or computer.
    • Enter "Sadhu Ashram, Ramgart Road, Aligarh" as your destination.
    • Follow the navigation instructions provided by Google Maps.

  3. By Local Transport:

    • Auto-rickshaw/Taxi: Hire an auto-rickshaw or taxi and inform the driver about your destination. Most local drivers should be familiar with Sadhu Ashram.
    • Bus: Check if there are any local buses that operate on Ramgart Road. Ask the bus conductor if the bus stops near Sadhu Ashram.

  4. Landmarks to Look For:

    • As you approach Ramgart Road, look for local landmarks that might help you confirm you’re on the right path, such as known shops, temples, or schools nearby.

  5. Ask for Directions:

    • If you're unsure, ask locals for directions to Sadhu Ashram on Ramgart Road. It's a known location in the area.

  6. Final Destination:

    • Once you reach Ramgart Road, Sadhu Ashram should be easy to spot. Look for any signage or ask nearby people to guide you to the exact location.

If you need detailed directions from a specific location or more information about Sadhu Ashram, feel free to ask

Read Complete Answer
sai raja 01 September,2024
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Trusted by 3,500+ universities and colleges globally | Accepted for migration visa applications to AUS, CAN, New Zealand , and the UK

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
Board Exam Date 2025 Live: Bihar Class 10, 12 model papers out, time table soon; updates on CBSE, UP
December 06, 2024 - 10:42 PM IST
CBSE Class 10 board exams from February 15 to March 18; download date sheet 2025 PDF
November 20, 2024 - 10:02 PM IST
CBSE Date Sheet 2025 Live: CBSE Class 10, 12 board exam timetable soon at cbse.gov.in; practical dates
November 14, 2024 - 03:21 PM IST
CBSE Date Sheet 2025 Live: CBSE to announce Class 10, 12 board exam dates soon at cbse.gov.in; sample paper
November 13, 2024 - 07:53 AM IST
CBSE Board Exam 2025: Class 10, 12 practical exam dates out at cbse.gov.in; passing marks
October 24, 2024 - 09:54 PM IST
CBSE urges schools to complete 100% registration of Class 9, 11 students by October 16; late fee for delays
October 11, 2024 - 08:56 AM IST
CBSE sample papers 2024-25 for Class 10, 12 out at cbseacademic.nic.in; marking scheme
September 05, 2024 - 07:38 PM IST

Stay up-to date with CBSE Class 10th News

Back to top